1. Introduction
Since the famous WASH report [
1] that followed the Three Mile Island nuclear accident, probabilistic risk, reliability and safety analyses have been developed considerably. They are nowadays applied to virtually all industrial systems the operation of which presents a risk for the systems themselves, their operators or their environment.
Probabilistic risk, reliability and safety assessment models describe how a system may degrade and eventually fail under the occurrence of random events such as failures of mechanical components, sudden changes in environmental conditions or human errors. They can be split into three nested categories: combinatorial models, state automata and process algebras [
2].
Combinatorial models are the simplest, but also by far the most widely used. In these models, the state of the system is described as a combination of the states of its components. As the number of possible states considered for each component is finite, and in general small, the number of possible states of the system is also finite, although subject to an exponential blow-up. Boolean models, i.e., fault trees, reliability block diagrams and event trees, belong to this category, see e.g., [
3,
4] for reference textbooks. So-called multistate systems [
5,
6,
7], i.e., extensions of Boolean models to the case where components can be in more than two—but still a finite number of—states, enter also in this category.
Intuitively, combinatorial models take a snapshot of the system at a given point in time. They do not consider the trajectory that lead the system from its initial state to its current state. Consequently, they can only approximate time dependencies induced for instance by cold-redundancies or reconfigurations. To take into account such dependencies, one needs more expressive models such as Markov chains [
8], stochastic Petri nets [
9], or guarded transition systems [
10,
11]. These models enter either in the category of state automata or in the category of process algebras. However, the more expressive the model, the more computationally expensive the calculation of probabilistic indicators from that model. Consequently, probabilistic risk, reliability and safety assessment models result always of a tradeoff between the accuracy of the description of the system under study and the ability to perform calculations on this description, see reference [
2] for an in-depth discussion. Moreover, the more expressive the model, the harder it is to design, to validate and to maintain. This is the reason why combinatorial models, and more specifically Boolean models, dominate the industrial practice.
It remains that, with the steadily increasing complexity of technical systems, the more expressive power we can have for the models, the better, with the proviso that the added expressive power does not degrade the computational complexity of assessments. This is why lots of efforts have been made in the recent years on the study of multistate systems. This is also what led us to introduce the algebraic concept of finite degradation structures [
12]. Finite degradation models generalize and unify both Boolean models and multistate systems. They can be seen as the most general mathematical framework that can be used to design probabilistic risk assessment models, while staying in the realm of combinatorial models.
Calculations performed on Boolean models belong formally to two distinct categories: qualitative assessments and quantitative assessments. The former aim primarily at extracting and classifying minimal cutsets. Minimal cutsets represent minimal scenarios of failure. The latter aim primarily at calculating probabilistic risk indicators such as the unavailability of the system (probability that the system is failed at time t), safety integrity levels or importance measures. In practice, this distinction is blurred because there are so many minimal cutsets that only the most relevant, i.e., the most probable, ones can be extracted. Moreover, the best way of calculating probabilistic indicators is to assess them via minimal cutsets. This is the reason why the extraction of the most probable minimal cutsets plays a central role in probabilistic risk and safety analyses.
Finite degradation structures formalize what is probably the most fundamental idea underlying all risk assessment methods: the states of a model represent essentially various levels of degradation of the system under study. Although these states cannot be totally ordered, they have rich algebraic structure that can be exploited both by analysts and by assessment algorithms: when studying a given level of degradation of the system, one is interested in the minimal conditions that produce this degradation level. These conditions are in turn characterized by the minimal states, according to the degradation order, in which the system is in the given degradation level. In other words, the notion of minimal cutset, or minimal state, of finite degradation models generalizes and sheds a new light on the one defined for fault trees.
There are essentially two families of algorithms to extract minimal cutsets. The first one consists of top-down algorithms. MOCUS [
13] and its modern versions such as the one implemented in RiskSpectrum [
14] and the one implemented in XFTA [
15], belong to this family. The second family consists of bottom-up algorithms based on the binary decision diagrams technology [
16,
17,
18]. We show here how to extend this technology so to handle finite degradation structures, via ideas introduced by Minato [
19] (in a different context). For this purpose, we introduce the notion of implicative normal form for formulas encoding discrete functions. We demonstrate a generic decomposition theorem making it possible the extraction of the most probable minimal states. This theorem generalizes the one of reference [
16], which is at core of minimal cutsets calculations.
The contribution of this article is thus fourfold. First, it shows how to generalize the concept of minimal cutsets to finite degradation models. Second, it demonstrates a decomposition theorem that makes possible to lift-up Boolean algorithms proposed in reference [
16] to finite degradation models. Third, it shows how to extend the binary decision diagram technology so to handle finite degradation models. Last, it discusses approximation schemes in the context of finite degradation models.
The remainder of this article is organized as follows.
Section 2 presents an illustrative example stemmed from the oil and gas industry.
Section 3 introduces finite degradation structures and finite degradation models.
Section 4 shows how to lift-up the notion of minimal cutset.
Section 5 shows how to extend the binary decision diagrams technology.
Section 6 discusses approximation schemes.
Section 7 provides some experimental results. Finally,
Section 8 concludes the article.
Appendix A presents the full model of the use case.
3. Finite Degradation Models
This section introduces finite degradation models which unify and generalize the various types of combinatorial models used in the framework of probabilistic risk, reliability and safety analyses.
3.3. Formulas
In the previous example, the state of the system is represented by a pair. Now if, for instance, the components A and B are in series, we can map each pair onto an element of , e.g. is mapped onto , is mapped onto , is mapped onto , and so on. There are indeed several ways to define such a mapping. Moreover the target finite degradation structure does not need to be the same as the source ones, which themselves may differ one another. In other words, it is possible to define a collection of operators on finite degradation structures.
In the sequel, we shall thus assume a finite set of finite degradation structures and a finite set of symbols called operators.
Each operator o of is associated with a mapping from , , into s, where both the ’s and s are finite degradation structures. n is the arity of o. is called the domain of o and is denoted . s is called the codomain of o and is denoted . The signature of o, which characterizes its arguments and return types, is denoted .
It is often, but not always, the case that operators are abstractions. Abstractions are surjective structure preserving mappings, i.e., an abstraction obeys the following conditions:
For all , .
.
such that .
As abstractions are epimorphisms in the sense of category theory, we shall use in the sequel the usual symbol ↠ for their signature, i.e., .
It is easy to check that the notion of abstraction generalizes the notion of monotone Boolean function.
As an illustration, one can consider the two binary operators ⧁ and ‖ from
into
. The operator ⧁ represents the series composition. It generalizes the Boolean operator ∨ (or). The operator ‖ represents the parallel composition. It generalizes the Boolean operator ∧ (and). These operators are defined in
Table 2.
It is easy to verify that the series operator ⧁ is not commutative but associative and that the parallel operator ‖ is both commutative and associative.
We can now define formulas of the finite degradation calculus.
Let be a finite set of finite degradation structures, let be a finite set of operators on defined as above, and finally, let be a finite set of symbols called variables. Each variable V of is assumed to take its value in the support set of one of the finite degradation structures of . This finite degradation structure is called the domain of V and is denoted .
The set of well formed (typed) formulas over , and is the smallest set such that:
Constants, i.e., members of support sets of finite degradation structures of , are well formed formulas. The type of a constant is the finite degradation structure it comes from.
Variables of are well-formed formulas. The type of a variable V is simply its domain.
If o is an operator of such that , and are well formed formulas of types , then is a well formed formula of type s.
In the sequel, we shall say simply formula instead of a well-formed formula.
The set of variables occurring in the formula f is denoted .
A variable valuation of f is a mapping from into , i.e., a function that associates with each variable a value of its domain.
f is interpreted as a mapping where s is the codomain of the outmost operator of f, by lifting up as usual variable valuations. Let be a variable valuation of , then:
If f is reduced to a constant c, then .
If f is reduced to a variable V, then .
If f is in the form , then .
3.4. Finite Degradation Models
Finite degradation models are obtained by lifting up fault tree constructions to the finite degradation calculus. Namely, a finite degradation model is a pair where:
, , is a finite set of state variables.
, , is a finite set of flow variables.
is a finite set of equations such that for :
- –
is the jth variable of .
- –
is a formula built over .
- –
We say that the flow variable depends on the (state or flow) variable V if either or there exists a variable that depends on V.
A finite degradation model is looped if one of its flow variable depends on itself. It is loop-free otherwise.
A finite degradation model is uniquely rooted if there is only one variable that occurs in no right member of an equation. Such a variable is a called the root of the model.
From now, we shall consider only well-typed, loop-free, uniquely rooted models.
It is easy to see that finite degradation models generalize fault trees: state and flow variables play respectively the roles of basic and internal events, while equations play the role of gates. Moreover, the root variable plays the role of the top event. The terms “state” and “flow” comes from guarded transition systems [
10].
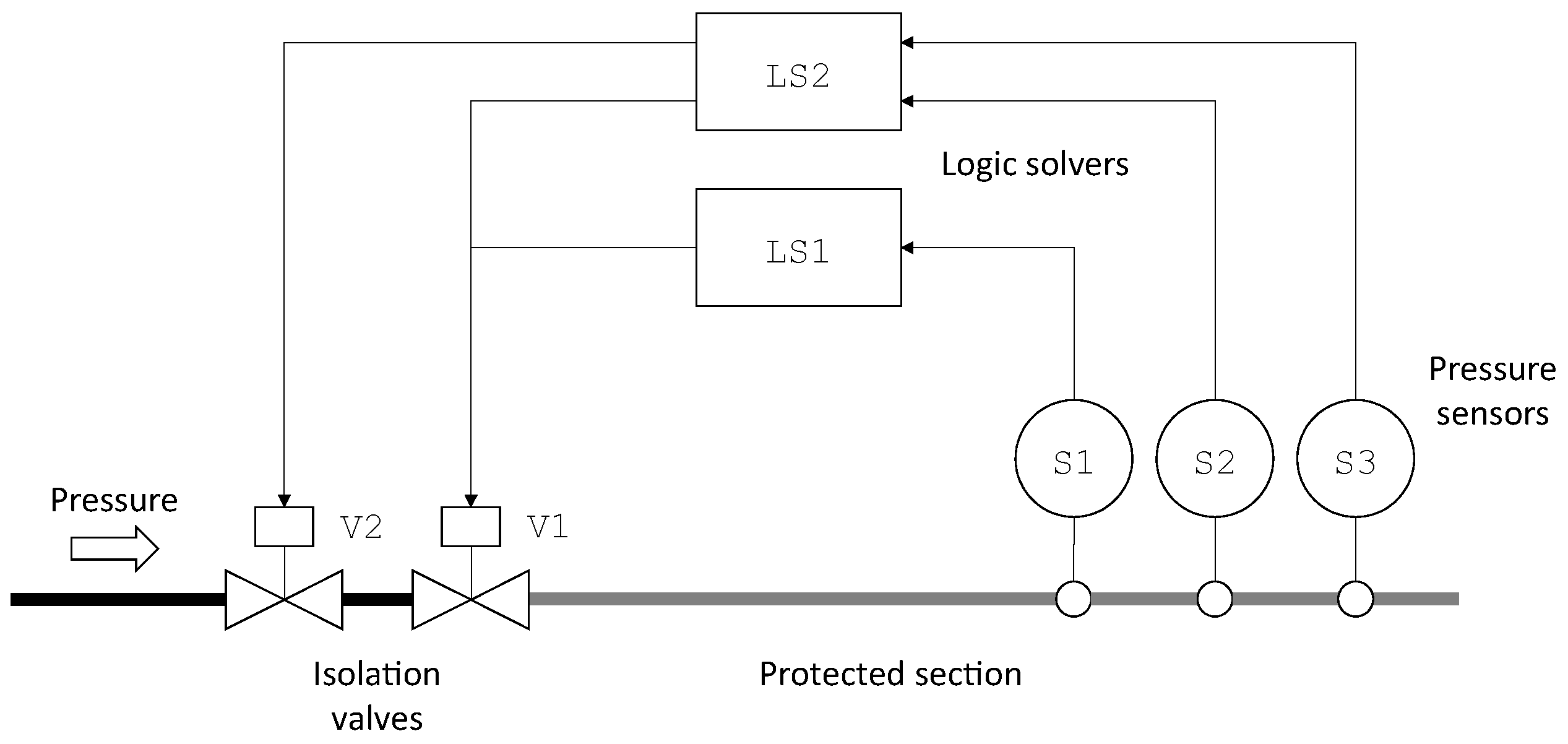
As an illustration, consider TA4 HIPPS presented
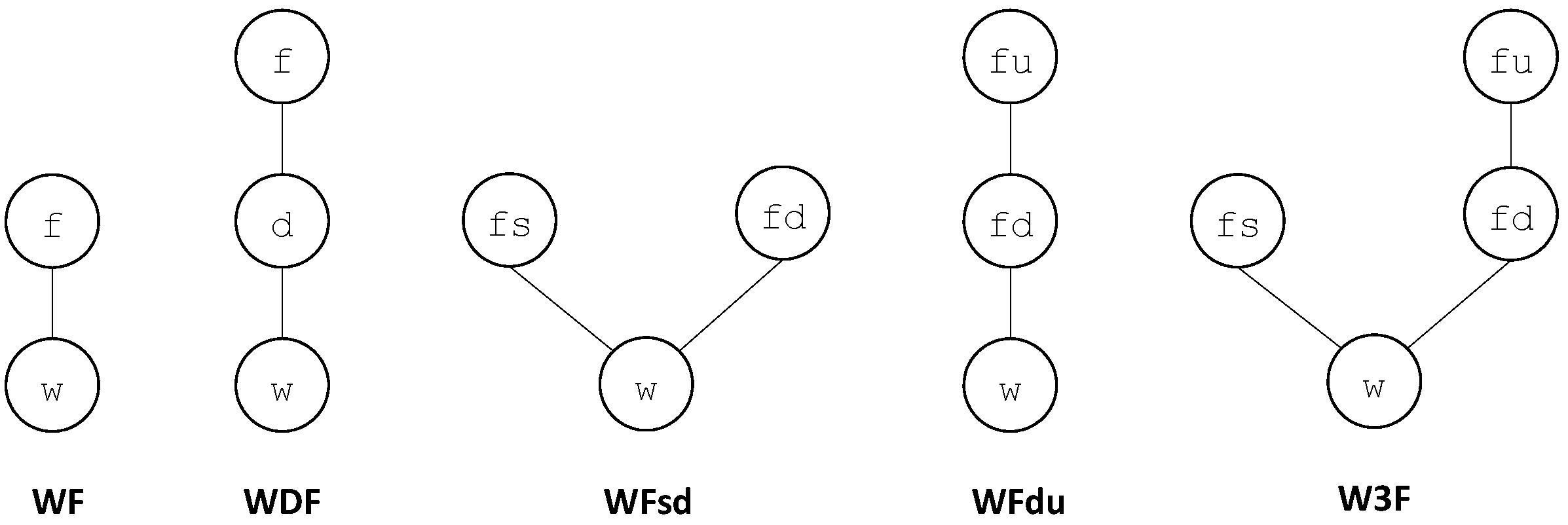
Section 2. We can use the finite degradation structure
W3F and the operators defined in
Table 2 to represent this system.
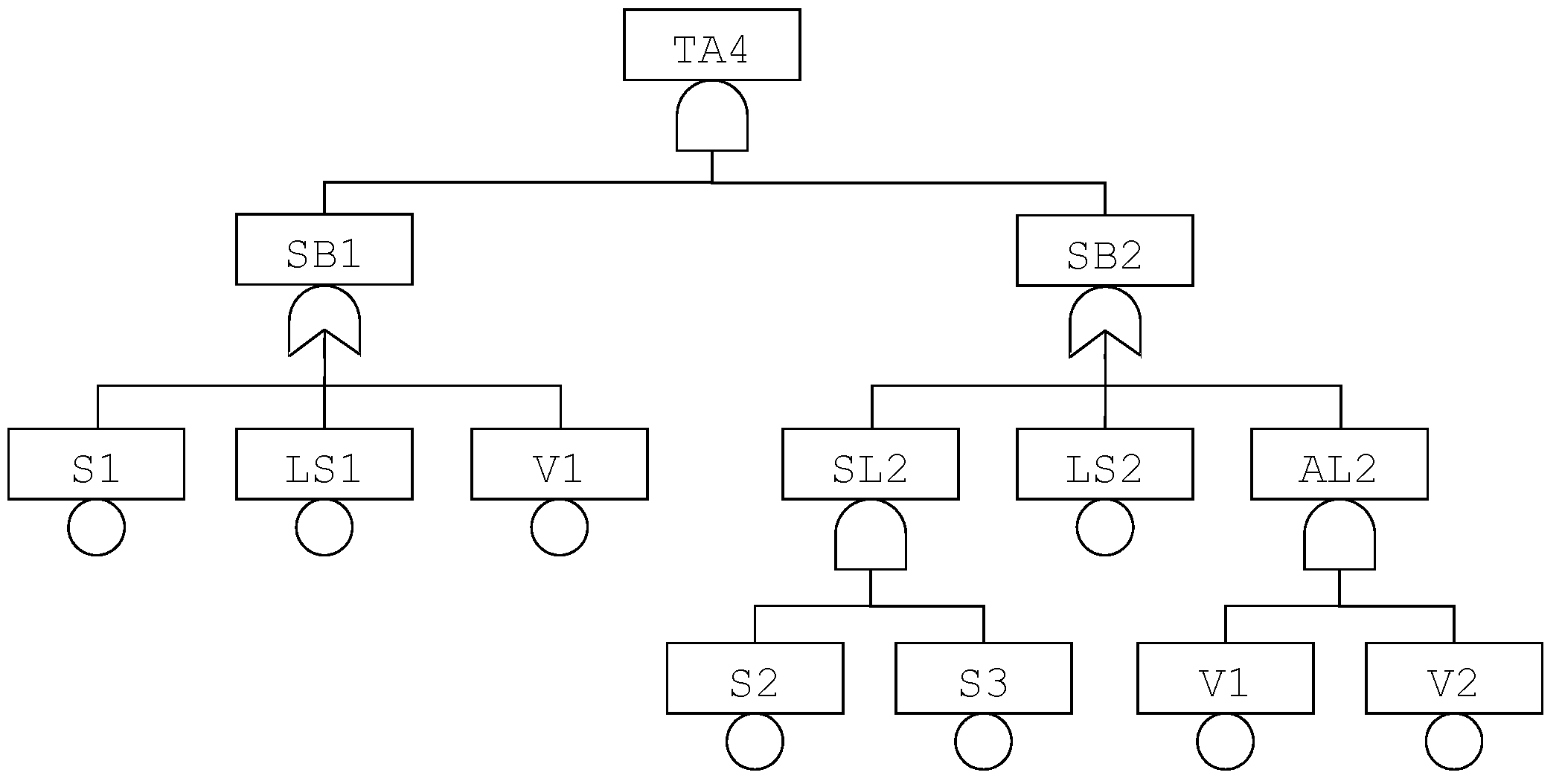
The fault tree pictured in
Figure 2 can be re-interpreted in this logic. Equations implementing this fault tree are given in
Table 3.
In this model, S1, S2, S3, LS1, LS2, V1 and V2 are state variables, while TA4, SB1, SB2, SL2 and AL2 are flow variables.
Note that LS1 and LS2 cannot take the value fu as we assumed that failures of logic solvers always detected. Similarly, V1 and V2 cannot take the value fs as we assumed that spurious closures of valves, if any, are immediately fixed.
3.5. Semantics
Let be a finite degradation model. A variable valuation of is a function , i.e., a function that associates with each variable V of a value in .
A variable valuation is admissible in the model if for each equation of .
The following property holds, thanks to the fact that the model is loop-free.
Lemma 1 (Unicity of admissible variable valuations). Let be a finite degradation model and σ be a partial variable valuation that assigns values only to state variables of . Then there is a unique way to extend σ into an admissible total assigment of variables of .
Note, is simply calculated bottom-up by propagating values in equations.
In the sequel, we shall denote , or simply when the model is clear from the context, this unique extension.
Consider for instance the model given in
Table 3 and the valuation of state variables
,
,
,
,
,
and
. Then,
is the total variable valuation such that
,
,
,
and finally
.
There is indeed a one-to-one correspondence between variable valuations and elements of . We shall thus make no distinction between them in the sequel.
It follows from the above lemma, that we can interpret a model
as a mapping:
Note that flow variables include in particular the root variable
R of the model. Therefore, if we restrict
to its
R component, we can interpret it as a mapping:
This is indeed true for any other flow variable.
The following result holds.
Lemma 2 (Coherent finite degradation models)
. Let be a uniquely rooted, loop-free finite degradation model, whose root variable is . If all operators used to build equations of are abstractions, then defines an abstraction: Lemma 2 generalizes the well-known result that a sufficient (but not necessary) condition for a fault tree to be coherent is that it is written using only ∧, ∨ and k-out-of-n connectives.
The finite degradation model given in
Table 3 is thus a mapping:
as the states of the three sensors are described with the finite degradation structure
, the states of the two logic solvers are described with the finite degradation structure
, the states of the two valves are described with the finite degradation structure
, and the state of the unique root variable (
TA4) is described with the finite degradation structure
.
Note that this model is not an abstraction, because the operator ⧁ introduces non-coherencies. Consider for instance the case where the three sensors are failed dangerous undetected and all other components are working. In this case, the HIPPS as a whole is failed dangerous undetected. Now, consider the case where the three sensors are failed dangerous undetected as previously but, in addition, the logic solver LS1 is failed safe. In this case, the closure of valves is triggered, even in absence of an overpressure. Consequently, the HIPPS as a whole is failed safe. The latter state is however clearly more degraded than the former. It is often the case that partial orders induce this kind of non-monotone behavior. This is one of the reason why handling different types of failures, as suggested by safety standards such as IEC61508, is far from easy when staying in the realm of Boolean models.
From now and for the sake of the simplicity, we shall omit brackets when it is clear from the context that we speak about the interpretation of a model and not the model itself.
4. Minimal Cutsets
The notion of minimal cutset plays a central role in system reliability theory, as well as in practical probabilistic risk analyses. Intuitively, in fault trees, a minimal cutset represents a minimal set of component failures that induces a failure of the system as a whole. In other words, minimal cutsets represent the most significant and in general the most probable scenarios of failure. This intuitive idea works fine for coherent models for which the notion of minimal cutset coincide with the classical notion of prime implicant. However, it needs to be refined to handle non-coherent ones [
16].
In this section, we shall lift-up the notion of minimal cutset to finite degradation models. We shall also characterize minimal cutsets in terms of states of finite degradation structures.
4.1. Definition
One of the main objective of probabilistic risk and safety analyses is to characterize dangerous states of the system under study as well as the cumulated probability of these states. Dangerous states are represented by biggest elements of finite degradation structures. We can formalize this idea by considering upper sets.
Let
be a finite degradation structure, an upper set of
is a subset
U of
C such that
, if
and
, then
. Upper sets are sometimes called upward closed sets [
24].
Let be finite degradation model with a root variable R and let U be an upper set of . We call the predicate an observer of .
As an illustration, in the finite degradation model given
Table 3, we could consider the observers
(the system is failed safe),
(the system is failed dangerous undetected),
(the system is failed dangerous) and
(the system is failed).
We are interested in characterizing the subset of valuations of the state variables whose admissible extension verifies , i.e., that satisfies the observer . To do so, we shall lift-up the notions of literals, product and minterm.
A literal over is an equality of the form , where V is a variable of and c is constant of .
A product over is a conjunct of literals over in which each variable of occurs at most once.
A minterm over is a product over in which each variable of occurs exactly once.
We denote by the set of minterms that can be built over a set of variables.
Minterms one-to-one correspond with variable valuations of : the variable valuation assigns the value c to the variable V if and only if the literal occurs in the corresponding minterm. Products one-to-one correspond thus with partial variable valuations.
Let be finite degradation model and be an observer for .
For each valuation
of the state variables, the root variable
R takes a certain value
. We do not care which specific value it takes, but whether this value belongs to
U or not. Consequently, we can simply consider
as a function from
into
, i.e., as the characteristic function of the set of state variable valuations
such that
, or equivalently as the set of minterms verifying the same condition. We denote by
this latter set:
Let
be a product over
, we can extend
to obtain a minterm over
as follows.
For instance, in our example, if
, then
is as follows.
We can now define minimal cutsets:
We denote by the set of minimal cutsets for the observer (in the model ).
For instance, in the model given
Table 3, the product
is a cutset for the observer
because
. However, it is not minimal because,
verifies also
and
. It is easy to verify that
is minimal if the valve
V1 is not failed undetected, then the first safety barrier
SB1 is not failed undetected, and if either sensors
S2 or
S3 are not failed dangerous, then the second safety barrier
SB2 is not failed dangerous, therefore it cannot produce a dangerous undetected failure of the HIPPS in combination with the dangerous undetected failure of the valve
V1.
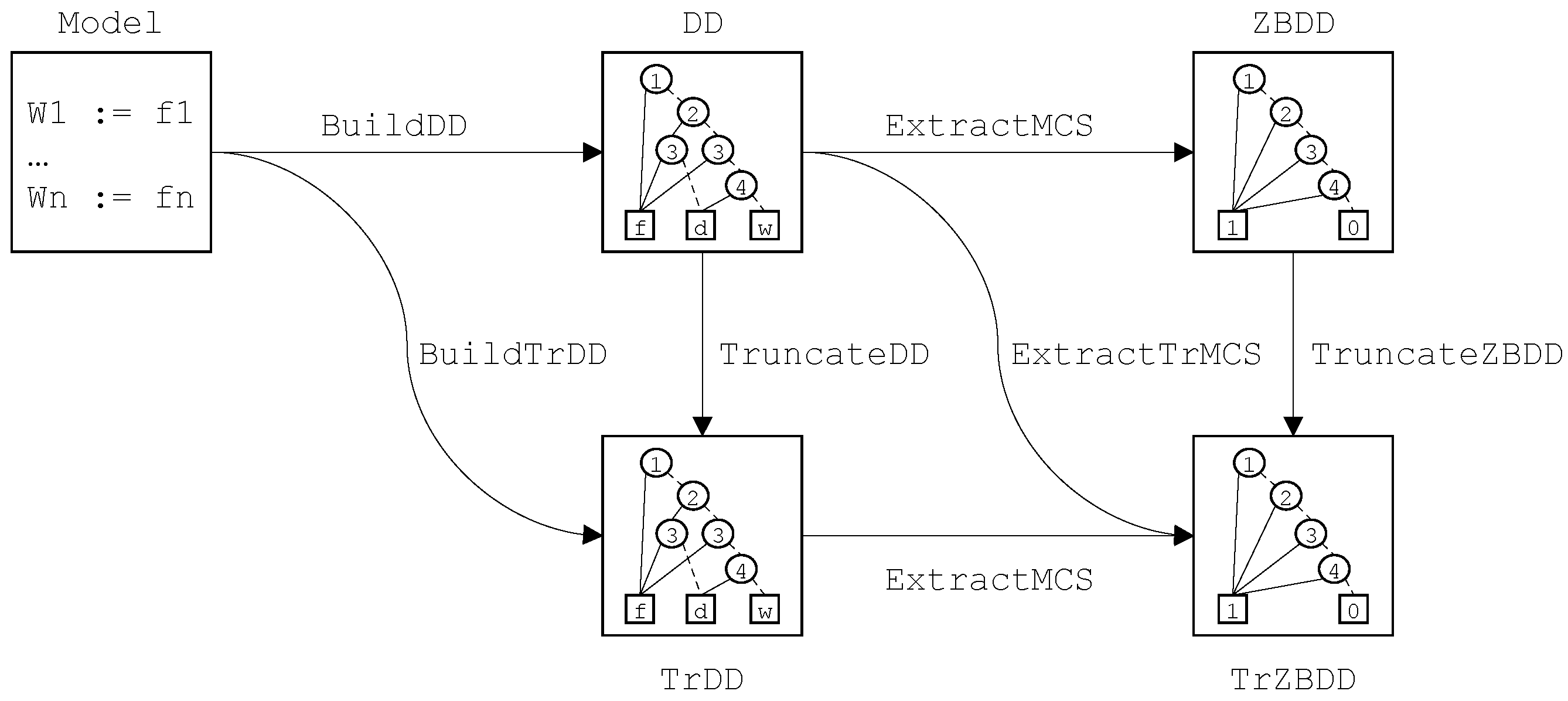
5. Decision Diagram Algorithms
The modern implementation of binary decision diagrams has been introduced by Bryant and his colleagues [
26]. We shall rely here on this implementation as well as on ideas introduced by Minato [
19]. The algorithms presented in this section generalize to finite degradation models those developed by Rauzy for Boolean models [
16].
5.2. Decision Diagrams
Let be finite degradation model. Each equation of describes a function from into . The decision diagram associated with the variable W encodes this function. To build this decision diagram, one needs first to build the decision diagrams associated with all variables of , then to build the decision diagram encoding f. The first step consists thus in building the decision diagrams associated with each variable by traversing bottom-up the model.
Building these decision diagrams requires choosing an order over the literals , where and , i.e., associating each literal with an index . This indexing must fulfill the following constraints.
Indices of the literals built over a variable must be consecutive, i.e., it is not allowed to intertwine indices associated with literals built over different variables.
For any variable and , if , then .
The justification for these two constraints will appear in the next section.
A decision diagram is a directed acyclic graph with three types of nodes:
The leaf nil.
Other leaves, which are labeled with constants.
Internal nodes, which are labeled with the index of a literal and have two out-edges: the then out-edge and the else out-edge.
In the sequel, we shall denote the leaf labeled with the constant c, and the internal node labeled with the index i and whose then and else out-edges point respectively to nodes m and n. m and n are called respectively the then-child and the else-child of the node .
Decision diagrams are ordered, i.e., that the index labeling an internal node is always smaller than the indices labeling its children (if they are internal nodes).
A decision diagram encodes a formula in implicative normal form. The semantics of decision diagrams is defined then recursively as follows.
Decision diagrams are built bottom-up, i.e., that nodes
m and
n are always built before the node
. This makes it possible to store nodes into a unique table. When one needs the leaf
or the internal node
, the unique table is looked up. If the node is already present in the table, it is returned. Otherwise, it is created and inserted in the table. This technique, introduced in reference [
26], ensures the unicity of each node in the table. It is one of the main reasons, if not the main reason, of the efficiency of the decision diagrams technology. The insertion and look-up in the unique table are implemented by means of hashing techniques, so to ensure a nearly linear complexity.
The semantics of decision diagrams makes it possible to simplify the representation. The node
encodes actually the formula
, which is equivalent to
.
is thus useless and can be replaced by
n. A decision diagram is reduced if it contains no node of the form
. This reduction generalizes to the one of Minato’s zero-suppressed binary decision diagrams [
19].
From now, we shall simply say the decision diagram, but we shall mean the reduced, ordered decision diagram.
5.3. Operations
The calculation of the decision diagram encoding a formula f is performed bottom-up. There are four cases:
, for some constant c. In this case, the unique table is looked up for the node , which is added if it did not exist before.
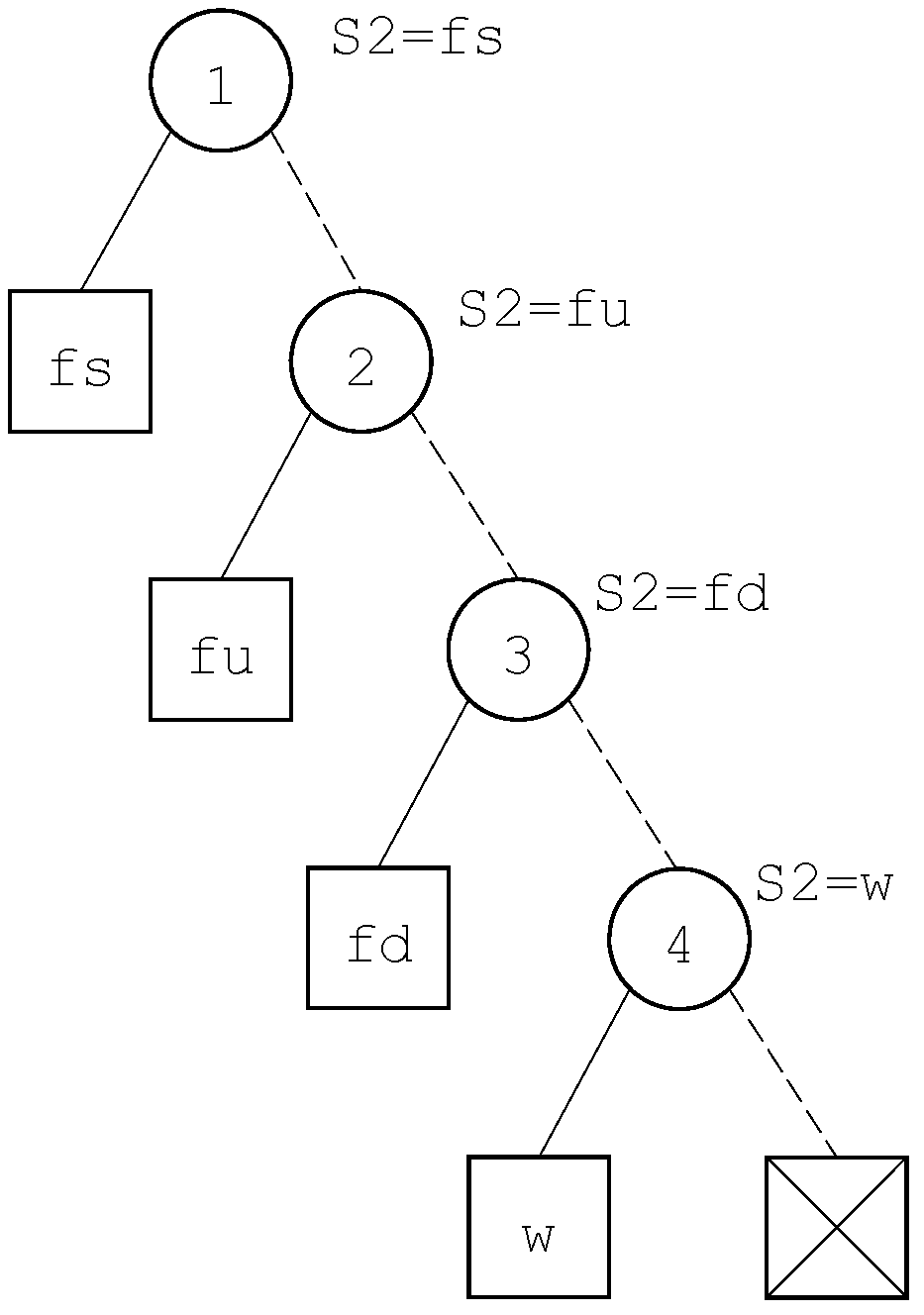
, for some state variable
V. In this case, the decision diagram associated with this variable is built. This decision diagram is made of a series of internal nodes in the form
, where
i is the index of the literal
, as illustrated in
Figure 5 for the variable
S2 of our example.
, for some flow variable W. In this case, the decision diagram associated with W is calculated (via the equation defining W) and returned.
for some operator . In this case, the decision diagrams for the arguments , …, are calculated, then the operator is applied onto these decision diagrams. The application of may require the applications of more primitive operators. For instance, the calculation of requires first the calculation of , then the calculation of .
Algorithm 1 gives the pseudo-code of the function that performs binary operations on decision diagrams. The algorithms for operations with different arities (unary, ternary,…) can be easily derived for this one.
The first step of the algorithm (line 2) consists in checking whether the result can be calculated directly, e.g., if the first argument is the leaf while computing a ⧁. If so, the result is returned. In general, when one of the arguments is , is returned.
Then, one looks whether the result on the operation has been cached (line 5). If so, the result is returned. Otherwise, it is computed and inserted into the cache (line 30). Caching techniques, which have been introduced for binary decision diagrams in the seminal article by Bryant et al. [
26], are the second pillar of the efficiency of the technology. As unique tables, caches are managed by means of hashing techniques. In case binary operators are commutative, the caching policy can be improved by setting an order over the arguments.
The core of the algorithm consists in a case study on the type of arguments. In the case where the first argument is a node and the second one a node such that the literals corresponding to indices i and j, are respectively and (line 17), the function must be recursively called on . However, it cannot be called on n, because the then-branch of n assigns also the variable V. This is the reason why the function GetOtherwiseChild is called.
In Algorithm 1, the function NewNode that creates a new node (e.g., line 29), checks whether the node r is , in which case it returns r0.
| Algorithm 1 Pseudo-code for the function that performs binary operation on decision diagrams. |
| 1 | define PerformBinaryOperation(op: operation, m: Node, n: Node) |
| 2 | r = CalculateTerminalResult(op, m, n) |
| 3 | if r!=None: |
| 4 | return r |
| 5 | r = LookForEntryInCache(op, m, n) |
| 6 | if r!=None: |
| 7 | return r |
| 8 | if m==□c and n==Δ(j,n1,n0): |
| 9 | r1 = PerformBinaryOperation(op, m, n1) |
| 10 | r0 = PerformBinaryOperation(op, m, n0) |
| 11 | r = NewNode(j, r1, r0) |
| 12 | else if m==Δ(i,m1,m0) and n==□(d): |
| 13 | r1 = PerformBinaryOperation(op, m1, n) |
| 14 | r0 = PerformBinaryOperation(op, m0, n) |
| 15 | r = NewNode(i, r1, r0) |
| 16 | else if m==Δ(i,m1,m0) and n==Δ(j,n1,n0) and i<j: |
| 17 | k = GetOtherwiseChild(i, n) |
| 18 | r1 = PerformBinaryOperation(op, m1, k) |
| 19 | r0 = PerformBinaryOperation(op, m0, k) |
| 20 | r = NewNode(i, r1, r0) |
| 21 | else if m==Δ(i,m1,m0) and n==Δ(j,n1,n0) and i>j: |
| 22 | k = GetOtherwiseChild(j, m) |
| 23 | r1 = PerformBinaryOperation(op, k, n1) |
| 24 | r0 = PerformBinaryOperation(op, k, n0) |
| 25 | r = NewNode(i, r1, r0) |
| 26 | else m==Δ(i,m1,m0) and n==Δ(i,n1,n0) |
| 27 | r1 = PerformBinaryOperation(op, m1, n1) |
| 28 | r0 = PerformBinaryOperation(op, m0, n0) |
| 29 | r = NewNode(i, r1, r0) |
| 30 | AddEntryToCache(op, m, n, r) |
| 31 | return r |
| 32 | |
| 33 | define GetOtherwiseChild(i: index, m: Node) |
| 34 | if m==Node(j, m1, m0) and Variable(i)==Variable(j) |
| 35 | return GetOtherwiseChild(i, m0) |
| 36 | return m |
Discussion
The algorithm to build the decision diagrams associated with variables of a finite degradation model is thus similar to the one to build the binary decision diagrams associated with variables of a Boolean model, e.g., fault tree or reliability block diagram. However, two nodes are used for each Boolean variable: one for the value 1 and one for the value 0. This induces an overcost compared to the algorithm dedicated to the binary case. However, this overcost is acceptable, especially when truncations are applied (see next section).
All complexity results that hold for binary decision diagrams see e.g., [
27] for a review, hold for decision diagrams as well. In particular, caching ensures that the worst case complexity of the function
PerformBinaryOperation is in the product of the sizes of its arguments (without caching, it is exponential).
It is well known that the size of binary decision diagrams, and therefore the efficiency of the whole method, depends heavily on the chosen variable ordering, see again [
27]. The same applies indeed to decision diagrams. As the calculation of an optimal ordering is computationally intractable, heuristics are applied which are essentially the same as for the Boolean case, see e.g., [
28]. The only difference regards dynamic reordering of decision diagrams, notably sifting [
29]. As indices of literals built over the variable must be consecutive, group sifting has to be applied rather than individual sifting.
Note finally that efficient algorithms exist to calculate probabilistic risk indicators such as the top-event probability or importance measures [
30]. These algorithms can be lifted-up to decision diagrams. The key idea is to extend the pivotal decomposition: assume that we have a decision diagram encoding a function
and that we want to calculate the probability
that
for some subset
U of
. Then the recursive equations to do so are as follows.
The mathematical definition of importance measures for finite degradation models is, however, non-trivial and will be the subject of a forthcoming article.