Privacy Preserving Data Publishing with Multiple Sensitive Attributes based on Overlapped Slicing

Abstract

Investigation into privacy preserving data publishing with multiple sensitive attributes is performed to reduce probability of adversaries to guess the sensitive values. Masking the sensitive values is usually performed by anonymizing data by using generalization and suppression techniques. A successful anonymization technique should reduce information loss due to the generalization and suppression. This research attempts to solve both problems in microdata with multiple sensitive attributes. We propose a novel overlapped slicing method for privacy preserving data publishing with multiple sensitive attributes. We used discernibility metrics to measure information loss. The experiment result shows that our method obtained a lower discernibility value than other methods.

1. Introduction

Privacy data in microdata become an important issue in information era. Microdata is a table that consist of data with individual description or single respondent, not aggregative data [1,2]. This data is individually explained in each record, and each record has one or more sensitive attribute [3]. Privacy in microdata protects confidential and personal data when the microdata is published. Most research, usually employed a single sensitive attribute, while in the real world, microdata is mostly used in multiple sensitive attributes. Only a few researches used multiple sensitive attributes, even some researchers treat multiple sensitive attributes as a single sensitive attribute by separating each attribute based on its sensitive attributes. This problem in privacy preserving data publishing emerged as a specific problem, which is concerning with privacy preserving data publishing with multiple sensitive attributes.

The model on privacy data started when Sweeney introduced k-anonymity for privacy preserving in both data publishing and data mining [4,5]. This model uses generalization and suppression to anonymize the quasi identifier attribute and handle linking attack in revealing the Governor data while Voter list data of Massachusetts and medical record in GIC data is linked. The problem for the model is that it still cannot deal with a homogeneity attack and background knowledge attack. A model which is called l-diversity, fixed both problems [6]. A Microdata satisfies l-diversity requirements, while it meets “l-well represented value” those are distinct l-diversity, entropy l-diversity, and recursive (c,l) diversity. It was simplified by p-sensitive k-anonymity proposed by Trutta that only deals with distinct l-diversity, but it covers handling homogeneity and background knowledge attack sufficiently [7]. Shortly, it is called p-sensitive. Unfortunately, most of the works on privacy preserving data publishing based on single sensitive attribute, while in the real world, it should be a multiple sensitive attributes problem. Some researches concerned with multiple sensitive attributes, but almost all of them only solved partial problems. When, k-anonymity, l-diversity, and p-sensitive are performed by anonymizing data, it tends to produce information loss. While we use anatomy [8], a model, which dissociates quasi identifier attributes and sensitive attributes, it produces minimum information loss.

The major problem of previous works is when a privacy model is applied to a microdata using any methods, it always produces information loss values. This work tried to minimize the information loss when anonymizing is conducted. This investigation started by distributing sensitive values. The sensitive values are distributed evenly in each bucket, which represents equivalence class. We also employed overlapped slicing not only for keeping the relationship between quasi identifier attributes and sensitive attributes, but also for scrambling the records to hold its privacy. It means that this work also aims to maintain its privacy but obtains better data utility.

This paper has some following contributions:

• We propose a microdata anonymization model using overlapped slicing for multiple sensitive attributes.
• We improve a distributional model for multiple sensitive attributes by ignoring generalization and suppression since both methods tend to produce information loss.
• We introduce an attack called relational attack that is a generalization of three types of attack: elimination attack, association disclosure attack, and full functional dependency attack.

The remaining of this paper is organized as follows. Section 2 explains related work. In Section 3, we describe privacy preserving data publishing concepts in anonymization, multiple sensitive attributes, slicing and overlapped slicing approach. Section 4 discusses our proposed model with its evaluation. We describe the discussion of our proposed model in Section 5. Finally, we conclude it in Section 6.

2. Related Work

The following are related to works, which are concerned with multiple sensitive attributes. Their works contained models and methods they used. First, research that focused on multiple sensitive attributes was conducted by Gal et al. [9]. The basic problem in their work was that while a model for single sensitive attribute applied well, it cannot just be implemented in multiple sensitive attributes. The model should be modified in a certain way, so that it can be worked well. k-anonymity was used by Gal et al., but it extended to l-diversity. They still utilized generalization and suppression for anonymizing the data. This model handles elimination attack, which was introduced only for multiple sensitive attributes. The results showed that the model is effective in solving its problem. Problems that Gal et al. did not pay attention to are the ignored relationship between quasi identifier attributes and sensitive attributes, and still produced information loss due to the utilization of generalization and suppression.

The next work introduced by Ye et al. [10] is called decomposition method and applied to l-diversity. The notion of this model is similar to anatomy by dividing the table into two, yet it still has sensitive attribute in quasi identifier. They implemented the decomposition method by adding noise to certain sensitive attributes for maintaining privacy. One sensitive attribute will be treated as a primary sensitive attribute. Experiment results demonstrated that this model was very effective, but it still does not pay enough attention to the correlation between quasi identifier and sensitive attributes.

A work was performed to extend decomposition [11]. Its method is called decomposition+ and used for fixing the disadvantages of the partition method. Decomposition+ uses distinct l-diversity as a privacy requirements model. By focusing on l-diversity, it is similar to p-sensitive. This model also overcomes the dynamic releases problem on previous research, but it still does not deal with high dimensional data and the sensitive attributes-quasi identifier relationship.

Other work on the privacy problem in multiple sensitive attributes is to handle the fully functional dependencies attack [12]. This attack is caused by the functional dependency of one sensitive attribute value to quasi identifier attribute value. Adversaries can infer other sensitive attributes by knowing functional dependency. Wang and Liu built a model called (l,d)-diversity to fix this problem. It works effectively, but since its usage of generalization, it produces information loss. Besides, they still did not consider distribution of sensitive attributes.

In multiple sensitive attributes, the relationship among sensitive attributes is considered as a threat. This threat became a basis for research by Liu [13] and called association disclosure. Its approach is based on sensitive attributes, which is divided into high-sensitive and low sensitive attributes. Liu used high-sensitive attributes for sorting the tuples. This method seems more effective since it declined its suppression ratio, but it still produced information loss.

Han et al. proposed a method called SLOMS [14]. This method is an extension of the slicing method only suitable for the single sensitive attribute [15]. SLOMS stands for Slicing on Multiple Sensitive attributes. Slicing method performs by partitioning table vertically. In a similar way, SLOMS works for multiple sensitive attributes into tables and they were bucketized on l-diversity privacy level. It still produced more information loss due to its usage of generalization and suppression.

A framework called ANGELMS was developed using MSB-KACA method [16]. This method also adopts the ANGEL method, which was proposed previously [17]. ANGEL stands for Anatomy and Generalization, while ANGELMS stands for Anatomy and Generalization for Multiple Sensitive attributes. Table is dissociated into two sub tables those are Batch Table (BT) and Generalized Table (GT). ANGELMS is not only adopting from ANGEL, but also following Slicing method in partitioning the table vertically. Since it still uses generalization, it produces information loss, which means reducing data utility. The dissociated tables also break correlation between each attribute, so it does not maintain on how sensitive attributes can influence quasi identifier and vice versa.

Anatomization with slicing emerged as a new model for multiple sensitive attributes [18]. This approach combines anatomy which segregate quasi identifier and sensitive attributes. Slicing approach is used separately on quasi identifier and sensitive attributes. This approach also adopted cloning method that proposed previously [19]. Three types of attack are handled, but the correlation of each attribute was not being considered.

The importance for distributing sensitive value is described in a work [20]. This work focused on how to control sensitive values so that the real ‘sensitive’ value will be difficult to relate to certain identity. The distribution formed quasi identifier group in p-sensitive privacy guarantee and generalized them. The model reduced probability of adversaries to do a relational attack. However, usage of generalization approach still reduced its data quality. Then, this work expanded and was fixed in distributing high-sensitive values evenly and simply [21]. The second work is conducted in real datasets, while the first is still in simulation design.

Distribution of sensitive values also had been conducted by Hasan et al. [22]. It is implemented to multiple independent data publishing and is used to assign sensitive values to the quasi identifier group. In order to create fake tuples in each quasi identifier group, this distribution is quite effective. However, Hassan applied his work to single sensitive attribute. A study of distribution of sensitive values that is applied to multiple sensitive attributes is conducted by Onashoga et al. [23]. Three phases are performed to complete his method, those are categorizing attributes, partition horizontally, and correlation operation in quasi identifier attributes. This method is called KC-Slice. An improvement of KC-Slice, called as Dynamic KC_i-Slice is proposed by Raju et al. [24]. The distribution of sensitive values is used when buckets are formed. Tuples are distributed evenly to each bucket based on high and low sensitive values. It is applied both in single and multiple sensitive attributes.

Nithya and Sheela also proposed a method in redistributing sensitive values [25]. The proposed method solved any hidden knowledge that can be appeared because any combination of sensitive values. This work is applied to multiple sensitive attributes, but the focus only redistributes its sensitive values. Another work in multiple sensitive attributes was proposed by Wang et al. [26]. This work configured microdata with two algorithms for satisfying t-closeness. It is effectively done and producing low information loss, but it is hard to achieve t-closeness [27]. This difficulty also led Agarwal and Sachdeva [28] in his work in the l-diversity level, which is called (P, U)-sensitive k-anonymity. The model ensures that p parameter like in p-sensitive, should be equal to the k parameter in k-anonymity. The symbol of U denotes union between p and k. In comparison to other methods, his work produced better running time and data utility. Unfortunately, it was conducted in single sensitive attribute only, not tried in multiple sensitive attributes yet. Agarwal also did not include how to distribute the sensitive values.

3. Privacy Preserving Data Publishing

This section describes the basis of anonymization on microdata, a microdata with multiple sensitive attributes, slicing method, and overlapped slicing.

3.1. Anonymization

Anonymization is a technique in privacy preserving data publishing (PPDP), therefore, it is better to discuss on PPDP first, to lead us to anonymization. PPDP is a field in privacy that protect individual privacy data when it is published. PPDP is used by some institution/organization when they want to publish their data, but its data contains some sensitive information. Such institutions include hospitals and any health institution since they have data of disease of patients and police departments with criminal data. Usually, PPDP is formed in table called microdata, a table with information is still not aggregated and related to individual information. PPDP does not concern with macrodata that data is being aggregated in a certain level.

The basic form of performing PPDP, a microdata table consists of four type of attributes that is T(EI, QI, SA, NA) [29]. T is a microdata table, EI is explicit identifier. Record owner can be identified explicitly by this attribute, such as name, employeeID. A Quasi Identifier (QI) is two or more attributes that appear since EI being hidden and QI does not explicitly identify but potentially identifies the record holder [29]. Sensitive attribute (SA) is an attribute that specifically consists of sensitive information about a person. Such attributes are disease, criminal records, salary (for some people). While a non-sensitive attribute is not included in three attributes above.

In PPDP, anonymization is a process to anonymize a microdata table, hence its sensitive data could not be linked to record the owner. Simply, it can be done by removing its explicit identifier like name or any id’s. Evidently, by joining some attributes to other corelated data, the combination of some attributes in QI [30] can reveal sensitive information. Sweeney proofed in [4], when William Weld, a former Governor of Massachusetts had data in medical health record joined with the voter list record. This combination of QI attributes is shown in Figure 1.

From Figure 1, it is clearly shown that ZIP, Birthdate and Sex appeared in two microdata can be linked and potentially reveal to certain record holder. The adversaries need to have some background information about the victim and victim’s QI [29]. This problem is handled by making ambiguous the linking parts, then the micro data should be mapped to anonymity data:

T’(QI’, SA, Non-SA)

QI’ is a pseudo-identifier, a QI is one or more attributes that have been anonymized by using generalization and/or suppression. Therefore, T’ is the anonymized table that contains ambiguous QI and this table is in a certain privacy guarantee level. For a common understanding we explain three types of privacy guarantee level, k-anonymity, l-diversity, and p-sensitive k-anonymity.

k-anonymity is a privacy guarantee that at least k number of records in a QI group that cannot be distinguished each other [4,31]. It refers to condition in a QI group (equivalence class) that a record cannot be distinguished with k-1 records. However, as we mentioned in Section 1, k-anonymity has a problem with homogeneity attack. We explain this attack by illustrating two tables below.

Table 1. A microdata table [3].

Age	Zip Code	Nationality	Disease
28	13053	Russian	Heart Disease
29	13068	American	Heart Disease
21	13068	Japanese	Viral Infection
23	13053	American	Viral Infection
50	14853	Indian	Cancer
55	14853	Russian	Heart Disease
47	14850	American	Viral Infection
49	14850	American	Viral Infection
31	13053	American	Cancer
37	13053	Indian	Cancer
36	13068	Japanese	Cancer
35	13068	American	Cancer

shows a microdata table without explicit identifier. It is not anonymized yet.

Table 2. Microdata in k-anonymity with k = 4 [3].

Age	Zip Code	Nationality	Disease
<30	130 **	*	Heart Disease
<30	130 **	*	Heart Disease
<30	130 **	*	Viral Infection
<30	130 **	*	Viral Infection
≥40	1485 *	*	Cancer
≥40	1485 *	*	Heart Disease
≥ 40	1485 *	*	Viral Infection
≥ 40	1485 *	*	Viral Infection
3 *	130 **	*	Cancer
3 *	130 **	*	Cancer
3 *	130 **	*	Cancer
3 *	130 **	*	Cancer

shows a microdata table after being anonymized to k-anonymity with k = 4.

Table 2 exhibits a privacy guarantee in k-anonymity with k = 4. Age, Zip code, and Nationality are quasi identifier attributes, while Disease is a sensitive attribute. Table 2 consists of three QI groups with each group contains at least four records (consequence of k = 4). In each group, each QI attribute is generalized or suppressed. Four record in first group: Age attribute is generalized one level (< 30) due to all four ages are under 30 years old. Zip code attribute is suppressed in two levels (130**) since they are similar in three first digit and distinct in two last digits, while Nationality attribute is performed in total suppression. Another two groups treat in similar way, but they are customized as privacy level needs. By performing k-anonymity, adversaries cannot easily guess a certain record holder. If adversaries know someone has an age of 47 and her/his Zip code area is 14850, adversaries only have probability equal to 0.33 to guess her/his disease. It can be Cancer, Heart Disease, or Viral Infection. This privacy guarantee is held because its QI attributes are generalized and suppressed so that creates ambiguous identifier. One record should be indistinguishable with other k-1 records in each QI group. However, a problem in the third QI group still appears (Table 2), if adversaries know the age of someone in this group, let us say, 35, adversaries can guess correctly due to all sensitive values in this group are cancer. This attack is called homogeneity attack.

From Table 4, homogeneity attack occurs not only when in a group all sensitive values are same, but also when sensitive values are skewed. Although, adversaries can not exactly guess, however, he/she have high probability when guess the sensitive value holder. In multiple sensitive attributes, this problem weakens its privacy since the correlation of any sensitive attributes in a group.

For handling this problem, a model called l-diversity was proposed [6]. A microdata is in l-diversity privacy guarantee if each group meets “l-well represented”. Machanavajjhala defined three types of l-well represented, those are distinct l-diversity, entropy l-diversity, and recursive (c,l) diversity. This model ensures every sensitive value in each group has to be varied. The more variation in each group, the better in l-diversity.

A model to simplify l-diversity is also built. It is p-sensitive k-anonymity, p-sensitive in short. This p-sensitive only needs a microdata to satisfy one of three types of l-well represented, that is distinct l-diversity. To satisfy p-sensitive or l-diversity a table should comply with k-anonymity first. Both models have same objective to protect microdata in anonymity by varying sensitive values.

Table 3. Microdata in p-sensitive privacy guarantee.

Age	Zip Code	Sex	Disease
20–29	130 **	F	Heart Disease
20–29	130 **	F	Heart Disease
20–29	130 **	F	Viral Infection
30–39	1485 *	M	Cancer
30–39	1485 *	M	Heart Disease
30–39	1485 *	M	Viral Infection
30–39	1485 *	M	Viral Infection

shows microdata table in l-diversity and p-sensitive privacy guarantee.

In the first group, there are two sensitive values, Heart disease and Viral Infection, and in the second group, three sensitive values appeared. This condition lead microdata in Table 3 to p-sensitive k-anonymity with k equals to 3 and p equals to 2.

3.2. Slicing

Slicing is a method that used in anonymizing data by using partition and bucketization. It uses vertical partitioning (column partition), horizontal partitioning (tuple partition), bucketizing, and its sliced table should be randomly permutated [15]. It is better to formalize this slicing method to clearly understanding. We follow the formulation of slicing from Li et.al [15].

Let T be a microdata table which consists n number of A attributes. $T=\left\{A\right\}$ where $A=\left\{A_1,A_2,\dots ,A_n\right\}$.

3.2.1. Attribute Partition

A tuple t∈T, t is a tuple of microdata table T, and t is represented as $t=\left(t{\left[A\right]}_1,t{\left[A\right]}_2,\dots ,t{\left[A\right]}_n\right)$, where $t\left[A_i\right]\left(1\le i\le n\right)$. Attribute partitioning is to partition attribute to more than one, so that each partition belongs to one subset as a partition, and each attribute’s subset is called an attribute, and union of these attributes is called column. Let be there are c attribute $A_1,A_2,\dots ,A_c$ then ${\cup }_{i=1}^c{A}_i=C$ and it is for any $1\le i_1\ne i_2\le c,A_{i_1}\cap A_{i_2}=\varnothing$. In single sensitive attribute, its sensitive attribute is put in the last position for easy representation.

3.2.2. Tuple Partition

Tuple partition is a partition of T that each partition belongs to exactly one subset. Each subset of tuple is called a bucket. Let assume, there are b buckets, $B_1,B_2,\dots ,B_b$ then ${\cup }_{i=1}^b{B}_i=T$ for any $1\le i_1\ne i_2\le b,B_{i_1}\cap B_{i_2}=\varnothing$. A bucket is not generalized or suppressed yet. It depends on the framework used in anonymizing microdata.

3.2.3. Slicing

Slicing a microdata table is when a microdata performed attribute partition, tuple partition and bucketizing for T.

Table 4. Attribute and tuple partition.

Age	Zip Code	Sex	Disease
25	13012	F	Heart Disease
23	13002	F	Heart Disease
28	13033	M	Viral Infection
34	14853	M	Cancer
39	14850	F	Heart Disease
33	14851	M	Viral Infection
31	14856	M	Viral Infection

shows attribute partition and tuple partition.

Table 4 and

Table 5. Sliced table.

(Age, Sex)	(Zip Code, Disease)
(25, F)	(13012, Heart Disease)
(23, F)	(13002, Heart Disease)
(28, M)	(13033, Viral Infection)
(34, M)	(14853, Cancer)
(39, F)	(14850, Heart Disease)
(33, M)	(14851, Viral Infection)
(31, M)	(14856, Viral Infection)

show slicing method. In Table 4, attribute partition is represented by {{Age}, {Zip code}, {Sex}, {Disease}}, while tuple partition is {{t₁, t₂, t₃},{t₄, t₅, t₆, t₇}}. In Table 5, attribute partition is represented by {{Age, Sex}, {Zip code, Disease}} while tuple partition is {{t₁, t₂, t₃},{t₄, t₅, t₆, t₇}}. A partition of tuple represents vertical partition, while attribute partition represents horizontal partition. When both partitions combine with random permutation of sensitive attribute values in each group, it is called the slicing method.

3.3. Overlapped Slicing

Overlapped slicing is an extension of slicing methods. The idea is to put an attribute into more than one column. It is performed by duplicating one sensitive attribute and put it into QI column. This will increase data utility since there is more attribute correlation. Let assume, $T=\left\{C_1,C_2,\dots ,C_c\right\}$. where C_c = S is sensitive column and C_i is QI column. In the slicing method, C_c contains not only a sensitive attribute, but also a QI attribute, as shown in Table 5. There is also a zipcode which is a QI attribute. In overlapped slicing, sensitive attribute like disease will be duplicated and put it into QI column. Therefore,

Table 6. Table after overlapped slicing.

(Age, Sex, Disease)	(Zip Code, Disease)
(25, F, Heart Disease)	(13012, Heart Disease)
(23, F, Heart Disease)	(13002, Heart Disease)
(28, M, Viral Infection)	(13033, Viral Infection)
(34, M, Cancer)	(14853, Cancer)
(39, F, Heart Disease)	(14850, Heart Disease)
(33, M, Viral Infection)	(14851, Viral Infection)
(31, M, Viral Infection)	(14856, Viral Infection)

describes overlapped slicing which is an extension of Table 5.

4. Proposed Model

This paper proposed a new model for privacy preserving data publishing, particularly for multiple sensitive attributes by distributing sensitive values in multiple sensitive attributes and then we extend slicing into overlapped slicing specifically overlapped slicing for multiple sensitive attributes. Sensitive attributes distribution is conducted for reducing relational attack [20] and we refine this attack in next subsection. Slicing increases the privacy guarantee, while overlapped slicing increases the data utility.

Figure 2 exhibits a framework of proposed model. This step of this model:

• Data Preprocessing
• Distribution, a step for distributing evenly the sensitive values,
• Slicing, a step to partition attributes and tuples,
• Overlapped Slicing, a step by extending slicing step and randomly permutated the records,
• Evaluation, we used a metrics called discernibility metrics.

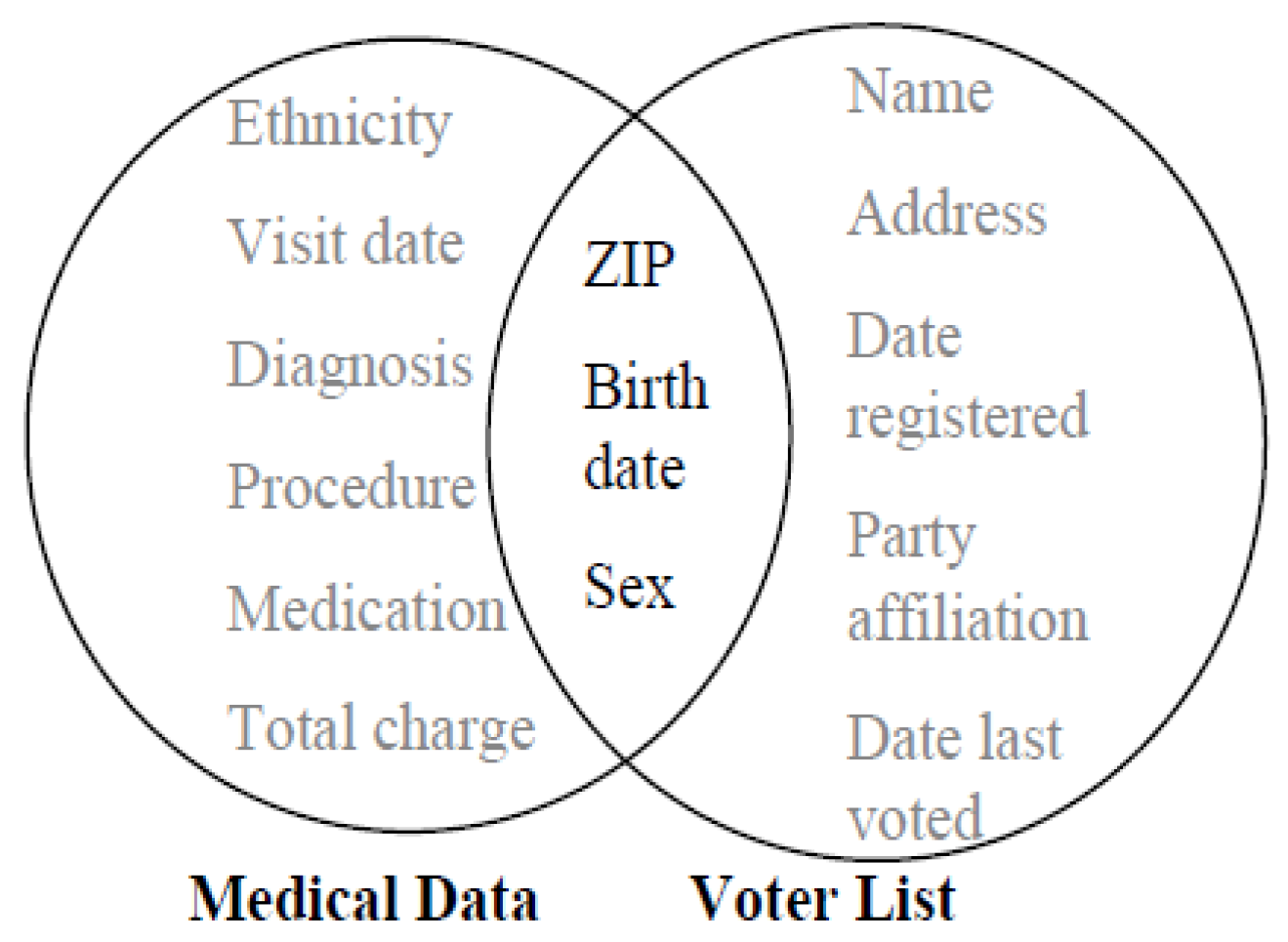
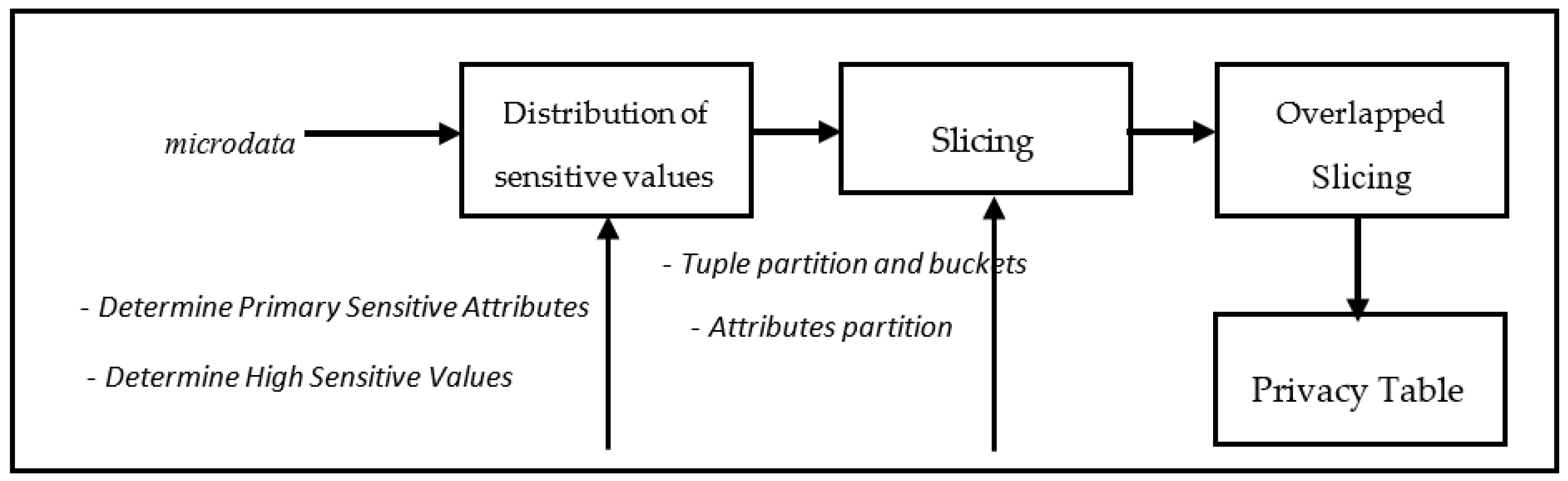
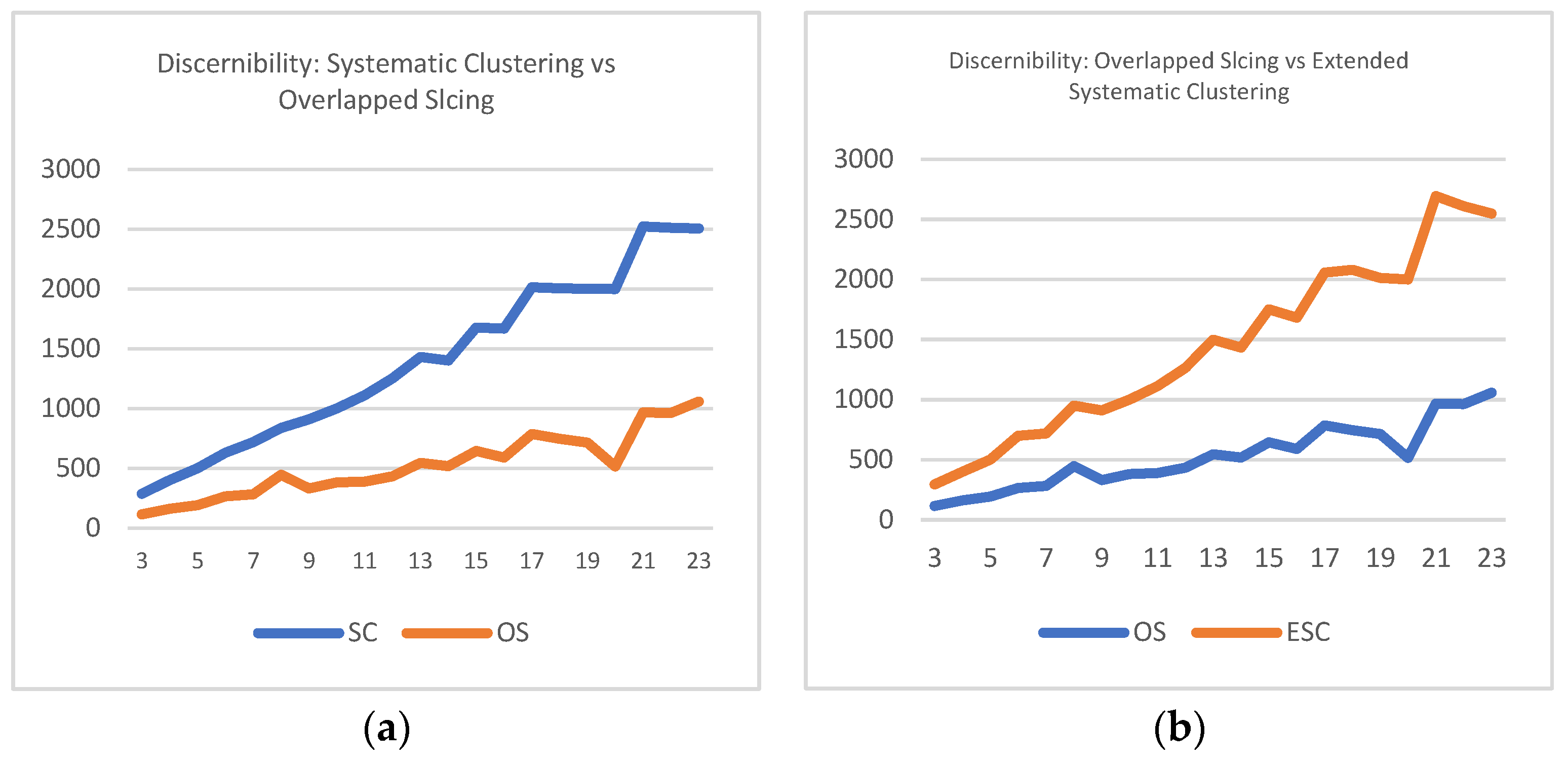
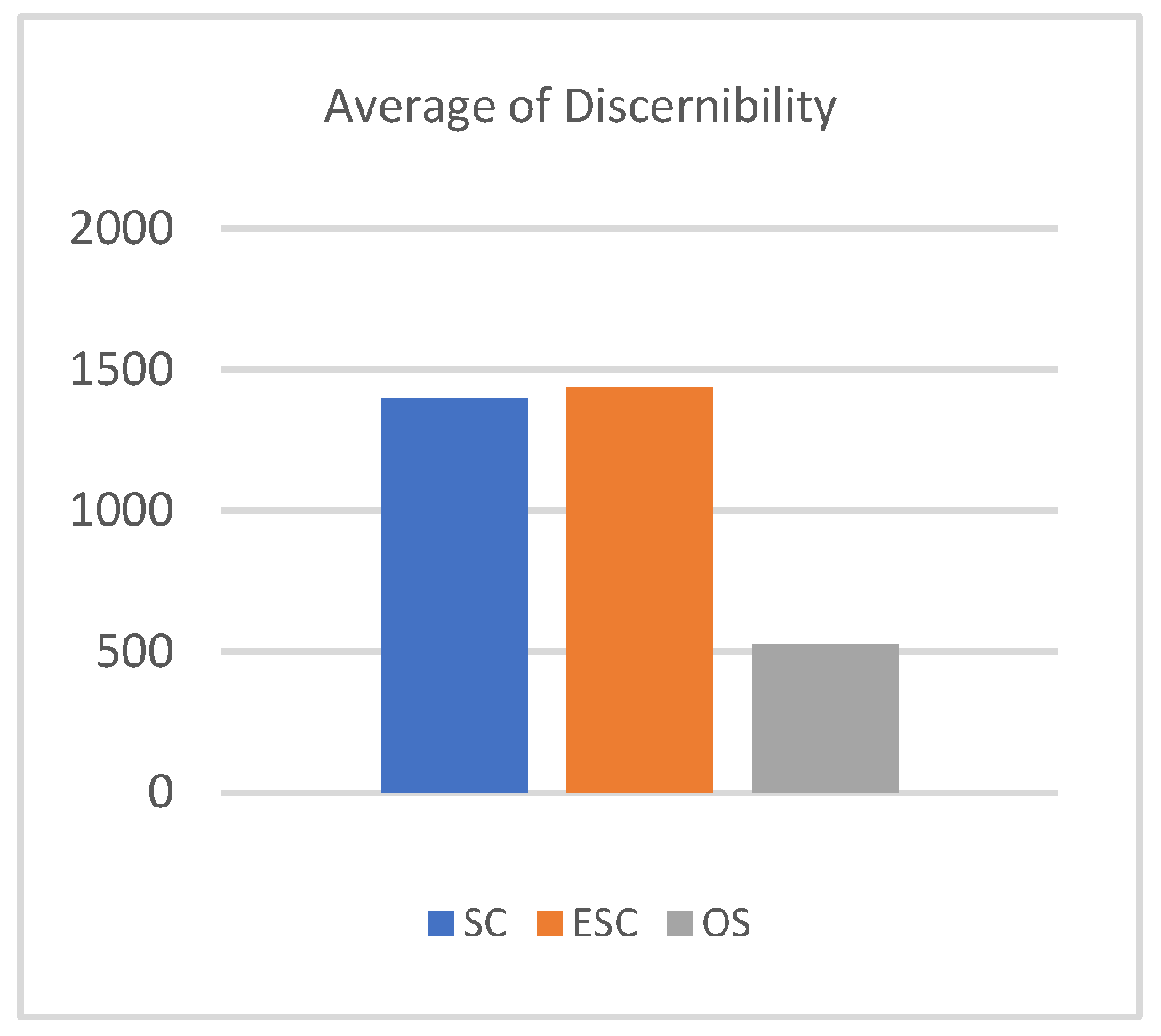
Processes number 2–4 are the main process of our proposed method. In data preprocessing, we removed missing values. We also set the quasi identifier attributes and sensitive attributes. We collected data from UCI machine learning repository which characteristics is microdata. In next subsection, we explain process number 2–5.

4.1. The Distribution of Sensitive Values

Many researches on PPDP did not set its sensitive attributes, whereas, it is very important to prevent a QI group, or a bucket obtains over sensitive values compare with others. This distribution also reduces the probability of relational attack, an attack that often reveals the privacy table containing multiple sensitive attributes.

Before we discuss distribution, it is better to describe relational attack. Relational attack is an attack that consists of three types attack, elimination attack [9], full functional dependency attack [9] and association disclosure attack [13]. These three types of attack concerned with multiple sensitive attributes since they have relation between sensitive attributes and quasi identifier attributes [9] or among sensitive attributes [9,13]. Since the characteristics are similar, we categorized these three attacks into relational attack.

We used distribution of sensitive values like our previous works [20,21]. Two steps are performed for distributing evenly the microdata table:

• Sensitive Attribute Setting
• Distribution of Sensitive Attribute Values

In our model, as in previous works described, a table with sensitive attributes more than three will be dissociated into two or more sub table with maximum number of sensitive attributes in a sub table are three. Each sub table has same QI attributes with different order after being set. In this paper we assume only two sensitive attributes as shown in

Table 7. Microdata with two quasi identifiers (QI) and two sensitive attributes (SA).

Age	Zip Code	Sex	Disease	Occupation
23	11222	F	Flu	Police
25	11234	F	Flu	Police
26	11323	M	Flu	Cook
27	11366	M	Flu	Teacher
29	12666	M	Cancer	Cook
31	12666	M	Bronchitis	Driver
33	12668	F	Bronchitis	Teacher
35	11660	M	Cancer	Teacher
38	12668	F	HIV	Banker
39	11360	M	HIV	Nurse

.

For setting the sensitive attributes, firstly we determined High-Sensitive Value (HSV) for each sensitive attribute. HSV is a value of sensitive attributes with confidential information and tends to be disgraceful by revealing it. Other sensitive values which is not categorized as HSV are called Less Sensitive Value (LSV).

In Table 7, HSV from Disease are HIV and Cancer, while from Occupation are Cook and Driver. Then, we determined Primary Sensitive Attributes (PSA), a sensitive attribute that contains HSV more than others. Other sensitive attributes are called Contributory Sensitive Attributes (CSA). PSA is put before CSA. In Table 7, Disease has 4 HSV (2 HIV and 2 Cancer), while Occupation only has three HSV (2 Cook and 1 Driver). Then, we decided Disease become PSA in this table and put before Occupation.

Next Step, we distribute evenly the sensitive values and form bucket or QI group with k parameter in k-anonymity. A distributional model in [20] is employed but by ignoring generalization and suppression. In our distributional model step number 1 to 3 has been performed, therefore we start to conduct step 4 and 5. The rule of distribution is explained as follows:

• Distribute evenly tuples that contain HSV in PSA to each bucket or group:
  • If all tuples that contain HSV in PSA have been distributed evenly, but there are still buckets or groups that have not being filled yet, then put tuples contain HSV in CSA to each group or bucket, otherwise tuples put randomly into buckets.
  • If all buckets have been filled by tuples with HSV from PSA, but there are still HSV in PSA, then repeat from first bucket to continue in distributing rest of tuples contain HSV.
• Check the table for privacy guarantee to satisfy p-sensitive. If it does not satisfy p-sensitive then exchange a non HSV tuple in the bucket to others with condition, the exchanged bucket still in p-sensitive privacy guarantee.

Table 8. Result of sensitive attributes distribution.

GroupID	Age	Zip code	Sex	Disease	Occupation
1	29	12666	M	Cancer	Cook
1	39	11360	M	HIV	Nurse
1	23	11222	F	Flu	Police
2	35	11660	M	Cancer	Teacher
2	26	11323	M	Flu	Cook
2	25	11234	F	Flu	Police
3	38	12668	F	HIV	Banker
3	31	12666	M	Bronchitis	Driver
3	27	11366	M	Flu	Teacher
3	33	12668	F	Bronchitis	Teacher

shows the result of sensitive attributes distribution which satisfy p-sensitive. It is obviously seen in Table 8 that each group satisfies k-anonymity with k = 3 and it also satisfies p-sensitive due to the fact that in each group, they have more than one sensitive value. We did not generalize and suppress to this table since this is not the released table. We anonymized this table in overlapped slicing stage with no generalization and suppression too. The reason is when a table is generalized or suppressed, it produces information loss.

Now, we formalize the distribution. If T is a microdata table, then T can be viewed horizontally and vertically. Horizontally, microdata T is:

$$T=\left\{QI,S\right\}$$

$$QI=\left\{Q{I}_1,Q{I}_2,\dots ,Q{I}_m\right\}$$

$$S=\left\{S_1,S_2,\dots ,S_n\right\}$$

where T is a microdata table that has been anonymized. QI are quasi identifier attributes, while S are sensitive attributes. $Q{I}_i$ are generalized and/or suppressed obtaining anonymity group.

$$S_i=\left\{HS{V}_1,HS{V}_2,\dots ,HS{V}_T,LS{V}_1,LS{V}_2,\dots ,LS{V}_q\right\}$$

$S_i$ denotes ith sensitive attributes, each of $S_i$ contains HSV and LSV which each attribute owns some HSVs (High-Sensitive Value) and LSVs (Less Sensitive Value). Those form horizontally microdata table, while vertically:

$$T=\left\{B_1,B_2,\dots ,B_p\right\}$$

$$B_i=\left\{r_1, r_2,\dots ,r_k\right\}, \left|B_i\right|\ge k$$

where T is a microdata table that has been anonymized. B_i is a bucket or quasi identifier group that contains at least k records, and k is parameter in k-anonymity, while r_i is ith record in $B_i$. $B_i\left[HS{V}_j\right]$ denotes matching bucket $\left[HS{V}_j\right]$ in $B_i$. Then the distribution is performed as shown below:

$$B\leftarrow {\forall }_{T}HS{V}_T$$

$$B\leftarrow \left\{B_1\right[{HSV}_1,B_2\left[{HSV}_2\right],\dots B_q\left[{HSV}_r\right\}$$

with a requirement $\left|B_i\left\{HS{V}_T\right\}\right|<k, if f \left|HSV\right|<\left|LSV\right|$, and k is parameter in k-anonymity. This requirement cannot be satisfied if total $\left|HSV\right|\ge \left|LSV\right|$ since probability of HSVs lie on a bucket can fill greater than k.

4.2. Slicing on Multiple Sensitive Attributes

Slicing of microdata T is performed by attribute and column partition. Microdata T can be viewed as a collection of attributes $T=\left\{A\right\}, A=\left\{A_1,A_2,\dots ,A_n\right\}$. They have attribute domain as $AD=\{D\left[A_1\right],D\left[A_2\right],\dots ,D\left[A_n\right]$. If tuple $t\in T$, then $t=\left(t\left[A_1\right],t\left[A_1\right],\dots ,t\left[A_n\right]\right)$ where $t\left[A_i\right]$ is value of tuple t with $\left(1\le i\le n\right)$.

Attribute partitioning is to partition attribute to more than one, so that each partition belongs to one subset as a partition, and each attribute’s subset is called an attribute, and union of these attribute is called column. Let there be c attribute $A_1,A_2,\dots ,A_c$ then ${\cup }_{i=1 }^c{A}_i=C$ and it is for any $1\le i_1\ne i_2\le c, A_{i_1}\cap A_{i_2}=\varnothing$. In single sensitive attribute, its sensitive attribute is put in the last position for easy representation. In multiple sensitive attributes, $A_n$ as the last attribute contains more than one attribute. $A_n$ represent multiple sensitive attributes as $A_n=\left(A_{n_1},A_{n_2},\dots ,A_{n_d}\right)$.

Tuple partition is a partition of T that each partition belongs to exactly one subset. Each subset of tuple is called a bucket. Let assume, there are b buckets, $B_1, B_2,\dots ,B_b$ then ${\cup }_{i=1 }^b{B}_i=T$ for any $1\le i_1\ne i_2\le b, B_{i_1}\cap B_{i_2}=\varnothing$. A Bucket is not generalized or suppressed yet. It depends on the framework used in anonymizing microdata.

In this stage, a slicing method for multiple sensitive attributes is conducted. It is adopted from slicing for single sensitive attribute [15]. This stage is performed by partitioning attributes and tuples. Then columns are formed which contain more than one attributes.

Table 9. Result of attribute partition.

Age	Zip Code	Sex	Disease	Occupation
29	12666	M	Cancer	Cook
39	11360	M	HIV	Nurse
23	11222	F	Flu	Police
35	11660	M	Cancer	Teacher
26	11323	M	Flu	Cook
25	11234	F	Flu	Police
38	12668	F	HIV	Banker
31	12666	M	Bronchitis	Driver
27	11366	M	Flu	Teacher
33	12668	F	Bronchitis	Teacher

shows the result after an attribute partition is performed. It is vertically partition for each attributes, Age and Zip code as QI attributes, Disease and Occupation as sensitive attributes. Slicing in Table 9 produced five columns, each column contains exactly one attribute. Age, Zip code, and Sex are QI attributes, Disease and Occupation are sensitive attributes, each attribute fills different column.

Table 10. Result of tuple partition.

Age	Zip Code	Sex	Disease	Occupation
29	12666	M	Cancer	Cook
39	11360	M	HIV	Nurse
23	11222	F	Flu	Police
35	11660	M	Cancer	Teacher
26	11323	M	Flu	Cook
25	11234	F	Flu	Police
38	12668	F	HIV	Banker
31	12666	M	Bronchitis	Driver
27	11366	M	Flu	Teacher
33	12668	F	Bronchitis	Teacher

shows result of tuple partition that partition the table horizontally. Each of horizontal partition is treated as a bucket with number of tuples follow k in k-anonymity. Next step, a slicing process by forming two columns with each column contains some attributes. A column represents as QI attribute and another one represents as sensitive attributes. But, one of three attributes in QI column will be put in another one to keep its correlation. Two attributes with most correlated is joined in first column are Age and Sex, while Zip code is put in next column.

Table 11. Sliced table.

(Age, Sex)	(Zip Code, Disease, Occupation)
(29, M)	(12666, Cancer, Cook)
(39, M)	(11360, HIV, Nurse)
(23, F)	(11222, Flu, Police)
(35, M)	(11660, Cancer, Teacher)
(26, M)	(11323, Flu, Cook)
(25, F)	(11234, Flu, Police)
(38, F)	(12668, HIV, Banker)
(31, M)	(12666, Bronchitis, Driver)
(27, M)	(11366, Flu, Teacher)
(33, F)	(12668, Bronchitis, Teacher)

shows the result of slicing method. First attribute has two columns, Age and Sex, second attribute contains three columns, Zip code, Disease, Occupation. In fact, Disease is a QI attribute, but it is put in an attribute contain sensitive columns to keep correlation between two attributes.

4.3. Overlapped Slicing on Multiple Sensitive Attributes

Overlapped slicing is to put one sensitive attribute in sensitive column into QI column. Overlapped slicing is an extension of slicing method and we implemented in multiple sensitive attributes. In overlapped slicing, the table does not only follow the slicing’s method but also the tuple in each bucket randomly permutated. Its aim is to improve data utility, while its privacy is maintained by permutating tuples in a bucket.

An attribute that chosen from sensitive column is CSA, because CSA does not potentially embarrass the holder. A microdata table T is given as:

$$T=\left\{QI,S\right\}$$

$$QI=\left\{Q{I}_1,Q{I}_2,\dots ,Q{I}_m\right\}, C_q={\cup }_1^{m}QI$$

$$S=\left\{S_1,S_2,\dots ,S_n\right\}, C_s={\cup }_1^{n}S$$

If $S_i$ is CSA then $QI=\left\{Q{I}_1,Q{I}_2,\dots ,Q{I}_m,S_i\right\}$, $S=\left\{S_1,S_2,\dots ,S_n\right\}$, and $T=\left\{C_q,C_s\right\}$. Vertically, in each bucket, its sensitive value is randomly permutated.

$$T=\left\{B_1,B_2,\dots ,B_p\right\}.$$

$$B_i=\left\{r_1, r_2,\dots ,r_k\right\}, \left|B_i\right|\ge k$$

Each tuple in a bucket is represented by $B_i=\left\{r_1\left[S_1,S_2,\dots ,S_n\right],r_2\left[S_1,S_2,\dots ,S_n\right],\dots ,r_k\left[S_1,S_2,\dots ,S_n\right]\right\}$. The notation describes value of sensitive attributes in ith record. $r_1\left[S_1,S_2,S_3\right]$ describe sensitive value of attribute S₁,S₂, and S₃ in record r₁. Simply we denote as $B_i=\left\{r_1\left[S{\left[r_1\right]}_1\right],r_2\left[S{\left[r_2\right]}_2\right],\dots ,r_k\left[S{\left[r_k\right]}_n\right]\right\}$. Then, we randomly permutate sensitive values in in bucket. Therefore, it could be $r_1\left[S{\left[r_3\right]}_1\right]$, $r_2\left[S{\left[r_1\right]}_2\right]$ or $r_3\left[S{\left[2\right]}_3\right]$. $r_1\left[S{\left[r_3\right]}_1\right]$ means record 1 in with the bucket contains sensitive values, which originally from record 3 in the bucket.

In

Table 12. Overlapped Slicing table.

(Age, Sex, Disease)	(Zip Code, Disease, Occupation)
(29, M, Cancer)	(12666, Cancer, Cook)
(39, M, HIV)	(11360, HIV, Nurse)
(23, F, Flu)	(11222, Flu, Police)
(35, M, Cancer)	(11660, Cancer, Teacher)
(26, M, Flu)	(11323, Flu, Cook)
(25, F, Flu)	(11234, Flu, Police)
(38, F, HIV)	(12668, HIV, Banker)
(31, M, Bronchitis)	(12666, Bronchitis, Driver)
(27, M, Flu)	(11366, Flu, Teacher)
(33, F, Bronchitis)	(12668, Bronchitis, Teacher)

, Disease is overlapped in first and second column. By overlapping this attribute, it will provide better data utility [15]. To maintain privacy guarantee, then tuples in each bucket from second columns is randomly permutated.

Table 13. Overlapped Slicing table with random permutation.

(Age, Sex, Disease)	(Zip Code, Disease, Occupation)
(39, M, HIV)	(11360, Cancer, Cook)
(29, M, Cancer)	(11222, HIV, Nurse)
(23, F, Flu)	(12666, Flu, Police)
(35, M, Cancer)	(11234, Flu, Cook)
(25, F, Flu)	(11323, Cancer, Police)
(26, M, Flu)	(11660, Flu, Teacher)
(27, M, Flu)	(12668, Bronchitis, Teacher)
(31, M, Bronchitis)	(11366, HIV, Banker)
(38, F, HIV)	(12668, Flu, Teacher)
(33, F, Bronchitis)	(12666, HIV, Driver)

below depicts how random permutation is performed in overlapped slicing. This random permutation creates fake tuples which not affected on information loss. From Table 13, values in each bucket in second column are randomly permutated to break linking between two columns. As shown in Table 12, in the first bucket, the values {(39, M, HIV), (29, M, Cancer), (23, F, Flu)} are randomly permutated, and the values {(11360, HIV, Cook), (11222, Flu, Nurse), (12666, Cancer, Police)} are randomly permutated also, therefore linking between both columns in one bucket is disguised. For example, in group 2 first tuple, {(35, M, Cancer), (11660, Cancer, Teacher)} is permutated to {(35, M, Cancer), (11234, Flu, Police)}. The second is fake tuple, because it is changed from the original tuple.

We assume table has been clustered into bucket based on quasi identifier. We briefly explain the overlapped slicing formally below, with OT is overlapped table.

Create Overlapped Table

$OT=\left\{Q,S\right\}$, where $Q=\left\{Q_1,Q_2,\dots ,Q_m\right\}$ and $S=\left\{S_1,S_2,\dots ,S_n\right\}$

Q is quasi identifier attributes, while S is sensitive attributes. Then, Q and S being overlapped:

$S\leftarrow \left\{Q_i\right\}$, $Q_i$ is randomly put from Q, $Q_i=Q_{OT}$

$Q\leftarrow \left\{S_i\right\}$ iff $S_i=CSA$ (CSA is Contributory Sensitive Attribute)

If number of CSA is more than one, then CSA is put randomly.

Then,

$$OT=\left\{\left(Q_1,Q_2,\dots ,Q_m, S_{CSA}\right),\{Q_{OT}, S_1,S_2,\dots ,S_n)\right\}$$

Create Fake tuples (by tuples random permutation)

for bucket $B=\left\{b_1,b_2,\dots ,b_r\right\}$, where $b_i=\left\{t_1,t_2,\dots ,t_p\right\}$, $B=\cup b_i$

domain of t, $t=\left\{t_1\left[S_1,S_2,\dots ,S_n\right],t_2\left[S_1,S_2,\dots ,S_n\right],\dots ,t_p\left[S_1,S_2,\dots ,S_n\right]\right\}$

b_i is a bucket contains t_i, where t_i is ith tuple in a bucket.

$$\begin{gathered} f\left(t\right)=rand\left[t_i\right]in{b}_i \\ {b}_i=random\left(t_p\left[S_i\right]\right) \end{gathered}$$

Overlapped slicing is a microdata table that satisfies overlapped attribute and tuple random permutation: $OT=\left\{Q,S\right\}$, where $Q=\left\{Q_1,Q_2,\dots ,Q_m\right\}$. and $S=\left\{S_1,S_2,\dots ,S_n\right\}$, overlapping with $S\leftarrow \left\{Q_i\right\}$, $Q\leftarrow \left\{S_i\right\}$ and bucket $b_i=\left\{t_1,t_2,\dots ,t_p\right\}$, $t=\left\{t_1\left[S_1,S_2,\dots ,S_n\right], t_2\left[S_1,S_2,\dots ,S_n\right],\dots ,t_p\left[S_1,S_2,\dots ,S_n\right]\right\}$, with $f\left(t\right)=rand\left[t_i\right]in b_i$ and $b_i=random\left(t_p\left[S_i\right]\right)$.

4.4. Privacy and Utility Analysis

Our method is able to guarantee against attribute disclosure attack based on l-diversity or p-sensitive privacy requirements. Table 13 satisfies 3-diversity because in all three sensitive attributes there are at least three diverse values. Then, we give an example on how the overlapped sliced table satisfies the privacy. Consider tuple t₁ in group 3 with QI values (27, M, Flu). In order to privacy analysis, adversaries can examine first column (Age, Sex, Disease) and he/she know that (27, M, Flu) must be in third bucket because no matching bucket in another two buckets. Therefore, adversaries are able to infer that (27, M, Flu) in bucket 3.

Then, adversaries check disease which is an overlapped attribute in Table 13. If adversaries refer to Table 12, then he/she can link exactly that (27, M, Flu) matches to (11366, Flu, Teacher). This matching tuple can lead adversaries with his/her background knowledge to guess who the holder is. However, by referring to Table 13, adversaries cannot guess correctly since sensitive values are randomized. If he/she take a tuple without check overlapped attribute, then its matching bucket is (12668, Bronchitis, Teacher). This lead to the mistake matching bucket. If he/she check the disease as overlapped attribute, its matching bucket is (12668, Flu, Teacher). This also lead to a mistake matching bucket since the sensitive values are randomly permutated. Therefore, its probability decreases from 1 bounded into 0.25. We can conclude that this table satisfies 3 diversity since other bucket contains three distinct values, although bucket 3 has 0.25 which means 4-diversity.

From a utility perspective, we can compare with generalization. In generalization, quasi identifiers are generalized or suppressed. For example, in Table 3, Age in first group is generalized to [20,29] and zipcode is suppressed two levels (130**). This is a condition of lossing information. Table with generalization and suppression in quasi identifiers has low utility because it can not be used completely. One do not know exactly the age in range [20,29] or do not know exact zipcode, whereas in data analysis, complete data is needed. Incomplete data will lead into poor analysis.

In overlapped slicing, as we see in Table 13, quasi identifiers are not generalized or suppressed. We run the technique by permuting randomly sensitive values in a bucket. This technique does not produce any information loss, tends to minimize information loss if it has to be generalized. However, this overlapped slicing produces fake tuples. It is a consequence of sensitive values permutation in a bucket. This fake tuples do not reduce utility of data, since the data still complete. One who uses the data in data analysis obtains better data than data with generalization.

4.5. Evaluation

For evaluation we used a measurement metrics tool which is called discernibility metrics [32,33]. Discernibility metrics measures number of tuples that cannot be distinguished to others, this metrics also measures penalty point to generalized tuples.

$$DM\left(T*\right)={{\displaystyle \sum }}_{t\in T}{\left|G_{T*}\left(t\right)\right|}^2$$

(1)

From formula (1), $DM\left(T*\right)$ is discernibility metrics value, while $G_{T*}\left(t\right)$ is number of generalized tuples. The higher discernibility value, the higher privacy, but the data utility is decreased. We used discernibility metrics rather than information loss metrics since we need to know briefly first on the strength of privacy. If it is measured by using discernibility metrics yields higher privacy, it is higher privacy also when information loss metrics is used. Both evaluation techniques are aligned in privacy and utility.

5. Experiment Result

This section explains data used and experiment result. Data is adjusted to the experiment needs and its result is compared with two other methods, those are systematic clustering and extended systematic clustering.

5.1. Data

We retrieved data from Adult datasets that available in UCI Machine Learning repository. We randomly choose 100 records. Adult datasets consist of 14 attributes, but we only used 6 attributes in this simulation. Those six attributes are categorized into 3 quasi identifier attributes and 3 sensitive attributes. We used Age, Sex, and Marital Status as quasi identifier attributes, while Education, Work Class, and Occupation as sensitive attributes. Since Education has more HSV than Work Class and Occupation, then we decided Education as Primary Sensitive Attribute, another two are Contributory Sensitive Attribute. The Adult datasets description is shown in

Table 14. Description of retrieved Adult datasets.

Attribute Name	Attribute Type	Distinct Value
Age	Numeric	21
Sex	Categorical	2
Marital Status	Categorical	6
Education	Categorical	14
Work Class	Categorical	6
Occupation	Categorical	12

below. The description below describes 100 records we retrieved.

This simulation used following criteria to evaluate our proposed model: (1) anonymity parameter k (3–23), (2) datasets 100, (3) Quasi identifier 3 attributes, (4) sensitive attribute 3 attributes.

5.2. Result

We performed our experiment to run overlapped slicing and compare with two other methods, systematic clustering and extended systematic clustering. Both are chosen since they run in systematic way, therefore those methods guarantee that outlier is minimized, while outliers produce more information loss. We used attribute age, sex, and marital status as quasi identifier attributes, while education, work class, and occupation as sensitive attributes.

Figure 3 exhibits discernibility value on overlapped slicing. In Figure 3a Discernibility value of overlapped slicing is compared with systematic clustering while in Figure 3b it is compared with extended systematic clustering. From Figure 3, it is obviously seen that overlapped slicing obtains discernibility value lower than systematic clustering and extended systematic clustering. This evaluation shows overlapped slicing outperforms two other methods in data utility.

Figure 4 shows the average of discernibility value by using overlapped slicing is below 1000, while systematic clustering and extended systematic clustering more than 1000. Overlapped slicing obtained 525.8, systematic clustering 1399.4, and extended systematic clustering 1438.2, respectively. This average value of discernibility strengthens overlapped slicing methods in holding better data utility than systematic clustering and extended systematic clustering.

6. Discussion

We conducted our experiment on overlapped slicing method. This method formed from extended systematic clustering, while it clustered the equivalence class/quasi identifier group. The result shows that our method obtained low discernibility value. This low value occurs because in overlapped slicing, we used the bucketize technique, where generalization and suppression are not mandatory. We only generalized age attribute, while another two did not generalize. In systematic clustering and extended systematic clustering generalization and suppression become a mandatory to anonymize quasi identifier group, while overlapped slicing mainly used permutation to sensitive attributes values for anonymizing table. This permutation is performed in a bucket. Those comparison clearly stated that discernibility value of overlapped slicing is lower than another two methods.

This investigation identified that overlapped slicing had successful in minimizing information loss due to two factors: (1) the overlapping stage, which keep correlation between QI and sensitive attributes, and (2) replacement of generalization and suppression in QI by randomly permutation of sensitive values in each bucket.

7. Conclusions

Overlapped slicing has been used with single sensitive attribute for privacy preserving data publishing. In this research, we proposed a novel overlapped slicing method with multiple sensitive attributes. The result shows that overlapped slicing performed better than systematic clustering and extended systematic clustering in data utility. We used discernibility metrics to evaluate them. Overlapped slicing obtained a lower discernibility value compared to the other two methods. The lower discernibility value means higher data utility. Our method has lower discernibility value since overlapped slicing used bucketize technique to anonymize data. Bucketize did not use generalization and suppression as mandatory.

Our future work will continue to investigate overlapped slicing by employing anatomy. Anatomy will dissociate quasi identifier attributes and sensitive attributes. It increases privacy, but it needs more investigation into data utility.