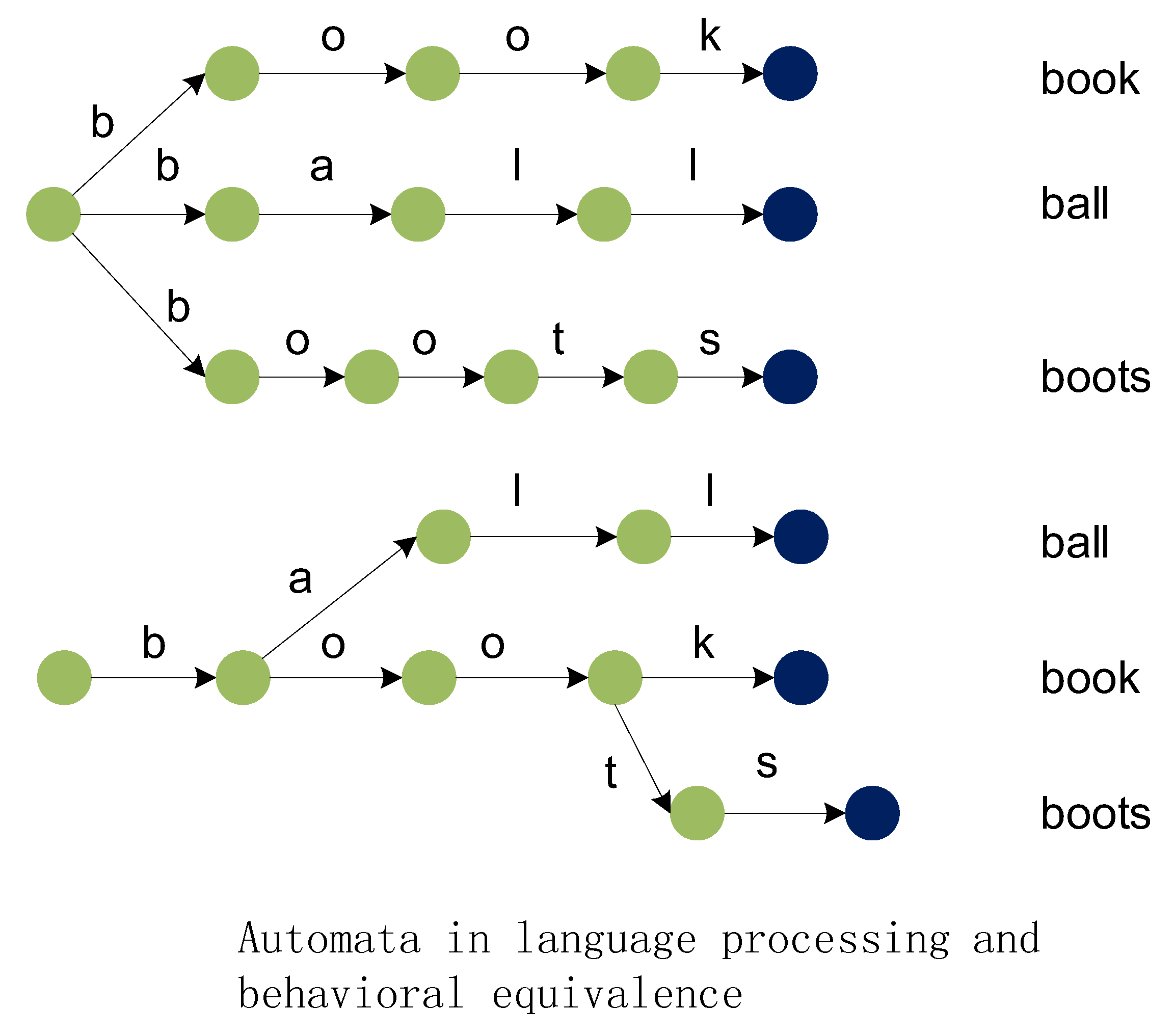1. Introduction
In the real world, there exist many systems exhibiting a hybrid discrete–continuous behavior, and the notion of hybrid automaton [
1] was introduced to model these hybrid systems. For example, embedded systems are often modeled as hybrid systems due to their involvement of both digital control software and analog plants, which physical process is often specified in the form of differential equations. Infinite states (or state explosion) due to the continuous behavior of the system are among the most challenging problems in verifying hybrid systems. In the traditional functional analysis domain, an efficient classical technique to tackle state explosion is equivalence [
2,
3]. In brief, the systems with the same functional behaviors are called equivalence. Functional equivalence simplifies the system by removing the duplicate branches. The papers by Glabbeek [
2,
3] proposed fourteen kinds of linear time-branching time equivalence relations, and the completed trace equivalence is a basic state-space equivalence relation, which can be used to further reduce the states of hybrid systems [
4,
5].
However, traditional equivalence techniques are based on absolute precision, which only gives the answer “yes” or “no”, not how much simulation. There is an example that illustrates that it is meaningful to introduce the deviation analysis to equivalence. Considering a microwave oven, if the microwave oven is required to heat to 100 C within 60 s but does so within 60.5 s (this is very common in life), and if a 0.5 s deviation is allowable, then the two systems are equivalent, or the two states can be merged. Otherwise, the two systems are not equivalent, or the two states cannot be merged. Especially in safety-critical cases, any deviation greater than zero seconds can be viewed as the presence of a bug. In reality, the parameters of hybrid systems are obtained by all kinds of measurements, which generally have a small number of errors. Since errors are inevitable, approximation analysis between the original system and the approximate system is very significant for the given permission precision.
In order to achieve this goal, this paper proceeds by defining two types of metrics, state metric
and trajectory metric
, to check how much a hybrid system
conforms to another hybrid system
. The
measures the distance of the states, while the
specifies the deviation of the system behaviors. Given a deviation
, the original ILAHS of
can be transformed to the approximate ILAHS of
. Then in trace equivalence semantics,
is further reduced to
with the same functions, and hence
is
-approximate trace equivalent to
. In particular,
is a traditional trace equivalence. At last, the decision problem that
is
-approximate to
can be reduced to semi-algebraic system solving (
SAS solving) [
6,
7,
8,
9,
10,
11].
There are several choices for metrics, such as bisimulation metrics [
12,
13], Lyapunov-like functions [
13], directed metrics [
14], and pseudo-ultrametrics [
15], most of which are required to satisfy intricate properties of simulation or bisimulation relations. In contrast, state metric
and trajectory metric
in this paper are based on Euclidean distance, which is an intuitive metric.
In this paper, we focus on a specific class of hybrid systems, namely, inhomogeneous linear algebraic hybrid systems (ILAHSs for short). It is well known that the most important analysis question for hybrid systems is the problem of reachability, which is computationally hard and undecidable for the general case and intractable even for the simplest subclasses [
1]. So it is doomed to be impossible to find a universal approach for this question without any simplifications or restrictions. ILAHSs, which are ubiquitous in reality, are a kind of classical hybrid systems with some simplifications.
Note that our approximation technology differs from those proposed in the papers [
16,
17,
18,
19,
20], which aim to construct an approximately reachable set. Most of the differential equations of hybrid systems, as we all know, cannot be solved analytically, and, therefore, the exact reachable set cannot be computed symbolically, so many papers developed a variety of methods that over-approximate or under-approximate the reachable set using varieties of set representations such as polyhedra [
21], zonotopes [
22], level sets, or ellipsoids [
23]. Our approximation technology is, however, to identify the approximate behavior equivalence among the hybrid systems. So far, there exist few papers focused on the approximation analysis of the ILAHS’ behavior equivalence [
4,
5,
24]. Unfortunately, their methods are based on
Matrix Jordan Standard Type, which only apply to special cases and cannot deal with the infinite trajectory condition, whereas our method can solve this problem.
The main contributions of this paper are as follows. First, we propose a new method for identifying equivalence, which applies to more general ILAHS. Second, not only is the finite trajectory condition defined, but the infinite trajectory condition is also defined. Third, compared to existing approaches, our method is based on Euclidean distance, which is an intuitive metric.
The remainder of this paper is organized as follows.
Section 2 recalls the preliminaries of our method, including hybrid system, inhomogeneous linear algebraic hybrid systems,
SAS, and so on. We define the approximate completed trace equivalence of ILAHS in
Section 3.
Section 4 presents a case study. Conclusions are given in
Section 5.
2. Preliminaries
In this section, we recall some concepts used throughout the paper. We first clarify some notation conventions. We use bold uppercase letters such as to denote matrices and denote the transpose and approximate matrix of , respectively. We use to denote vectors. We denote as an assignment of variables .
Hybrid automata, first proposed by Rajeev Alur et al. [
25], are a mathematical model to describe a system containing continuous and discrete components. Many other models for hybrid systems can be found in [
26,
27,
28,
29]. In this paper, we adopt the model proposed in [
1] as our modeling framework. A hybrid system can then be defined as:
Definition 1 (Hybrid System). A hybrid system consists of the following components:
L: a finite set of locations (or modes).
V: a set of real-valued system variables. The hybrid state space is denoted by , a state is denoted by , and is a continuous state of the variables over the real numbers.
: a set of discrete transitions. A discrete transition consists of the pre- and post-locations of the transition , a guard , which is a boolean function of the variables V, and an action , which is an assignment over the variables V and . V denotes the current-state variables, and denotes the next-state variables.
: continuous evolution, a map that maps each location to a differential rule , of the form . The differential rule specifies how the system variables evolve at the location ℓ, which is also known as a vector field or a flow field.
: a map that maps each location to a location condition (location invariant) that is an assertion over V.
: the initial location.
Θ: an assertion specifying the initial condition.
The behaviors of hybrid systems are expressed as trajectories.
Definition 2 (Trajectory)
. A trajectory of a hybrid system is an (in)finite sequence of states of the formsuch that,Initiation: specifies an initial state. Furthermore, for each consecutive state pair , one of the two evolution conditions below is satisfied:
Discrete evolution:There exists a transition such that τ is enabled, i.e., = true and .
Continuous evolution: , and there exists a time interval , , along with a smooth (continuous and differentiable to all orders) function such that g evolves from to according to the differential rule at location ℓ, while satisfying the location condition . Formally,
- 1.
and ;
- 2.
.
A state is reachable if it appears in some trajectory of . The set of all reachable states of is denoted by Reach().
With some restrictions, a hybrid system can be specialized into an inhomogeneous linear algebraic hybrid system, which is ubiquitous in reality [
4,
5,
24].
Definition 3 (Inhomogeneous linear algebraic hybrid system, ILAHS). ILAHS is a kind of hybrid system with simplifications: for continuous evolution, , where .
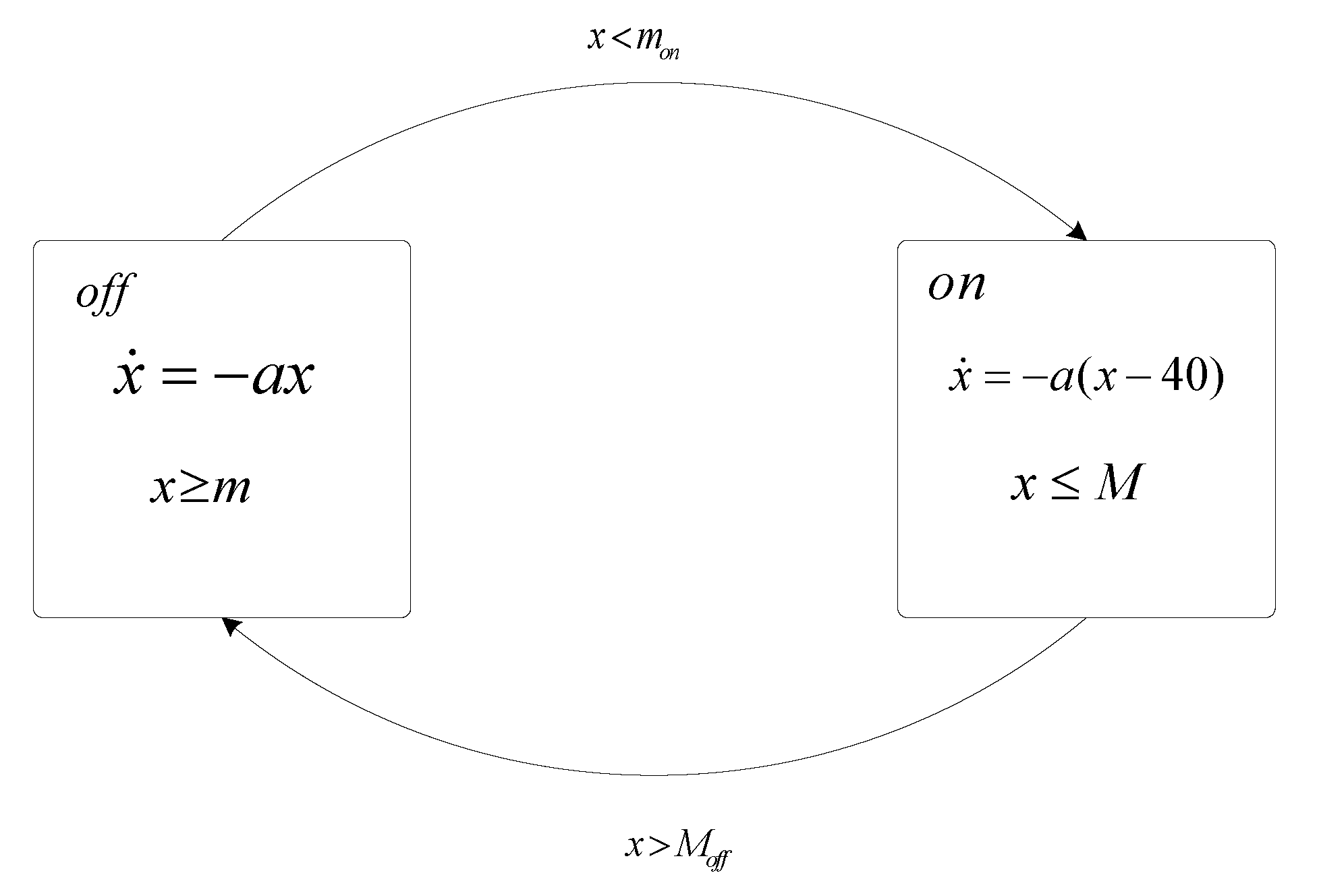
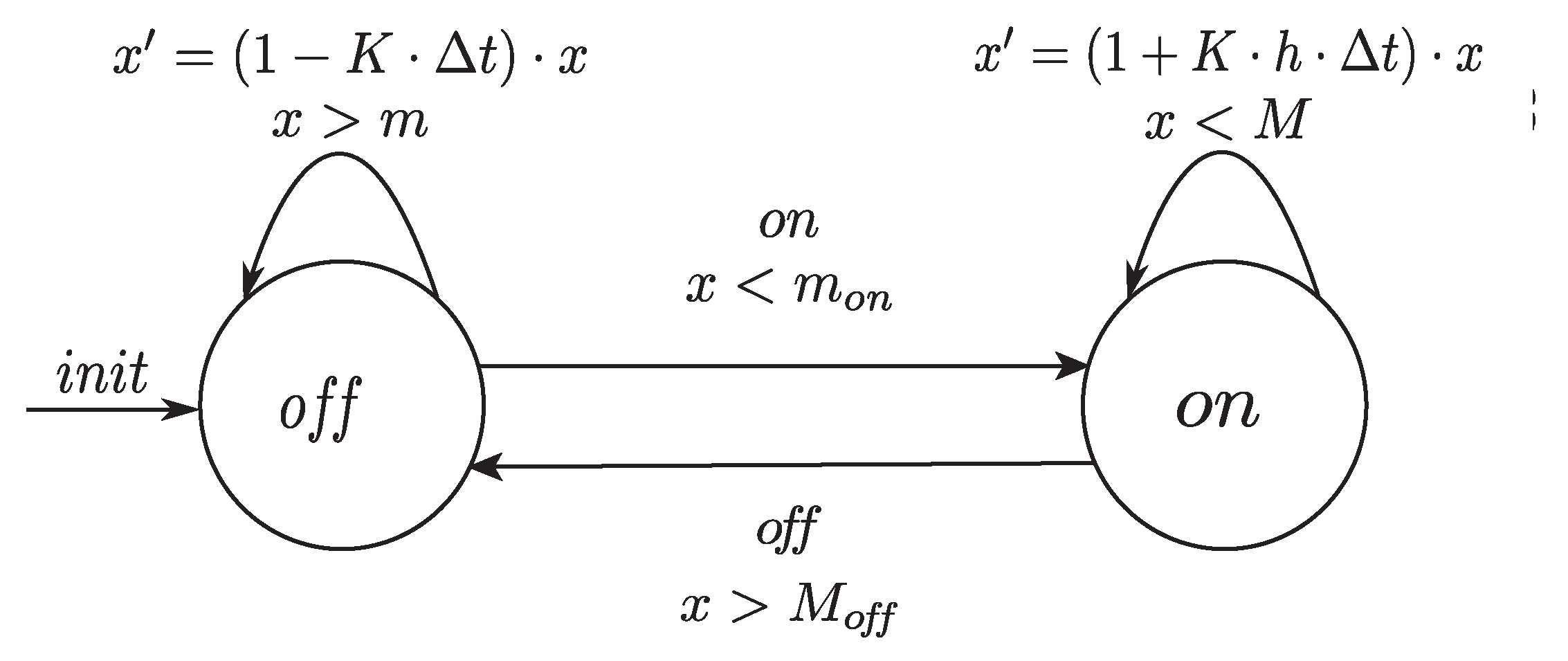
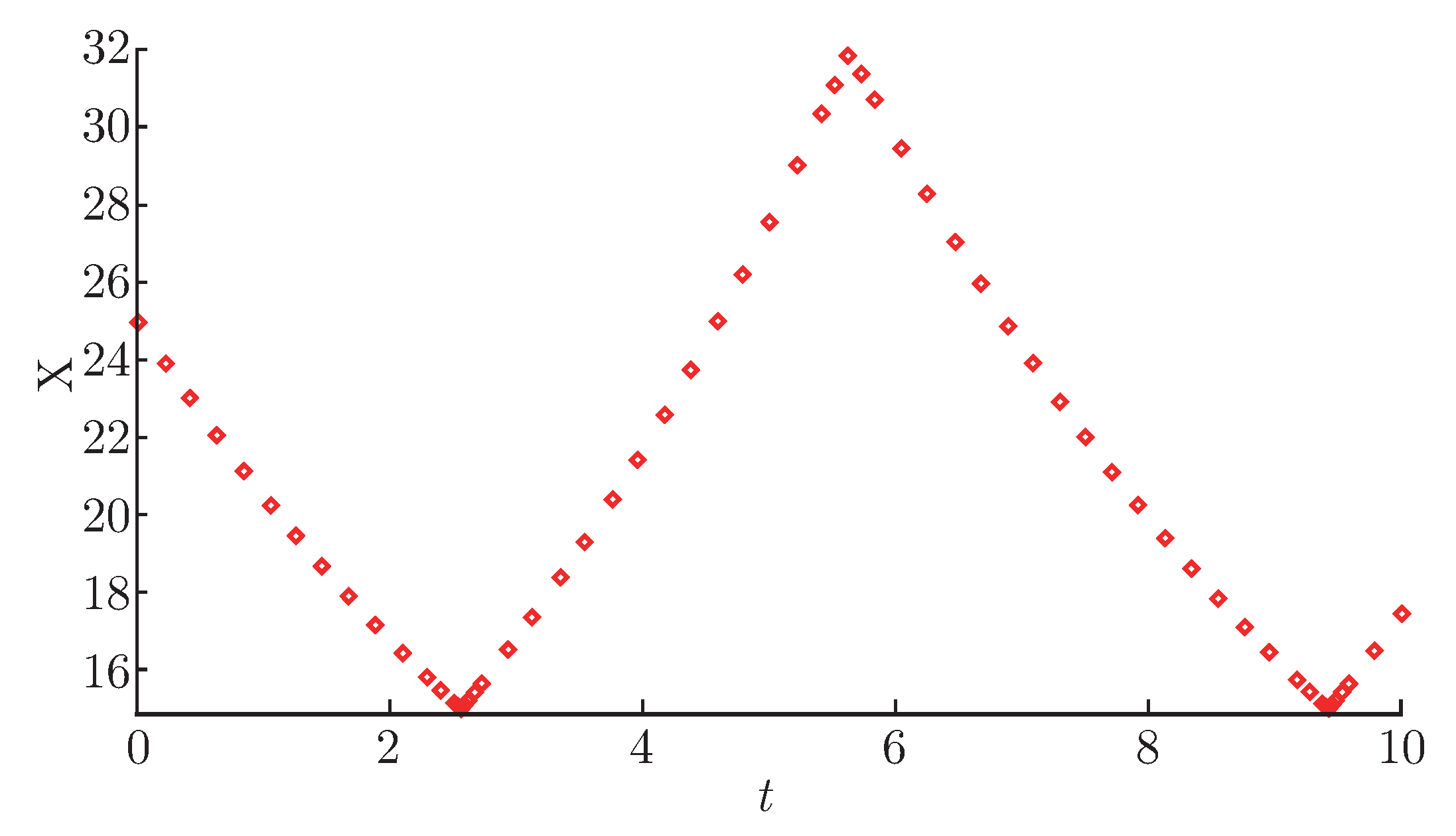
Example 1 (A thermostat)
. Consider a room being heated by a radiator controlled by a thermostat, one of the typical introductory examples of hybrid systems. This system has both a continuous state and two discrete states. The continuous state is the temperature in the room . The discrete states, , reflect whether the radiator is on or off. The evolution of x is governed by a differential equation, while the evolution of L is through jumps. It is very convenient to compactly describe such hybrid systems by mixing the differential equation with the directed graph notation (shown in Figure 1).Computers are used as control systems for a wide variety of industrial and consumer devices. However, the working principle of computers is fundamentally discrete rather than continuous. When the time x is discretized, the general hybrid system (Figure 1) can be turned into an ILAHS(Figure 2), whereThe ILAHS’ behaviors are expressed as trajectories. For instance, we assume that , , , , , , and . If the initial temperature of the room is C, then one possible trajectory is as follows (Figure 3): Definition 4 (Metric). For a set X, a metric on X is a function such that
- 1.
for all if and only if ;
- 2.
, for all ; and
- 3.
for all .
Note that the condition (1) expresses that
implies
. If
does not necessarily mean that
, the metric is called a pseudo-metric [
12].
Definition 5 (Trace Equivalence). is a trace of a process p, if there exists a process q, such that . Let denote the set of traces of p. Two processes p and q are trace equivalent if . In trace semantics, two processes are identified iff they are trace equivalent.
Trace semantics is based on the idea that two processes are to be identified if they allow the same set of observations, where an observation simply consists of a sequence of actions performed by the process in succession (
Figure 4). More details can be found in the paper [
2].
However,
consists of abstract actions, which are unable to express the exchange details of the data stream. In 2008, Sankaranarayanan et al. [
30] defined a hybrid system program model with polynomial equations that took the place of abstract actions and opened up a new method of hybrid system design and verification based on polynomial algebra. For example, the transition
with
indicates the relation
, the variable
x refers to the current state, and
to the next state of a transition.
Definition 6 (Completed Trace Equivalence)
. is a completed trace of a process p, if there exists a process q, such that and . Let denote the set of completed traces of p. Two processes p and q are completed trace equivalent if and . In completed trace semantics, two processes are identified iff they are completed trace equivalent (Figure 5). Obviously, the trace equivalence can be regarded as a simpler version of the completed trace equivalence.
Definition 7 (Semi-Algebraic System)
. A semi-algebraic system (SAS for short) is a conjunctive polynomial formula of the following form:where , and are all in . An SAS is usually denoted by a quadruple , where and . An SAS is called parametric if , otherwise it is constant. For , what we are concerned about is the real solutions of the equations () under the constraints (). More specifically, assuming S is a constant , the interesting questions are how to compute the number of real solutions of S, and if the number is finite, how to compute these real solutions. Assuming S is parametric , the interesting problem is the so-called real solution classification, which is to determine the condition on the parameters such that the system has the prescribed number of distinct real solutions, which is possibly infinite.
To address this issue, Yang et al. [
6] first defined the key concept of border polynomial(BP), based on which an algorithm is proposed. For more details, please refer to [
7,
8,
9,
10,
11]. This algorithm has been improved and implemented by Xia as the Maple package DISCOVERER [
31]. Since 2009, the main functions of DISCOVERER have been integrated into the RegularChains library of Maple. Since then, the implementation has been improved by Chen et al. [
32,
33,
34]. Thus, the experiment in this paper requires a version of Maple higher than Maple 13.
Example 2. Prove that under the constraints , i.e., In other words,
where
In order to prove (
4) with Maple, we first start Maple and load two relative packages of
RegularChains as follows.
> with (RegularChains):
> with (ParametricSystemTools):
> with (SemiAlgebraicSetTools):
Then we define an order of the unknowns:
> R:= PolynomialRing ([a, b, c]):
Then, by calling
>RealRootClassification ([abc-1], [a,b,c], [-f], [ ], 2, 0, R):
we will know at once that the inequality holds.
3. -Approximate Completed Trace Equivalence of ILAHS
In this section, we define
-approximate completed trace equivalence of ILAHS and propose the discriminant conditions based on
SAS. Assuming
is an ILAHS and
is a trajectory of
,
is an original (or theoretical) transition matrix,
is discrete evolution, for simplicity,
, and so on.
is an approximate (or actual) matrix with respect to
, so we have another trajectory,
If a given derivation
is allowable, we aim to check whether two trajectories are identical; if every trajectory of two ILAHSs is identical, the two hybrid systems are identical with respect to derivation
.
To measure the behavior of the hybrid system, this paper defines two types of metrics based on the Euclidean metric: the state metric and the trajectory metric . measures the distance of states, while specifies the similarity of two systems’ behaviors.
Definition 8 (State Metric)
. State metric is Euclidean metric: such thatIf , can be abbreviated as . Definition 9 (Trajectory Metric)
. Trajectory metric is defined as the minimum distance of relevant states, i.e., Definition 10 (-Approximate States). Given a deviation ε, is ε-approximate to iff .
Definition 11 (-Approximate Trajectories). Given a deviation ε and two trajectories and , is ε-approximate to iff .
Definition 12 (-Approximate Completed Trace Equivalence of ILAHS). Given a deviation ε, if all completed traces of two ILAHSs are ε-approximate trajectories, then the two ILAHSs are ε-approximate completed trace equivalence.
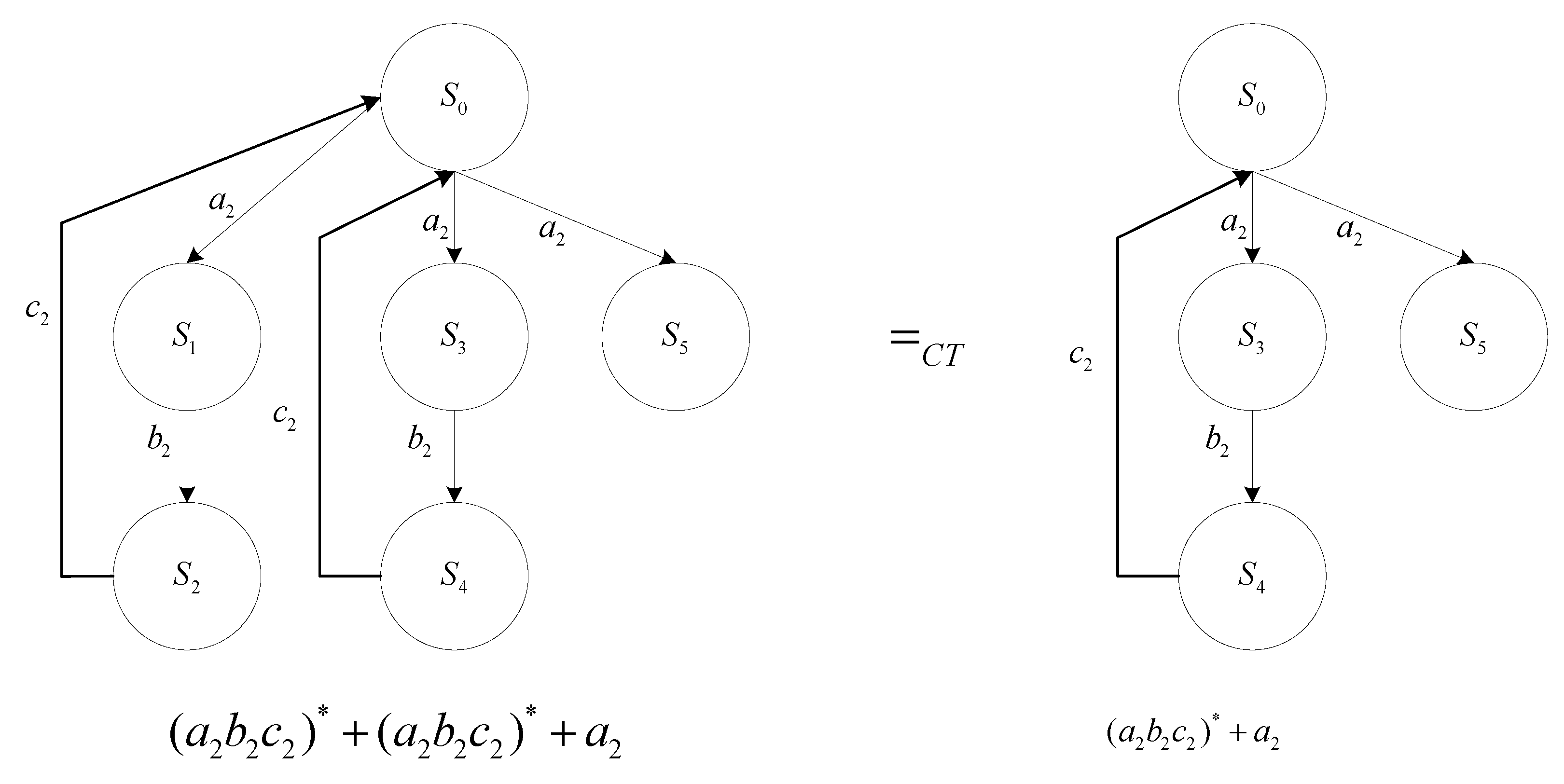
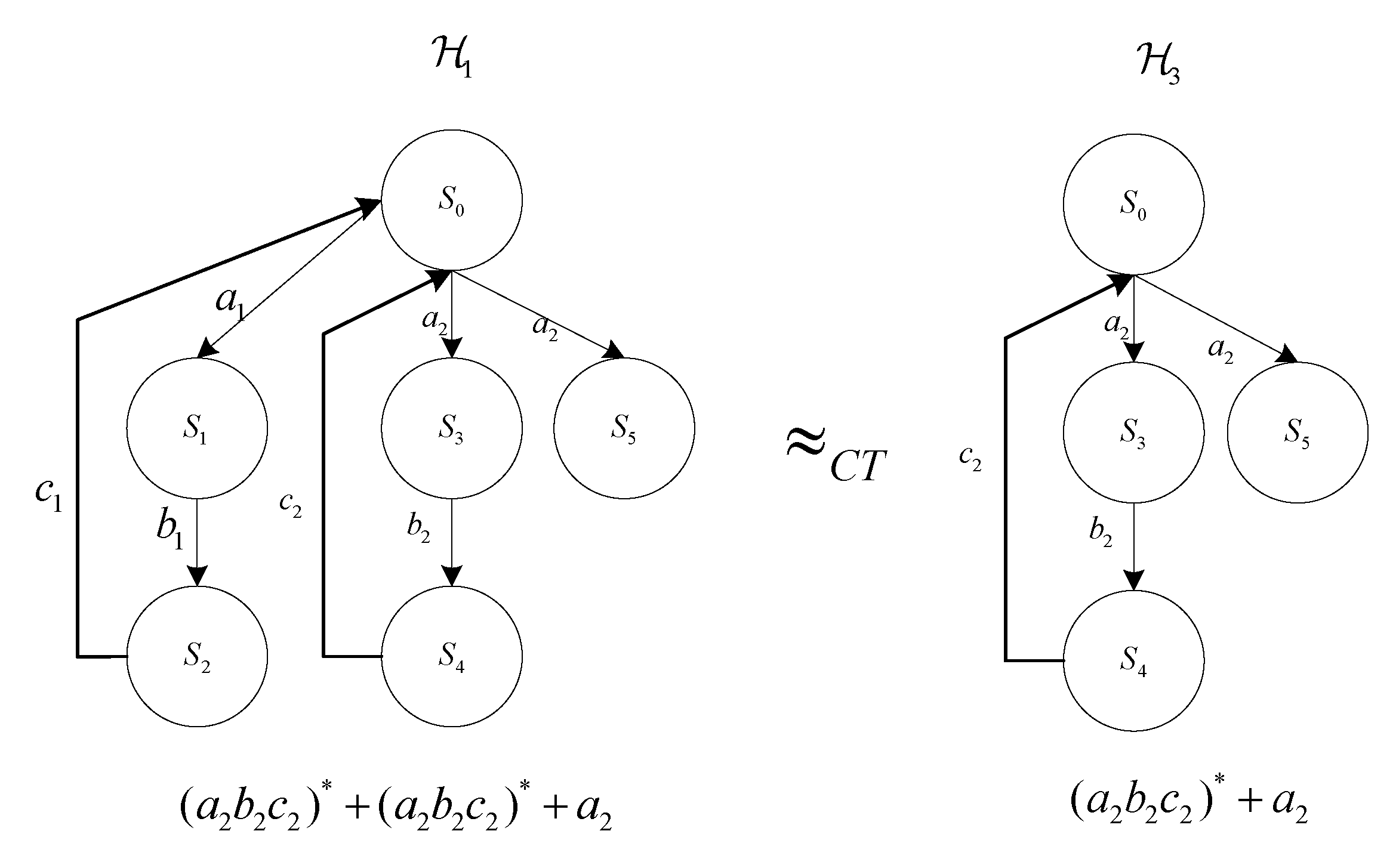
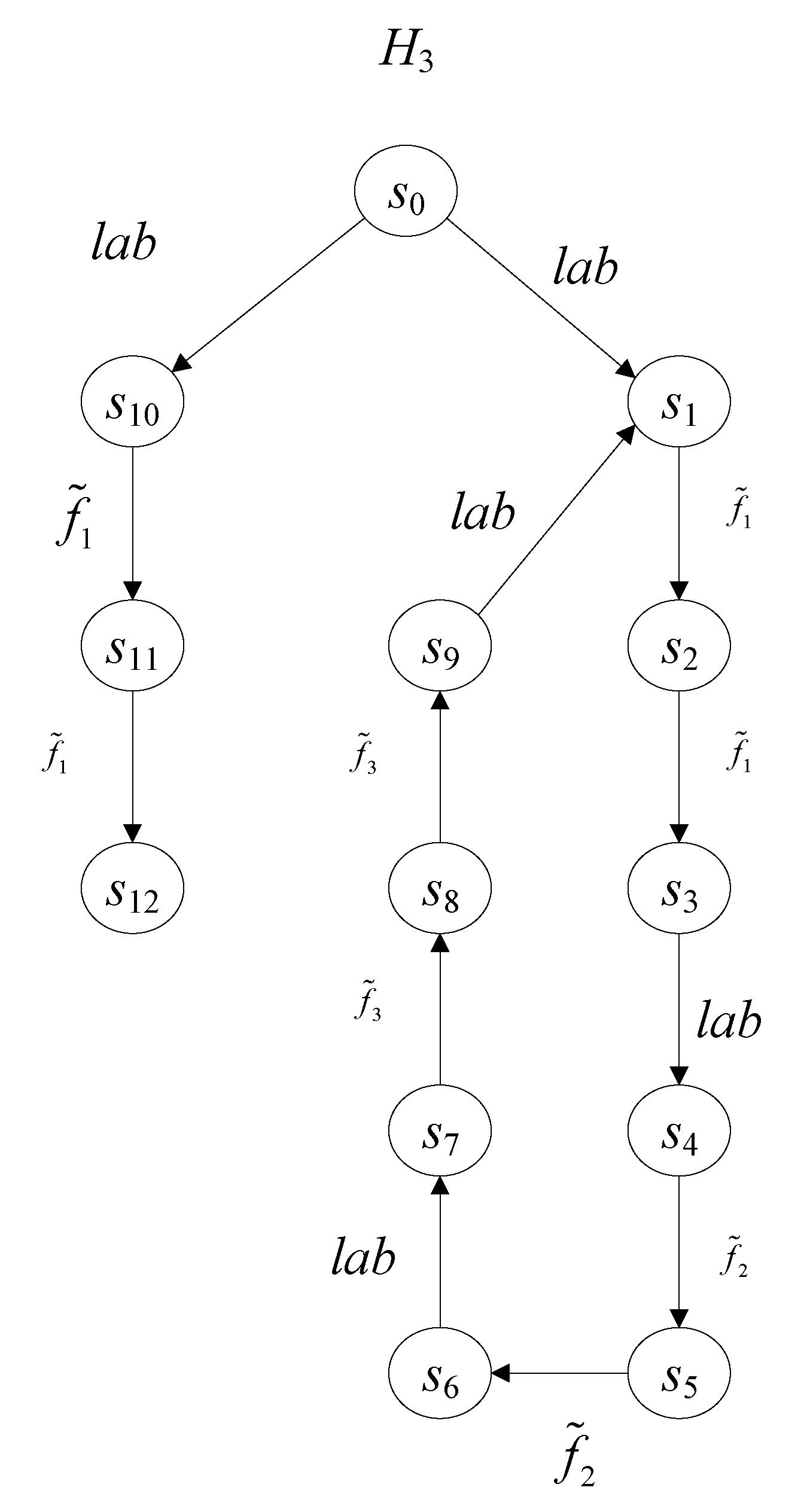
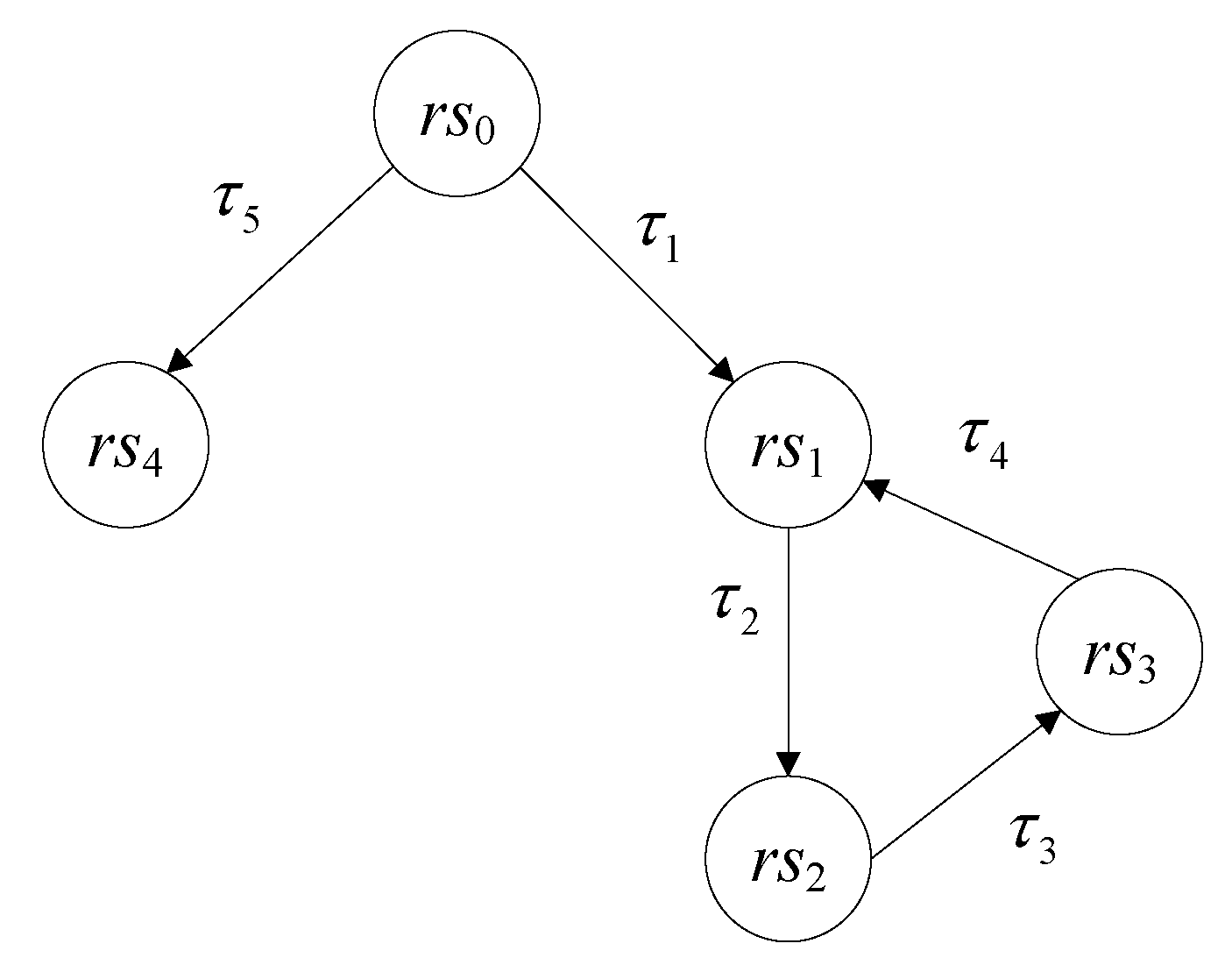
In
Figure 6,
is an original ILAHS, given a deviation
,
and
are completed trace equivalence, in the semantics of completed trace equivalence,
is identical to
.
Obviously, involves fewer states than ; in other words, by approximate completed trace equivalence, the research on hybrid systems can be simplified.
Since there exist two categories of trajectories in completed trace equivalence (
Figure 6), the infinite trajectory
and the finite trajectory
, there are two corresponding decision conditions, the finite trajectory condition and the infinite trajectory condition. For simplicity, assume discrete evolution such as
.
Definition 13 (Finite Trajectory Condition)
. For a finite trajectory such that The infinite trajectory condition is defined by the inductive method.
Definition 14 (Infinite Trajectory Condition)
. For an infinite trajectory such thatfor every , (8) and (9) have no solution. The condition Initiation shows that the deviation of two states is initially less than ; the condition Consecution shows that deviation less than is preserved by the loop.
Complexity Analysis: Take (
9) for example. Assuming
,
, our method consists of three main steps. In the first step, we transform the equations of (
9) into triangular sets (i.e., equations in the triangular form) by Ritt–Wu’s method. By [
35], the complexity of this step is
. The second step is to compute a border polynomial (BP) from the triangularized systems through resultant computation. By [
35], the complexity of computing the BP is at most
. Finally, we use the PCAD(partial cylindrical algebraic decomposition) algorithm with the BP to obtain the real solution classification; the complexity of this step is at most
, where
, the highest degree of BP.
A Special Case: The approaches proposed in papers [
4,
5,
24] use the Frobenius norm to study approximate equivalence of real-time linear algebraic hybrid automaton. Their approaches can only apply to a class of special matrices. We now prove that their approaches are a special case of our approach.
We first introduce the conclusions in their papers [
4,
5,
24].
For
and its approximate matrix
, which are
nonsingular matrices, the eigenvalues of matrix
A are
, and there exists an orthogonal matrix
U:
Then, for a deviation and , if are -approximate to , and , are -approximate to .
This conclusion is equivalent to (
11) ⊧ (
13) for an existing constant
.
Proof. ∴
i.e., for every
,
in other words, (
11) ⊧ (
13). □