A Novel Multi-Attribute Decision Making Method Based on The Double Hierarchy Hesitant Fuzzy Linguistic Generalized Power Aggregation Operator
Abstract
1. Introduction
2. Preliminaries
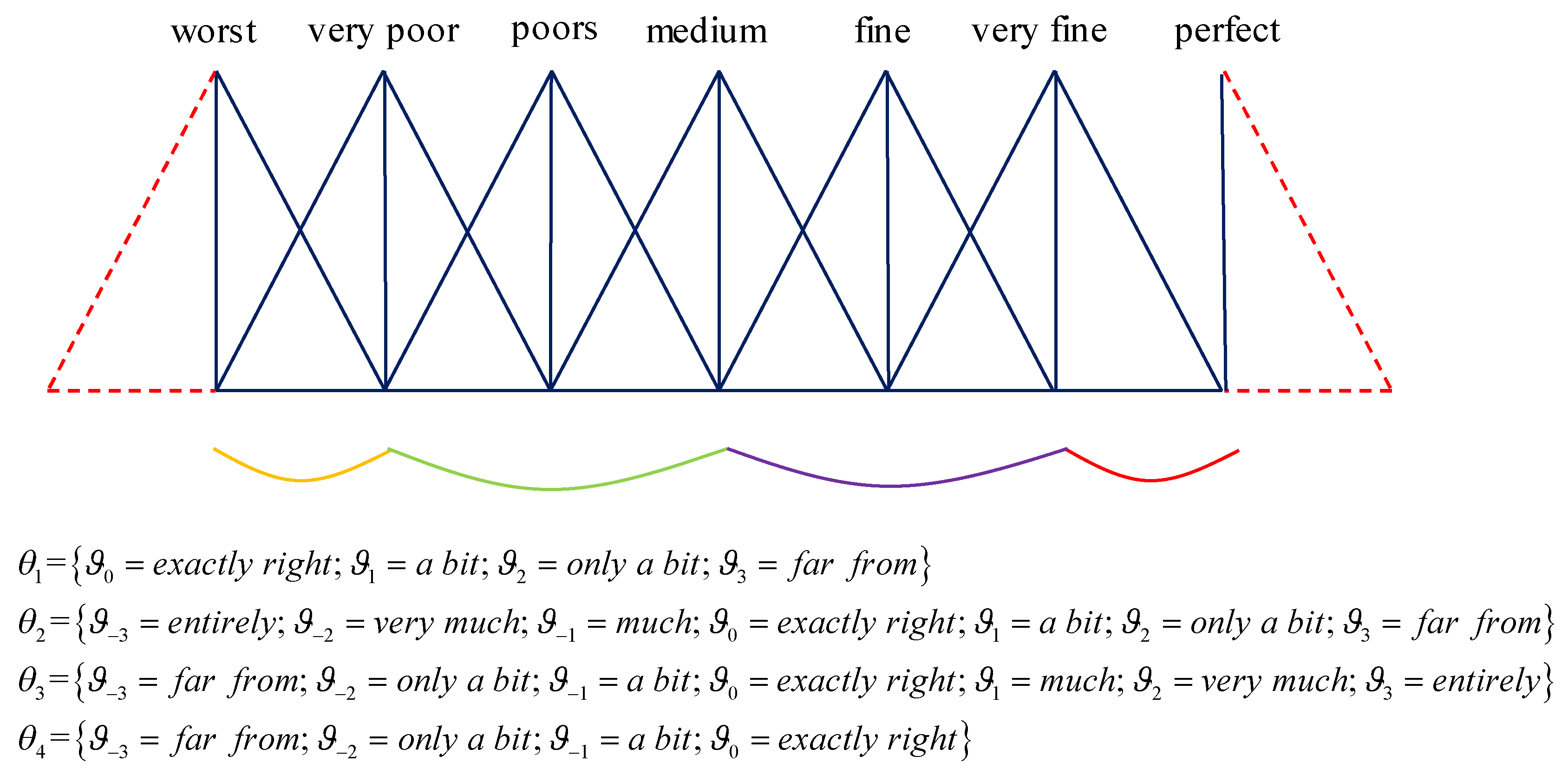
2.1. Double Hierarchy Hesitant Fuzzy Linguistic Term Set
- Supposethenis superior to
- Supposethenis indifference with
2.2. The Generalized Power Average (GPA) Operator
3. Double Hierarchy Hesitant Fuzzy Linguistic Generalized Power Aggregation Operators
3.1. DHHFLGPA Operator and Its Weight Form
3.2. DHHFLGPG Operator and Its Weight Form
4. The MADM Method Based on the Proposed Operator
5. Numerical Example
5.1. Decision Steps
5.2. Sensitivity Analysis
5.3. Comparative Analysis
- (1)
- The DHHFLTS is made up of two hierarchy LTSs, in which the SHLTS indicates a further explanation or elaborate presentation of a given LT contained in the first hierarchy LTS. In other words, several buttons are installed to the LT contained in the first hierarchy LTS to depict its true extent. Therefore, compared with HFLTS, the DHHFLTS can express information more comprehensively and accurately. For instance, when the DMs want to express their view “Between far from poor and much fine”, it is more precise to use the DHHFLTS than the HFLTS . Obviously, the DHHFLTS can depict the DM’s complex cognition and information more accurately.
- (2)
- The proposed operators take the support degree between any two inputs into consideration. When the evaluation value of alternatives under a certain attribute is closer, the attribute should be given a greater weight. Hence, the approaches can weaken the impact of unjustified extremum on the aggregation results. Additionally, the newly proposed operators are related to the parameter , which is given by the DMs on account of the extent of their adventure appetite. Nonetheless the HFLWA and HFLWG operators with the absence of any parameter thus fail to imitate the DM’s adventure preference. For the sake of further showing this advantage of proposed method, an example can be given as follows.
5.4. Availability Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nunić, Z. Evaluation and selection of Manufacturer PVC carpentry using FUCOM-MABAC model. ORESTA 2018, 1, 13–28. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Liu, P. Multiple attribute group decision making based on q-rung orthopair fuzzy Heronian mean operators. Int. J. Intell. Syst. 2018, 33, 2341–2363. [Google Scholar] [CrossRef]
- Pamučar, D.; Lukovac, V.; Božanić, D.; Komazec, N. Multi-criteria FUCOM-MAIRCA model for the evaluation of level crossings, case study in the Republic of Serbia. ORESTA 2018, 1, 108–129. [Google Scholar] [CrossRef]
- Fazlollahtabar, H.; Smailbašić, A.; Stević, Ž. FUCOM method in group decision-making, Selection of forklift in a warehouse. Decis. Mak. Appl. Manag. Eng. 2019, 2, 49–65. [Google Scholar] [CrossRef]
- Vesković, S.; Stević, Ž.; Stojić, G.; Vasiljević, M.; Milinković, S. Evaluation of the railway management model by using a new integrated model DELPHI-SWARA-MABAC. Decis. Mak. Appl. Manag. Eng. 2018, 1, 34–50. [Google Scholar] [CrossRef]
- Karabasevic, D.; Popovic, G.; Stanujkic, D.; Maksimovic, M.; Sava, C. An approach for hotel type selection based on the single-valued intuitionistic fuzzy numbers. CO Publ. 2019, 1–2, 7. [Google Scholar]
- Liu, Z.; Li, L.; Li, J. q-Rung orthopair uncertain linguistic partitioned Bonferroni mean operators and its application to multiple attribute decision-making method. Int. J. Intell. Syst. 2019, 34, 2490–2520. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.; Liang, X. Multiple attribute decision-making method for dealing with heterogeneous relationship among attributes and unknown attribute weight information under q-rung orthopair fuzzy environment. Int. J. Intell. Syst. 2018, 33, 1900–1928. [Google Scholar] [CrossRef]
- Levrat, E.; Voisin, A.; Bombardier, S. Subjective evaluation of car seat comfort with fuzzy set techniques. Int. J. Intell. Syst. 1997, 12, 891–913. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mizumoto, M.; Tanaka, K. Some properties of fuzzy sets of type 2. Inf. Control 1976, 31, 312–340. [Google Scholar] [CrossRef]
- Martinez, L.; Herrera, F. An overview on the 2-tuple linguistic model for computing with words in decision making, Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Gou, X.; Liao, H.; Xu, Z. Double hierarchy hesitant fuzzy linguistic term set and MULTIMOORA method, A case of study to evaluate the implementation status of haze controlling measures. Inf. Fusion 2017, 38, 22–34. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Distance and similarity measures for hesitant fuzzy linguistic termets and their application in multi-criteria decision making. Inf. Sci. 2014, 271, 125–142. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Herrera-Viedma, E.; Herrera, F. Hesitant fuzzy linguistic term set and its application in decision making, a state-of-the-art survey. Int. J. Fuzzy Syst. 2018, 20, 2084–2110. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.; Liao, H. Multiple criteria decision making based on Bonferroni means with hesitant fuzzy linguistic information. Soft Comput. 2017, 21, 6515–6529. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, C. On the use of multiplicative consistency in hesitant fuzzy linguistic preference relations. Knowl. Based Syst. 2014, 72, 13–27. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Chen, Q. An outranking approach for multi-criteria decision-making with hesitant fuzzy linguistic term sets. Inf. Sci. 2014, 280, 338–351. [Google Scholar] [CrossRef]
- Liao, H.; Gou, X.; Xu, Z.; Zeng, X.J.; Herrera, F. Hesitancy degree-based correlation measures for hesitant fuzzy linguistic term sets and their applications in multiple criteria decision making. Inf. Sci. 2020, 508, 275–292. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.; Liao, H. Multiple criteria decision making based on distance and similarity measures under double hierarchy hesitant fuzzy linguistic environment. Comput. Ind. Eng. 2018, 126, 516–530. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.; Herrera, F. Consensus reaching process for large-scale group decision making with double hierarchy hesitant fuzzy linguistic preference relations. Knowl. Based Syst. 2018, 157, 20–33. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Qu, Q. Double Hierarchy Hesitant Fuzzy Linguistic Mathematical Programming Method for MAGDM Based on Shapley Values and Incomplete Preference Information. IEEE Access 2018, 6, 74162–74179. [Google Scholar] [CrossRef]
- Krishankmar, R.; Subrajaa, L.S.; Ravichandran, K.S.A. Framework for Multi-Attribute Group Decision-Making Using Double Hierarchy Hesitant Fuzzy Linguistic Term Set. Int. J. Fuzzy Syst. 2019, 21, 1130–1143. [Google Scholar] [CrossRef]
- Wang, J.; Lu, J.P.; Wei, G.; Lin, R.; Wei, C. Models for MADM with Single-Valued Neutrosophic 2-Tuple Linguistic Muirhead Mean Operators. Mathematics 2019, 7, 442. [Google Scholar] [CrossRef]
- He, J.H.; Wang, X.D.; Zhang, R.T.; Li, L. Some q-Rung Picture Fuzzy Dombi Hamy Mean Operators with Their Application to Project Assessment. Mathematics 2019, 7, 468. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P. Intuitionistic uncertain linguistic partitioned Bonferroni means and their application to multiple attribute decision-making. Int. J. Syst. Sci. 2017, 48, 1092–1105. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Cardinal, W. Individualistic ethics, and interpersonal comparisons of utility. J. Political Econ. 1955, 63, 309–321. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions, A Guide for Practitioners; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Bonferroni, C. Sulle medie multiple di potenze. Boll. Dell’unione Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Yager, R.R. The power average operator. IEEE Trans. Syst. Man Cybern. A 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, H.; Liu, J. Generalized power aggregation operators and their applications in group decision making. Comput. Ind. Eng. 2012, 62, 989–999. [Google Scholar] [CrossRef]
- Liu, P.; Wang, Y. Multiple attribute group decision making methods based on intuitionistic linguistic power generalized aggregation operators. Appl. Soft Comput. 2014, 17, 90–104. [Google Scholar] [CrossRef]
- Liu, P.; Yu, X. 2-Dimension uncertain linguistic power generalized weighted aggregation operator and its application in multiple attribute group decision making. Knowl. Based Syst. 2014, 57, 69–80. [Google Scholar] [CrossRef]
- Liu, P.; Liu, Y. An approach to multiple attribute group decision making based on intuitionistic trapezoidal fuzzy power generalized aggregation operator. Int. J. Comput. Int. Syst. 2014, 7, 291–304. [Google Scholar] [CrossRef]
- Wu, Q.; Wu, P.; Zhou, Y. Some 2-tuple linguistic generalized power aggregation operators and their applications to multiple attribute group decision making. J. Intell. Fuzzy Syst. 2015, 29, 423–436. [Google Scholar] [CrossRef]
- Zhang, Z. Hesitant fuzzy power aggregation operators and their application to multiple attribute group decision making. Inf. Sci. 2013, 234, 150–181. [Google Scholar] [CrossRef]
- Wang, X.; Triantaphyllou, E. Ranking irregularities when evaluating alternatives by using some ELECTRE methods. Omega 2008, 36, 45–63. [Google Scholar] [CrossRef]
- Xu, X.; Hao, J.; Yu, L.; Deng, Y. Fuzzy Optimal Allocation Model for Task-Resource Assignment Problem in Collaborative Logistics Network. IEEE Trans. Fuzzy Syst. 2019, 27, 1112–1125. [Google Scholar] [CrossRef]
| 0.2583 | 0.0722 | 0.3111 | |
| 0.1917 | 0.0611 | 0.2333 | |
| 0.1833 | 0.0639 | 0.2111 | |
| 0.1083 | 0.0333 | 0.1667 |
| 0.1722 | 0.0750 | 0.3222 | |
| 0.1278 | 0.0972 | 0.3778 | |
| 0.1222 | 0.0972 | 0.3667 | |
| 0.0722 | 0.0972 | 0.3778 |
| 0.1444 | 0.2250 | 0.3778 | |
| 0.1222 | 0.2917 | 0.3889 | |
| 0.1278 | 0.2917 | 0.3556 | |
| 0.0667 | 0.2917 | 0.3667 |
| 0.1556 | 0.2417 | 0.0944 | |
| 0.1167 | 0.2833 | 0.0972 | |
| 0.1056 | 0.2750 | 0.0889 | |
| 0.0833 | 0.2833 | 0.0917 |
| Ranking | ||
|---|---|---|
| Operator | Expected/Score Values | Ranking |
|---|---|---|
| Operators | Expected/Score Values | Ranking |
|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhao, X.; Li, L.; Wang, X.; Wang, D. A Novel Multi-Attribute Decision Making Method Based on The Double Hierarchy Hesitant Fuzzy Linguistic Generalized Power Aggregation Operator. Information 2019, 10, 339. https://doi.org/10.3390/info10110339
Liu Z, Zhao X, Li L, Wang X, Wang D. A Novel Multi-Attribute Decision Making Method Based on The Double Hierarchy Hesitant Fuzzy Linguistic Generalized Power Aggregation Operator. Information. 2019; 10(11):339. https://doi.org/10.3390/info10110339
Chicago/Turabian StyleLiu, Zhengmin, Xiaolan Zhao, Lin Li, Xinya Wang, and Di Wang. 2019. "A Novel Multi-Attribute Decision Making Method Based on The Double Hierarchy Hesitant Fuzzy Linguistic Generalized Power Aggregation Operator" Information 10, no. 11: 339. https://doi.org/10.3390/info10110339
APA StyleLiu, Z., Zhao, X., Li, L., Wang, X., & Wang, D. (2019). A Novel Multi-Attribute Decision Making Method Based on The Double Hierarchy Hesitant Fuzzy Linguistic Generalized Power Aggregation Operator. Information, 10(11), 339. https://doi.org/10.3390/info10110339




