Efficient Detection of Ventricular Late Potentials on ECG Signals Based on Wavelet Denoising and SVM Classification
Abstract
1. Introduction
2. Prior Research
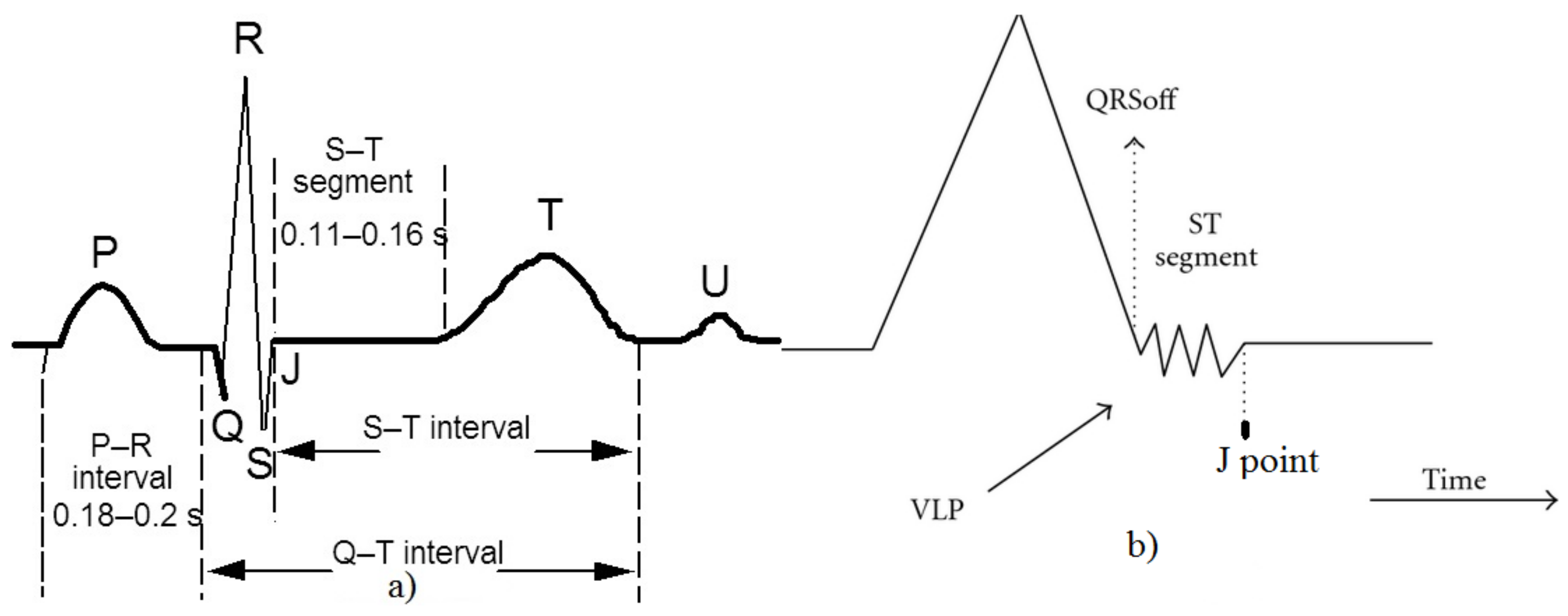
3. Ventricular Late Potential Characteristics
4. Techniques Adopted for the Method Implementation
4.1. Wavelet Transform
4.2. Support Vector Machine
- x ∈ Rn as a vector which represents a pattern to be classified;
- y as a scalar which represents the class label (i.e., y ∈ {±1});
- S = {(xi, yi); I = 1, 2, …, l} for a given set of l training examples.
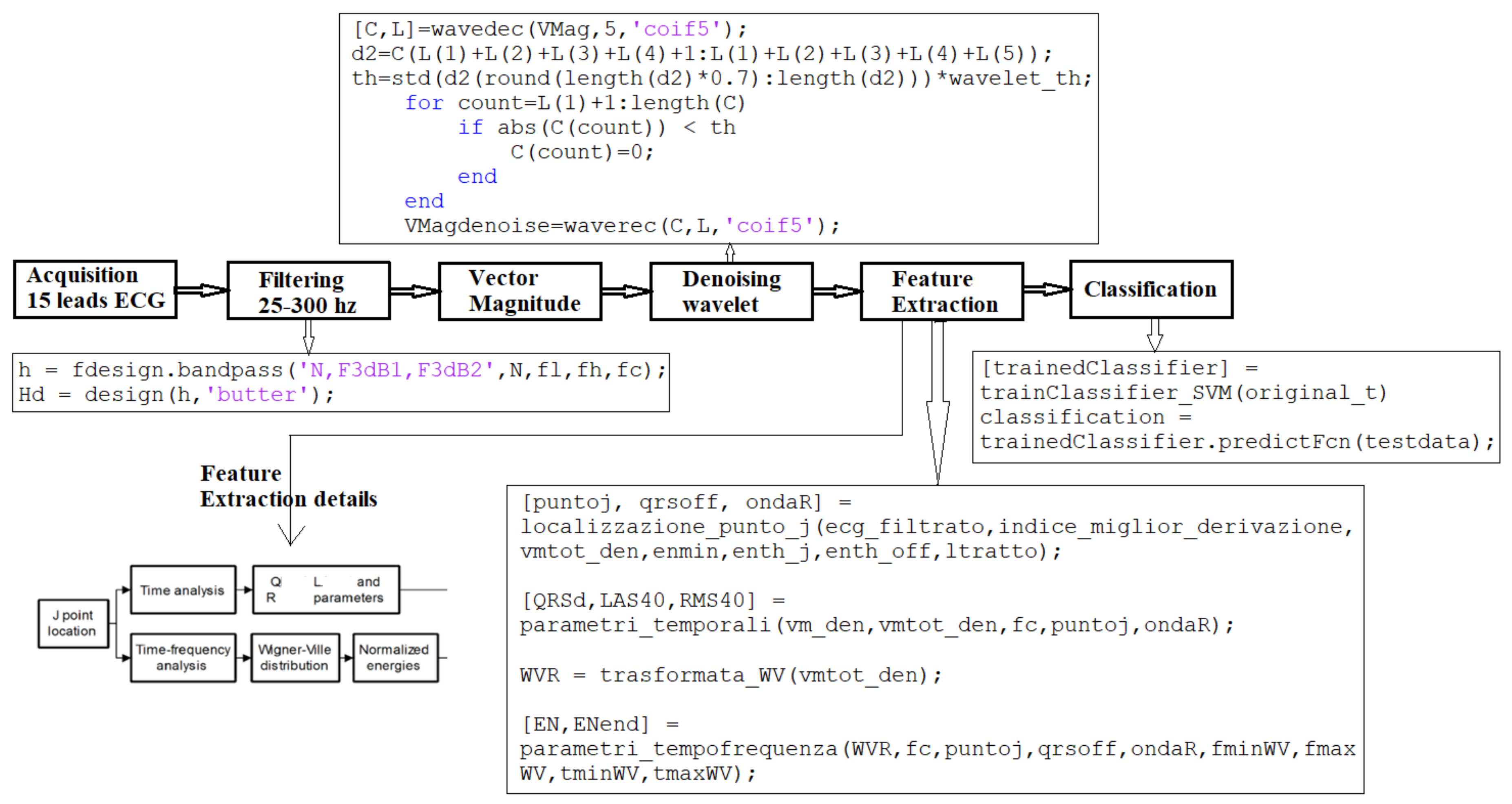
5. Developed Method for VLP Detection
5.1. Step I: Signal Preprocessing
5.1.1. Filtering
- remove both the DC component and the signal wandering due to low frequency terms;
- limit the noise energy by restricting the bandwidth of the acquired HR-ECG signal to the components of interest.
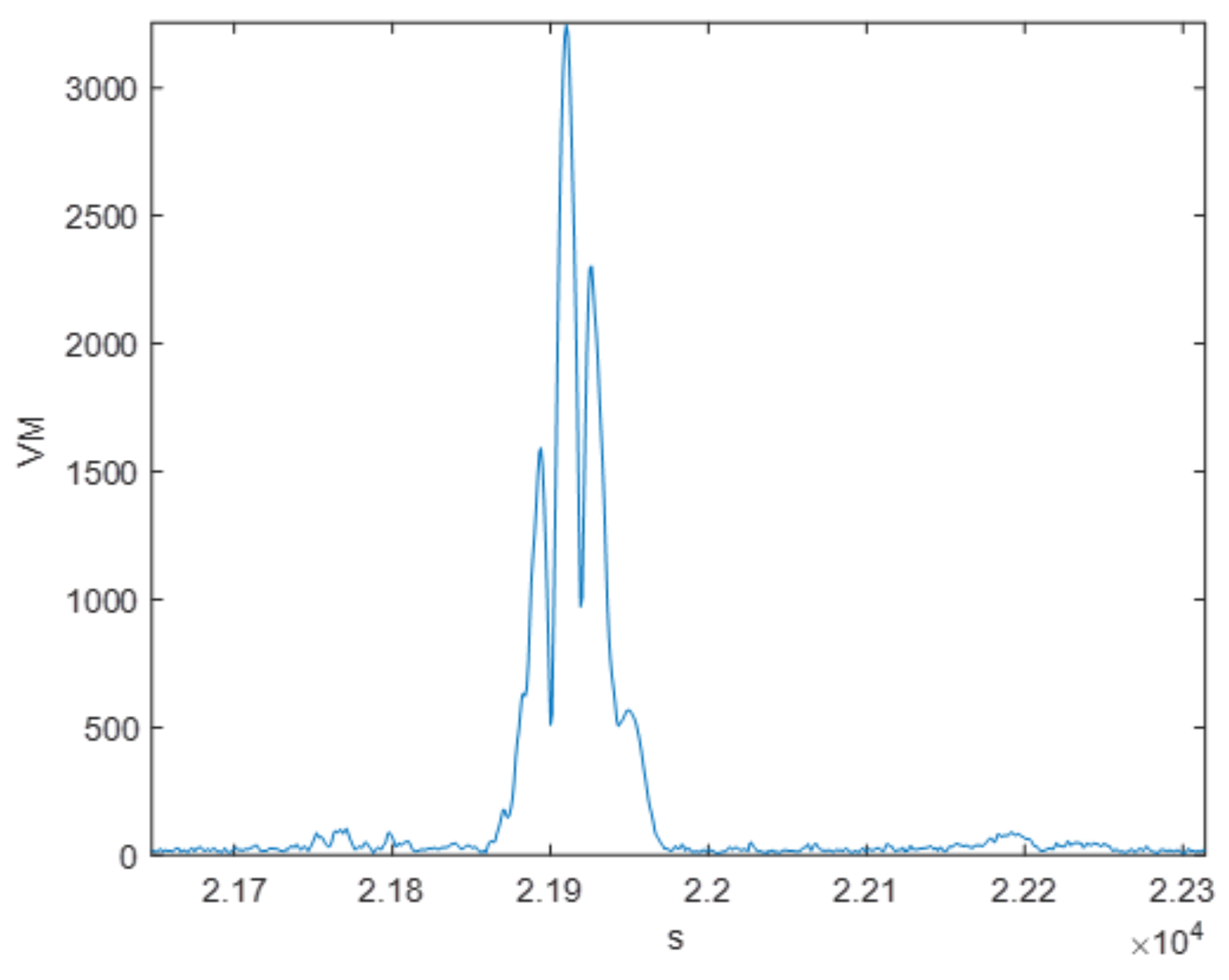
5.1.2. Vector Magnitude Evaluation
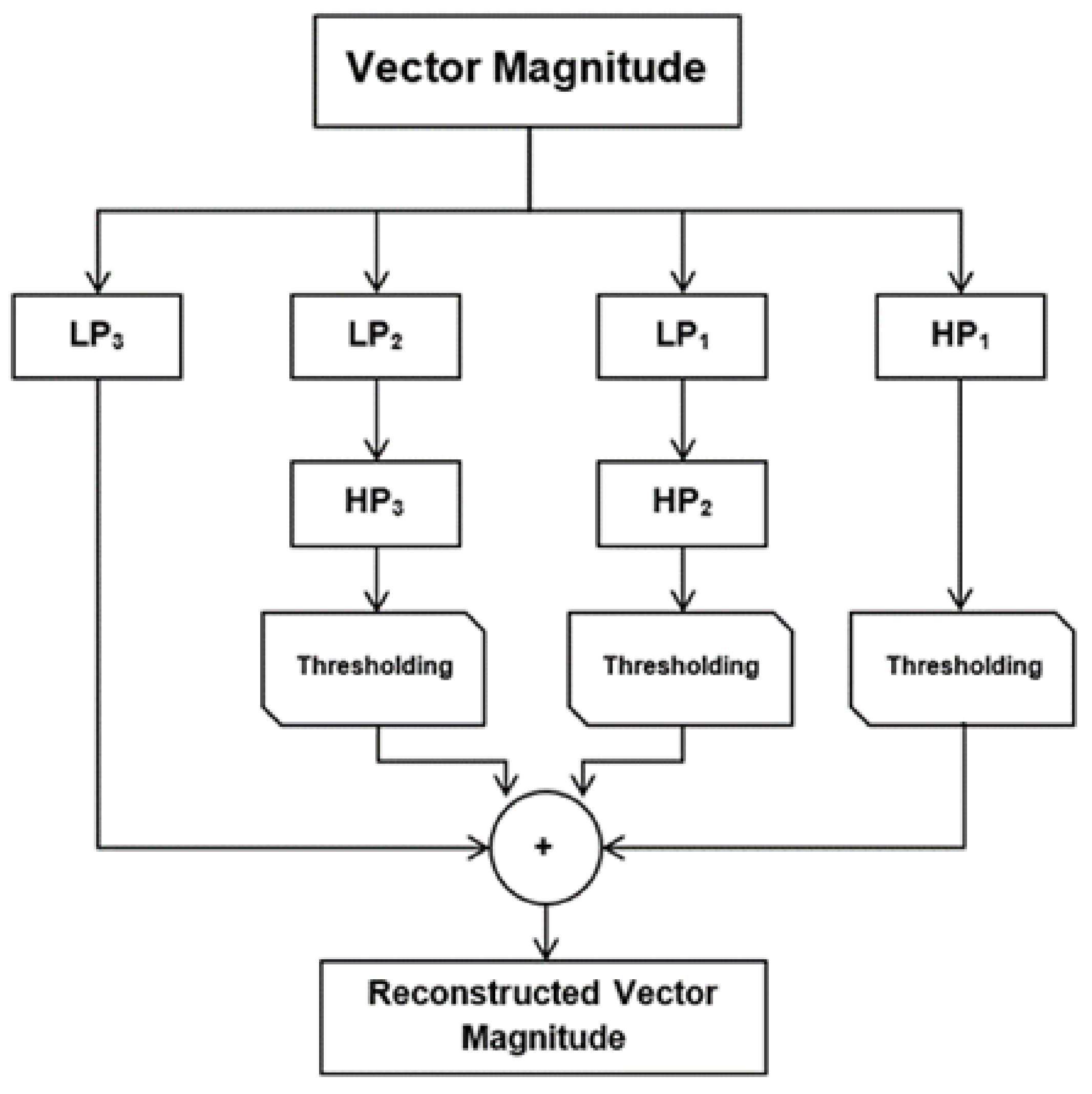
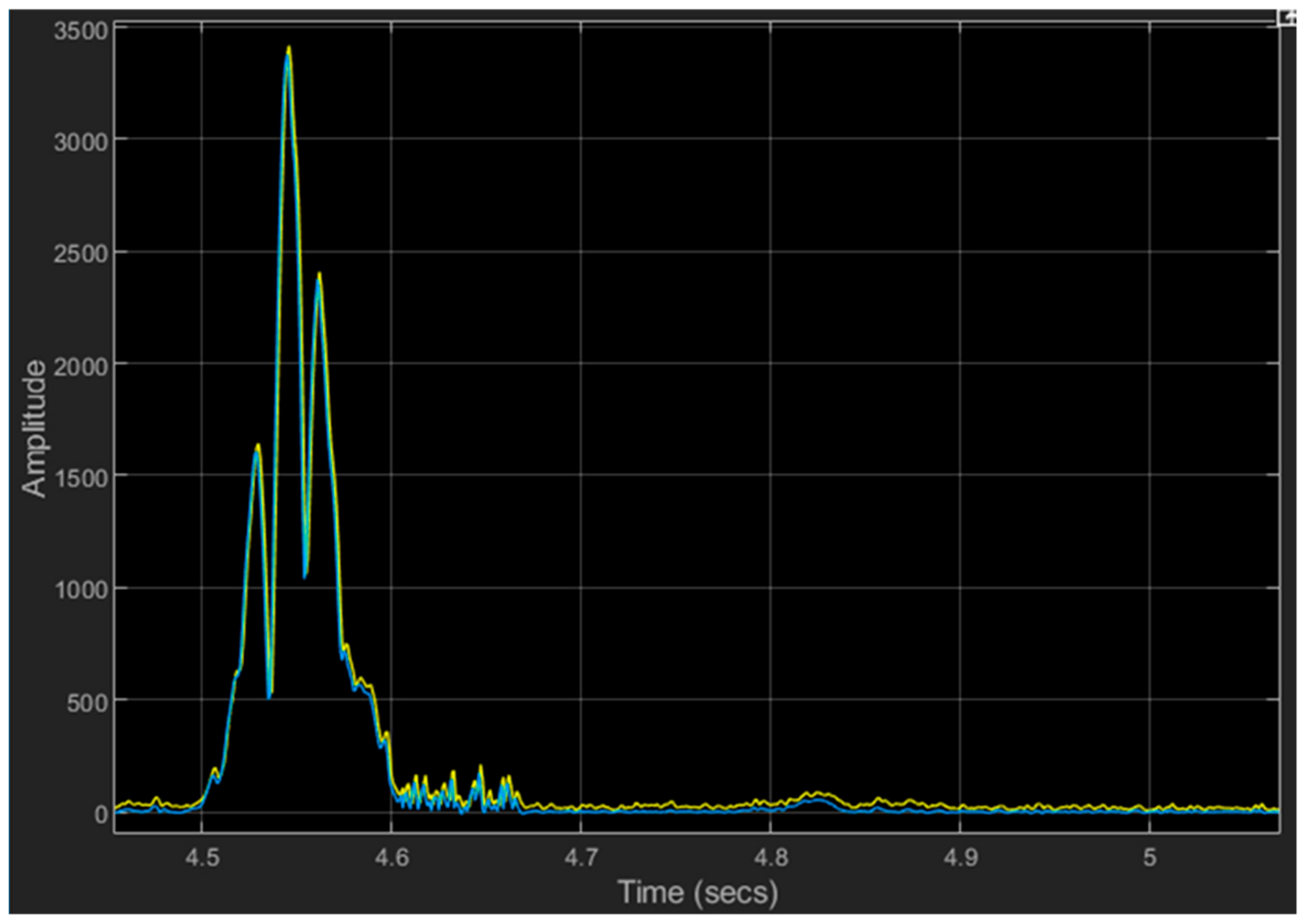
5.1.3. Wavelet Denoising
5.2. Step II: Feature Extraction
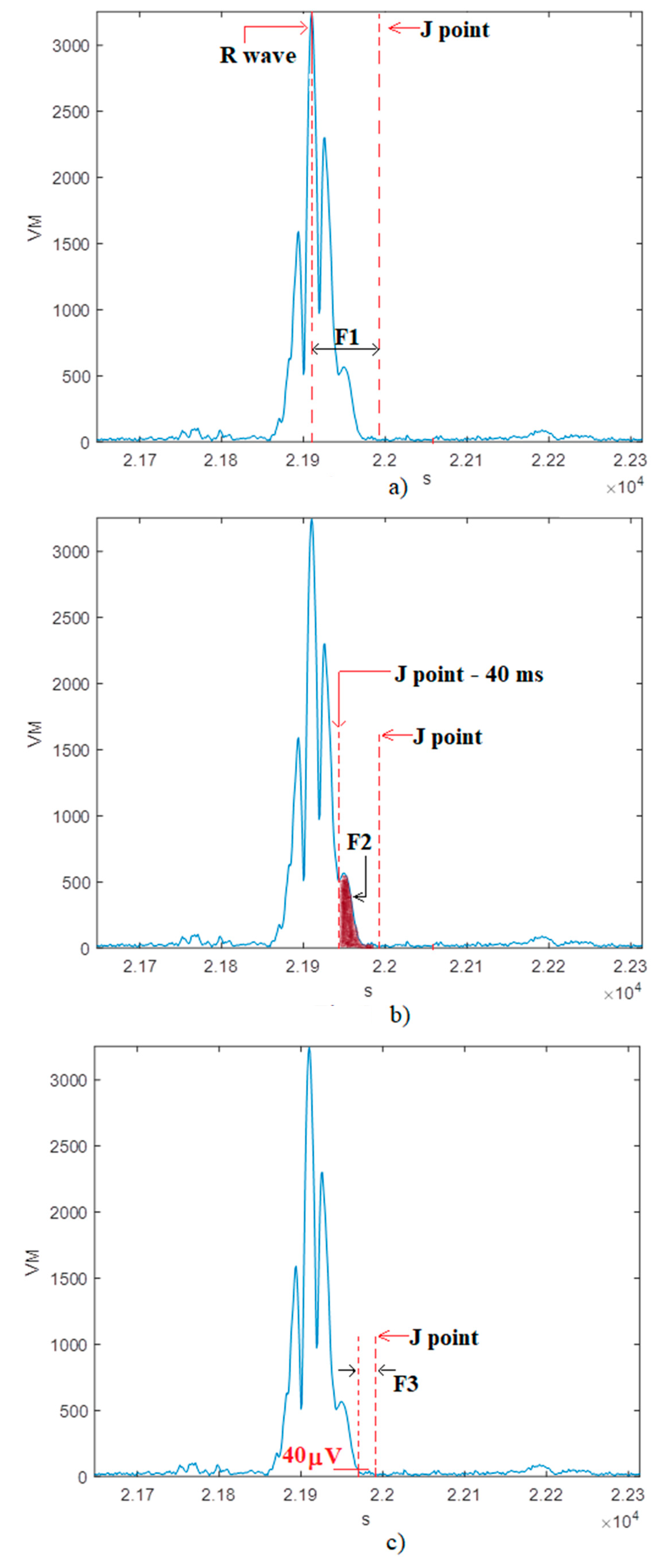
- F1: time lag between the R peak and the J point;
- F2: root mean square voltage of the terminal 40 ms of the QRS complex;
- F3: amount of time during which the QRS complex remains below 40 µV;
- F4: EVLP/EQRS;
- F5: EEND/EQRS.
- EEND is the energy calculated in an area next to the QRSoff point;
- EQRS is the energy of the QRS complex;
- EVLP is the energy of the VLP.
- QRSoff is the end of the QRS complex;
- TFR is the two-dimensional matrix resulting from the Wigner Ville distribution of the signal [55];
- ki is a normalization parameter defined as the product between the row and column numbers of the considered region in the TFR matrix;
- tmin = J point − 55 ms;
- tmax = J point + 25 ms;
- fmin = 55 Hz;
- fmax = 300 Hz;
5.3. Step III: Classification
6. Performance Evaluation
6.1. Database Used as Test Bench
6.2. Evaluation Parameters
- TP (number of true positives) is the number of correct identifications of VLPs inside the HR-ECG record under test;
- FN (the number of false negatives) is the number of VLPs present in the HR-ECG that the algorithm is not able to detect;
- FP (the number of false positives) is the number of VLPs detected by the algorithm but are actually not present in the HR-ECG;
- TN (the number of true negatives) is the number of HR-ECG records that the procedure considers without VLPs that actually do not have VLPs.
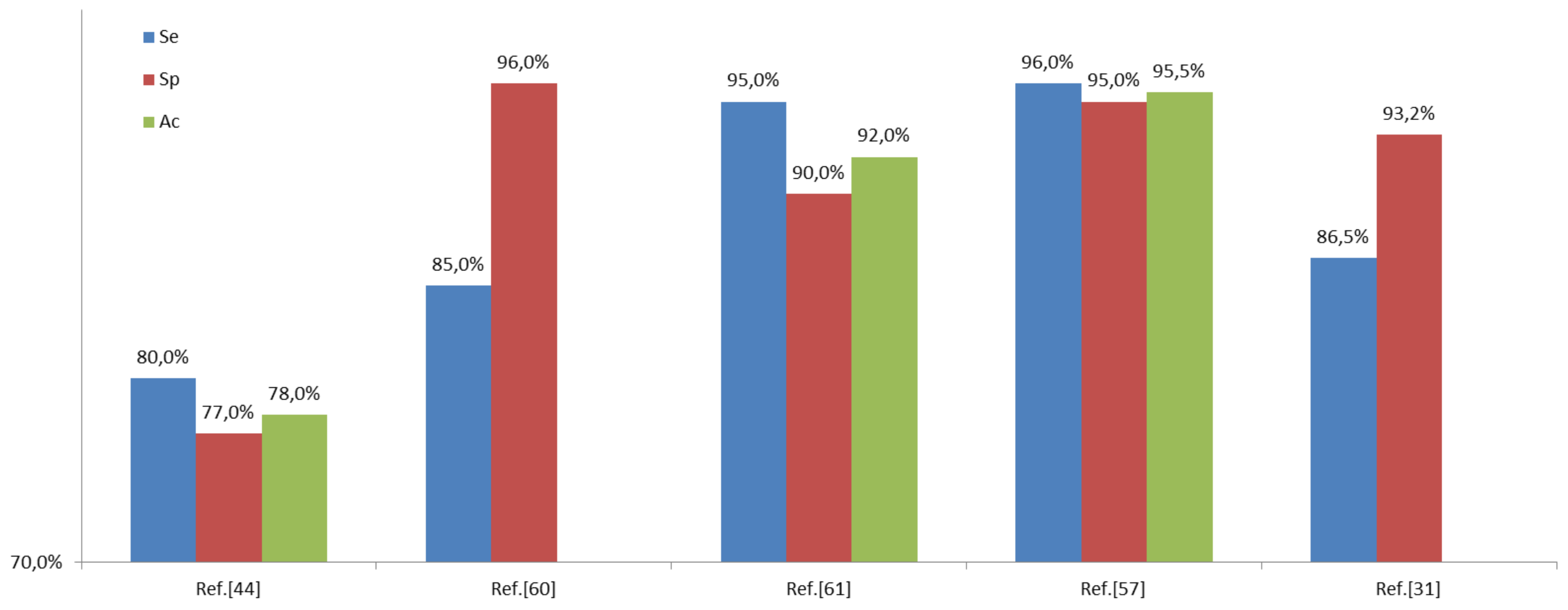
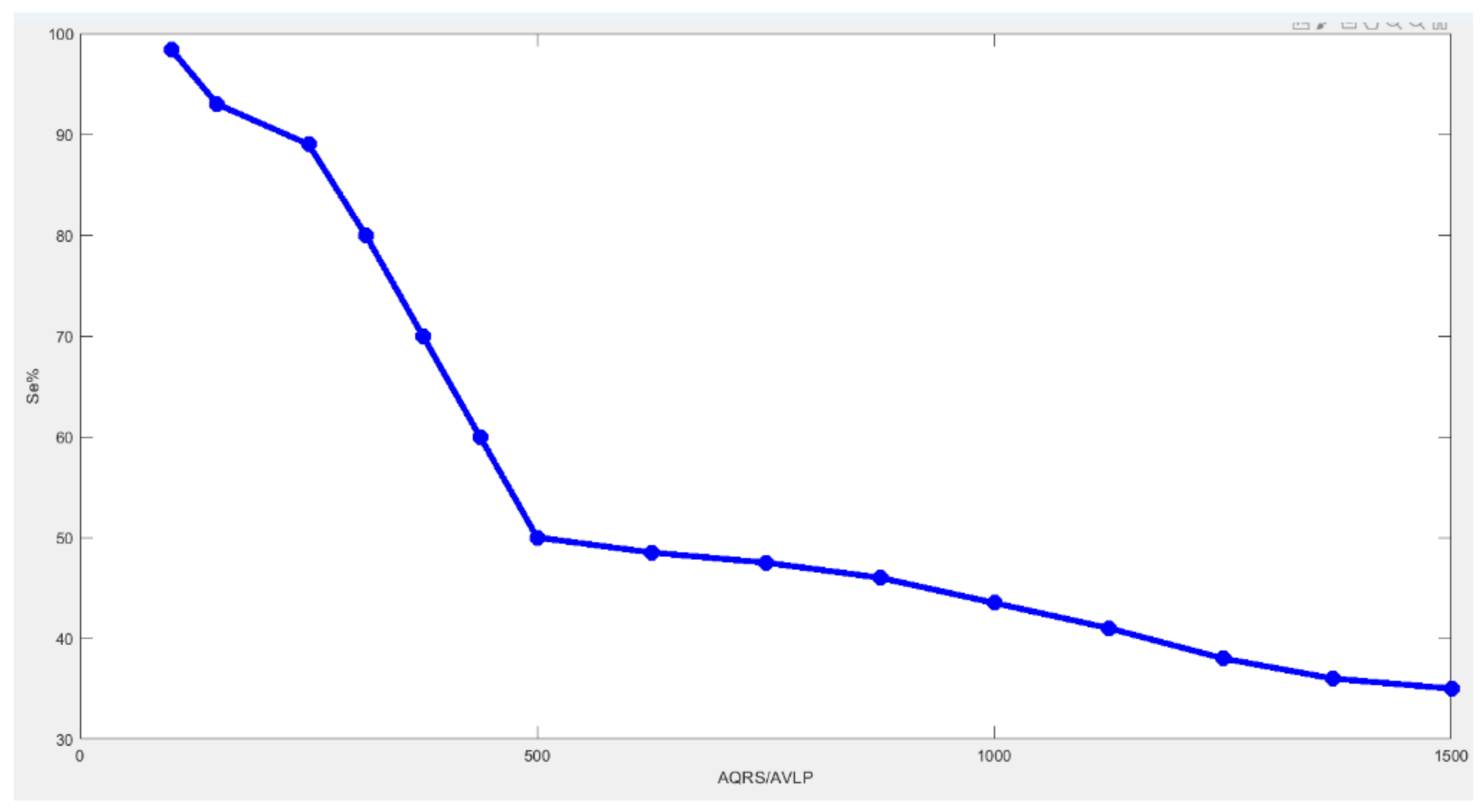
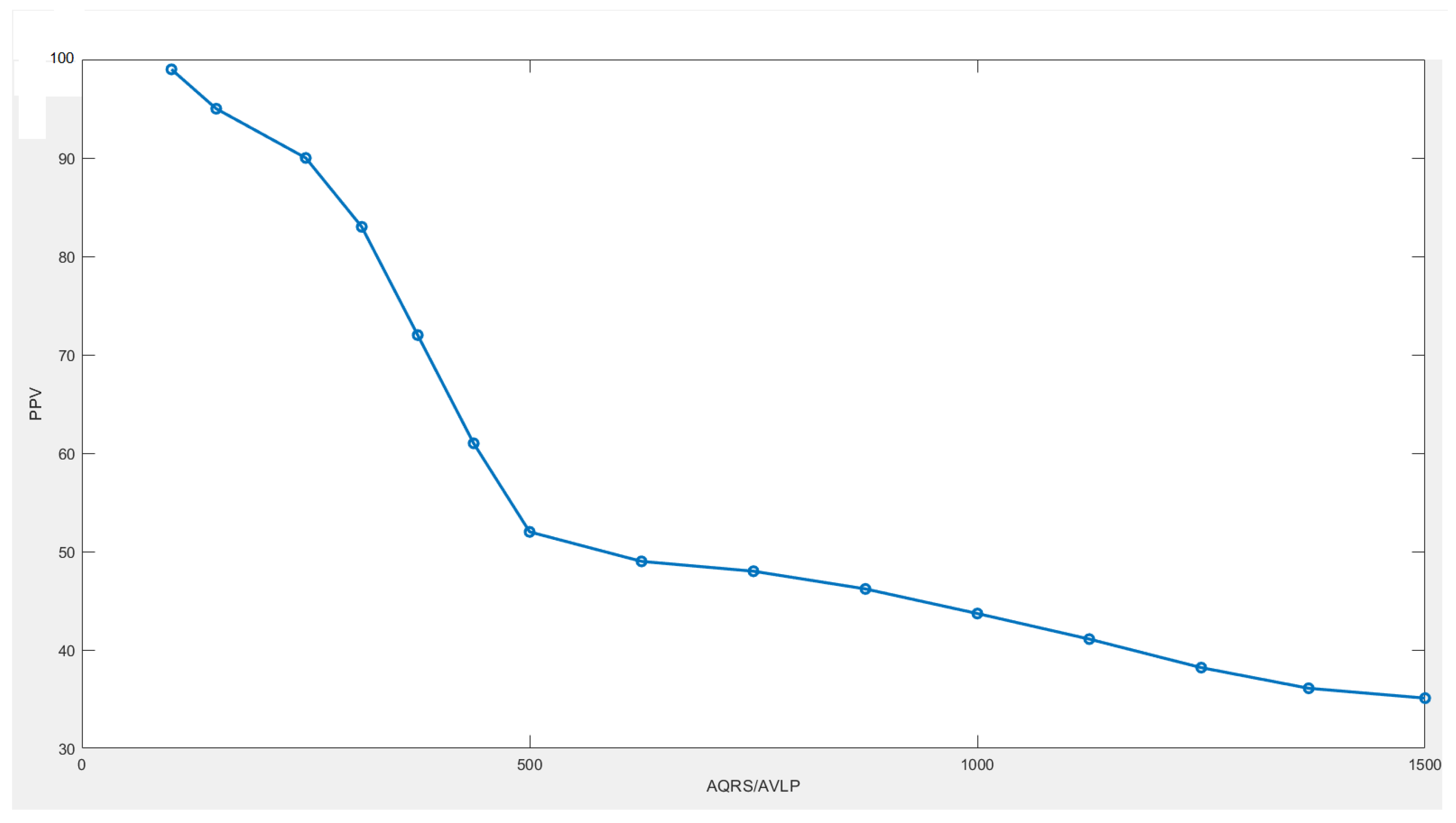
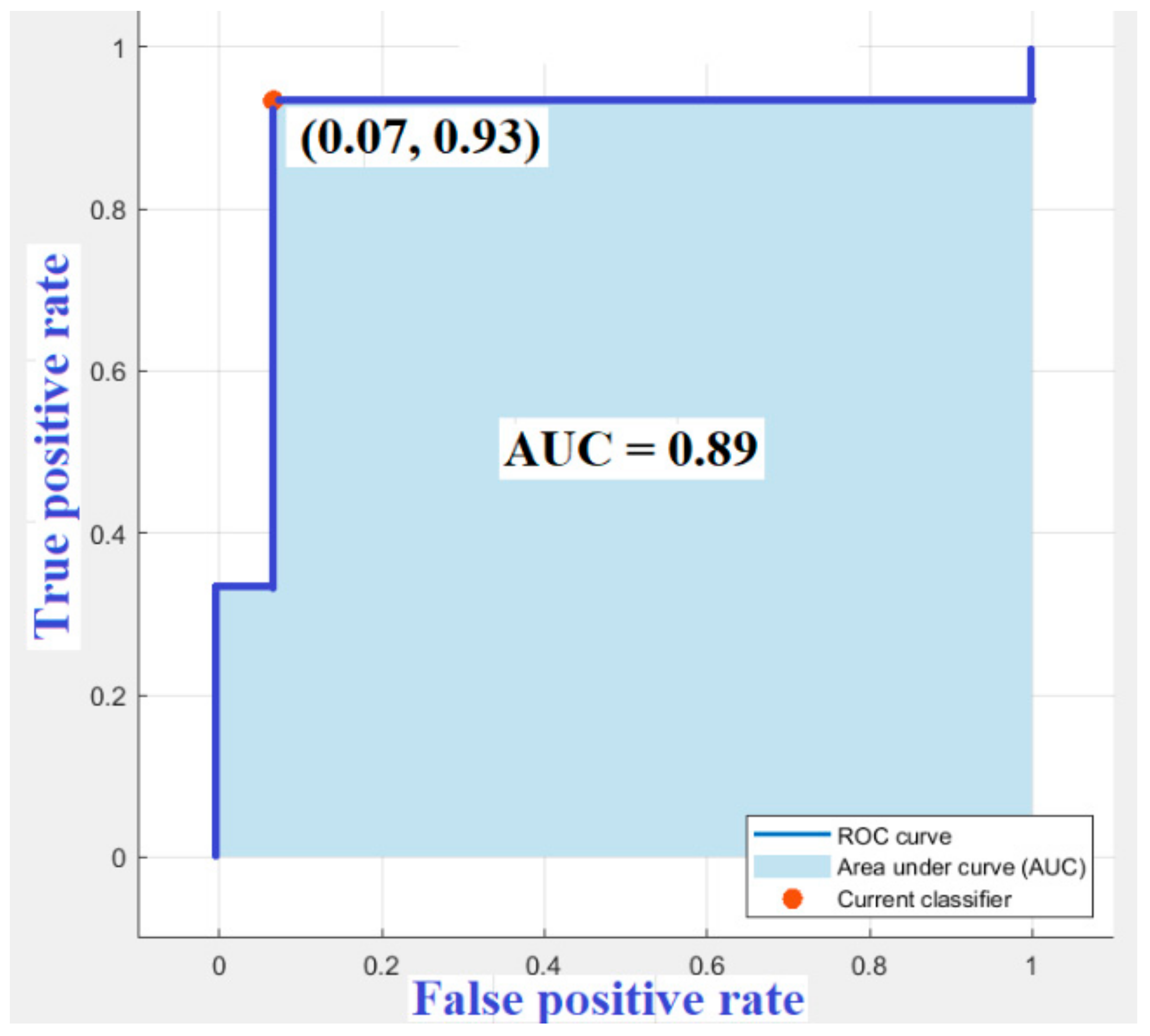
6.3. Results
7. Discussions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Impedovo, D.; Pirlo, G. eHealth and artificial intelligence. Information 2019, 10, 117. [Google Scholar] [CrossRef]
- Giorgio, A.; Guaragnella, C. ECG Signal Denoising using Wavelet for the VLP effective detection on FPGA. In Proceedings of the AEIT 2018, Bari, Italy, 3–5 October 2018. [Google Scholar]
- Baumann, B. Polarization sensitive optical coherence tomography: A review of technology and applications. Appl. Sci. 2017, 7, 474. [Google Scholar] [CrossRef]
- Rizzi, M.; D’aloia, M.; Cice, G. Computer aided evaluation (CAE) of morphologic changes in pigmented skin lesions. Lect. Notes Comput. Sci. 2015, 9281, 250–257. [Google Scholar]
- Brem, R. Potential Benefits of Computer-Aided Detection for Cancer Identification and Treatment. JAMA Intern. Med. 2016, 176, 410. [Google Scholar] [CrossRef]
- D’Aloia, M.; Cortone, F.; Cice, G.; Russo, R.; Rizzi, M.; Longo, A. Improving energy efficiency in building system using a novel people localization system. In Proceedings of the 2016 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS), Bari, Italy, 13–14 June 2016; pp. 1–6. [Google Scholar]
- Qin, C.; Yao, D.; Shi, Y.; Song, Z. Computer-aided detection in chest radiography based on artificial intelligence: A survey. BioMed. Eng. Online 2018, 17, 113–136. [Google Scholar] [CrossRef]
- Rizzi, M.; D’Aloia, M. Computer aided system for breast cancer diagnosis. Biomed. Eng. Appl. Basis Commun. 2014, 26, 3–11. [Google Scholar] [CrossRef]
- Rejdak, K.; Rubaj, A.; Głowniak, A.; Furmanek, K.; Kutarski, A.; Wysokiński, A.; Stelmasiak, Z. Analysis of ventricular late potentials in signal–averaged ECG of people with epilepsy. Epilepsia 2011, 52, 2118–2124. [Google Scholar] [CrossRef]
- Giorgio, A. Health panel: A platform useful to physicians for fast and easy managing of FPGA-based medical devices. IJMEI 2019, 11, 116–151. [Google Scholar] [CrossRef]
- Santangeli, P.; Infusino, F.; Sgueglia, G.A.; Sestito, A.; Lanza, G.A. Ventricular late potentials: A critical overview and current applications. J. Electrocardiol. 2008, 4, 318–324. [Google Scholar] [CrossRef]
- Wang, J.; Sui, X.T.; Sun, Y.X.; Li, Y.; Yang, G.; Xu, F.; Zhang, Y.L.; Zhang, X.G. Differences of Ventricular Late Potential between Acute STEMI and NSTEMI Patients. West Indian Med. J. 2013, 62, 721–723. [Google Scholar]
- Lutfi, M.F. Ventricular late potential in cardiac syndrome X compared to coronary artery disease. BMC Cardiovasc. Disord. 2017, 17, 35–40. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tatsumi, H.; Takagi, M.; Nakagawa, E.; Yamashita, H.; Yoshiyama, M. Risk stratification in patients with Brugada syndrome: analysis of daily fluctuations in 12-lead electrocardiogram (ECG) and signal-averaged electrocardiogram (SAECG). J. Cardiovasc. Electrophysiol. 2006, 17, 705–711. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, A.L.; Cavalvanti, P.S.; Lombardi, F.; Nunes, M.C.; Barros, M.V.; Rocha, M.C. Prognostic value of signal-averaged electrocardiogram in Chagas disease. J. Cardiovasc. Electrophysiol. 2008, 19, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Folino, A.F.; Bauce, B.; Frigo, G.; Nava, A. Long-term follow-up of the signal averaged ECG in arrhythmogenic right ventricular cardiomyopathy: Correlation with arrhythmic events and echocardiographic findings. Europace 2006, 8, 423–429. [Google Scholar] [CrossRef] [PubMed]
- Riaz, B.; Majeed, M.I.; Khan, M.A. Association of ventricular late potentials with left ventricular Hypertrophy in patients with systemic arterial hypertension. Pak. Armed Forces Med. J. 2016, 66, 841–844. [Google Scholar]
- Kowalewski, M.A.; Urban, M.; Florys, B.; Peczynska, J. Late potentials: Are they related to cardiovascular complications in children with type 1 diabetes? J. Diabetes Complicat. 2002, 16, 263–270. [Google Scholar] [CrossRef]
- Lalani, A.P.; Kanna, B.; John, J.; Ferrick, K.J.; Huber, M.S.; Shapiro, L.E. Abnormal signal-averaged electrocardiogram (SAECG) in obesity. Obes. Res. 2000, 8, 20–28. [Google Scholar] [CrossRef]
- Babaev, A.A.; Vloka, M.E.; Sadurski, R.; Steinberg, J.S. Influence of age on atrial activation as measured by the P-wave signal-averaged electrocardiogram. Am. J. Cardiol. 2000, 86, 692–695. [Google Scholar] [CrossRef]
- Mirza, M.; Strunets, A.; Shen, W.K.; Jahangir, A. Mechanisms of arrhythmias and conduction disorders in older adults. Clin. Geriatr. Med. 2012, 28, 555–573. [Google Scholar] [CrossRef]
- Couderc, J.P.; Chevalier, P.; Fayn, J.; Rube, P.; Touboul, P. Identification of post-myocardial infarction patients prone to ventricular tachycardia using time–frequency analysis of QRS and ST segments. Europace 2000, 2, 141–153. [Google Scholar] [CrossRef]
- Digiovanni, S.L.; Guaragnella, C.; Rizzi, M.; Falagario, M. Healthcare system: A digital green filter for smart health early cervical cancer diagnosis. In Proceedings of the IEEE 2nd International Forum on Research and Technologies for Society and Industry Leveraging a Better Tomorrow, RTSI 2016, Bologna, Italy, 7–9 September 2016. [Google Scholar]
- Mandala, S.; Di, T.C. ECG Parameters for Malignant Ventricular Arrhythmias: A Comprehensive Review. J. Med. Biol. Eng. 2017, 37, 441–453. [Google Scholar] [CrossRef] [PubMed]
- Guaragnella, C.; Giorgio, A.; Rizzi, M. Marginal Component Analysis of ECG Signals for Beat-to-Beat Detection of Ventricular Late Potentials. Electronics 2019, 8, 1000. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Simson, M.B. Use of Signals in the Terminal QRS Complex to Identify Patients with Ventricular Tachycardia after Myocardial Infarction. Circulation 1981, 64, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.C.; Hu, W.C. Analysis of Unpredictable Intra-QRS Potentials Based on Multi-Step Linear Prediction Modeling for Evaluating the Risk of Ventricular Arrhythmias. In Proceedings of the Computers in Cardiology, Durham, NC, USA, 30 September–3 October 2007; pp. 793–796. [Google Scholar]
- Speranza, G.; Bonato, P.; Antolini, R. Analyzing late ventricular potentials. IEEE Eng. Med. Biol. Mag. 1996, 15, 88–94. [Google Scholar] [CrossRef]
- Mitchell, R.H.; Escalona, O. Discriminating At-Risk Post-MI Patients by Fractal Dimension Analysis of the Late Potential Attractor. In Proceedings of the 20th Annual. Conference of the IEEE Engineering in Medicine Biology Society, Hong Kong, China, 1 November 1998; pp. 1573–1575. [Google Scholar]
- Orosco, L.L.; Laciar, E. Analysis of ventricular late potentials in high resolution ECG records by time-frequency representations. Latin Am. Appl. Res. 2009, 39, 255–260. [Google Scholar]
- Schels, H.F.; Haberl, R.; Jilge, G.; Steinbigler, P.; Steimbeck, G. Frequency Analysis of the Electrocardiogram Maximum Entropy Method for Identification of Patients with Sustained Ventricular. IEEE Trans. Biomed. Eng. 1991, 38, 821–826. [Google Scholar] [CrossRef]
- Voss, A.; Kurths, J.; Fiehring, H. Frequency Domain Analysis of Highly Amplified ECG on the Basis of Maximum Entropy Spectral Estimation. Med. Biol. Eng. Comput. 1992, 30, 277–282. [Google Scholar] [CrossRef]
- Bianchi, A.M.; Mainardi, L.T.; Castiglioni, D.; Dalla Vecchia, L.; Lombardi, F.; Cerutti, S. Time-Variant Autoregressive Spectral Analysis for the Detection of Ventricular Late Potentials. In Proceedings of the IEEE/15th Annual Conference Engineering Medical Biology Society, San Diego, CA, USA, 31 October 1993; pp. 719–720. [Google Scholar]
- Makijarvi, M.; Fetsch, T.; Reinhardt, L.; Martinez-Rubio, A.; Shenasa, M.; Borggrefe, M.; Breithardt, G. Comparison and combination of late potentials and spectral turbulence analysis to predict arrhythmic events after myocardial infarction in the Post-Infarction Late Potential (PILP) Study. Eur. Heart J. 1995, 16, 651–659. [Google Scholar] [CrossRef]
- Vázquez, R.; Caref, E.B.; Torres, F.; Reina, M.; Huet, J.; Guerrero, J.A.; El-Sherif, N. Comparison of the New Acceleration Spectrum Analysis with Other Time and Frequency-Domain Analyses of the Signal Averaged Electrocardiogram. Eur. Heart J. 1998, 19, 628–637. [Google Scholar] [CrossRef][Green Version]
- Reyna-Carranza, M.A.; Bravo-Zanoguera, M.E.; Arriola, H.G.; Lópe, R. Study of the noise ventricular late potentials sensibility on the Wigner distribution time-frequency plane. In Proceedings of the 2012 Pan American Health Care Exchanges, Miami, FL, USA, 26–31 March 2012. [Google Scholar]
- Giorgio, A.; Guaragnella, C.; Giliberti, D.A. Improving ECG signal denoising using wavelet transform for the prediction of malignant arrhythmias. Int. J. Med. Eng. Inform. 2019, in press. [Google Scholar]
- Mousa, A.; Yilmaz, A. A method based on wavelet analysis for the detection of ventricular late potentials in ECG signals. In Proceedings of the 44th IEEE 2001 Midwest Symposium on Circuits and Systems, Dayton, OH, USA, 14–17 August 2001. [Google Scholar]
- Subramanian, A.S.; Gurusamy, G.; Selvakumarc, G. Detection of Ventricular Late Potentials Using Wavelet Transform and ANT Colony Optimization. In Proceedings of the AIP Conference 1298, 331, Oregon, Portland, 21–22 July 2010. [Google Scholar]
- Yang, W.Q. Adaptive enhancement of ventricular late potentials using orthogonal beat-to-beat recording. In Proceedings of the 14th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Paris, France, 29 October–1 November 1992; pp. 492–493. [Google Scholar]
- Mitchell, R.H. Evaluation of adaptive line enhancement for beat-to-beat detection of ventricular late Potentials. Electron. Lett. 1999, 35, 1037–1038. [Google Scholar] [CrossRef]
- Meste, O.; Rix, H.; Caminal, P. Ventricular late potentials characterization in time-frequency domain by means of a wavelet transform. IEEE Trans. Biomed. Eng. 1994, 41, 625–633. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Qian, Y.; Gao, Z.; Lin, J. A Novel Method for Beat-to-Beat Detection of Ventricular Late Potentials. IEEE Trans. Biomed. Eng. 2001, 48, 931–935. [Google Scholar]
- Laciar, E.; JanÈ, R. Analysis of beat-to-beat variability of ventricular late potentials by a spectro-temporal technique in patients with Chagasí disease. In Proceedings of the 26th Annual International Conference of the IEEE EMBS, San Francesco, CA, USA, 1–5 September 2004; pp. 3605–3608. [Google Scholar]
- Khan, M.A.; Majeed, S.M.I.; Sarwar, M. Effect of noise on identification of ventricular late potentials. Pak. Armed Forces Med. J. 2015, 65, S5–S10. [Google Scholar]
- Giorgio, A. A New FPGA-based Medical Device for The Real Time Prevention of The Risk of Arrhythmias. Int. J. Appl. Eng. Res. 2016, 11, 6013–6017. [Google Scholar]
- D’Aloia, M.; Longo, A.; Rizzi, M. Noisy ECG Signal Analysis for Automatic Peak Detection. Information 2019, 10, 35. [Google Scholar] [CrossRef]
- Rizzi, M.; D’Aloia, M.; Guaragnella, C.; Castagnolo, B. Health care improvement: Comparative analysis of two CAD systems in mammographic screening. IEEE Trans. Syst. Man. Cybern.-Part A Syst. Hum. 2012, 42, 1385–1395. [Google Scholar] [CrossRef]
- Breithardt, G.; Cain, M.E.; El-Sherif, N.; Flowers, N.C.; Hombach, V.; Janse, M.; Simson, M.B.; Steinbeck, G. Standards for analysis of ventricular late potentials using high-resolution or signal-averaged electrocardiography: A statement by a task force committee of the European Society of Cardiology, the American Heart Association, and the American College of Cardiology. J. Am. Coll. Cardiol. 1991, 17, 999–1006. [Google Scholar]
- Aqil, M.; Jbari, A.; Bourouhou, A. ECG Signal Denoising by Discrete Wavelet Transform. Int. J. Online Eng. 2017, 13, 51–68. [Google Scholar] [CrossRef]
- Rizzi, M.; D’Aloia, M.; Russo, R.; Cice, G.; Stanisci, S.; Montingelli, A.; Longo, A. Lightweight Signal Analysis for R-Peak Detection. Available online: https://pdfs.semanticscholar.org/4c83/08905c139b66dc85ea90aae0c873103582b6.pdf (accessed on 15 October 2019).
- Giorgio, A. A Model for the Real Time Detection of Ventricular Late Potentials Oriented to Embedded Systems Implementation. Int. J. Adv. Eng. Res. Appl. 2016, 1, 500–511. [Google Scholar]
- Gadaleta, M.; Giorgio, A. A Method for Ventricular Late Potentials Detection Using Time-Frequency Representation and Wavelet Denoising. ISRN Cardiol. 2012, 2012, 9. [Google Scholar] [CrossRef] [PubMed]
- Rahati, S.; Bajestani, G.S.; Falsoleiman, H.; Heidari-Bokavi, A. Wavelet transform application in time frequency enhancement for ventricular late potential better detection. In Proceedings of the BioMedical Engineering and Informatics: New Development and the Future-1st International Conference on BioMedical Engineering and Informatics (BMEI’08), Sanya, China, 27–30 May 2008; pp. 295–300. [Google Scholar]
- Crispi, A.T. Improving ventricular late potentials detection effectiveness. Ph.D. Thesis, The University of New Brunswick, Fredericton and Sanit John, NB, Canada, 2002. [Google Scholar]
- Zandi, A.S.; Moradi, M.H. Quantitative evaluation of a wavelet-based method in ventricular late potential detection. Pattern Recognit. 2006, 39, 1369–1379. [Google Scholar] [CrossRef]
- D’Aloia, M.; Rizzi, M.; Russo, R.; Notarnicola, M.; Pellicani, L. A marker-based image processing method for detecting available parking slots from UAVs. Lect. Notes Comput. Sci. 2015, 9281, 275–281. [Google Scholar]
- Hajian-Tilaki, K. Receiver Operating Characteristic (ROC) Curve Analysis for Medical Diagnostic Test Evaluation. Caspian J. Intern. Med. 2013, 4, 627–635. [Google Scholar] [PubMed]
- Bunluechokchai, S. Detection of Wavelet Transform-Processed Ventricular Late Potentials and Approximate Entropy. Comput. Cardiol. 2003, 30, 549–552. [Google Scholar]
- Zandi, A.S.; Moradi, M.H. Detection of ventricular late potentials in high-resolution ECG signals by a method based on the continuous wavelet transform and artificial neural networks. WSEAS Trans. Electron. 2004, 1, 471–475. [Google Scholar]
- Mandrekar, J.N. Receiver Operating Characteristic Curve in Diagnostic Test Assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef]
| VLP Present in the HR-ECG | VLP Not Present in the HR-ECG | Total | |
|---|---|---|---|
| VLP detected by the tool in the HR-ECG | TP | FP | TP + FP |
| VLP undetected by the tool in the HR-ECG | FN | TN | |
| Total | TP + FN | FP + TN |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorgio, A.; Rizzi, M.; Guaragnella, C. Efficient Detection of Ventricular Late Potentials on ECG Signals Based on Wavelet Denoising and SVM Classification. Information 2019, 10, 328. https://doi.org/10.3390/info10110328
Giorgio A, Rizzi M, Guaragnella C. Efficient Detection of Ventricular Late Potentials on ECG Signals Based on Wavelet Denoising and SVM Classification. Information. 2019; 10(11):328. https://doi.org/10.3390/info10110328
Chicago/Turabian StyleGiorgio, Agostino, Maria Rizzi, and Cataldo Guaragnella. 2019. "Efficient Detection of Ventricular Late Potentials on ECG Signals Based on Wavelet Denoising and SVM Classification" Information 10, no. 11: 328. https://doi.org/10.3390/info10110328
APA StyleGiorgio, A., Rizzi, M., & Guaragnella, C. (2019). Efficient Detection of Ventricular Late Potentials on ECG Signals Based on Wavelet Denoising and SVM Classification. Information, 10(11), 328. https://doi.org/10.3390/info10110328







