A Comparison of Reinforcement Learning Algorithms in Fairness-Oriented OFDMA Schedulers
Abstract
1. Introduction
1.1. Motivation
1.2. Challenges and Solutions
2. Related Work
2.1. Paper Contributions
2.2. Paper Organization
3. OFDMA Scheduling Model
4. Intra-Class Fairness Controlling System
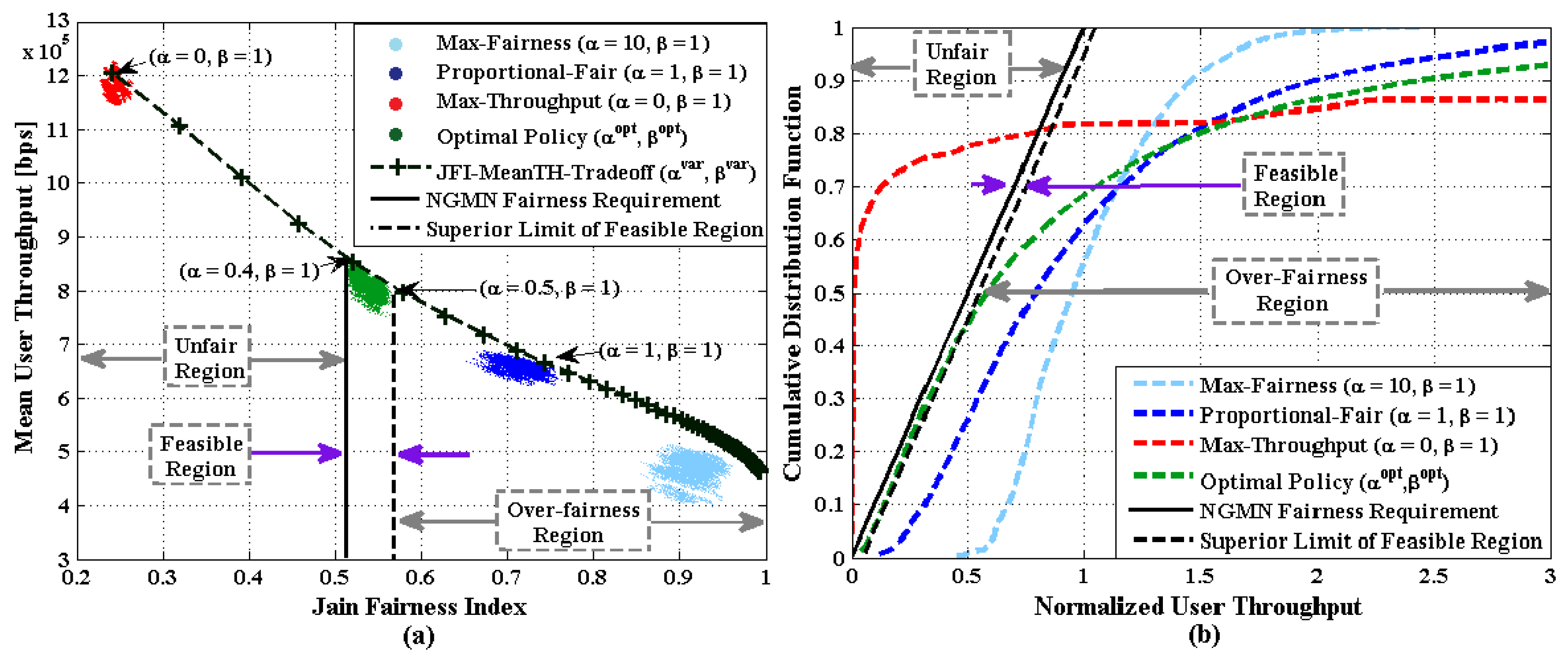
4.1. Throughput-Fairness Trade-off Concept
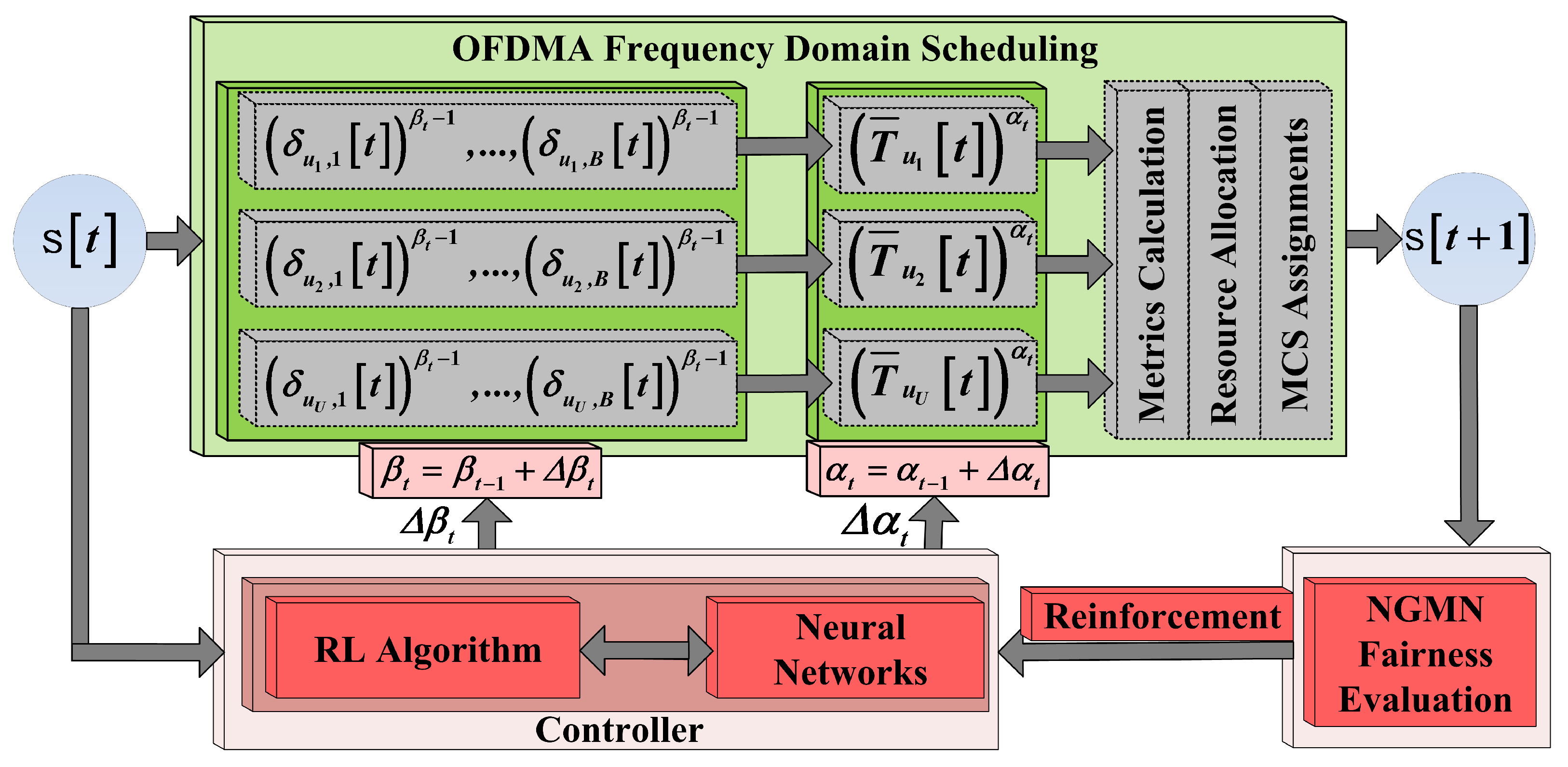
4.2. Proposed System
5. Learning Framework
5.1. Scheduler-Controller Interaction
5.1.1. States
5.1.2. Actions
5.1.3. Reward Functions
5.2. Learning Functions
5.3. Approximation of Learning Functions with Feed Forward Neural Networks
5.4. Training the Feed Forward Neural Networks
5.4.1. Forward Propagation
5.4.2. Backward Propagation
5.5. Exploration Types
5.6. RL Algorithms
6. Simulation Results
6.1. Parameter Settings
Network and Controller Settings
6.2. Learning Stage
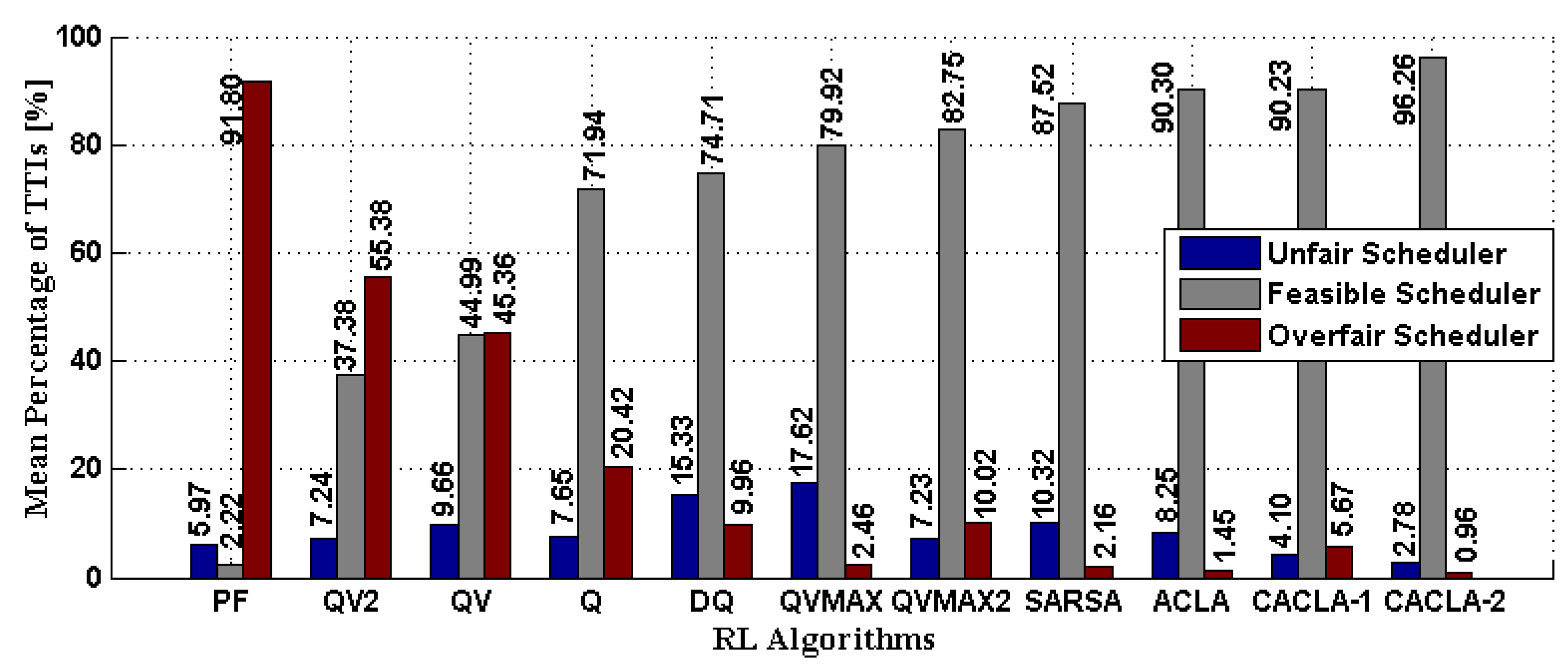
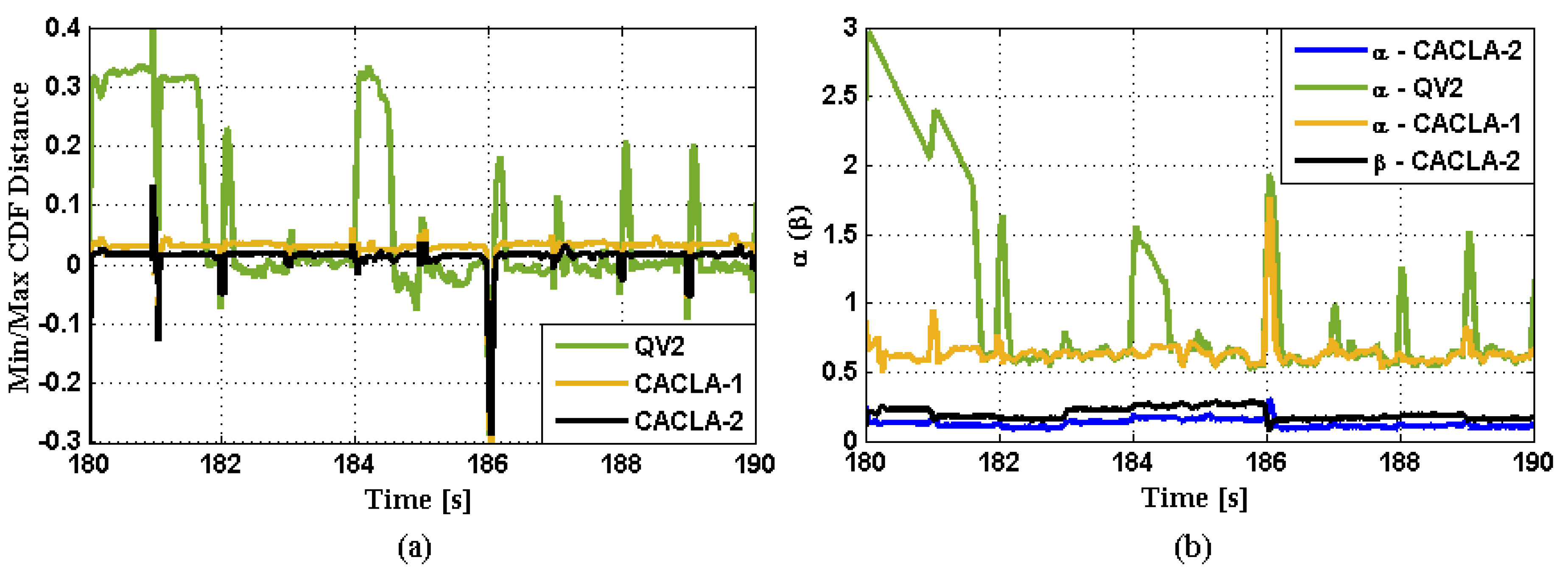
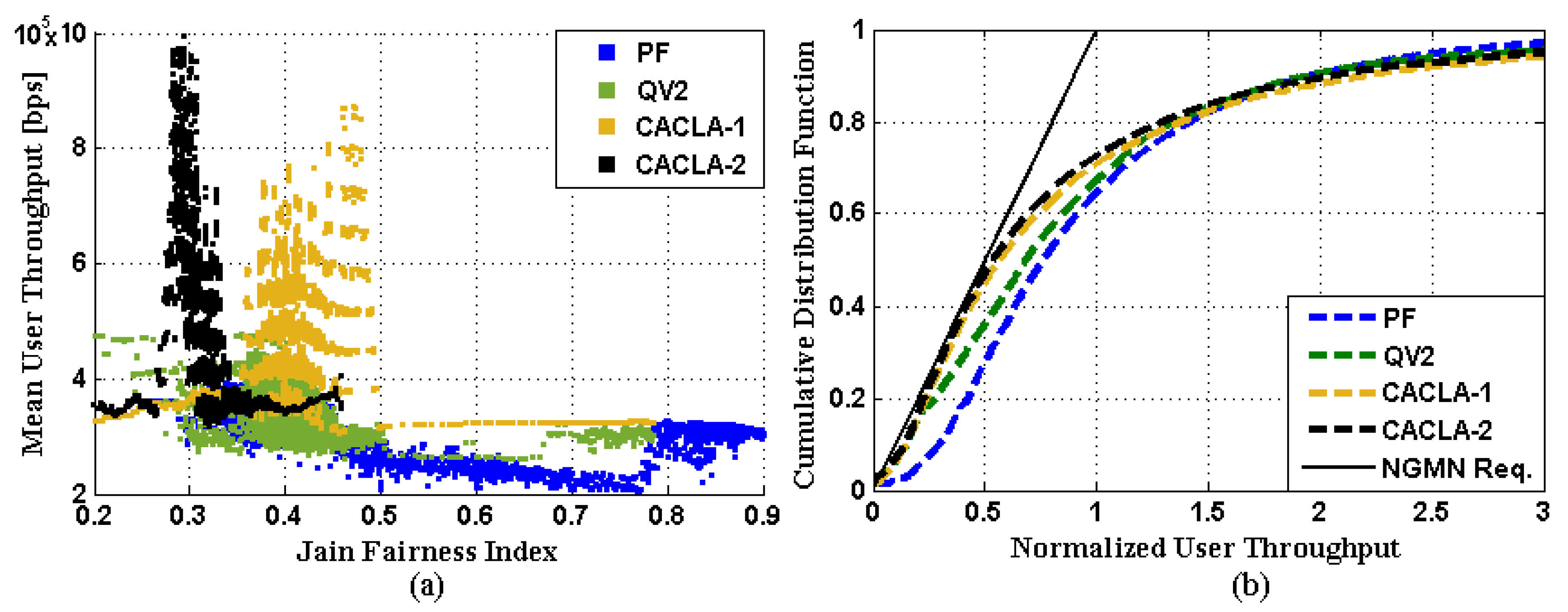
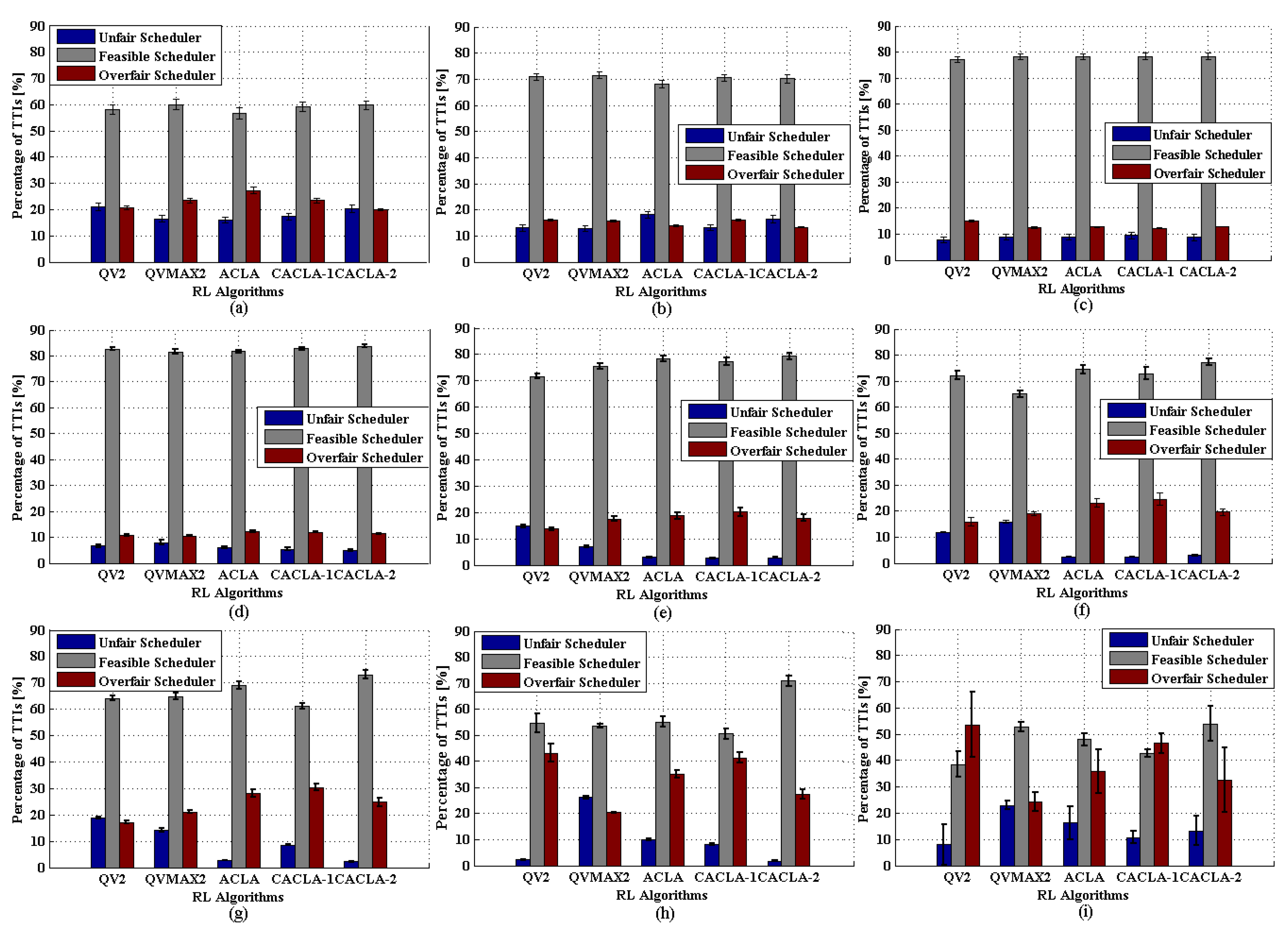
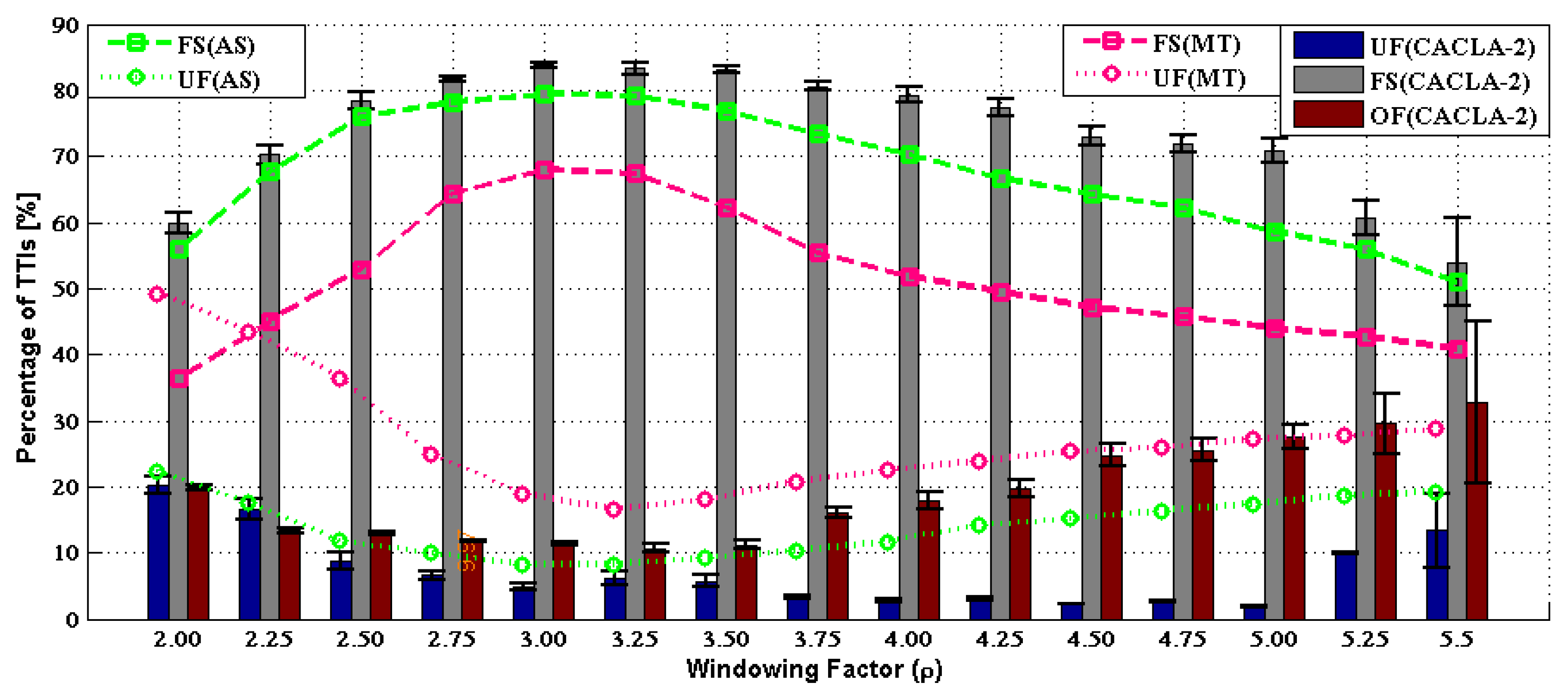
6.3. Exploitation Stage
6.4. General Remarks
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 3, 1065–1082. [Google Scholar] [CrossRef]
- Calabrese, F.D.; Wang, L.; Ghadimi, E.; Peters, G.; Hanzo, L.; Soldati, P. Learning Radio Resource Management in RANs: Framework, Opportunities, and Challenges. IEEE Commun. Mag. 2018, 56, 138–145. [Google Scholar] [CrossRef]
- Comsa, I.-S.; Trestian, R. Information Science Reference. In Next-Generation Wireless Networks Meet Advanced Machine Learning Applications; Comsa, I.-S., Trestian, R., Eds.; IGI Global: Hershey, PA, USA, 2019. [Google Scholar]
- Comsa, I.-S. Sustainable Scheduling Policies for Radio Access Networks Based on LTE Technology. Ph.D. Thesis, University of Bedfordshire, Luton, UK, November 2014. [Google Scholar]
- Comsa, I.-S.; Zhang, S.; Aydin, M.; Kuonen, P.; Trestian, R.; Ghinea, G. Enhancing User Fairness in OFDMA Radio Access Networks Through Machine Learning. In Proceedings of the 2019 Wireless Days (WD), Manchester, UK, 24–26 June 2019; pp. 1–8. [Google Scholar]
- Capozzi, F.; Piro, G.; Grieco, L.A.; Boggia, G.; Camarda, P. Downlink Packet Scheduling in LTE Cellular Networks: Key Design Issues and a Survey. IEEE Commun. Surv. Tutor. 2013, 15, 678–700. [Google Scholar] [CrossRef]
- Comsa, I.-S.; Zhang, S.; Aydin, M.; Chen, J.; Kuonen, P.; Wagen, J.-F. Adaptive Proportional Fair Parameterization Based LTE Scheduling Using Continuous Actor-Critic Reinforcement Learning. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Austin, TX, USA, 8–12 December 2014; pp. 4387–4393. [Google Scholar]
- Comsa, I.-S.; Aydin, M.; Zhang, S.; Kuonen, P.; Wagen, J.-F.; Lu, Y. Scheduling Policies Based on Dynamic Throughput and Fairness Tradeoff Control in LTE-A Networks. In Proceedings of the IEEE Local Computer Networks (LCN), Edmonton, AB, Canada, 8–11 September 2014; pp. 418–421. [Google Scholar]
- Shi, H.; Prasad, R.V.; Onur, E.; Niemegeers, I. Fairness in Wireless Networks: Issues, Measures and Challenges. IEEE Commun. Surv. Tutor. 2014, 16, 5–24. [Google Scholar]
- Jain, R.; Chiu, D.; Hawe, W. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems; Technical Report TR-301; Eastern Research Laboratory, Digital Equipment Corporation: Hudson, MA, USA, 1984; pp. 1–38. [Google Scholar]
- Next Generation of Mobile Networks (NGMN). NGMN Radio Access Performance Evaluation Methodology. In A White Paper by the NGMN Alliance. 2008, pp. 1–37. Available online: https://www.ngmn.org/wp-content/uploads/NGMN_Radio_Access_Performance_Evaluation_Methodology.pdf (accessed on 12 October 2019).
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press Cambridge: Cambridge, MA, USA, 2018. [Google Scholar]
- Iacoboaiea, O.C.; Sayrac, B.; Jemaa, S.B.; Bianchi, P. SON Coordination in Heterogeneous Networks: A Reinforcement Learning Framework. IEEE Trans. Wirel. Commun. 2016, 15, 5835–5847. [Google Scholar] [CrossRef]
- Simsek, M.; Bennis, M.; Guvenc, I. Learning based Frequency and Time-Domain Inter-Cell Interference Coordination in HetNets. IEEE Trans. Veh. Technol. 2015, 64, 4589–4602. [Google Scholar] [CrossRef]
- De Domenico, A.; Ktenas, D. Reinforcement Learning for Interference-Aware Cell DTX in Heterogeneous Networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Zhang, L.; Tan, J.; Liang, Y.-C.; Feng, G.; Niyato, D. Deep Reinforcement Learning-Based Modulation and Coding Scheme Selection in Cognitive Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2019, 18, 3281–3294. [Google Scholar] [CrossRef]
- Naparstek, O.; Cohen, K. Deep Multi-User Reinforcement Learning for Distributed Dynamic Spectrum Access. IEEE Trans. Wirel. Commun. 2019, 18, 310–323. [Google Scholar] [CrossRef]
- Comsa, I.-S.; Aydin, M.; Zhang, S.; Kuonen, P.; Wagen, J.-F. Reinforcement Learning Based Radio Resource Scheduling in LTE-Advanced. In Proceedings of the International Conference on Automation and Computing, Huddersfield, UK, 10–10 September 2011; pp. 219–224. [Google Scholar]
- Comsa, I.-S.; Aydin, M.; Zhang, S.; Kuonen, P.; Wagen, J.-F. Multi Objective Resource Scheduling in LTE Networks Using Reinforcement Learning. Int. J. Distrib. Syst. Technol. 2012, 3, 39–57. [Google Scholar] [CrossRef][Green Version]
- Comsa, I.-S.; De-Domenico, A.; Ktenas, D. Method for Allocating Transmission Resources Using Reinforcement Learning. U.S. Patent Application No. US 2019/0124667 A1, 25 April 2019. [Google Scholar]
- He, J.; Tang, Z.; Tang, Z.; Chen, H.-H.; Ling, C. Design and Optimization of Scheduling and Non-Orthogonal Multiple Access Algorithms with Imperfect Channel State Information. IEEE Trans. Veh. Technol. 2018, 67, 10800–10814. [Google Scholar] [CrossRef]
- Shahsavari, S.; Shirani, F.; Erkip, E. A General Framework for Temporal Fair User Scheduling in NOMA Systems. IEEE J. Sel. Top. Signal Process. 2019, 13, 408–422. [Google Scholar] [CrossRef]
- Kaneko, M.; Yamaura, H.; Kajita, Y.; Hayashi, K.; Sakai, H. Fairness-Aware Non-Orthogonal Multi-User Access with Discrete Hierarchical Modulation for 5G Cellular Relay Networks. IEEE Access 2015, 3, 2922–2938. [Google Scholar] [CrossRef]
- Ahmed, F.; Dowhuszko, A.A.; Tirkkonen, O. Self-Organizing Algorithms for Interference Coordination in Small Cell Networks. IEEE Trans. Veh. Technol. 2017, 66, 8333–8346. [Google Scholar] [CrossRef]
- Zabini, F.; Bazzi, A.; Masini, B.M.; Verdone, R. Optimal Performance Versus Fairness Tradeoff for Resource Allocation in Wireless Systems. IEEE Trans. Wirel. Commun. 2017, 16, 2587–2600. [Google Scholar] [CrossRef]
- Ferdosian, N.; Othman, M.; Mohd Ali, B.; Lun, K.Y. Fair-QoS Broker Algorithm for Overload-State Downlink Resource Scheduling in LTE Networks. IEEE Syst. J. 2018, 12, 3238–3249. [Google Scholar] [CrossRef]
- Trestian, R.; Comsa, I.S.; Tuysuz, M.F. Seamless Multimedia Delivery Within a Heterogeneous Wireless Networks Environment: Are We There Yet? IEEE Commun. Surv. Tutor. 2018, 20, 945–977. [Google Scholar] [CrossRef]
- Schwarz, S.; Mehlfuhrer, C.; Rupp, M. Throughput Maximizing Multiuser Scheduling with Adjustable Fairness. In Proceedings of the IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–5. [Google Scholar]
- Proebster, M.; Mueller, C.M.; Bakker, H. Adaptive Fairness Control for a Proportional Fair LTE Scheduler. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Instanbul, Turkey, 26–30 September 2010; pp. 1504–1509. [Google Scholar]
- Comsa, I.-S.; Aydin, M.; Zhang, S.; Kuonen, P.; Wagen, J.-F. A Novel Dynamic Q-learning-based Scheduler Technique for LTE-advanced Technologies Using Neural Networks. In Proceedings of the IEEE Local Computer Networks (LCN), Clearwater, FL, USA, 22–25 October 2012; pp. 332–335. [Google Scholar]
- Comsa, I.-S.; De-Domenico, A.; Ktenas, D. QoS-Driven Scheduling in 5G Radio Access Networks—A Reinforcement Learning Approach. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar]
- Comsa, I.-S.; Trestian, R.; Ghinea, G. 360∘ Mulsemedia Experience over Next Generation Wireless Networks—A Reinforcement Learning Approach. In Proceedings of the Tenth International Conference on Quality of Multimedia Experience (QoMEX), Cagliari, Italy, 29 May–1 June 2018; pp. 1–6. [Google Scholar]
- Comsa, I.-S.; Zhang, S.; Aydin, M.; Kuonen, P.; Yao, L.; Trestian, R.; Ghinea, G. Towards 5G: A Reinforcement Learning-based Scheduling Solution for Data Traffic Management. IEEE Trans. Net. Serv. Manag. 2018, 15, 1661–1675. [Google Scholar] [CrossRef]
- Comsa, I.-S.; Zhang, S.; Aydin, M.E.; Kuonen, P.; Trestian, R.; Ghinea, G. Guaranteeing User Rates with Reinforcement Learning in 5G Radio Access Networks. In Next-Generation Wireless Networks Meet Advanced Machine Learning Applications; Comsa, I.S., Trestian, R., Eds.; IGI Global: Hershey, PA, USA, 2019; pp. 163–198. [Google Scholar]
- Piro, G.; Grieco, L.A.; Boggia, G.; Capozzi, F.; Camarda, P. Simulating LTE cellular systems: An Open-Source Framework. IEEE Trans. Veh. Technol. 2011, 60, 498–513. [Google Scholar] [CrossRef]
- Song, G.; Li, Y. Utility-based Resource Allocation and Scheduling in OFDM-based Wireless Broadband Networks. IEEE Commun. Mag. 2005, 43, 127–134. [Google Scholar] [CrossRef]
- Comsa, I.-S.; Zhang, S.; Aydin, M.E.; Kuonen, P.; Trestian, R.; Ghinea, G. Machine Learning in Radio Resource Scheduling. In Next-Generation Wireless Networks Meet Advanced Machine Learning Applications; Comsa, I.S., Trestian, R., Eds.; IGI Global: Hershey, PA, USA, 2019; pp. 24–56. [Google Scholar]
- Wiering, M.A.; van Hasselt, H.; Pietersma, A.-D.; Schomaker, L. Reinforcement Learning Algorithms for Solving classification Problems. In Proceedings of the IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning, Paris, France, 11–15 April 2011; pp. 1–6. [Google Scholar]
- Szepesvari, C. Algorithms for Reinforcement Learning: Synthesis Lectures on Artificial Intelligence and Machine Learning; Morgan: San Rafael, CA, USA, 2010. [Google Scholar]
- Van Hasselt, H.P. Insights in Reinforcement Learning Formal Analysis and Empirical Evaluation of Temporal- Difference Learning Algorithms. Ph.D. Thesis, University of Utrecht, Utrecht, The Netherlands, 2011. [Google Scholar]
- van Hasselt, H. Double Q-learning. Adv. Neural. Inf. Process. Syst. 2011, 23, 2613–2622. [Google Scholar]
- Rummery, G.A.; Niranjan, M. Online Q-Learning Using Connectionist Systems; Technical Note; University of Cambridge: Cambridge, UK, 1994. [Google Scholar]
- Wiering, M. QV(lambda)-Learning: A new On-Policy Reinforcement Learning Algorithm. In Proceedings of the 7th European Workshop on Reinforcement Learning, Utrecht, The Netherlands, 20–21 October 2005; pp. 17–18. [Google Scholar]
- Wiering, M.A.; van Hasselt, H. The QV Family Compared to Other Reinforcement Learning Algorithms. In Proceedings of the IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning, Nashville, TN, USA, 30 March–2 April 2009; pp. 101–108. [Google Scholar]
- van Hasselt, H.; Wiering, M.A. Using Continuous Action Spaces to Solve Discrete Problems. In Proceedings of the International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 1149–1156. [Google Scholar]
- Adam, S.; Busoniu, L.; Babuska, R. Experience Replay for Real-Time Reinforcement Learning Control. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 201–212. [Google Scholar] [CrossRef]
- Proebster, M.C. Size-Based Scheduling to Improve the User Experience in Cellular Networks. Ph.D. Thesis, Universität Stuttgart, Stuart, Germany, 2016. [Google Scholar]
| Parameter | Value |
|---|---|
| System Bandwidth/Cell Radius | 20 MHz (100 RBs)/1000 m |
| User Speed/Mobility Model | 120 Kmph/Random Direction |
| Channel Model | Jakes Model |
| Path Loss/Penetration Loss | Macro Cell Model/10 dB |
| Interfered Cells/Shadowing STD | 6/8 dB |
| Carrier Frequency/DL Power | 2 GHz/43 dBm |
| Frame Structure | FDD |
| CQI Reporting Mode | Full-band, periodic at each TTI |
| Physical Uplink Control CHannel | |
| (PUCCH) Model | Errorless |
| Scheduler Types | SP-GPF, DP-GPF, MT [28], AS [29], RL Policies |
| Traffic Type | Full Buffer |
| No. of schedulable users | 10 each TTI |
| RLC Automatic Repeat reQuest (ARQ) | Transmission Mode |
| Adaptive Modulation and Coding | |
| (AMC) Levels | QPSK, 16-QAM, 64-QAM |
| Target Block Error Rate (BLER) | 10% |
| Number of Users | Variable: 15-120 |
| RL Algorithms | Q-Learning [12], Double-Q-Learning [41], SARSA [42], QV [43], QV2 [44], QVMAX [44], QVMAX2 [44], ACLA [38], CACLA-1 [45], CACLA-2 [45] |
| Exploration (learning and ER)/Exploitation | 4000 s (1000 s ER)/200 s for Q, DQ, and SARSA 3000 s/200 s for actor-critic RL |
| Forgetting factor (), windowing Factor | , |
| RL Algs. | Learning Rate | Learning Rate | Discount Factor | Exploration |
|---|---|---|---|---|
| Q-Learning | − | 0.99 | -greedy | |
| DQ-Learning | − | 0.99 | -greedy | |
| SARSA | − | 0.99 | Boltzmann | |
| QV | 0.99 | Boltzmann | ||
| QV2 | 0.95 | Boltzmann | ||
| QVMAX | 0.99 | Boltzmann | ||
| QVMAX2 | 0.95 | Boltzmann | ||
| ACLA | 0.99 | -greedy | ||
| CACLA-1 | 0.99 | -greedy | ||
| CACLA-2 | 0.99 | -greedy |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comșa, I.-S.; Zhang, S.; Aydin, M.; Kuonen, P.; Trestian, R.; Ghinea, G. A Comparison of Reinforcement Learning Algorithms in Fairness-Oriented OFDMA Schedulers. Information 2019, 10, 315. https://doi.org/10.3390/info10100315
Comșa I-S, Zhang S, Aydin M, Kuonen P, Trestian R, Ghinea G. A Comparison of Reinforcement Learning Algorithms in Fairness-Oriented OFDMA Schedulers. Information. 2019; 10(10):315. https://doi.org/10.3390/info10100315
Chicago/Turabian StyleComșa, Ioan-Sorin, Sijing Zhang, Mehmet Aydin, Pierre Kuonen, Ramona Trestian, and Gheorghiță Ghinea. 2019. "A Comparison of Reinforcement Learning Algorithms in Fairness-Oriented OFDMA Schedulers" Information 10, no. 10: 315. https://doi.org/10.3390/info10100315
APA StyleComșa, I.-S., Zhang, S., Aydin, M., Kuonen, P., Trestian, R., & Ghinea, G. (2019). A Comparison of Reinforcement Learning Algorithms in Fairness-Oriented OFDMA Schedulers. Information, 10(10), 315. https://doi.org/10.3390/info10100315







