A Novel Multi-Criteria Decision-Making Model: Interval Rough SAW Method for Sustainable Supplier Selection
Abstract
:1. Introduction
2. Literature Review
2.1. Review of Applying the FUCOM Method in Various Fields
2.2. Review of Applying Multi-Criteria Methods in the Integration with Rough Numbers
2.3. Selection of Suppliers over the Last Five Years
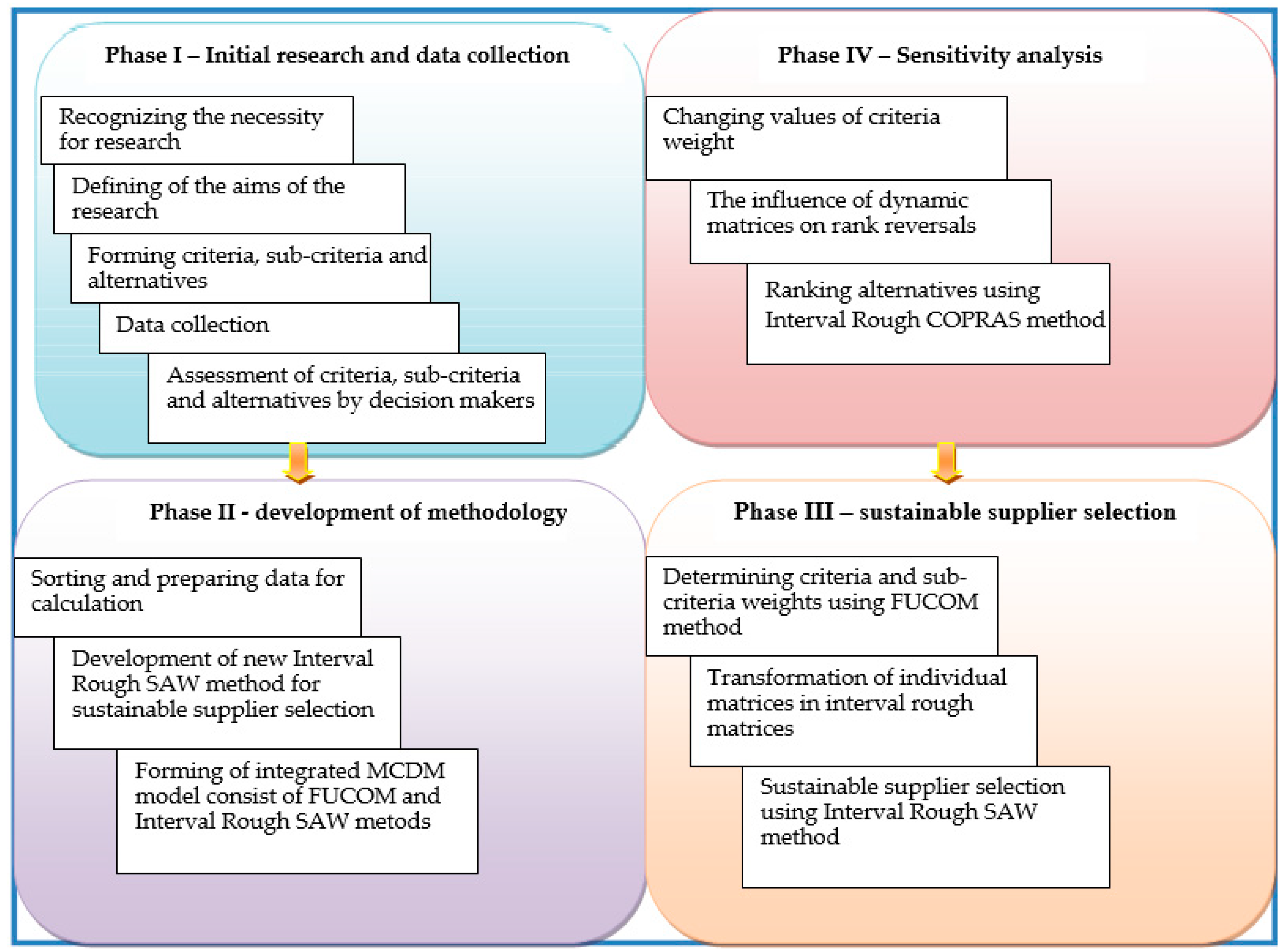
3. Methods
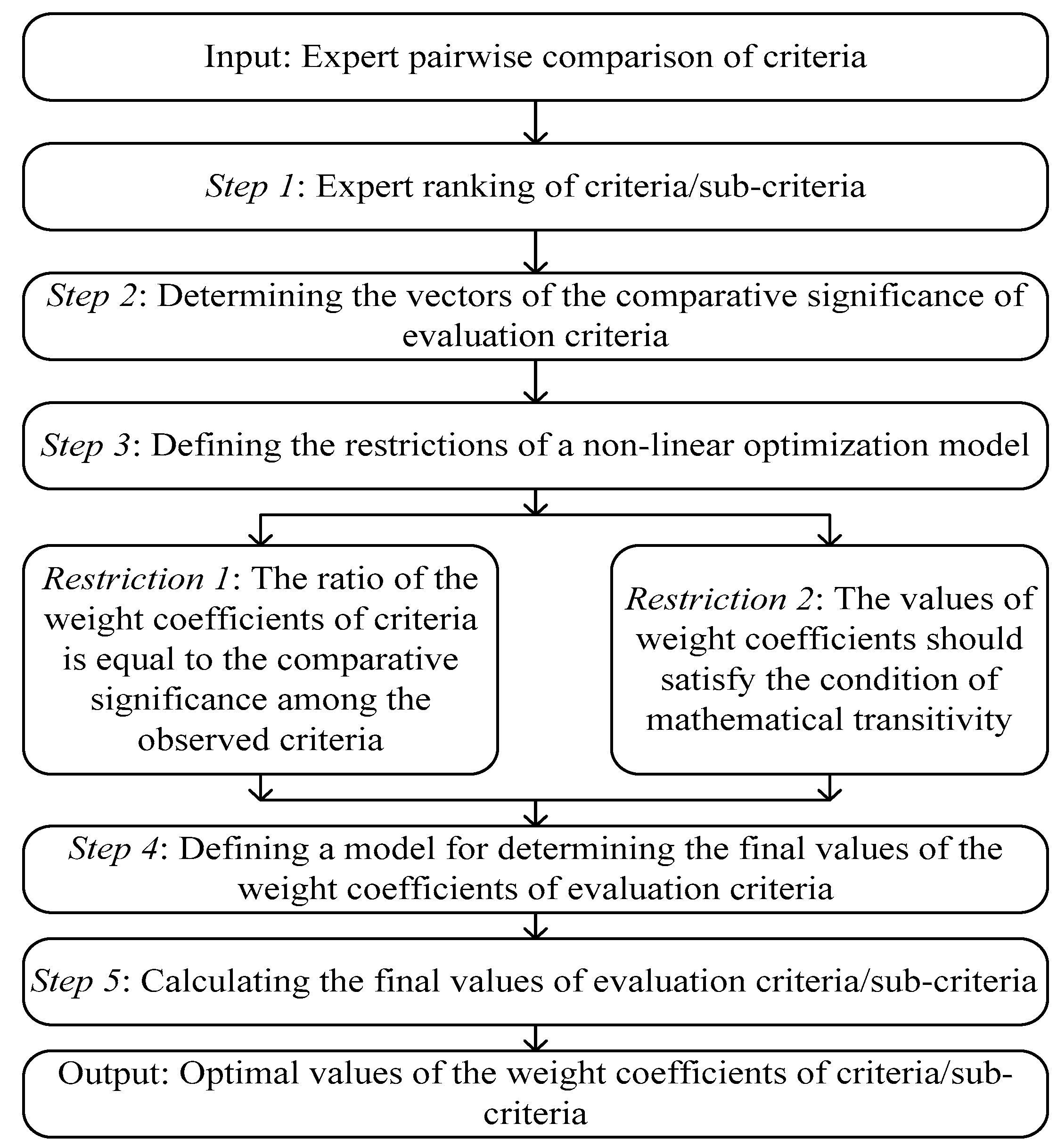
3.1. Full Consistency Method (FUCOM)
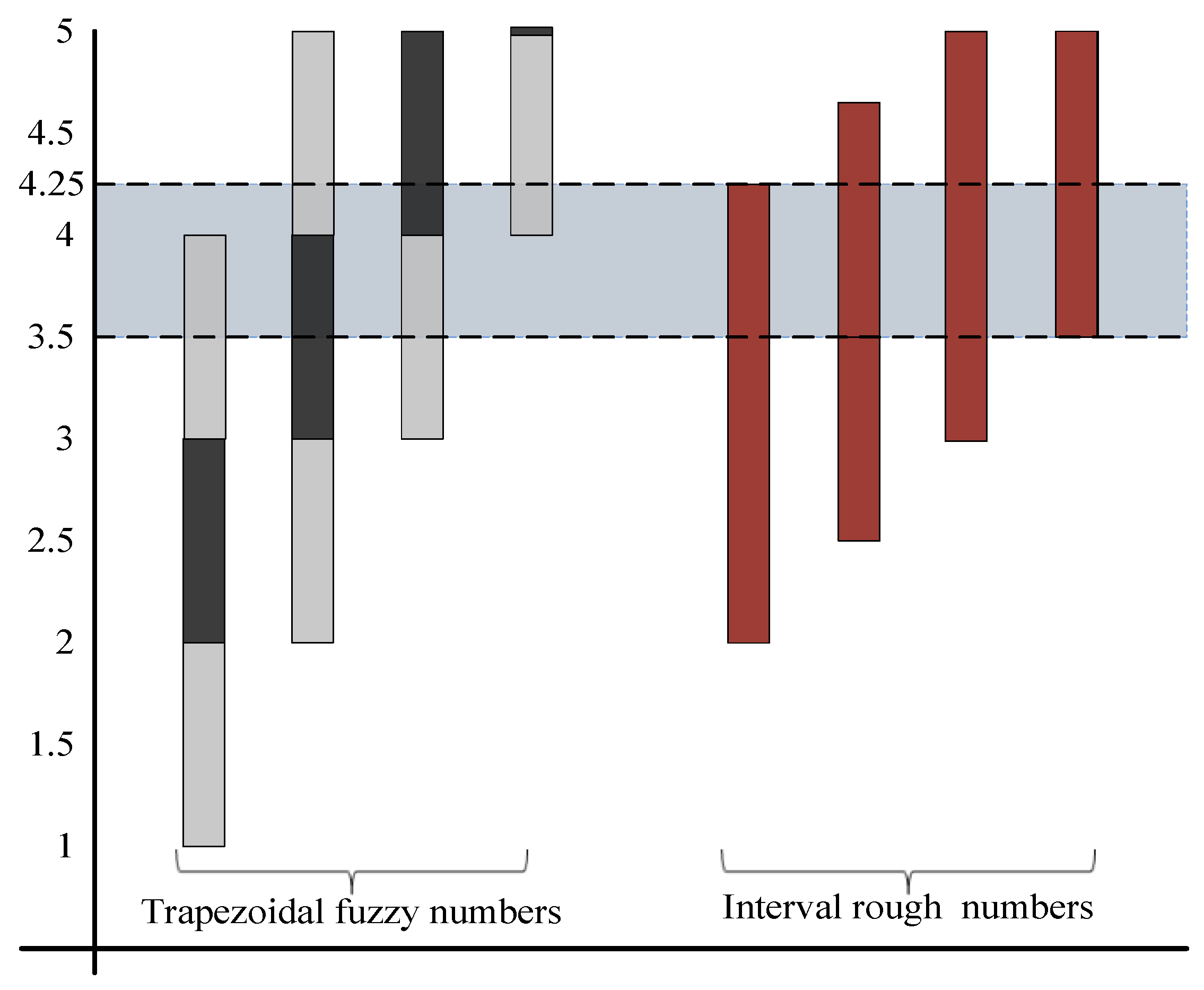
3.2. Interval Rough Numbers
3.3. Interval Rough SAW Method
4. Results
- Sub-criteria of the group of economic criteria C1: C11—cost / price; C12—quality; C13—flexibility; C14—productivity; C15—financial capacity; C16—partnerships; and C17—ecological innovations
- Sub-criteria of the group of social criteria C2: C21—reputation; C22—work safety; C23—employees’ rights; C24—local community influence; C25—training of employees; C26—respect for rights and policies; and C27—release of information.
- Sub-criteria of the group of environmental criteria C3: C31 — environmental image; C32—recycling; C33—pollution control; C34—environmental management system; C35—environmentally friendly products; C36—resource consumption; and C37—green competencies.
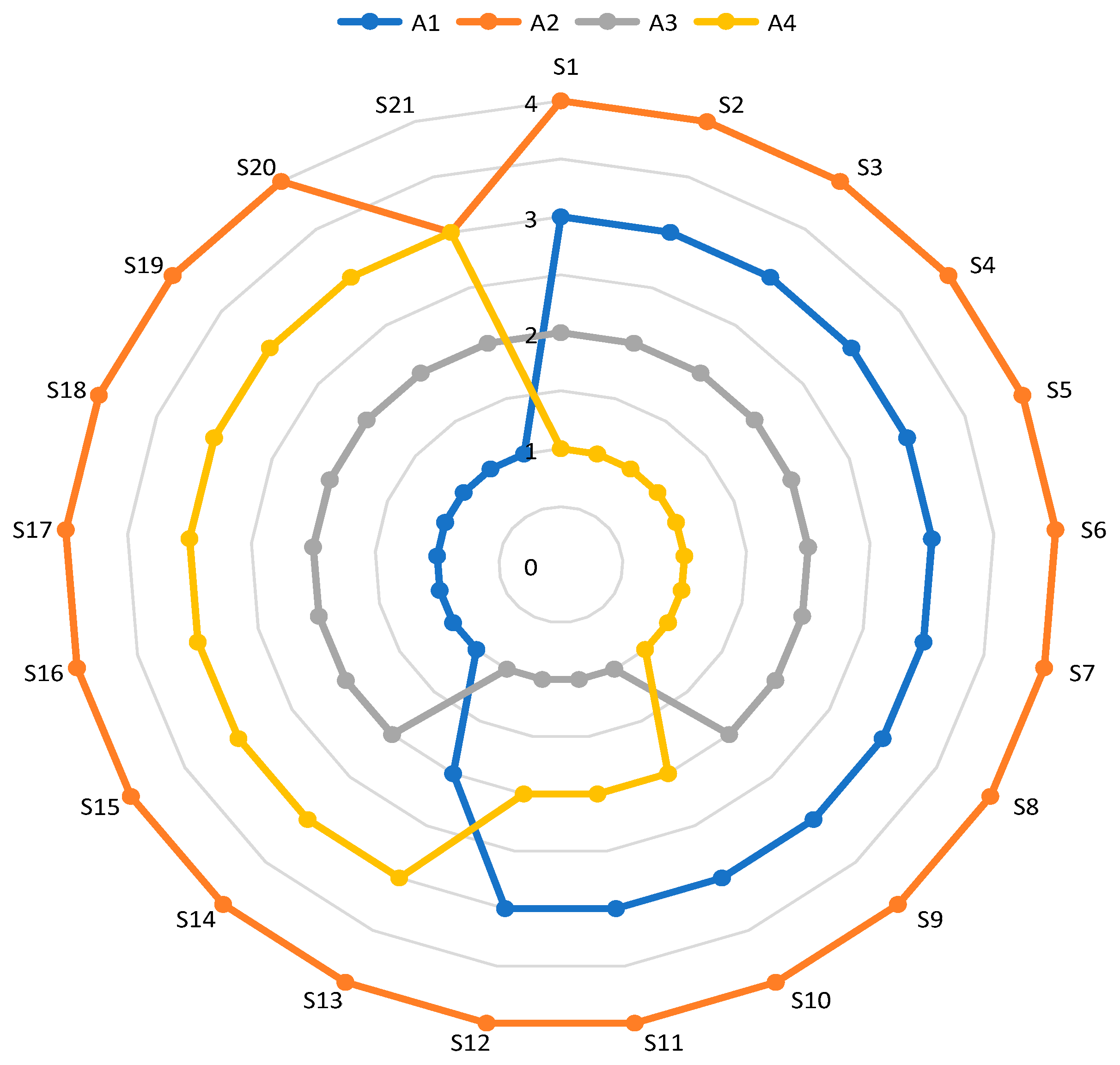
5. Sensitivity Analysis
5.1. Changing the Weights of Criteria
5.2. Influence of Dynamic Matrices on Rank Change
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pamučar, D.; Stević, Ž.; Sremac, S. A new model for determining weight coefficients of criteria in mcdm models: Full consistency method (fucom). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef]
- Pamučar, D.; Lukovac, V.; Božanić, D.; Komazec, N. Multi-criteria FUCOM-MAIRCA model for the evaluation of level crossings: Case study in the Republic of Serbia. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 108–129. [Google Scholar] [CrossRef]
- Prentkovskis, O.; Erceg, Ž.; Stević, Ž.; Tanackov, I.; Vasiljević, M.; Gavranović, M. A new methodology for improving service quality measurement: Delphi-FUCOM-SERVQUAL model. Symmetry 2018, 10, 757. [Google Scholar] [CrossRef]
- Nunić, Z. Evaluation and selection of Manufacturer PVC carpentry using FUCOM-MABAC model. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 13–28. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Nunić, Z.; Stjepanović, Ž.; Prentkovskis, O. A novel rough range of value method (R-ROV) for selecting automatically guided vehicles (AGVs). Stud. Inform. Control 2018, 27, 385–394. [Google Scholar] [CrossRef]
- Fazlollahtabar, H.; Smailbašić, A.; Stević, Ž. FUCOM method in group decision-making: Selection of forklift in a warehouse. Decis. Mak. Appl. Manag. Eng. 2019, 2, 49–65. [Google Scholar] [CrossRef]
- Bozanic, D.; Tešić, D.; Kočić, J. Multi-criteria FUCOM-Fuzzy MABAC model for the selection of location for construction of single-span bailey bridge. Decis. Mak. Appl. Manag. Eng. 2019, 2, 132–146. [Google Scholar] [CrossRef]
- Badi, I.; Abdulshahed, A. Ranking the Libyan airlines by using full consistency method (FUCOM) and analytical hierarchy process (AHP). Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 1–14. [Google Scholar] [CrossRef]
- Noureddine, M.; Ristic, M. Route planning for hazardous materials transportation: Multicriteria decision making approach. Decis. Mak. Appl. Manag. Eng. 2019, 2, 66–85. [Google Scholar] [CrossRef]
- Nenadić, D. Ranking dangerous sections of the road using MCDM model. Decis. Mak. Appl. Manag. Eng. 2019, 2, 115–131. [Google Scholar] [CrossRef]
- Erceg, Ž.; Mularifović, F. Integrated MCDM model for processes optimization in supply chain management in wood company. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 37–50. [Google Scholar] [CrossRef]
- Matić, B.; Jovanović, S.; Das, D.K.; Zavadskas, E.K.; Stević, Ž.; Sremac, S.; Marinković, M. A New Hybrid MCDM Model: Sustainable Supplier Selection in a Construction Company. Symmetry 2019, 11, 353. [Google Scholar] [CrossRef]
- Durmić, E. Evaluation of criteria for sustainable supplier selection using FUCOM method. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 91–107. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Vasiljević, M.; Stojić, G.; Korica, S. Novel integrated multi-criteria model for supplier selection: Case study construction company. Symmetry 2017, 9, 279. [Google Scholar] [CrossRef]
- Stević, Ž.; Tanackov, I.; Vasiljević, M.; Rikalović, A. Supplier evaluation criteria: AHP rough approach. In Proceedings of the XVII International Scientific Conference on Industrial Systems, Novi Sad, Serbia, 4–6 October 2017; pp. 298–303. [Google Scholar]
- Shidpour, H.; Da Cunha, C.; Bernard, A. Group multi-criteria design concept evaluation using combined rough set theory and fuzzy set theory. Expert Syst. Appl. 2016, 64, 633–644. [Google Scholar] [CrossRef]
- Tiwari, V.; Jain, P.K.; Tandon, P. Product design concept evaluation using rough sets and VIKOR method. Adv. Eng. Inform. 2016, 30, 16–25. [Google Scholar] [CrossRef]
- Zhu, G.N.; Hu, J.; Qi, J.; Gu, C.C.; Peng, Y.H. An integrated AHP and VIKOR for design concept evaluation based on rough number. Adv. Eng. Inform. 2015, 29, 408–418. [Google Scholar] [CrossRef]
- Shen, K.Y.; Tzeng, G.H. A novel bipolar MCDM model using rough sets and three-way decisions for decision aids. In Proceedings of the 2016 Joint 8th International Conference on Soft Computing and Intelligent Systems (SCIS) and 17th International Symposium on Advanced Intelligent Systems (ISIS), Sapporo, Japan, 25–28 August 2016; pp. 53–58. [Google Scholar]
- Karavidić, Z.; Projović, D. A multi-criteria decision-making (MCDM) model in the security forces operations based on rough sets. Decis. Mak. Appl. Manag. Eng. 2018, 1, 97–120. [Google Scholar] [CrossRef]
- Shen, K.Y.; Hu, S.K.; Tzeng, G.H. Financial modeling and improvement planning for the life insurance industry by using a rough knowledge based hybrid MCDM model. Inf. Sci. 2017, 375, 296–313. [Google Scholar] [CrossRef]
- Stojić, G.; Stević, Ž.; Antuchevičienė, J.; Pamučar, D.; Vasiljević, M. A novel rough WASPAS approach for supplier selection in a company manufacturing PVC carpentry products. Information 2018, 9, 121. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Stević, Ž.; Tanackov, I.; Prentkovskis, O. A novel multicriteria approach-rough step-wise weight assessment ratio analysis method (R-SWARA) and its application in logistics. Stud. Inform. Control 2018, 27, 97–106. [Google Scholar] [CrossRef]
- Aydogan, E.K. Performance measurement model for Turkish aviation firms using the rough-AHP and TOPSIS methods under fuzzy environment. Expert Syst. Appl. 2011, 38, 3992–3998. [Google Scholar] [CrossRef]
- Kusi-Sarpong, S.; Bai, C.; Sarkis, J.; Wang, X. Green supply chain practices evaluation in the mining industry using a joint rough sets and fuzzy TOPSIS methodology. Resour. Policy 2015, 46, 86–100. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z.; Zhu, B. A rough TOPSIS approach for failure mode and effects analysis in uncertain environments. Qual. Reliab. Eng. Int. 2014, 30, 473–486. [Google Scholar] [CrossRef]
- Su, C.H.; Chen KT, K.; Fan, K.K. Rough set theory based fuzzy TOPSIS on serious game design evaluation framework. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Khan, C.; Anwar, S.; Bashir, S.; Rauf, A.; Amin, A. Site selection for food distribution using rough set approach and TOPSIS method. J. Intell. Fuzzy Syst. 2015, 29, 2413–2419. [Google Scholar] [CrossRef] [Green Version]
- Vasiljević, M.; Fazlollahtabar, H.; Stević, Ž.; Vesković, S. A rough multicriteria approach for evaluation of the supplier criteria in automotive industry. Decis. Mak. Appl. Manag. Eng. 2018, 1, 82–96. [Google Scholar] [CrossRef]
- Pamučar, D.; Stević, Ž.; Zavadskas, E.K. Integration of interval rough AHP and interval rough MABAC methods for evaluating university web pages. Appl. Soft Comput. 2018, 67, 141–163. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. Supplier evaluation and selection in fuzzy environments: A review of MADM approaches. Econ. Res. Ekon. Istraživanja 2017, 30, 1073–1118. [Google Scholar] [CrossRef]
- Arabsheybani, A.; Paydar, M.M.; Safaei, A.S. An integrated fuzzy MOORA method and FMEA technique for sustainable supplier selection considering quantity discounts and supplier’s risk. J. Clean. Prod. 2018, 190, 577–591. [Google Scholar] [CrossRef]
- Luthra, S.; Govindan, K.; Kannan, D.; Mangla, S.K.; Garg, C.P. An integrated framework for sustainable supplier selection and evaluation in supply chains. J. Clean. Prod. 2017, 140, 1686–1698. [Google Scholar] [CrossRef]
- Awasthi, A.; Govindan, K.; Gold, S. Multi-tier sustainable global supplier selection using a fuzzy AHP-VIKOR based approach. Int. J. Prod. Econ. 2018, 195, 106–117. [Google Scholar] [CrossRef]
- Yadav, V.; Sharma, M.K. Multi-criteria decision making for supplier selection using fuzzy AHP approach. Benchmarking Int. J. 2015, 22, 1158–1174. [Google Scholar] [CrossRef]
- Azimifard, A.; Moosavirad, S.H.; Ariafar, S. Selecting sustainable supplier countries for Iran’s steel industry at three levels by using AHP and TOPSIS methods. Resour. Policy 2018, 57, 30–44. [Google Scholar] [CrossRef]
- Badi, I.; Abdulshahed, A.M.; Shetwan, A. A case study of supplier selection for a steelmaking company in Libya by using the Combinative Distance-based ASsessment (CODAS) model. Decis. Mak. Appl. Manag. Eng. 2018, 1, 1–12. [Google Scholar] [CrossRef]
- Rezaei, J.; Nispeling, T.; Sarkis, J.; Tavasszy, L. A supplier selection life cycle approach integrating traditional and environmental criteria using the best worst method. J. Clean. Prod. 2016, 135, 577–588. [Google Scholar] [CrossRef]
- Karsak, E.E.; Dursun, M. An integrated fuzzy MCDM approach for supplier evaluation and selection. Comput. Ind. Eng. 2015, 82, 82–93. [Google Scholar] [CrossRef]
- Azadnia, A.H.; Saman MZ, M.; Wong, K.Y. Sustainable supplier selection and order lot-sizing: An integrated multi-objective decision-making process. Int. J. Prod. Res. 2015, 53, 383–408. [Google Scholar] [CrossRef]
- Girubha, J.; Vinodh, S.; Kek, V. Application of interpretative structural modelling integrated multi criteria decision making methods for sustainable supplier selection. J. Model. Manag. 2016, 11, 358–388. [Google Scholar] [CrossRef]
- Öztürk, B.A.; Özçelik, F. Sustainable supplier selection with a fuzzy multi-criteria decision making method based on triple bottom line. Bus. Econ. Res. J. 2014, 5, 129. [Google Scholar]
- Mehregan, M.R.; Hashemi, S.H.; Karimi, A.; Merikhi, B. Analysis of interactions among sustainability supplier selection criteria using ISM and fuzzy DEMATEL. Int. J. Appl. Decis. Sci. 2014, 7, 270–294. [Google Scholar] [CrossRef]
- Jia, P.; Govindan, K.; Choi, T.M.; Rajendran, S. Supplier selection problems in fashion business operations with sustainability considerations. Sustainability 2015, 7, 1603–1619. [Google Scholar] [CrossRef]
- Su, C.M.; Horng, D.J.; Tseng, M.L.; Chiu, A.S.; Wu, K.J.; Chen, H.P. Improving sustainable supply chain management using a novel hierarchical grey-DEMATEL approach. J. Clean. Prod. 2016, 134, 469–481. [Google Scholar] [CrossRef]
- Mohammed, A.; Setchi, R.; Filip, M.; Harris, I.; Li, X. An integrated methodology for a sustainable two-stage supplier selection and order allocation problem. J. Clean. Prod. 2018, 192, 99–114. [Google Scholar] [CrossRef] [Green Version]
- Duntsch, I.; Gediga, G. The rough set engine GROBIAN. In Proceedings of the 15th IMACS World Congress, Berlin, Germany, 24–29 August 1997; pp. 613–618. [Google Scholar]
- Stević, Ž.; Pamučar, D.; Kazimieras Zavadskas, E.; Ćirović, G.; Prentkovskis, O. The selection of wagons for the internal transport of a logistics company: A novel approach based on rough BWM and rough SAW methods. Symmetry 2017, 9, 264. [Google Scholar] [CrossRef]
- Kirkwood, C.W. Strategic Decision Making: Multi-Objective Decision Analysis with Spreadsheets; Duxbury Press: Belmont, Australia, 1997. [Google Scholar]
- Kahraman, Y.R. Robust Sensitivity Analysis for Multi-Attribute Deterministic Hierarchical Value Models; Storming Media: Washington, DC, USA, 2002. [Google Scholar]
- Pamučar, D.; Božanić, D.; Lukovac, V.; Komazec, N. Normalized weighted geometric bonferroni mean operator of interval rough numbers-application in interval rough dematel-copras model. Facta Univ. Ser. Mech. Eng. 2018, 16, 171–191. [Google Scholar] [CrossRef]
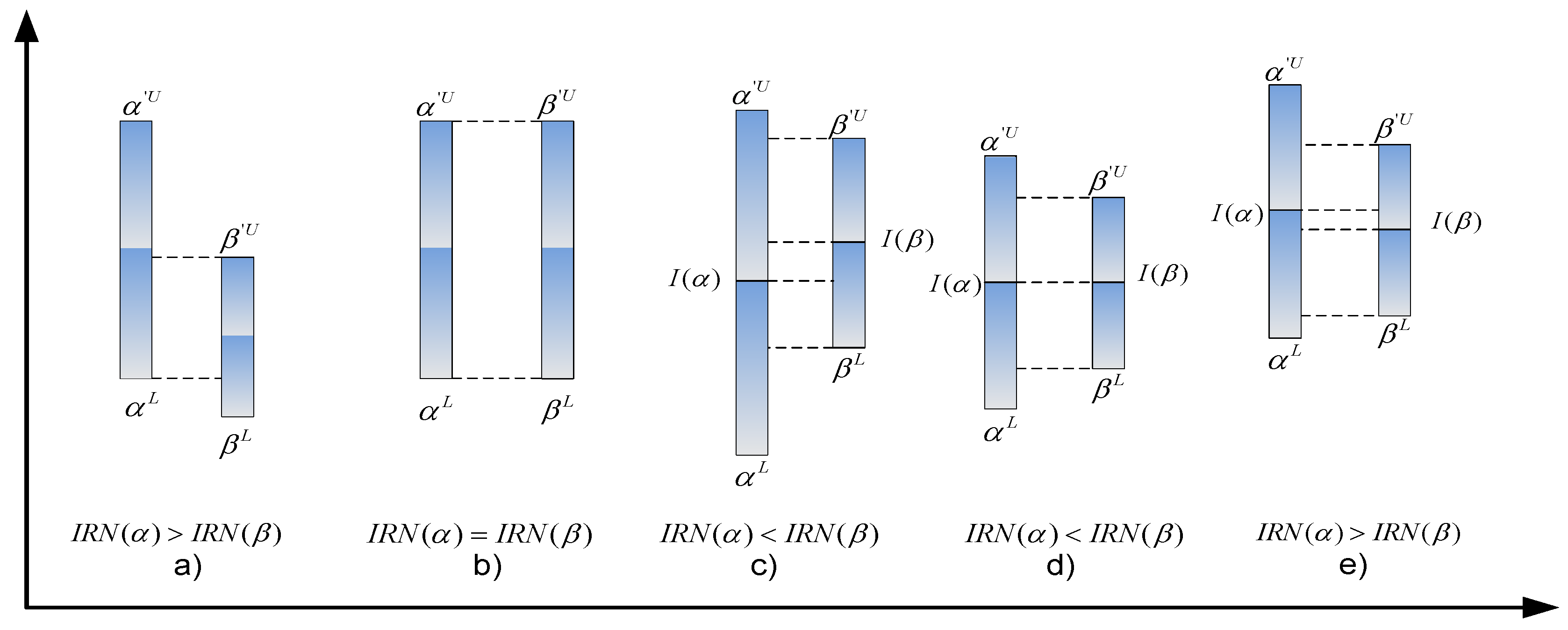
| Criterion | Experts | |||
|---|---|---|---|---|
| E1 | E2 | E3 | E4 | |
| wi | (2;3) | (3;4) | (4;5) | (5;5) |
| A1 | A2 | A3 | A4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | E1 | E2 | E3 | E1 | E2 | E3 | E1 | E2 | E3 | |
| C11 | (1;1) | (2;3) | (1;2) | (1;2) | (3;4) | (3;3) | (1;2) | (2;2) | (2;2) | (1;2) | (3;3) | (2;3) |
| C12 | (7;8) | (7;7) | (7;8) | (7;7) | (6;7) | (6;7) | (7;8) | (7;7) | (6;7) | (7;7) | (6;7) | (6;7) |
| C13 | (5;6) | (4;5) | (5;6) | (5;6) | (4;5) | (4;5) | (7;8) | (6;7) | (5;5) | (7;7) | (6;7) | (6;6) |
| C14 | (7;7) | (6;7) | (6;7) | (6;6) | (5;6) | (6;6) | (7;7) | (6;7) | (5;5) | (7;7) | (6;6) | (6;7) |
| C15 | (5;5) | (4;5) | (5;5) | (6;7) | (5;6) | (5;5) | (6;6) | (6;7) | (6;6) | (7;8) | (7;7) | (6;6) |
| C16 | (7;8) | (7;8) | (7;8) | (6;7) | (5;6) | (5;6) | (6;7) | (6;6) | (6;6) | (6;7) | (6;6) | (7;8) |
| C17 | (6;6) | (5;6) | (5;5) | (6;6) | (5;5) | (4;5) | (6;7) | (5;6) | (5;6) | (7;7) | (6;7) | (5;6) |
| C21 | (5;6) | (5;5) | (4;5) | (6;6) | (6;7) | (5;6) | (7;7) | (7;7) | (6;6) | (7;8) | (7;7) | (6;6) |
| C22 | (5;5) | (4;5) | (5;5) | (6;6) | (5;5) | (4;4) | (7;8) | (6;7) | (4;5) | (7;7) | (6;6) | (5;6) |
| C23 | (5;6) | (5;5) | (5;6) | (6;7) | (6;7) | (5;5) | (6;7) | (6;7) | (4;5) | (6;6) | (5;6) | (4;5) |
| C24 | (3;4) | (3;3) | (2;3) | (3;4) | (3;3) | (3;4) | (4;4) | (4;5) | (3;3) | (4;5) | (4;4) | (4;4) |
| C25 | (3;4) | (3;4) | (3;4) | (6;6) | (5;5) | (4;5) | (6;6) | (4;5) | (4;4) | (6;7) | (5;6) | (5;6) |
| C26 | (5;5) | (4;5) | (4;5) | (6;6) | (5;6) | (5;6) | (6;6) | (6;7) | (5;5) | (6;6) | (6;7) | (6;6) |
| C27 | (3;3) | (3;3) | (2;2) | (5;6) | (4;5) | (3;4) | (6;7) | (6;6) | (4;4) | (6;7) | (6;6) | (4;5) |
| C31 | (4;5) | (4;4) | (5;6) | (4;4) | (4;5) | (5;5) | (5;6) | (5;6) | (4;5) | (6;6) | (6;6) | (5;6) |
| C32 | (6;6) | (6;6) | (5;6) | (5;6) | (5;5) | (5;6) | (6;7) | (6;7) | (5;6) | (6;6) | (6;6) | (4;5) |
| C33 | (4;4) | (4;4) | (6;6) | (5;5) | (5;6) | (5;6) | (6;6) | (5;5) | (4;4) | (5;6) | (6;6) | (4;5) |
| C34 | (3;4) | (3;3) | (4;4) | (4;4) | (4;5) | (4;4) | (6;6) | (5;5) | (2;3) | (6;6) | (5;5) | (3;4) |
| C35 | (5;6) | (4;5) | (4;5) | (4;4) | (3;4) | (4;4) | (6;6) | (5;5) | (3;4) | (5;5) | (4;5) | (5;5) |
| C36 | (4;4) | (5;5) | (5;5) | (4;5) | (5;5) | (5;5) | (4;5) | (5;5) | (6;6) | (3;4) | (4;4) | (3;4) |
| C37 | (3;4) | (4;4) | (3;4) | (4;5) | (3;4) | (4;4) | (5;5) | (4;5) | (3;4) | (5;5) | (5;6) | (4;4) |
| A1 | A2 | A3 | A4 | |
|---|---|---|---|---|
| C11 | [1.11, 1.55]; [1.5, 2.5] | [1.89, 2.78]; [2.5, 3.5] | [1.45, 1.89]; [2, 2] | [1.5, 2.5]; [2.45, 2.89] |
| C12 | [7, 7]; [7.45, 7.89] | [6.11, 6.55]; [7, 7] | [6.45, 6.89]; [7.11, 7.55] | [6.11, 6.55]; [7, 7] |
| C13 | [4.45, 4.89]; [5.45, 5.89] | [4.11, 4.55]; [5.11, 5.55] | [5.5, 6.5]; [5.89, 7.39] | [6.11, 6.55]; [6.45, 6.89] |
| C14 | [6.11, 6.55]; [7, 7] | [5.45, 5.89]; [5.45, 5.89] | [5.5, 6.5]; [5.89, 6.78] | [6.11, 6.55]; [6.45, 6.89] |
| C15 | [4.45, 4.89]; [5, 5] | [5.11, 5.55]; [5.5, 6.5] | [6, 6]; [6.11, 6.55] | [6.45, 6.89]; [6.5, 7.5] |
| C16 | [7, 7]; [8, 8] | [5.11, 5.55]; [6.11, 6.55] | [6, 6]; [6.11, 6.55] | [6.11, 6.55]; [6.5, 7.5] |
| C17 | [5.11, 5.55]; [5.45, 5.89] | [4.5, 5.5]; [5.11, 5.55] | [5.11, 5.55]; [6.11, 6.55] | [5.5, 6.5]; [6.45, 6.89] |
| C21 | [4.45, 4.89]; [5.11, 5.55] | [5.45, 5.89]; [6.11, 6.55] | [6.45, 6.89]; [6.45, 6.89] | [6.45, 6.89]; [6.5, 7.5] |
| C22 | [4.45, 4.89]; [5, 5] | [4.5, 5.5]; [4.5, 5.5] | [4.89, 6.39]; [5.89, 7.39] | [5.5, 6.5]; [6.11, 6.55] |
| C23 | [5, 5]; [5.45, 5.89] | [5.45, 5.89]; [5.89, 6.78] | [4.89, 5.78]; [5.89, 6.78] | [4.5, 5.5]; [5.45, 5.89] |
| C24 | [2.45, 2.89]; [3.11, 3.55] | [3, 3]; [3.45, 3.89] | [3.45, 3.89]; [3.5, 4.5] | [4, 4]; [4.11, 4.55] |
| C25 | [3, 3]; [4, 4] | [4.5, 5.5]; [5.11, 5.55] | [4.22, 5.11]; [4.5, 5.5] | [5.11, 5.55]; [6.11, 6.55] |
| C26 | [4.11, 4.55]; [5, 5] | [5.11, 5.55]; [6, 6] | [5.45, 5.89]; [5.5, 6.5] | [6, 6]; [6.11, 6.55] |
| C27 | [2.45, 2.89]; [2.45, 2.89] | [3.5, 4.5]; [4.5, 5.5] | [4.89, 5.78]; [4.89, 6.39] | [4.89, 5.78]; [5.5, 6.5] |
| C31 | [4.11, 4.55]; [4.5, 5.5] | [4.11, 4.55]; [4.45, 4.89] | [4.45, 4.89]; [5.45, 5.89] | [5.45, 5.89]; [6, 6] |
| C32 | [5.45, 5.89]; [6, 6] | [5, 5]; [5.45, 5.89] | [5.45, 5.89]; [6.45, 6.89] | [4.89, 5.78]; [5.45, 5.89] |
| C33 | [4.22, 5.11]; [4.22, 5.11] | [5, 5]; [5.45, 5.89] | [4.5, 5.5]; [4.5, 5.5] | [4.5, 5.5]; [5.45, 5.89] |
| C34 | [3.11, 3.55]; [3.45, 3.89] | [4, 4]; [4.11, 4.55] | [3.28, 5.28]; [3.89, 5.39] | [3.89, 5.39]; [4.5, 5.5] |
| C35 | [4.11, 4.55]; [5.11, 5.55] | [3.45, 3.89]; [4, 4] | [3.89, 5.39]; [4.5, 5.5] | [4.45, 4.89]; [5, 5] |
| C36 | [4.45, 4.89]; [4.45, 4.89] | [4.45, 4.89]; [5, 5] | [4.5, 5.5]; [5.11, 5.55] | [3.11, 3.55]; [4, 4] |
| C37 | [3.11, 3.55]; [4, 4] | [3.45, 3.89]; [4.11, 4.55] | [3.5, 4.5]; [4.45, 4.89] | [4.45, 4.89]; [4.5, 5.5] |
| A1 | A2 | A3 | A4 | |
|---|---|---|---|---|
| C11 | [0.44, 1.03], [0.97, 1.8] | [0.32, 0.62], [0.84, 1.06] | [0.56, 0.78], [0.79, 1.38] | [0.38, 0.63], [0.6, 1.33] |
| C12 | [0.89, 0.94], [1.06, 1.13] | [0.77, 0.88], [1, 1] | [0.82, 0.92], [1.02, 1.08] | [0.77, 0.88], [1, 1] |
| C13 | [0.6, 0.76], [0.83, 0.96] | [0.56, 0.71], [0.78, 0.91] | [0.74, 1.01], [0.9, 1.21] | [0.83, 1.02], [0.98, 1.13] |
| C14 | [0.87, 0.94], [1.07, 1.15] | [0.78, 0.84], [0.83, 0.96] | [0.79, 0.93], [0.9, 1.11] | [0.87, 0.94], [0.98, 1.13] |
| C15 | [0.59, 0.75], [0.73, 0.78] | [0.68, 0.85], [0.8, 1.01] | [0.8, 0.92], [0.89, 1.02] | [0.86, 1.06], [0.94, 1.16] |
| C16 | [0.88, 0.88], [1.14, 1.14] | [0.64, 0.69], [0.87, 0.94] | [0.75, 0.75], [0.87, 0.94] | [0.76, 0.82], [0.93, 1.07] |
| C17 | [0.74, 0.86], [0.84, 1.07] | [0.74, 0.86], [0.79, 1.01] | [0.74, 0.86], [0.94, 1.19] | [0.8, 1.01], [0.99, 1.25] |
| C21 | [0.59, 0.75], [0.74, 0.86] | [0.73, 0.91], [0.89, 1.02] | [0.86, 1.06], [0.94, 1.07] | [0.86, 1.06], [0.94, 1.16] |
| C22 | [0.6, 0.8], [0.77, 0.91] | [0.61, 0.9], [0.69, 1] | [0.66, 1.05], [0.91, 1.34] | [0.74, 1.06], [0.94, 1.19] |
| C23 | [0.74, 0.85], [0.93, 1.08] | [0.8, 1], [1, 1.24] | [0.72, 0.98], [1, 1.24] | [0.66, 0.93], [0.93, 1.08] |
| C24 | [0.54, 0.73], [0.78, 0.89] | [0.66, 0.73], [0.86, 0.97] | [0.76, 0.95], [0.88, 1.13] | [0.88, 0.97], [1.03, 1.14] |
| C25 | [0.46, 0.49], [0.72, 0.78] | [0.69, 0.9], [0.92, 1.09] | [0.64, 0.84], [0.81, 1.08] | [0.78, 0.91], [1.1, 1.28] |
| C26 | [0.63, 0.74], [0.83, 0.83] | [0.78, 0.91], [1, 1] | [0.83, 0.96], [0.92, 1.08] | [0.92, 0.98], [1.02, 1.09] |
| C27 | [0.38, 0.53], [0.42, 0.59] | [0.54, 0.82], [0.78, 1.12] | [0.75, 1.05], [0.85, 1.31] | [0.75, 1.05], [0.95, 1.33] |
| C31 | [0.69, 0.76], [0.76, 1.01] | [0.69, 0.76], [0.76, 0.9] | [0.74, 0.82], [0.93, 1.08] | [0.91, 0.98], [1.02, 1.1] |
| C32 | [0.79, 0.91], [1.02, 1.1] | [0.73, 0.78], [0.93, 1.08] | [0.79, 0.91], [1.1, 1.26] | [0.71, 0.9], [0.93, 1.08] |
| C33 | [0.72, 0.94], [0.77, 1.02] | [0.85, 0.92], [0.99, 1.18] | [0.76, 1.01], [0.82, 1.1] | [0.76, 1.01], [0.99, 1.18] |
| C34 | [0.57, 0.79], [0.64, 0.97] | [0.73, 0.89], [0.76, 1.14] | [0.6, 1.17], [0.72, 1.35] | [0.71, 1.2], [0.83, 1.38] |
| C35 | [0.74, 0.89], [0.95, 1.25] | [0.62, 0.76], [0.74, 0.9] | [0.7, 1.05], [0.83, 1.24] | [0.8, 0.96], [0.93, 1.12] |
| C36 | [0.64, 0.8], [0.82, 0.9] | [0.62, 0.71], [0.82, 0.9] | [0.56, 0.69], [0.73, 0.89] | [0.78, 0.89], [1.13, 1.29] |
| C37 | [0.57, 0.79], [0.82, 0.9] | [0.63, 0.86], [0.84, 1.02] | [0.64, 1], [0.91, 1.1] | [0.81, 1.09], [0.92, 1.24] |
| Si | AV | Rank | |||
|---|---|---|---|---|---|
| 0.680 | 0.838 | 0.882 | 1.061 | 0.865 | 3 |
| 0.671 | 0.821 | 0.863 | 1.016 | 0.842 | 4 |
| 0.737 | 0.931 | 0.901 | 1.154 | 0.931 | 2 |
| 0.765 | 0.943 | 0.942 | 1.159 | 0.952 | 1 |
| Criteria | Criteria | ||||
|---|---|---|---|---|---|
| C1 | 0.097 | C8 | 0.051 | C15 | 0.034 |
| C2 | 1.000 | C9 | 0.069 | C16 | 0.043 |
| C3 | 0.067 | C10 | 0.036 | C17 | 0.053 |
| C4 | 0.096 | C11 | 0.028 | C18 | 0.031 |
| C5 | 0.064 | C12 | 0.038 | C19 | 0.035 |
| C6 | 0.069 | C13 | 0.046 | C20 | 0.022 |
| C7 | 0.052 | C14 | 0.043 | C21 | 0.027 |
| Criteria | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | S14 | S15 | S16 | S17 | S18 | S19 | S20 | S21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.0971 | 0.0000 | 0.0671 | 0.0960 | 0.0636 | 0.0694 | 0.0520 | 0.0509 | 0.0694 | 0.0358 | 0.0277 | 0.0382 | 0.0462 | 0.0428 | 0.0335 | 0.0428 | 0.0532 | 0.0312 | 0.0347 | 0.0220 | 0.0266 |
| C2 | 0.0923 | 0.0500 | 0.0637 | 0.0912 | 0.0604 | 0.0659 | 0.0494 | 0.0483 | 0.0659 | 0.0340 | 0.0264 | 0.0362 | 0.0439 | 0.0406 | 0.0318 | 0.0406 | 0.0505 | 0.0297 | 0.0329 | 0.0209 | 0.0253 |
| C3 | 0.0874 | 0.1000 | 0.0603 | 0.0864 | 0.0572 | 0.0624 | 0.0468 | 0.0458 | 0.0624 | 0.0323 | 0.0250 | 0.0343 | 0.0416 | 0.0385 | 0.0302 | 0.0385 | 0.0479 | 0.0281 | 0.0312 | 0.0198 | 0.0239 |
| C4 | 0.0825 | 0.1500 | 0.0570 | 0.0816 | 0.0540 | 0.0590 | 0.0442 | 0.0432 | 0.0590 | 0.0305 | 0.0236 | 0.0324 | 0.0393 | 0.0364 | 0.0285 | 0.0364 | 0.0452 | 0.0265 | 0.0295 | 0.0187 | 0.0226 |
| C5 | 0.0777 | 0.2000 | 0.0536 | 0.0768 | 0.0509 | 0.0555 | 0.0416 | 0.0407 | 0.0555 | 0.0287 | 0.0222 | 0.0305 | 0.0370 | 0.0342 | 0.0268 | 0.0342 | 0.0425 | 0.0250 | 0.0277 | 0.0176 | 0.0213 |
| C6 | 0.0728 | 0.2500 | 0.0503 | 0.0720 | 0.0477 | 0.0520 | 0.0390 | 0.0382 | 0.0520 | 0.0269 | 0.0208 | 0.0286 | 0.0347 | 0.0321 | 0.0251 | 0.0321 | 0.0399 | 0.0234 | 0.0260 | 0.0165 | 0.0199 |
| C7 | 0.0680 | 0.3000 | 0.0469 | 0.0672 | 0.0445 | 0.0486 | 0.0364 | 0.0356 | 0.0486 | 0.0251 | 0.0194 | 0.0267 | 0.0324 | 0.0299 | 0.0235 | 0.0299 | 0.0372 | 0.0218 | 0.0243 | 0.0154 | 0.0186 |
| C8 | 0.0631 | 0.3500 | 0.0436 | 0.0624 | 0.0413 | 0.0451 | 0.0338 | 0.0331 | 0.0451 | 0.0233 | 0.0180 | 0.0248 | 0.0301 | 0.0278 | 0.0218 | 0.0278 | 0.0346 | 0.0203 | 0.0225 | 0.0143 | 0.0173 |
| C9 | 0.0583 | 0.4000 | 0.0402 | 0.0576 | 0.0382 | 0.0416 | 0.0312 | 0.0305 | 0.0416 | 0.0215 | 0.0166 | 0.0229 | 0.0277 | 0.0257 | 0.0201 | 0.0257 | 0.0319 | 0.0187 | 0.0208 | 0.0132 | 0.0160 |
| C10 | 0.0534 | 0.4500 | 0.0369 | 0.0528 | 0.0350 | 0.0382 | 0.0286 | 0.0280 | 0.0382 | 0.0197 | 0.0153 | 0.0210 | 0.0254 | 0.0235 | 0.0184 | 0.0235 | 0.0292 | 0.0172 | 0.0191 | 0.0121 | 0.0146 |
| C11 | 0.0486 | 0.5000 | 0.0335 | 0.0480 | 0.0318 | 0.0347 | 0.0260 | 0.0254 | 0.0347 | 0.0179 | 0.0139 | 0.0191 | 0.0231 | 0.0214 | 0.0168 | 0.0214 | 0.0266 | 0.0156 | 0.0173 | 0.0110 | 0.0133 |
| C12 | 0.0437 | 0.5500 | 0.0302 | 0.0432 | 0.0286 | 0.0312 | 0.0234 | 0.0229 | 0.0312 | 0.0161 | 0.0125 | 0.0172 | 0.0208 | 0.0192 | 0.0151 | 0.0192 | 0.0239 | 0.0140 | 0.0156 | 0.0099 | 0.0120 |
| C13 | 0.0388 | 0.6000 | 0.0268 | 0.0384 | 0.0254 | 0.0277 | 0.0208 | 0.0203 | 0.0277 | 0.0143 | 0.0111 | 0.0153 | 0.0185 | 0.0171 | 0.0134 | 0.0171 | 0.0213 | 0.0125 | 0.0139 | 0.0088 | 0.0106 |
| C14 | 0.0340 | 0.6500 | 0.0235 | 0.0336 | 0.0223 | 0.0243 | 0.0182 | 0.0178 | 0.0243 | 0.0125 | 0.0097 | 0.0134 | 0.0162 | 0.0150 | 0.0117 | 0.0150 | 0.0186 | 0.0109 | 0.0121 | 0.0077 | 0.0093 |
| C15 | 0.0291 | 0.7000 | 0.0201 | 0.0288 | 0.0191 | 0.0208 | 0.0156 | 0.0153 | 0.0208 | 0.0108 | 0.0083 | 0.0114 | 0.0139 | 0.0128 | 0.0101 | 0.0128 | 0.0160 | 0.0094 | 0.0104 | 0.0066 | 0.0080 |
| C16 | 0.0243 | 0.7500 | 0.0168 | 0.0240 | 0.0159 | 0.0173 | 0.0130 | 0.0127 | 0.0173 | 0.0090 | 0.0069 | 0.0095 | 0.0116 | 0.0107 | 0.0084 | 0.0107 | 0.0133 | 0.0078 | 0.0087 | 0.0055 | 0.0066 |
| C17 | 0.0194 | 0.8000 | 0.0134 | 0.0192 | 0.0127 | 0.0139 | 0.0104 | 0.0102 | 0.0139 | 0.0072 | 0.0055 | 0.0076 | 0.0092 | 0.0086 | 0.0067 | 0.0086 | 0.0106 | 0.0062 | 0.0069 | 0.0044 | 0.0053 |
| C18 | 0.0146 | 0.8500 | 0.0101 | 0.0144 | 0.0095 | 0.0104 | 0.0078 | 0.0076 | 0.0104 | 0.0054 | 0.0042 | 0.0057 | 0.0069 | 0.0064 | 0.0050 | 0.0064 | 0.0080 | 0.0047 | 0.0052 | 0.0033 | 0.0040 |
| C19 | 0.0097 | 0.9000 | 0.0067 | 0.0096 | 0.0064 | 0.0069 | 0.0052 | 0.0051 | 0.0069 | 0.0036 | 0.0028 | 0.0038 | 0.0046 | 0.0043 | 0.0034 | 0.0043 | 0.0053 | 0.0031 | 0.0035 | 0.0022 | 0.0027 |
| C20 | 0.0049 | 0.9500 | 0.0034 | 0.0048 | 0.0032 | 0.0035 | 0.0026 | 0.0025 | 0.0035 | 0.0018 | 0.0014 | 0.0019 | 0.0023 | 0.0021 | 0.0017 | 0.0021 | 0.0027 | 0.0016 | 0.0017 | 0.0011 | 0.0013 |
| C21 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stević, Ž.; Durmić, E.; Gajić, M.; Pamučar, D.; Puška, A. A Novel Multi-Criteria Decision-Making Model: Interval Rough SAW Method for Sustainable Supplier Selection. Information 2019, 10, 292. https://doi.org/10.3390/info10100292
Stević Ž, Durmić E, Gajić M, Pamučar D, Puška A. A Novel Multi-Criteria Decision-Making Model: Interval Rough SAW Method for Sustainable Supplier Selection. Information. 2019; 10(10):292. https://doi.org/10.3390/info10100292
Chicago/Turabian StyleStević, Željko, Elmina Durmić, Mladen Gajić, Dragan Pamučar, and Adis Puška. 2019. "A Novel Multi-Criteria Decision-Making Model: Interval Rough SAW Method for Sustainable Supplier Selection" Information 10, no. 10: 292. https://doi.org/10.3390/info10100292







