Networked Euler-Lagrangian Systems Synchronization under Time-Varying Communicating Delays
Abstract
1. Introduction
2. Preliminaries
3. Modelling and Problem Formulation
3.1. Euler-Lagrange Dynamics
3.2. Kinematics
3.3. Control Objective
4. Cooperative Task-Space Synchronous Protocol Design
5. Stability Analysis
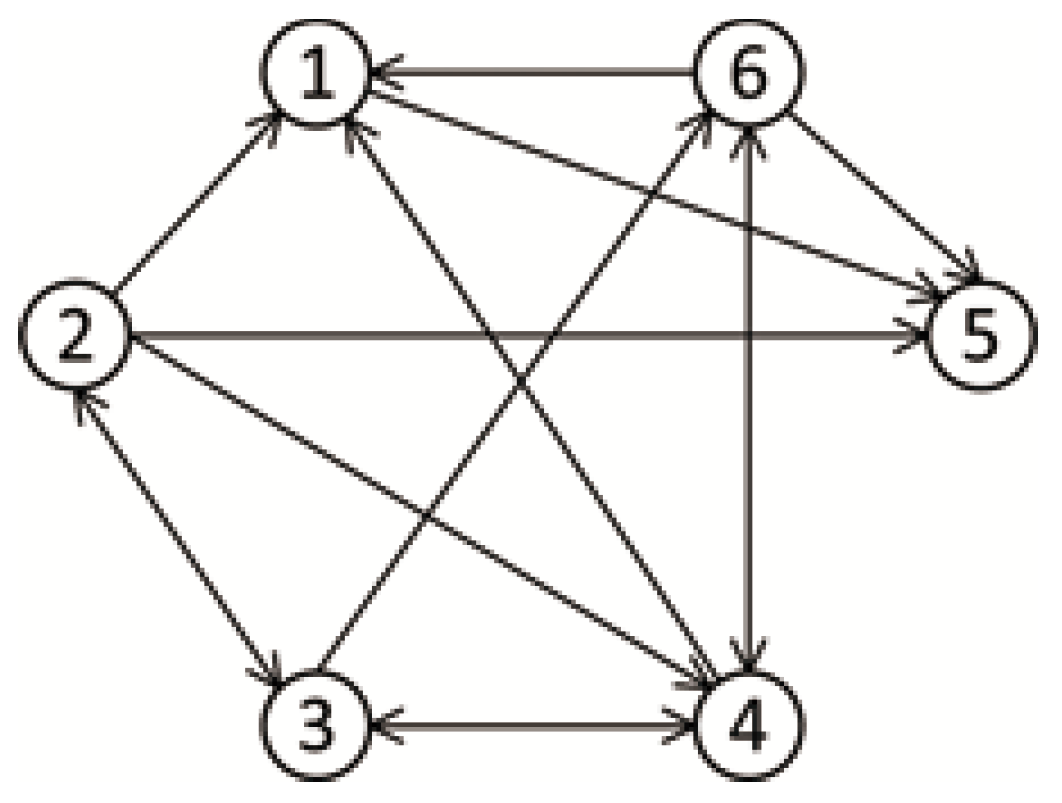
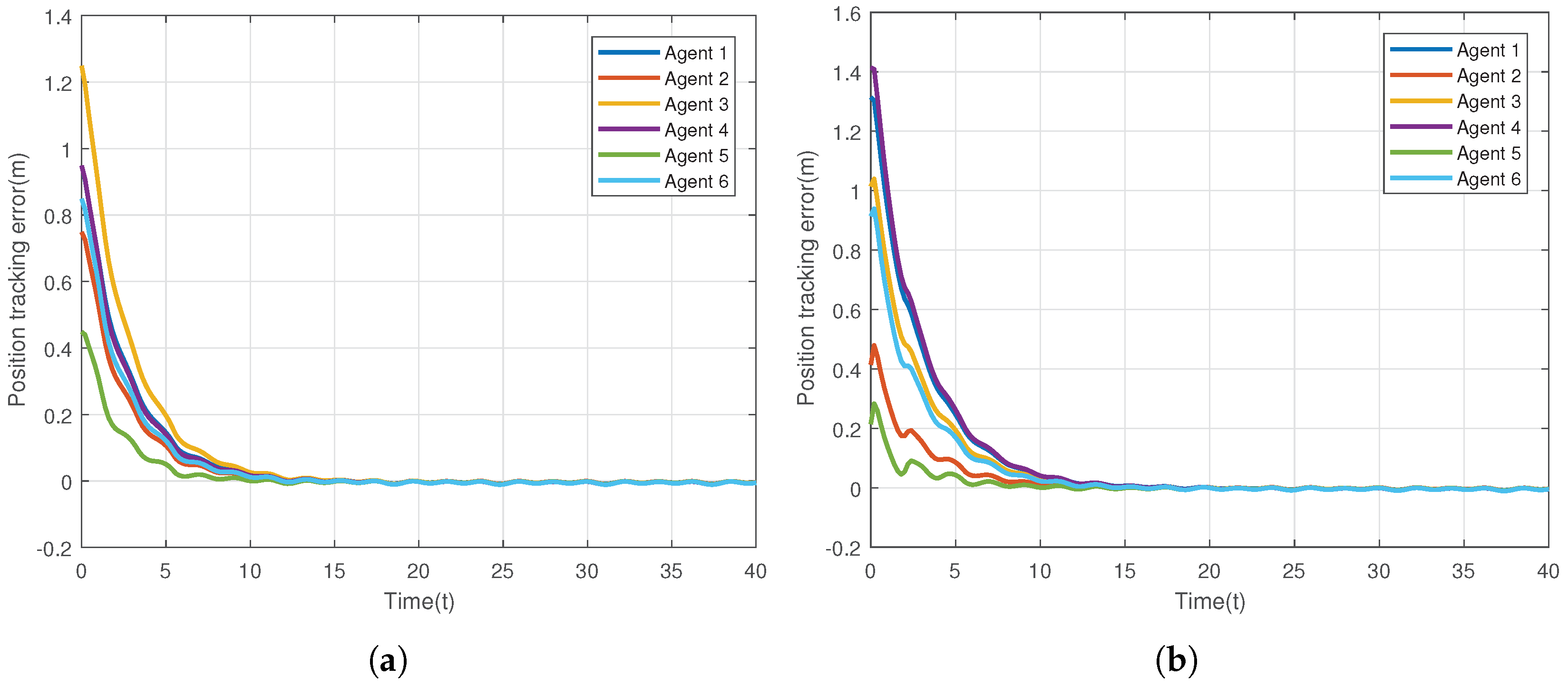
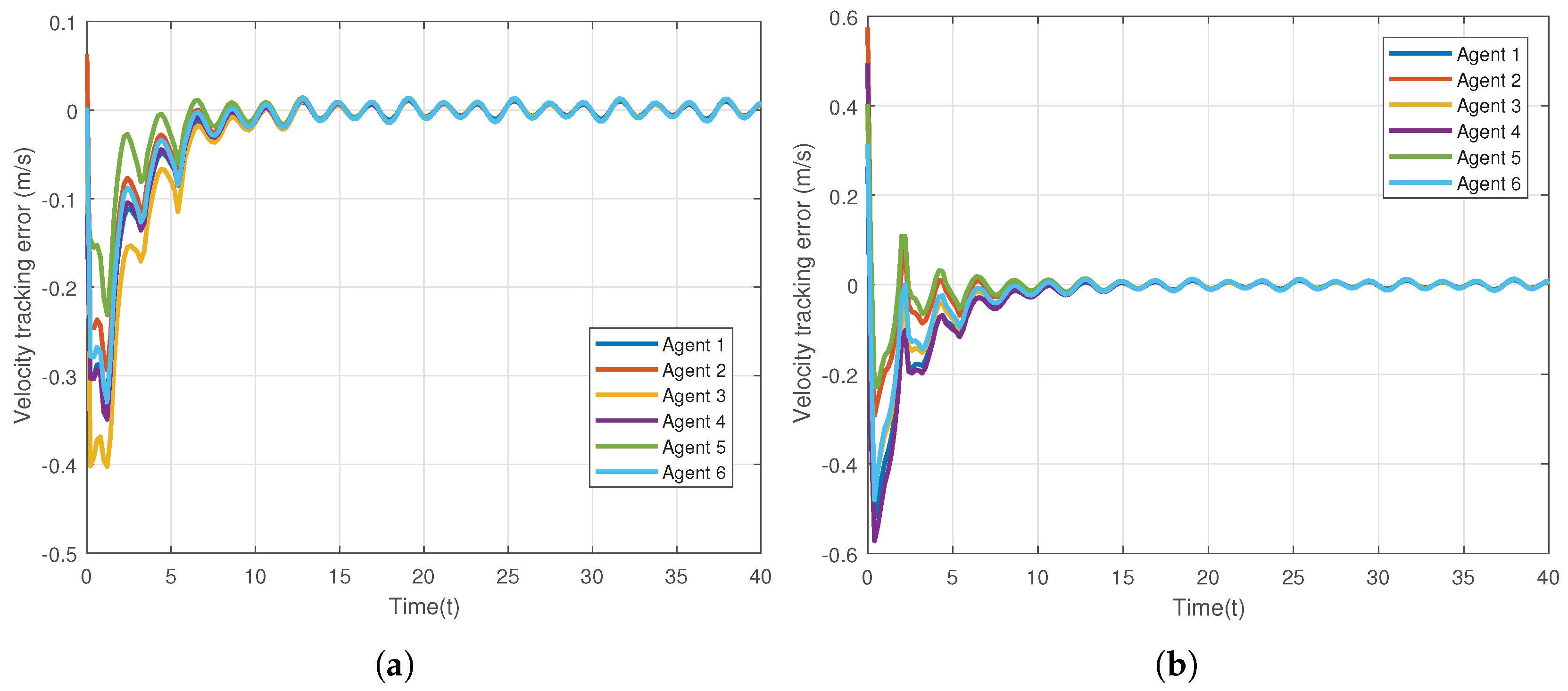
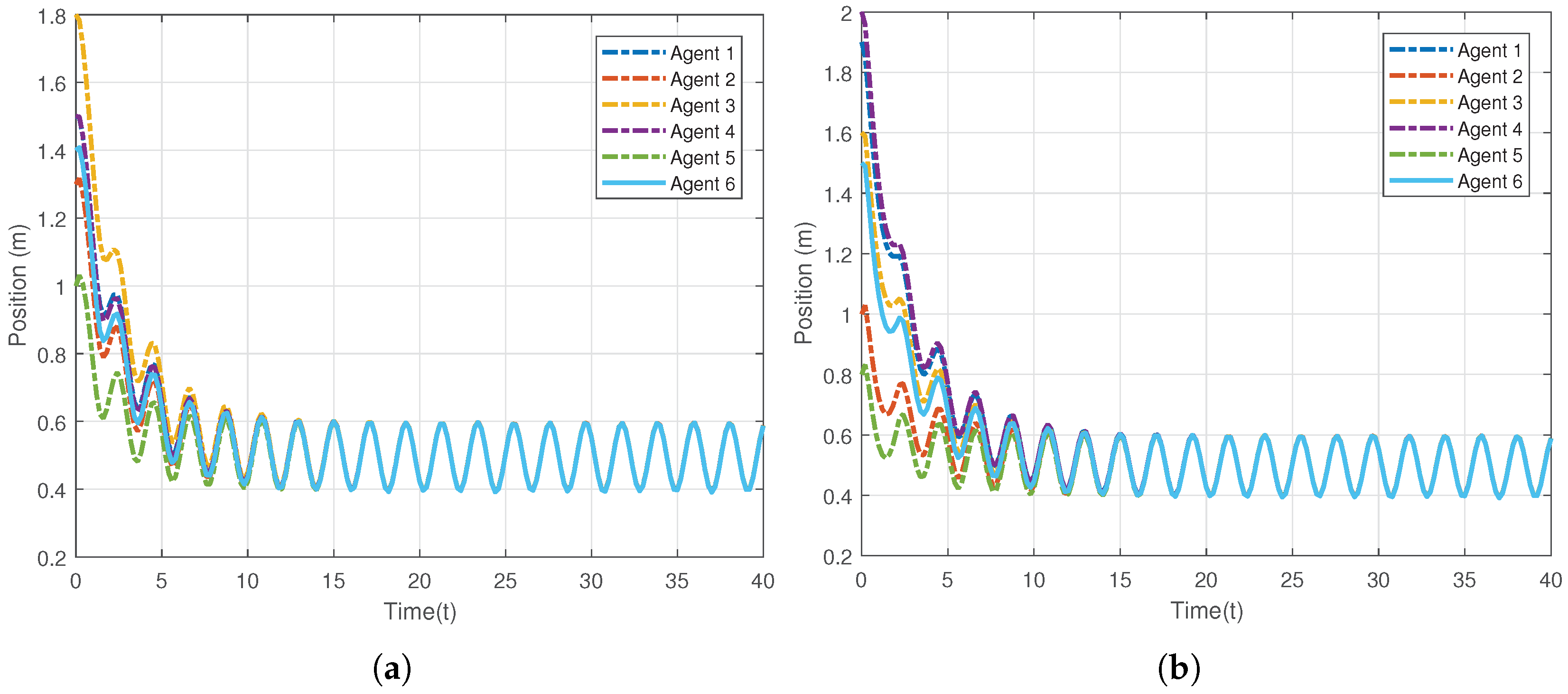
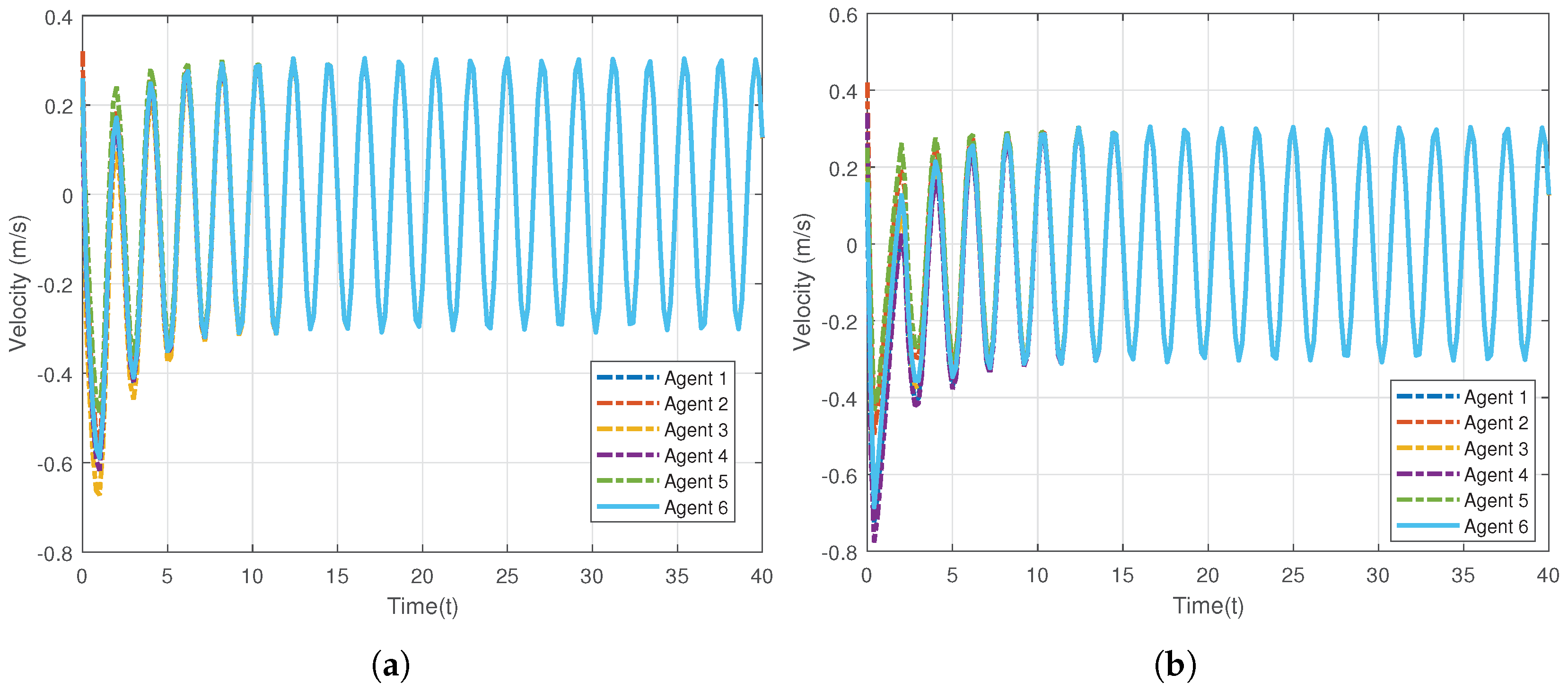
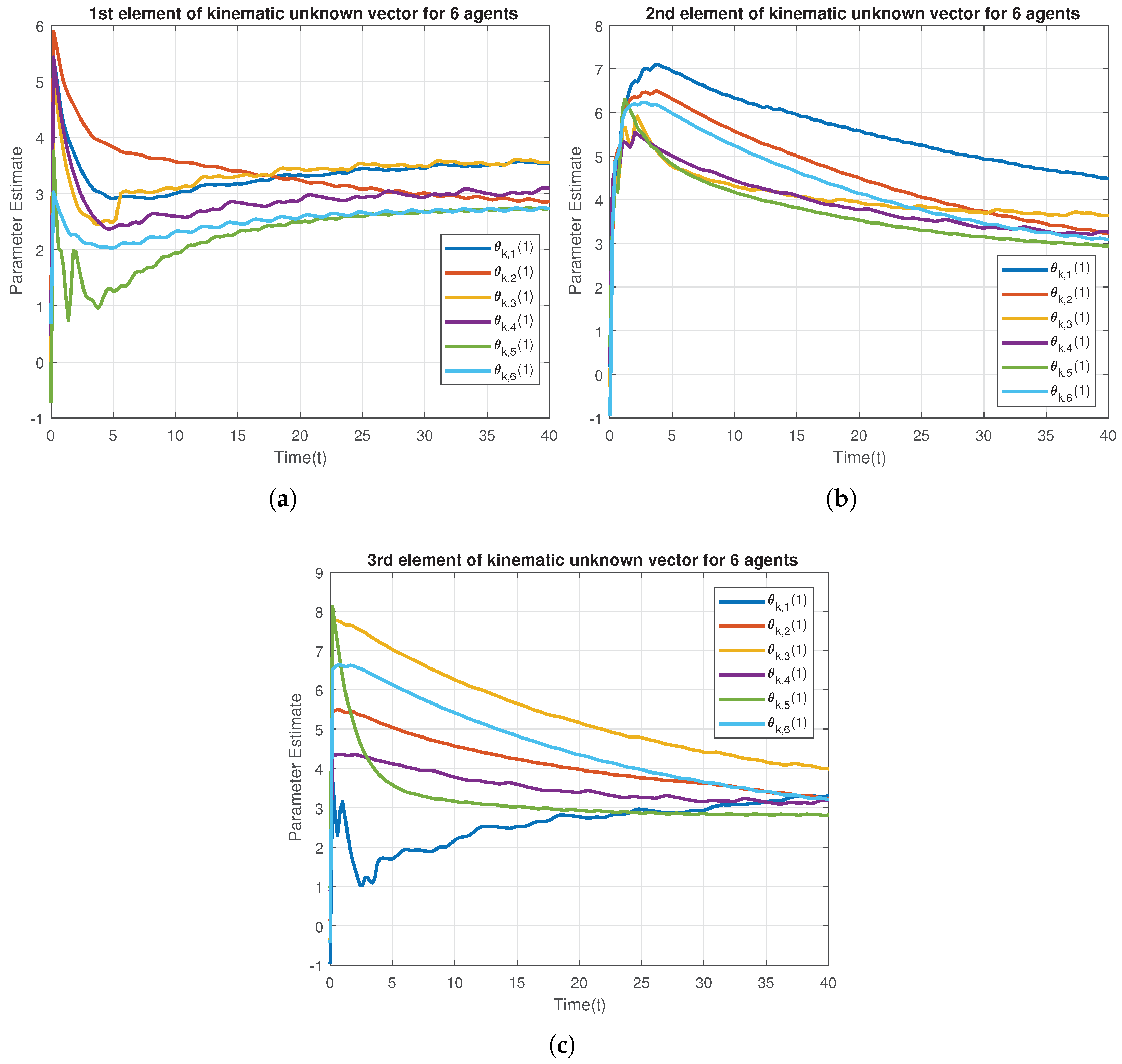
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rahman, A.A.; Ashraf, M.; Van Oorschot, P.C. CPV: Delay-Based Location Verification for the Internet. IEEE Trans. Dependable Secure Comput. 2017, 14, 130–144. [Google Scholar]
- Liu, Y.; Liu, A.; Hu, Y.; Li, Z.; Choi, Y.; Sekiya, H.; Li, J. FFSC: An Energy Efficiency Communications Approach for Delay Minimizing in Internet of Things. IEEE Access 2017, 4, 3775–3793. [Google Scholar] [CrossRef]
- Bashan, A.; Bartsch, R.P.; Kantelhardt, J.W.; Havlin, S.; Ivanov, P. Network physiology reveals relations between network topology and physiological function. Nat. Commun. 2012, 3, 702. [Google Scholar] [CrossRef] [PubMed]
- Bartsch, R.P.; Liu, K.K.; Bashan, A.; Pch, I. Network Physiology: How Organ Systems Dynamically Interact. PLoS ONE 2015, 10, e0142143. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.L.; Bartsch Ronny, P.; Lin, A.; Mantegna Rosario, N.; Plamen, C.I. Plasticity of brain wave network interactions and evolution across physiologic states. Front. Neural Circuits 2015, 9, 62. [Google Scholar] [CrossRef]
- Chase Ivan, D. Cooperative and Noncooperative Behavior in Animals. Am. Nat. 1980, 115, 827–857. [Google Scholar] [CrossRef]
- Rilling, J.K.; Demarco, A.C.; Hackett, P.D.; Thompson, R.; Ditzen, B.; Patel, R.; Pagnoni, G. Effects of intranasal oxytocin and vasopressin on cooperative behavior and associated brain activity in men. Psychoneuroendocrinology 2012, 37, 447–461. [Google Scholar] [CrossRef]
- Wang, H. Consensus of Networked Mechanical Systems with Time Delays: A Unified Framework. IEEE Trans. Autom. Control 2013. [Google Scholar] [CrossRef]
- Islam, S.; Liu, P.X.; Saddik Abdulmotaleb, E. Observer-based force reflecting robust coordination control for networked bilateral shared telerobotic system. Int. J. Control 2018. [Google Scholar] [CrossRef]
- Chopra, N.; Spong Mark, W. Adaptive Synchronization of Bilateral Teleoperators with Time Delay. Automatica 2008, 44, 2142–2148. [Google Scholar] [CrossRef]
- Nitendra, N.; Enver, T.; Darren, D. Teleoperation with kinematically redundant robot manipulators with sub-task objectives. Robotica 2009, 27, 1027–1038. [Google Scholar]
- Lorenzo, S.; Cristian, S.; Alessio, L.; Cesare, F. Decentralized Control of Cooperative Robotic Systems for Arbitrary Setpoint Tracking while Avoiding Collisions. IFAC-Pap. Online 2015, 48, 57–62. [Google Scholar]
- Cheah, C.C.; Liu, C.; Slotine, J.J.E. Adaptive Tracking Control for Robots with Unknown Kinematic and Dynamic Properties; Sage Publications Inc.: Thousand Oaks, CA, USA, 2006. [Google Scholar]
- Nikhil, C.; Chen, L.Y. Controlled Synchronization of Mechanical Systems. In Proceedings of the ASME 2008 Dynamic Systems and Control Conference, Ann Arbor, MI, USA, 20–22 October 2008; pp. 1221–1228. [Google Scholar]
- Alexander, F.J.; Murray Richard, M. Information flow and cooperative control of vehicle formations. IFAC Proc. 2002, 35, 115–120. [Google Scholar]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Lin, Z.; Broucke, M.; Francis, B. Local control strategies for groups of mobile autonomous agents. IEEE Trans. Autom. Control 2004, 49, 622–629. [Google Scholar] [CrossRef]
- Olfatisaber, R.; Murray Richard, M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ziyang, M.; Zhongkui, L.; Athanasios, V.; Shiming, C. Delay-Induced Synchronization of Identical Linear Multiagent Systems. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 43, 476–489. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, T.; Yang, G.H.; Liang, H. Distributed Cooperative Optimal Control for Multiagent Systems on Directed Graphs: An Inverse Optimal Approach. IEEE Trans. Cybern. 2015, 45, 1315–1326. [Google Scholar] [CrossRef]
- Wang, T.; Qiu, J.; Shen, Y.; Gao, H.; Fan, J.; Chai, T. Performance-Based Adaptive Fuzzy Tracking Control for Networked Industrial Processes. IEEE Trans. Cybern. 2016, 46, 1760–1770. [Google Scholar] [CrossRef]
- Li, T.; Zhao, H. Global finite-time adaptive control for uncalibrated robot manipulator based on visual servoing. ISA Trans. 2017. [Google Scholar] [CrossRef]
- Wang, H. Adaptive visual tracking for robotic systems without image-space velocity measurement. Automatica 2015, 55, 294–301. [Google Scholar] [CrossRef]
- Wang, H. Adaptive Control of Robot Manipulators With Uncertain Kinematics and Dynamics. IEEE Trans. Autom. Control 2017, 62, 948–954. [Google Scholar] [CrossRef]
- Wang, T.; Qiu, J.; Gao, H. Adaptive Neural Control of Stochastic Nonlinear Time-Delay Systems with Multiple Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2016, 99, 1–9. [Google Scholar] [CrossRef]
- Zhang, F.; Dawson, D.M.; De Queiroz, M.S.; Dixon, W.E. Global adaptive output feedback tracking control of robot manipulators. IEEE Trans. Autom. Control 2002, 45, 1203–1208. [Google Scholar] [CrossRef]
- Ren, W. Distributed leaderless consensus algorithms for networked Euler–Lagrange systems. Int. J. Control 2009, 82, 2137–2149. [Google Scholar] [CrossRef]
- Jo, C.S.; Jacques, S.J. Cooperative Robot Control and Concurrent Synchronization of Lagrangian Systems. IEEE Trans. Robot. 2007, 25, 686–700. [Google Scholar]
- Chopra, N.; Spong, M.W. Output Synchronization of Nonlinear Systems with Time Delay in Communication. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4986–4992. [Google Scholar]
- Liu, Y.C.; Chopra, N. Controlled Synchronization of Heterogeneous Robotic Manipulators in the Task Space. IEEE Trans. Robot. 2012, 28, 268–275. [Google Scholar] [CrossRef]
- Emmanuel, N.; Romeo, O.; Luis, B.; David, H. Synchronization of Networks of Nonidentical Euler-Lagrange Systems with Uncertain Parameters and Communication Delays. IEEE Trans. Autom. Control 2011, 56, 935–941. [Google Scholar]
- Liu, Y.C.; Chopra, N. Synchronization of networked robotic systems on strongly connected graphs. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 3194–3199. [Google Scholar]
- Wang, H. Passivity based synchronization for networked robotic systems with uncertain kinematics and dynamics. Automatica 2013, 49, 755–761. [Google Scholar] [CrossRef]
- Liang, X.; Wang, H.; Liu, Y.H.; Chen, W.; Hu, G.; Zhao, J. Adaptive Task-Space Cooperative Tracking Control of Networked Robotic Manipulators Without Task-Space Velocity Measurements. IEEE Trans. Cybern. 2015, 46, 2386–2398. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Min, X.; Ahmed, A.; Tasawar, H. Bifurcations in a delayed fractional complex-valued neural network. Appl. Math. Comput. 2017, 292, 210–227. [Google Scholar] [CrossRef]
- Fei, Z.; Guan, C.; Gao, H. Exponential Synchronization of Networked Chaotic Delayed Neural Network by a Hybrid Event Trigger Scheme. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2558–2567. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Huang, L.; Tang, L.; Zhuang, J. Generalized pinning synchronization of delayed Cohen-Grossberg neural networks with discontinuous activations. Neural Netw. 2018, 104, 80–92. [Google Scholar] [CrossRef] [PubMed]
- Zouari, F.; Ibeas, A.; Boulkroune, A.; Cao, J.; Mehdi, M.A. Adaptive neural output-feedback control for nonstrict-feedback time-delay fractional-order systems with output constraints and actuator nonlinearities. Neural Netw. 2018, 105, 256–276. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.H.; Wang, H.; Chen, W.; Zhou, D. Adaptive visual servoing using common image features with unknown geometric parameters. Automatica 2013, 49, 2453–2460. [Google Scholar] [CrossRef]
- Cheng, L.; Hou, Z.G.; Tan, M.; Liu, D. Multi-Agent Based Adaptive Consensus Control for Multiple Manipulators with Kinematic Uncertainties. In Proceedings of the 2008 IEEE International Symposium on Intelligent Control, San Antonio, TX, USA, 3–5 September 2008; pp. 189–194. [Google Scholar]
- Li, X.; Luo, X.; Wang, J.; Zhu, Y.; Guan, X. Bearing-Based Formation Control of Networked Robotic Systems with Parametric Uncertainties. Neurocomputing 2018. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Y. Task-Space Consensus of Networked Robotic Systems: Separation and Manipulability. arXiv, 2018; arXiv:1702.06265. [Google Scholar]
- Chris, G.; Gordon, R. Algebraic Graph Theory; World Book Inc.: Chicago, IL, USA, 2004. [Google Scholar]
- Slotine, J.-J.E.; Jean-Jacques, E.; Li, W. Applied Nonlinear Control; China Machine Press: Beijing, China, 2004. [Google Scholar]
- Wang, H.; Liu, Y.H. Adaptive Visual Servoing of Robot Manipulators Using Uncalibrated Eye-in-hand Visual Feedback. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 386–391. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhao, Z.; Li, T. Networked Euler-Lagrangian Systems Synchronization under Time-Varying Communicating Delays. Information 2019, 10, 14. https://doi.org/10.3390/info10010014
Wang H, Zhao Z, Li T. Networked Euler-Lagrangian Systems Synchronization under Time-Varying Communicating Delays. Information. 2019; 10(1):14. https://doi.org/10.3390/info10010014
Chicago/Turabian StyleWang, Hongjun, Zhuoqun Zhao, and Tao Li. 2019. "Networked Euler-Lagrangian Systems Synchronization under Time-Varying Communicating Delays" Information 10, no. 1: 14. https://doi.org/10.3390/info10010014
APA StyleWang, H., Zhao, Z., & Li, T. (2019). Networked Euler-Lagrangian Systems Synchronization under Time-Varying Communicating Delays. Information, 10(1), 14. https://doi.org/10.3390/info10010014





