Semantic Distance Spreading Across Entities in Linked Open Data ^†

Abstract

Recommender systems can utilize Linked Open Data (LOD) to overcome some challenges, such as the item cold start problem, as well as the problem of explaining the recommendation. There are several techniques in exploiting LOD in recommender systems; one approach, called Linked Data Semantic Distance (LDSD), considers nearby resources to be recommended by calculating a semantic distance between resources. The LDSD approach, however, has some drawbacks such as its inability to measure the semantic distance resources that are not directly linked to each other. In this paper, we first propose another variation of the LDSD approach, called wtLDSD, by extending indirect distance calculations to include the effect of multiple links of differing properties within LOD, while prioritizing link properties. Next, we introduce an approach that broadens the coverage of LDSD-based approaches beyond resources that are more than two links apart. Our experimental results show that approaches we propose improve the accuracy of the LOD-based recommendations over our baselines. Furthermore, the results show that the propagation of semantic distance calculation to reflect resources further away in the LOD graph extends the coverage of LOD-based recommender systems.

1. Introduction

Information is generally available online through various mediums such as the world wide web (WWW). This information is primarily provided as unstructured data, such as text that lacks sufficient information for advanced applications to exploit the content effectively. The desire to address this problem has led to the development of new standards and formats that enable consumption and distribution of publicly structured data between different parties; this structured shareable data is known as Linked Open Data (LOD). There are four principles of Linked Open Data [1]. Firstly, the Uniform Resource Identifier (URI) must be used to identify resources in any LOD dataset. Secondly, HTTP URIs must be used to look up resources. Thirdly, useful information must be provided on standard formats (e.g., RDF, SPARQL) at each URI. Lastly, resources are linked for further exploration. There are over one thousand linked data datasets in different fields [2]; some specialize in a particular knowledge domain such as books or music while others are generic, covering many cross-domain concepts such as the popular LOD provider, DBpedia [3]. Due to the extensive offering of structured data in different domains, LOD has been investigated in the field of recommender systems. In particular, LOD provides comprehensive open datasets with multi-domain concepts and relationships to each other, and these relationships enable recommender systems to identify relevant concepts across collections [4]. Furthermore, the LOD standards and techniques facilitate the task of recommender systems by providing standard interfaces for retrieving the data (e.g., RDF, SPARQL), eliminating the need for additional raw data processing. LOD also provides ontological knowledge of data that allows recommender systems to identify the relationship between concepts [5].

The usage of LOD has been explored in different ways in recommender systems, mainly by exploiting its graph nature representation or by various statistical measures [6]. Content-based recommender systems recommend items based on their similarity to the preferences of the user. There are various approaches to estimate the similarity between entities: Distance-based, feature-based, statistical, and hybrid approaches [7]. Distance-based methods estimate the similarity between entities through a distance function such as SimRank [8], PageRank [9], and HITS [10]. Feature-based methods assume that entities can be represented as feature sets, and the similarity of entities is based on the common characteristics between their feature sets; e.g., the Jaccard index [11], Dice’s coefficient [12], and Tversky [13]. Statistical-based similarity methods rely on statistical data generated from the entity underline information and the hybrid methods combines some of these approaches into one.

One approach that exploits the graph structure of LOD estimates resource relatedness as a function of their semantic distance in the graph. The intuition behind this approach is that the more resources linked to each other in the LOD graph, the more related they are. 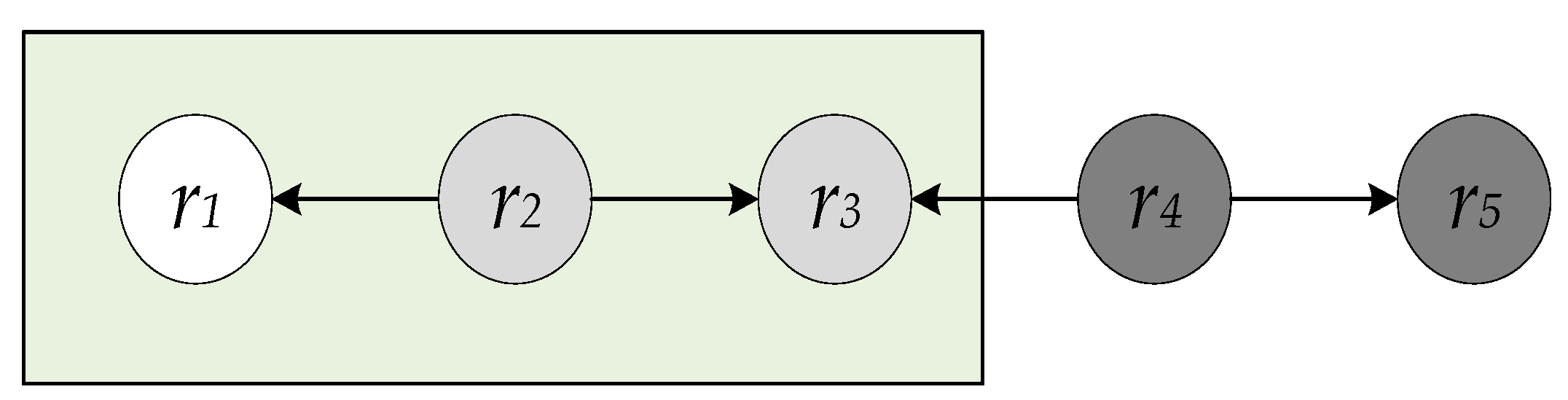This intuition is the principal of LOD resource relatedness measures, the Linked Data Semantic Distance (LDSD) [14], along with a more recent measure based on it, Resource Similarity (Resim) [15]. One of the disadvantages of the LDSD approach is that it calculates only the semantic distance between directly connected resources or indirectly via an intermediate resource. As a result, resources located more than two links away are automatically considered unrelated to each other. For instance, Figure 1 shows an example snapshot of a LOD dataset with five resources. In this example, resources r₂ and r₃ are reachable to the resource r₁ in LDSD; however, resources r₄ and r₅ are not reachable to resource r₁ and therefore are considered as unrelated to r₁. In contrast, Resim improves this limitation by including an additional measure of similarity exclusively to resources that are more than two links apart. However, this additional measure calculates the similarity between resources based on their properties only without considering the graph structure for these more distant resources.

In this paper, we first extend the indirect distance calculations in LDSD to include the effect of multiple links of differing properties within LOD while prioritizing link properties [16]. This extension is incorporated within LDSD to measure the effect of including heterogeneous link types in the calculation of semantic distance, resulting in a new variation of the LDSD approach, called wtLDSD. Next, we introduce an approach that extends the coverage of LDSD-based semantic distance approaches to resources that are more than two links apart [17]. This approach is beneficial in several ways; one of which is to enrich related resources for those isolated resources with sparse links to others. Notably, there is a strong correlation between LOD-based recommender systems performance and the number of resource links, as the accuracy of LOD-based recommender systems declines for sparse resources [15]. Therefore, propagating semantic links further through the graph of LOD increases resource coverage and may lead to a larger recall. Furthermore, even for well-linked resources, propagating links more widely might be beneficial for recommending related resources from another domain, e.g., linking a movie to a related book.

To accomplish this propagation, we utilize an all-pairs shortest path algorithm, the famous Floyd–Warshall algorithm [18], to propagate the semantic distances throughout the graph of linked resources. For the evaluation, we conducted an experiment to estimate the relatedness between musical artists in DBpedia, and it showed that our approach not only increases the span of the semantic distance calculations; it also improves the accuracy of the resulting recommendations over LDSD-based approaches.

This paper is organized as follows: Section 2 presents the related work, followed by background information about Linked Data Semantic Distance (LDSD) in Section 3. Next, Section 4 extends the indirect distance calculations to include the effect of multiple links of differing properties within LOD. Section 5 proposes a propagating approach that extends semantic distance calculations. Section 6 then presents the evaluation of the approaches we propose. Lastly, Section 7 summaries this document and discusses future work.

2. Related Work

There are several works that have focused on distance-based similarity approaches in LOD. Passant [14] introduced an approach, named Linked Data Semantic Distance (LDSD), that enables recommender systems to utilize LOD by estimating the similarity between LOD resources. This similarity is estimated by calculating a semantic distance between LOD resources. This approach depends on only direct links between resources as well as indirect resources through an intermediate resource to compute a semantic distance. Exploiting this approach, Passant in [19] has built a recommender system for music, called dbrec, that utilizes the popular LOD provider, DBpedia, to recommend musical artists and bands. The first step in this system is creating a reduced LOD dataset to enable efficient semantic distance computations. Next, semantic distances are calculated between each pair of resources that represent musical artists or bands using LDSD. Lastly, related musical artists or bands are predicted for the user. Piao et al. [15] introduced another variation of the linked data semantic distance approach named Resource Similarity (Resim) that refined the original LDSD to overcome some of its weaknesses such as equal self-similarity, symmetry, and minimality. They also enhanced Resim in [20] by applying some normalization methods that rely on path occurrences in the data set. They also expanded the number of resources that participate in the semantic distance by using a property-based similarity measure for resources more than two links away. Similarly, Leal et al. [21] introduced another semantic relatedness approach, called Shakti, that estimated the relatedness between LOD resources. The relatedness in this approach is measured through resources proximity. Particularly, the proximity is measured based on the number of indirect links between resources penalized by their distance length. Though, LDSD and Resim accuracy outperform Shakti as confirmed by [15]. Besides, Alfarhood et al. [16] presented improved resource semantic relatedness approaches, wLDSD and wResim, which introduced weights for every link-based calculation in LDSD and Resim. These weights are predicted by estimating the correlation between link properties with their linked resource classes.

Different from distance-based similarity approaches, Likavec et al. [22] proposed a feature-based similarity measure, called Sigmoid similarity, for domain specific ontologies. This method is based on the Dice measure and takes the underlying hierarchy into account. The main idea behind this approach is that similarity between entities increases when they share common features. Additionally, Meymandpour and Davis [7] introduced a semantic similarity measure, called PICSS, based on common and characteristic features between resources. Thus, the similarity between two resources increases when they share more informative features such as features with a low number of occurrences. In addition, Traverso-Ribón and Vidal [23] proposed a semantic similarity approach, called GARUM, based on machine learning. In this approach, a supervised regression algorithm receives several similarity measures of hierarchy, neighborhood, shared information, and attributes and then predicts a final similarity score. The intuition behind this approach is that knowledge represented in the entities accurately describes the entities and makes it possible to determine more precise similarity values. Nguyen et al. [24] studied the usage of two structural context similarity approaches of graphs, SimRank and PageRank, in the domain of LOD recommender systems. They show that the two metrics are capable in this application, and they can generate some novel recommendations but with a high-performance cost.

Damljanovic et al. [4] presented a LOD-based concept recommender system that helps users to improve their web search by using appropriate concept tags and topics. They used both a graph-based and a statistical-based method to estimate concept similarities. They found that the graph-based method outperforms their baseline in accuracy whereas the statistical technique produced better-unexpected results. Likewise, Fernández-Tobías et al. [25] have developed a LOD-based cross-domain recommender system to link concepts from two different domains. They first extract information about the two domains from the LOD datasets, and they then connect concepts using a graph-based distance.

Di Noia et al. [26] demonstrated that LOD could be effectively employed in content-based recommender systems to overcome issues such as the cold start problem. They introduced a content-based recommender system that uses LOD datasets, in particular, DBpedia, Freebase, and LinkedMDB to recommend movies. Their system gathers contextual information about movies such as actors, directors, and genres from LOD datasets, and it then applies a content-based recommendation algorithm to generate recommendation results. Additionally, Ostuni et al. [27] presented a hybrid LOD-based recommender system that relies on users’ implicit feedback. Semantic information about items from the user profile and items in DBpedia are combined into one graph in which path-based features could be extracted from. Ostuni et al. [28] also introduced a content-based recommender system based on semantic item similarities in DBpedia. The semantic similarity between resources is estimated using a neighborhood-based graph kernel that finds local neighborhoods of these items. Figueroa et al. [29] presented a framework, called AlLied, to deploy and various recommendation algorithms in LOD. This framework allows algorithms to be tested with different domains and datasets.

Clearly, there is an active research community working on the concept of exploiting LOD in recommender systems. Our proposed work builds on these projects but differs in that it expands the coverage and accuracy of LDSD-based approaches.

3. Background

Linked Open Data (LOD) is a graph representation of interlinked data in which resources (nodes) are linked semantically to each other by links (edges) which define the relationship between these resources. In this paper, we use a similar definition for LOD datasets to the one stated in [14]:

A Linked Open Data dataset is a graph G such as G = (R, L, I) in which:

• R = {r₁, r₂, …, r_x} is a set of resources identified by their URI (Unique universal identifier),
• L = {l₁, l₂, …, l_y} is a set of typed links identified by their URI,
• I = {i₁, i₂, …, i_z} is a set of instances of these links between resources, such as i_i = <l_j, r_a, r_b>.

In graphs, links could indicate relatedness between resources, so the more linked the resources the more related they are. In this context, a direct connection between two resources exists when there is a distinct direct link (directional edge) between them. Thus, we define a direct distance (C_d) between two resources r_a and r_b through a link with a property l_i is equal to one if there a link with a property l_i exists that links the resource r_a to the resource r_b. The direct distance (C_d) is defined as:

$$C_d\left(l_i,r_a,r_b\right)=\{\begin{array}{cc}1\hfill & \hfill \mathrm{if} \mathrm{the} \mathrm{link} \langle l_i,r_a,r_b\rangle \mathrm{exists}\\ 0\hfill & \hfill \mathrm{otherwise}\end{array}.$$

(1)

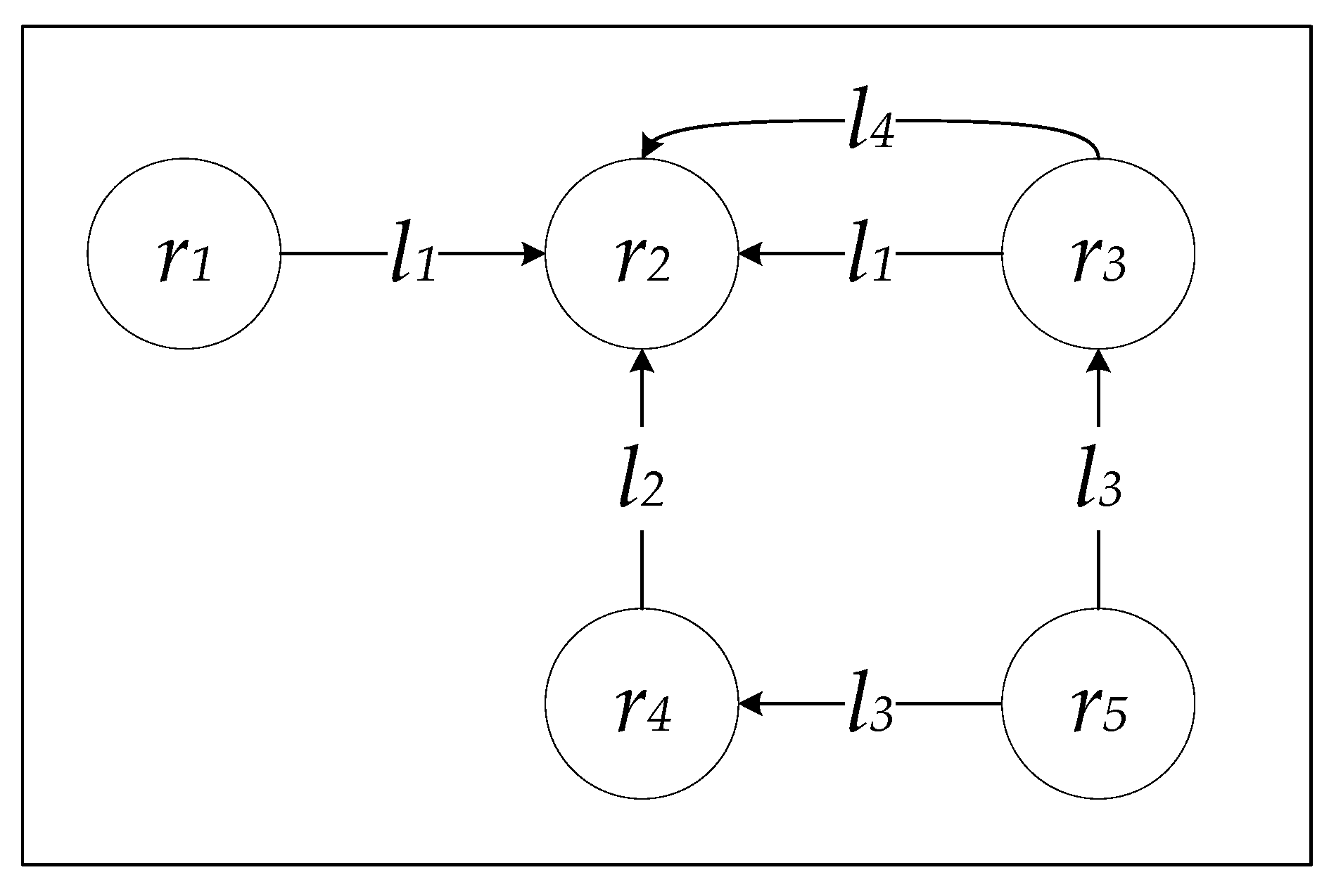
Following the example displayed in Figure 2, the direct distance between r₃ and r₂ is two ($C_d\left(r_3,r_2\right)=2$) because they are linked by links l₁ and l₄, and the direct distance between r₂ and r₃ is zero ($C_d\left(r_2,r_3\right)=0$) as there are no direct links originating from r₂.

Resources are not always linked directly to each other; they can be indirectly linked through other resources. Thus, indirect connectivity between two resources happens when they are linked via another resource, and these connections can be either incoming or outgoing from the intermediate resource. Accordingly, there are two types of indirect connections: Incoming and outgoing. Formally, an incoming indirect distance (C_ii) between two resources r_a and r_b is equal to one if there exists a resource r_c such that r_c is directly linked to both r_a and r_b via links of property l_i. The incoming indirect distance (C_ii) is defined as:

$$C_{ii}\left(l_i,r_c,r_a,r_b\right)=\{\begin{array}{cc}1\hfill & \hfill \left\{\exists r_c| \langle l_i,r_c,r_a\rangle \&\langle l_i,r_c,r_b\rangle \right\}\\ 0\hfill & \hfill \mathrm{otherwise}\end{array}.$$

(2)

Similarly, an outgoing indirect distance (C_io) between two resources r_a and r_b is equal to one if there exists a resource r_c such that both r_a and r_b are directly linked to r_c via links of property l_i. The outgoing indirect distance (C_io) is defined as:

$$C_{io}\left(l_i,r_c,r_a,r_b\right)=\{\begin{array}{cc}1\hfill & \hfill \left\{\exists r_c│\langle l_i,r_a,r_c\rangle \&\langle l_i,r_b,r_c\rangle \right\}\\ 0\hfill & \hfill \mathrm{otherwise}\end{array}.$$

(3)

The aforementioned indirect distance notation can be generalized for all intermediate resources as defined below (These versions of C_i accept three inputs instead of four as in the regular C_i):

$$C_{ii}\left(l_i,r_a,r_b\right)={\displaystyle \sum }_n{C}_{ii}\left(l_i,r_n,r_a,r_b\right),$$

$$C_{io}\left(l_i,r_a,r_b\right)={\displaystyle \sum }_n{C}_{io}\left(l_i,r_n,r_a,r_b\right).$$

According to the example in Figure 2, the incoming indirect distance between r₃ and r₄ is one ($C_{ii}\left(r_3,r_4\right)=1$) through the resource r₅ linked by the link property l₃, however, the outgoing indirect distance between r₃ and r₄ is zero ($C_{io}\left(r_3,r_4\right)=0$) since there is no resource such that both r₃ and r₄ are directly linked to through the same link property.

Linked Data Semantic Distance (LDSD)

Utilizing the direct and indirect distance concepts, [14] outlines an approach that measures the relatedness between two resources in the LOD. This approach is called Linked Data Semantic Distance (LDSD) and defined as:

$$LDSD\left(r_a,r_b\right)=\frac{1}{1+DC\left(r_a,r_b\right)+DC\left(r_b,r_a\right)+I{C}_i\left(r_a,r_b\right)+I{C}_o\left(r_a,r_b\right)},$$

(4)

where $DC\left(r_a,r_b\right)$ is the direct distance (C_d) between the resources r_a and r_b normalized by the log of all outgoing links from r_a, and it can be calculated as:

$$DC\left(r_a,r_b\right)={\displaystyle \sum }_i\frac{C_d\left(l_i,r_a,r_b\right)}{1+\log \left({{\displaystyle \sum }}_n{C}_d\left(l_i,r_a,r_n\right)\right)}.$$

$DC\left(r_b,r_a\right)$ is the direct distance (C_d) between the resources r_b and r_a normalized by the log of all outgoing links from r_b, and it can be calculated as:

$$DC\left(r_b,r_a\right)={\displaystyle \sum }_i\frac{C_d\left(l_i,r_b,r_a\right)}{1+\log \left({{\displaystyle \sum }}_n{C}_d\left(l_i,r_b,r_n\right)\right)}.$$

$I{C}_i\left(r_a,r_b\right)$ is the incoming indirect distance (C_ii) between the resources r_a and r_b normalized by the log of all incoming indirect links from r_a, and it can be calculated as:

$$I{C}_i\left(r_a,r_b\right)={\displaystyle \sum }_i\frac{C_{ii}\left(l_i,r_a,r_b\right)}{1+\log \left({{\displaystyle \sum }}_n{C}_{ii}\left(l_i,r_a,r_n\right)\right)}.$$

$I{C}_o\left(r_a,r_b\right)$ is the outgoing indirect distance (C_io) between the resources r_a and r_b normalized by the log of all outgoing indirect links from r_a, and it can be calculated as:

$$I{C}_o\left(r_a,r_b\right)={\displaystyle \sum }_i\frac{C_{io}\left(l_i,r_a,r_b\right)}{1+\log \left({{\displaystyle \sum }}_n{C}_{io}\left(l_i,r_a,r_n\right)\right)}.$$

The LDSD approach produces semantic distances values that range from zero to one. When a semantic distance between two resources equals zero, it means that the two resources are 100% related to each other. On the other hand, if it equals one, it indicates that there is no relatedness whatsoever between these two resources. Nevertheless, LDSD employs only the direct distance (C_d) and the indirect distance (C_ii and C_io) in calculating the semantic distance, and it does not include other resources that are located more than one resource away. Therefore, those other resources are automatically considered unrelated to each other.

4. Typeless Indirect Semantic Distance

One of the advantages of LOD is the massive amount of interconnected information, but the sheer volume of data causes several challenges. One of these challenges is that data accuracy in LOD can vary from one dataset to another and even within a given dataset. Several LOD datasets, including DBpedia, have their data composed and linked via human effort. For example, a link in DBpedia that represents the relationship between a song and its album can have different properties (labels) such as “fromAlbum” or “title” depending on the editor who updated the song or album page in Wikipedia. However, when applying LOD in recommender systems, the recommender system must be capable of recommending items even if the resources to be recommended are linked using different properties. Therefore, it may be necessary for a recommender system to consider the relationship between resources even when their links have different properties. This case is especially true when mining a relationship from multiple LOD datasets, each of which may have its own ontology or set of link properties. Despite this, the indirect distance (C_i) of LDSD does not consider these cases when calculating the indirect distance. In this section, we asses extending indirect distance calculations to include the effect of multiple links of differing properties within LOD. This extension is incorporated within LDSD to estimate the effect of including heterogeneous link properties in the semantic distance calculation.

Following the example in Figure 2, the outgoing indirect distance between r₁ and r₄ is zero ($C_{io}\left(r_1,r_4\right)=0$) since there is no resource such that both r₁ and r₄ are directly linked to through the same link property. However, both r₁ and r₄ are directly connected to r₂ but this is via different link properties (l₁ and l₂). In this section, we develop a typeless incoming and outgoing indirect distance between two resources r_a and r_b to broaden the indirect distance to include cases where the two resources can be linked by two different link properties (l_k and l_p) as displayed in Figure 3.

Formally, the incoming typeless indirect distance, TIC_i, between two resources r_a and r_b is the sum of the incoming typeless indirect link distance, TILC_i, of all links that connect them as follows:

$$TI{C}_i\left(r_a,r_b\right)={\displaystyle \sum }_n{\displaystyle \sum }_j{\displaystyle \sum }_{k}TIL{C}_i\left(l_j,l_k,r_n,r_a,r_b\right).$$

(5)

The Incoming Typeless Indirect Link Distance (TILC_i) between two resources r_a and r_b is equal to one if there is a resource r_n such that r_n is directly connected to both r_a and r_b via links of properties l_k and l_p, and it is defined as:

$$TIL{C}_i\left(l_k,l_p,r_n,r_a,r_b\right)=\{\begin{array}{cc}1\hfill & \hfill \left\{\exists r_n|\langle l_k,r_n,r_a\rangle \&\langle l_p,r_n,r_b\rangle \right\}\\ 0\hfill & \hfill \mathrm{otherwise}\end{array}.$$

Similarly, the outgoing typeless indirect distance, TIC_o, between two resources r_a and r_b is the sum of the outgoing typeless indirect link distance, TILC_o, of all links that connect them as follows:

$$TI{C}_o\left(r_a,r_b\right)={\displaystyle \sum }_n{\displaystyle \sum }_j{\displaystyle \sum }_{k}TIL{C}_o\left(l_j,l_k,r_n,r_a,r_b\right).$$

(6)

The Outgoing Typeless Indirect Link Distance (TILC_o) between two resources r_a and r_b is equal to one if there is a resource r_n such that both r_a and r_b are directly connected to r_n via links of properties l_k and l_p, and it is defined as:

$$TIL{C}_o\left(l_k,l_p,r_n,r_a,r_b\right)=\{\begin{array}{cc}1\hfill & \hfill \left\{\exists r_n│\langle l_k,r_a,r_n\rangle \&\langle l_p,r_b,r_n\rangle \right\}\\ 0\hfill & \hfill \mathrm{otherwise}\end{array}.$$

Even though $C_{io}\left(r_1,r_4\right)=0$ as previously stated, the outgoing typeless indirect distance between r₁ and r₄ is one ($TI{C}_o\left(r_1,r_4\right)=1$) through the resource r₂ with the links properties (l₁, l₂), which shows that r₁ and r₄ are indirectly connected to each other with the typeless variation.

The typeless indirect link distance (TILC) notation can be generalized for all intermediate resources as:

$$TIL{C}_i\left(l_k,l_p,r_a,r_b\right)={\displaystyle \sum }_n{\displaystyle \sum }_j{\displaystyle \sum }_{k}TIL{C}_i\left(l_j,l_k,r_n,r_a,r_b\right),$$

$$TIL{C}_o\left(l_k,l_p,r_a,r_b\right)={\displaystyle \sum }_n{\displaystyle \sum }_j{\displaystyle \sum }_{k}TIL{C}_o\left(l_j,l_k,r_n,r_a,r_b\right).$$

Weighted Typeless Linked Data Semantic Distance (wtLDSD)

Based on the extended indirect distance calculations to include the effect of multiple links of differing properties within LOD, we introduce another variation of the LDSD approach that measures the effect of including heterogeneous link properties in the semantic distance calculation. This new variation, called wtLDSD, is based on the work we introduced in [16]:

$$wtLDSD\left(r_a,r_b\right)=\frac{1}{1+WDC{}^{\prime }{}^{\left(r_a,r_b\right)}+WDC{}^{\prime }{}^{\left(r_b,r_a\right)}+WTI{C^{\prime }}_i\left(r_a,r_b\right)+WTI{C^{\prime }}_o\left(r_a,r_b\right)},$$

(7)

where $WDC{}^{\prime }\left(r_a,r_b\right)$ is the direct distance (C_d) weighted by $W_{l_i}$ for each link with a property l_i as follows:

$$WDC{}^{\prime }\left(r_a,r_b\right)={{\displaystyle \sum }}_i\left(\frac{C_d\left(l_i,r_a,r_b\right)}{1+\log \left({{\displaystyle \sum }}_n{C}_d\left(l_i,r_a,r_n\right)\right)}\times W_{l_i}\right).$$

$WDC{}^{\prime }\left(r_b,r_a\right)$ is the direct distance (C_d) weighted by $W_{l_i}$ for each link with a property l_i as follows:

$$WD{C{}^{\prime }}^{\left(r_b,r_a\right)}={\displaystyle \sum }_i\left(\frac{C_d\left(l_i,r_b,r_a\right)}{1+\log \left({{\displaystyle \sum }}_n{C}_d\left(l_i,r_b,r_n\right)\right)}\times W_{l_i}\right).$$

$WTIC{{}^{\prime }}_i\left(r_a,r_b\right)$ is the incoming typeless indirect distance (TIC_i) between resources r_a and r_b normalized by the log of all incoming typeless indirect links to the resource r_a and weighted by $W_{l_j}$ or $W_{l_k}$ for each link of types l_j or l_k correspondingly as follows:

$$WTIC{{}^{\prime }}_i\left(r_a,r_b\right)={\displaystyle \sum }_j\left({\displaystyle \sum }_k\frac{TIL{C}_i\left(l_j,l_k,r_a,r_b\right)}{1+\log \left(TIL{C}_i\left(l_j,l_k,r_a,n_r\right)\right)}\times W_{l_k}\right)\times W_{l_j}.$$

$WTIC{{}^{\prime }}_o\left(r_a,r_b\right)$ is the outgoing typeless indirect distance (TIC_o) between resources r_a and r_b normalized by the log of all outgoing typeless indirect links from the resource r_a and weighted by $W_{l_j}$ or $W_{l_k}$ for each link of types l_j or l_k correspondingly as follows:

$$WTIC{{}^{\prime }}_o\left(r_a,r_b\right)={\displaystyle \sum }_j\left({\displaystyle \sum }_k\frac{TIL{C}_i\left(l_j,l_k,r_a,r_b\right)}{1+\log \left(TIL{C}_i\left(l_j,l_k,r_a,n_r\right)\right)}\times W_{l_k}\right)\times W_{l_j}.$$

The value of every weight $W_{l_j}$ or $W_{l_k}$ is a positive rational number between zero and one ($0\le W_{l_j}\le 1$) and ($0\le W_{l_k}\le 1$). The weight of each link ($W_{l_j}$ or $W_{l_k}$) can be calculated using several approaches, and we use the Resource-Specific Link Awareness Weights (RSLAW) as it was the best performing approach in [16]. The weighting factors $W_{l_j}$ and $W_{l_k}$ are introduced in every link-based operation. Thus, higher direct and indirect distance values are produced for those links with high weights ($W_{l_j}$ and $W_{l_k})$; on the contrary, less emphasis is resulted on these links when they have a low weight, while some link properties are cancelled if their corresponding weight is zero.

5. Semantic Distance Spreading Approach

There are some challenges in including more than one intermediate node in computing the semantic distance such as efficiency. The time complexity undergoes combinatorial explosion in propagating weights throughout the graph. Computing all semantic distance weights between all resources has an upper bound of O(nⁿ) where n is the number of resources in the graph, evidently intractable in LOD since it consists of millions of resources. Thus, we propose in this section an approach that first calculates the semantic distance between each directly linked resource pair in the LOD graph, and then propagates these values for other indirectly connected resources with an all-pair shortest path algorithm to compute the final semantic distance values between all resource pairs. This approach first reduces the original LOD graph to include only resources that are under consideration by the recommender system and then their final semantic distances will be computed using the reduced graph. The proposed approach relies on the Floyd–Warshall algorithm that finds the shortest paths in a weighted graph, and it is presented in Algorithm 1.

Since the set R is previously defined as the set of all resources in the linked data dataset, a subset of R can be defined by the recommender system to designate the resources that have the potential to be included in the recommendation results. The purpose of this resource list is to increase the efficiency of the system by limiting the resource classes to those of interest to the recommender system. As a result, propagated semantic distances are calculated between resource pairs in this list only. For example, a musical recommender system can limit this set to only resources that represent musical artists and bands. Formally, γ is a set of resources with a resource class intended for recommendation specified by the recommender system (γ ⊆ R).

The proposed approach starts by creating a |γ| × |γ| matrix labeled from 1 to |γ| for both rows and columns, and each label represents a resource. Then, this matrix is initialized with either 0.0 for the distance from each resource to itself, 1.0 otherwise. Unlike the original Floyd–Warshall algorithm in which the matrix is initialized with infinity (∞), the value 1.0 here represents the maximum semantic distance referring value that reflects the lack of any relatedness.

The time complexity of this algorithm for the average and the worst-case performance is Θ(|γ|³) assuming that the semantic distances between each pair of resources exist and have already been computed.

Algorithm 1: The semantic distance spreading algorithm.

1  let d be a |γ| × |γ| array of minimum semantic distances 2  for i from 1 to |γ| 3   for j from 1 to |γ| 4    if i==j 5     d[i][j] = 0 6    else 7     d[i][j] = 1 8  for each resource pair (ra, rb) ∈ γ 9   d[ra][rb] = SemanticDistance(ra, rb) 10   for k from 1 to |γ| 11    for i from 1 to |γ| 12     for j from 1 to |γ| 13      if d[i][j] > 1 − ((1 − d[i][k]) × (1 − d[k][j])) 14       d[i][j] = 1 − ((1 − d[i][k]) × (1 − d[k][j])) 15      end if

5.1. LOD Graph Reduction

After initializing the semantic distance matrix (d) with whichever value zero or one, the approach proceeds to compute the semantic distance between each resource pair (r_a, r_b) that is part of γ using any semantic distance approach such as LDSD or wtLDSD (lines 8 and 9 in Algorithm 1). This step reduces the whole LOD graph to contain only γ resources. For instance, Figure 4 displays an example of a snapshot of a LOD dataset. In this instance, resources r₁, r₃, and r₅ have the same resource class (e.g., MusicalArtist) that is a subset of γ whereas resource r₂ and r₄ have different resource classes (e.g., Album or MusicalWork) that are not subsets of γ. Thus, this algorithm computes the semantic distance between resources r₁, r₃, and r₅ only, and it results in semantic distance values between these pairs. However, resources r₂ and r₄ contribute to the semantic distance calculation because resources r₁, r₃, and r₅ are indirectly linked through these resources which the LDSD approach takes into consideration in its indirect distance component.

5.2. Semantic Distance Propagation

After calculating semantic distance values between all resources pairs (as lines 8 and 9 of the algorithm), the Floyd–Warshall algorithm is applied to find the ideal path that achieves the lowest semantic distance value by comparing all available paths in the reduced graph. The intuition behind spreading semantic distances is that relatedness can be propagated through resources considering that semantic distance values reflect this spreading. For example, if a resource r_a is considered 50% related to a resource r_b, and the resource r_b is considered 50% related to a resource r_c then we can say that the resource r_a is 25% related to the resource r_c (50% of the 50%). In this application, the Floyd–Warshall algorithm is viable since semantic distance values are positive values ranging from zero to one, where zero represents a 100% relatedness whereas the value one represents no relatedness whatsoever.

The semantic distance matrix is updated by investigating each resource as an intermediate resource. Thus, this algorithm considers all resources one after another and updates all shortest paths including the current resource as an intermediate resource. There are three phases in this algorithm:

• The intermediate resource (k) iteration as in line 10
• The source resource (i) iteration as in line 11
• The destination resource (j) iteration as in line 12

When an intermediate resource (k) is chosen between resources i and j, it can contribute to a lower semantic distance if the semantic distance value through it is lower than the current value (lines 13 and 14). Different from the original Floyd–Warshall that considers distances as integer numbers, our comparison adopts semantic distance values that range from zero to one. Besides, semantic distances propagation is accomplished via the multiplication operation, so that the loss of semantic distance is proportional to the amount of propagation in the graph from the original resources.

6. Evaluation

The accuracy of recommender systems can be evaluated using two approaches: Rating prediction and ranking [30]. The rating prediction method compares the prediction rating of a specific algorithm to ground truth while the ranking approach compares a ranked list of recommended items to set aside items in a user profile. We implement the latter approach in this paper.

6.1. Dataset and Methodology

We conducted an experiment to measure the effectiveness of our proposed variation of the LDSD (wtLDSD) in addition to applying the semantic distance propagation algorithm to both the original LDSD and the new variation, wtLDSD, resulting in two new approaches pLDSD and pwtLDSD. We compared these methods against three baselines LDSD, Resim [15], and Jaccard Index [11]. The Jaccard Index is chosen to represent other similarity measures exploiting Linked Open Data since it has shown promising performances in [31].

The weights of links in the wtLDSD methods are generated using the Resource-Specific Link Awareness Weights (RSLAW) described in [16].

The Jaccard Index, also known as the Jaccard Similarity Coefficient, is a statistical measure to approximate the similarity between two sets. It is estimated by dividing the number of items shared by the sets by the total number of items in either set as defined below:

$$\mathrm{Jaccard}\left(r_a,r_b\right)=\frac{\left|N\left(r_a\right){\displaystyle \cap }N\left(r_b\right)\right|}{\left|N\left(r_a\right){\displaystyle \cup }N\left(r_b\right)\right|},$$

(8)

such that $N\left(r_a\right)$ is the set of neighboring resources to a resource r_a. which is directly linked to each member of the set.

Similar to some related works in this field [14,19,24], we applied our experiment in the music domain to estimate the relatedness between musical artists and bands in DBpedia. We used a dataset from the second Linked Open Data-enabled recommender systems challenge, which includes personal preferences (likes) of some Facebook users in several fields including musical preferences. Each item in this dataset is linked to the corresponding resource in DBpedia. The total number of music preferences of users is 1,013,973 with an average of 19.47 preferences per user for a total of 52,069 users. We estimated the semantic distance between all resources in the dataset on a live DBpedia server (version 2015-10). We randomly picked 500 users with at least 10 preferences from the dataset above. Five preferences per user were kept for testing while the other preferences were used to create a user profile for each user. We then generated a list of recommended resources for each user based on the similarity of the user and each resource in the dataset. The similarity score between each user and resource was estimated based on the semantic distance produced by each approach as follows:

$$\mathrm{similarity}\left(u_i,r_a\right)=\frac{{{\displaystyle \sum }}_{r_b\in Profile\left(u_i\right)}\left(1-SemanticDistance\left(r_a,r_b\right)\right)}{\left|Profile\left(u_i\right)\right|},$$

(9)

where $SemanticDistance\left(r_a,r_b\right)$ is the semantic distance approach used for the evaluation (Jaccard, LDSD, Resim, wtLDSD, pLDSD, or pwtLDSD). $Profile\left(u_i\right)$ is the user profile of the user u_i which includes all resources that the user u_i has liked minus five resources (those reserved for testing purposes).

The resulting resource list was sorted in a descending order per user; then test resources were used to measure the effectiveness of each semantic distance method using the standard metrics F₁ Score and the Mean Reciprocal Rank (MRR). The F₁ score, the harmonic mean of precision and recall, is defined as:

$$F_1=2\times \frac{precision\times recall}{precision+recall}.$$

(10)

Additionally, the Mean Reciprocal Rank (MRR) that takes into account how early a relevant result appears within ranked results is calculated as:

$$MRR=\frac{{{\displaystyle \sum }}_{i=1}^{\left|Q\right|}\frac{1}{ran{k}_i}}{\left|Q\right|},$$

(11)

where rank_i is the highest rank of relevant results in a query Q_i.

6.2. Results

The results of the experiment using the F₁ score and MRR measurements are presented in

Table 1. Experiment Results.

	Jaccard	LDSD	Resim	wtLDSD	pLDSD	pwtLDSD
MRR	0.010	0.028	0.037	0.043	0.044	0.050
F1@5	0.009	0.031	0.049	0.050	0.051	0.065
F1@10	0.011	0.044	0.053	0.065	0.059	0.075
F1@20	0.012	0.046	0.051	0.063	0.058	0.079

. The F₁ score values are presented at different ranked results cutoffs, namely, 5, 10 and 20.

As shown in Table 1, our weighted typeless variation wtLDSD outperformed the original LDSD in all metrics (F₁ and MRR), and this result was statistically significant (p < 0.05) based on a paired student t-test. The MRR score of the wtLDSD approach was 0.043 versus 0.028 for the original LDSD and 0.037 for Resim. Similarly, the F₁ score confirms the results of the MRR metric with a score of 0.050 for wtLDSD for the top five results, compared to a score of 0.031 for the original LDSD and 0.049 for Resim. These results also hold at other results cutoff points as displayed in Figure 5. In particular, the F₁ score at the top 10 results for wtLDSD was 0.065, compared to a score of 0.044 for LDSD and 0.053 for Resim. Additionally, The F₁ score at the top 20 results for wtLDSD was 0.063, compared to a score of 0.046 for LDSD and 0.051 for Resim. These results show the importance of leveraging link weights in semantic distance computation since the accuracy of the recommender system improves even when typeless indirect connectivity is used.

Additionally, the propagated approaches (pLDSD and pwtLDSD) outperformed all the baselines in all metrics (F₁ and MRR). The MRR score of the pLDSD approach was 0.044 versus 0.028 for the original LDSD, an improvement of 57%, whereas it was 0.050 for pwtLDSD versus 0.043 for wtLDSD, an improvement of 16%. The F₁ score also confirms the results of the MRR metric with a score of 0.051 for pLDSD for the top five results, compared to a score of 0.031 for the original LDSD while it was 0.065 for pwtLDSD versus 0.050 for wtLDSD. These results are also valid at the other cutoff points (@10 and @20).

The pwtLDSD gained the highest accuracy among all the approaches presented in this document with an improvement of 78% over LDSD and 35% over Resim. It also gained an improvement of 16% over our variation, wtLDSD. Altogether, these results demonstrate that the propagation of semantic distances beyond resources that are more than two links apart enhances the accuracy of LOD-based recommender systems.

Recommender systems are evaluated not only through their accuracy; they can also be evaluated according to other criteria, including their coverage. It is notable that our propagated approaches (pLDSD and pwtLDSD) have increased the coverage over our baselines. As mentioned earlier, semantic distance calculations on a pair of resources generate results on a scale of 0 (no distance apart, so perfectly identical) to 1 (as far away as possible, so entirely unrelated). Therefore, the related results are defined as all resources with a semantic distance of less than 1.0 while non-related resources are those with a semantic distance that is exactly 1.0.

Table 2. The coverage of the propagated approaches vs. others.

	LDSD	Resim	wtLDSD	pLDSD	pwtLDSD
Coverage	10%	61%	9%	85%	90%

displays the coverage of each approach. The coverage here is defined as the average number of related results for each resource, and it is defined below:

$$Coverage=\frac{{{\displaystyle \sum }}_{r_i}\left(\frac{{{\displaystyle \sum }}_{r_j\in N\left(r_i\right)}1}{n}\right)}{n}\times 100,$$

(12)

where n is the number of resources in the dataset, and N(r_i) is the set of resources whose semantic distances are less than one from r_i.

The results show that the coverage of each approach increases with a maximum increase of 81% (pwtLDSD vs. wtLDSD). Due to this increase in coverage, the recommender system has access to more related resources that may result in an improved novelty of the recommendation results.

7. Conclusions

In this work, we first introduced a new variation of the LDSD, called wtLDSD, by extending the indirect distance calculations to include the effect of multiple links of differing properties within LOD while prioritizing link properties. Next, we presented a new method of calculating semantic distance in LOD that that broadens the coverage of LDSD-based approaches beyond resources that are more than two links apart. We utilized an all-pair shortest path algorithm, the Floyd–Warshall algorithm, to efficiently compute semantic distances. Our evaluation shows that approaches we propose not only expand the number of resources involved in semantic distance computations (with a maximum coverage increment of 80% compared to LDSD); it also improves the accuracy of the resulting recommendations over LDSD-based approaches.

In the future, we will study the effects of our propagation approach based on other similarity approaches. Furthermore, we will evaluate other similarity approaches that work with unstructured data to include the textual content of resource properties in the similarity estimation. In addition, we will analyze the effects of the proposed approaches on different domains such as books and movies as well as perform cross-domain recommendations.