Throughput of Wireless-Powered Based Multiuser System with Large-Scale Distributed Antennas
Abstract
1. Introduction
- An efficient energy and information transfer transmission scheme is proposed. In the downlink phase, to save the signaling and RF chains overhead, the RAU with the shortest distance towards a UE is selected for the WET. In the uplink phase, the wireless data transmission probability of a UE is developed. Then, the UEs which satisfy the WIT requirement transmit data to the central processor (CP) according to the “harvest-then-transmit” protocol.
- The asymptotic throughput for an arbitrary UE is derived in closed-form by exploiting the ZF detection (ZFD) and the MMSE detection (MMSED) to separate data information among different UEs. Besides, the optimal time fraction used for EH is obtained by maximizing the asymptotic throughput.
- Performance results are provided to validate the theoretical analysis and show the impacts on the throughput performance from various parameters. The average throughput of the cell is also calculated through numerical analysis, which can provide guidelines for the network analysis and optimization.
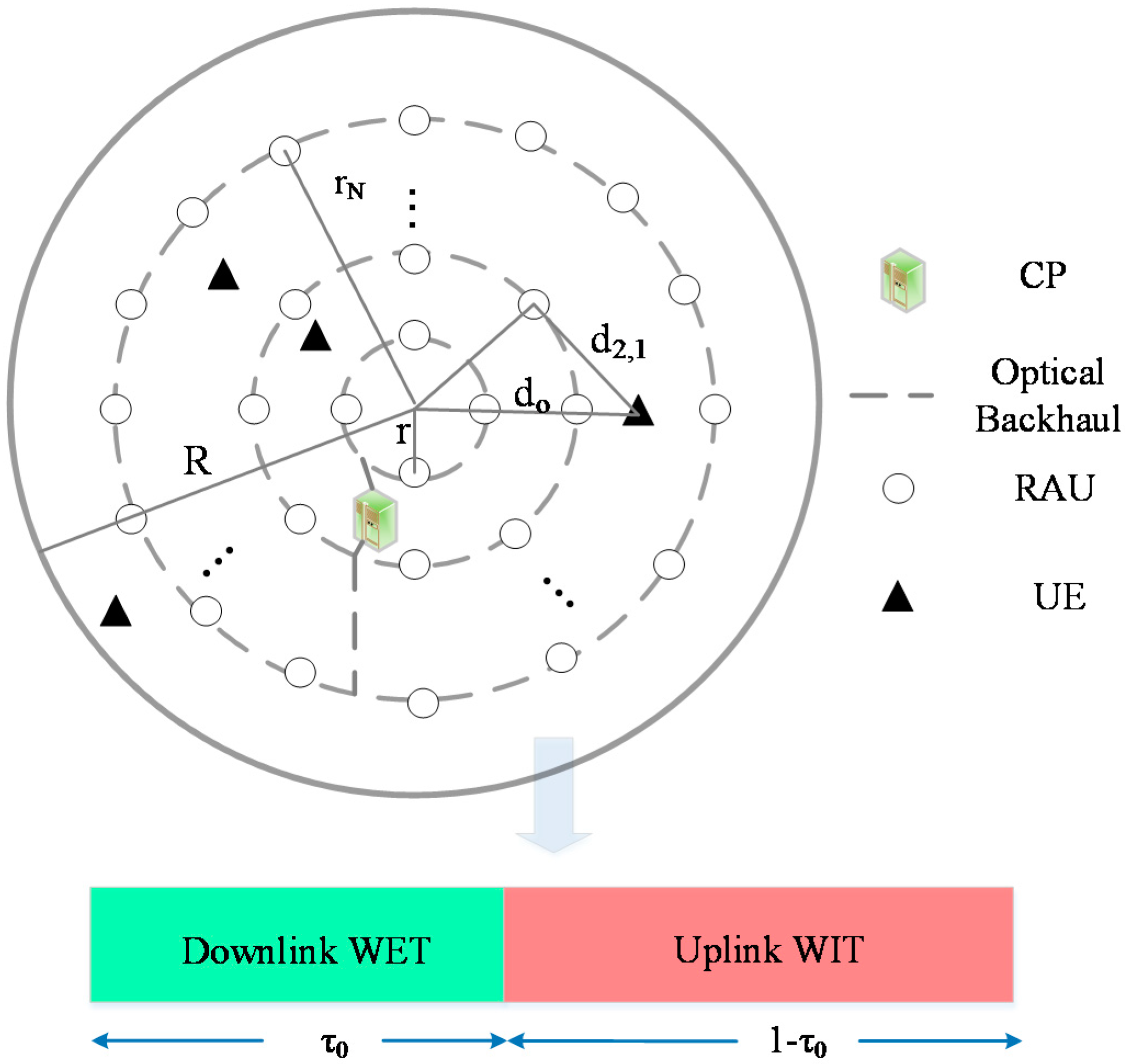
2. System Model
- Downlink WET: In , each UE harvests energy from the selected RAU with the shortest distance.
- Uplink WIT: Firstly, we analyze the information transmission probability of a UE. Only if the power used for information transmission in is no less than the transmit sensitivity, the UE can send its data to the CP at threshold power. To separate different data information among () UEs, ZFD is employed.
2.1. WET Model
2.2. WIT Model
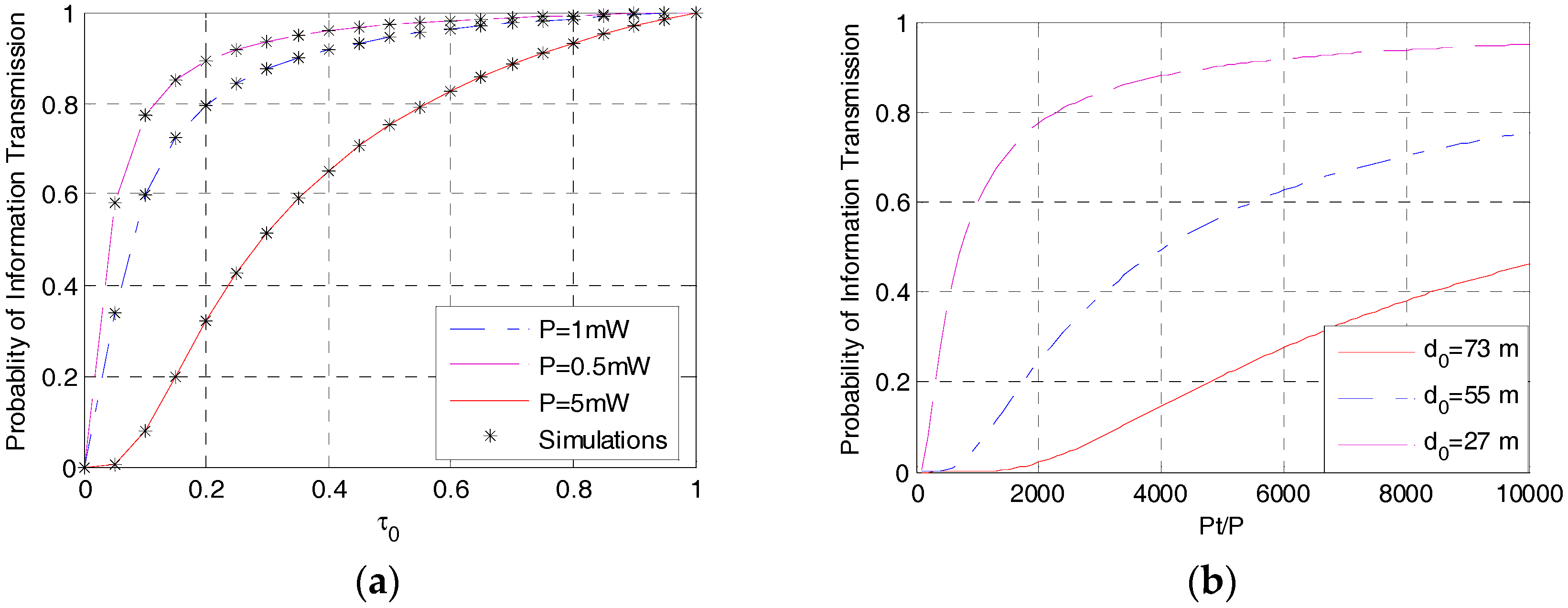
3. Information Transmission Probability for a UE
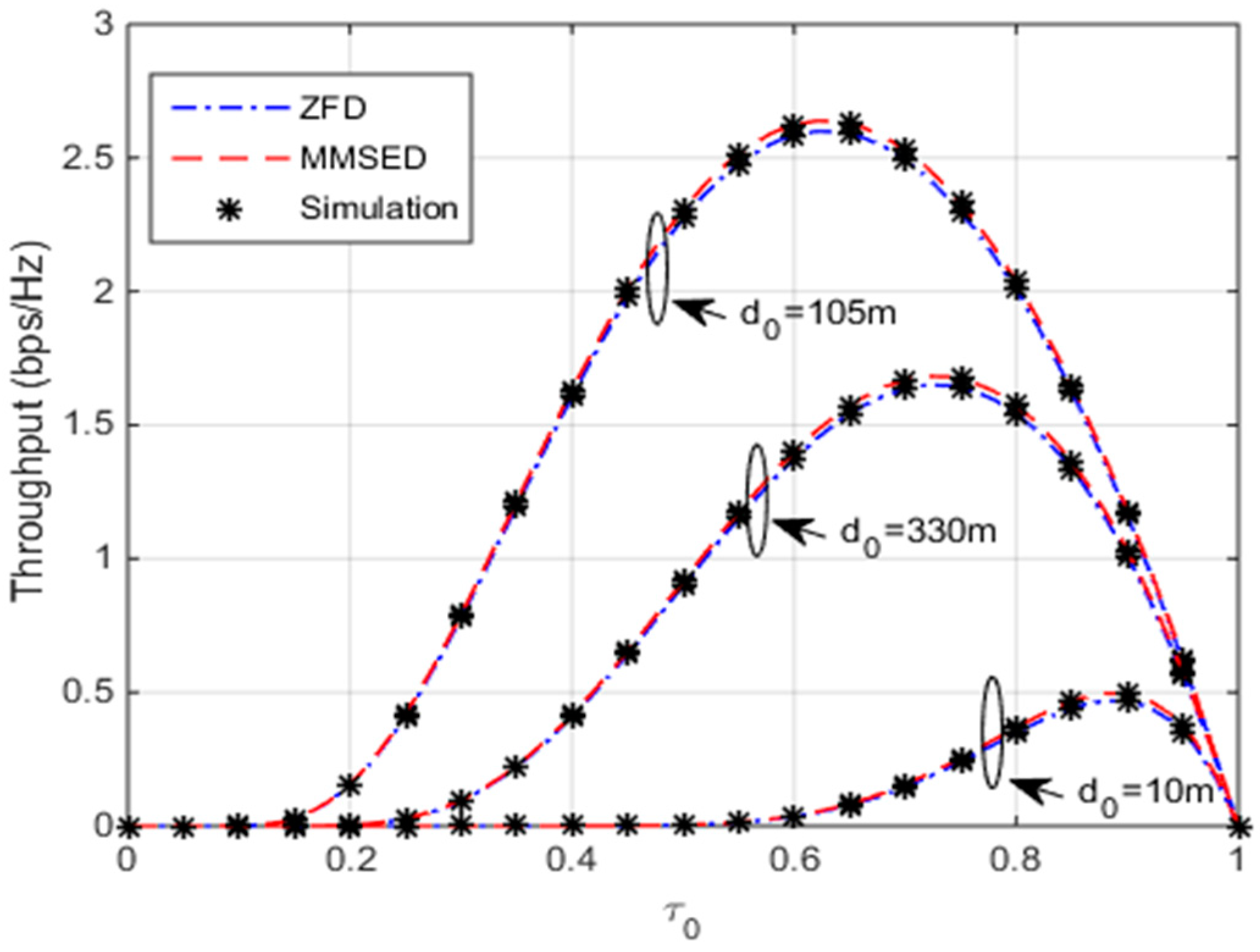
4. Asymptotic Throughput
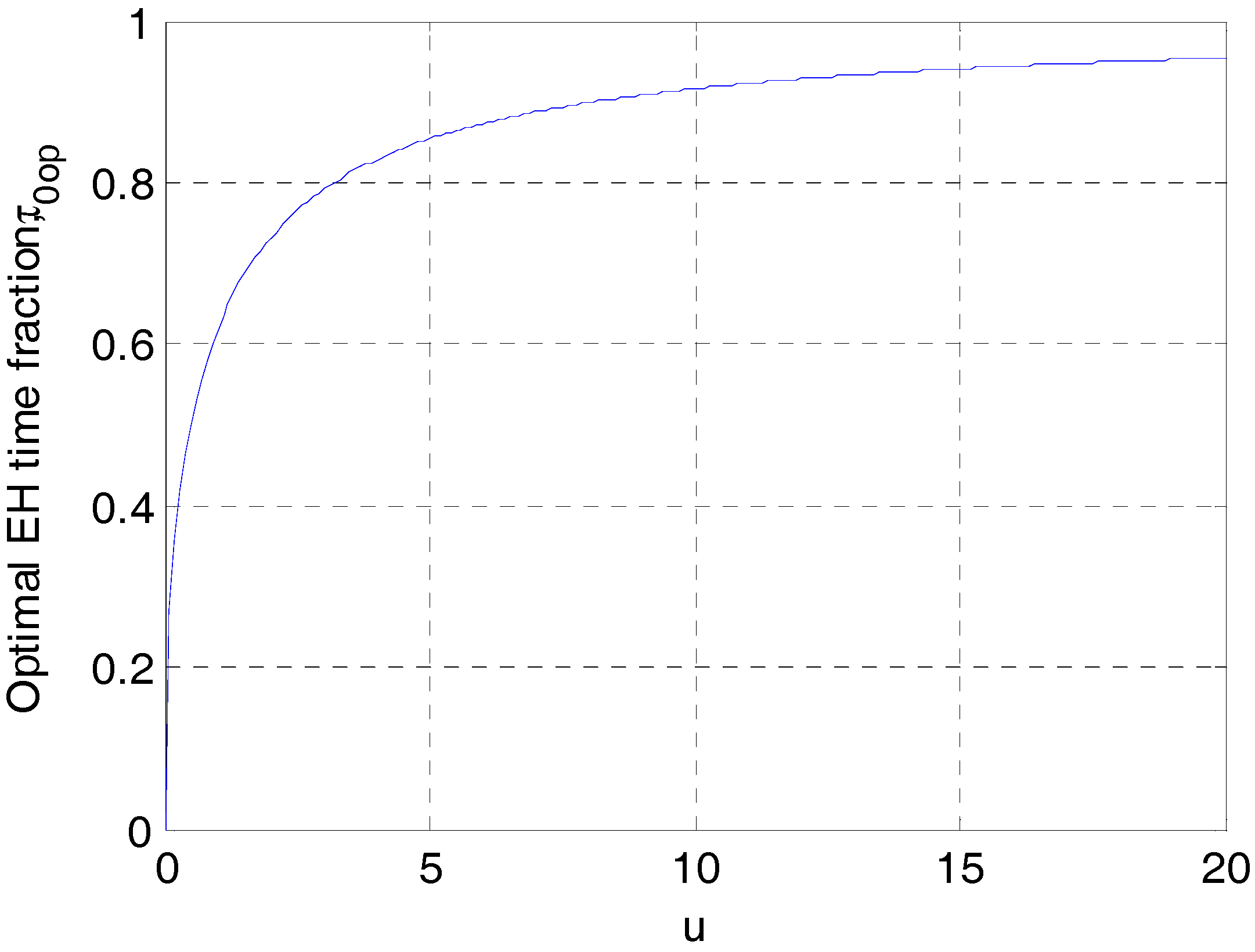
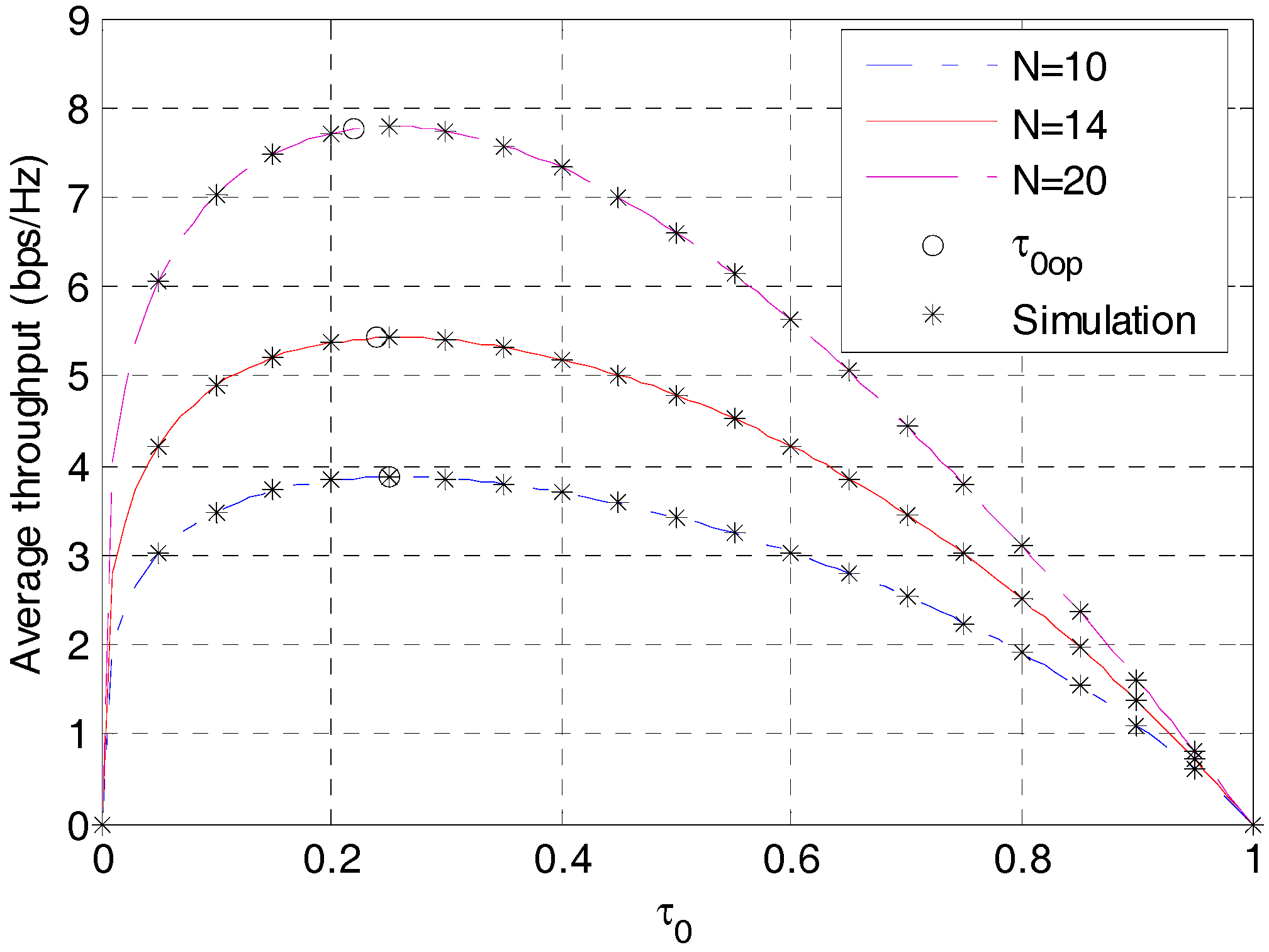
5. Optimization of Energy Harvesting Time
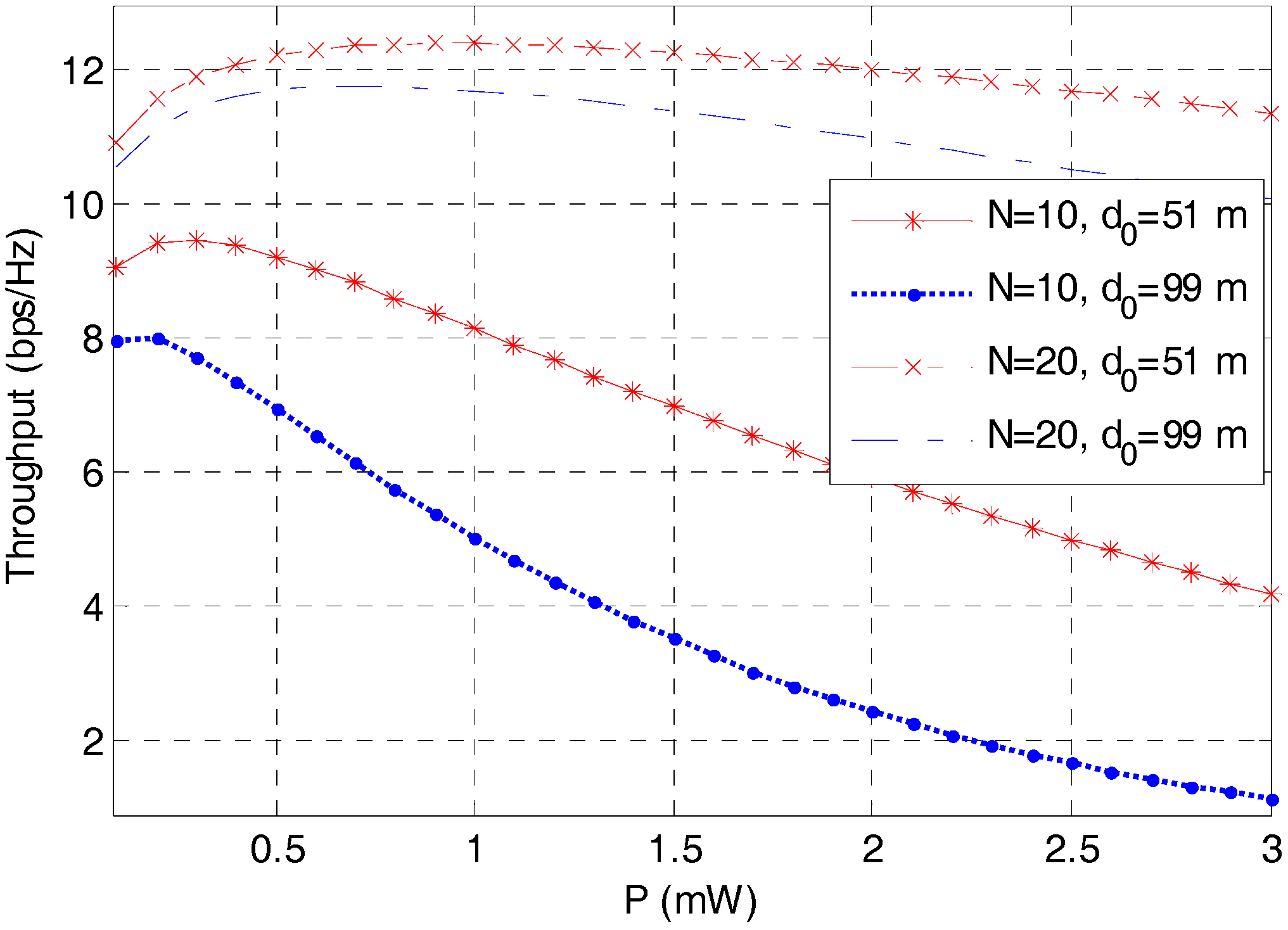
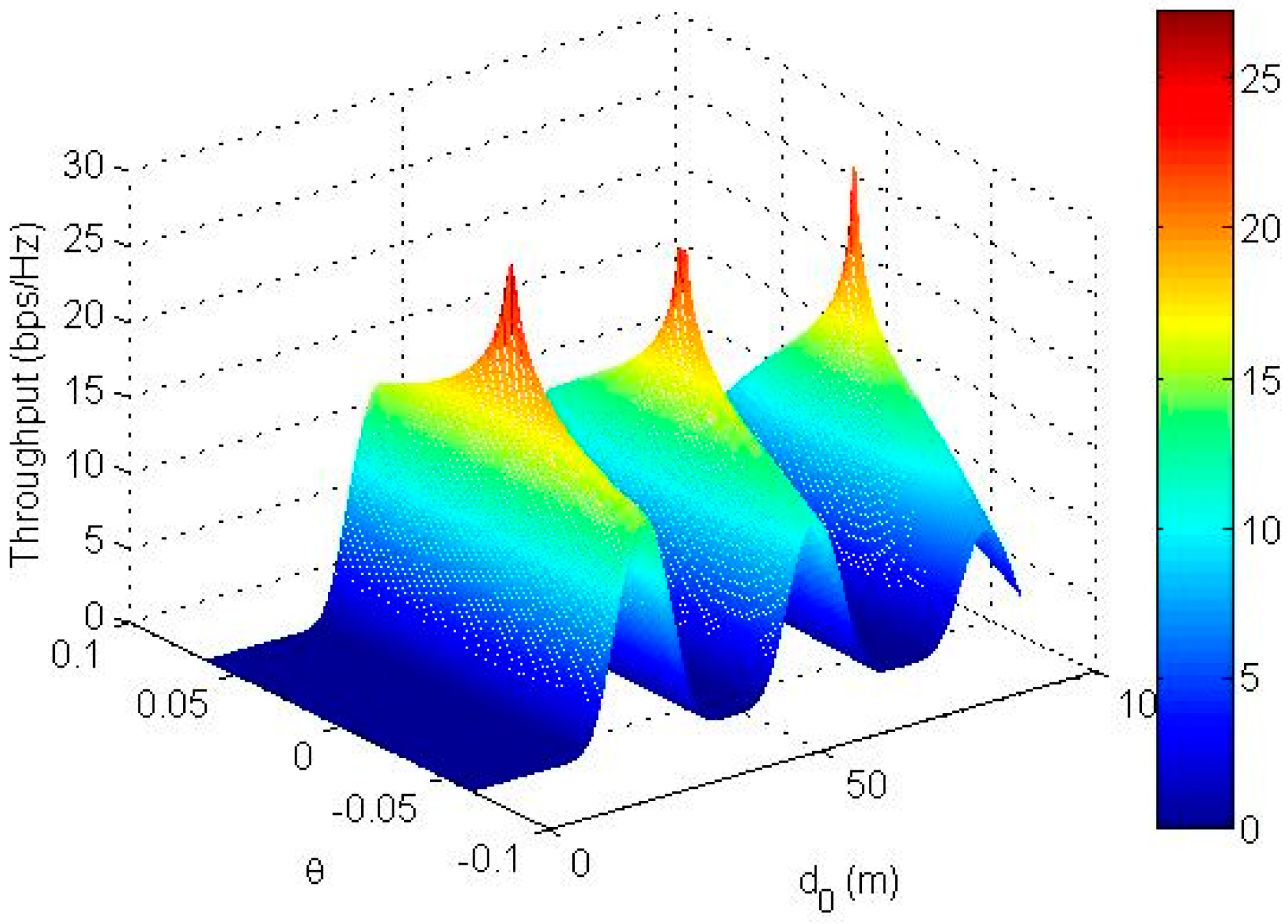
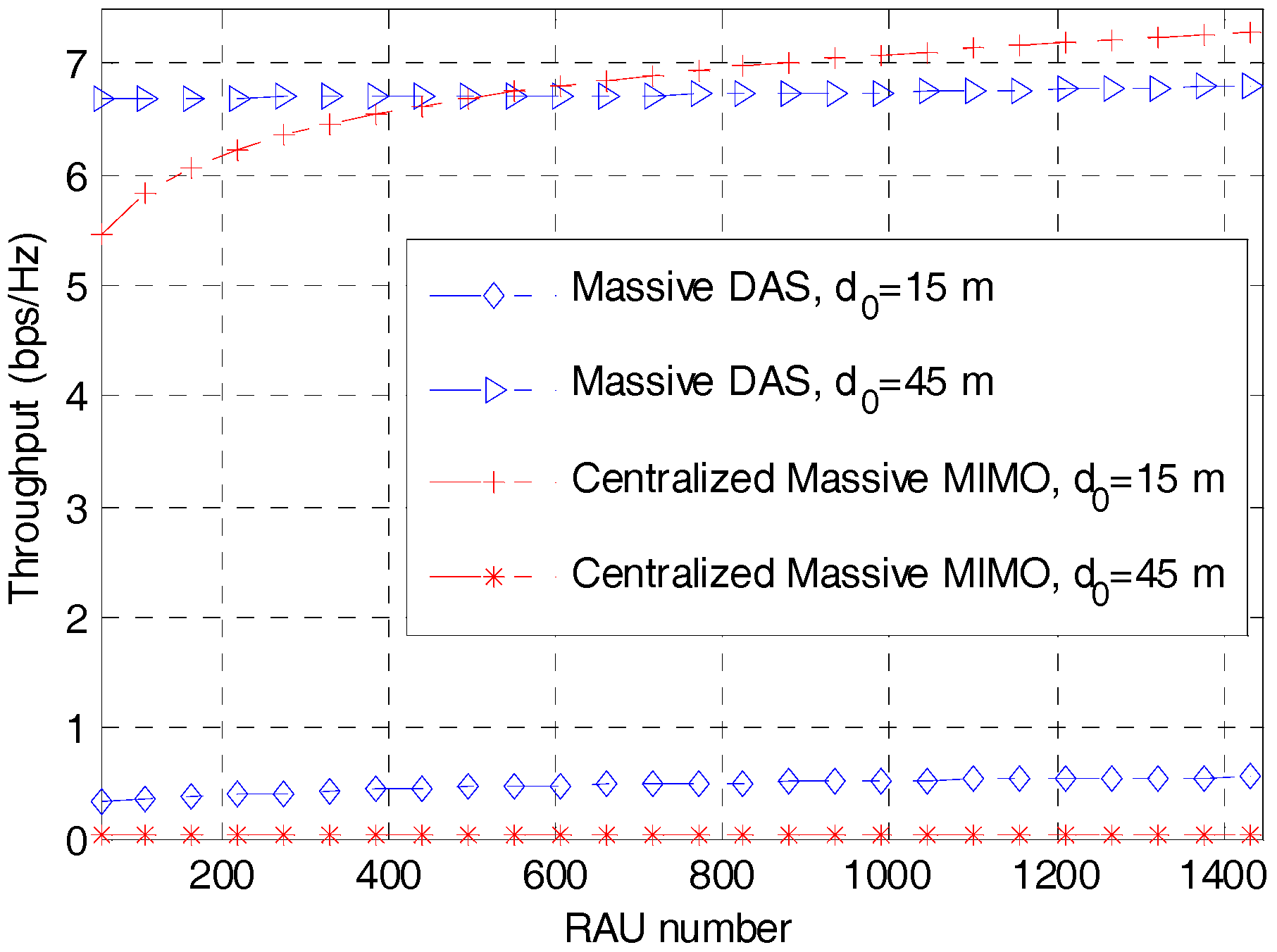
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Larsson, E.; Edfors, O.; Tufvesson, F.; Marzetta, T. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Guo, K.; Guo, Y.; Ascheid, G. Security-constrained power allocation in MU-massive-MIMO with distributed antennas. IEEE Trans. Wirel. Commun. 2016, 15, 8139–8153. [Google Scholar] [CrossRef]
- Bogale, T.E.; Le, L.B. Massive MIMO and mmwave for 5G wireless hetNet: Potential benefits and challenges. IEEE Veh. Technol. Mag. 2016, 11, 64–75. [Google Scholar] [CrossRef]
- Shirazinia, A.; Dey, S.; Ciuonzo, D.; Rossi, P.S. Massive MIMO for decentralized estimation of a correlated source. IEEE Trans. Signal Process. 2016, 64, 2499–2512. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, J.; Swindlehurst, A.L.; López-Salcedo, J.A. Massive MIMO for wireless sensing with a coherent multiple access channel. IEEE Trans. Signal Process. 2015, 63, 3005–3017. [Google Scholar] [CrossRef]
- Mai, V.V.; Jeong, Y.; Shin, H. Error exponents for distributed detection. IEEE Commun. Lett. 2016, 58, 121–124. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S.; Dey, S. Massive MIMO channel-aware decision fusion. IEEE Trans. Signal Process. 2015, 63, 604–619. [Google Scholar] [CrossRef]
- Ding, G.; Gao, X.; Xue, Z.; Wu, Y.; Shi, Q. Massive MIMO for distributed detection with transceiver impairments. IEEE Trans. Veh. Technol. 2018, 67, 604–617. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Salvo Rossi, P.; Dey, S. Massive MIMO meets decision fusion: Decode-and-fuse vs. decode-then-fuse. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 265–268. [Google Scholar]
- Lee, K.; Yoon, C.; Jo, O.; Lee, W. Joint optimization of spectrum sensing and transmit power in energy harvesting-based cognitive radio networks. IEEE Access 2018, 6, 30653–30662. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, M.; Liu, Y. Energy-efficient SWIPT in IoT distributed antenna systems. IEEE Internet Things J. 2018, 5, 2646–2656. [Google Scholar] [CrossRef]
- Yang, G.; Ho, C.K.; Zhang, R.; Guan, Y.L. Throughput optimization for massive MIMO systems powered by wireless energy transfer. IEEE J. Sel. Areas Commun. 2015, 33, 1640–1650. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Zheng, K. Downlink hybrid information and energy transfer with massive MIMO. IEEE Trans. Wirel. Commun. 2016, 15, 1309–1322. [Google Scholar] [CrossRef]
- Huang, K.; Lau, V.K.N. Enabling wireless power transfer in cellular networks: Architecture, modeling and deployment. IEEE Trans. Wirel. Commun. 2014, 13, 902–912. [Google Scholar] [CrossRef]
- Tang, H.; Xie, X.; Chen, J. X-duplex relay with self-interference signal energy harvesting and its hybrid mode selection method. In Proceedings of the 27th Wireless and Optical Communication Conference (WOCC), Hualien, Taiwan, 30 April–1 May 2018; pp. 1–6. [Google Scholar]
- Licea, D.B.; Zaidi, S.A.R.; Mclernon, D.; Ghogho, M. Improving radio energy harvesting in robots using mobility diversity. IEEE Trans. Signal Process. 2016, 64, 2065–2077. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Chen, X. Energy-efficient optimization for wireless information and power transfer in large-scale MIMO systems employing energy beamforming. IEEE Wirel. Commun. Lett. 2013, 2, 667–670. [Google Scholar] [CrossRef]
- Zhai, C.; Liu, J.; Zheng, L. Cooperative spectrum sharing with wireless energy harvesting in cognitive radio network. IEEE Trans. Veh. Technol. 2015, 65, 5303–5316. [Google Scholar] [CrossRef]
- Zhai, C.; Liu, L.; Zheng, L. Relay based spectrum sharing with secondary users powered by wireless energy harvesting. IEEE Trans. Commun. 2016, 64, 1875–1887. [Google Scholar] [CrossRef]
- Yuan, F.; Jin, S.; Huang, Y.; Wong, K.; Zhang, Q.T.; Zhu, H. Joint wireless information and energy transfer in massive distributed antenna systems. IEEE Commun. Mag. 2015, 53, 109–116. [Google Scholar] [CrossRef]
- Yang, A.; Jing, Y.; Xing, C.; Fei, Z.; Kuang, J. Performance analysis and location optimization for massive MIMO systems with circularly distributed antennas. IEEE Trans. Wirel. Commun. 2015, 14, 5659–5671. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Zhu, P.; You, X. Spectral efficiency analysis of single-cell multi-user large-scale distributed antenna system. IET Commun. 2014, 12, 2213–2221. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Zhu, P.; You, X. Spectral efficiency analysis of large-scale distributed antenna system in a composite correlated Rayleigh fading channel. IET Commun. 2015, 9, 681–688. [Google Scholar] [CrossRef]
- Guo, K.; Mukherjee, S.; Ascheid, G. Wireless information and power transfer in MU-massive-MIMO with distributed antennas. In Proceedings of the 2017 International Symposium on Wireless Communication Systems (ISWCS), Bologna, Italy, 28–31 August 2017; pp. 228–233. [Google Scholar]
- Sun, Q.; Jin, S.; Wang, J.; Zhang, Y.; Gao, X.; Wong, K. Downlink massive distributed antenna systems scheduling. IET Commun. 2015, 9, 1006–1016. [Google Scholar] [CrossRef]
- Choi, W.; Andrews, I.G. Downlink performance and capacity of distributed antenna systems in a multicell environment. IEEE Trans. Wirel. Commun. 2007, 6, 69–73. [Google Scholar] [CrossRef]
- Tabassum, H.; Hossain, E. On the deployment of energy sources in wireless-powered cellular networks. IEEE Trans. Commun. 2015, 63, 3391–3404. [Google Scholar] [CrossRef]
- Li, J.; Yan, J.; Zhao, L.; Dong, Q. Antenna selection and transmit beamforming optimisation with partial channel state information in distributed antenna systems. IET Commun. 2014, 8, 2272–2280. [Google Scholar] [CrossRef]
- Li, H.; Koudouridis, G.; Zhang, J. Antenna selection schemes for energy efficiency in distributed antenna systems. In Proceedings of the IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 5619–5623. [Google Scholar]
- Wang, Q.; Liu, J.; Zheng, L. Exact error rate of dual-channel receiver with remote antenna unit selection in multicell networks. Ksii Trans. Internet Inf. Syst. 2016, 10, 548–557. [Google Scholar] [CrossRef]
- Wang, Q.; Xiong, H.; Yu, S. Throughput of wireless-powered massive distributed antenna systems over composite fading channels. J. Commun. 2017, 12, 24–31. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, P.; Chen, M. Antenna location design for generalized distributed antenna systems. IEEE Commun. Lett. 2009, 13, 315–317. [Google Scholar] [CrossRef]
- Park, E.; Lee, S.; Lee, I. Antenna placement optimization for distributed antenna systems. IEEE Trans. Wirel. Commun. 2012, 11, 2468–2477. [Google Scholar] [CrossRef]
- Hoydis, J.; Brink, S.; Debbah, M. Massive MIMO in UL/DL cellular systems: How many antennas do we need? IEEE J. Sel. Areas Commun. 2013, 31, 160–171. [Google Scholar] [CrossRef]
- Hochwald, M.; Marzetta, T.; Tarokh, V. Multiple-antenna channel hardening and its implications for rate feedback and scheduling. IEEE Trans. Inf. Theory 2004, 50, 1893–1909. [Google Scholar] [CrossRef]
- Gao, X.; Edfors, O. Linear pre-coding performance in measured very-large MIMO channels. In Proceedings of the IEEE VTC, San Francisco, CA, USA, 5–8 September 2011; pp. 1–5. [Google Scholar]
- Ngo, H.; Larsson, E.; Marzetta, T. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar] [CrossRef]
- Wagner, S.; Couillet, R.; Debbah, M.; Slock, D.T.M. Large system analysis of linear precoding in correlated MISO broadcast channels under limited feedback. IEEE Trans. Inf. Theory 2012, 58, 4509–4537. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Seires and Products; Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Choi, W.; Kim, J.K. Forward-link capacity of a DS/CDMA system with mixed multivariate sources. IEEE Trans. Veh. Technol. 2001, 50, 737–749. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Wei, J.; Guo, W. Throughput of Wireless-Powered Based Multiuser System with Large-Scale Distributed Antennas. Information 2019, 10, 13. https://doi.org/10.3390/info10010013
Wang Q, Wei J, Guo W. Throughput of Wireless-Powered Based Multiuser System with Large-Scale Distributed Antennas. Information. 2019; 10(1):13. https://doi.org/10.3390/info10010013
Chicago/Turabian StyleWang, Qing, Jingbo Wei, and Weidong Guo. 2019. "Throughput of Wireless-Powered Based Multiuser System with Large-Scale Distributed Antennas" Information 10, no. 1: 13. https://doi.org/10.3390/info10010013
APA StyleWang, Q., Wei, J., & Guo, W. (2019). Throughput of Wireless-Powered Based Multiuser System with Large-Scale Distributed Antennas. Information, 10(1), 13. https://doi.org/10.3390/info10010013



