Abstract
Pyrrolidinium-based ionic liquids with anions of the per(fluoroalkylsulfonyl)imide family are particularly interesting for their use as electrolytes in lithium batteries. These ions have several geometric isomers and the presence of different ion conformers and their distribution affects the ILs (Ionic liquids) physical and chemical properties. In the present work, we report the temperature dependence of the infrared spectra of the N-butyl-N-methyl-pyrrolidinium(trifluoromethanesulfonyl)(nonafluorobutanesulfonyl)imide (PYR14‑IM14) ionic liquid; DFT (Density Functional Theory) calculations performed with different models provides indications about the IM14 conformers and their vibrational spectra. Moreover the temperature dependence of the intensity of the lines identified as markers of different conformers provide indications about the conformers’ distribution and the difference of their enthalpy in the liquid phase.
1. Introduction
Ionic liquids (ILs) are salts with melting point below 100 °C, which have been largely studied in recent years due to their peculiar properties [1,2,3], such as a wide liquidus range associated with a low melting point, negligible vapor pressure, chemical and electrochemical stabilities up to high temperatures, and high ionic conductivity, which make them attractive not only for catalytic reactions and synthesis but also for energy applications [1,2,3,4,5].
They are typically formed by organic cations, like imidazolium, pyrrolidinium, ammonium or alkyl phosphonium, and organic/inorganic anions, like hexafluorophosphate, tetrafluoroborate, triflate, dicyanamide, tetracyanamethanide, or bis(trifluoromethanesulfonyl)imide (TFSI) [1,2,3,4]. The physical and chemical properties of these compounds are influenced by the nature of the ions and by their structure. Indeed, all of the properties of ILs are the consequence of competitive microscopic interaction forces, the balance of which can generate an extremely rich scenario. In particular, these interactions can be finely tuned by assembling different combinations of cations and anions or by changing the length and the type of the side chains of the composing ions [4]. Many of the ions composing the ILs have geometric isomers, which can coexist in the liquid state according to the Boltzmann distribution. For some ions, conformers can be identified by means of spectroscopic techniques, such as Raman and infrared spectroscopy, combined to ab initio or DFT (Density Functional Theory) calculations of the vibration frequencies [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].
In previous works [6,10,11,15,16,17,18,19] we investigated, by means of vibrational spectroscopies, the conformers of several ions largely used in the design of applicative ILs, since using ab initio calculations of the infrared-active intramolecular vibrations, it was possible to assign the experimental lines to the various ions composing the liquid, and even to their different conformers. Moreover, we reported the temperature and pressure dependence of the infrared absorption spectra of these ILs both in the liquid and in the solid phase in order to ascertain the changes of the intramolecular structure, and in particular of the conformer distribution induced by the crystallization/melting process. We focused on cations belonging to the pyrrolidinum and ammonium families and on imide anions such asbis(fluorosulfonyl)imide (FSI) and bis(trifluoromethanesulfonyl)imide (TFSI).
The TFSI anion is a flexible molecule that can adopt two energetically inequivalent conformations, the transoid and the cisoid forms, differing in energy by only 2.2 kJ/mol [7,9,13,16]. This ion has been widely studied by vibrational spectroscopies since it possesses very well detectable bands: in particular in the infrared spectra trans-TFSI displays a strong absorption around 628 cm−1, while cis-TFSI shows two bands centered at 602 and 650 cm−1 [7,10]. Moreover, the temperature dependence of the intensities of the peaks attributed to different conformers can provide information about the energy separation of the various conformers [12] and their concentration, which affects the IL’s physical and chemical properties in both the liquid and solid phases. Indeed, the molecular configurations of anions and cations is a key point to understand the dependence of the macroscopic properties of the ILs on their ionic composition. Regarding TFSI, the transoid conformer with a C2 symmetry is more stable than the cisoid one, which has a C1 symmetry [7,10,12], however, due to the low energy separation both conformers are present in the liquid state. Instead, the relative concentration of the TFSI conformers in the different phases of the ILs strongly depends on the cation, as we showed by comparing the temperature dependence of the infrared spectra of two ammonium-based ILs sharing the same TFSI anion, and having different cations: N-trimethyl-N-propylammonium TFSI and N-trimethyl-N-hexylammonium TFSI. As expected, the liquid phases of the two liquids are all characterized by the presence of both TFSI conformers. However, the solid phase shows different behavior for the two compounds: in solid TMPA-TFSI, the relative concentration of the conformers is strongly shifted toward a predominance of the transoid conformer; on the contrary, the solid TMHA‑TFSI retains only the cis-TFSI, even if this rotamer is less thermodynamically stable. We also showed that the study of the relative concentration of the two anion conformers as a function of temperature and pressure provides information about the phase diagram [6,11,16,18,19].
Also the bis(fluorosulfonyl)imide (FSI) ion has two conformers: one with C2 (trans) [15,21,22] and the other with C1 (cis) symmetry [15,21,22,23]. The former is more stable, while the latter has a higher energy by about 4.5 kJ/mol; moreover they both give rise to well detectable bands in the IR spectrum that can be used as a marker of their presence [15].
Concerning cations, conformational analyses are more complex as many ions have an alkyl chain which considerably increases the number of single bonds around which one can have rotations. Some conformational analysis exists for selected cations of the families of pyrrolidinium [14,17,24], imidazolium [25,26] and ammonium [10,11]. Pyrrolidinium based ILs have been largely investigated for their potential application in electrochemistry; and, in particular, extensive investigations of the N-butyl-N-methyl-pyrrolidinium (PYR14) cation conformers was performed [14,27,28]. Our recent calculations [28] showed that the PYR14 ion possesses 33 conformers. The most stable is called equatorial-envelope, and it has a planar configuration of the four carbon atoms of the C4N ring (envelope) and the butyl group at the equatorial position against these four atoms. At an energy only 1.8 kJ/mol higher, one finds the axial-envelope configurations, with the butyl group at an axial position against the four carbon atoms of the pyrrolidinium ring. About 3 kJ/mol higher than the most stable one, we find the twist-axial conformer, in which two atoms of the C4N ring are located above and below the plane constructed by the other three atoms. Higher energy conformer were found to span the entire energy range between 3 and 25 kJ/mol. The envelope and twist conformers can easily convert one into the other by means of pseudorotations, and, since the reported difference in energy between the different conformers is low [14,28], it has been suggested that these two conformers are both present in equilibrium in PYR14‑TFSI [14].
Indeed, the N-alkyl-N-methylpyrrolidiniumbis(trifluoromethanesulfonyl)imide ILs have been largely studied due to their potential use as electrolytes in lithium batteries, for which it is important to widen the liquidus range by shifting the melting temperature to lower temperatures. To achieve this goal several combinations of cations belonging to the pyrrolidinium family and appropriate anions of the per(fluoroalkylsulfonyl)imide family have been studied [5,29,30,31,32]. In particular calorimetric measurements [5,30,32] showed that an increase in the difference between the cation and the anion sizes induces a lowering of the melting transition temperature that ends in a very difficult crystallization, as observed in ILs containing (trifluoromethanesulfonyl)(nonafluorobutanesulfonyl)imide (such as PYR14‑IM14 or PYR13‑IM14), for which only a glass transition is detected around 190 K despite the repeated thermal cycles carried out at low rates and at low temperatures. A similar behavior has been reported also for PYR14 (nonafluorobutanesulfonyl)(toluenesulfonyl)imide (PYR14‑IMT4) [5], indicating that the unfavorable packing of strongly asymmetric anions such as IM14 or IMT4 remarkably lowers the cation-anion lattice energy and hinders the crystallization of the ionic liquid materials [30].
To our knowledge, except for the previously reported TSFI and FSI anion, a systematic conformational analysis of various anions of the per(fluoroalkylsulfonyl)imide family and their vibrational spectra is still lacking. To fill this gap, in this work, we present an experimental and computational study of the IM14 anion. In particular we report the temperature dependence of the infrared spectra of the PYR14‑IM14 (structural formula in Scheme 1); DFT calculations performed with different models provides indications about the IM14 conformers and their vibrational spectra. Indeed, only a conformational search by DFT was reported for IM14 [32]. The comparison of the computational results with the experimental vibrational lines allows the detection of lines which can be used as good markers of the occurrence of the two lower energy anion conformers. Moreover, the temperature dependence of the intensity of those lines provides indications about the difference of the enthalpy of different conformers of the liquid phase.
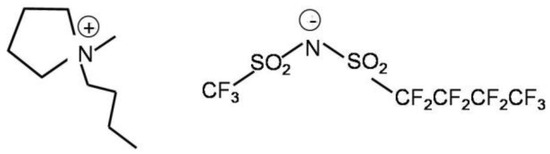
Scheme 1.
Structural formula of PYR14. IM14: left, PYR14+ cation; right, IM14− anion.
2. Results and Discussion
The infrared spectra of the PYR14-IM14 ionic liquid measured in the frequency range between 400 and 1500 cm−1 at two different temperatures (e.g., around room temperature and at 180 K) are reported in Figure 1. It must be noticed that the spectrum was measured up to 3600 cm−1 (see Figure S1 in the supplementary Material) and the absence of absorptions lines in the range between 1600 and 1700 cm−1 (O-H bending modes) and between 3200 and 3600 cm−1 (O-H stretching modes) ruled out the presence of water in the sample. In order to ascribe single vibration lines to the conformers of the composing ions we performed calculations of their vibrational frequencies and intensity.
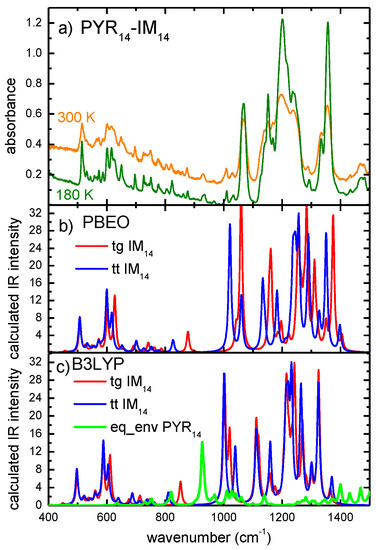
Figure 1.
Comparison between the experimental absorbance of the PYR14-IM14 measured at two different temperatures (a) and the calculated absorptions of the two IM14 conformers (results from PBE0 (Perdew-Burke-Ernzerhof) model in (b) and from B3LYP model in panel (c) and of the eq-env PYR14 conformer (B3LYP (Becke, 3-parameter, Lee-Yang-Parr) model in (c), in the frequency range between 400 and 1500 cm−1. For a better comparison the calculated intensity of the PYR14 conformer is multiplied by a factor of five.
For the PYR14 cation, we considered only the lowest energy conformer which corresponds to the equatorial-envelope (eq-env) geometry [27,28] and we reported in Figure 1c the theoretical absorption spectrum obtained with the vibration frequencies and infrared intensities of the lines previously calculated by us by means of density functional theory at the level of the B3LYP (Becke, 3-parameter, Lee-Yang-Parr) approximation [27]. This approach has been already used to study the infrared spectrum of the PYR14-TFSI and its modifications induced by the interaction with a membrane [27]. It must be noticed that, in Figure 1, the calculated spectrum of the cation conformer is plotted multiplied by a factor of five for a better comparison, since the intensity obtained for its vibrational lines is very weak in this frequency range, compared to those obtained for the anion conformers, as we show in the following:
Indeed, for the IM14 anion, the conformational analysis performed by means of Spartan software (Wavefunction Inc., Irvine, CA, USA) indicates that this ion possesses 74 conformers, but calculations pointed out the occurrence of two low energy configurations, in agreement with previous partial DFT calculations [32]. The most stable configuration is called all-trans (tt), while at an energy 1.8 kJ/mol higher we found the trans-gauche (tg) conformer. The geometry of these two lowest energy conformers is reported in Figure 2, while their atomic positions are reported in the supporting info, Tables S1 and S2, respectively.
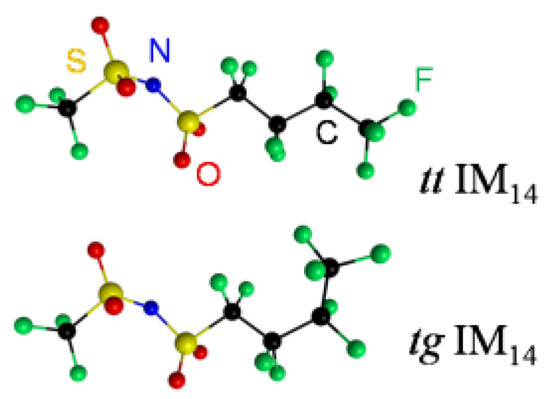
Figure 2.
Equilibrium geometry of the two lowest energy IM14 conformers, tt IM14 and tg IM14, as obtained by DFT calculations.
The higher energy conformers span the entire energy range up to ~19 kJ/mol.
The vibration frequencies and their intensity were calculated for both IM14 conformers by means of two models: the B3LYP is commonly used for calculations on ions composing ionic liquids [6,10,13,14,15]; the BPE0 model, that has been reported to give better agreement with the experimental vibration frequencies than the B3LYP model in the bis(trifluoromethanesulfonyl)imide ion [15]. The unscaled calculated frequency values obtained by both methods are reported in the supporting materials, in Table S3, while the absorption spectra generated from these values between 400 and 1500 cm−1 with no scaling factor are reported in Figure 1b,c.
The comparison of the experimental absorbance with the calculated vibration lines provides evidence that the liquid shows the presence of the two anion conformers at both temperatures. In fact the lines below 700 cm−1 and between 1000 and 1500 cm−1 in the spectrum can be due either to the tg or the tt conformer or their superposition, so that the absence of one of them could not be excluded, whereas the contribution of the cation conformer in this frequency range is negligible, except for the line at 950 cm−1. Moreover, the cation lines calculated with the PBE0 model coincide very well with the experimental lines. The frequencies obtained by the B3LYP model are, instead, underestimated and a scaling factor of 1.02 would be necessary to obtain a good agreement with the data. This better coincidence indicates a better performance of the PBE0 model, as already reported for the FSI anion, and it is worth noting that this model is much less time consuming than B3LYP.
As reported in Figure 1, between 1000 and 1400 cm−1 there are several intense absorption lines due to the two anion conformers, but they result quite superimposed in the experimental spectrum and therefore they are difficult to be used as markers of the two configurations. Instead, as better displayed in Figure 3, around 600 cm−1, there are two clearly distinguishable lines, at 616 and 626 cm−1, which can be assigned to the S-N-S in plane bending mode respectively of the tt and of tg IM14 conformers and, therefore, could be used as markers of presence of the two conformers. Indeed, absorbance spectra collected at various temperatures between 300 and 180 K (Figure 3) show that these two lines are present in the whole measured temperature range, even if their relative intensities change with temperature. It has been already reported that this PYR14‑IM14 undergoes a glass transition around 190 K [5,29,30,31,32]; therefore, the present measurements indicate that the two conformers are present both in the liquid and in the glassy state.
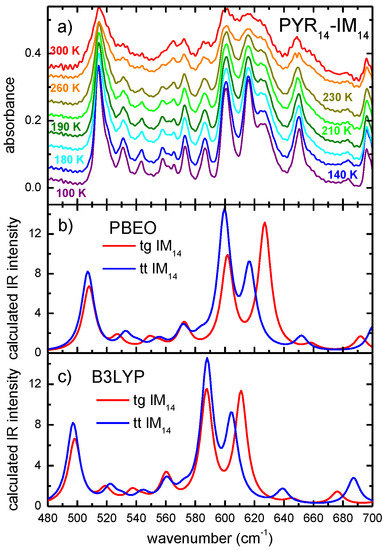
Figure 3.
Comparison between the experimental temperature dependence of the absorbance of the PYR14-IM14 (a) and the calculated absorptions of the two IM14 conformers (results from PBE0 model in (b) and from the B3LYP model in (c) in the frequency range between 550 and 700 cm−1.
The temperature dependence of the absorbance spectrum allows the study of the temperature evolution of the concentration of the two conformers of IM14. The ratio of the conformers’ concentration, r, in a liquid is proportional to the ratio of the intensities of the spectral bands attributable to specific conformers [12]. In the present case, we can distinguish a band at 616 cm−1 due to the low energy tt IM14 and a band at 626 cm−1 which is attributable to the higher energy tg IM14 conformer.
Therefore, we define the ratio of the two conformer concentration, Cx, as:
where Ix designates the integrated IR (Infrared) intensity of the band centered at wavenumber x [12]. The following equation holds for the equilibrium constant, K, between conformers. In the liquid state:
where R is the gas constant, T is the temperature and ∆H and ∆S are the enthalpy and entropy differences between the conformers. Considering that the ratio between the conformer concentrations is proportional to the equilibrium constant K ∝ r, one obtains:
where c is a constant [12].
In the present case we considered Itg = I626 and Itt = I616.
Figure 4 shows the plot of ln(r) vs. 1/T, which verifies the Arrhenius dependence of the concentration from temperature, since there is a straight linear dependence of ln(r) on 1/T for our liquid. This linear dependence in the temperature range above 190 K allows the calculation of ∆H, which is found to be positive and equal to 0.98 ± 0.3 kJ/mol, further confirming that the tt IM14 conformer is the more energetically favored.
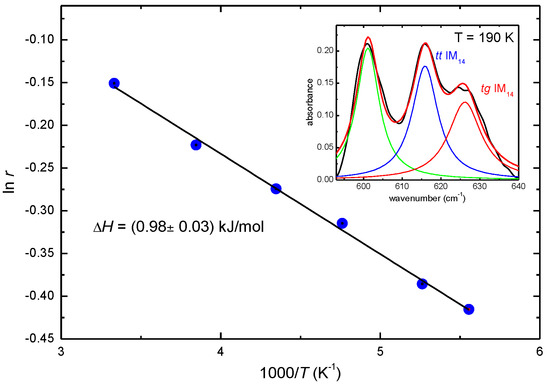
Figure 4.
Temperature dependence of the logarithm of the ratio of the intensities of the bands due to the two IM14 conformers and best fit line. In the inset an example of the fit of the absorbance spectrum and deconvolution into the contributions of the conformers is reported.
The presently reported study provides evidence that a careful comparison of computational results and experimental data is able to identify the lowest energy conformers also of complex systems, such as the presently investigated, in which a total number of 74 conformers is expected.
3. Materials and Methods
3.1. Experimental
The liquid N-butyl-N-methylpyrrolidinium (trifluoromethanesulfonyl)(nonafluorobutanesulfonyl) imide (Pyr14-IM14) was synthesized by a procedure developed at ENEA and described in detail elsewhere [29,30].
Infrared spectroscopy measurements were performed by means of a Bruker IFS 125 HR spectrometer (Bruker Corporation, Billerica, MA, USA) at the AILES beamline of the SOLEIL Synchrotron [33,34]. The spectra were recorded in the mid infrared range (400–6000 cm−1) at a resolution of 0.5 cm−1, by combining a potassium bromide beamsplitter and a wide-band bolometer detector from Infrared Laboratories. A thin layer of the IL was placed between the diamond windows of a vacuum tight cell. All measurements were performed in high vacuum (p < 10−4 mbar), in order to avoid contaminations and absorption bands due to H2O and CO2. The transmission was calculated using the spectrum of the bare optical windows as a reference. Transmission measurements were converted to absorbance data. The samples were cooled down to 100 K by means of a Cryomec cryopump with a temperature rate of 5 K/min, and data were collected on heating at the same rate between this minimum temperature and 300 K.
3.2. Computational
Spartan software [35,36] was employed to find preliminary geometries of the conformers of the (trifluoromethanesulfonyl)(nonafluorobutanesulfonyl)imides ion by means of force field models, which were afterwards optimized by means of the Firefly package [37,38] performing DFT calculations with the 6-31G∗∗basis set by means of two different theories: B3LYP or PBE0. The combination B3LYP theory and 6-31G∗∗basis set has been largely used in the literature in order to investigate the vibrational properties of ionic liquids. However, in the case of the bis(trifluoromethanesulfonyl)imide and the bis(fluorosulfonyl)imide ion [15,16] it has been shown that the PBE0 functional gives better agreement with the experimental vibrational spectra. Therefore, here we compare the two models for the trifluoromethanesulfonyl)(nonafluorobutanesulfonyl)imides ion.
After the geometry optimization, the vibrational frequencies and the IR intensities were calculated. The wxMacMolPlt software (NCSA, Urbana, IL, USA) was used to visualize the molecular geometries and vibrations [39]. The IR spectrum of each conformer was simulated by summing Lorentzian curves centered at each calculated IR vibration frequency with a fixed 10 cm−1 peak width.
4. Conclusions
In the present work we report the infrared spectrum of the PYR14‑IM14 ionic liquid and its temperature dependence. DFT calculations performed with different models provides indications about the IM14 conformers and their vibrational spectra. In particular the markers of the occurrence of the two low-energy conformers (the all-trans (tt) and the trans‑gauche (tg) conformer), were identified in the spectrum. An analysis of the temperature dependence of these lines shows that these two conformers are both present in the glassy and in the liquid phase, and the difference of their enthalpy in the liquid phase is calculated.
Supplementary Materials
The following are available online at www.mdpi.com/2078-1547/8/1/7/S1, Table S1: Atomic positions of conformer tg IM14 of the trifluoromethanesulfonyl)(nonafluorobutanesulfonyl)imides ion (the three coordinates are reported in Å), Table S2: Atomic positions of conformer tg IM14 of the trifluoromethanesulfonyl)(nonafluorobutanesulfonyl)imides ion (the three coordinates are reported in Å), Table S3: Unscaled calculated frequency and intensity of the vibrations of the two conformers of the trifluoromethanesulfonyl)(nonafluorobutanesulfonyl)imides ion, with the two theories: PBE0 and B3LYP, Figure S1: Absorbance of the PYR14-IM14 measured at 300 K in the frequency range between 1300 and 1700 cm−1 (panel a) and between 2700 and 3600 cm−1 (panel b). Lines due to C-H bending and stretching modes are indicated, while the absence of absorptions lines in the range between 1600 and 1700 cm−1 (O-H bending modes) and between 3200 and 3600 cm−1 (O-H stretching modes) rules out the presence of water.
Acknowledgments
We wish to thank Pascale Roy and Jean-Blaise Brubach for assistance at the AILES beamline of the Synchrotron Soleil. This study was performed beamtime # 20160058 at the Soleil Synchrotron.
Author Contributions
Giovanni Battista Appetecchi synthesized the materials; Annalisa Paolone performed the experiments and the DFT calculations; Oriele Palumbo and Francesco Trequattrini analyzed the data; Oriele Palumbo wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Welton, T. Ionic liquids in catalysis. Coord. Chem. Rev. 2004, 248, 2459–2477. [Google Scholar] [CrossRef]
- Navarra, M.A. Ionic liquids as safe electrolyte components for Li-metal and Li-ion batteries. Mat. Res. Soc. Bull. 2013, 38, 548–553. [Google Scholar] [CrossRef]
- Armand, M.; Endres, F.; MacFarlane, D.R.; Ohno, H.; Scrosati, B. Ionic-liquid materials for the electrochemical challenges of the future. Nat. Mater. 2009, 8, 621–629. [Google Scholar] [CrossRef] [PubMed]
- Matic, A.; Scrosati, B. Ionic liquids for energy applications. MRS Bull. 2013, 38, 533–537. [Google Scholar] [CrossRef]
- Kunze, M.; Jeong, S.; Paillard, E.; Winter, M.; Passerini, S. Melting behavior of pyrrolidinium-based ionic liquids and their binary mixtures. J. Phys. Chem. 2010, 114, 12364–12369. [Google Scholar] [CrossRef]
- Palumbo, O.; Vitucci, F.M.; Trequattrini, F.; Paolone, A. A study of the conformers of the N,N-diethyl-N-methyl-N-propylammonium ion by means of infrared spectroscopy and DFT calculations. Vib. Spec. 2015, 80, 11–16. [Google Scholar] [CrossRef]
- Herstedt, M.; Smirnov, M.; Johansson, P.; Chami, M.; Grondin, J.; Servant, L.; Lassègues, J.C. Spectroscopic characterization of the conformational states of the bis(trifluoromethanesulfonyl)imide anion (TFSI−). J. Raman Spectrosc. 2005, 36, 762–770. [Google Scholar] [CrossRef]
- Fujii, K.; Takamuku, T.; Kanzaki, R.; Umebayashi, Y.; Ishiguro, S.-I. Conformational equilibrium of bis(trifluoromethanesulfonyl)imide anion of a room-temperature ionic liquid: Raman spectroscopic study and DFT calculations. J. Phys. Chem. 2006, 110, 8179–8183. [Google Scholar] [CrossRef] [PubMed]
- Canongia Lopes, J.N.; Shimizu, K.; Pádua, A.A.H.; Umebayashi, Y.; Fukuda, S.; Fujii, K.; Ishiguro, S.-I. A tale of two ions: The conformational landscapes of bis(trifluoromethanesulfonyl) amide and N,N-dialkylpyrrolidinium. J. Phys. Chem. B 2008, 112, 1465–1472. [Google Scholar] [CrossRef] [PubMed]
- Vitucci, F.M.; Trequattrini, F.; Palumbo, O.; Brubach, J.-B.; Roy, P.; Paolone, A. Infrared spectra of bis(trifluoromethanesulfonyl)imide based ionic liquids: Experiments and DFT simulations. Vib. Spec. 2014, 74, 81–87. [Google Scholar] [CrossRef]
- Vitucci, F.M.; Trequattrini, F.; Palumbo, O.; Brubach, J.-B.; Roy, P.; Navarra, M.A.; Panero, S.; Paolone, A. Stabilization of different conformers of bis(trifluoromethanesulfonyl)imide anion in ammonium based ionic liquids at low temperatures. J. Phys. Chem. 2014, 118, 8758–8764. [Google Scholar] [CrossRef] [PubMed]
- Martinelli, A.; Matic, A.; Johansson, P.; Jacobsson, P.; Börjesson, L.; Fernicola, A.; Panero, S.; Scrosati, B.; Ohno, H. Conformational evolution of TFSI- in protic and aprotic ionic liquids. J. Raman Spectrosc. 2011, 42, 522–528. [Google Scholar] [CrossRef]
- Fujii, K.; Seki, S.; Fukuda, S.; Kanzaki, R.; Takamuku, T.; Umebayashi, Y.; Ichiguro, S.-I. Anion conformation of low-viscosity room temperature ionic liquid 1-ethyl-3methylimidazolium bis(fluorosulfonyl)imide. J. Phys. Chem. 2007, 111, 12829–12833. [Google Scholar] [CrossRef] [PubMed]
- Fujimori, T.; Fujii, K.; Kanzaki, R.; Chiba, K.; Yamamoto, H.; Umebayashi, Y.; Ishiguro, S.-I. Conformational structure of room temperature ionic liquid N-butyl-N-methyl-pyrrolidiniumbis(trifluoromethanesulfonyl)imide—Raman spectroscopic study and DFT calculations. J. Mol. Liquids 2007, 131–132, 216–224. [Google Scholar] [CrossRef]
- Gatto, S.; Palumbo, O.; Caramazza, S.; Trequattrini, F.; Postorino, P.; Appetecchi, G.B.; Paolone, A. The infrared spectrum of bis(fluorosulfonyl)imide revisited: attractive performances of the PBE0/6–31G∗∗ model. Vib. Spec. 2016, 82, 16–21. [Google Scholar] [CrossRef]
- Palumbo, O.; Trequattrini, F.; Vitucci, F.M.; Navarra, M.A.; Panero, S.; Paolone, A. An infrared spectroscopy study of the conformational evolution of the bis(trifluoromethanesulfonyl)imide ion in the liquid and in the glass state. Adv. Condens. Matter Phys. 2015, 2015, 176067. [Google Scholar] [CrossRef]
- Trequattrini, F.; Palumbo, O.; Gatto, S.; Appetecchi, G.B.; Paolone, A. A computational and experimental study of the conformers of pyrrolidinium ionic liquid cations containing an ethoxy group in the alkyl side chain. Adv. Chem. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Capitani, F.; Gatto, S.; Postorino, P.; Palumbo, O.; Trequattrini, F.; Deutsch, M.; Brubach, J.-B.; Roy, P.; Paolone, A. The complex dance of the two conformers of bis(trifluoromethanesulfonyl)imide as a function of pressure and temperature. J. Phys. Chem. 2016, 120, 1312–1318. [Google Scholar] [CrossRef] [PubMed]
- Capitani, F.; Trequattrini, F.; Palumbo, O.; Paolone, A.; Postorino, P. Phase transitions of PYR14-TFSI as a function of pressure and temperature: The competition between smaller volume and lower energy conformer. J. Phys. Chem. 2016, 120, 2921–2928. [Google Scholar] [CrossRef] [PubMed]
- Sobczyk, L.; Chudoba, D.; Tolstoy, P.M.; Filarowski, A. Some brief notes on theoretical and experimental investigations of intramolecular hydrogen bonding. Molecules 2016, 21, 1657–1676. [Google Scholar] [CrossRef] [PubMed]
- Farrugia, L.J.; Holfter, H.; Klapötke, T.M. Preparation and X-ray crystal structure of caesiumimidodisulphuryl fluoride Cs[N(SO2F)2]. J. Fluor. Chem. 1996, 78, 51–53. [Google Scholar] [CrossRef]
- Matsumoto, K.; Oka, T.; Nohira, T.; Hagiwara, R. Polymorphism of alkali bis(fluorosulfonyl)amides (M[N(SO2F)2], M = Na, K, and Cs). Inorg. Chem. 2013, 52, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Beran, M.; Príhoda, J.; Žák, Z.; Cerník, M. A new route to the syntheses of alkali metal bis(fluorosulfuryl)imides: Crystal structure of LiN(SO2F)2. Polyhedron 2006, 25, 1292–1298. [Google Scholar] [CrossRef]
- Ishida, H. Conformations of pyrrolidinium ion studied by molecular orbital calculations. Z. Naturforsch. 2000, 55a, 665–666. [Google Scholar]
- Lassègues, J.C.; Grondin, J.; Holomb, R.; Johansson, P. Raman and AB initio study of the conformational isomerism in the 1-ethyl-3-methyl-imidazolium bis(trifluoromethanesulfonyl)imide ionic liquid. J. Raman Spectrosc. 2007, 3, 551–558. [Google Scholar] [CrossRef]
- Ribeiro, M.C. High viscosity of imidazolium ionic liquids with the hydrogen sulfate anion: A raman spectroscopy study. J. Phys. Chem. 2012, 116, 7281–7290. [Google Scholar] [CrossRef] [PubMed]
- Vitucci, F.M.; Palumbo, O.; Trequattrini, F.; Brubach, J.-B.; Roy, P.; Meschini, I.; Croce, F.; Paolone, A. Interaction of 1-butyl-1-methylpyrrolidinium bis(trifluoromethanesulfonyl)imide with an electrospun PVdF membrane: Temperature dependence of the concentration of the anion conformers. J. Chem. Phys. 2015, 143, 143. [Google Scholar] [CrossRef] [PubMed]
- Palumbo, O.; Trequattrini, F.; Vitucci, F.M.; Paolone, A. Relaxation dynamics and phase transitions in ionic liquids: viscoelastic properties from the liquid to the solid state. J. Phys. Chem. 2015, 119, 12905–12911. [Google Scholar] [CrossRef]
- Montanino, M.; Alessandrini, F.; Passerini, S.; Appetecchi, G.B. Water-based synthesis of hydrophobic ionic liquids for high-energyelectrochemical devices. Electrochim. Acta 2013, 96, 124–133. [Google Scholar] [CrossRef]
- Jeremias, S.; Carewska, M.; Conte, L.; Passerini, S.; Appetecchi, G.B. Asymmetry effect of novel per(fluoroalkylsulfonyl)imide anions in pyrrolidinium ionic liquids. RSC Adv. 2013, 3, 17755–17761. [Google Scholar] [CrossRef]
- Castiglione, F.; Raos, G.; Appetecchi, G.B.; Montanino, M.; Passerini, S.; Moreno, M.; Famulari, A.; Mele, A. Blending ionic liquids: How physico-chemical properties change. Phys. Chem. Chem. Phys. 2010, 12, 1784–1792. [Google Scholar] [CrossRef] [PubMed]
- Russina, O.; Lo Celso, F.; Di Michiele, M.; Passerini, S.; Appetecchi, G.B.; Castiglione, F.; Mele, A.; Caminiti, R.; Triolo, A. Mesoscopic structural organization in triphilic room temperature ionic liquids. Faraday Discuss. 2013, 167, 499–513. [Google Scholar] [CrossRef] [PubMed]
- Roy, P.; GuidiCestelli, M.; Nucara, A.; Marcouille, O.; Calvani, P.; Giura, P.; Paolone, A.; Mathis, Y.-L.; Gerschel, A. Spectral distribution of infrared synchrotron radiation by an insertion device and its edges: A comparison between experimental and simulated spectra. Phys. Rev. Lett. 2000, 84, 483–486. [Google Scholar] [CrossRef] [PubMed]
- Roy, P.; Brubach, J.-B.; Calvani, P.; De Marzi, G.; Filabozzi, A.; Gerschel, A.; Giura, P.; Lupi, S.; Marcouille, O.; Mermet, A.; et al. Infrared synchrotron radiation: From the production to the spectroscopic and microscopic applications. Nucl. Instrum. Methods Phys. Res. Sect. 2001, 426, 467–468. [Google Scholar] [CrossRef]
- Shao, Y.; Molnar, L.F.; Jung, Y.; Kussmann, J.; Ochsenfeld, C.; Brown, S.T.; Gilbert, A.T.B.; Slipchenko, L.V.; Levchenko, S.V.; O’Neill, D.P.; et al. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [Google Scholar] [CrossRef] [PubMed]
- Hehre, W.J. A Guide to Molecular Mechanics and Quantum Chemical Calculations; Wavefunction, Inc.: Irvine, CA, USA, 2003. [Google Scholar]
- Granovsky, A.A. Firefly version 8.0. Available online: http://classic.chem.msu.su/gran/firefly/index.html (accessed on 21 February 2017).
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Bode, B.M.; Gordon, M.S. MacMolPlt: A graphical user interface for GAMESS. J. Mol. Graphics and Modeling 1999, 16, 133–138. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).