1. Introduction
The search for a mathematical description of reality has a rich and long history [
1]. Biological problems, however, have resisted outright general mathematization and prompted several discussions about the nature of living phenomena and their similarity/radical difference with the rest of the physical world [
2] in this respect. There is, nevertheless, ample evidence that mathematical tools and models (with a varying degree of phenomenological content and fundamental roots) have played a major role and helped in understanding the evolution of various biological systems and populations.
Among all of these developments, population dynamics has a history of almost a century of successful mathematical models, as pioneered by Lotka [
3], Volterra [
4] and others [
5]. As is well known, a general Lotka-Volterra type equation relates the rate of change of the number of individuals of one population to the population itself and other functions involving features that contribute to it. This is conceptually quite simple and flexible enough to accommodate a variety of known biological features that determine the evolution of a given population. However, and quite analogously to the Aristotelian view of physical dynamics, the rate of change is a first order derivative and, therefore, is not sensitive to anything, but the instantaneous variations. On this basis, the Lotka-Volterra type of description has been criticized in the past, and several authors [
6,
7,
8] pioneered the formulation of a second order formalism to deal with the temporal variation of the rate of change. The reasons for this “Galilean turn” have been discussed elsewhere [
9,
10] and established the second order theory on quite firm grounds. It has been shown that a second order theory complies with the recorded evidence of population dynamics and offers a new perspective of several observed phenomena.
The aim of this work is to present and discuss a second order description of the biodiversity (more specifically, the number of genera
) inspired by this Galilean approach. We shall show in
Section 2 below that a fundamental equation for the evolution of
can be constructed and justified. The general character of the solutions and their relevance to the existing fossil record (including massive extinctions, with the particular example of the Permo-Triassic recovery phase) will be the subject of
Section 3. The conclusions of this work will be presented in
Section 4.
2. Second Order Formalism in Population Dynamics and Its Extension to Biodiversity
The basic idea of the inertial (Galilean) approach to population dynamics, as discussed by Guinzburg and Colvayn [
9], starts with the mathematical form of Malthus’ law of population growth: in the absence of external perturbations and given unlimited resources, a population
will grow exponentially
; with
the grow rate. This simple expression can be immediately put in the form:
and interpreted as showing that there is no net “acceleration” in this case to the function
. The introduction of “external forces” (or rather particularly, predator-prey interactions, finite population limits,
etc.) is quite straightforward and assumes the general form
at the r.h.s. (in the first order Lotka-Volterra theory, Equation 1 is replaced by
and
, respectively, yielding a quite different view of the population evolution without any inertia). A complete dynamical description is thus achieved, and its solutions can be compared to actual population data, as discussed in [
10,
11,
12] and many other publications. For instance, the “accelerated death” of bacteria subject to sudden starvation is indicative of a second order theory in which the death rate can vary.
The extension to tackle the biodiversity problem within this Galilean description framework starts with an analogous postulate, which is even more transparent than the Malthusian law, because it does not involve a logarithmic function: in the absence of any perturbation, the number of genera
(assumed to represent biodiversity, so chosen to avoid the problems faced at the lowest species level) will tend to a constant in time, that is:
This is of course a direct consequence of
at sufficiently long times of the unperturbed system, when all “forces” cancel out in steady state. The main idea here is that life develops unperturbed, and after a certain time, the number of genera does not change for fixed external conditions (see, for instance, [
10]). Note that the general inertial view of Mc Shea and Brandon [
12] of a zero-force law (that is, the increase of diversity and complexity with time in the absence of any “force”) is also included in this description. Equation (2) sates that the growth should be linear with time at most. Strictly speaking, a number of fluctuations seem unavoidable, and we should write something like
, the average number of genera, as a true stochastic variable (see
Section 4), but for the moment, we will retain the simpler continuum picture.
2.1. Motivating Basic Ecological Forces
As a further development, we shall assume that putative “forces” stressing the ecosystem on the right hand side are represented by a general function
, to be determined for specific cases. An obvious choice for one of these forces is to assume that the rate of change of the growth rate is proportional to the number of genera
itself, having in mind that it is reasonable to expect an increasing number of genera when the diversity is correspondingly large for a process even happening at a constant/growing rate. For a given maximum number of genera
(the asymptotic value of
at sufficient large times, akin to the carrying capacity discussed in population dynamics [
11]), which will be different for different environments, this “force” can be written as:
with
complying with Equation (2) when this term vanishes for long times and
. Other “forces” may be added depending on the situation, for example a constant force (note that
from Equation (3) is already of this type) or a force proportional to the rate itself
, (
), interpreted as environmental effects that slow down the response of
acting as ecological “friction”. This simple term introduces a damping timescale
possibly related to the action of the biosphere in the relaxation of perturbations, much in the same way as is observed in other natural systems (see below). It is clear that non-linear terms containing both
and
in the polynomials or other complex functions may be expected on general grounds, but shall not be addressed in this exploratory work. Therefore, the simplest form for the complete differential description of
reads:
with
a constant stress, to be refined later if necessary.
2.2. Simple Solutions
The “inertial” solution when
becomes asymptotically constant is, by construction, the behavior to be expected for an unperturbed system. For shorter times, however, the system may show a different transient evolution provided the initial condition determines a non-zero constant initially, and therefore, a linear growth should result after the transient, recovery phase set by a sudden perturbation.
In a more general case and provided that the “forces” are fairly represented by Equation (4), the stationary solutions are analogous to a damped harmonic oscillator. These may be written as
, with
. Depending on the relation between
and
, a damped oscillatory, critically damped or overdamped behavior results [
13,
14]. The last two solutions possess a characteristic timescale, but no period. The period of the first solution is altered by the damping term with respect to its “natural” value
. Note that we have ignored for the moment the constant term related to the value
and the constant
, which would induce a phase difference, as is well known from the general study of harmonic oscillators.
Taking advantage of the extensive studies performed in several contexts of the damped harmonic oscillator, we may immediately write down one of the most interesting solutions of possible biological interest: the response of the system to a sudden, shortly-lived, large perturbation of the type
. The delta function with unity amplitude as an impulsive force model yields the so-called Green function as the general homogeneous solution:
where
are the roots of the quadratic equation
. Again, real (damped) or imaginary (oscillatory) values may be obtained, depending on the hierarchy between
and
. In particular, when the friction is neglected (
), the Green function has the simple form
for
; thus, a sinusoidal decay is obtained.
Generally, when a more complex force on the r.h.s. is acting on the system, it would produce a variation of
, written as its convolution with the Green function, namely:
which allows a complete description whenever a long-term force needs to be modeled (for example, a change in atmospheric composition or some other long-term environmental effect). It should be noted that the precise modeling of evolutionary forces is largely unknown, and even the most natural choice may not have a mathematical form easy to grasp and employ in the r.h.s. [
15]. With the presentation of these mathematical tools, we will try to interpret the recorded fossil history in the next section, paying attention to the biological meaning of the presented formal solutions
3. Comparison with Existing Fossil Records
The study of the biosphere’s diversity history is a delicate business, since various biases could occur and mask fundamental facts. Compilations of marine taxa collected from a variety of sources has been the main source for these studies, and generally speaking, they have shown an initial Cambrian radiation followed by a fluctuating pattern affected by large extinctions and, finally (starting in the Triassic), a large exponential-like increase, often taken as a radiation [
16]. Synoptic data gathered by Sepkoski [
17] have been a chief element leading to this view of diversity since the Cambrian explosion.
Recent work on this problem [
18], however, challenged the former general vision. The main improvement has been a careful treatment of the sampling and taxa identification issues, both somewhat problematic in previous works. The new diversity curve, precisely
vs. time (Figure 1 of [
18]), has been discussed at length and displays, according to these authors, some novel features to be noted. A very general conclusion of the study is that the net increase in diversity was modest and may be limited overall, not exceeding a small numerical factor since the beginning of the records. In particular, it seems that the
increase since the beginning of the Paleogene was about 15% at most. They also obtained that the Meso-Cenozoic radiation started before the late Cretaceous and is not as dramatic as previously thought. Some of the “Big Five” extinctions stand very clearly in the new curve, and some appear less dramatic than before within this 11 My bin of data subject to the procedures detailed in [
18].
The application of the results of
Section 2 to this curve must be done with great care, and we can only advance some general qualitative trends in the present work. First, we note that constant periods (notably the whole Paleogene plateau) plus (linear?) risings and drops are the rule, rather than the exception in this curve. This suggests the purely inertial view of the diversity evolution on the Earth, subject to changes epoch-by-epoch and complying with the expectation of a generally increasing trend for the upper limit (
) as argued by many researchers [
19,
20,
21]. It may be even possible to embrace massive extinctions without a major departure of the inertial view, although then, some non-linear force or sudden perturbation should be invoked to model the extinctions themselves. This is where the Green function of the last Section is a useful tool: a sudden large perturbation of short (geological) duration will then produce a recovery with constants
, which are functions of
directly related to the observed
evolution, provided reliable, higher resolution curves can be obtained instead of the relatively large 11 My binning considered in [
18]. It is important to note that due to the “extant genera” problem of Alroy
et al. [
18], the curve may underestimate the growth near present times, a feature that is not problematic in the original Sepkoski compilation [
22].
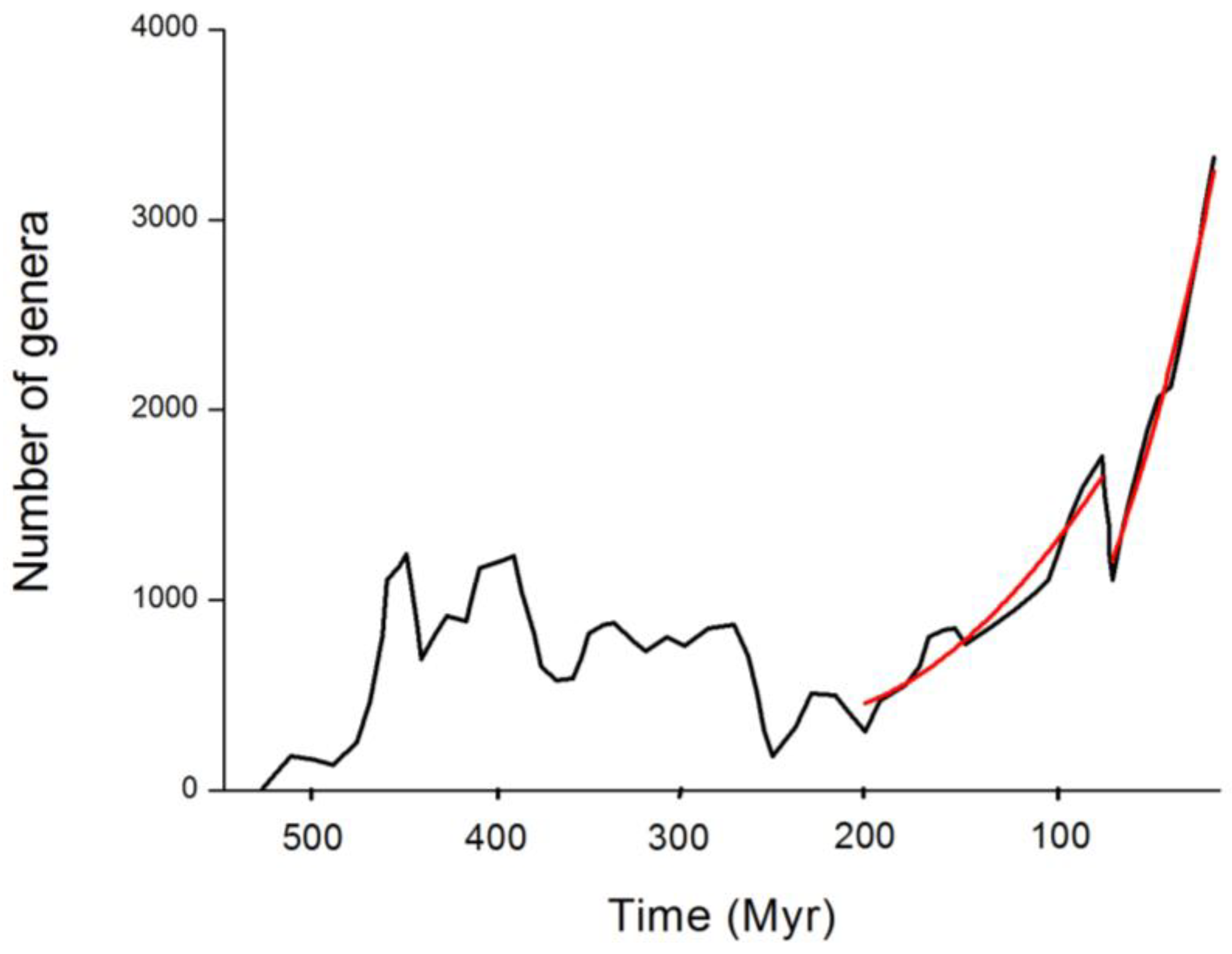
Figure 1 displays a simple prediction of the model in the long-term recovery leading to steady states after two large extinctions. It is assumed here that the extinction event resets the conditions, creating a constant ecological stress
of different magnitude on the r.h.s. of Equation (4) and also that the
compensate for each other. The solutions are then parabolic in time. This is as acceptable as an exponential growth in both situations.
Figure 1.
Best fits to the long-term recovery after the Triassic-Jurassic (left red segment) and Cretaceous-Paleogene (right red segment) extinctions. The black curve is the data by Sepkoski [
22], which suggests a more dramatic growth for the latter and overall for
. The model performs well within a quadratic evolution steaming from the solutions of
.
Figure 1.
Best fits to the long-term recovery after the Triassic-Jurassic (left red segment) and Cretaceous-Paleogene (right red segment) extinctions. The black curve is the data by Sepkoski [
22], which suggests a more dramatic growth for the latter and overall for
. The model performs well within a quadratic evolution steaming from the solutions of
.
In addition to these steady states, the recent work by Burgess, Bowring and Shen [
23] provides an excellent opportunity to test the quantitative short-term recovery response of the system described by Equation (4) to a sudden perturbation modeled as a delta function in time, that is its Green function Equation (5). The authors constructed a time history of the end-Permian mass extinction based onU-Pb zircon dates from five volcanic ashes in the well-studied site of Meshian, China. Using this chronology, the duration of the extinction itself was determined to be 60 ± 48 kiloyears (that is, virtually instantaneous from a geological point of view and even more instantaneous when the fossil record is analyzed [
24,
25]) and a plot of carbonate carbon isotopic composition history plotted for the aftermath. Under the assumption that the latter quantity is a proxy for the
(which is, nevertheless, subject to some caveats), a comparison with the theoretical picture may be attempted. A “best fit” curve is shown in blue. The agreement is not satisfactory, although the calculated
is acceptable, and a decaying amplitude plus a quasi-frequency (of around 2.6 My
−1) in the late curve are present.
Two general remarks may be in order to achieve a better understanding of the global features. First, the reports on the existence of a 5–10 My recovery timescale present in this extinction [
26,
27,
28] could be directly associated with the exponentially decaying amplitude of the transient originated by the presence of a timescale τ ≡ 1/β, clearly seen in the fit, which falls precisely in this range. Its origin is suggested to be related to the environment itself, rather than being a result of the specific trigger mechanism. In fact, the suggestion [
29] that the dynamics of extinctions should shift from just the abiotic effects to the study of a trophic + non-trophic chain of interactions characteristic of the collapse of the biosphere suggest an exploration of the origin of this timescale from first principles. Second, we believe that the poor agreement of the peaks seen in the fit has to be traced back to the presence of a single frequency in the Green function Equation (5). Actually, the knowledge of dynamical systems similar to those described by Equation (4) suggests that the data curve is the result of a beat between two different frequencies. Therefore, the presented description is still short of providing a satisfactory quantitative picture of the recovery of
after an extinction event (
Figure 2).
Figure 2.
A comparison between the Green function response Equation (5) (blue curve) with the time-resolved data corresponding to the Permo-Triassic extinction event analyzed by Burgess, Bowring and Shen [
23] (black curve). The origin of the time axis has been set to the end of the extinction interval given by these authors. See the text for details.
Figure 2.
A comparison between the Green function response Equation (5) (blue curve) with the time-resolved data corresponding to the Permo-Triassic extinction event analyzed by Burgess, Bowring and Shen [
23] (black curve). The origin of the time axis has been set to the end of the extinction interval given by these authors. See the text for details.
On the other hand, an important claim in the literature [
30,
31] is about a strong periodicity of ~62 My in the fossil record. One of the suggested explanations is that short-lived and long-lived genera behave differently in secular timescales and produce a sinusoidal pattern. This feature has no room in a formalism that treats
as a single quantity without discriminating both types of genera. However, it is fair to state that such a description would be richer and possibly related to the problem just discussed above, for which we have no answer by now.
We finally point out that an attempt to study the global diversity recoveries has been published by Kirchner and Weil [
32], and a lagged correlation (at ≈10 My) between extinction and origination rates is reported (
is just the difference of both), even outside the Big Five extinctions. If true, this timescale appears to be a robust property of the global ecosystem and, therefore, also related to a combination of
(and, as pointed out above, perhaps other participating quantities or more complex forms of these parameters), helping to unravel the nature of a successful mathematical description. It is important to note in this context that such a lagged correlation is equivalent to a phase difference in the oscillator-like picture and can be easily justified, being a very common feature of oscillator-like dynamics [
14] that remains to be studied.
4. Conclusions
We have outlined in this work a theory of global diversity based on a second-order differential equation. Just like its analogue in population dynamics [
9], the Galilean (inertial) character of the resulting description has some advantages over a first-order “Aristotelian” approach, but it is premature to insist on its advantages until the features are developed and compared in more detail with the existing records. At face value, the history of diversity on the planet shows the features of the inertial behavior. In other words, a naive qualitative analysis could conclude that the inertial description of Equation (2) suffices to account for most of the reconstructed marine genera curve [
18], at least outside of the massive extinction episodes and for relatively short timescales. Alternatively, a different (quadratic) behavior is obtained if the system becomes stressed by a constant force, possibly after an extinction event, resetting the environmental/trophic conditions. After the transient and provided that the forces cancel out quick enough, the system could enter the inertial regime again in which Equation (2) applies and the diversity evolves linearly or tends to a constant instead, or it could evolve quadratically if stressed by a constant ecological force
. It is more difficult to obtain and justify these behaviors within a first-order (Aristotelian) formalism, and there are hints for their presence in the
vs. time actual curves.
Geological long-term trends need also to consider the issue of changing conditions, together with the existence of a growing
. Extinctions themselves pose a different problem not present in a pure inertial view: either a large external perturbation should be introduced (like the exogenous Alvarez
et al. [
33] asteroid), breaking the inertial behavior; or an explicit non-linearity related to the environment/population itself should be identified and modeled. In the first case, Green functions could be more or less directly used to infer the character of relevant quantities, while in the second case, the need of a deeper mathematically-oriented discussion of the biological interactions would be called for, and we would not be dealing with a pure “Galilean” system any more. For the moment, we have established that in the specific comparison with the short-term recovery after the P-T extinction, the Green function of the simplest equation lacks enough features to describe the detailed time-resolved history [
23], pointing towards a more complex form than the one suggested in Equation (4). Alternatively, one can attempt a different class of descriptions, starting from the analysis of the endogenous/exogenous relation, and try to “build-up” the patterns of extinctions, as recently shown by Stollmeier, Geisel and Nagler [
34].
It should be acknowledged that, strictly speaking, a stochastic term added to the oscillator forces would produce an even better description, since an average
would emerge naturally from the effects of the expected fluctuating effects of the environment. Such an improvement is also on the list of future tasks, and the present discussion is intended just to open the debate on these issues.