1. Introduction
Climate change (CC) is expected to significantly decrease annual rainfall in the Mediterranean region [
1,
2,
3], as increase in surface temperature is expected through the end of this century. Projections by the fifth iteration of the Intergovernmental Panel on Climate Change (IPCC) point towards a “likely to very likely” decrease in precipitation over the Mediterranean by 30–45%, especially if temperature rises by 1.4 °C [
4,
5]. IPCC further projects that over the coming years, meteorological droughts and floods in the region will increase in intensity and frequency, seriously altering the ecological and hydrological patterns of the rivers and streams.
The transition from flow conditions to dry river beds creates an ecosystem vulnerable to climate change and flow variability [
6]. Under the pressure of the climate change, the number of intermittent-flow streams is expected to increase in the future. Nowadays, intermittent-flow streams experience dry phases following a natural, periodical pattern and cover almost 30% of the total length of rivers at global scale [
7]. Only in the 19 European countries, the terrestrial area covered by intermittent streams of known hydrological regime (due to existing gauging stations) reaches 10,180 km
2, almost 11% of these countries’ terrestrial territory [
8]. In arid and semi-arid parts of the world, their exploitation is intensive, involving water storage for irrigation or hydropower generation, surface and groundwater pumping, channelization and urbanization of some parts.
Statistics show that hydropower plants produce around 20% of the electricity consumed on a global scale and 50% of that produced in the United States. More than 60 countries in the world have made important investments in hydropower plants [
9]. For instance, in Greece, the installed hydropower potential exceeds 3061 MW [
10]. The use of hydroelectric power is expected to increase in the future due to the possible exhaustion of conventional fossil fuels and the shift to more sustainable renewable energy resources. Small rivers (<2 m
3s
−1) hide high potential for run-of-the-river (RoR) hydroelectric power generation, which is a more sustainable solution towards dam construction or other renewable sources, as there is not any disturbance in the river regime and limited socioeconomic impacts [
11]. In particular, the investment in RoR plants is crucial in moving to clean energy solutions with zero environmental footprint, especially in Natura 2000 areas. However, RoR plants are dynamic systems with the river flow as a crucial parameter that affects their operation. The operation of turbines follows the weather conditions and the flow response to rainfall or snowpack melting. Consequently, the plant operation and efficiency are strongly depended on the flow transition following climatic conditions and the long-term CC impact on flow variation.
By 2023, Greece is planning to replace existing lignite power plants with renewable energy solutions. Starting in 1954 with the construction of Louros hydropower reservoir, the Hellenic public power corporation (PPC) produces today more than 3173 MW energy from the large hydropower plants and ~300 MW from the 78 small hydropower plants (SHP). A SHP can be characterized as producing power less than 15 MW. The majority of SHPs are located at mountainous terrains facing particular operation conditions (e.g., environmental flow, turbine max and min discharge, shortage of operational days, intermittent energy source). Unfortunately, Greece, with thousands of intermittent streams, operated 2940 water mills in the past and nowadays has fewer than 100 SHPs in operation. Until now, there is no study examining the potential of intermittent rivers to serve small hydropower plants. The objective of the current study is (a) to investigate the current status of the small hydropower plants in Greece, (b) to explore the hydropower potential of intermittent-flow streams, and (c) to make recommendations for the hydrological models and tools used in the design of the SHP in river basins of intermittent flow.
Tsiknias River (Lesvos, Greece) is used as a case study to understand the effect of intermittency impact into the river flow regime and hydropower production. In order to assess the flow regime of Tsiknias River and to put forward management recommendations related to hydropower production, hydrological model simulations up to the year 2020 were conducted for the site. The flow duration curve (FDC) is used as a tool to correlate the hydrological regime to the hydropower potential by calculating the capacity factor index (CF), which represents the mean annual power of the hydropower plant.
2. Methodology
The main methodological steps include (a) an extended literature review related to explore the SHP status and perspectives in Greece; (b) spatial, flow and climate data collection of the Tsiknias River basin as a representative case study of a small river with a mountainous and intermittent flow; (c) the use of Modello Idrologico SemiDistribuito in continuo (MISDc) (Matlab code) [
12] to conduct hydrologic analysis of the historical conditions and climate change scenario inputs. (d); the use of the flow duration curve (FDC) in designing SHPs.
2.1. Study Area
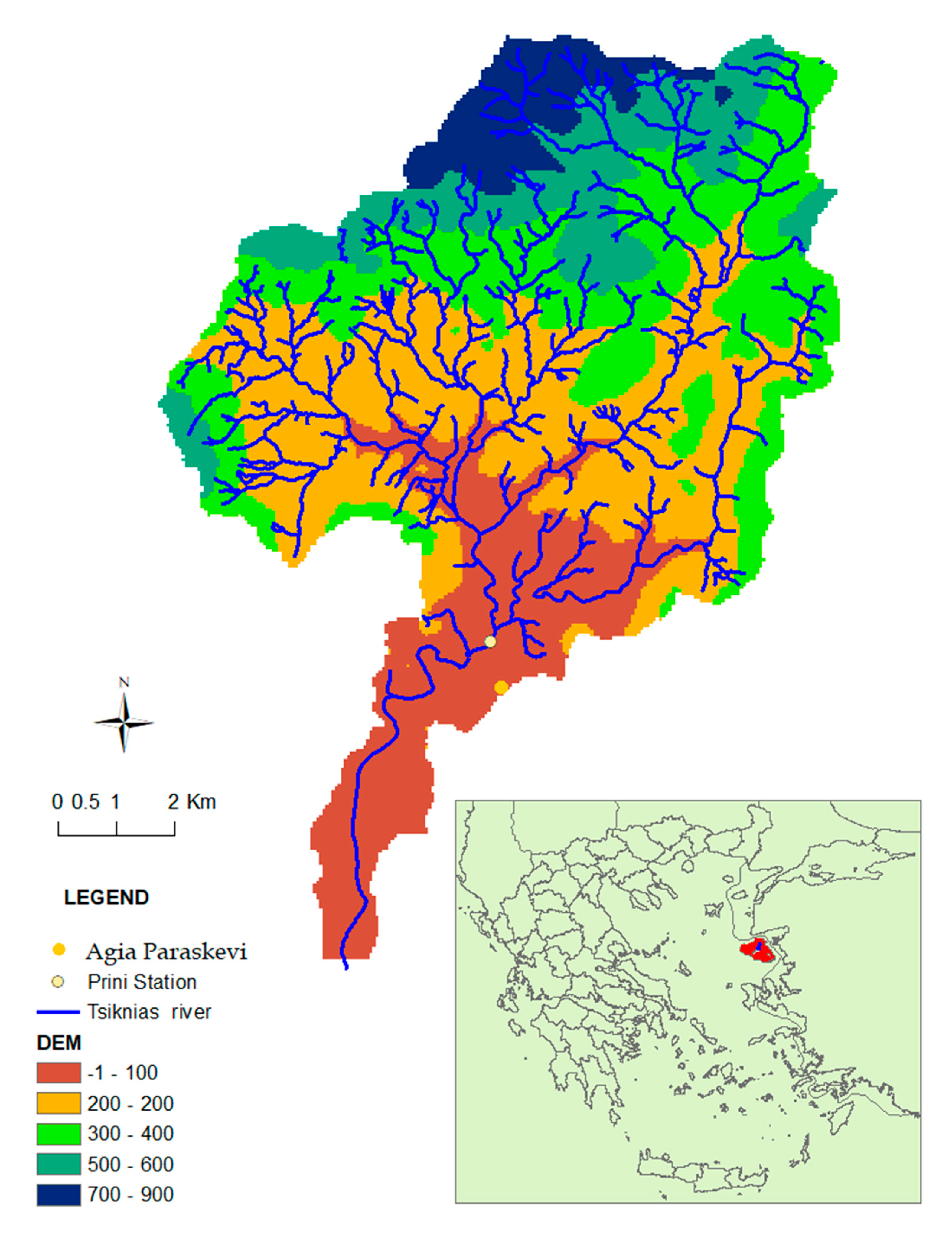
The Tsiknias River catchment, located in the north-central part of Lesvos, Greece (
Figure 1), flows south into the island’s Gulf of Kalloni and through the settlement of Kalloni. The catchment is approximately 91.3 km
2 in size and encompasses a lowland and low mountainous environment with its highest point of elevation being 968 m (Bormann et al., 2018). Tsiknias River is a major river discharging into the closed gulf of Kalloni in terms of water amount and nutrient load contribution. The area is of a Mediterranean climate type and is primarily occupied by agriculture (olive groves), grassland, and brushland habitats, with some small pine and oak forests at the northern tip of the catchment [
13]. The soil in the largest part of the area originates from various lithological formations such as volcanic lava, pyroclastics, and ignimbrite. Only in small segments and especially at the mouth of the river, the soil is composed of torrential concentration/fluvial deposits (clays, sands, fluvial deposits). The soils of the study site are of shallow depth (from 5 to 30 cm) to moderately deep depth (from 30 to 65 cm), are well drained, [
14] and the maintenance of terraced fields by the farmers prevents soil erosion [
15]. The river experiences flash flooding during the rainy season (November to April) and reaches no-flow during summer months, with major flood events causing extensive economic damage in Agia Paraskevi village and in the main road close to the river estuaries [
16]. The mean outflow of the river is estimated to be 21.4 hm
3 and the annual loads of nitrogen and phosphorus flowing into the Gulf of Kalloni are approximately 23 t N and 8.5 t P [
17].
The river experiences intermittent flow, flash flooding and long dry periods annually and the effects of climate change on these flow variations should be considered in the management of water bodies. The adaptation of non-conventional water resources measures (i.e., the construction of a reservoir to serve the operation of a small hydropower plant), riverbank protection measures to control flood-prone areas and the high energy demands of the area, and the effect of CC on the environment are subjects of continuous discussion at community and municipality levels. Using hydrological modeling to simulate climate change scenarios at the level of specific river catchments can be indispensable in guiding management strategy [
18].
The meteorological station in Agia Paraskevi (95 m elevation) operates in the basin, recording precipitation, wind speed, wind direction, solar radiation, cloud cover, humidity, and barometric pressure, with an annual mean rain value of 664 mm. Water level data used in the modeling were sourced from the telemetric station (Prini bridge) installed in 2014 which records flows at 15 min intervals [
19].
2.2. Continuous Rainfall-Runoff Model—MISDc (Matlab Code) Model Setup
The lumped version of the “Modello Idrologico SemiDistribuito in continuo” (MISDc) is used in this study to simulate an hourly time scale of the river flow. The model was developed for the simulation of flood events on a half-hourly time scale and consists of two components: (a) a soil water balance model that estimates the soil moisture temporal pattern, extracting the initial soil moisture conditions for the second component and (b) an event-based rainfall-runoff model for flood hydrograph simulation. The two models are coupled through a simple linear relationship that is derived from extended field work taken place at experimental catchments located in central Italy [
6]. A nonlinear power function is used to relate the soil moisture storage of the model and the baseflow. MISDc is applied in several catchments in Italy and across Europe. It is freely available on the researchgate website [
20]. Its strengths are its simplicity in visualizing the surface flow of the river, the limited number of calibrated parameters and its high performance in semi-arid areas. Applications of the MISDc model include stream flow prediction, runoff forecasting and hydrologic extremes [
21,
22,
23,
24,
25].
For the study of the Tsiknias basin, MISDc is used as a lumped model, considering the entire basin as one single discharge point. For this particular case, the model was calibrated with flow data (from Prini gauging station) of hourly time steps for the period from October 2017 to January 2020 and validated for the period of July 2014 to November 2016. The input meteorological time-series covered the period of 2011 to 2020. Daily time step meteorological data (temperature and precipitation) are available for the period if 1956 to 2020. The meteorological station of Mytilene airport operated by the Hellenic Meteorological Service was used as a reference meteorological station for the correction and filling of missing data of Agia Paraskevi using the inverse distance weighting (IDW) method. The missing data were less than 0.1%. The MISDc model requires three input datasets: precipitation, temperature and flow time series. The model was run several times by calculating the Nash–Sutcliffe efficiency (NSE) values (Equation (1)) and Kling–Gupta efficiency (KGE) (Equation (2)) until the simulated graph patterns followed those of the observed graph patterns to a sufficient degree and the NSE value approximated one (1).
The MISDc model includes twelve (12) model parameters related to three modules: (a) the soil water balance model, (b) the soil conservation service curve number, and (c) the routing module. A standard gradient-based automatic optimization method in used by the model to maximize an objection function by selecting an optimum set of calibrated parameters. The objective function measures the Euclidean distance from the ideal point (unity) of the Pareto front (unity) and is called the modified dimensionless Kling–Gupta efficiency statistic [
22].
The following equation was used to calculate Nash–Sutcliffe efficiency (NSE). The value of NSE for a “perfect fit” is one. The equation describing Reff is the following:
where
Qsim is the simulated flow;
Qobs is the observed flow;
is the mean of the observed flow.
Additionally, the Kling–Gupta efficiency (KGE) is used to count the model efficiency, covering several weaknesses or perceived shortcomings in NSE.
The KGE is calculated as
where
σobs is the standard deviation in observations,
σsim the standard deviation in simulations,
the simulation mean, and
the observation mean. Values of KGE close to one (1) indicate perfect agreement between simulations and observation values.
The capacity factor (CF) is the ratio of the annual average power in relation to the maximum produced in a power plant (Equation (3)) and is a crucial design parameter of the plant.
where
Pmax is the rated power (in kW) and
Pm the average annual power (in kW).
Additionally, the CF is estimated on an annual scale in relation to the design discharge (
Qd)
Annual energy (
Ea in kWh/year) is calculated from the CF according the formula
Lower values of the CF are used in storage-type hydropower plants (~20%) and much higher values in RoR plants (~80%) [
26]. If the plant is designed with a low design discharge (
Qd) which corresponds to high CF values, then either a small part of the hydropower potential is exploited (in the case of perennial flow) or the operation of the plant is strongly dependent on the flow regime fluctuation (in case of torrential flow). However, in a river with a constant flow, the selection of the design discharge has very little impact on annual energy production. In contrast, in an intermittent-flow river, the design discharge selection is crucial for plant viability. In more torrent-type streams, where the basin permeability is very low and the river becomes dry during the summer, the design flow has a high impact on plant performance [
26].
The flow duration curve (FDC) visually represents the hydrological regime, synthesized by the permeability of the various soil types and land use, the water management practices and climate characteristics of the river basin. The FDC relates the duration of each flow value in days (d) or as a percentage (p) of time.
3. Results
3.1. Status of Small Hydropower Plants in Greece
The development of large hydroelectric projects (HEPs) is part of the strategic planning of Greece towards energy independence and, in the last decade, has represented part of the “decarbonization” of electrical energy production and optimal integration of renewables. To date, Public Power Corporation (PPC) Hellas and PPC Renewables, have been responsible for the development of large HEPs (15 units) and SHPs (17 units) with a total power output of more than 3.4 GW with an average annual production equal to 5.3TWh, while the total useful reservoir volume is equal to 5.7 billion cubic meters (bcm). Private investments also resulted in the operation of 61 SHPs [
27] with a total installed power of 223 MW. In total, the installed power of SHPs in Greece reaches 300 MW.
Figure 2 shows the locations of 192 SHPs that are either in operation (78 active plants of 107 fully operated plants) [
28] or are under construction or in progress of the authorization process (85 plants). Despite the significant hydropower potential of Greek streams, a very slow development rate of SHPs is observed. SHPs exploit less than 10% of the existing hydropower potential in low-flow streams in Greece, a very small amount in relation to the 70% of the European Union.
The majority of the SHPs are installed in mountainous streams or in the outlet of reservoirs. Unfortunately, there is not any information about the flow status of the streams or the days that the existing SHPs are in operation. However, numerous SHPs are located in small flow streams (<2 m3/s) and are subject to flow variation or experience no-flow during the summer, such as the SHP of Krathis River in Peloponnese, Greece.
The excessively strict rules imposed on the environmental licensing of the SHP have resulted in the establishment of a highly complex, time-consuming licensing framework for the SHP, which has led to substantially suspending of its environmental impact assessment (EIA). The EIA of SHPs located into the Natura 2000 area in particular were strongly influenced by the Water Framework Directive and others similar legislations. Several reasons inhibit the completion of the authorization procedure, such as deficiencies of legal frameworks, irregular bureaucratic requirements and delays, local peculiarities and local society reactions. A direct result of the complex and time-consuming licensing process (~7 years) is the requirement to spend significant amounts of money on the development of projects, which are often disproportionate to their size. A consequent result of the time-consuming licensing process is that other renewable technologies (wind and solar energy) are more competitive than the hydropower projects. Parts of the terrestrial country, characterized by morphology of significant investment interest, are already officially or unofficially “closed” by electricity, such as the regions of Peloponnese or Thrace. “Naeras” in Ikaria island, is the first hybrid energy project in Greece that combines wind and hydraulic power.
Therefore, the development rate of SHPs is about 0.3%, and only 3.5% of the installed renewable resource power is generated by SHPs. Environmental concerns and luck regarding objective information or misinformation in some instances, at a societal level, slowed the rate of development for SHPs at a national level. In addition to this, an important reason that has also affected the development of new projects is the recent financial crisis and the subsequent recession, which reduced investment in such projects.
3.2. Tsiknias River
Tsiknias River is selected for the current study for several reasons, i.e., (a) the existence in the past of water mills in its courses; (b) the intermittent character of its flow; (c) the existence of a long time-series of meteorological and flow data; and (d) the objective of the North Aegean water management plan is the construction of a water-storage reservoir (10 Mm
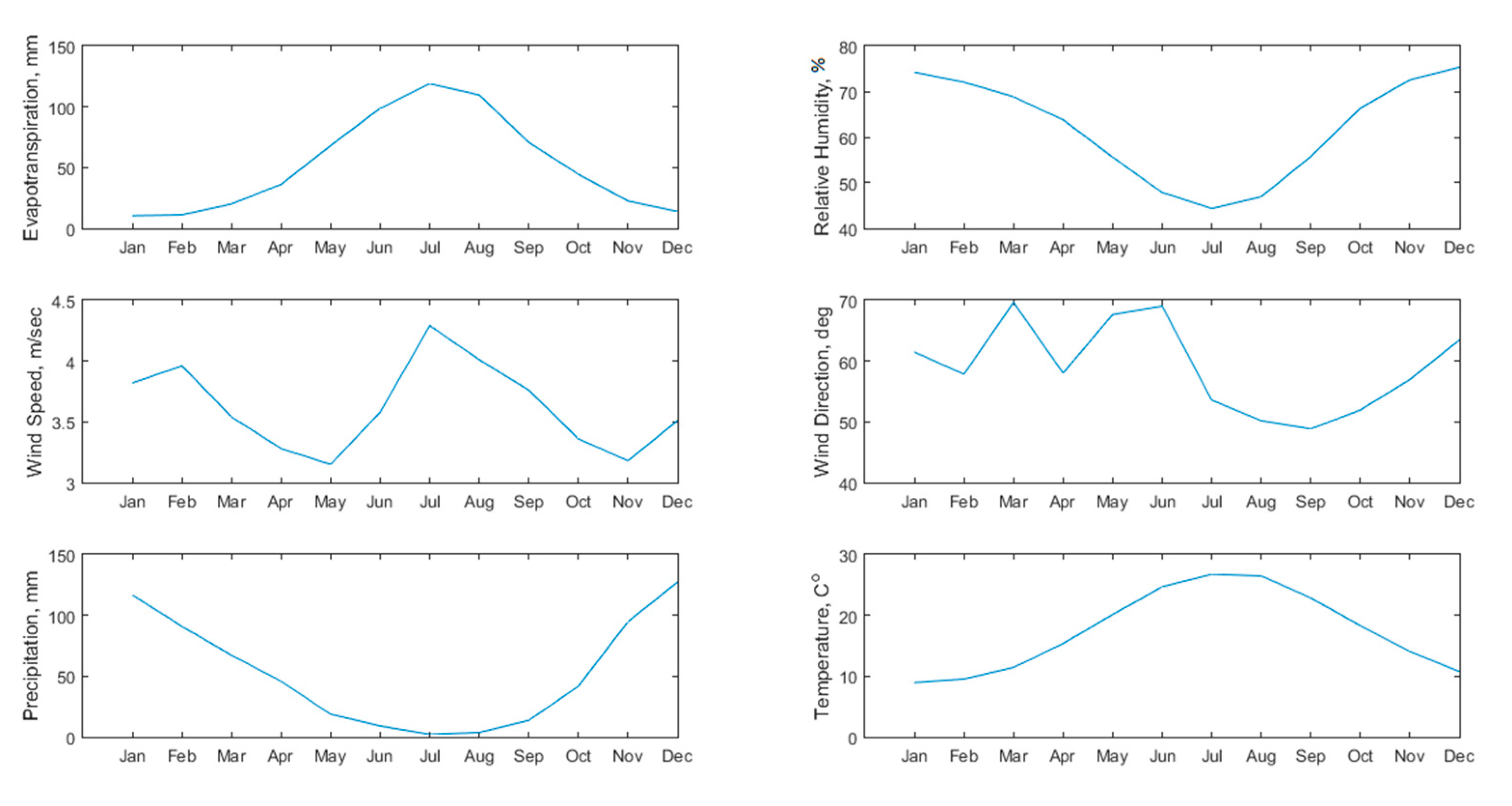
3 capacity) close to river estuaries. The Tsiknias basin is characterized by high variation in precipitation and evapotranspiration during the year (630 mm and 1052 mm mean annual height, respectively). Maximum values of air temperature, evapotranspiration and wind speed are observed in July–August and the maximum precipitation in December (~130 mm/month). In the summer period, the lowest values of precipitation and relative humidity are observed (
Figure 3). The analysis of precipitation records of Agia Paraskevi station shows a precipitation pattern of high intensity. Tsiknias River flows during the winter period from November to April with an average flow of 0.92 m
3/s. The maximum flow is observed during high rainfall events. For instance, in December of 2017 (30/12/2017), the major flood event of the hydrologic year is measured with a flood peak of 237 m
3/s (hourly flow value) and a 15 h duration, originated by a 47 mm precipitation height.
The calibration of the flow resulted in a set of final parameter values (see
Table 1) that gave much better model efficiency values (NSE = 0.6; KGE = 0.8) when compared with previous studies [
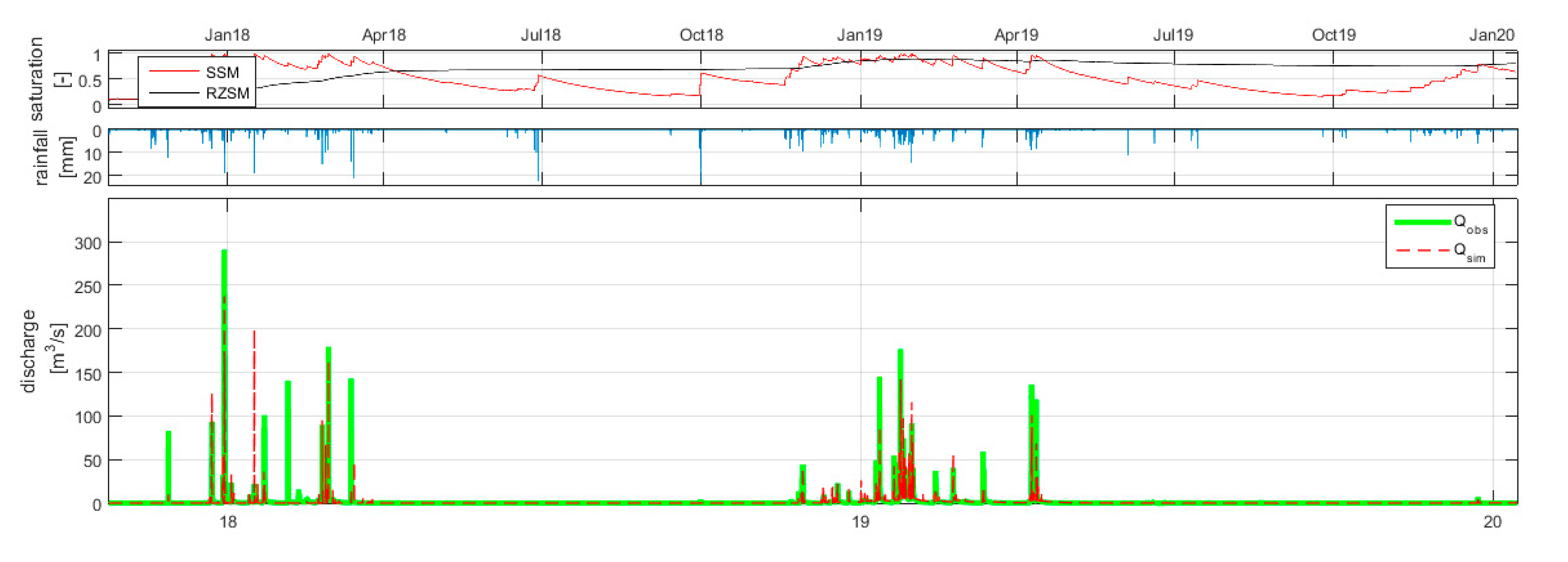
19]. The validation performance of the model gave the KGE value of 0.5, which is mostly related to specific weakness of the observed data (observation of flow increase without rain and changing geometry of the location where the logger is installed due to severe erosion).
Figure 4 shows the hydrograph of observed vs. simulated flow for the calibration period demonstrating the model’s ‘fit’ and the variation of precipitation and soil saturation in the basin for the same reference period (October 2017 to January 2020).
As illustrated from the calibrated hydrograph (
Figure 4), Tsiknias River experienced high discharge and flush floods corresponding to the area’s rainy season. The floods show high seasonality, most of them occurring between the months of October and February. They are characterized as short duration floods with a rapid water level increase resulting from high-intensity short-duration storms [
16]. Similarly, lower discharges are observed between June and August, which corresponds to the drier periods.
3.3. Flow Duration Curve (FDC)
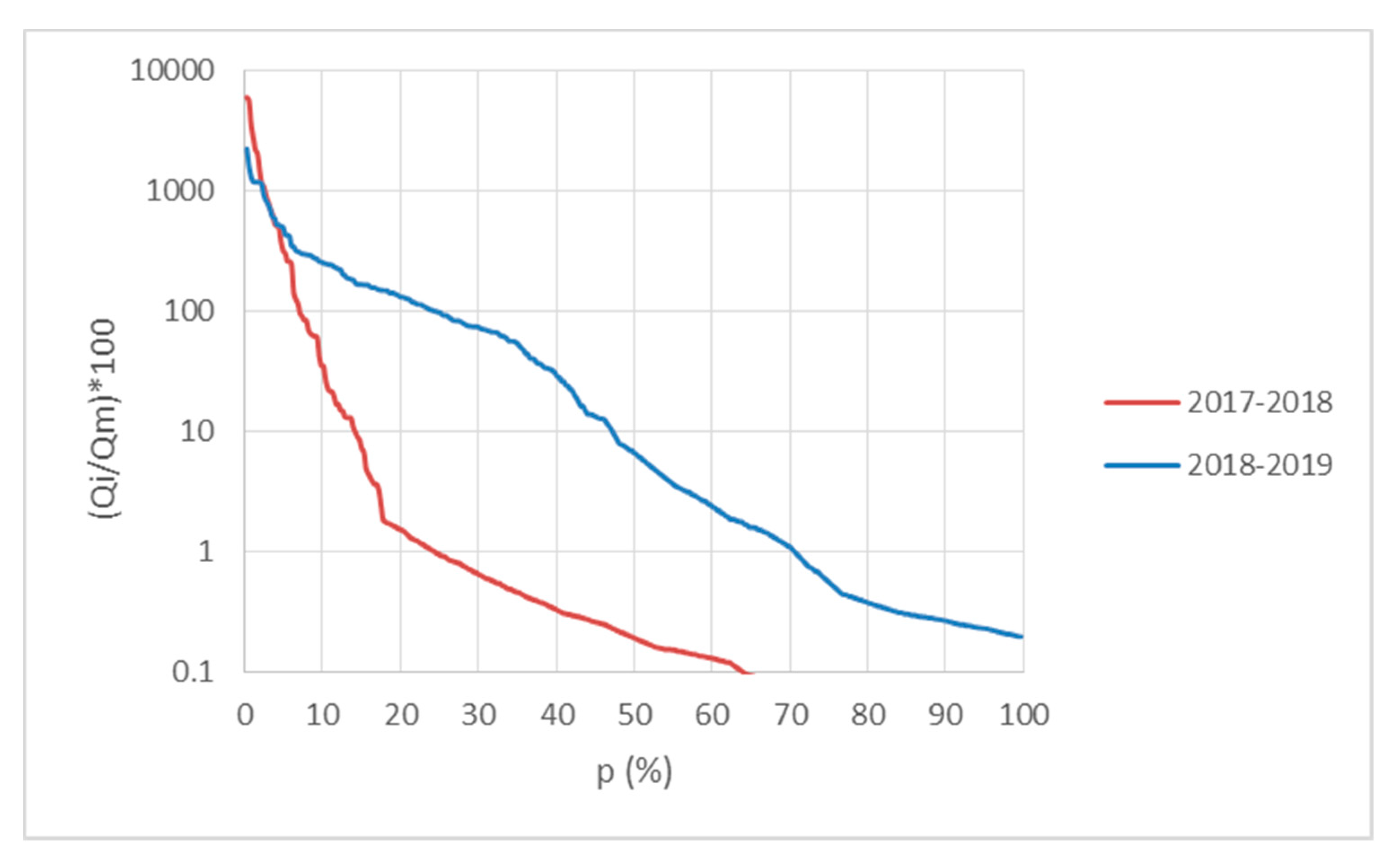
The flow intermittency has a serious effect also on the hydropower capacity of the small streams. The flow duration curve (FDC) is essential for the estimation of their hydropower capacity (
Figure 5). The mean annual FDC is constructed according the standardized non-parametric procedure developed by Vogel and Vennessey (1994) with the duration of one hydrologic year [
29]. In this approach, if the flow data series covers N years, we obtain N separately of the FDC and the mean annual FDC is thus calculated by assigning the mean flow value among the available N to each duration on the x-axis. To facilitate the comparison of the run-off regime of the studied rivers, each river discharge, Qi, is standardized by the mean annual flow, Q
m, of the river. The resulting graph (
Figure 5) uses a logarithmic scale for the discharge axis in order to show low flows more clearly [
26].
For Tsiknias River with a variation in mean daily flow between 0 and 237 m
3s
−1 and a mean flow of 0.92 m
3s
−1, the majority of the high flows are found within the time duration of 0 to 10% (
Figure 5). The study of Liucci et al. (2014) suggests the calculation of the slope from the mean annual FDC graph in the straight line within the range of durations p (%) from 20% to 95%; but for temporary streams, there are very small flow or zero flow values in the durations p > 70%. The slope of the annual FDC (
Figure 5) is constant between the intervals 20 to 70% and is between 2.5 to 5% for the calibrated period. The capacity factor is estimated in relation to the design discharge according to Equation (4). Higher design discharge values correspond to lower CF values.
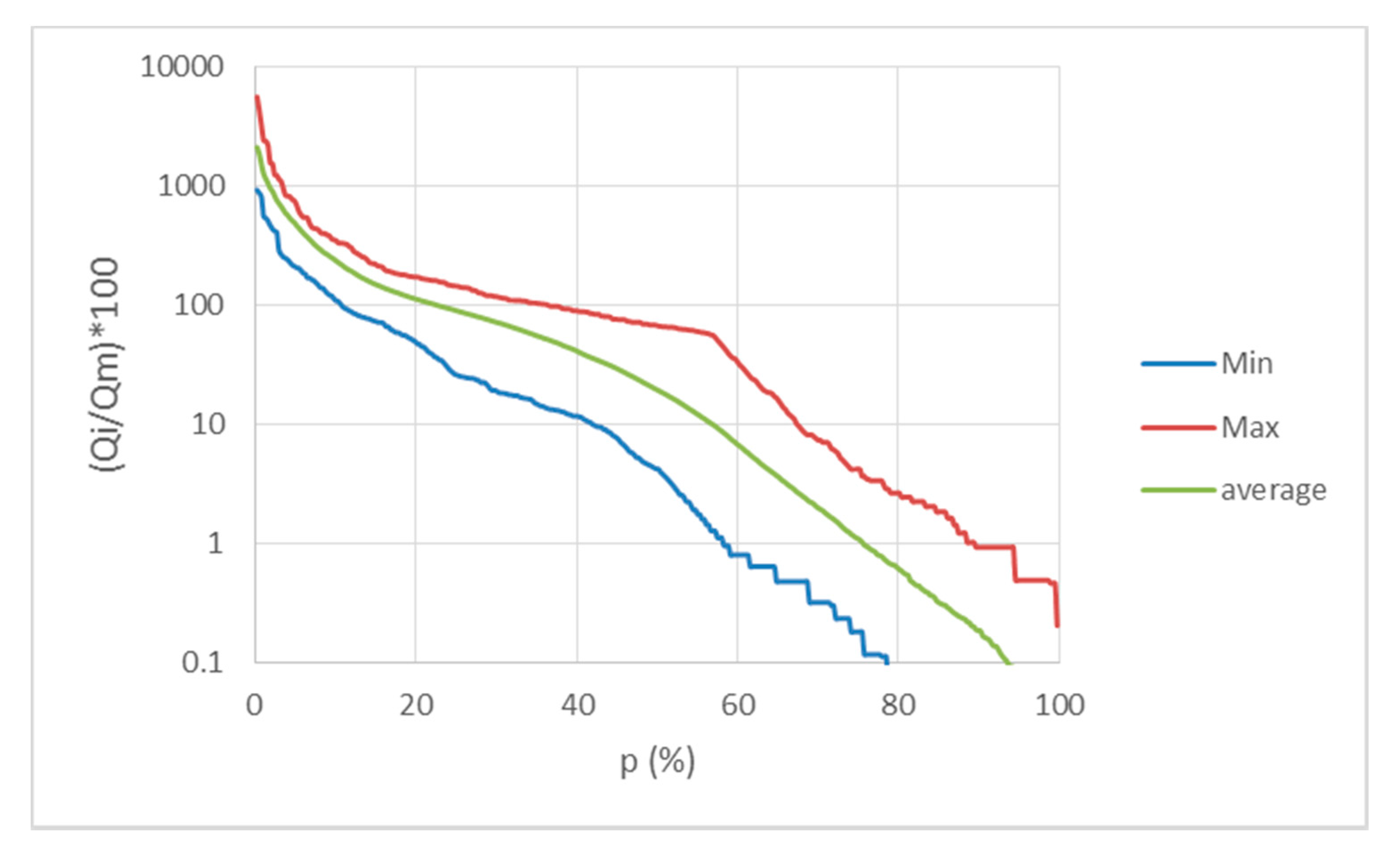
Nowadays, SHPs are designed for a 50 year lifespan. The MISDc model is used to simulate the 50 years (1956–2005) and the average, minimum and maximum annual FDC is constructed for the site for the 50-year period (
Figure 6). It is observed that in time duration >60%, the flows are very small and there is no linear response of the graph. The 50-year simulation indicates that the river can maintain the flow needed for hydropower production by up to 60% of the time. The selection of RoR or storage-type hydropower involves optimizing the operating conditions of the plant in relation to the cost benefit of the business.
3.4. Comparison with Intermittent Streams of Crete
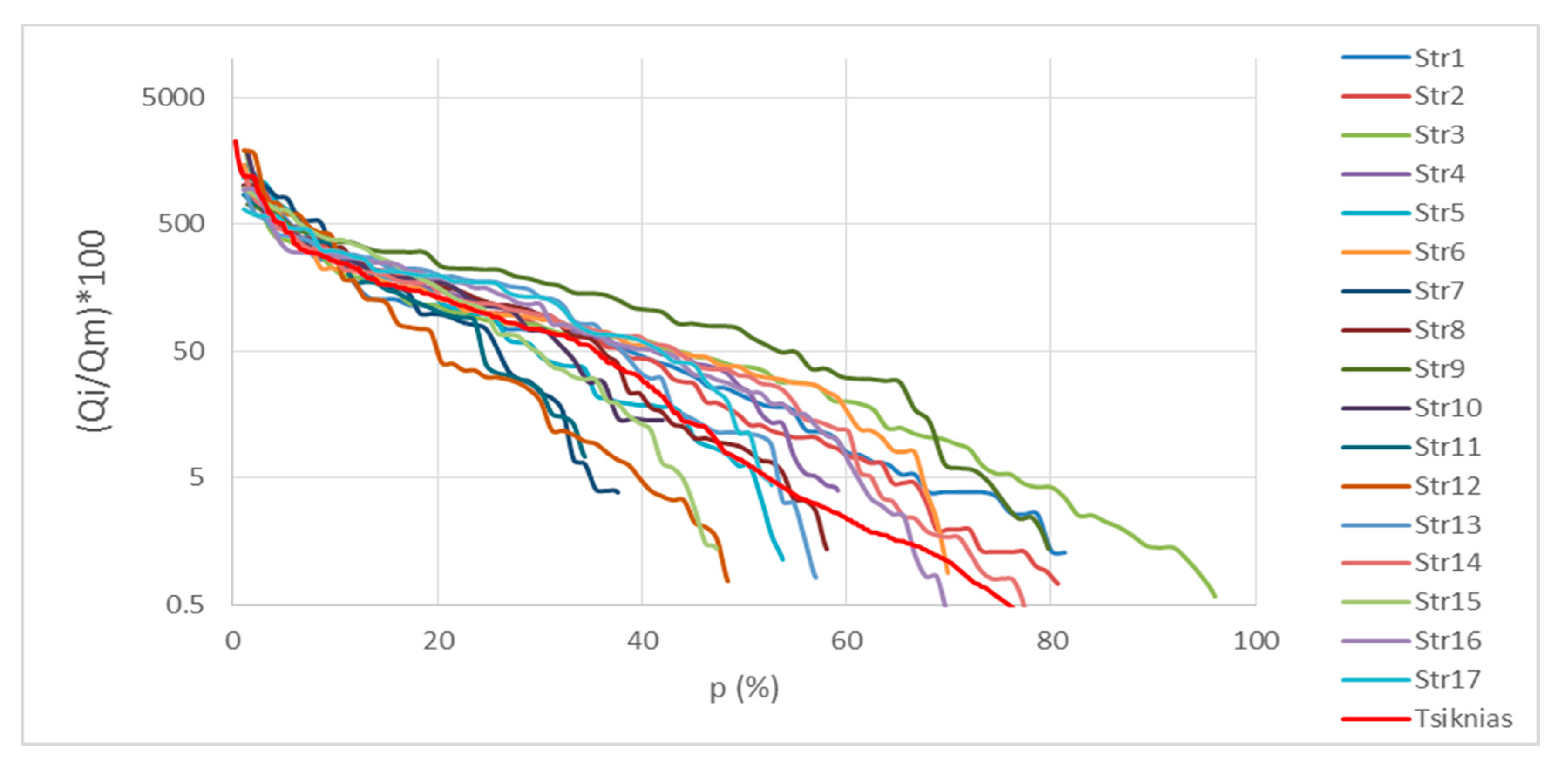
To verify our assumption that temporary rivers can serve SHPs, 17 intermittent streams from the island of Crete were investigated.
Table 2 presents the main characteristics of the streams and
Figure 7 shows the mean annual FDC curves of the streams for the period of 1990 to 1996. Six of the Cretan streams with durations of no-flow less than 40% are selected to estimate slope “a” of the mean annual FDC. The slope ranges between 2.1 to 4.6%, almost in the same interval of the Tsiknias River annual FDC graph. The low slope values indicate streams of low permeability and torrential character of the flow.
4. Discussion
The MISDc model performs the simulation of Tsiknias river basin to a high standard, even in an hourly time-scale. The model captured both the low and high flows very well. However, in intermittent streams, due to the small water volumes, data quality and accuracy remain big issues. These streams are ungauged or have very sparse data, which makes their hydrological study more difficult. In addition, in the case of gauging streams, the water level is sensitive to the slightest changes in rain intensity and storm-affected areas, variables that are often not recorded by the existing meteorological stations due to positional or instrumental errors. However, in small streams (with a flow less than 2.0 m3/s), local storms may increase the water level significantly, without any recording of precipitation in the rain-gauging station. On the other hand, the high-density rain gauge network increases the ongoing costs of monitoring the basin.
During heavy rains of high intensity and short duration (<1 day) that are frequent in arid and semi-arid parts of the world, huge amounts of rainwater are converted into runoff. Water balance estimations in Mediterranean catchments highlight the greater importance of water volumes conveyed upstream than those downstream, thus reflecting the morphometric and lithologic parameters of the watersheds [
30]. Furthermore, the water volume corresponding to the highest values of discharge is much higher than that corresponding to the low streamflow and, in particular, to the baseflow component. It is therefore essential for the design of small hydroelectric plants to be accurate in measuring/predicting high flows. The MISDc model, due to its ability to simulate hourly flows and its very good performance at high flows, provides accurate high flows and therefore has a high efficiency in the accuracy and reliability of the FDCs produced [
31]. The results obtained for Tsiknias River using MISDc are of similar magnitude as those reported in the literature [
22,
32] that reported that the NSE range is close to 0.60 in small Mediterranean catchments.
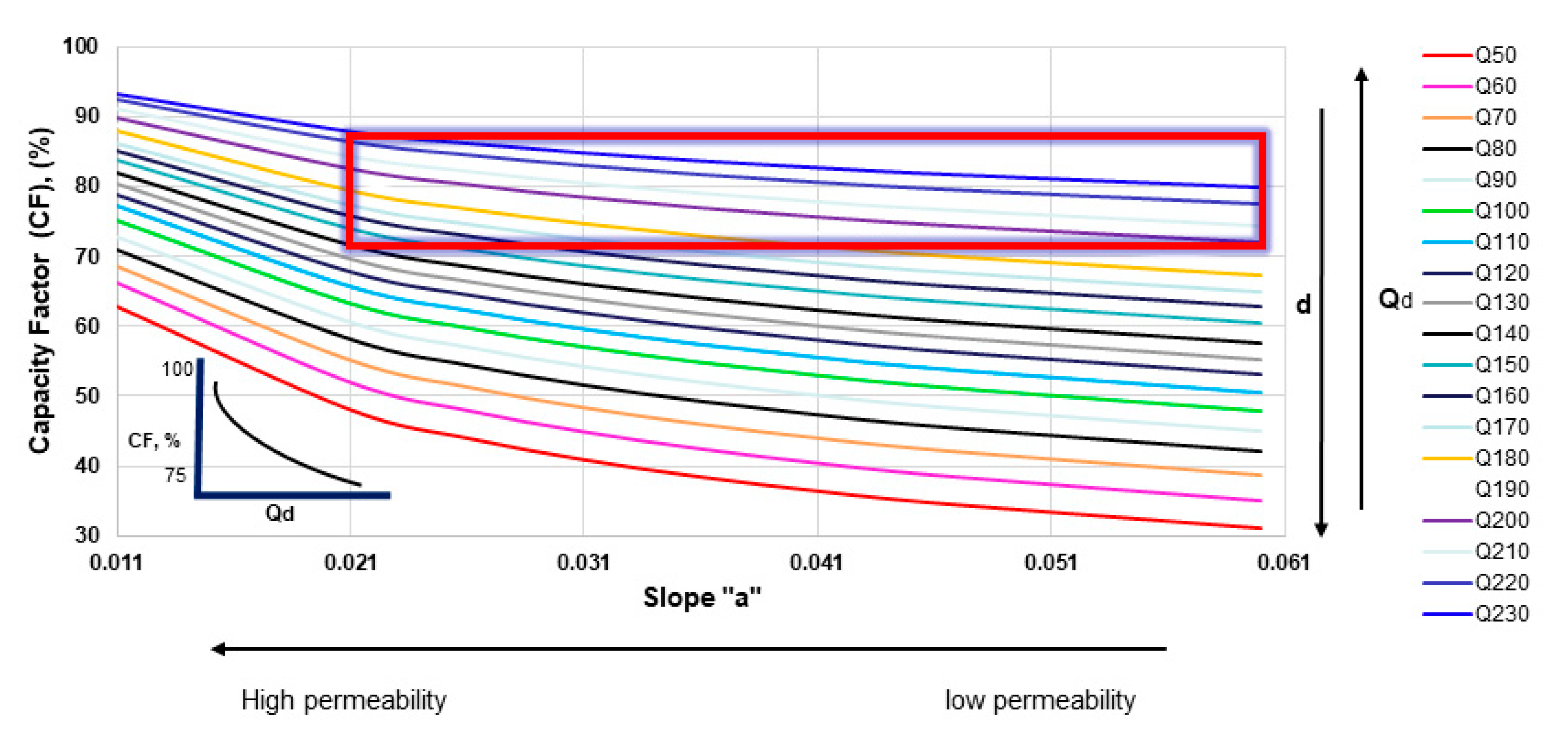
The FDC is a very important tool to study and assess the hydropower potential of intermittent streams. Considering the relation between the slope of the annual FDC “a” and the capacity factor,
Figure 8 graphically visualizes the domain area of the intermittent streams. The current study showed that slope “a” ranges between 0.021 to 0.046 and the capacity factor may remain higher than 75%, as shown by the red box found in the upper right corner of
Figure 8. A serious limitation in the design of the RoR plants in intermittent-flow streams is the limited number of operational days of the plant due to the dry river bed. Low design discharge values are considered to maintain high CF values, otherwise the storage-type SHP may be selected.
Small RoR hydroelectric reservoirs are already operating or are in planning processes in many parts of the world. The small number of SHPs in Greece does not coincide with the established traditions of water power use in the country’s history. The 2940 water mills operated in Greece in the past are found at moderate restorable conditions, meaning that they have technically or even economically feasible hydropower potential [
33]. In a small intermittent stream river, Krathis River, in the Peloponnese, a small hydropower plant of 2.8 MW installed hydropower and of 10 GWh annual potential power (Tsivlos plant) operates, even though the river experiences flow 70% of the time. Furthermore, in the north Peloponnese, the small hydroelectric plant of Glavkos operates with 4.1 MW installed hydropower and 11.4 GWh annual potential power [
34].
All Greek islands are strongly dependent on energy production by the burning of fossil fuels, and the shift to renewable resources is becoming a necessity to overcome energy poverty of households during the era of the economic recession [
35]. In this context, the main goal of the energy policy is the complete decarbonization of the country by 2023 (much earlier than the European goal). Greece is in the process of completing the legal framework for electric mobility, and the action plan for a circular economy and the biodiversity strategy could make the greatest contributions to rebuild a more resilient, sustainable and future-safe country.
SHPs are totally absent from Greek islands, despite the high numbers of water mills operating in the past. For instance, in Lesvos island, 217 water mills operated in the last century, with 137 mills established in perennial-flow small streams and 80 in intermittent-flow streams [
36]. Nowadays, none of these mills are active and there is no plan for SHP operation in the existing water mill locations. Currently, the energy demands of the island are covered by burning oil fuels and diesel, and energy policy-makers plan to invest in electrical submarine cables for energy supply. In the future, hydropower exploitation plans may contribute to the sustainability and energy autonomy of the island.
The water bodies of the Greek islands reveal high vulnerability despite the good supply of water from annual rainfall the islands receive in relation to the demand stemming from various sectors [
37]. Analysis indicated that the hydrogeological systems of the islands have significant vulnerabilities emanating from both natural and anthropogenic pressures in addition to a poor adaptive capacity to counter perturbations [
38,
39]. The literature demonstrates that community-based methods and participatory approaches can greatly enhance a project’s level of success, for example, in the design of a water management plan or an energy sustainability plan [
40,
41]. Similarly, the creation of hydropower exploitation plans in the temporary river basins could also benefit from community involvement. Experts in participatory approaches could facilitate involving the community in the design of the plan. The management of the Natura 2000 areas is an important issue of social and economic character. The execution of plans without involving all the social actors can lead to a long period of social conflicts and huge delays in the licensing procedure. The case-study of the Kalloni catchment related to environmental sustainability [
40] has shown that a better cooperation among politicians, NGOs and the local community is needed for a sustainable future, both of the natural area and of the economy and quality of life of the local community.
5. Conclusions
The regime of the intermittent-flow river is heavily influenced by the natural fluctuation of temperature and rainfall height and experiences extreme drought and flush flooding events. The precise quantification of the flow variation is better explained by running more efficient models of small time-steps, such as the MISDc model. Proper analysis of the simulation results of the MISDc model can guide stakeholders and decision makers in making the right decisions in exploiting the hydropower of intermittent-flow rivers.
As we move into a time in which mineral resources are exhausted, using hydropower in small rivers, even in those characterized by intermittency, will be a serious blow to energy efficiency in the coming decades, especially for small islands that depended on carbon fuel burning. The exploitation of the hydropower of intermittent-flow rivers comes into question, and especially the use of the environmentally friendly RoR plants. However, the design of hydropower plants should consider the annual FDC to investigate the influence of the flow regime on the capacity factor of the plant.
Even though the RoR plants operation coincides with the negligible environmental and ecological impact, their technical details should be carefully evaluated under the scope of the flow fluctuation, especially those located in arid and semi-arid areas. In conclusion, SHPs in Greece and in many other countries of the world are important for energy production. The exploitation of hydropower production of small streams is strongly depended on the knowledge of all the environmental variables, such as precipitation and flow volume variation, but also the impact of human intervention in the water budget (due to over pumping, irrigation needs, water storage or diversion).
Finally, hydropower exploitation plans should be designed considering the impact of climate change, but also following new designs to take into account citizen participation, continuing education and information and the cooperation of all stakeholders.