Abstract
A new and universal theoretical approach to the dynamics of the transient state in elementary physico-chemical processes, called dozy-chaos mechanics (Egorov, V.V. Heliyon Physics 2019, 5, e02579), is introduced to a wide general readership.
1. Introduction
In a publication of Petrenko and Stein [1], it is demonstrated that “the feasibility of the theory of extended multiphonon electron transitions” [2,3,4] “for the description of optical spectra of polymethine dyes and J-aggregates using quantum chemistry”. A recent publication by the same authors [5] “demonstrates the feasibility and applicability of the theory of extended multiphonon electron transitions for the description of nonlinear optical properties of polymethine dyes using quantum chemistry and model calculations”. About twenty years have passed since the first publications on the theory of extended multiphonon electron transitions [2,3,4], however, apart from the author of this theory and this paper, only Petrenko and Stein managed to use their results constructively, despite their promising character [1,5,6], and despite the fact that for a long time, the new theory has been constantly in the field of view of a sufficiently large number of researchers (see, e.g., [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]). The low demand in practice for the new, promising theory is associated not only with its complexity (however, we note that this theory is the simplest theory of all its likely future and more complex modifications [6]), but also with an insufficiently clear presentation of its physical foundations in the author’s pioneering works [2,3,4]. This lack of clarity is expressed, in particular, in the title of the new theory as “the theory of extended multiphonon electron transitions”, which, following the pioneering articles of the author, is used by Petrenko and Stein in their articles. Over the past twenty years, the physical interpretation of the new theory has been significantly improved by the author, as expressed in his recent review [6], as well as in a number of publications preceding it [32,33,34,35,36,37,38,39,40,41]. However, these results on improved physical interpretation are not taken into account by Petrenko and Stein [1,5]. This shortcoming can be compensated by a concept review of the author, according to which, for example, it would be more correct to present the new theory not as “the theory of extended multiphonon electron transitions” [1,2,3,4,5], but as dozy-chaos mechanics [6], in other words, not as some effective but nevertheless particular theory, but as a fundamentally new and universal approach to the theoretical description of the dynamics in the transient state of elementary physico-chemical processes. This concept review is provided below and is intended for a wide audience.
2. Dozy-Chaos Mechanics on a Qualitative Level of Consideration
2.1. Full-Fledged Electron-Nuclear Motion in the Transient State of Molecular Quantum Transitions, Singularity in Their Rates, and the Franck–Condon Principle as a Primitive Singularity Damper
Quantum mechanics as a fundamental theory and the main component of modern theoretical physics works well in atomic and nuclear physics, but it stops working as well in molecular and chemical physics. The reason for this is the appearance of a singularity there in the probabilities of quantum transitions per unit time or, in other words, in the transition rate constants when going beyond the adiabatic approximation [6]. As is well known, the Born–Oppenheimer adiabatic approximation (see [6,42] and references therein), which is the basis of modern molecular physics, solid state physics, quantum chemistry, and other disciplines, allows us to solve problems related to the elucidation of the structure of physical and chemical objects. It is based on the use of a huge difference in the masses of light electrons and heavy atomic nuclei, which leads to a very fast adjustment of the distribution of the electron charge to the motion of slowly moving nuclei. As a result, the electrons form an electrical potential in which the nuclei make their oscillations. In the adiabatic approximation, only the motion of nuclei is dynamically full-fledged; the electrons play a dynamically passive role, which is reduced exclusively to the formation of electric potential for the motion of nuclei. When the molecule is optically excited, it is assumed that the quantum transition of an electron occurs at the turning point of the nuclei making classical oscillations. This assumption constitutes the essence of the Franck–Condon principle (see [6,42] and references therein), which is introduced into molecular physics as some addition to quantum mechanics for calculating the rates of molecular quantum transitions. Thus, with the standard consideration of molecular quantum transitions, that is, consideration within the framework of quantum mechanics in the adiabatic approximation, supplemented by the Franck–Condon principle, the motion of electrons is dynamically primitive, under which there is a forbiddance on the exchange of energy and motion between electrons and nuclei. This forbiddance can be removed if we go beyond the adiabatic approximation, thus ensuring, along with the nuclei, a full-fledged dynamic for electrons. However, in this case of the dynamically full-fledged motion of both nuclear and electronic subsystems of the molecule, due to the incommensurability of the masses of these strongly interacting (according to Coulomb’s law) subsystems, we get a singularity in the rates of quantum transitions. We dampen this singularity in the framework of the so-called dozy-chaos mechanics [6], see details below. In the standard molecular quantum mechanics, which is not singular only in the adiabatic approximation and thanks to it, both the adiabatic approximation and the Franck–Condon principle itself play together the role of such a damper of the singular transition rates [6]. In contrast to the adiabatic dynamics, where electrons are dynamically primitive, while nuclei oscillate, the Franck–Condon principle makes the motion of electrons to be full-fledged when they perform a quantum jump at turning points of nuclei, that is, where the fixed nuclei are dynamically primitive. It is the cases of this kind of “shutdown” from the full-fledged dynamic process of one of the subsystems of the molecule, electrons or nuclei, which ensure the true applicability of quantum mechanics to molecular systems [6].
2.2. Potential Box with a Movable Wall and Dozy Chaos as a Damper of the Singularity
The aforementioned singularity and the possibility of its damping can be easily demonstrated by the example of a one-dimensional potential box with one movable wall, which is connected to the abscissa axis by a certain movable hinge (Figure 1). Suppose that this hinge can be both ideal and non-ideal, that is, to ensure the movement of the wall along the abscissa axis with absolutely no friction, and with some friction. Suppose that the case of infinitely large friction, or in other words, the case of an absolutely fixed wall corresponds to some primitive model of an atom. Then both cases with a movable wall moving without friction and with friction, we are forced to attribute to some primitive model of the molecule, where the movement of the wall models the reorganization of its nuclear subsystem as a result of the electronic transition. It already follows from the aforementioned evaluative judgments (Section 2.1) that standard quantum mechanics is not able to describe theoretically molecules and molecular systems in their entire dynamic completeness. It can describe them only in stationary states, taken in the adiabatic approximation, which in our model correspond to the case of a fixed wall, by which, in turn, we simulate an atom. It can be said that the adiabatic approximation reduces the problem of the theoretical description of a molecule to the problem of describing an atom, in which the dynamics of a quantum transition can, as a rule, be neglected. What cannot be said about a molecule, in which the dynamics of a quantum transition cannot be neglected, since, in addition to the electronic transition, there is a reorganization of the nuclear subsystem, which is forced to adjust to the distribution of the electron charge in a new electronic state. Such a reorganization, as we indicated above, corresponds to the displacement of the wall of the potential box during the electronic transition in our primitive model of the molecule.
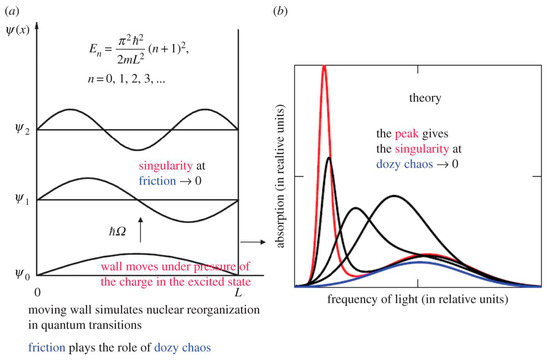
Figure 1.
Singularity in the rate of molecular quantum transitions: a potential box with a movable wall (a) and the optical absorption band shape dependent on the dozy chaos available to a given quantum transition (b); the band shape with the strongly pronounced peak (J-band) corresponds to the least dozy chaos [37]. The wall is fastened to the abscissa axis by a freely movable hinge and can move with a certain friction or without friction against the axis. Such a wall simulates the environmental nuclear reorganization in the molecular “quantum” transitions, where dozy chaos plays the role of friction. In the theory [6], this results in the dozy-chaos dependent optical absorption band being displaced to the red spectral region and narrowed (b). The position, the intensity and the width of the optical absorption band are determined by the ratio between the dozy-chaos energy and the reorganization energy (see Section 3). The smaller the value of is, the higher the degree of organization of the molecular “quantum” transition, and the more the intensity and less the width of the optical band (b). The position of the wing maximum is determined by the energy , whereas the position of the peak is determined by the energy [37]. (Original citation)—reproduced by permission of The Royal Society of Chemistry.
Suppose first that the hinge fastening the wall to the abscissa axis is ideal, and in the process of electronic transition caused, for example, by optical excitation from the ground state, our wall can move along the abscissa axis without friction. As is known, in the case of a quantum transition of an electron from the ground state to the first excited state, there occurs a redistribution of the electron charge, concentrated in the middle of the potential box, towards its edges. Such a redistribution of the charge causes pressure on its walls, with the result that the movable wall comes into very rapid motion. This, in turn, leads to a rapid and unlimited increase in the width of the potential box, with the result that the energy level of the excited electronic state rapidly tends downward to coincide with the energy level of the ground state. As a result, the rate of the electron transition tends to infinity, in other words, we have a singularity in this rate.
If the hinge fastening the wall with the abscissa axis is not ideal, that is, in the process of an electron transition the wall moves with some friction, then during the transition the wall will not have time to go to infinity, and the rate of the electron transition will have a normal finite value. Such a wall movement with friction in a potential box corresponds to the chaotic nature of the reorganization of the nuclear subsystem in a molecule during an electron transition in it. This chaos is called dozy chaos [32,33] (Figure 1), since it occurs in the nuclear and electronic motion in the process of a “quantum” transition (in a transient state) only and is absent in the initial and final (adiabatic) states [6]. Due to dozy chaos, the energy spectrum of the electron and nuclear movements in the transient state is continuous, which corresponds to the classical nature of the motion of both the nuclei and the electron. Such a classical motion of electrons and nuclei in a transient state is no longer described by standard quantum mechanics. On the other hand, the structures of the electron–nuclear system of the molecule in the ground and excited states, due to the reorganization of both the electron and nuclear subsystems, differ sharply and are described, as a rule, quite well within the framework of the adiabatic approximation in standard quantum mechanics. Thus, the initial and final states of the molecule can be regarded as quantum states, whereas the transient state is chaotic and of the classical nature. Therefore, molecular quantum transitions can be called dozy-chaos transitions. The corresponding new theory that describes these dozy-chaos molecular transitions is called dozy-chaos mechanics [6]. The simplest example of dozy-chaos mechanics is dozy-chaos mechanics of elementary electron–charge transfers in condensed media in chemical physics [6]. To date, on the basis of this new theory, it has been possible to systematically explain a large amount of experimental data on the optical spectra of polymethine dyes and their various aggregates [1,5,6,39], as well as a number of other fundamental experimental data in physical chemistry [6].
3. Dozy-Chaos Mechanics: Hamiltonian, Green’s Function, and Dozy Chaos
The Hamiltonian for the theoretical description of the elementary electron transfers between its donor 1 and acceptor 2, which are immersed in a condensed medium, has the form [2,3,4,6,32,33,37,39,41]
where is the effective mass of the electron, is the electron’s radius vector, are the real normal phonon coordinates, are the eigenfrequencies of normal nuclear vibrations, and is the phonon index; is the electron–phonon coupling term. In comparison with the Hamiltonian in the standard theory of many-phonon transitions (see [43]), in the theory of elementary electron transfers the Hamiltonian is complicated merely by an extra electron potential well set apart from the original well by the distance [3,4]. The nuclear reorganization energy (see Section 2.2 and Figure 1) is defined as follows [6,39,41]
where are the shifts of the normal phonon coordinates , which correspond to the shifts in the equilibrium positions of the nuclei, caused by the presence of an electron in the medium on the donor 1 or on the acceptor 2.
As shown in [3,4,6], within the framework of standard quantum mechanics, the taking into account of the dynamics of the transient state by the Green’s function method using Hamiltonian (1) leads to a significant singularity in the rates of “quantum” transitions. This singularity is the result of a full-fledged account of the dynamic interaction of light electrons and very heavy nuclei in the transient state [6,32,33,37,39,41] (see Section 2.1), in other words, the consequence of considering their joint motion beyond the Born–Oppenheimer adiabatic approximation and the Franck–Condon principle (see [6,42] and references therein). This singularity can be easily demonstrated by the example of a one-dimensional potential box with a moving wall [6,32,33,37,39,41] (Section 2.2). In this example, the box is a primitive model of a molecule or electron donor–acceptor system, and the moving wall models the reorganization of the nuclear subsystem of the molecule or the reorganization of environmental nuclei [6].
The general expression for the spectral representation of the total Green function of the system G has the form:
where are the eigenfunctions of the total Hamiltonian of the system, in our case, the Hamiltonian (1); is the set of all electronic and nuclear coordinates; are the eigenvalues of , and is the exact value of the total energy of the system; () is the standard, infinitesimally small imaginary additive, the energy denominator vanishes when . The aforementioned singularity in the rates of “quantum” transitions is eliminated by replacing in the energy denominator of the Green’s function (3) with a finite quantity [2,3,4,6,32,33,37,39,41]. Such a replacement serves as the basis for constructing a new theory—dozy-chaos mechanics of elementary electron transfers in condensed matter [6].
Successful comparison of the new theory with a large number of experimental data, for example, on the optical spectra of polymethine dyes and their aggregates shows that the value far exceeds the magnitude of the quantum of nuclear vibrations : . The energy could be interpreted as the width of the electron-vibrational energy levels in the transient molecular state, which provides the exchange of energy and motion between the electron and the nuclei in the transient state. However, due to the anomalously large values indicated above, this exchange occurs so intensely that it leads to dozy chaos [32,33] in the motion of both the vibrating nuclei and the electron itself (Section 2.2). Dozy chaos is a mix of chaotic motions of the electronic charge, nuclear reorganization, and the electromagnetic field (dozy-chaos radiation) via which the electrons and nuclei interact in the transient state [35,36]. The energy is called dozy-chaos energy [32,33] (see Figure 1). Since the electron is a light and mobile elementary particle in comparison with heavy nuclei, it is precisely the electron that provokes chaos in the vibrational motion of nuclei in the transient state to coordinate their spatial configuration with the new distribution of the electron charge in the final state. Thus, from a physical point of view, we are talking about the discovery in theory of a new property of an electron [6]. In atoms, an electron makes quantum jumps from one discrete energy level to another, while in molecules, to transfer from one adiabatic state to another, the electron provokes chaos in the vibrational motion of nuclei to control their motion in the transient state. In other words, a light electron, by provoking dozy chaos, shifts the very heavy nuclei to new equilibrium positions of their vibrational motions. Therefore, the new theory is called dozy-chaos mechanics [6] (Section 2.2). On the other hand, this name of the theory follows from the fact that it is a generalization of the well-known theory of many-phonon transitions [43], which, in turn, is a quantum mechanics of condensed matter, which takes into account the reorganization of nuclear vibrations during electron transitions. This generalization consists in taking into account the chaotic electron–nuclear dynamics in the transient state [6].
It is known from the theory of many-phonon transitions [43] that the main contribution to the shifts of the normal phonon coordinates during electron transitions and, accordingly, to the reorganization energy (Equation (2)) is made, as a rule, by optical phonons, which are often considered in the framework of the Einstein model . The dozy-chaos energy can be considered in a sense as the imaginary part of a complex reorganization energy in which the reorganization energy is its real part [37]. Moreover, as the comparison of theory with experiment shows, the energy is comparable to the energy : [2,3,4,32,33,37,38,39,41]. Therefore, it can be assumed that the main mechanism of the occurrence of dozy chaos is determined by the interaction of the electron (its charge and spin) with the bound (induction) electromagnetic field of optical phonons. A more definite answer to this question can be obtained in the framework of the future quantum-classical electrodynamics, which will be a generalization of dozy-chaos (quantum-classical) mechanics, just as standard quantum electrodynamics [44,45,46] is a generalization of quantum mechanics [47,48].
4. Dozy-Chaos Mechanics, Quantum Mechanics, and Classical Mechanics: Some Analogy
The aforementioned replacement of the value in the energy denominator of Green’s function by its finite one, which eliminates the singularity in the rates of molecular “quantum” transitions (Section 3), takes physical theory beyond the scope of quantum mechanics and provides us with dozy-chaos mechanics, similar to how the introduction of the finite value of the elementary action, the Planck constant , which eliminates the singularity in the spectrum of an absolutely black body [49]
took the physical theory beyond the scope of classical mechanics and gave us subsequently quantum mechanics itself ( is the circular frequency of the radiation, and is the absolute temperature; see Figure 2) [6].
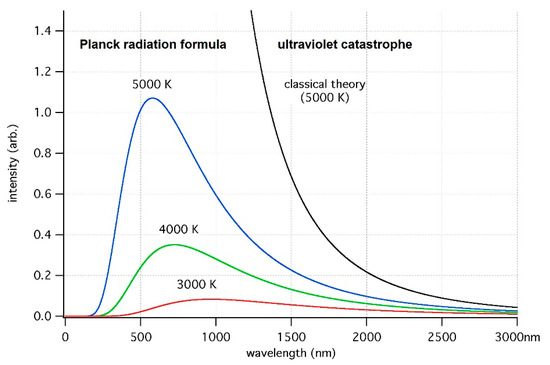
Figure 2.
Distribution function of black light (Equation (4)) and singularity in this function in the framework of classical mechanics (on the right). The wavelength , indicated on the x-axis, corresponds to the frequency by the standard formula ( is the speed of light in vacuum).
5. Dynamic Electron–Nuclear–Reorganization Resonance
One of the main results of dozy-chaos mechanics is a dynamic electron–nuclear–reorganization resonance (the so-called transferon resonance) [3,4] (see also [6]) or, according to [5], the Egorov resonance
where is the characteristic time of motion of the electron in the donor–acceptor system, and is the characteristic time of motion of the reorganization of nuclear vibrations in the environment. These times are obtained by the following equations
where is the distance between the donor and the acceptor of an electron ( is equal to the length of the polymethine chain—the main optical chromophore of polymethine dyes, see Section 7) [2,3,4,32,33,37,39,41], is the binding energy of the electron on the donor 1 (electronic energy of the ground state of the dye) [2,3,4,32,33,37,39,41], and
where is the energy of reorganization of the nuclear vibrations in the medium (see Section 3, Equation (2)). Thus, the Egorov resonance is the resonance between the characteristic frequency associated with the motion of the electron in the space between its donor and the acceptor and the characteristic frequency associated with the movement of the reorganization of the nuclei of the environment in which the donor and acceptor of the electron are immersed. In other words, the Egorov resonance is an important special case in the dynamics of the transient state of elementary electron transfers in condensed matter [6,39,41].
6. Absorption and Luminescence Spectra
The energy of the absorbed photon and the heat energy [43] are related by the law of conservation of energy:
where is the electron binding energy on the acceptor 2 and the quantity defines the thermal effect energy (the heat energy) in elementary electron-transfer processes. The wavelength , indicated on the x-axis in Figure 4 below, corresponds to the frequency in Equation (8) by the standard formula ( is the refractive index). The conservation law (Equation (8)) corresponds to the entire shape of the optical band as a whole: by varying the heat energy , we vary the frequency of light and determine one or another part of the absorption band [2,3,4,6,32,33,37,39,41,43].
In the analytical result for the shape of the optical bands of polymethine dye monomers and their J-aggregates [2,3,4,6,39,41], the transition from absorption spectra to luminescence spectra is carried out by changing the sign before the heat energy () [41,43] and the length of the optical chromophore (electron-charge-transfer distance) () [41].
7. Optical Electron-Transfer-Polymethine-Chain Chromophore
The simplest example of the considered molecular “quantum” transitions with the dynamics of their transient states taken into account is the “quantum” transitions in the main optical chromophore of monomers of polymethine dyes placed in a solvent—in the system “polymethine chain + environment”. According to the concept of the so-called ideal polymethine state (IPS), formulated by Dӓhne [50], the main element of a chromophore in the monomer of polymethine dyes—the polymethine chain has a markedly extended -electron-charge density. It strongly alternates along the quasi-linear polymethine chain and is alternately redistributed on optical excitation (see Figure 3) [51].

Figure 3.
Ideal polymethine state (IPS) [50,51]. Charges reside on carbon atoms of the polymethine chain in the ground state; charges: 1, positive; 2, negative [37]. The polymethine chain length is defined as the distance between nitrogen atoms N. (Original citation)—Reproduced by permission of The Royal Society of Chemistry.
For the first excited state of IPS, the moment of electron transition is directed along the polymethine chain [51], and this corresponds to the elementary electron-charge transfer along the chain [2,3,4,32,33,37,39,41]. Therefore, in Equations (1) and (6) (see Section 3 and Section 5, respectively) the distance can be regarded as the polymethine chain length (see the caption to Figure 3). The thiapolymethinecyanine discussed in Section 8 belongs to IPS.
The specific alternating charge structure of the quasi-linear polymethine chain allows almost neglecting tunnel effects of electron-charge transfers between neighboring carbon atoms inside the chain and so to reduce completely the problem of the electron charge alternately redistributed on optical excitation to that of electron transfer to the distance with the tunnel parameter which is taken close to unity [2,3,4,32,33,37,39,41].
In addition, due to the sufficiently long quasi-linear polymethine chain, one can neglect nuclear motion in a chain itself in the transient state and only take into account the interaction of electron-charge transfers with the nuclear environment [2,3,4,32,33,37,39,41]. Such a physical picture is clearly confirmed in the Egorov resonance (Equations (5)–(7)) region by quantum–chemical calculations [1,5] for thiacyanine [1] and thiapyrylocyanine [5].
8. Implementation of the Dynamic Electron–Nuclear–Reorganization Resonance in the Optical Band Shape
Experimentally, the dynamic electron–nuclear–reorganization resonance (the Egorov resonance, see Section 5) manifests itself, for example, in polymethine dyes [2,3,4,32,33,37,39,41], namely, in the resonance nature of the dependence of the shape of the optical absorption band on the length of the polymethine chain (see Figure 4). The optical band with corresponds to the Egorov resonance or is close to it.
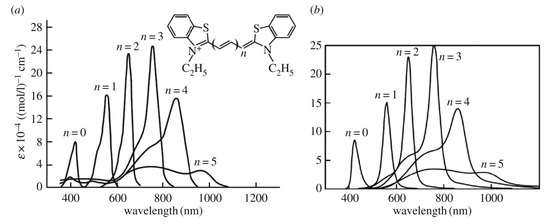
Figure 4.
Experimental [52,53] (a) and theoretical [4] (b) monomer’s optical absorption spectra dependent on the length of the polymethine chain , where are certain roughly equal bond lengths in the chain (thiapolymethinecyanine in methanol at room temperature; is the extinction coefficient) [37,39,54]. The optical absorption band with corresponds to the dynamic electron–nuclear–reorganization resonance (the Egorov resonance, see Section 5) or is close to it. (Original citation)—reproduced by permission of The Royal Society of Chemistry.
The weakening of the interaction of the electron with the medium as a result of the transition from a more polar solvent to a less polar solvent, that is, when moving to the smaller values of the nuclear reorganization energy , leads, according to Equations (5)–(7), to a shift of the Egorov resonance to the region of larger lengths of the polymethine chain [1,39], which is consistent with experimental data in [55].
9. Dozy-Chaos Mechanics and the Franck–Condon Principle
We note that the Franck–Condon principle itself, which involves the classical motion of nuclei “towards” a quantum electronic transition at their turning point (Section 2.1), essentially serves as a prerequisite for creating dozy-chaos (quantum–classical) mechanics [6]. However, an attempt to formalize the Franck–Condon principle in the framework of quantum mechanics leads to a singularity in the rates of “quantum” transitions, which is eliminated in a regular way only in dozy-chaos (quantum–classical) mechanics [6].
10. Conclusions
As it follows from Section 1, future research should focus on generalizing dozy-chaos mechanics to nonlinear optical processes, which are important in a variety of applications [5], in particular, in the imaging of cancerous tumors [56] and cells [57] and in photodynamic therapy [58,59]. Based on the dozy-chaos mechanics of nonlinear optical processes, the optical resolution of the corresponding medical devices can be improved.
On the other hand, from the point of view of theoretical physics, it is of interest to formulate dozy-chaos mechanics in which the initial Hamiltonian is Hermitian (see Equation (1)) [6], as in the well-known theory of many-phonon transitions [43], in the language of non-Hermitian Hamiltonians (see, e.g., [60,61,62,63,64,65,66,67]). In other words, it is of interest to solve the inverse problem: by the form of the complete Green function of the system (Equation (3)), in which the infinitesimal imaginary additive in the energy denominator of its spectral representation is replaced by a finite value, to find the form of the original non-Hermitian Hamiltonian that corresponds to such a modified Green function. In dozy-chaos mechanics, in contrast to the initial Hermitian Hamiltonian with linear electron–nuclear (–phonon) interaction (term in Equation (1)), in the non-Hermitian Hamiltonian obtained from the solution of the inverse problem, the electron–nuclear interaction can turn out to be nonlinear.
If we consider our commitment to the axiomatic construction of fundamental physical theories based on the Hamiltonian formalism being unshakable, a successful solution of the inverse problem can raise the status of dozy-chaos mechanics to the status of quantum mechanics and classical mechanics. This new quantum mechanics, taking into account the classical nature of the transient electron–nuclear state, could then be called quantum–classical mechanics, which, however, has already been made in advance in [6,41].
It is well known that the basic dynamic equation of quantum mechanics, the Schrödinger equation, is an analytical analogue of the Hamilton–Jacobi equation for action in classical mechanics. What is the analogue of the Schrödinger equation in quantum–classical mechanics? Is there such an analogy?
Funding
This work was supported by the Ministry of Science and Higher Education within the State assignment Federal Scientific Research Center “Crystallography and Photonics” Russian Academy of Sciences.
Conflicts of Interest
The author declares no conflict of interest.
References
- Petrenko, A.; Stein, M. Molecular Reorganization energy as a key determinant of J-band formation in J-aggregates of polymethine dyes. J. Phys. Chem. A 2015, 119, 6773–6780. [Google Scholar] [CrossRef]
- Egorov, V.V. Electron-transfer approach to the nature of the optical lineshape for molecular J-aggregates. Chem. Phys. Lett. 2001, 336, 284–291. [Google Scholar] [CrossRef]
- Egorov, V.V. On electrodynamics of extended multiphonon transitions and nature of the J-band. Chem. Phys. 2001, 269, 251–283. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the optical transition in polymethine dyes and J-aggregates. J. Chem. Phys. 2002, 116, 3090–3103. [Google Scholar] [CrossRef]
- Petrenko, A.; Stein, M. Toward a molecular reorganization energy-based analysis of third-order Nonlinear optical properties of polymethine dyes and J-aggregates. J. Phys. Chem. A 2019, 123, 9321–9327. [Google Scholar] [CrossRef]
- Egorov, V.V. Quantum-classical mechanics as an alternative to quantum mechanics in molecular and chemical physics. Heliyon Phys. 2019, 5, e02579. [Google Scholar] [CrossRef]
- Struganova, I.A.; Lim, H.; Morgan, S.A. The Influence of Inorganic Salts and Bases on the Formation of the J-band in the Absorption and Fluorescence Spectra of the Diluted Aqueous Solutions of TDBC. J. Phys. Chem. B 2002, 106, 11047–11050. [Google Scholar] [CrossRef]
- Struganova, I.A.; Hazell, M.; Gaitor, J.; McNally-Carr, D.; Živanović, S. Influence of Inorganic Salts and Bases on the J-Band in the Absorption Spectra of Water Solutions of 1,1‘-Diethyl-2,2‘-cyanine Iodide. J. Phys. Chem. A 2003, 107, 2650–2656. [Google Scholar] [CrossRef]
- Zhang, Z.; Achilefu, S. Synthesis and Evaluation of Polyhydroxylated Near-Infrared Carbocyanine Molecular Probes. Org. Lett. 2004, 6, 2067–2070. [Google Scholar] [CrossRef]
- Abdel-Halim, S.T.; Awad, M.K. Absorption, fluorescence, and semiempirical ASED-MO studies on a typical Brooker’s merocyanine dye. J. Mol. Struct. 2005, 754, 16–24. [Google Scholar] [CrossRef]
- Li, C.; Greenwood, T.R.; Bhujwalla, Z.M.; Glunde, K. Synthesis and Characterization of Glucosamine-Bound Near-Infrared Probes for Optical Imaging. Org. Lett. 2006, 8, 3623–3626. [Google Scholar] [CrossRef] [PubMed]
- Eisfeld, A.; Briggs, J. The shape of the J-band of pseudoisocyanine. Chem. Phys. Lett. 2007, 446, 354–358. [Google Scholar] [CrossRef]
- Roden, J.; Eisfeld, A.; Briggs, J. The J- and H-bands of dye aggregate spectra: Analysis of the coherent exciton scattering (CES) approximation. Chem. Phys. 2008, 352, 258–266. [Google Scholar] [CrossRef][Green Version]
- Kaiser, T.E.; Stepanenko, V.; Würthner, F. Fluorescent J-Aggregates of Core-Substituted Perylene Bisimides: Studies on Structure−Property Relationship, Nucleation−Elongation Mechanism, and Sergeants-and-Soldiers Principle. J. Am. Chem. Soc. 2009, 131, 6719–6732. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, T.E.; Scheblykin, I.G.; Thomsson, D.; Würthner, F. Temperature-dependent exciton dynamics in J-Aggregates—When disorder plays a role. J. Phys. Chem. B 2009, 113, 15836–15842. [Google Scholar] [CrossRef]
- Kalimuthu, P.; John, S.A. Nanostructured Aggregates ofmeso-Tetramesitylporphyrin on Solid Substrate. Langmuir 2009, 25, 12414–12418. [Google Scholar] [CrossRef]
- Bouit, P.-A.; Aronica, C.; Toupet, L.; Le Guennic, B.; Andraud, C.; Maury, O. Continuous Symmetry Breaking Induced by Ion Pairing Effect in Heptamethine Cyanine Dyes: Beyond the Cyanine Limit. J. Am. Chem. Soc. 2010, 132, 4328–4335. [Google Scholar] [CrossRef]
- Würthner, F.; Kaiser, T.E.; Saha-Möller, C.R. J-Aggregates: From serendipitous discovery to supramolecular engineering of functional dye materials. Angew. Chem. Int. Ed. 2011, 50, 3376–3410. [Google Scholar] [CrossRef]
- Somaschi, N.; Mouchliadis, L.; Coles, D.; Perakis, I.E.; Lidzey, D.G.; Lagoudakis, P.G.; Savvidis, P.G. Ultrafast polariton population build-up mediated by molecular phonons in organic microcavities. Appl. Phys. Lett. 2011, 99, 143303-1–143303-3. [Google Scholar] [CrossRef]
- Matsumoto, S.; Horiguchi-Babamoto, E.; Eto, R.; Sato, S.; Kobayashi, T.; Naito, H.; Shirod, M.; Takahashie, H. J-aggregate structure in a chloroform solvate of a 2,3-dicyanopyrazine dye—Separation of two-dimensional stacking dye layers by solvate formation. Dyes Pigm. 2012, 95, 431–435. [Google Scholar] [CrossRef][Green Version]
- Dubinina, T.V.; Tomilova, L.G.; Zefirov, N.S. Synthesis of phthalocyanines with an extended system of pi-electron conjugation. Russ. Chem. Rev. 2013, 82, 865–895. [Google Scholar] [CrossRef]
- Suponitsky, K.Y.; Masunov, A.E. Supramolecular step in design of nonlinear optical materials: Effect of π…π stacking aggregation on hyperpolarizability. J. Chem. Phys. 2013, 139, 094310. [Google Scholar] [CrossRef]
- Frost, J.E.; Jones, G.A. A quantum dynamical comparison of the electronic couplings derived from quantum electrodynamics and Förster theory: Application to 2D molecular aggregates. New J. Phys. 2014, 16, 113067. [Google Scholar] [CrossRef]
- Bergendahl, L.T.; Paterson, M.J. Excited states of porphyrin and porphycene aggregates: Computational insights. Comput. Theor. Chem. 2014, 1040–1041, 274–286. [Google Scholar] [CrossRef]
- Rubia-Payá, C.; Giner-Casares, J.J.; Miguel, G.; Martín-Romero, M.T.; Möbius, D.; Camacho, L. Aggregation and structural study of the monolayers formed by an amphiphilic thiapentacarbocyanine. RSC Adv. 2015, 5, 32227–32238. [Google Scholar] [CrossRef]
- Masunov, A.E.; Anderson, D.; Freidzon, A.Y.; Bagaturyants, A.A. Symmetry-Breaking in Cationic Polymethine Dyes: Part 2. Shape of Electronic Absorption Bands Explained by the Thermal Fluctuations of the Solvent Reaction Field. J. Phys. Chem. A 2015, 119, 6807–6815. [Google Scholar] [CrossRef]
- Bricks, J.L.; Slominskii, Y.L.; Panas, I.; Demchenko, A.P.; Slominsky, Y.L.; Demchenko, A. Fluorescent J-aggregates of cyanine dyes: Basic research and applications review. Methods Appl. Fluoresc. 2018, 6. [Google Scholar] [CrossRef]
- Hestand, N.J.; Spano, F.C. Expanded Theory of H- and J-Molecular Aggregates: The Effects of Vibronic Coupling and Intermolecular Charge Transfer. Chem. Rev. 2018, 118, 7069–7163. [Google Scholar] [CrossRef]
- Guerrini, M.; Cocchi, C.; Calzolari, A.; Varsano, D.; Corni, S. Interplay between Intra- and Intermolecular Charge Transfer in the Optical Excitations of J-Aggregates. J. Phys. Chem. C 2019, 123, 6831–6838. [Google Scholar] [CrossRef]
- Guerrini, M.; Calzolari, A.; Varsano, D.; Corni, S. Quantifying the Plasmonic Character of Optical Excitations in a Molecular J-Aggregate. J. Chem. Theory Comput. 2019, 15, 3197–3203. [Google Scholar] [CrossRef]
- Von Weber, A.; Stanley, P.; Jakob, M.; Kartouzian, A.; Heiz, U. Tunable Induced Circular Dichroism in Thin Organic Films. J. Phys. Chem. C 2019, 123, 9255–9261. [Google Scholar] [CrossRef]
- Egorov, V.V.; Alfimov, M.V. Theory of the J-band: From the Frenkel exciton to charge transfer. Phys. Usp. 2007, 50, 985–1029. [Google Scholar] [CrossRef]
- Egorov, V.V. Theory of the J-band: From the Frenkel exciton to charge transfer. Phys. Proc. 2009, 2, 223–326, [Proc. 15th Int. Conf. Lumin. Opt. Spectr. Cond. Matter—ICL ’2008, Lyon, France, 7–11 July 2008]. [Google Scholar] [CrossRef][Green Version]
- Egorov, V.V. Optical line shapes for polymethine dyes and their aggregates: Novel theory of quantum transitions and its correlation with experiment. J. Lumin. 2011, 131, 543–547, [Proc. 17th Int. Conf. on Dynamical Processes in Excited States of Solids (DPC’10), Argonne Nat. Lab., Argonne, Illinois, USA, 20–25 June 2010]. [Google Scholar] [CrossRef]
- Egorov, V.V. Discovery of Dozy Chaos and Discovery of Quanta: Analogy Being in Science and Perhaps in Human Progress; Stavrinides, S.G., Banerjee, S., Caglar, H., Ozer, M., Eds.; In Proceedings of the Chaos and Complex Systems: Proceedings of the 4th International Interdisciplinary Chaos Symp., Antalya, Turkey, 29 April–2 May, 2012; Springer: Berlin, Germany, 2013; pp. 41–46. [Google Scholar] [CrossRef]
- Egorov, V.V. Dozy Chaos in Chemistry: Simplicity in Complexity; Stavrinides, S.G., Banerjee, S., Caglar, H., Ozer, M., Eds.; In Proceedings of the Chaos and Complex Systems: Proceedings of the 4th International Interdisciplinary Chaos Symp., Antalya, Turkey, 29 April–2 May, 2012; Springer: Berlin, Germany, 2013; pp. 219–224. [Google Scholar] [CrossRef]
- Egorov, V.V. Optical lineshapes for dimers of polymethine dyes: Dozy-chaos theory of quantum transitions and Frenkel exciton effect. RSC Adv. 2013, 3, 4598–4609. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the narrow optical band in H*-aggregates: Dozy-chaos–exciton coupling. AIP Adv. 2014, 4, 077111. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the optical band shapes in polymethine dyes and H-aggregates: Dozy chaos and excitons. Comparison with dimers, H*- and J-aggregates. R. Soc. Open Sci. 2017, 4. [Google Scholar] [CrossRef]
- Egorov, V.V. Where and why quantum mechanics ceases to work in molecular and chemical physics. In Proceedings of the European XFEL Theory Seminar, Schenefeld, Hamburg, Germany, 6 March 2018; Available online: https://indico.desy.de/indico/event/20069/ (accessed on 21 February 2018).
- Egorov, V.V. Quantum-classical mechanics: Luminescence spectra in polymethine dyes and J-aggregates. Nature of the small Stokes shift. Res. Phys. 2019, 13. [Google Scholar] [CrossRef]
- Mustroph, H. Potential-Energy Surfaces, the Born-Oppenheimer Approximations, and the Franck-Condon Principle: Back to the Roots. Chem. Phys. Chem. 2016, 17, 2616–2629. [Google Scholar] [CrossRef]
- Perlin, Y.E. Modern methods in the theory of many-phonon processes. Sov. Phys. Uspekhi 1964, 6, 542–565. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the emission and absorption of radiation. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Fermi, E. Quantum theory of radiation. Rev. Mod. Phys. 1932, 4, 87–132. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Davydov, A.S. Quantum Mechanics; Pergamon Press: Oxford, UK, 1976. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Planck, M. On the law of distribution of energy in the normal spectrum. Ann. Phys. (Leipzig) 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Dähne, S. Color and Constitution: One Hundred Years of Research. Science 1978, 199, 1163–1167. [Google Scholar] [CrossRef]
- Kachkovskii, A.D. The nature of electronic transitions in linear conjugated systems. Russ. Chem. Rev. 1997, 66, 647–664. [Google Scholar] [CrossRef]
- Brooker, L.G.S.; Sprague, R.H.; Smyth, C.P.; Lewis, G.L. Color and Constitution. I. Halochromism of Anhydronium Bases Related to the Cyanine Dyes1. J. Am. Chem. Soc. 1940, 62, 1116–1125. [Google Scholar] [CrossRef]
- James, T.H. (Ed.) The Theory of the Photographic Process; Macmillan: New York, NY, USA, 1977. [Google Scholar]
- Egorov, V.V. Dryad Digital Repository. Data from. R. Soc. Open Sci. 2017, 4. [Google Scholar] [CrossRef]
- Kachkovski, O.; Tolmachov, O.; Slominskii, Y.; Kudinova, M.; Derevyanko, N.; Zhukova, O. Electronic properties of polymethine systems 7: Soliton symmetry breaking and spectral features of dyes with a long polymethine chain. Dyes Pigm. 2005, 64, 207–216. [Google Scholar] [CrossRef]
- James, N.S.; Chen, Y.; Joshi, P.; Ohulchanskyy, T.Y.; Ethirajan, M.; Henary, M.; Strekowsk, L.; Pandey, R.K. Evaluation of Polymethine Dyes as Potential Probes for Near Infrared Fluorescence Imaging of Tumors: Part–1. Theranostics 2013, 3, 692–702. [Google Scholar] [CrossRef]
- König, S.G.; Krämer, R. Accessing Structurally Diverse Near-Infrared Cyanine Dyes for Folate Receptor-Targeted Cancer Cell Staining. Chem. A Eur. J. 2017, 23, 9306–9312. [Google Scholar] [CrossRef]
- Usama, S.M.; Thavornpradit, S.; Burgess, K. Optimized Heptamethine Cyanines for Photodynamic Therapy. ACS Appl. Bio Mater. 2018, 1, 1195–1205. [Google Scholar] [CrossRef]
- Atchison, J.; Kamila, S.; Nesbitt, H.; Logan, K.A.; Nicholas, D.M.; Fowley, C.; Davis, J.; Callan, J.F.; McHale, A.P.P.; Callan, J.F. Iodinated cyanine dyes: A new class of sensitisers for use in NIR activated photodynamic therapy (PDT). Chem. Commun. 2017, 53, 2009–2012. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1118. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Sergi, A. Matrix Algebras in Non-Hermitian Quantum Mechanics. Commun. Theor. Phys. 2011, 56, 96–98. [Google Scholar] [CrossRef][Green Version]
- Sergi, A.; Zloshchastiev, K.G. Non-hermitian quantum dynamics of a two-level system and models of dissipative environments. Int. J. Mod. Phys. B 2013, 27. [Google Scholar] [CrossRef]
- Sergi, A. Embedding quantum systems with a non-conserved probability in classical environments. Theor. Chem. Acc. 2015, 134. [Google Scholar] [CrossRef]
- Zloshchastiev, K. Non-Hermitian Hamiltonians and stability of pure states. Eur. Phys. J. D 2015, 69. [Google Scholar] [CrossRef]
- Sergi, A.; Giaquinta, P.V. Linear Quantum Entropy and Non-Hermitian Hamiltonians. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. (NY) 2017, 385, 162–179. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).