Dozy-Chaos Mechanics for a Broad Audience
Abstract
1. Introduction
2. Dozy-Chaos Mechanics on a Qualitative Level of Consideration
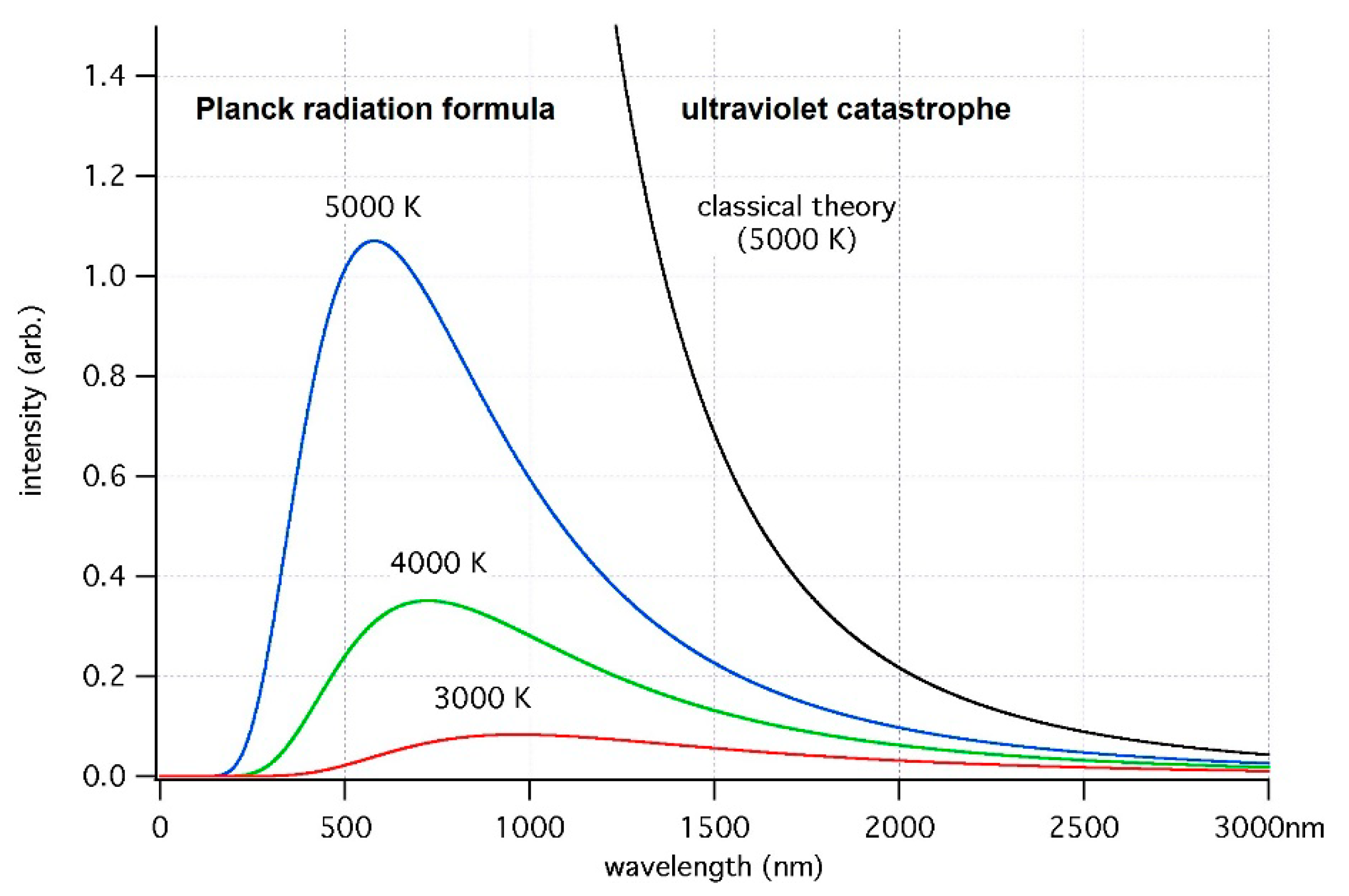
2.1. Full-Fledged Electron-Nuclear Motion in the Transient State of Molecular Quantum Transitions, Singularity in Their Rates, and the Franck–Condon Principle as a Primitive Singularity Damper
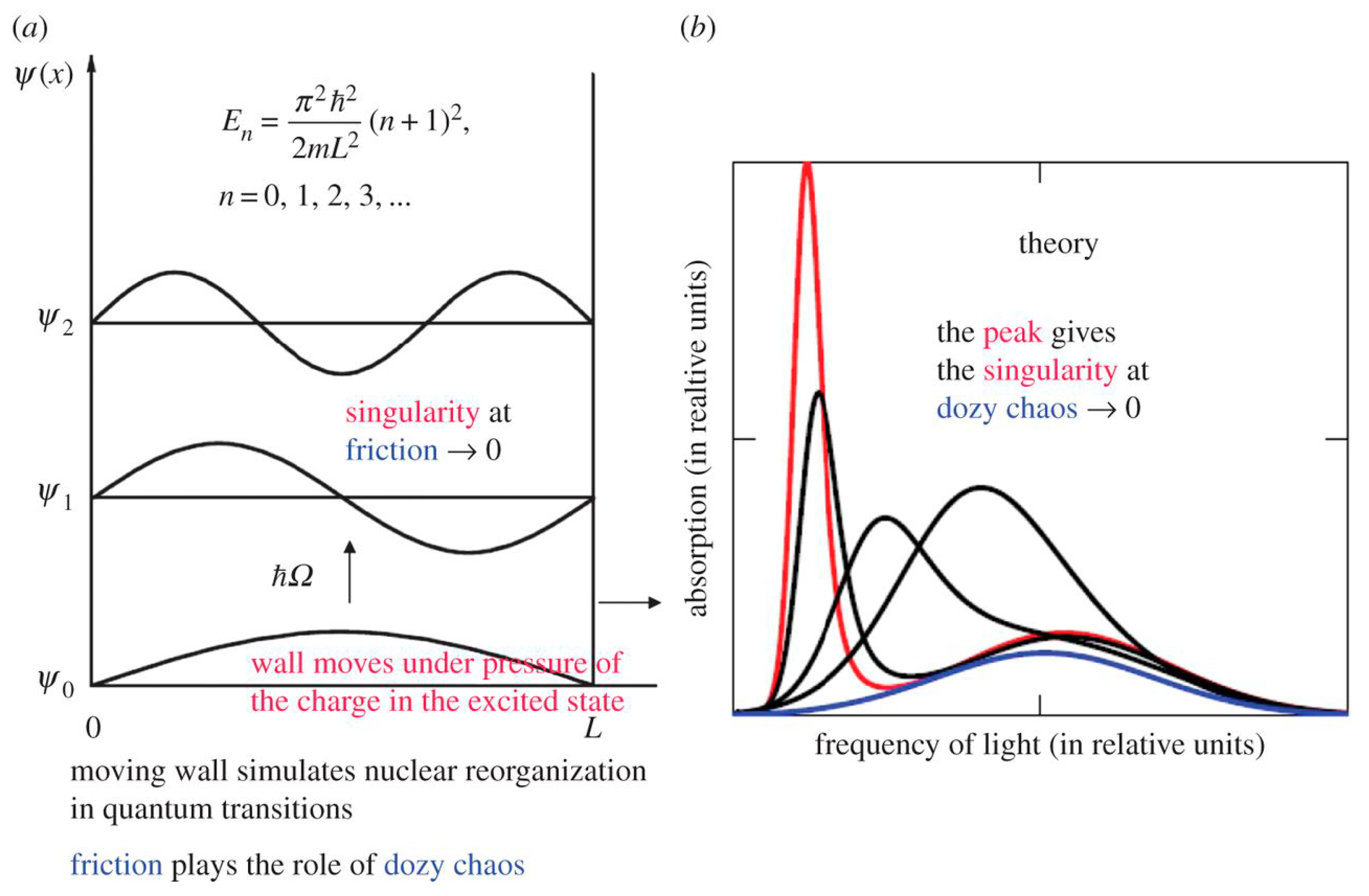
2.2. Potential Box with a Movable Wall and Dozy Chaos as a Damper of the Singularity
3. Dozy-Chaos Mechanics: Hamiltonian, Green’s Function, and Dozy Chaos
4. Dozy-Chaos Mechanics, Quantum Mechanics, and Classical Mechanics: Some Analogy
5. Dynamic Electron–Nuclear–Reorganization Resonance
6. Absorption and Luminescence Spectra
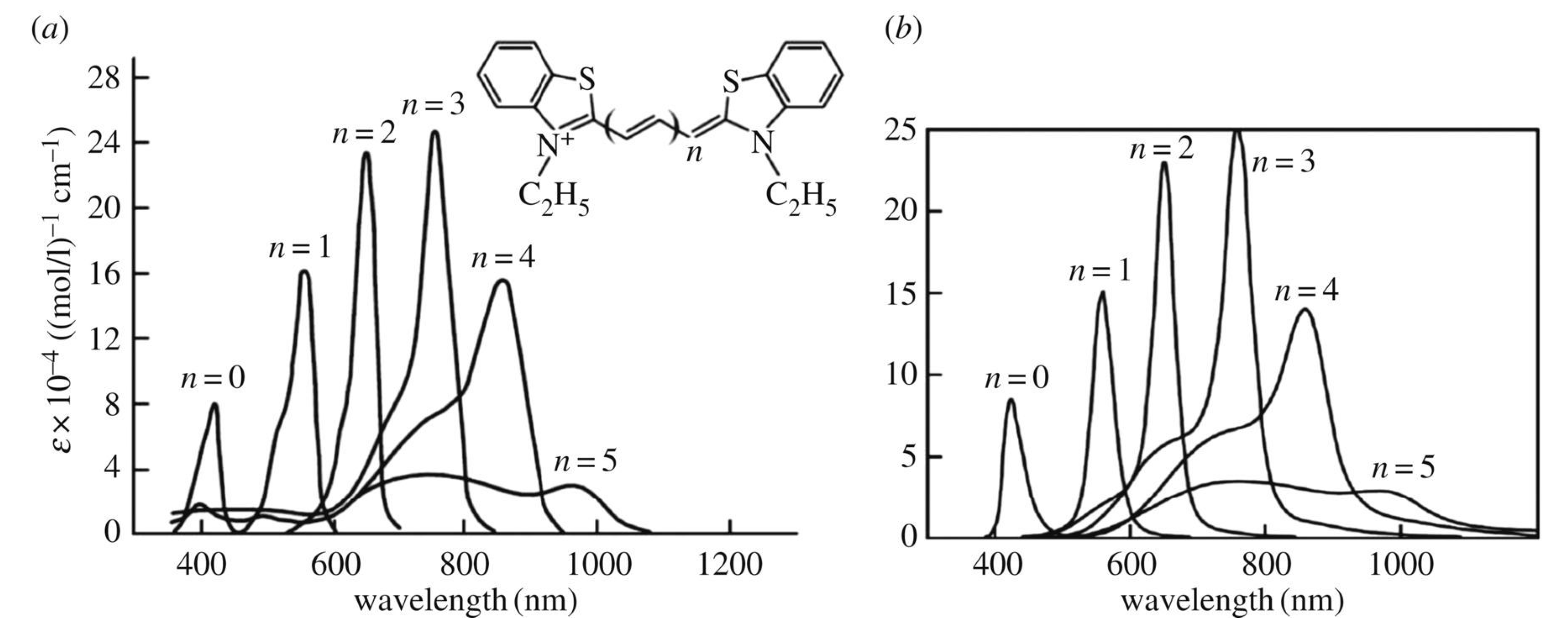
7. Optical Electron-Transfer-Polymethine-Chain Chromophore
8. Implementation of the Dynamic Electron–Nuclear–Reorganization Resonance in the Optical Band Shape
9. Dozy-Chaos Mechanics and the Franck–Condon Principle
10. Conclusions
Funding
Conflicts of Interest
References
- Petrenko, A.; Stein, M. Molecular Reorganization energy as a key determinant of J-band formation in J-aggregates of polymethine dyes. J. Phys. Chem. A 2015, 119, 6773–6780. [Google Scholar] [CrossRef]
- Egorov, V.V. Electron-transfer approach to the nature of the optical lineshape for molecular J-aggregates. Chem. Phys. Lett. 2001, 336, 284–291. [Google Scholar] [CrossRef]
- Egorov, V.V. On electrodynamics of extended multiphonon transitions and nature of the J-band. Chem. Phys. 2001, 269, 251–283. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the optical transition in polymethine dyes and J-aggregates. J. Chem. Phys. 2002, 116, 3090–3103. [Google Scholar] [CrossRef]
- Petrenko, A.; Stein, M. Toward a molecular reorganization energy-based analysis of third-order Nonlinear optical properties of polymethine dyes and J-aggregates. J. Phys. Chem. A 2019, 123, 9321–9327. [Google Scholar] [CrossRef]
- Egorov, V.V. Quantum-classical mechanics as an alternative to quantum mechanics in molecular and chemical physics. Heliyon Phys. 2019, 5, e02579. [Google Scholar] [CrossRef]
- Struganova, I.A.; Lim, H.; Morgan, S.A. The Influence of Inorganic Salts and Bases on the Formation of the J-band in the Absorption and Fluorescence Spectra of the Diluted Aqueous Solutions of TDBC. J. Phys. Chem. B 2002, 106, 11047–11050. [Google Scholar] [CrossRef]
- Struganova, I.A.; Hazell, M.; Gaitor, J.; McNally-Carr, D.; Živanović, S. Influence of Inorganic Salts and Bases on the J-Band in the Absorption Spectra of Water Solutions of 1,1‘-Diethyl-2,2‘-cyanine Iodide. J. Phys. Chem. A 2003, 107, 2650–2656. [Google Scholar] [CrossRef]
- Zhang, Z.; Achilefu, S. Synthesis and Evaluation of Polyhydroxylated Near-Infrared Carbocyanine Molecular Probes. Org. Lett. 2004, 6, 2067–2070. [Google Scholar] [CrossRef]
- Abdel-Halim, S.T.; Awad, M.K. Absorption, fluorescence, and semiempirical ASED-MO studies on a typical Brooker’s merocyanine dye. J. Mol. Struct. 2005, 754, 16–24. [Google Scholar] [CrossRef]
- Li, C.; Greenwood, T.R.; Bhujwalla, Z.M.; Glunde, K. Synthesis and Characterization of Glucosamine-Bound Near-Infrared Probes for Optical Imaging. Org. Lett. 2006, 8, 3623–3626. [Google Scholar] [CrossRef] [PubMed]
- Eisfeld, A.; Briggs, J. The shape of the J-band of pseudoisocyanine. Chem. Phys. Lett. 2007, 446, 354–358. [Google Scholar] [CrossRef]
- Roden, J.; Eisfeld, A.; Briggs, J. The J- and H-bands of dye aggregate spectra: Analysis of the coherent exciton scattering (CES) approximation. Chem. Phys. 2008, 352, 258–266. [Google Scholar] [CrossRef][Green Version]
- Kaiser, T.E.; Stepanenko, V.; Würthner, F. Fluorescent J-Aggregates of Core-Substituted Perylene Bisimides: Studies on Structure−Property Relationship, Nucleation−Elongation Mechanism, and Sergeants-and-Soldiers Principle. J. Am. Chem. Soc. 2009, 131, 6719–6732. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, T.E.; Scheblykin, I.G.; Thomsson, D.; Würthner, F. Temperature-dependent exciton dynamics in J-Aggregates—When disorder plays a role. J. Phys. Chem. B 2009, 113, 15836–15842. [Google Scholar] [CrossRef]
- Kalimuthu, P.; John, S.A. Nanostructured Aggregates ofmeso-Tetramesitylporphyrin on Solid Substrate. Langmuir 2009, 25, 12414–12418. [Google Scholar] [CrossRef]
- Bouit, P.-A.; Aronica, C.; Toupet, L.; Le Guennic, B.; Andraud, C.; Maury, O. Continuous Symmetry Breaking Induced by Ion Pairing Effect in Heptamethine Cyanine Dyes: Beyond the Cyanine Limit. J. Am. Chem. Soc. 2010, 132, 4328–4335. [Google Scholar] [CrossRef]
- Würthner, F.; Kaiser, T.E.; Saha-Möller, C.R. J-Aggregates: From serendipitous discovery to supramolecular engineering of functional dye materials. Angew. Chem. Int. Ed. 2011, 50, 3376–3410. [Google Scholar] [CrossRef]
- Somaschi, N.; Mouchliadis, L.; Coles, D.; Perakis, I.E.; Lidzey, D.G.; Lagoudakis, P.G.; Savvidis, P.G. Ultrafast polariton population build-up mediated by molecular phonons in organic microcavities. Appl. Phys. Lett. 2011, 99, 143303-1–143303-3. [Google Scholar] [CrossRef]
- Matsumoto, S.; Horiguchi-Babamoto, E.; Eto, R.; Sato, S.; Kobayashi, T.; Naito, H.; Shirod, M.; Takahashie, H. J-aggregate structure in a chloroform solvate of a 2,3-dicyanopyrazine dye—Separation of two-dimensional stacking dye layers by solvate formation. Dyes Pigm. 2012, 95, 431–435. [Google Scholar] [CrossRef][Green Version]
- Dubinina, T.V.; Tomilova, L.G.; Zefirov, N.S. Synthesis of phthalocyanines with an extended system of pi-electron conjugation. Russ. Chem. Rev. 2013, 82, 865–895. [Google Scholar] [CrossRef]
- Suponitsky, K.Y.; Masunov, A.E. Supramolecular step in design of nonlinear optical materials: Effect of π…π stacking aggregation on hyperpolarizability. J. Chem. Phys. 2013, 139, 094310. [Google Scholar] [CrossRef]
- Frost, J.E.; Jones, G.A. A quantum dynamical comparison of the electronic couplings derived from quantum electrodynamics and Förster theory: Application to 2D molecular aggregates. New J. Phys. 2014, 16, 113067. [Google Scholar] [CrossRef]
- Bergendahl, L.T.; Paterson, M.J. Excited states of porphyrin and porphycene aggregates: Computational insights. Comput. Theor. Chem. 2014, 1040–1041, 274–286. [Google Scholar] [CrossRef]
- Rubia-Payá, C.; Giner-Casares, J.J.; Miguel, G.; Martín-Romero, M.T.; Möbius, D.; Camacho, L. Aggregation and structural study of the monolayers formed by an amphiphilic thiapentacarbocyanine. RSC Adv. 2015, 5, 32227–32238. [Google Scholar] [CrossRef]
- Masunov, A.E.; Anderson, D.; Freidzon, A.Y.; Bagaturyants, A.A. Symmetry-Breaking in Cationic Polymethine Dyes: Part 2. Shape of Electronic Absorption Bands Explained by the Thermal Fluctuations of the Solvent Reaction Field. J. Phys. Chem. A 2015, 119, 6807–6815. [Google Scholar] [CrossRef]
- Bricks, J.L.; Slominskii, Y.L.; Panas, I.; Demchenko, A.P.; Slominsky, Y.L.; Demchenko, A. Fluorescent J-aggregates of cyanine dyes: Basic research and applications review. Methods Appl. Fluoresc. 2018, 6. [Google Scholar] [CrossRef]
- Hestand, N.J.; Spano, F.C. Expanded Theory of H- and J-Molecular Aggregates: The Effects of Vibronic Coupling and Intermolecular Charge Transfer. Chem. Rev. 2018, 118, 7069–7163. [Google Scholar] [CrossRef]
- Guerrini, M.; Cocchi, C.; Calzolari, A.; Varsano, D.; Corni, S. Interplay between Intra- and Intermolecular Charge Transfer in the Optical Excitations of J-Aggregates. J. Phys. Chem. C 2019, 123, 6831–6838. [Google Scholar] [CrossRef]
- Guerrini, M.; Calzolari, A.; Varsano, D.; Corni, S. Quantifying the Plasmonic Character of Optical Excitations in a Molecular J-Aggregate. J. Chem. Theory Comput. 2019, 15, 3197–3203. [Google Scholar] [CrossRef]
- Von Weber, A.; Stanley, P.; Jakob, M.; Kartouzian, A.; Heiz, U. Tunable Induced Circular Dichroism in Thin Organic Films. J. Phys. Chem. C 2019, 123, 9255–9261. [Google Scholar] [CrossRef]
- Egorov, V.V.; Alfimov, M.V. Theory of the J-band: From the Frenkel exciton to charge transfer. Phys. Usp. 2007, 50, 985–1029. [Google Scholar] [CrossRef]
- Egorov, V.V. Theory of the J-band: From the Frenkel exciton to charge transfer. Phys. Proc. 2009, 2, 223–326, [Proc. 15th Int. Conf. Lumin. Opt. Spectr. Cond. Matter—ICL ’2008, Lyon, France, 7–11 July 2008]. [Google Scholar] [CrossRef][Green Version]
- Egorov, V.V. Optical line shapes for polymethine dyes and their aggregates: Novel theory of quantum transitions and its correlation with experiment. J. Lumin. 2011, 131, 543–547, [Proc. 17th Int. Conf. on Dynamical Processes in Excited States of Solids (DPC’10), Argonne Nat. Lab., Argonne, Illinois, USA, 20–25 June 2010]. [Google Scholar] [CrossRef]
- Egorov, V.V. Discovery of Dozy Chaos and Discovery of Quanta: Analogy Being in Science and Perhaps in Human Progress; Stavrinides, S.G., Banerjee, S., Caglar, H., Ozer, M., Eds.; In Proceedings of the Chaos and Complex Systems: Proceedings of the 4th International Interdisciplinary Chaos Symp., Antalya, Turkey, 29 April–2 May, 2012; Springer: Berlin, Germany, 2013; pp. 41–46. [Google Scholar] [CrossRef]
- Egorov, V.V. Dozy Chaos in Chemistry: Simplicity in Complexity; Stavrinides, S.G., Banerjee, S., Caglar, H., Ozer, M., Eds.; In Proceedings of the Chaos and Complex Systems: Proceedings of the 4th International Interdisciplinary Chaos Symp., Antalya, Turkey, 29 April–2 May, 2012; Springer: Berlin, Germany, 2013; pp. 219–224. [Google Scholar] [CrossRef]
- Egorov, V.V. Optical lineshapes for dimers of polymethine dyes: Dozy-chaos theory of quantum transitions and Frenkel exciton effect. RSC Adv. 2013, 3, 4598–4609. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the narrow optical band in H*-aggregates: Dozy-chaos–exciton coupling. AIP Adv. 2014, 4, 077111. [Google Scholar] [CrossRef]
- Egorov, V.V. Nature of the optical band shapes in polymethine dyes and H-aggregates: Dozy chaos and excitons. Comparison with dimers, H*- and J-aggregates. R. Soc. Open Sci. 2017, 4. [Google Scholar] [CrossRef]
- Egorov, V.V. Where and why quantum mechanics ceases to work in molecular and chemical physics. In Proceedings of the European XFEL Theory Seminar, Schenefeld, Hamburg, Germany, 6 March 2018; Available online: https://indico.desy.de/indico/event/20069/ (accessed on 21 February 2018).
- Egorov, V.V. Quantum-classical mechanics: Luminescence spectra in polymethine dyes and J-aggregates. Nature of the small Stokes shift. Res. Phys. 2019, 13. [Google Scholar] [CrossRef]
- Mustroph, H. Potential-Energy Surfaces, the Born-Oppenheimer Approximations, and the Franck-Condon Principle: Back to the Roots. Chem. Phys. Chem. 2016, 17, 2616–2629. [Google Scholar] [CrossRef]
- Perlin, Y.E. Modern methods in the theory of many-phonon processes. Sov. Phys. Uspekhi 1964, 6, 542–565. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the emission and absorption of radiation. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Fermi, E. Quantum theory of radiation. Rev. Mod. Phys. 1932, 4, 87–132. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Davydov, A.S. Quantum Mechanics; Pergamon Press: Oxford, UK, 1976. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Planck, M. On the law of distribution of energy in the normal spectrum. Ann. Phys. (Leipzig) 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Dähne, S. Color and Constitution: One Hundred Years of Research. Science 1978, 199, 1163–1167. [Google Scholar] [CrossRef]
- Kachkovskii, A.D. The nature of electronic transitions in linear conjugated systems. Russ. Chem. Rev. 1997, 66, 647–664. [Google Scholar] [CrossRef]
- Brooker, L.G.S.; Sprague, R.H.; Smyth, C.P.; Lewis, G.L. Color and Constitution. I. Halochromism of Anhydronium Bases Related to the Cyanine Dyes1. J. Am. Chem. Soc. 1940, 62, 1116–1125. [Google Scholar] [CrossRef]
- James, T.H. (Ed.) The Theory of the Photographic Process; Macmillan: New York, NY, USA, 1977. [Google Scholar]
- Egorov, V.V. Dryad Digital Repository. Data from. R. Soc. Open Sci. 2017, 4. [Google Scholar] [CrossRef]
- Kachkovski, O.; Tolmachov, O.; Slominskii, Y.; Kudinova, M.; Derevyanko, N.; Zhukova, O. Electronic properties of polymethine systems 7: Soliton symmetry breaking and spectral features of dyes with a long polymethine chain. Dyes Pigm. 2005, 64, 207–216. [Google Scholar] [CrossRef]
- James, N.S.; Chen, Y.; Joshi, P.; Ohulchanskyy, T.Y.; Ethirajan, M.; Henary, M.; Strekowsk, L.; Pandey, R.K. Evaluation of Polymethine Dyes as Potential Probes for Near Infrared Fluorescence Imaging of Tumors: Part–1. Theranostics 2013, 3, 692–702. [Google Scholar] [CrossRef]
- König, S.G.; Krämer, R. Accessing Structurally Diverse Near-Infrared Cyanine Dyes for Folate Receptor-Targeted Cancer Cell Staining. Chem. A Eur. J. 2017, 23, 9306–9312. [Google Scholar] [CrossRef]
- Usama, S.M.; Thavornpradit, S.; Burgess, K. Optimized Heptamethine Cyanines for Photodynamic Therapy. ACS Appl. Bio Mater. 2018, 1, 1195–1205. [Google Scholar] [CrossRef]
- Atchison, J.; Kamila, S.; Nesbitt, H.; Logan, K.A.; Nicholas, D.M.; Fowley, C.; Davis, J.; Callan, J.F.; McHale, A.P.P.; Callan, J.F. Iodinated cyanine dyes: A new class of sensitisers for use in NIR activated photodynamic therapy (PDT). Chem. Commun. 2017, 53, 2009–2012. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1118. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Sergi, A. Matrix Algebras in Non-Hermitian Quantum Mechanics. Commun. Theor. Phys. 2011, 56, 96–98. [Google Scholar] [CrossRef][Green Version]
- Sergi, A.; Zloshchastiev, K.G. Non-hermitian quantum dynamics of a two-level system and models of dissipative environments. Int. J. Mod. Phys. B 2013, 27. [Google Scholar] [CrossRef]
- Sergi, A. Embedding quantum systems with a non-conserved probability in classical environments. Theor. Chem. Acc. 2015, 134. [Google Scholar] [CrossRef]
- Zloshchastiev, K. Non-Hermitian Hamiltonians and stability of pure states. Eur. Phys. J. D 2015, 69. [Google Scholar] [CrossRef]
- Sergi, A.; Giaquinta, P.V. Linear Quantum Entropy and Non-Hermitian Hamiltonians. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. (NY) 2017, 385, 162–179. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egorov, V.V. Dozy-Chaos Mechanics for a Broad Audience. Challenges 2020, 11, 16. https://doi.org/10.3390/challe11020016
Egorov VV. Dozy-Chaos Mechanics for a Broad Audience. Challenges. 2020; 11(2):16. https://doi.org/10.3390/challe11020016
Chicago/Turabian StyleEgorov, Vladimir V. 2020. "Dozy-Chaos Mechanics for a Broad Audience" Challenges 11, no. 2: 16. https://doi.org/10.3390/challe11020016
APA StyleEgorov, V. V. (2020). Dozy-Chaos Mechanics for a Broad Audience. Challenges, 11(2), 16. https://doi.org/10.3390/challe11020016




