Scour Characteristics and Equilibrium Scour Depth Prediction around Umbrella Suction Anchor Foundation under Random Waves
Abstract
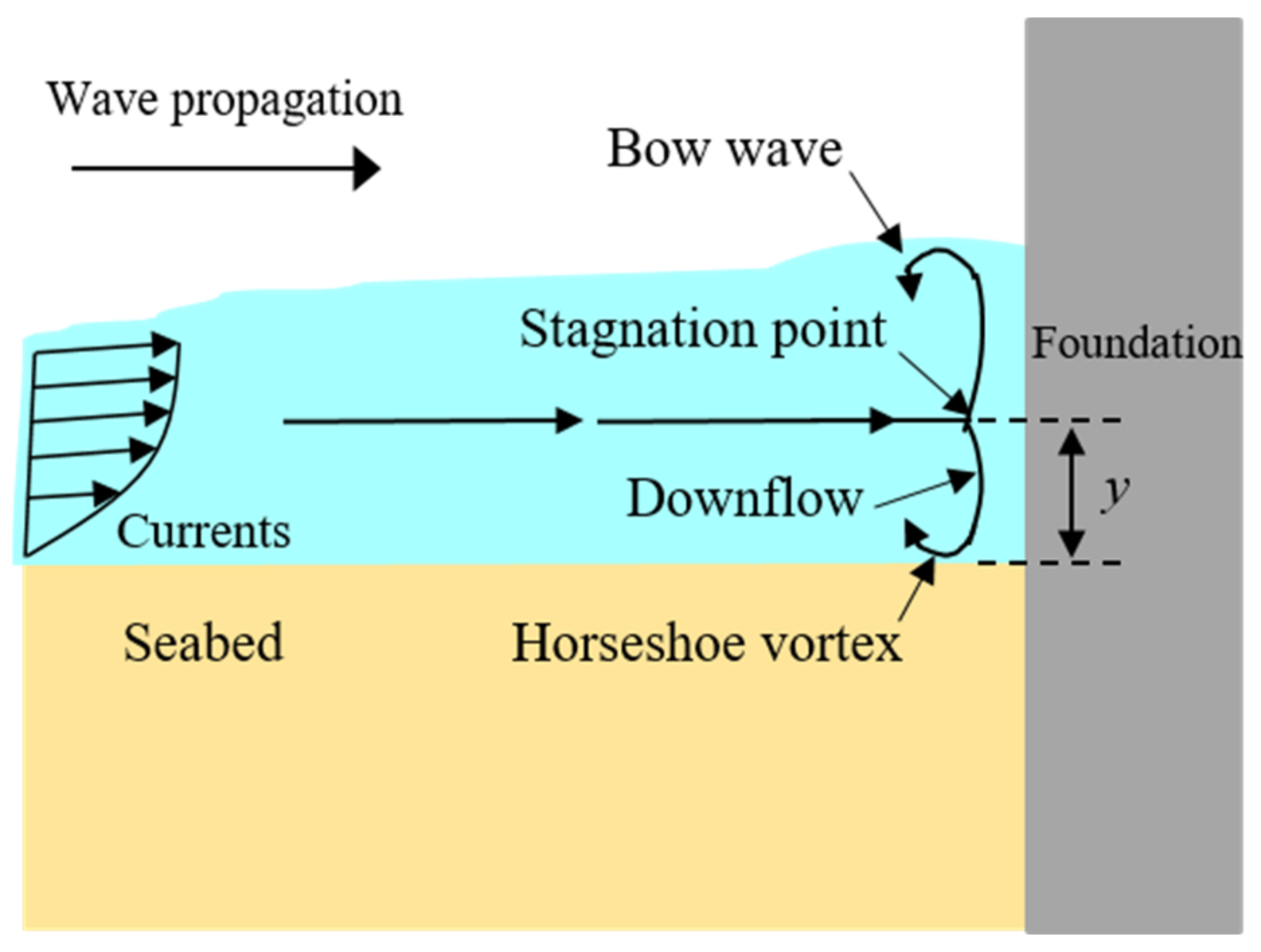
:1. Introduction
2. Numerical Method
2.1. Governing Equations of Flow
2.2. Turbulent Model
2.3. Sediment Scour Model
2.3.1. Entrainment and Deposition
2.3.2. Bed Load Transport
2.3.3. Suspended Load Transport
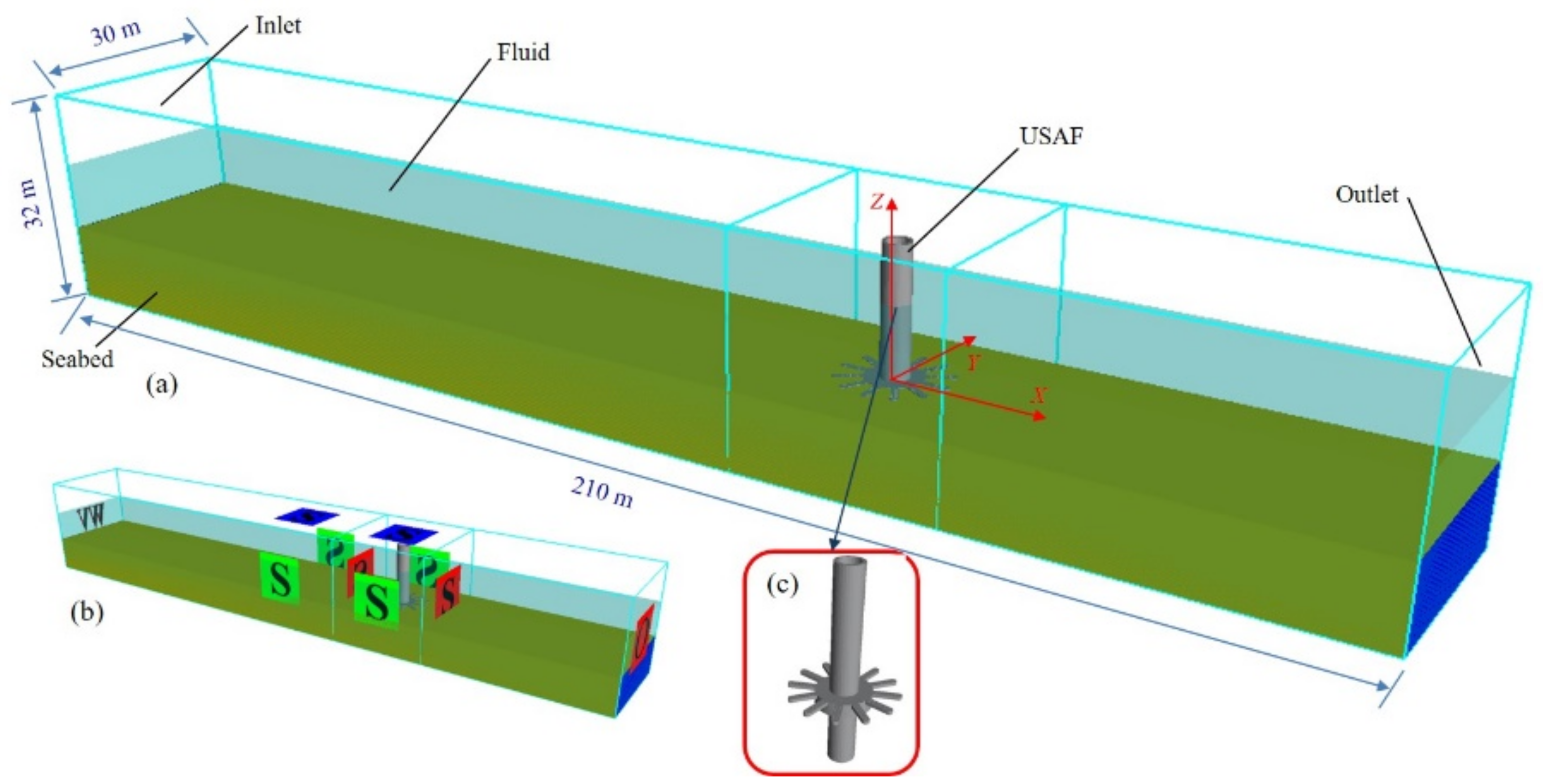
3. Model Setup
3.1. Mesh Geometric Dimensions
3.2. Boundary Conditions
3.3. Wave Parameters
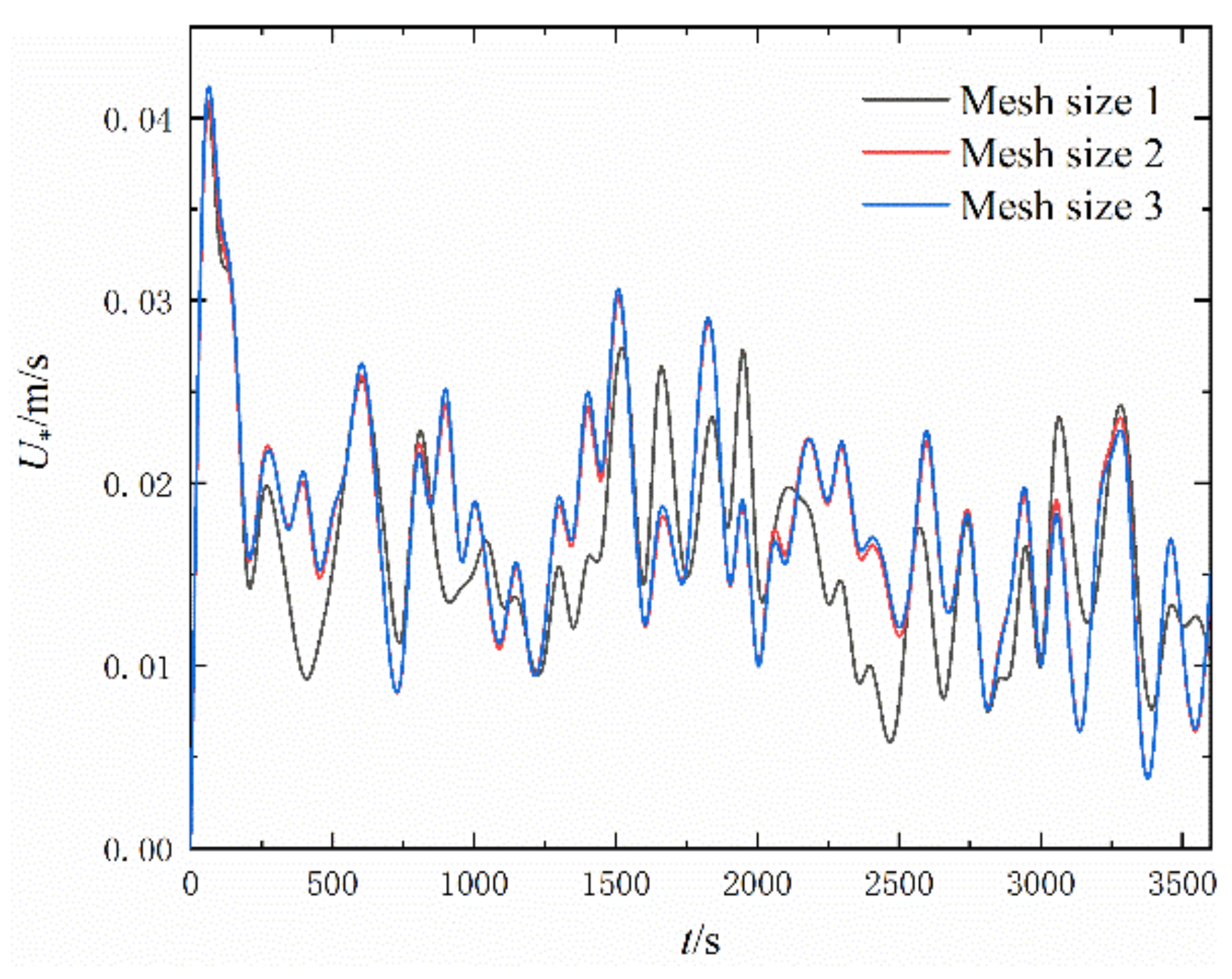
3.4. Mesh Sensitivity
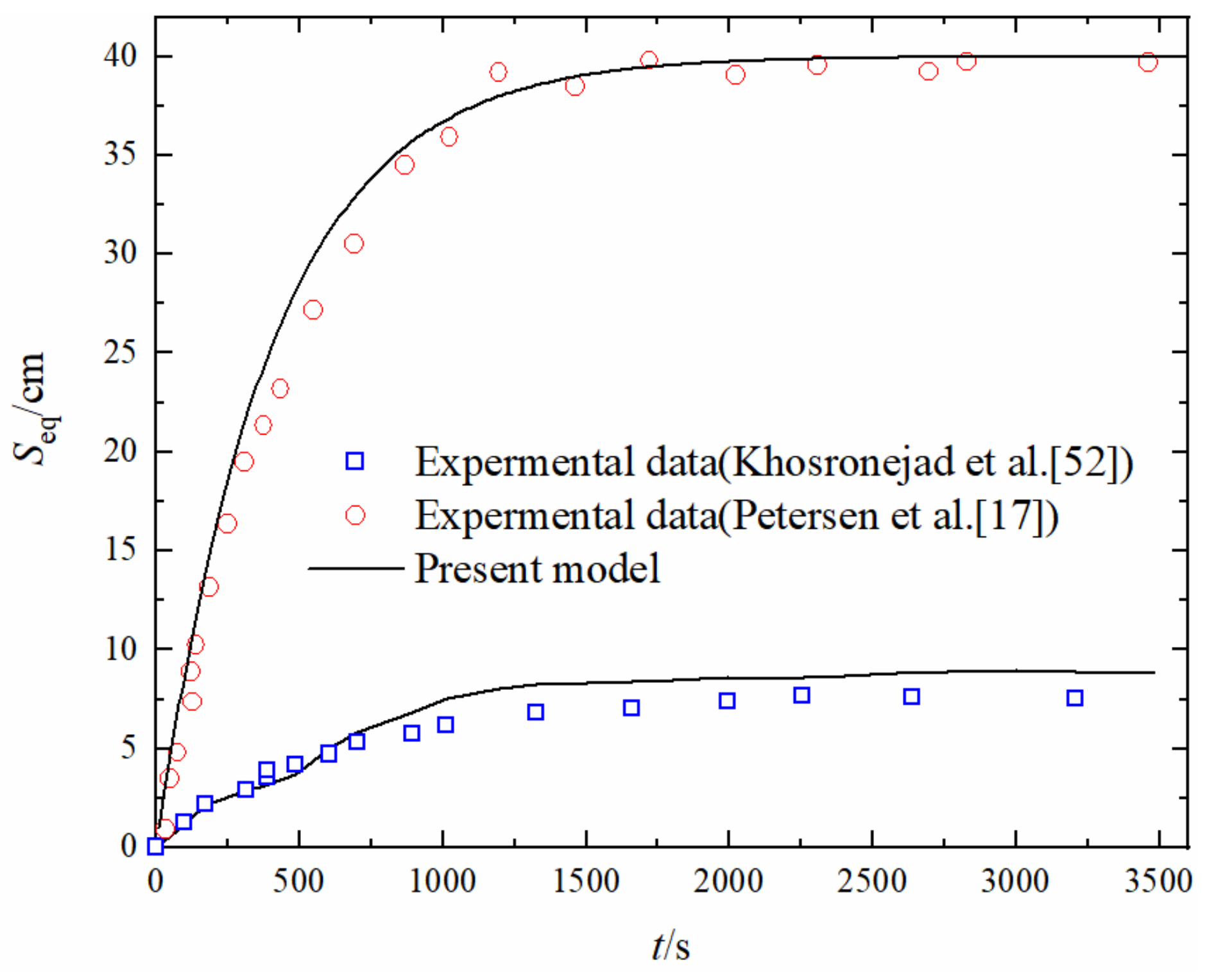
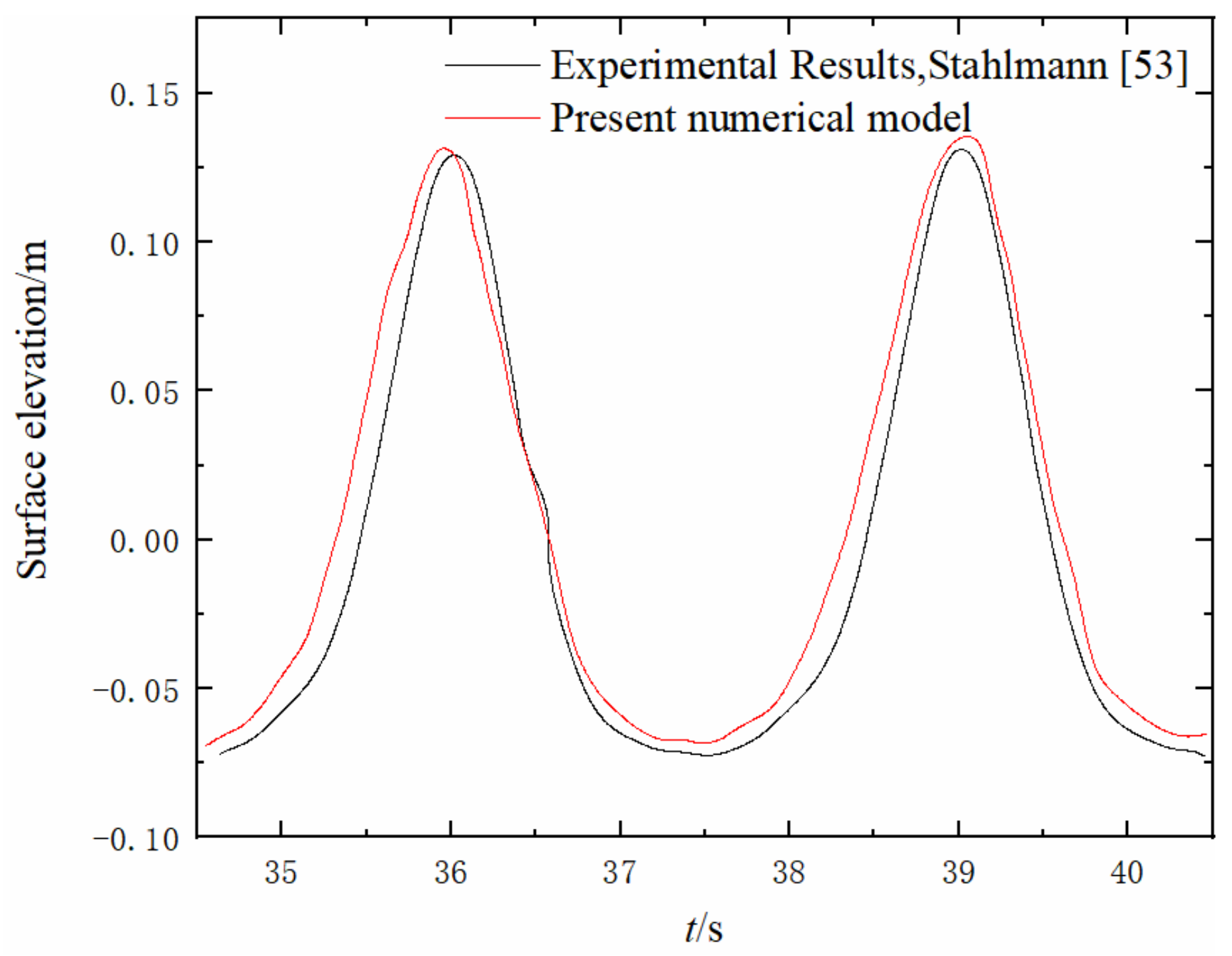
3.5. Model Validation
4. Numerical Results and Discussions
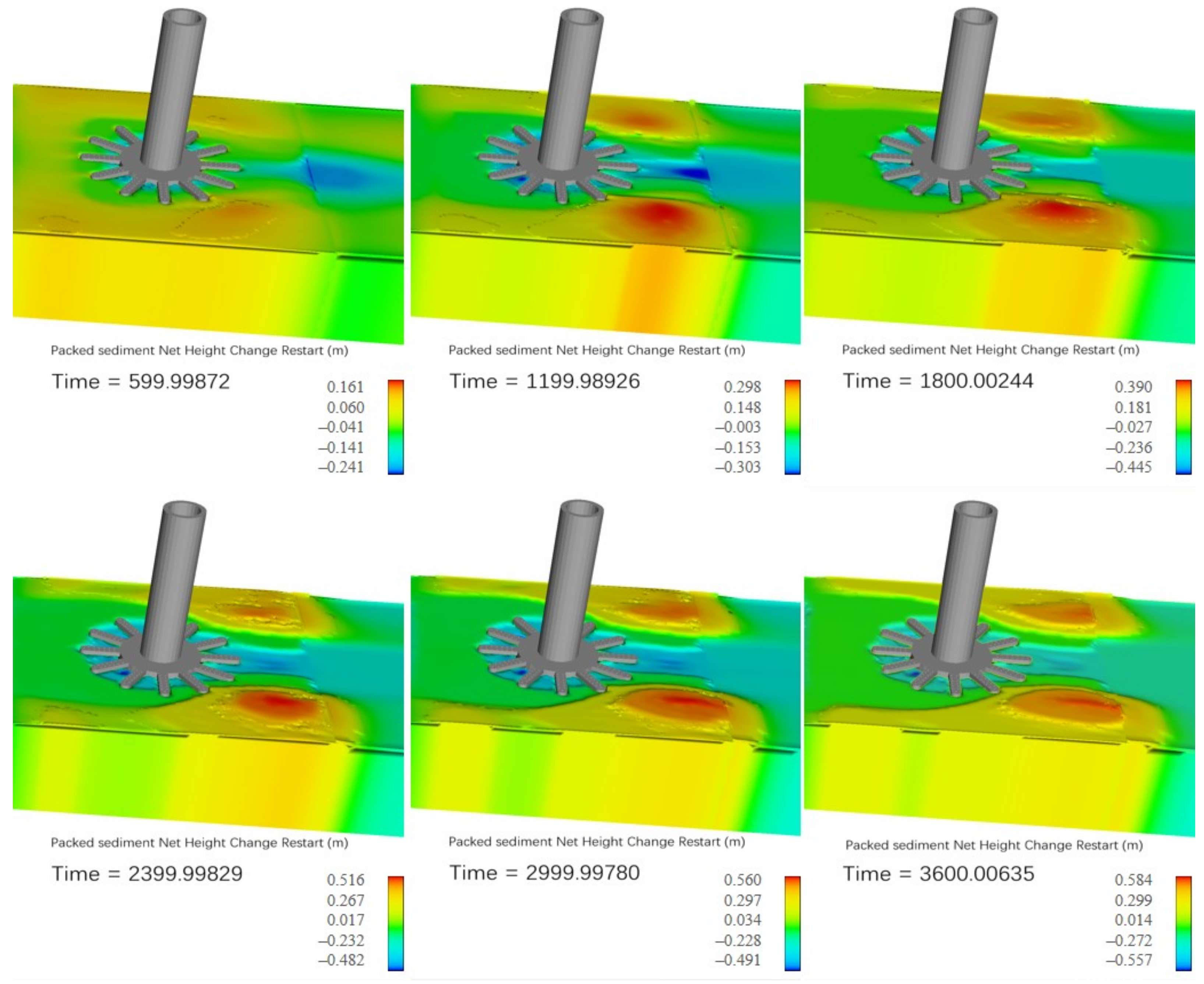
4.1. Scour Evolution
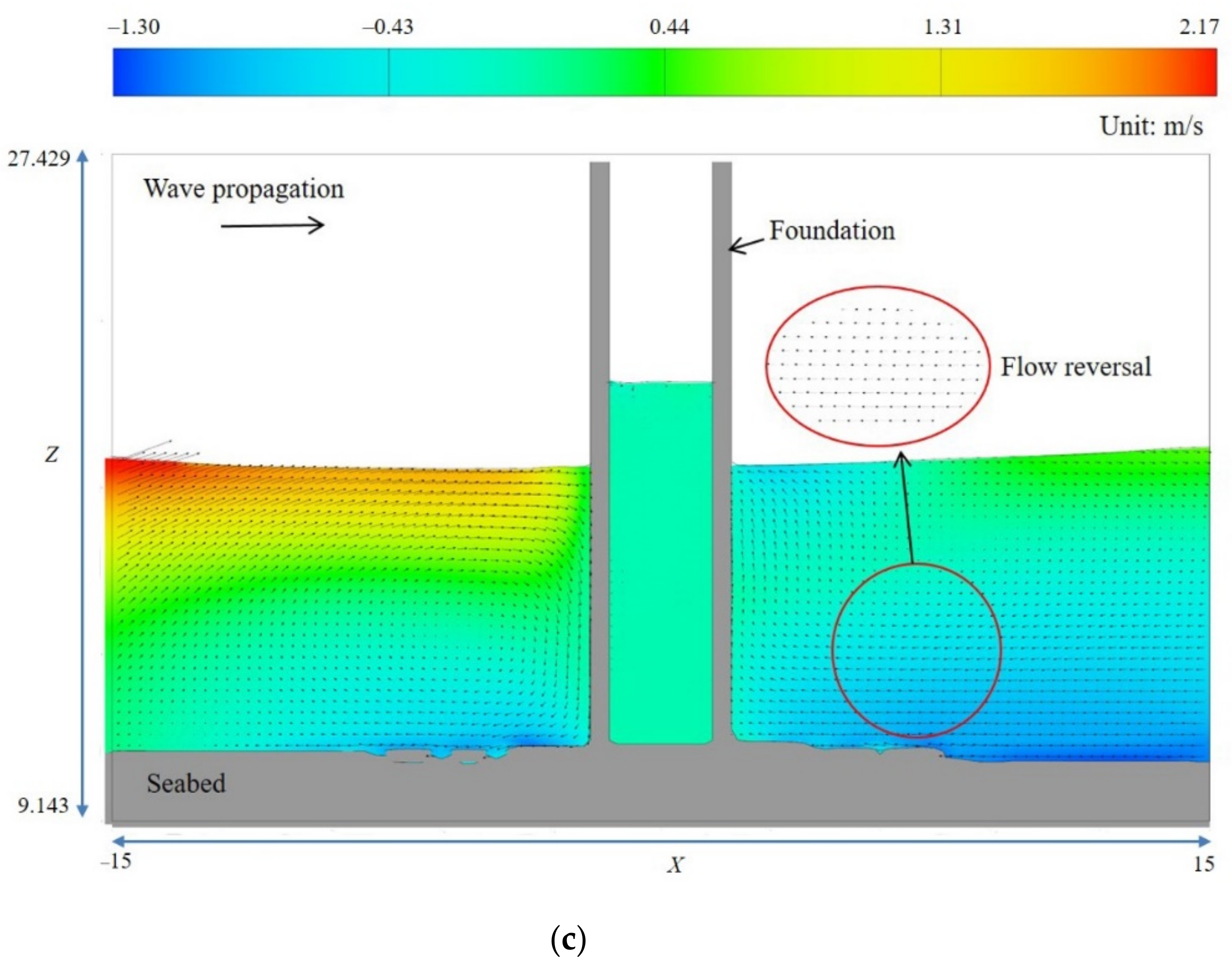
4.2. Scour Mechanism under Random Waves
4.3. Equilibrium Scour Depth
4.4. Parametric Study
4.4.1. Influence of Froude Number
4.4.2. Influence of Euler Number
5. Conclusions
- (1)
- The packed sediment scour model and the RNG k−ε turbulence model were used to simulate the sand particles transport processes and the flow field around UASF respectively. The scour evolution obtained by the present model agrees well with the experimental results of Khosronejad et al. [52], Petersen et al. [17], Sumer and Fredsøe [16] and Schendel et al. [22], which indicates that the present model is accurate and reasonable for depicting the scour morphology around UASF under random waves.
- (2)
- The vortex system at wave crest phase is mainly related to the scour process around USAF under random waves. The maximum scour depth appeared at the lee-side of the USAF at the initial stage (t < 1200 s). Subsequently, when t > 2400 s, the location of the maximum scour depth shifted to the upside of the USAF at an angle of about 45° with respect to the wave propagating direction.
- (3)
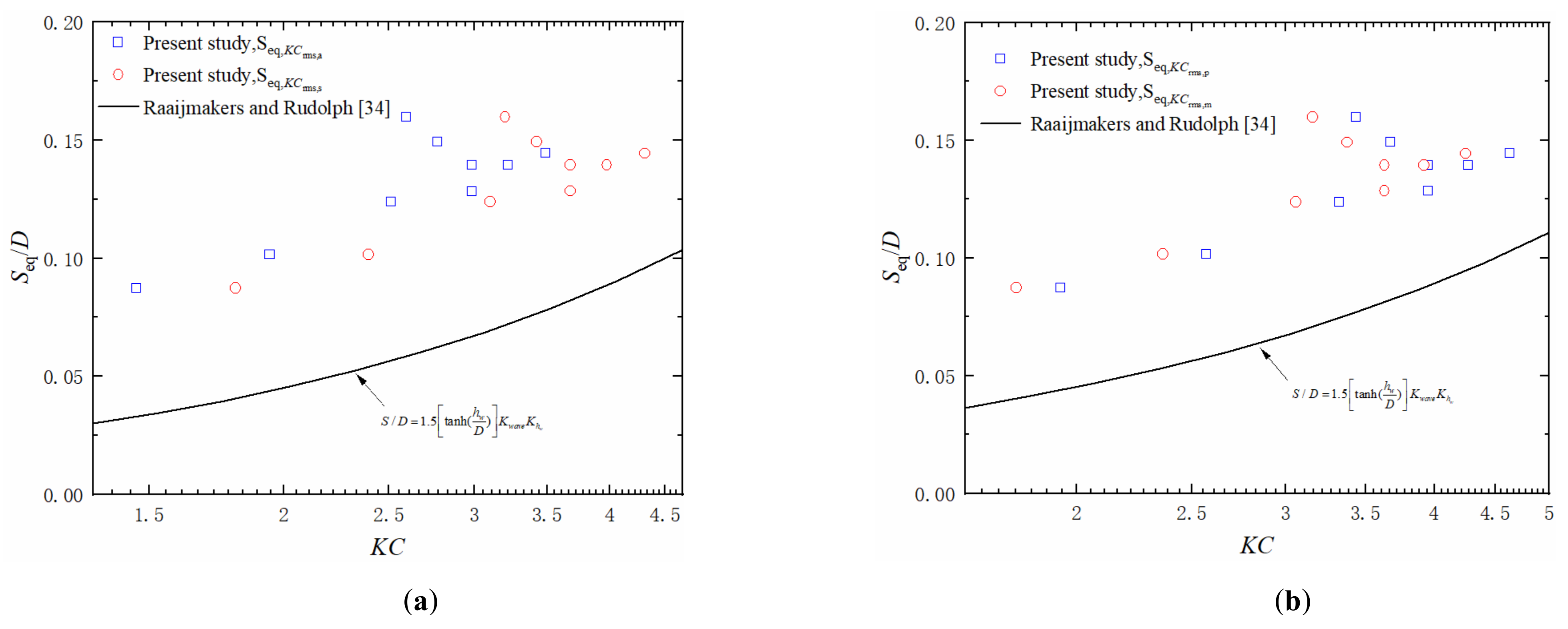
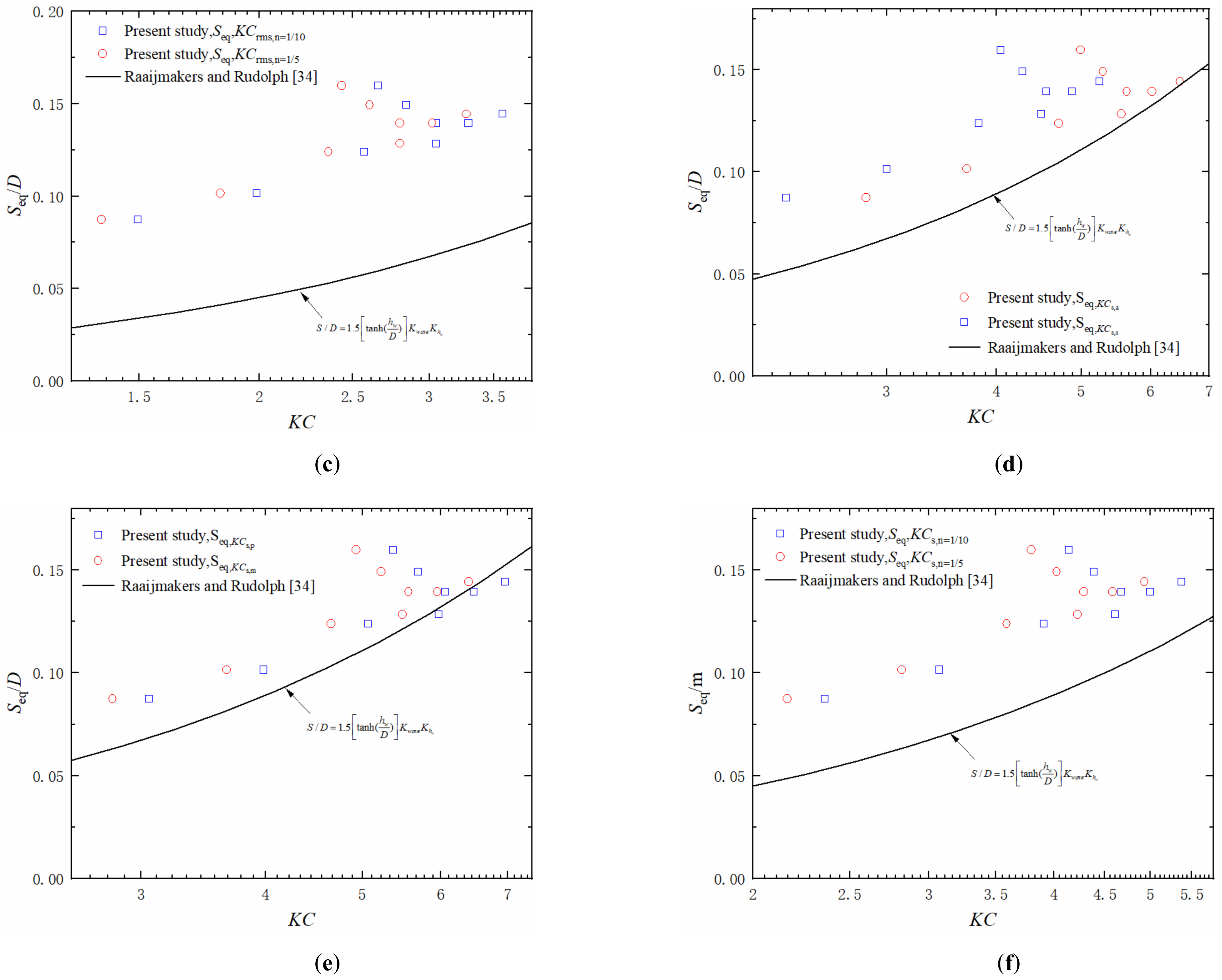
- The error is negligible and the Raaijmakers’s model is of relatively high accuracy for predicting scour around USAF under random waves when KC is calculated by KCs,p. Given that, a further revision model (Equation (31)) was proposed according to Raaijmakers’s model to predict the equilibrium scour depth around USAF under random waves and it shows good agreement with the simulating results of the present study when KCs,p < 8.
- (4)
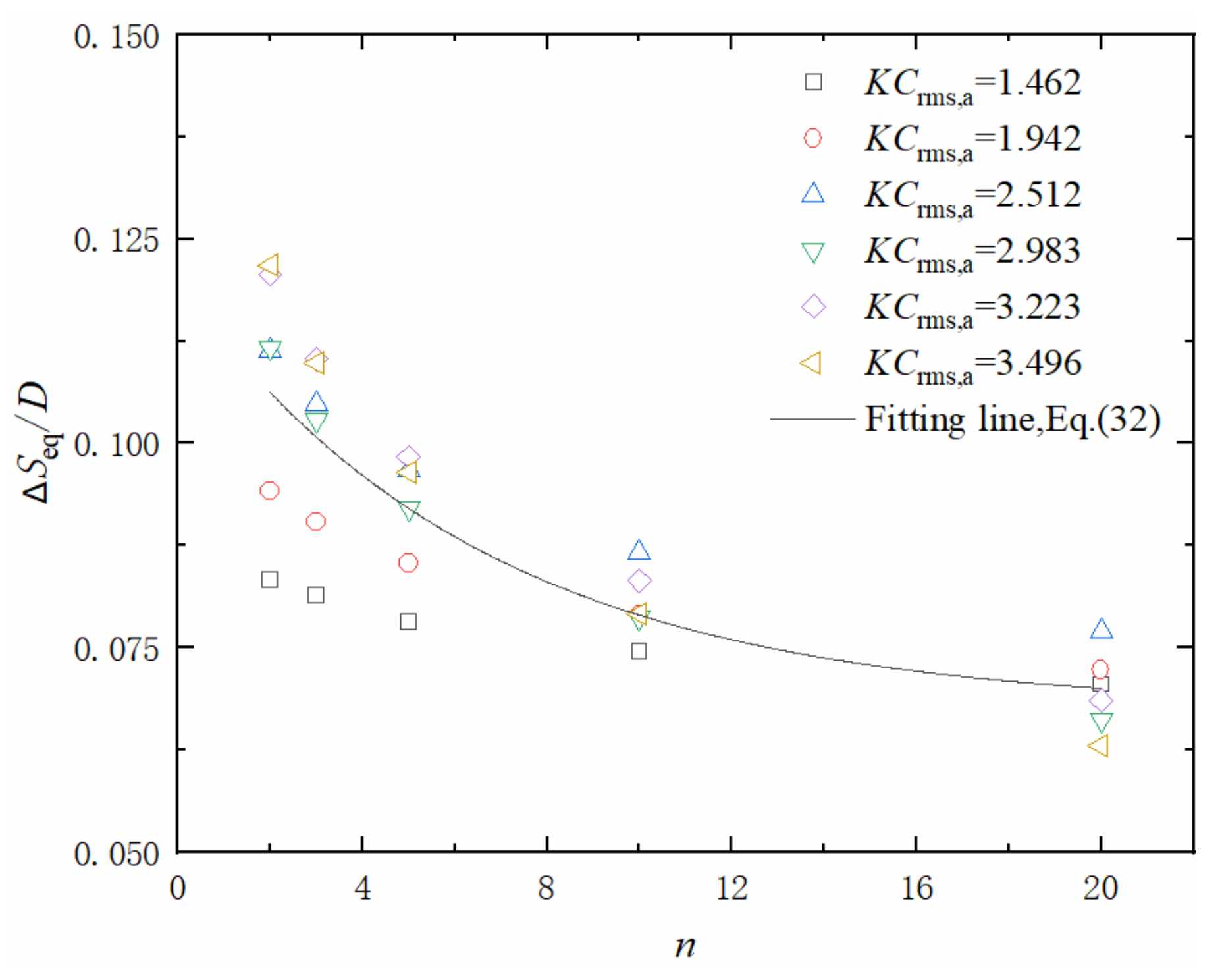
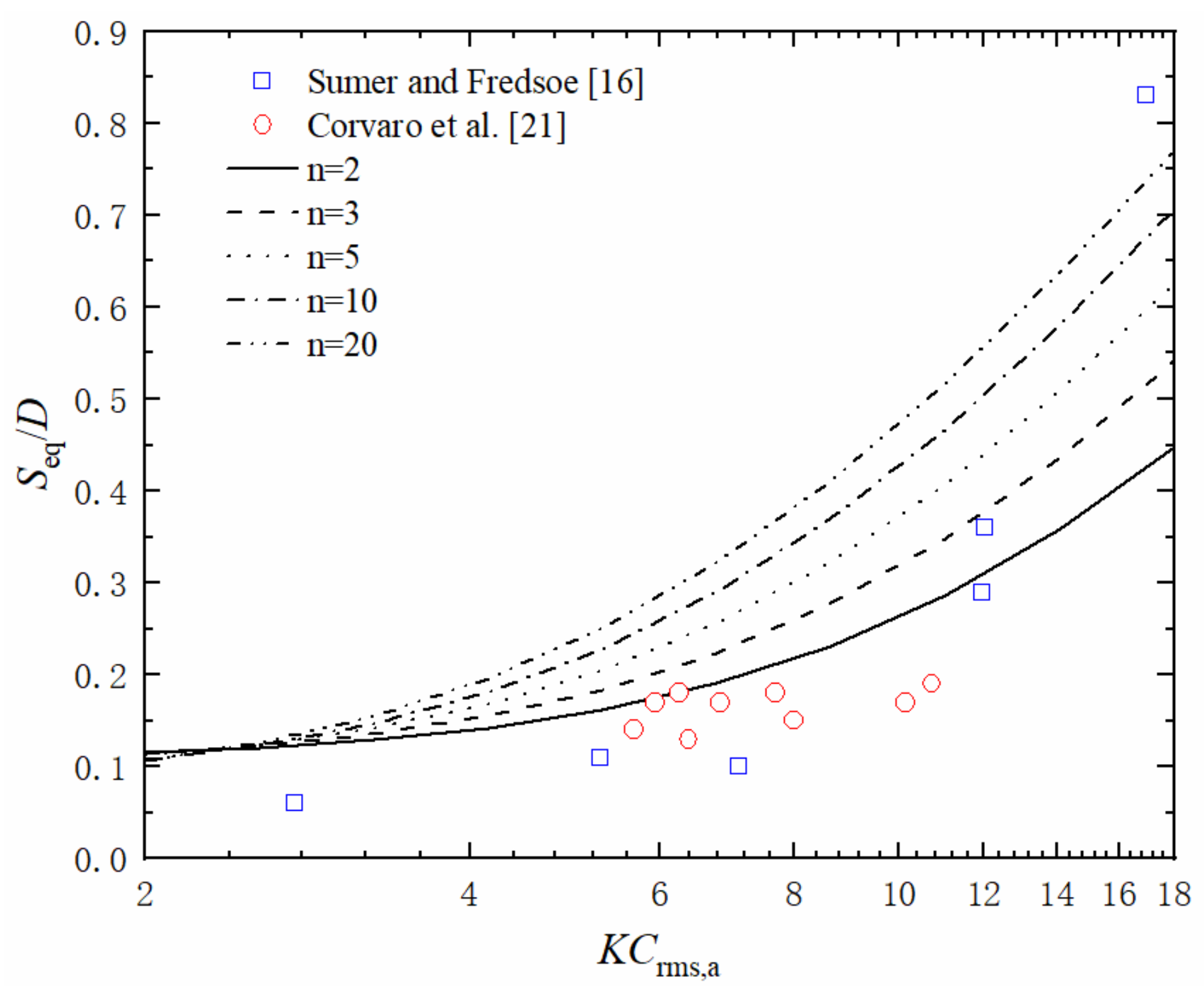
- Another further revision model (Equation (33)) was proposed according to the stochastic model established by Myrhaug and Rue [37] to predict the equilibrium scour depth around USAF under random waves, and the predicting results are the most favorable for n = 10 when KCrms,a < 4. However, contrary to the case of low KCrms,a, the predicting results are the most favorable for n = 2 when KCrms,a > 4 by the comparison with experimental results of Sumer and Fredsøe [16] and Corvaro et al. [21].
- (5)
- The same formula (Equation (37)) is applicable to express the relationship of Seq/D with Eu or Fr, and it can be inferred that the higher Fr and Eu both lead to the more intensive horseshoe vortex and larger Seq.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sumer, B.M.; Fredsøe, J.; Christiansen, N. Scour Around Vertical Pile in Waves. J. Waterw. Port. Coast. Ocean Eng. 1992, 118, 15–31. [Google Scholar] [CrossRef]
- Rudolph, D.; Bos, K. Scour around a monopile under combined wave-current conditions and low KC-numbers. In Proceedings of the 6th International Conference on Scour and Erosion, Amsterdam, The Netherlands, 1–3 November 2006; pp. 582–588. [Google Scholar]
- Nielsen, A.W.; Liu, X.; Sumer, B.M.; Fredsøe, J. Flow and bed shear stresses in scour protections around a pile in a current. Coast. Eng. 2013, 72, 20–38. [Google Scholar] [CrossRef]
- Ahmad, N.; Bihs, H.; Myrhaug, D.; Kamath, A.; Arntsen, Ø.A. Three-dimensional numerical modelling of wave-induced scour around piles in a side-by-side arrangement. Coast. Eng. 2018, 138, 132–151. [Google Scholar] [CrossRef]
- Li, H.; Ong, M.C.; Leira, B.J.; Myrhaug, D. Effects of Soil Profile Variation and Scour on Structural Response of an Offshore Monopile Wind Turbine. J. Offshore Mech. Arct. Eng. 2018, 140, 042001. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Liu, S. Dynamic analysis of umbrella suction anchor foundation embedded in seabed for offshore wind turbines. Géoméch. Energy Environ. 2017, 10, 12–20. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F.; Vanem, E.; Carvalho, H.; Correia, J.A.F.D.O. Editorial: Advanced research on offshore structures and foundation design: Part 1. Proc. Inst. Civ. Eng. Marit. Eng. 2019, 172, 118–123. [Google Scholar] [CrossRef]
- Chavez, C.E.A.; Stratigaki, V.; Wu, M.; Troch, P.; Schendel, A.; Welzel, M.; Villanueva, R.; Schlurmann, T.; De Vos, L.; Kisacik, D.; et al. Large-Scale Experiments to Improve Monopile Scour Protection Design Adapted to Climate Change—The PROTEUS Project. Energies 2019, 12, 1709. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; De Vos, L.; Chavez, C.E.A.; Stratigaki, V.; Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F.; Troch, P. Large Scale Experimental Study of the Scour Protection Damage Around a Monopile Foundation Under Combined Wave and Current Conditions. J. Mar. Sci. Eng. 2020, 8, 417. [Google Scholar] [CrossRef]
- Sørensen, S.P.H.; Ibsen, L.B. Assessment of foundation design for offshore monopiles unprotected against scour. Ocean Eng. 2013, 63, 17–25. [Google Scholar] [CrossRef]
- Prendergast, L.; Gavin, K.; Doherty, P. An investigation into the effect of scour on the natural frequency of an offshore wind turbine. Ocean Eng. 2015, 101, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Fazeres-Ferradosa, T.; Chambel, J.; Taveira-Pinto, F.; Rosa-Santos, P.; Taveira-Pinto, F.; Giannini, G.; Haerens, P. Scour Protections for Offshore Foundations of Marine Energy Harvesting Technologies: A Review. J. Mar. Sci. Eng. 2021, 9, 297. [Google Scholar] [CrossRef]
- Yang, Q.; Yu, P.; Liu, Y.; Liu, H.; Zhang, P.; Wang, Q. Scour characteristics of an offshore umbrella suction anchor foundation under the combined actions of waves and currents. Ocean Eng. 2020, 202, 106701. [Google Scholar] [CrossRef]
- Yu, P.; Hu, R.; Yang, J.; Liu, H. Numerical investigation of local scour around USAF with different hydraulic conditions under currents and waves. Ocean Eng. 2020, 213, 107696. [Google Scholar] [CrossRef]
- Sumer, B.M.; Christiansen, N.; Fredsøe, J. The horseshoe vortex and vortex shedding around a vertical wall-mounted cylinder exposed to waves. J. Fluid Mech. 1997, 332, 41–70. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour around Pile in Combined Waves and Current. J. Hydraul. Eng. 2001, 127, 403–411. [Google Scholar] [CrossRef]
- Petersen, T.U.; Sumer, B.M.; Fredsøe, J. Time scale of scour around a pile in combined waves and current. In Proceedings of the 6th International Conference on Scour and Erosion, Paris, France, 27–31 August 2012. [Google Scholar]
- Petersen, T.U.; Sumer, B.M.; Fredsøe, J.; Raaijmakers, T.C.; Schouten, J.-J. Edge scour at scour protections around piles in the marine environment—Laboratory and field investigation. Coast. Eng. 2015, 106, 42–72. [Google Scholar] [CrossRef]
- Qi, W.; Gao, F. Equilibrium scour depth at offshore monopile foundation in combined waves and current. Sci. China Ser. E Technol. Sci. 2014, 57, 1030–1039. [Google Scholar] [CrossRef] [Green Version]
- Larsen, B.E.; Fuhrman, D.R.; Baykal, C.; Sumer, B.M. Tsunami-induced scour around monopile foundations. Coast. Eng. 2017, 129, 36–49. [Google Scholar] [CrossRef] [Green Version]
- Corvaro, S.; Marini, F.; Mancinelli, A.; Lorenzoni, C.; Brocchini, M. Hydro- and Morpho-dynamics Induced by a Vertical Slender Pile under Regular and Random Waves. J. Waterw. Port. Coast. Ocean Eng. 2018, 144, 04018018. [Google Scholar] [CrossRef]
- Schendel, A.; Welzel, M.; Schlurmann, T.; Hsu, T.-W. Scour around a monopile induced by directionally spread irregular waves in combination with oblique currents. Coast. Eng. 2020, 161, 103751. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Taveira-Pinto, F.; Romão, X.; Reis, M.; das Neves, L. Reliability assessment of offshore dynamic scour protections using copulas. Wind. Eng. 2018, 43, 506–538. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Welzel, M.; Schendel, A.; Baelus, L.; Santos, P.R.; Pinto, F.T. Extended characterization of damage in rubble mound scour protections. Coast. Eng. 2020, 158, 103671. [Google Scholar] [CrossRef]
- Tavouktsoglou, N.S.; Harris, J.M.; Simons, R.R.; Whitehouse, R.J.S. Equilibrium Scour-Depth Prediction around Cylindrical Structures. J. Waterw. Port. Coast. Ocean Eng. 2017, 143, 04017017. [Google Scholar] [CrossRef] [Green Version]
- Ettema, R.; Melville, B.; Barkdoll, B. Scale Effect in Pier-Scour Experiments. J. Hydraul. Eng. 1998, 124, 639–642. [Google Scholar] [CrossRef]
- Umeda, S. Scour Regime and Scour Depth around a Pile in Waves. J. Coast. Res. Spec. Issue 2011, 64, 845–849. [Google Scholar]
- Umeda, S. Scour process around monopiles during various phases of sea storms. J. Coast. Res. 2013, 165, 1599–1604. [Google Scholar] [CrossRef]
- Baykal, C.; Sumer, B.; Fuhrman, D.R.; Jacobsen, N.; Fredsøe, J. Numerical simulation of scour and backfilling processes around a circular pile in waves. Coast. Eng. 2017, 122, 87–107. [Google Scholar] [CrossRef] [Green Version]
- Miles, J.; Martin, T.; Goddard, L. Current and wave effects around windfarm monopile foundations. Coast. Eng. 2017, 121, 167–178. [Google Scholar] [CrossRef] [Green Version]
- Miozzi, M.; Corvaro, S.; Pereira, F.A.; Brocchini, M. Wave-induced morphodynamics and sediment transport around a slender vertical cylinder. Adv. Water Resour. 2019, 129, 263–280. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, Y.; Zhang, S.; Shi, Z.; Chen, X.; Xu, Y.; Tang, Y. Experimental study on scour around a composite bucket foundation due to waves and current. Ocean Eng. 2019, 189, 106302. [Google Scholar] [CrossRef]
- Carreiras, J.; Larroudé, P.; Seabra-Santos, F.; Mory, M. Wave Scour Around Piles. In Proceedings of the Coastal Engineering 2000, American Society of Civil Engineers (ASCE), Sydney, Australia, 16–21 July 2000; pp. 1860–1870. [Google Scholar]
- Raaijmakers, T.; Rudolph, D. Time-dependent scour development under combined current and waves conditions—Laboratory experiments with online monitoring technique. In Proceedings of the 4th International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008; pp. 152–161. [Google Scholar]
- Khalfin, I.S. Modeling and calculation of bed score around large-diameter vertical cylinder under wave action. Water Resour. 2007, 34, 357. [Google Scholar] [CrossRef] [Green Version]
- Zanke, U.C.; Hsu, T.-W.; Roland, A.; Link, O.; Diab, R. Equilibrium scour depths around piles in noncohesive sediments under currents and waves. Coast. Eng. 2011, 58, 986–991. [Google Scholar] [CrossRef]
- Myrhaug, D.; Rue, H. Scour below pipelines and around vertical piles in random waves. Coast. Eng. 2003, 48, 227–242. [Google Scholar] [CrossRef]
- Myrhaug, D.; Ong, M.C.; Føien, H.; Gjengedal, C.; Leira, B.J. Scour below pipelines and around vertical piles due to second-order random waves plus a current. Ocean Eng. 2009, 36, 605–616. [Google Scholar] [CrossRef]
- Myrhaug, D.; Ong, M.C. Random wave-induced onshore scour characteristics around submerged breakwaters using a stochastic method. Ocean Eng. 2010, 37, 1233–1238. [Google Scholar] [CrossRef]
- Ong, M.C.; Myrhaug, D.; Hesten, P. Scour around vertical piles due to long-crested and short-crested nonlinear random waves plus a current. Coast. Eng. 2013, 73, 106–114. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Yakhot, V.; Smith, L.M. The renormalization group, the e-expansion and derivation of turbulence models. J. Sci. Comput. 1992, 7, 35–61. [Google Scholar] [CrossRef]
- Mastbergen, D.R.; Berg, J.V.D. Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons. Sedimentology 2003, 50, 625–637. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands; Thomas Telford Ltd.: London, UK, 1998. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Zhou, X.-L.; Wang, J.-H. Numerical investigation of local scour around three adjacent piles with different arrangements under current. Ocean Eng. 2017, 142, 625–638. [Google Scholar] [CrossRef]
- Yu, Y.X.; Liu, S.X. Random Wave and Its Applications to Engineering, 4th ed.; Dalian University of Technology Press: Dalian, China, 2011. [Google Scholar]
- Pang, A.; Skote, M.; Lim, S.; Gullman-Strand, J.; Morgan, N. A numerical approach for determining equilibrium scour depth around a mono-pile due to steady currents. Appl. Ocean Res. 2016, 57, 114–124. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Three-dimensional interaction of waves and porous coastal structures using Open-FOAM®. Part I: Formulation and validation. Coast. Eng. 2014, 83, 243–258. [Google Scholar] [CrossRef]
- Corvaro, S.; Crivellini, A.; Marini, F.; Cimarelli, A.; Capitanelli, L.; Mancinelli, A. Experimental and Numerical Analysis of the Hydrodynamics around a Vertical Cylinder in Waves. J. Mar. Sci. Eng. 2019, 7, 453. [Google Scholar] [CrossRef] [Green Version]
- Flow3D User Manual, version 11.0.3; Flow Science, Inc.: Santa Fe, NM, USA, 2013.
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Stahlmann, A. Experimental and Numerical Modeling of Scour at Foundation Structures for Offshore Wind Turbines. Ph.D. Thesis, Franzius-Institute for Hydraulic, Estuarine and Coastal Engineering, Leibniz Universität Hannover, Hannover, Germany, 2013. [Google Scholar]
- Breusers, H.N.C.; Nicollet, G.; Shen, H. Local Scour Around Cylindrical Piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Schendel, A.; Hildebrandt, A.; Goseberg, N.; Schlurmann, T. Processes and evolution of scour around a monopile induced by tidal currents. Coast. Eng. 2018, 139, 65–84. [Google Scholar] [CrossRef]







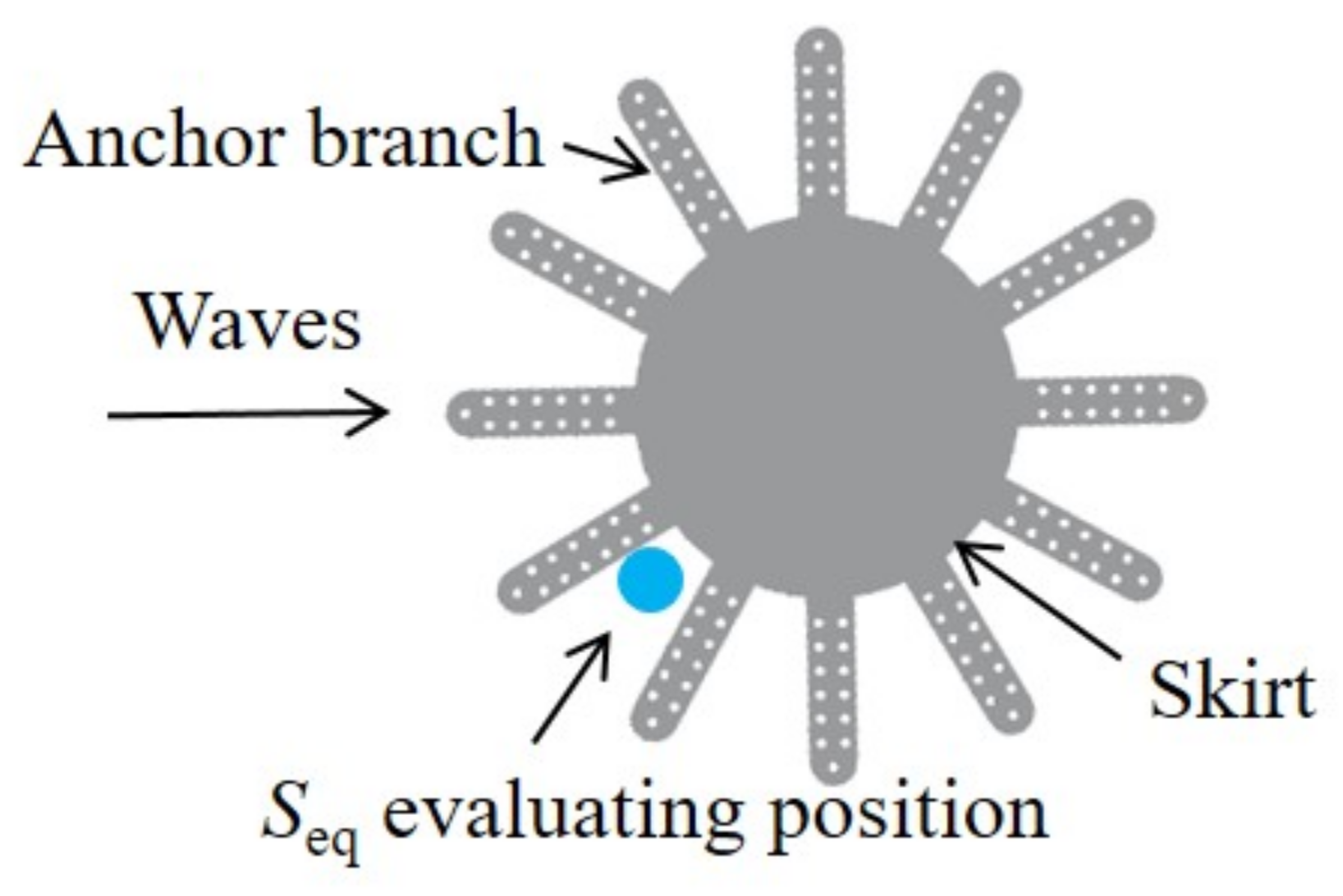







| Item | Dimension/m |
|---|---|
| Main tube height | 11.2 |
| Main tube diameter | 4 |
| Main tube wall thickness | 0.02 |
| Tube skirt height | 2 |
| Tube skirt diameter | 8 |
| Tube skirt wall thickness | 0.02 |
| Anchor branch length | 4 |
| Anchor branch thickness | 0.048 |
| Case | Water Depth/m | Significant Wave Height H1/3/m | Peak Period Tp/s | ε | Ur |
|---|---|---|---|---|---|
| 1 | 8 | 3.0 | 8.79 | 0.029 | 0.658 |
| 2 | 8 | 3.5 | 9.53 | 0.029 | 0.928 |
| 3 | 8 | 4.0 | 10.37 | 0.028 | 1.282 |
| 4 | 8 | 4.5 | 10.76 | 0.029 | 1.567 |
| 5 | 8 | 5.0 | 11.19 | 0.030 | 1.898 |
| 6 | 9 | 5.0 | 11.19 | 0.030 | 1.480 |
| 7 | 10 | 5.0 | 11.19 | 0.030 | 1.184 |
| 8 | 11 | 5.0 | 11.19 | 0.030 | 0.965 |
| 9 | 12 | 5.0 | 11.19 | 0.030 | 0.800 |
| Case | Uwm,rms | KCrms,a | KCrms,p | KCrms,s | KCrms,m | KCrms,n = 1/10 | KCrms,n = 1/5 |
|---|---|---|---|---|---|---|---|
| 1 | 0.882 | 1.462 | 1.938 | 1.805 | 1.781 | 1.496 | 1.372 |
| 2 | 1.080 | 1.940 | 2.573 | 2.396 | 2.364 | 1.986 | 1.822 |
| 3 | 1.285 | 2.511 | 3.330 | 3.101 | 3.060 | 2.571 | 2.358 |
| 4 | 1.470 | 2.981 | 3.953 | 3.681 | 3.633 | 3.052 | 2.799 |
| 5 | 1.655 | 3.490 | 4.629 | 4.309 | 4.253 | 3.573 | 3.277 |
| 6 | 1.526 | 3.219 | 4.270 | 3.975 | 3.923 | 3.296 | 3.023 |
| 7 | 1.414 | 2.982 | 3.955 | 3.682 | 3.634 | 3.053 | 2.800 |
| 8 | 1.314 | 2.773 | 3.677 | 3.424 | 3.379 | 2.839 | 2.604 |
| 9 | 1.229 | 2.593 | 3.439 | 3.202 | 3.160 | 2.655 | 2.435 |
| Case | Uwm,s | KCs,s | KCs,p | KCs,a | KCs,m | KCs,n = 1/10 | KCs,n = 1/5 |
|---|---|---|---|---|---|---|---|
| 1 | 1.390 | 2.844 | 3.055 | 2.303 | 2.807 | 2.358 | 2.163 |
| 2 | 1.670 | 3.705 | 3.980 | 3.001 | 3.657 | 3.072 | 2.818 |
| 3 | 1.955 | 4.719 | 5.068 | 3.822 | 4.657 | 3.913 | 3.588 |
| 4 | 2.220 | 5.561 | 5.973 | 4.503 | 5.488 | 4.611 | 4.229 |
| 5 | 2.489 | 6.482 | 6.963 | 5.250 | 6.398 | 5.375 | 4.929 |
| 6 | 2.314 | 6.026 | 6.472 | 4.880 | 5.947 | 4.997 | 4.582 |
| 7 | 2.165 | 5.639 | 6.056 | 4.567 | 5.565 | 4.676 | 4.288 |
| 8 | 2.033 | 5.296 | 5.688 | 4.289 | 5.227 | 4.391 | 4.027 |
| 9 | 1.919 | 4.998 | 5.368 | 4.048 | 4.933 | 4.144 | 3.801 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Liu, H.; Leng, H.; Yu, P.; Wang, X. Scour Characteristics and Equilibrium Scour Depth Prediction around Umbrella Suction Anchor Foundation under Random Waves. J. Mar. Sci. Eng. 2021, 9, 886. https://doi.org/10.3390/jmse9080886
Hu R, Liu H, Leng H, Yu P, Wang X. Scour Characteristics and Equilibrium Scour Depth Prediction around Umbrella Suction Anchor Foundation under Random Waves. Journal of Marine Science and Engineering. 2021; 9(8):886. https://doi.org/10.3390/jmse9080886
Chicago/Turabian StyleHu, Ruigeng, Hongjun Liu, Hao Leng, Peng Yu, and Xiuhai Wang. 2021. "Scour Characteristics and Equilibrium Scour Depth Prediction around Umbrella Suction Anchor Foundation under Random Waves" Journal of Marine Science and Engineering 9, no. 8: 886. https://doi.org/10.3390/jmse9080886
APA StyleHu, R., Liu, H., Leng, H., Yu, P., & Wang, X. (2021). Scour Characteristics and Equilibrium Scour Depth Prediction around Umbrella Suction Anchor Foundation under Random Waves. Journal of Marine Science and Engineering, 9(8), 886. https://doi.org/10.3390/jmse9080886




