Deep Learning Convolutional Neural Network Applying for the Arctic Acoustic Tomography Current Inversion Accuracy Improvement
Abstract
:1. Introduction
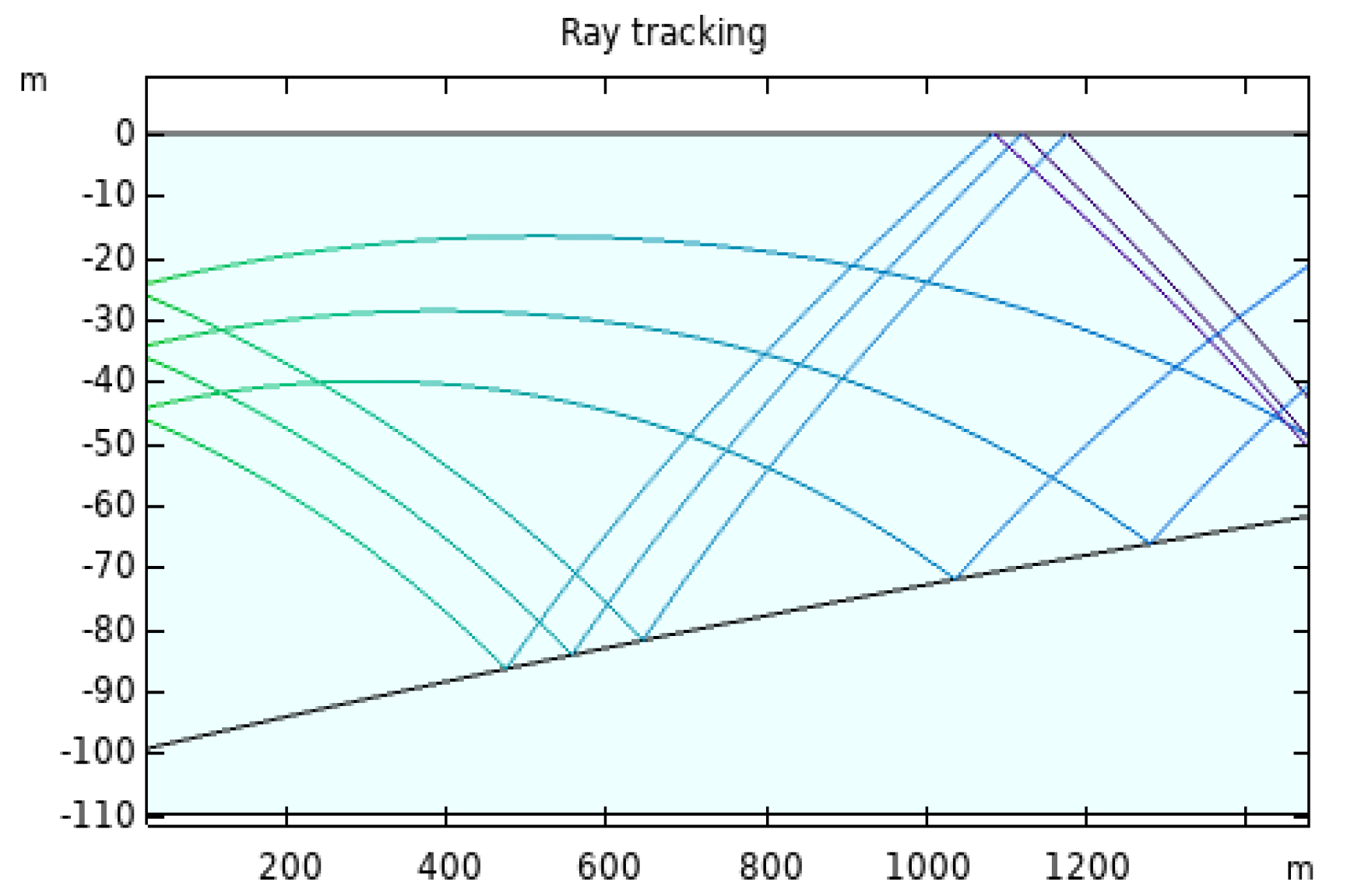
2. Acoustic Tomography Reciprocal Transmission and Flow Field Calculation
2.1. Acoustic Tomography Reciprocal Transmission
2.2. Flow Field Acoustic Tomography Least Square Method
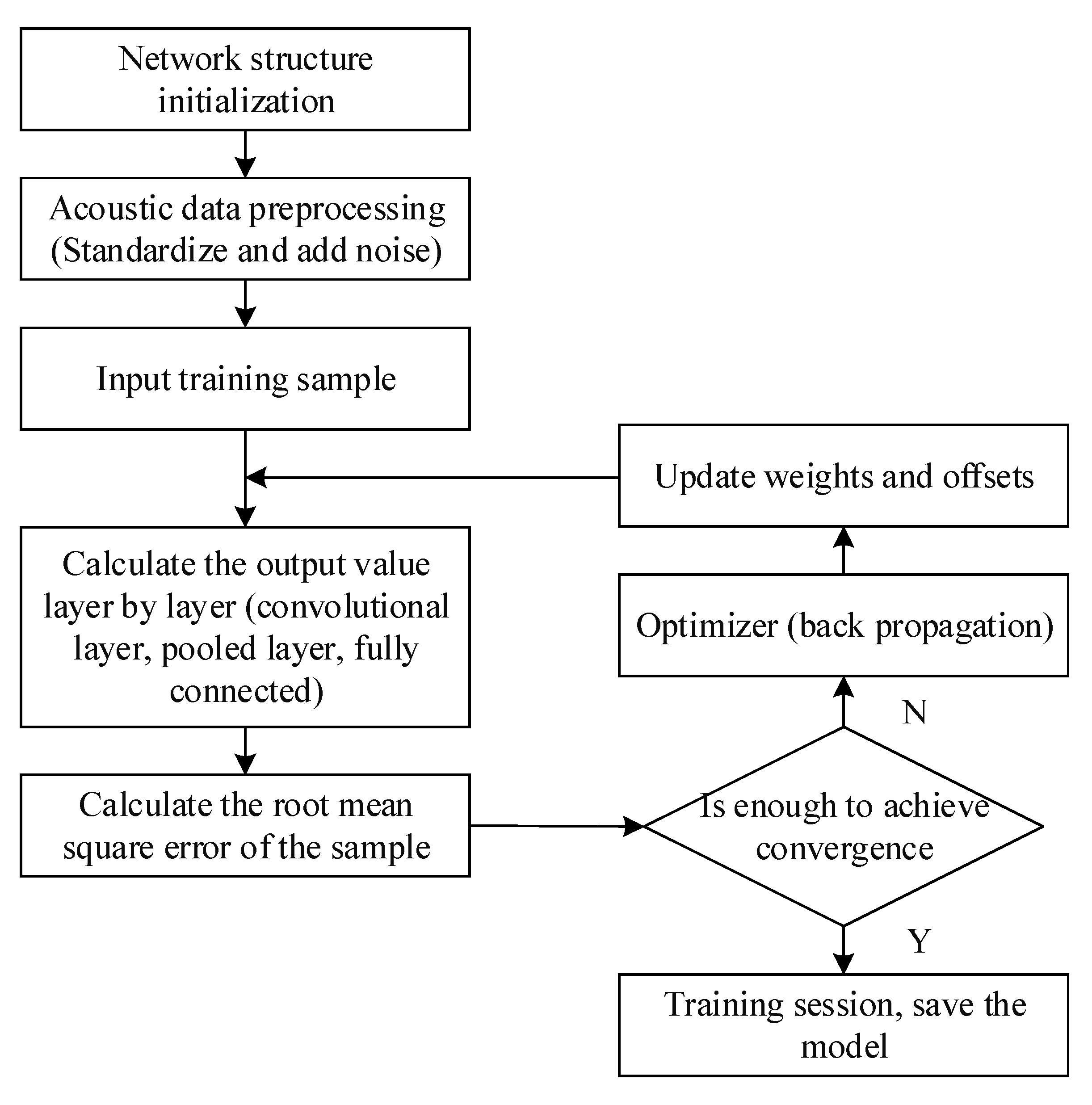
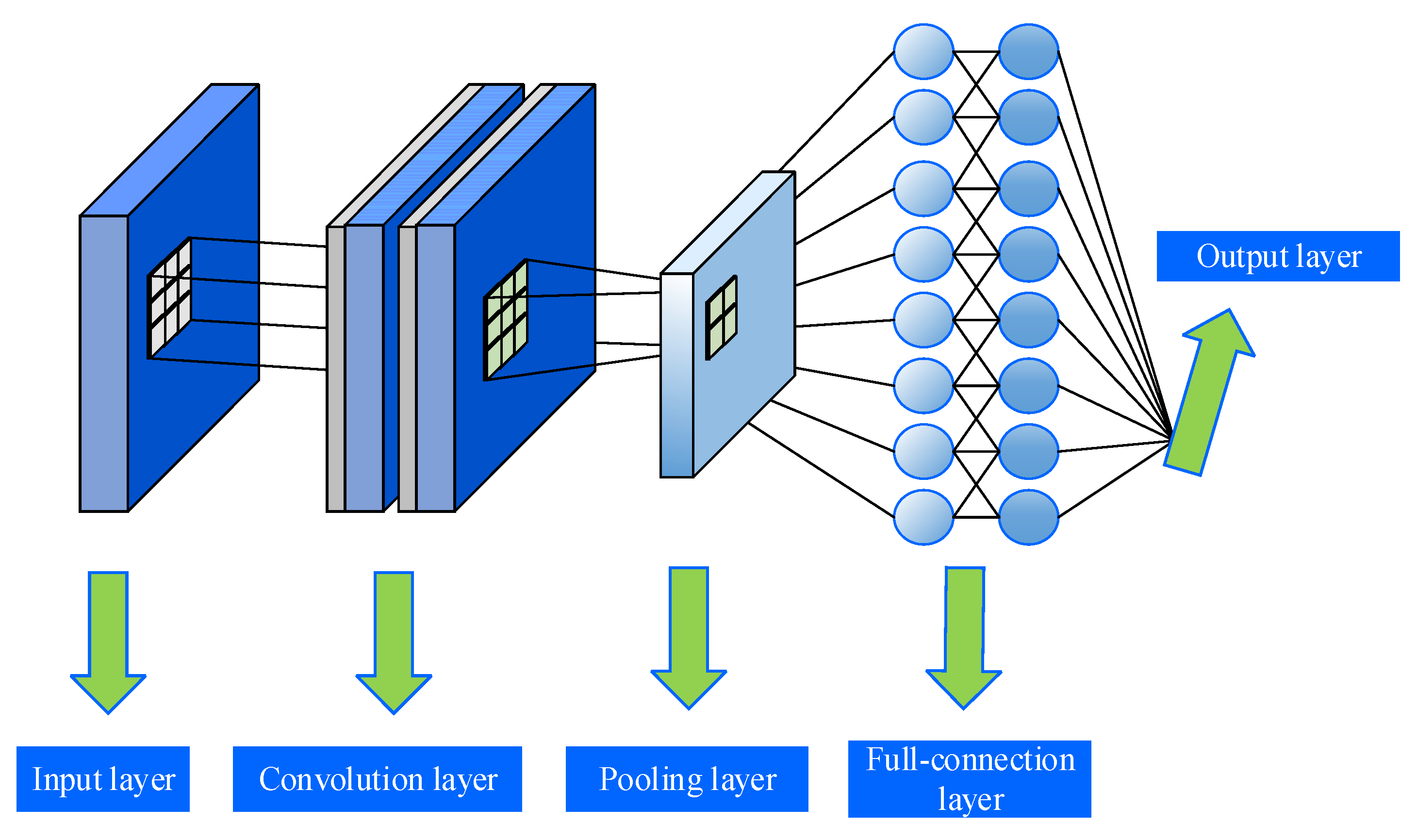
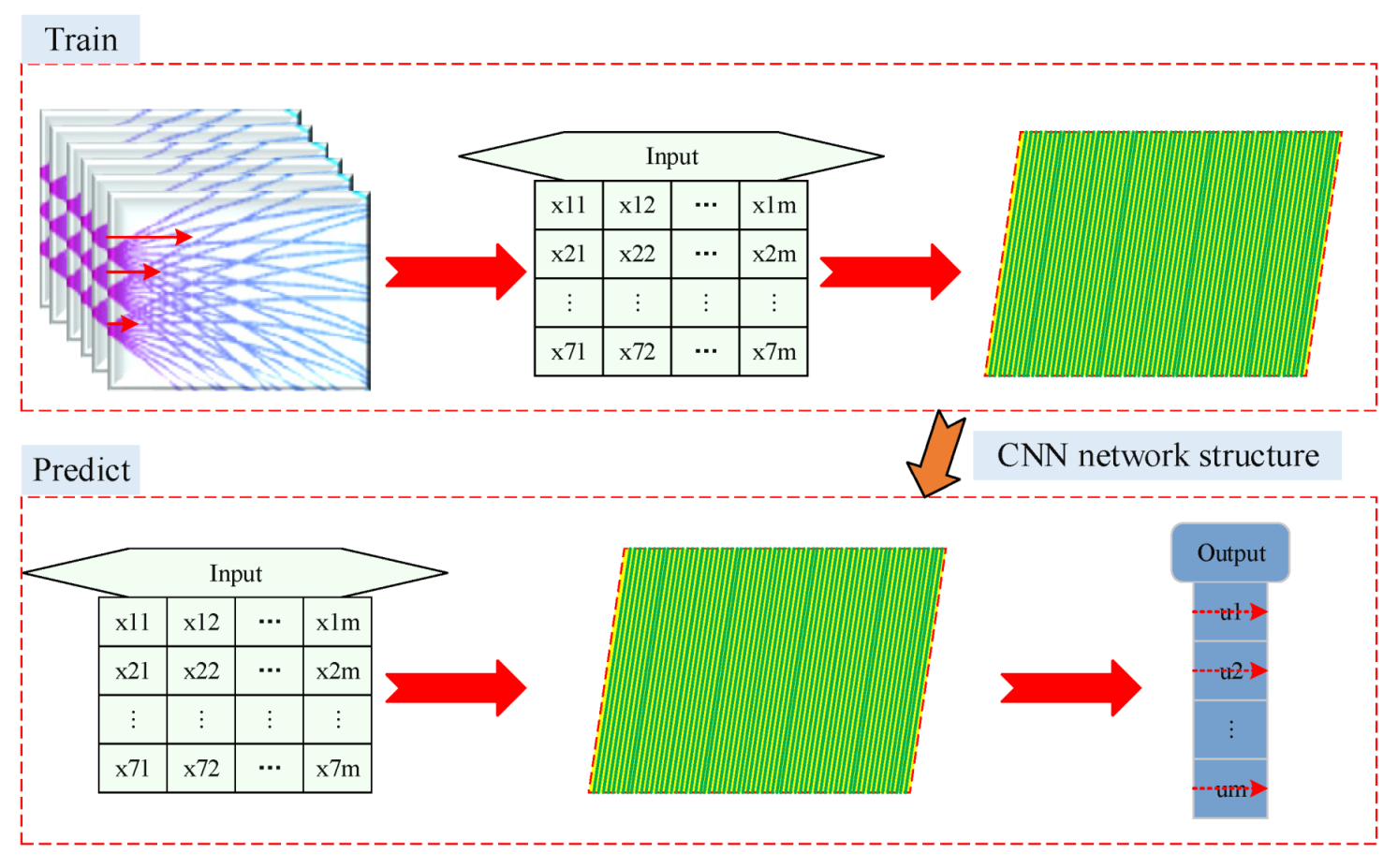
2.3. Flow Field Acoustic Tomography Based on CNN
3. Modeling and Simulation
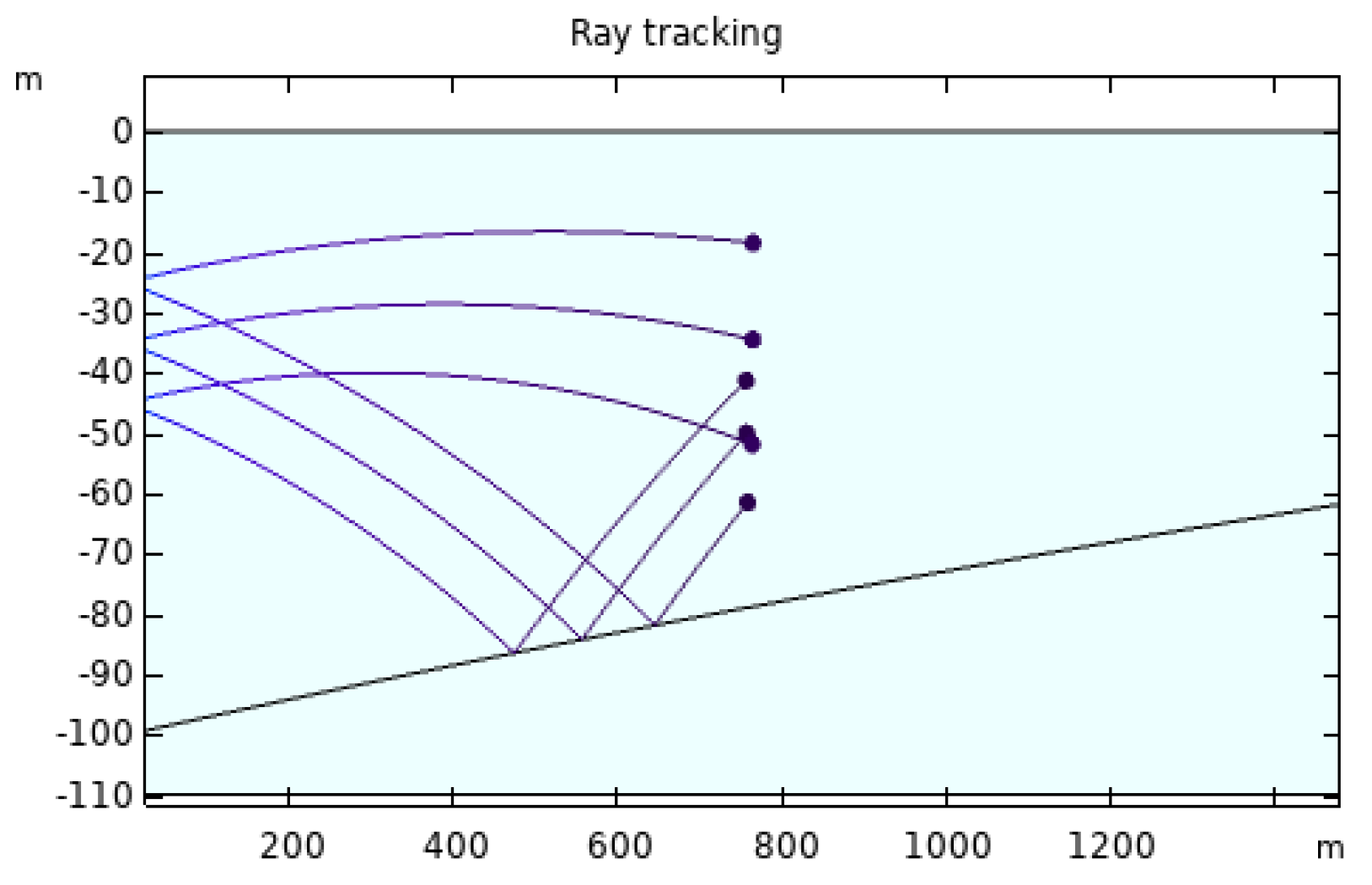
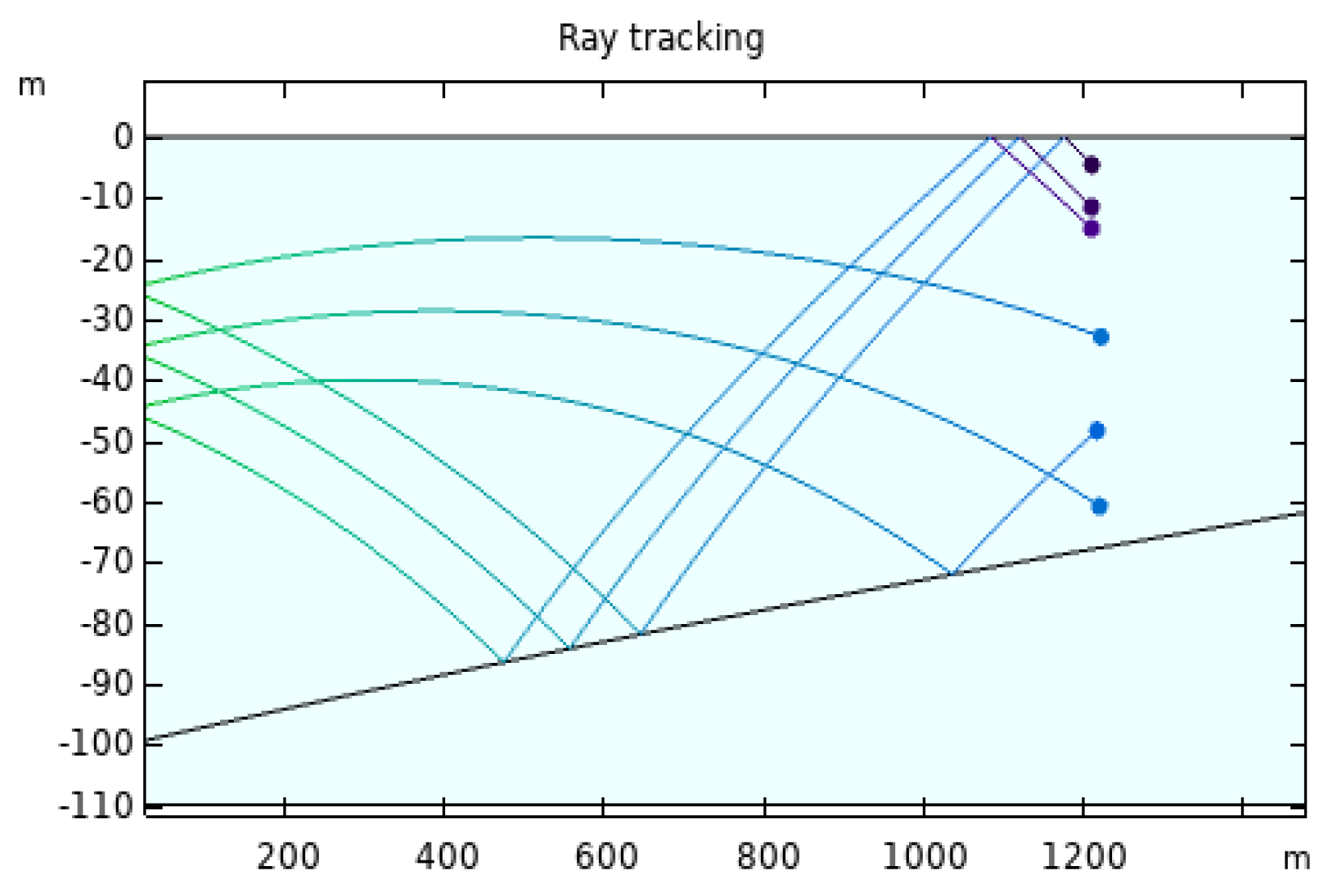
3.1. Model Establishment
3.2. Flow Field Acoustic Tomography Error and Accuracy Judgment Index
4. Simulation Results
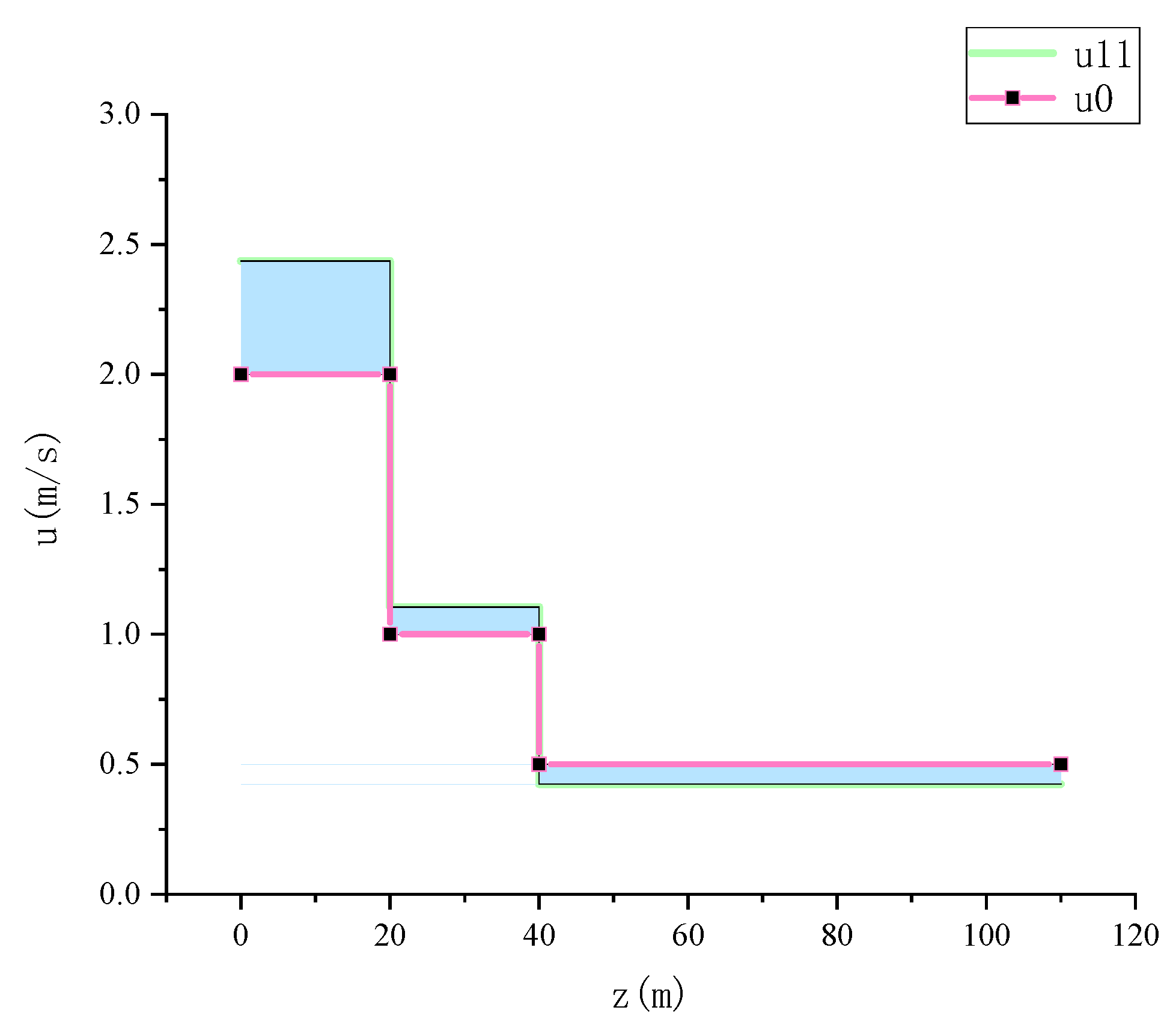
4.1. Least Squares Simulation Results
4.2. Implementation of CNN
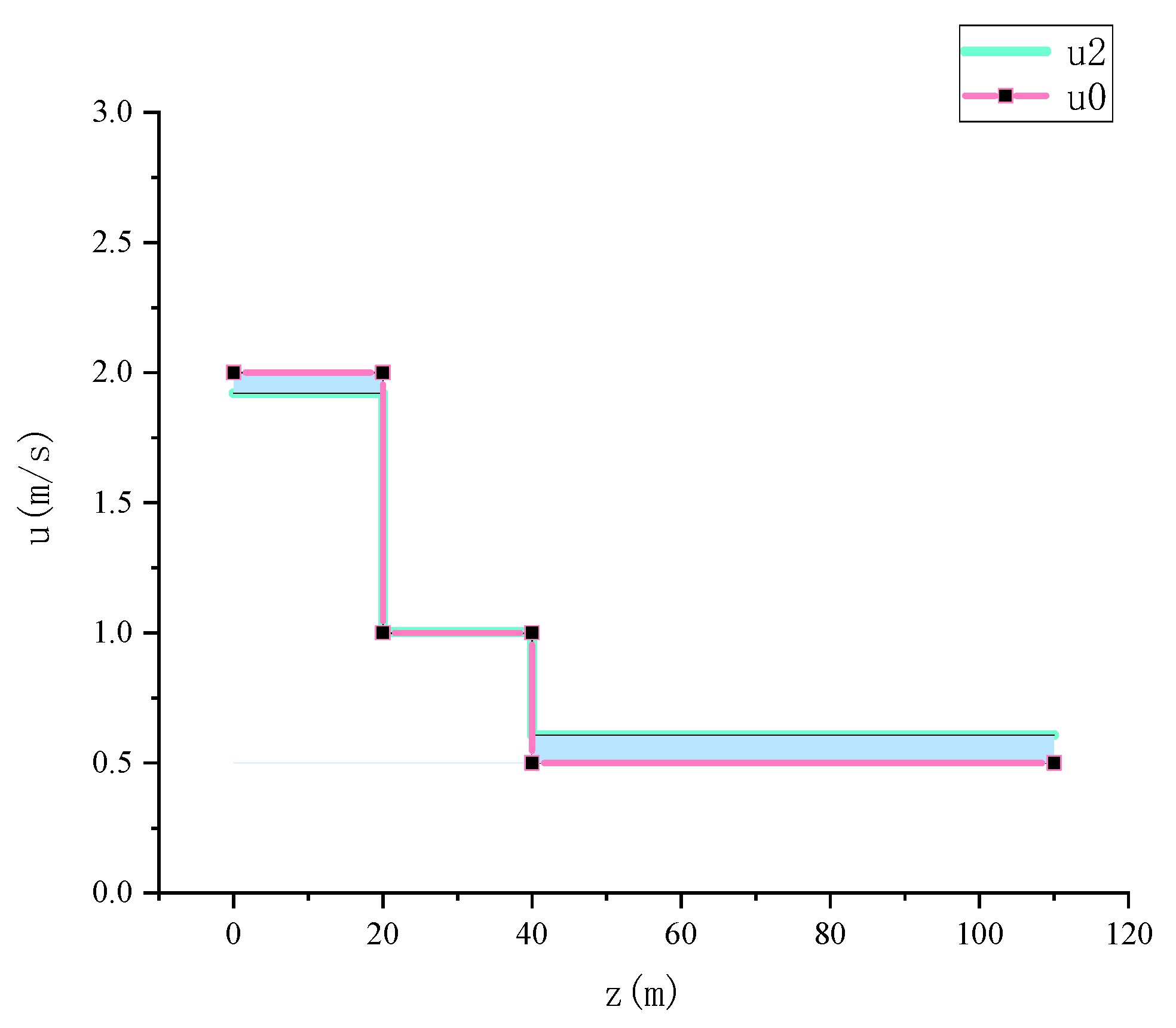
4.3. Experimental Analysis of CNN
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maeda, K.; Kimura, N.; Yamaguchi, H. Temporal and spatial change in the relationship between sea-ice motion and wind in the Arctic. Polar Res. 2020, 39. [Google Scholar] [CrossRef]
- Wunsch, M.C. Ocean acoustic tomography: A scheme for large scale monitoring. Deep Sea Res. 1979. [Google Scholar] [CrossRef]
- Zhang, Y.; Maslowski, W.; Semtner, A.J. Impact of mesoscale ocean currents on sea ice in high-resolution Arctic ice and ocean simulations. J. Geophys. Res. Oceans 1999, 104, 18409–18429. [Google Scholar] [CrossRef] [Green Version]
- Spindel, R.C.; Worcester, P.F. Ocean Acoustic Tomography. Sci. Am. 1990, 263, 94–99. [Google Scholar] [CrossRef]
- Skarsoulis, E.K. A matched-peak inversion approach for ocean acoustic travel-time tomography. J. Acoust. Soc. Am. 2000, 107, 1324–1332. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, N.; Huang, C.-F.; Kaneko, A.; Liu, C.-T.; Howe, B.M.; Wang, Y.-H.; Yang, Y.; Lin, J.; Zhu, X.-H.; Gohda, N. Measuring the Kuroshio Current with ocean acoustic tomography. J. Acoust. Soc. Am. 2013, 134, 3272–3281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, G.; Pan, H.; Zhang, Q.; Lv, X.; Zhao, W.; Gao, Y. Determination of Harmonic Parameters with Temporal Variations: An Enhanced Harmonic Analysis Algorithm and Application to Internal Tidal Currents in the South China Sea. J. Atmos. Ocean. Technol. 2018, 35. [Google Scholar] [CrossRef]
- Dushaw, B.D.; Sagen, H. The role of simulated small-scale ocean variability in inverse computations for ocean acoustic tomography. J. Acoust. Soc. Am. 2017, 142, 3541. [Google Scholar] [CrossRef] [PubMed]
- Dushaw, B.D.; Sagen, H. On the effects of small-scale variability on acoustic propagation in Fram Strait: The tomography forward problem. J. Acoust. Soc. Am. 2016, 140, 1286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Callaham, J.; Maeda, K.; Brunton, S.L. Robust flow field reconstruction from limited measurements via sparse representation. Phys. Rev. Fluids 2019, 4, 103907. [Google Scholar] [CrossRef] [Green Version]
- Mustaqeem; Kwon, S. 1D-CNN: Speech Emotion Recognition System Using a Stacked Network with Dilated CNN Features. Comput. Mater. Con. 2021, 67, 4039–4059. [Google Scholar] [CrossRef]
- Stéphan, Y.; Thiria, S.; Badran, F. Application of multilayered neural networks to ocean acoustic tomography inversions. Inverse Probl. Eng. 1996, 3, 281–304. [Google Scholar] [CrossRef]
- Narvekar, C.; Rao, M. Flower classification using CNN and transfer learning in CNN- Agriculture Perspetive. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, 3–5 December 2020. [Google Scholar] [CrossRef]
- Powell, B.S.; Kerry, C.G.; Cornuelle, B.D. Using a numerical model to understand the connection between the ocean and acoustic travel-time measurements. J. Acoust. Soc. Am. 2013, 134, 3211–3222. [Google Scholar] [CrossRef] [PubMed]
- Skarsoulis, E.; Piperakis, G.; Kalogerakis, M.; Sagen, H. Ocean acoustic tomography: Travel-time inversion in the eastern Fram Strait. J. Acoust. Soc. Am. 2008, 123, 2991. [Google Scholar] [CrossRef]
- Frederick, C.; Villar, S.; Michalopoulou, Z.H. Seabed classification using physics-based modeling and machine learning. J. Acoust. Soc. Am. 2020, 148, 859–872. [Google Scholar] [CrossRef] [PubMed]
- Lähivaara, T.; Kärkkäinen, L.; Huttunen, J.; Hesthaven, J.S. Deep convolutional neural networks for estimating porous material parameters with ultrasound tomography. J. Acoust. Soc. Am. 2018, 143, 1148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, F.; Ma, J. Deep-learning inversion: A next generation seismic velocity-model building method. Geophysics 2019, 1–133. [Google Scholar] [CrossRef] [Green Version]
- Etter, P.C. Underwater Acoustic Modeling and Simulation; Spon Press (Tay & Francis Group): London, UK, 2003. [Google Scholar] [CrossRef]
- Comanducci, L.; Bestagini, P.; Tagliasacchi, M.; Sarti, A.; Tubaro, S. Reconstructing Speech from CNN Embeddings. IEEE. Signal. Proc. Let. 2021, 28, 952–956. [Google Scholar] [CrossRef]
- Blondel, P.; Sagen, H.; Martin, B.; Pettit, E.; Tegowski, J.; Thodes, A.; Tollefsen, D.; Worcester, P. Report of the Polar Session, Oceanoise2015: Report of the Round Table Session on Polar Noise. Available online: http://oceanoise2015.com/?page_id=789 (accessed on 6 July 2021).




| Forward Propagation Time/s | Backward Propagation Time/s | △t/s | |
|---|---|---|---|
| 1 | 0.9908667974750063 | 0.9921370357778033 | −0.001270238 |
| 2 | 0.9814290042702533 | 0.9832276442346188 | −0.00179864 |
| 3 | 0.9911920895784465 | 0.9924207624924704 | −0.001228673 |
| 4 | 0.9845382912123009 | 0.9855862764180756 | −0.001047985 |
| 5 | 0.9909932804115785 | 0.9922227519661865 | −0.001229472 |
| 6 | 0.9861684623886157 | 0.9869143234892909 | −0.000745861 |
| 0–20 | 20–40 | 40–110 | Condition Number | Mean Absolute Error | |
|---|---|---|---|---|---|
| 3 | 2.43632 | 1.10469 | 0.42396 | 6.07417 | 0.15831 |
| MAPE | 0.21816 | 0.10469 | 0.15208 | ||
| 4 | 2.24261 | 1.01349 | 0.77710 | 6.69373 | 0.229665 |
| MAPE | 0.121305 | 0.01349 | 0.5542 | ||
| 5 | 2.74908 | 0.68197 | 0.75077 | 7.74111 | 0.398037 |
| MAPE | 0.37454 | 0.31803 | 0.50154 | ||
| 6 | 2.5162 | 0.8419 | 0.7991 | 9.0633 | 0.338133 |
| MAPE | 0.2581 | 0.1581 | 0.5982 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, K.; Xu, J.; Wang, Z.; Lu, C.; Fan, L.; Li, Z.; Zhou, J. Deep Learning Convolutional Neural Network Applying for the Arctic Acoustic Tomography Current Inversion Accuracy Improvement. J. Mar. Sci. Eng. 2021, 9, 755. https://doi.org/10.3390/jmse9070755
Jin K, Xu J, Wang Z, Lu C, Fan L, Li Z, Zhou J. Deep Learning Convolutional Neural Network Applying for the Arctic Acoustic Tomography Current Inversion Accuracy Improvement. Journal of Marine Science and Engineering. 2021; 9(7):755. https://doi.org/10.3390/jmse9070755
Chicago/Turabian StyleJin, Kangkang, Jian Xu, Zichen Wang, Can Lu, Long Fan, Zhongzheng Li, and Jiaxin Zhou. 2021. "Deep Learning Convolutional Neural Network Applying for the Arctic Acoustic Tomography Current Inversion Accuracy Improvement" Journal of Marine Science and Engineering 9, no. 7: 755. https://doi.org/10.3390/jmse9070755
APA StyleJin, K., Xu, J., Wang, Z., Lu, C., Fan, L., Li, Z., & Zhou, J. (2021). Deep Learning Convolutional Neural Network Applying for the Arctic Acoustic Tomography Current Inversion Accuracy Improvement. Journal of Marine Science and Engineering, 9(7), 755. https://doi.org/10.3390/jmse9070755






