An FTC Design via Multiple SOGIs with Suppression of Harmonic Disturbances for Five-Phase PMSG-Based Tidal Current Applications
Abstract
1. Introduction
2. System Modeling and Problem Formulation
- Swell effects and turbulences are not considered for the tidal current speed;
- Only the 1st and 3rd harmonic components in back-EMFs are considered;
- Harmonic disturbances are discussed under a single-phase open case;
- The permanent magnets are surface mounted on the rotor of the five-phase PMSG used in the simulation setup and the laboratory prototype;
- Magnetic curve is linear;
- Eddy currents, iron losses are negligible;
- Stator phase windings are star-connected and neutral wire is absent.
2.1. Model of Tidal Current Turbine
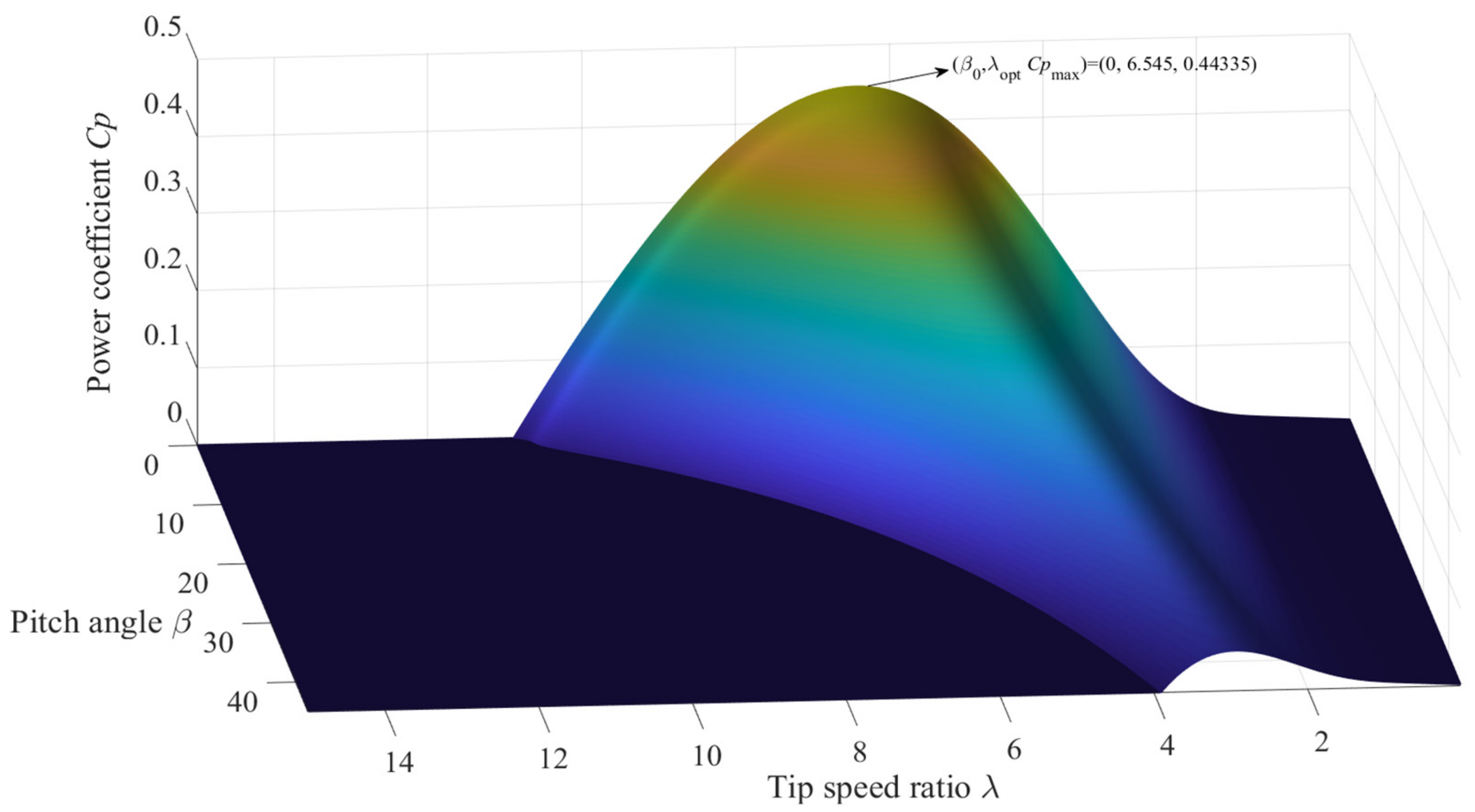
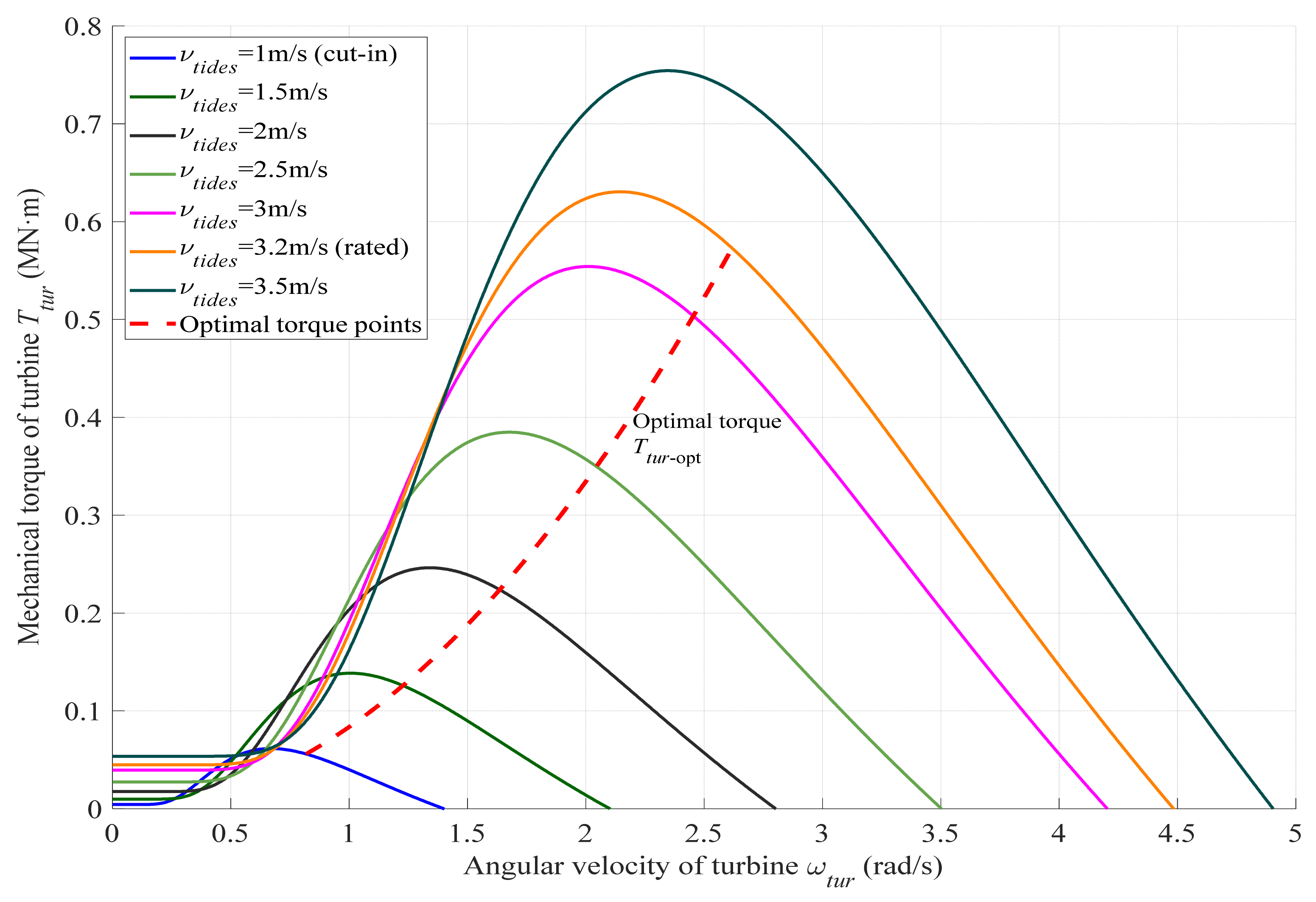
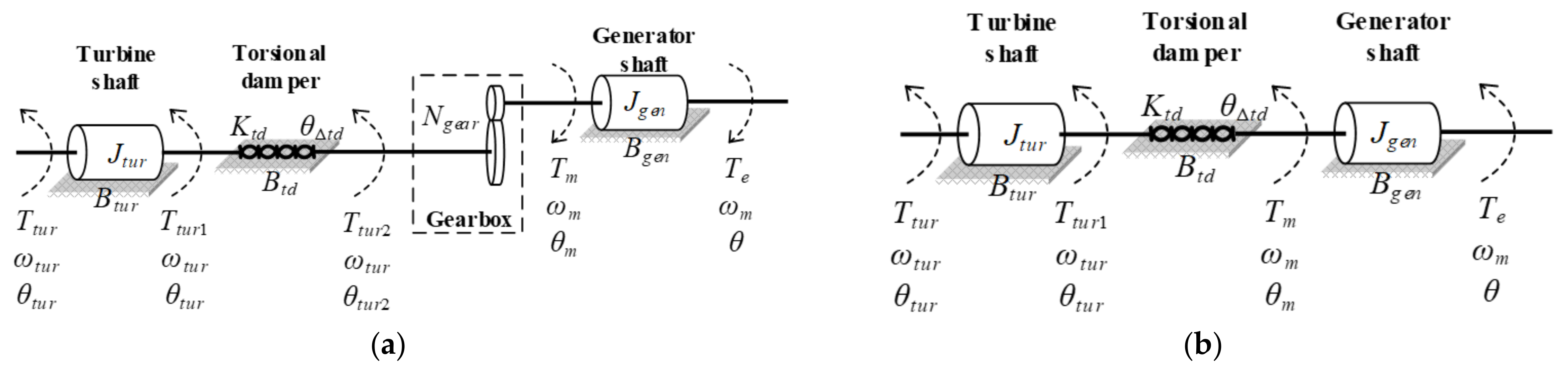
2.2. Mechanical Model of Drive Train
2.3. Modeling of Five-Phase PMSG in Healthy Conditions
2.4. Modelling of Five-Phase PMSG with Single-Phase Open
2.5. Additional Harmonic Disturbances Subject to Single-Phase Open
3. Multiple SOGIs-Based Model-Free FTC Strategy
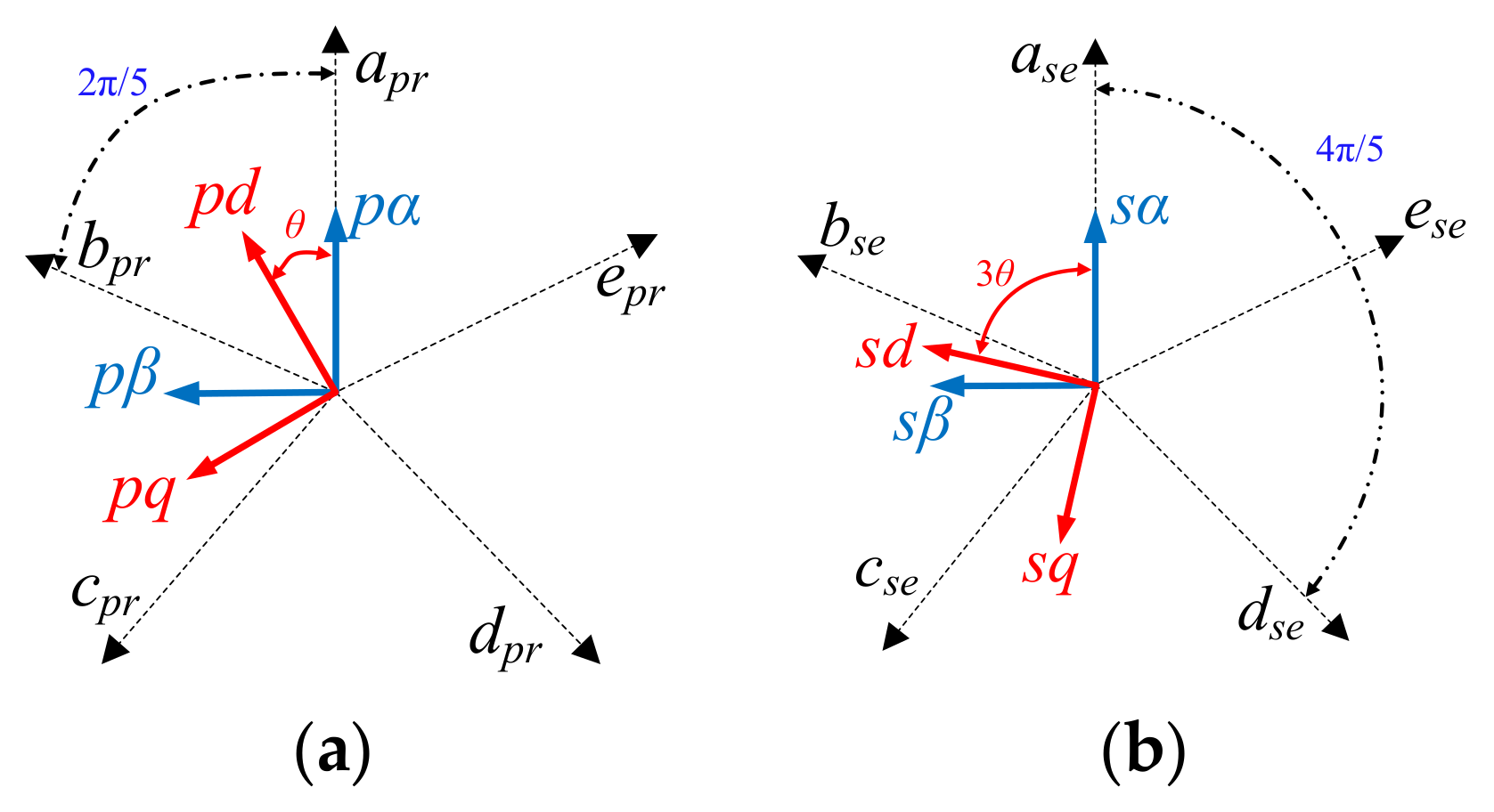
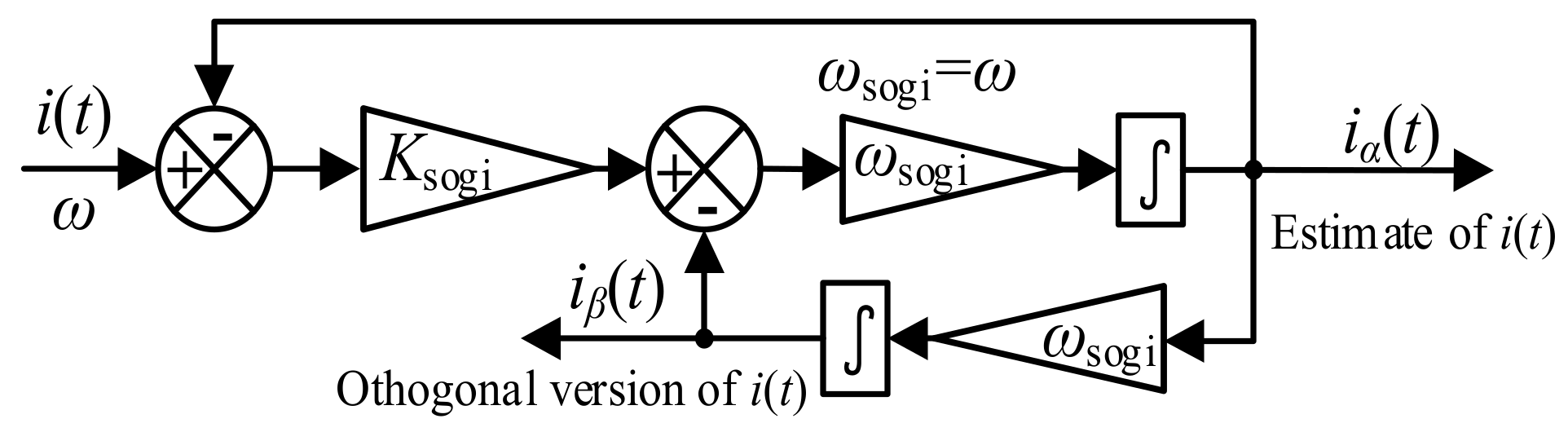
3.1. Single SOGI and Multiple SOGIs
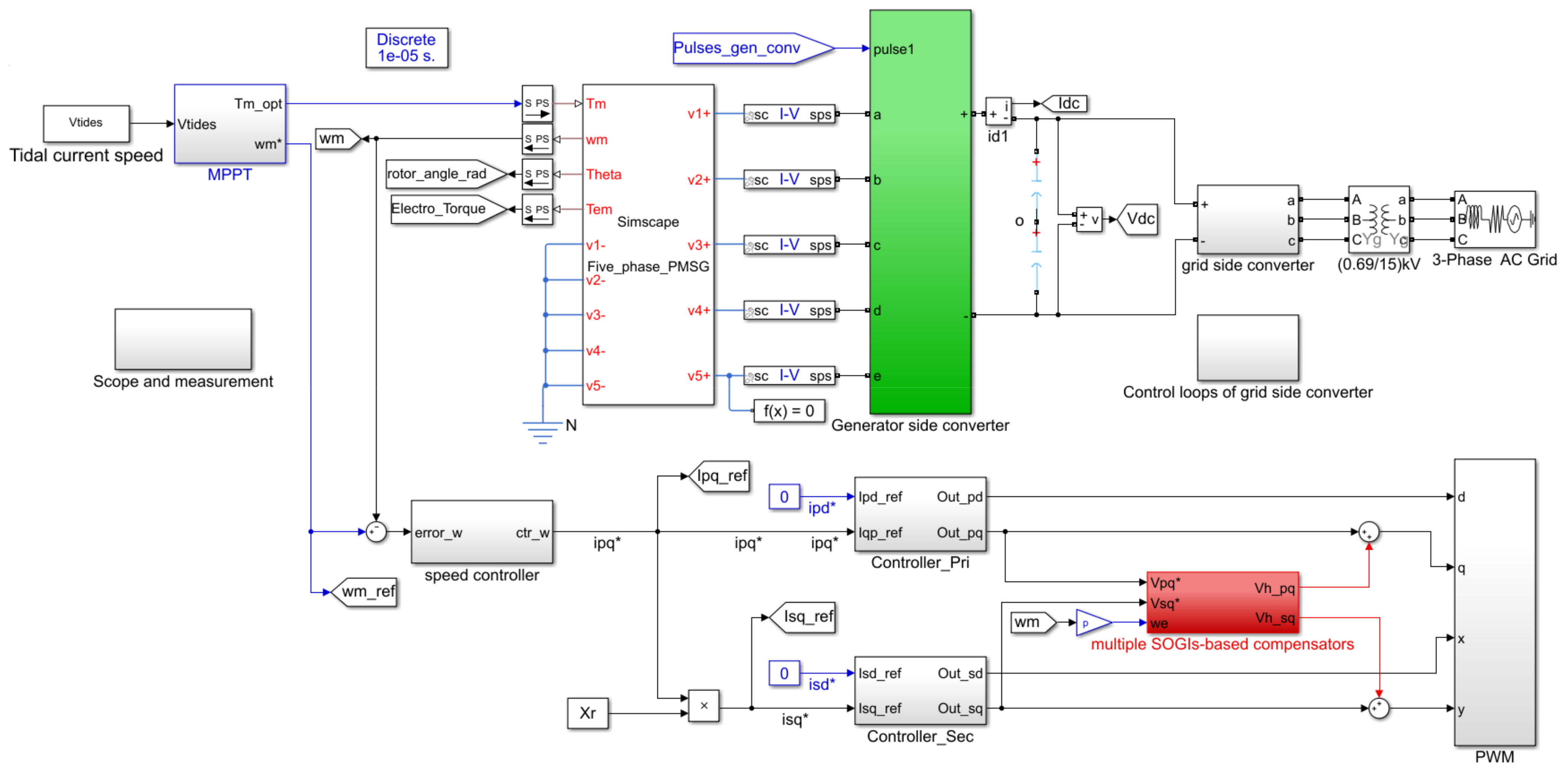
3.2. Multiple SOGIs-Based Model-Free FTC Design for Five-Phase PMSG-Based TCECS
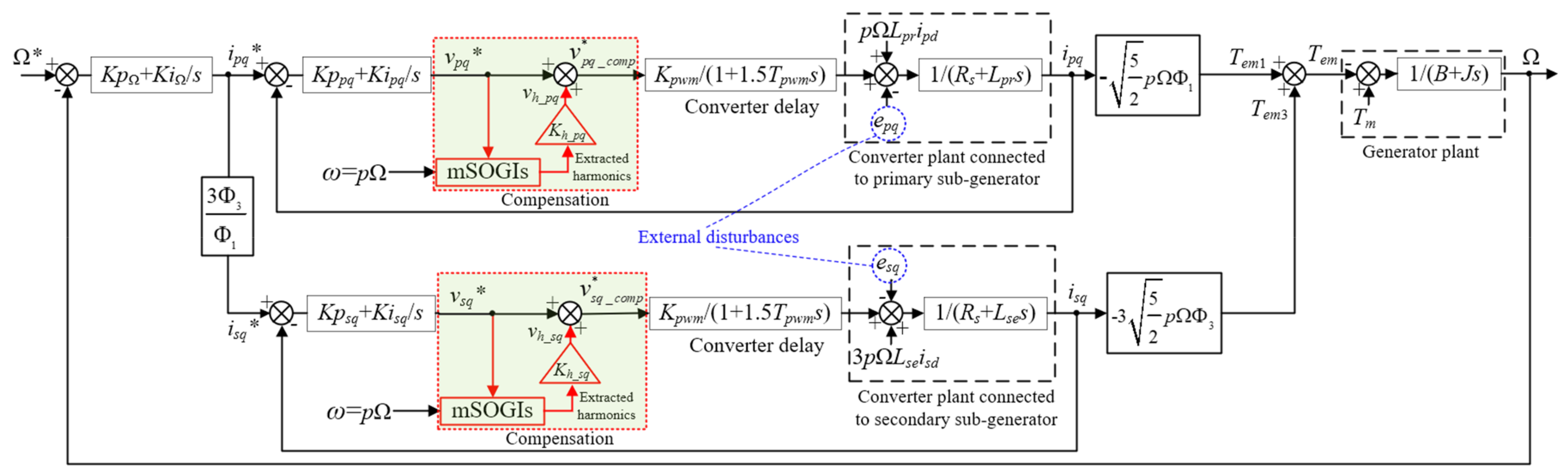
4. Simulation Test by Real Power Scale Tidal Current Turbine Systems
4.1. Comparison of Performance Using Five-Phase and Three-Phase PMSG
4.2. Test of Fault-Tolerant Performance
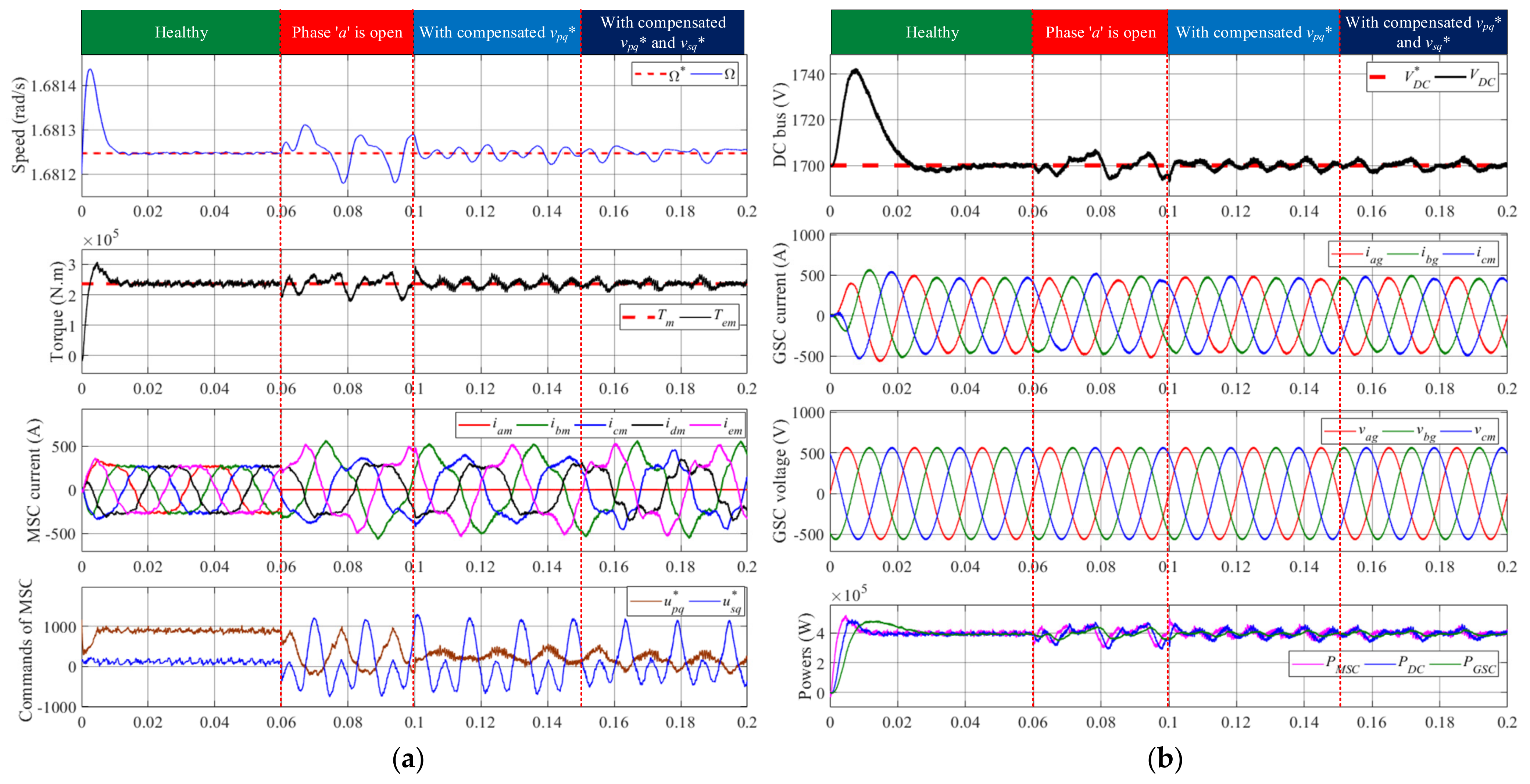
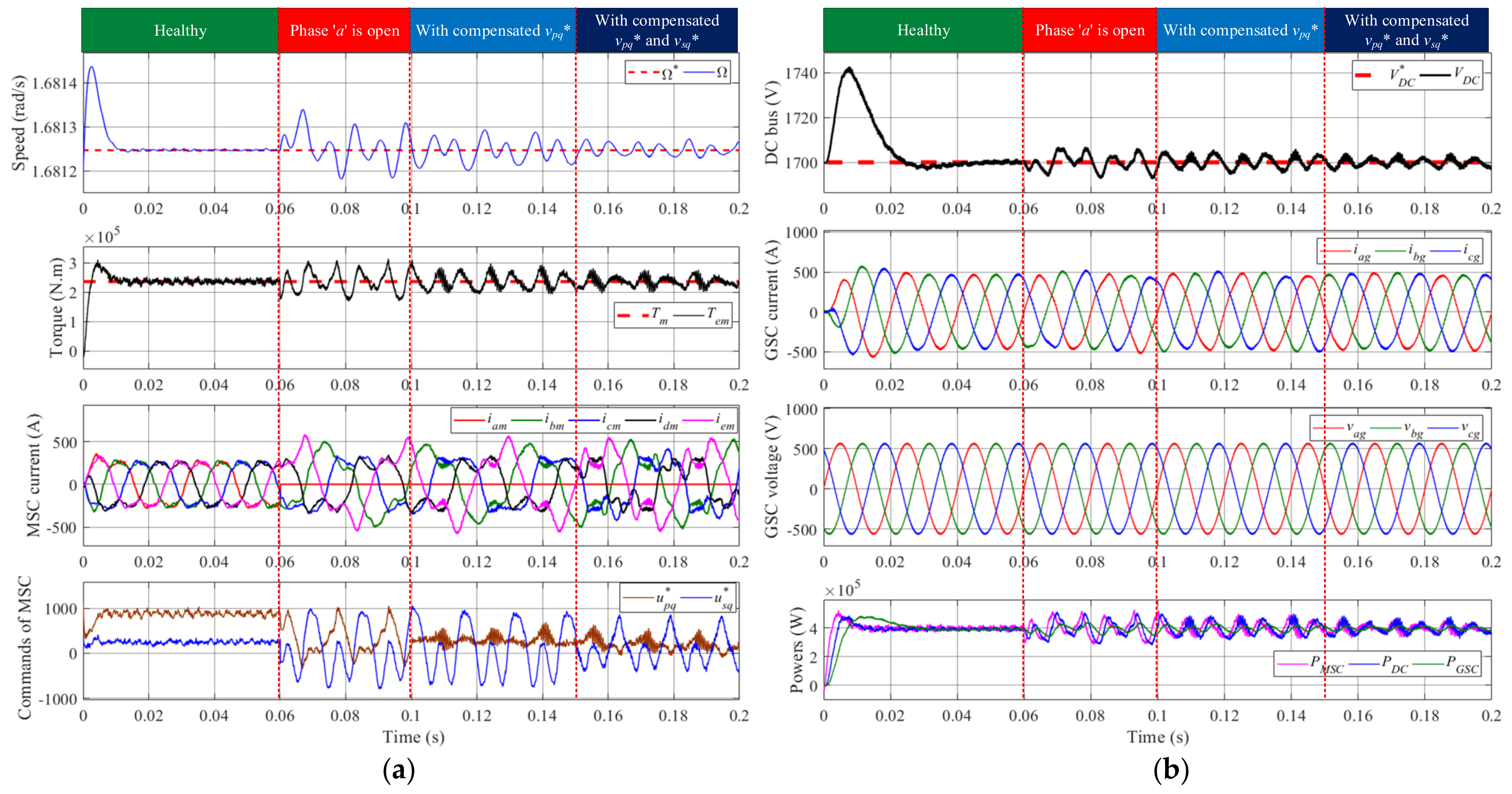
- Under small third harmonic fluxFigure 12a,b present the simulation test results of the machine side, DC bus voltage and grid side when Φ1 is 30 times more than Φ3 under operation at 0.393 MW. The fundamental frequency of the grid side is 50 Hz. With appropriate initializations, the whole system can reach the controlled mode at 0.04 s. At 0.06 s, phase “a” is set as an open circuit. At 0.1 s, the mSOGIs-based compensator for vpq* is activated. The other compensator for vsq* is then introduced after 0.05 s. From the first and second subplots in Figure 12a, it is clear that the speed fluctuations and torque ripples are suppressed via the compensators. The compensator for vsq* is used to constraint the harmonic disturbances in the secondary sub-generator, which is helpful in strengthening the fault tolerance combining with the compensator for the principal sub-generator. In the process of compensations, the perturbated degree of the control commands vpq* and vsq* are also reduced, according to the last subplot in Figure 12a, so as to directly reconfigure the PWM drive signals for the machine-side converter. However, the voltage command vsq* in the last subplot in the Figure 12a is much lower than vpq* in healthy conditions, while the fluctuation of vsq* is greater than vpq* once the single phase is open. Too great compensation for vsq* will worsen the suppression behaviors against the fluctuations, which will result in more perturbations in other control loops under the dual-loop control framework, such as the unconsidered d-axis control loops. That is to say, perturbations can “transfer” into other control loops. Consequently, the compensation gains are finally set as Kh_pq = 1 and Kh_sq = 0.1.In DC bus and grid side, as Figure 12b, the DC voltage, phase current as well as the output power of the grid-side converter (GSC) also perform attenuations of fluctuations under the single-phase open condition as the compensators are put into use. In detail, the power conversion processes create delays in the starting stage through the MSC and GSC. In steady states under healthy conditions, the powers in machine side, DC bus and grid side are almost equal. With compensations in faulty conditions, it is obvious that the fluctuations of power are also constrained. This is beneficial from the adopted fault-tolerant compensators in machine side. As a result, the proposed mSOGIs-based compensators are able to maintain the performance of the whole back-to-back conversion chain.Figure 12. Simulation result of compensation in q-axis current control loops when Φ1/Φ3 = 30: (a) machine-side waveforms; (b) DC bus voltage and grid-side waveforms.Figure 12. Simulation result of compensation in q-axis current control loops when Φ1/Φ3 = 30: (a) machine-side waveforms; (b) DC bus voltage and grid-side waveforms.
- Under significant third harmonic fluxIn Figure 13, the magnet flux Φ1 is nine times of Φ3, which means that the third harmonic component in the back-EMFs is more significant in both healthy and faulty conditions. Fluctuations in machine side and grid side are well compensated, and their performance analysis is consistent with Figure 12. The only difference is that the gain of compensator Kh_sq for vsq* should be increased to adapt to the greater disturbances in the more important secondary sub-generator, and avoid injecting external interferences from the compensators. Thus, the compensation gains Kh_pq and Kh_sq are set as 1 and 0.35 m respectively.It should be noted that the test results in Figure 13, under a significant third harmonic flux, are independent to the MPPT characteristics. The nominal Φ3 related to the characteristics in Figure 3 is equal to 0.082 Wb. That is, Figure 12 shows a working point with νtides = 2.055 m/s in the MPPT characteristics. Figure 13 is performed to test the fault-tolerant control behaviors of the proposed FTC method under a condition of a greater trapezoidal deformation for the back-EMFs by increasing the flux parameter Φ3 in the numerical model and control strategy. The simulation results show that the proposed method can adapt well to the five-phase PMSG with different trapezoidal back-EMFs.
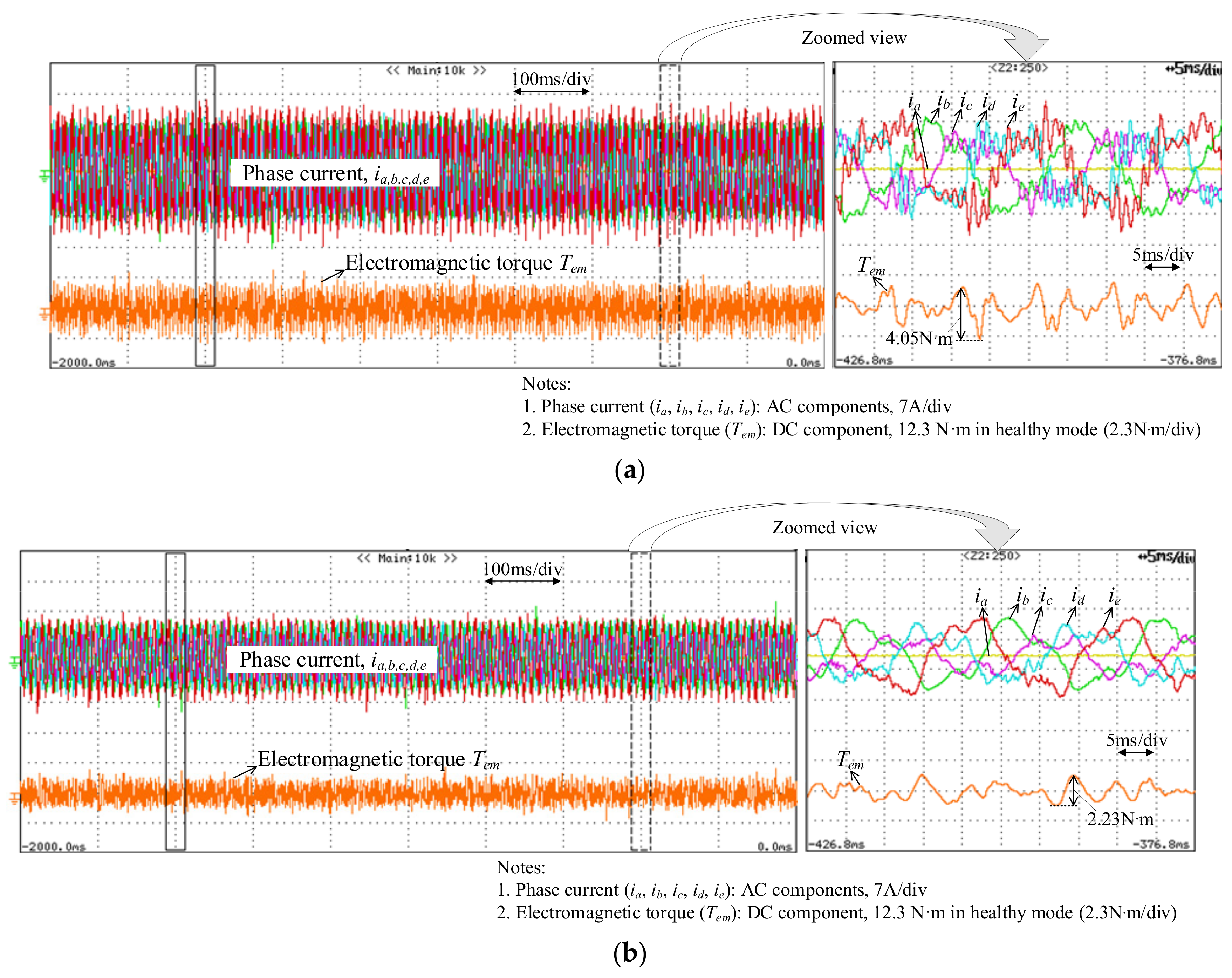
5. Experimental Verifications
5.1. Harmonic Compensation Behaviors in Healthy Conditions
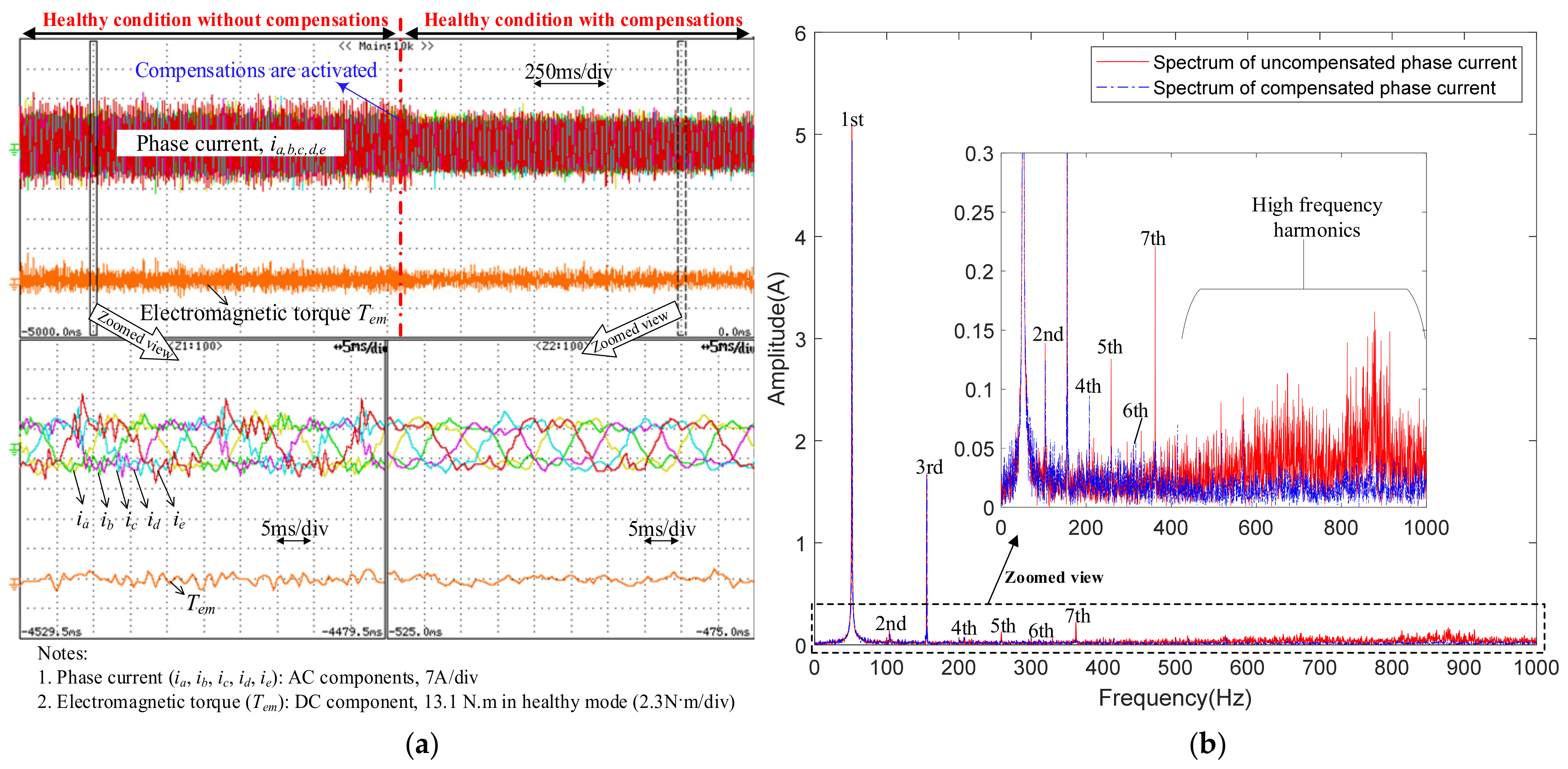
5.2. Fault Tolerance in Single-Phase Open Conditions
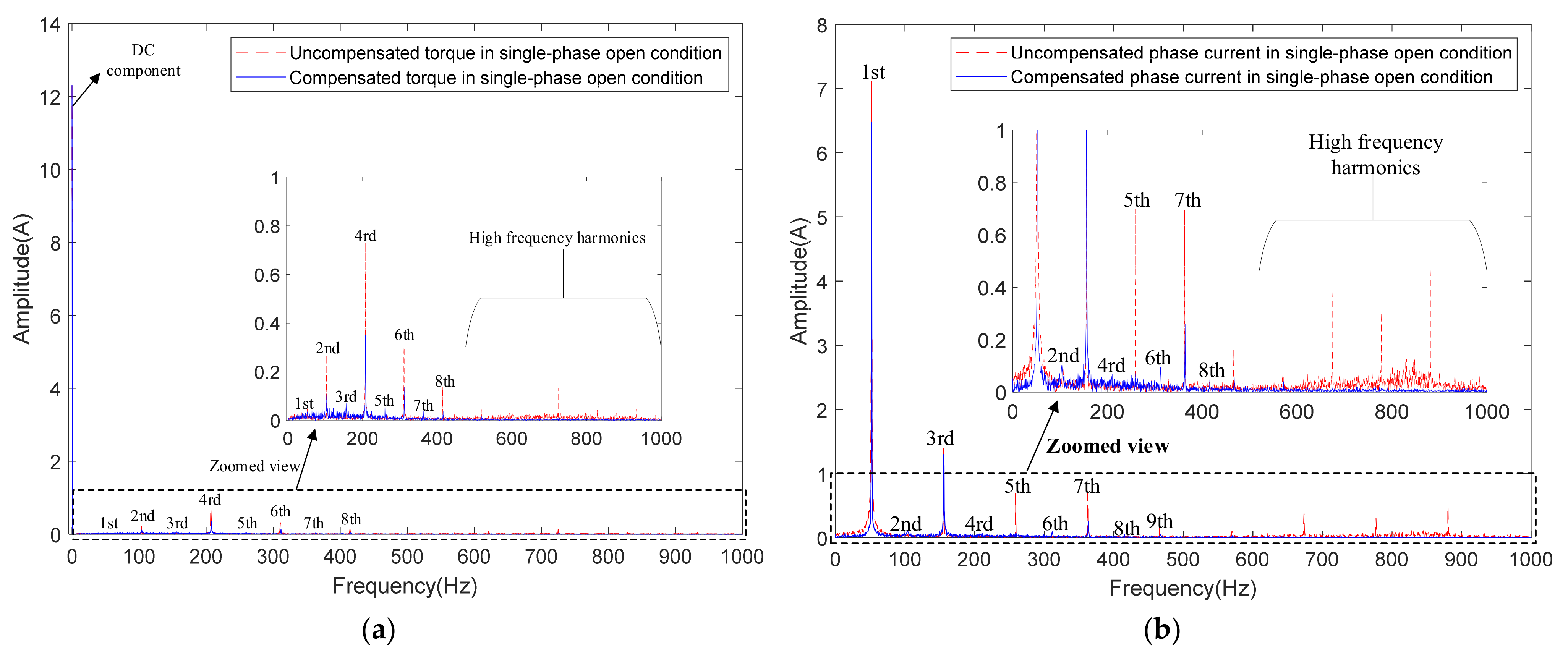
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Description | Value |
|---|---|---|
| Jtur | Inertia of turbine | 1.3131 × 106 kg∙m2 |
| Pm_rated | Generator rated power (at 50 Hz) | 1.5 MW |
| Vdc | DC-bus rated voltage | 1700 V |
| ωm_rated | Rotor-rated angular velocity (at 50 Hz) | 2.618 rad/s |
| npp | Pole pair number | 120 |
| Φ1 | Magnet flux in principle sub-generator | 2.458 Wb |
| Φ3 | Magnet flux in secondary sub-generator | 0.2731 Wb or 0.082 Wb |
| Rs | Generator stator resistance | 0.0081 Ω |
| Lpr | Principle sub-generator inductances | 1.2 mH |
| Lse | Secondary sub-generator inductances | 0.88 mH |
| Cdc | DC-bus capacitor | 13 mF |
| Rf | Grid-side resistance | 0.1 mΩ |
| Lf | Grid-side inductance | 1.5 mH |
| Symbol | Description | Value |
|---|---|---|
| Pnorminal | Nominal power of generator (at 110 Hz) | 3.3 kW |
| BM_dc | Friction coefficient of DC motor’s shaft | 0.091 |
| Bgen | Friction coefficient of generator’s shaft | 0.123 |
| JM_dc | Inertia of DC motor | 0.02 kg·m2 |
| Jgen | Inertia of generator | 0.00137 kg·m2 |
| ωm_norminal | Nominal angular velocity of generator | 230.3835 rad/s |
| p | Number of pole pairs | 3 |
| Φ1, Φ3 | Magnet fluxes | 0.150 Wb, 0.0149 Wb |
| Rs | Stator resistance | 0.540 Ω |
| Load | Resistive load | 242 Ω |
| Lpr, Lse | Equivalent inductance | 5.1 mH, 3.2 mH |
| Tpwm | Switching period | 0.1 ms |
| Kh_pq, Kh_sq | Compensation gains | 0.55 |
Appendix B
References
- Sala, G.; Mengoni, M.; Rizzoli, G.; Degano, M.; Zarri, L.; Tani, A. Impact of star connection layouts on the control of multiphase induction motor drives under open-phase fault. IEEE Trans. Ind. Electron. 2021, 36, 3717–3726. [Google Scholar]
- Huang, W.; Hua, W.; Chen, F.; Hu, M.; Zhu, J. Model predictive torque control with svm for five-phase pmsm under open-circuit fault condition. IEEE Trans. Power Electron. 2020, 35, 5531–5540. [Google Scholar] [CrossRef]
- Cervone, A.; Slunjski, M.; Levi, E.; Brando, G. Optimal third-harmonic current injection for asymmetrical multiphase permanent magnet synchronous machines. IEEE Trans. Ind. Electron. 2021, 68, 2772–2783. [Google Scholar] [CrossRef]
- Xiong, C.; Guan, T.; Zhou, P.; Xu, H. A fault-tolerant foc strategy for five-phase spmsm with minimum torque ripples in the full torque operation range under double-phase open-circuit fault. IEEE Trans. Ind. Electron. 2020, 67, 9059–9072. [Google Scholar] [CrossRef]
- Hang, J.; Wu, H.; Zhang, J.; Ding, S.; Huang, Y.; Hua, W. Cost functionbased open-phase fault diagnosis for pmsm drive system with model predictive current control. IEEE Trans. Power Electron. 2021, 36, 2574–2583. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Wang, F.; Chen, Z. Fault-tolerant consensus control with control allocation in a leader-following multi-agent system. J. Frankl. Inst. J. Frankl. I. 2020, 357, 9614–9632. [Google Scholar] [CrossRef]
- Wang, X. Active fault tolerant control for unmanned underwater vehicle with sensor faults. IEEE Trans. Instrum. Meas. 2020, 69, 9485–9495. [Google Scholar] [CrossRef]
- Jainm, T.; Yamé, J.J.; Sauter, D. Active Fault-Tolerant Control Systems, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–9. [Google Scholar]
- Lan, J.; Patton, R.J. Integrated design of fault-tolerant control for nonlinear systems based on fault estimation and t–s fuzzy modeling. IEEE Trans. Fuzzy Syst. 2017, 25, 1141–1154. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Zhao, W.; Chen, Q.; Xu, G. Third harmonic current injection in fault-tolerant five-phase permanent-magnet motor drive. IEEE Trans. Power Electron. 2018, 33, 6970–6979. [Google Scholar] [CrossRef]
- Tian, B.; Sun, L.; Molinas, M.; An, Q.T. Repetitive control based phase voltage modulation amendment for foc-based five-phase pmsms under single-phase open fault. IEEE Trans. Ind. Electron. 2021, 68, 1949–1960. [Google Scholar] [CrossRef]
- Boem, F.; Gallo, A.J.; Raimondo, D.M.; Parisini, T. Distributed faulttolerant control of large-scale systems: An active fault diagnosis approach. IEEE Control Netw. Syst. 2020, 7, 288–301. [Google Scholar] [CrossRef]
- Zhang, H.; Han, J.; Luo, C.; Wang, Y. Fault-tolerant control of a nonlinear system based on generalized fuzzy hyperbolic model and adaptive disturbance observer. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2289–2300. [Google Scholar] [CrossRef]
- Liu, D.; Yang, Y.; Li, L.; Ding, S.X. Control performance-based faulttolerant control strategy for singular systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 2398–2407. [Google Scholar] [CrossRef]
- Liu, Z.; Houari, A.; Machmoum, M.; Benkhoris, M.F.; Tang, T.H. An Active FTC Strategy Using Generalized Proportional Integral Observers Applied to Five-Phase PMSG based Tidal Current Energy Conversion Systems. Energies 2020, 13, 6645. [Google Scholar] [CrossRef]
- Kiselev, A.; Catuogno, G.R.; Kuznietsov, A.; Leidhold, R. Finitecontrol- set mpc for open-phase fault-tolerant control of pm synchronous motor drives. IEEE Trans. Ind. Electron. 2020, 67, 4444–4452. [Google Scholar] [CrossRef]
- Azizi, A.; Nourisola, H.; Shoja-Majidabad, S. Fault tolerant control of wind turbines with an adaptive output feedback sliding mode controller. Renew. Energy 2019, 135, 55–65. [Google Scholar] [CrossRef]
- Rodríguez, P.; Luna, A.; Candela, I.; Mujal, R.; Teodorescu, R.; Blaabjerg, F. Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions. IEEE Trans. Ind. Electron. 2011, 58, 127–138. [Google Scholar] [CrossRef]
- Torres, L.; Jiménez-Cabas, J.; González, O.; Molina, L.; López-Estrada, F.-R. Kalman Filters for Leak Diagnosis in Pipelines: Brief History and Future Research. J. Mar. Sci. Eng. 2020, 8, 173. [Google Scholar] [CrossRef]
- Tian, G.; Zhou, Q.; Birari, R.; Qi, J.; Qu, Z. A hybrid-learning algorithm for online dynamic state estimation in multimachine power systems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5497–5508. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Jiang, Y.; Yin, S. Fault-tolerant control of time-delay markov jump systems with itô stochastic process and output disturbance based on sliding mode observer. IEEE Trans. Ind. Informat. 2018, 14, 5299–5307. [Google Scholar] [CrossRef]
- Liu, W.; Li, P. Disturbance observer-based fault-tolerant adaptive control for nonlinearly parameterized systems. IEEE Trans. Ind. Electron. 2019, 66, 8681–8691. [Google Scholar] [CrossRef]
- Yao, X.; Wu, L.; Guo, L. Disturbance-observer-based fault tolerant control of high-speed trains: A markovian jump system model approach. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1476–1485. [Google Scholar] [CrossRef]
- Gou, B.; Ge, X.L.; Pu, J.K.; Feng, X.Y. A fault diagnosis and fault tolerant control method for DC-link circuit using notch filter in power traction converter. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3230–3235. [Google Scholar]
- Hu, P.F.; He, Z.X.; Li, S.Q.; Guerrero, J.M. Non-ideal proportional resonant control for modular multilevel converters under sub-module fault conditions. IEEE Trans. Energy Convers. 2019, 34, 1741–1750. [Google Scholar] [CrossRef]
- Lewis, M.; O’Hara Murray, R.; Fredriksson, S.; Maskell, J.; Fockert, A.D.; Neill, S.P.; Robins, P.E. A standardised tidal-stream power curve, optimised for the global resource. Renew. Energy 2021, 170, 1308–1323. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T.; Krismer, F.; Looser, A.; Schweizer, M.; Friedemann, R.A.; Steimer, P.K.; Bevirt, J.B. Conceptualization and multiobjective optimization of the electric system of an airborne wind turbine. IEEE Trans. Emerg. Sel. Top. Power Electron. 2013, 1, 73–103. [Google Scholar] [CrossRef]
- Liu, Z.; Houari, A.; Machmoum, M.; Benkhoris, M.F.; Tang, T. A second order filter-based fault detection method for five-phase permanent magnet synchronous generators. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 4827–4832. [Google Scholar]
- Kestelyn, X.; Semail, E. A vectorial approach for generation of optimal current references for multiphase permanent-magnet synchronous machines in real time. IEEE Trans. Ind. Electron. 2011, 58, 5057–5065. [Google Scholar] [CrossRef]
- Hwang, J.; Wei, H. The current harmonics elimination control strategy for six-leg three-phase permanent magnet synchronous motor drives. IEEE Trans. Power Electron. 2014, 29, 3032–3040. [Google Scholar] [CrossRef]
- Xiao, F.; Dong, L.; Li, L.; Liao, X. A frequency-fixed sogi-based pll for single-phase grid-connected converters. IEEE Trans. Power Electron. 2017, 32, 1713–1719. [Google Scholar] [CrossRef]
- Pham, H.; Bourgeot, J.; Benbouzid, M. Fault-tolerant finite control set-model predictive control for marine current turbine applications. IET Renew. Power Gener. 2018, 12, 415–421. [Google Scholar] [CrossRef]
- Mekri, F.; Elghali, S.B.; Benbouzid, M.E.H. Fault-Tolerant Control Performance Comparison of Three- and Five-Phase PMSG for Marine Current Turbine Applications. IEEE Trans. Sustain. Energy 2013, 4, 425–433. [Google Scholar] [CrossRef]
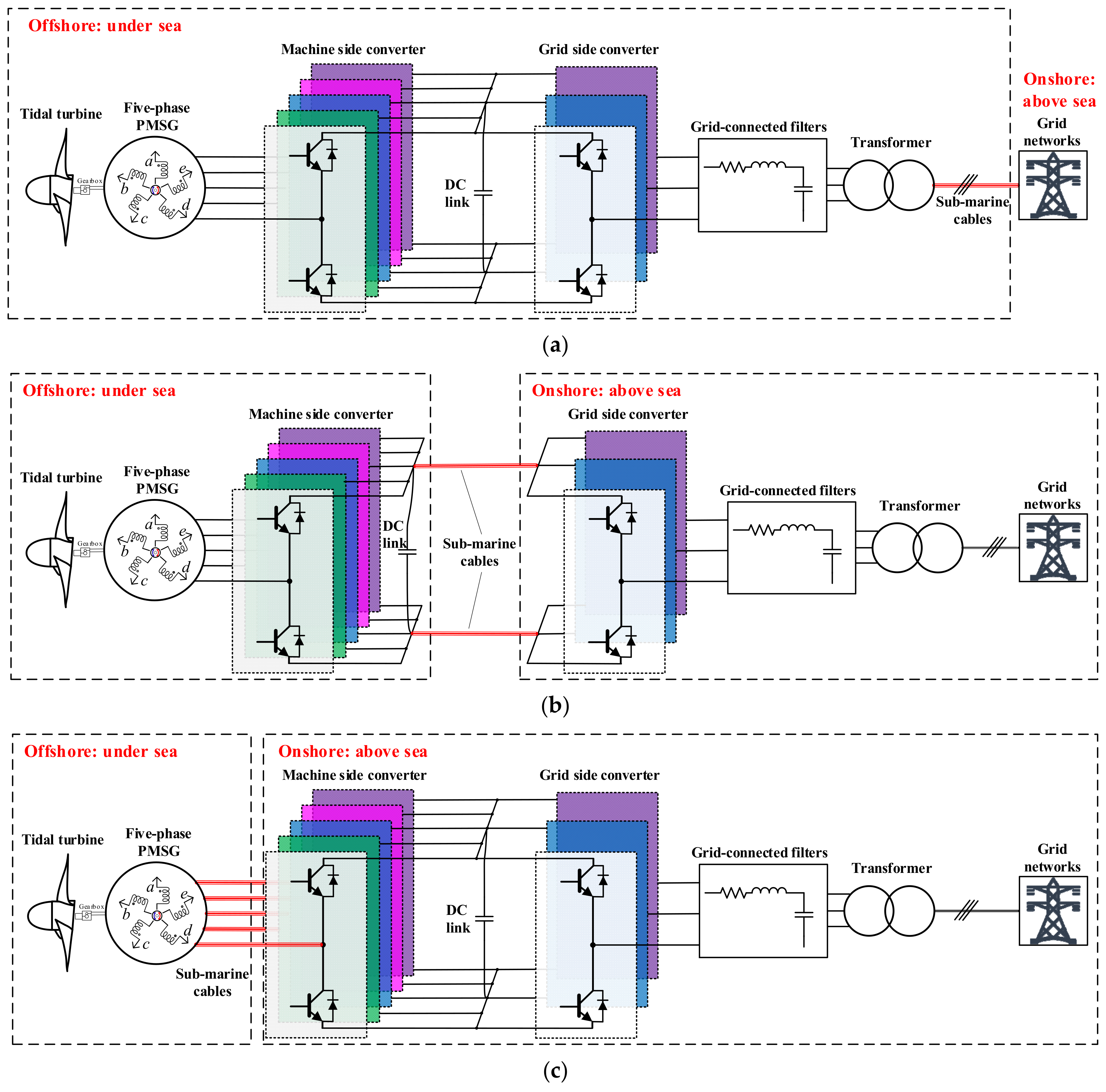




| Symbol | Value | Symbol | Value |
|---|---|---|---|
| C1 | 0.6406 | C4 | 10.778 |
| C2 | 116.664 | C5 | 16 |
| C3 | 0.4 | C6 | 0.0053 |
| Conditions | Healthy | Single-Phase Open (e.g., Phase “a” Is Open) | |
|---|---|---|---|
| Frames | |||
| Original Frame | phase ‘a’ | Mainly contains 1st and 3rd harmonics (Others are regarded as disturbances) | Almost equal to 0 |
| phase ‘b’ | Mainly contains 1st, 3rd, 5th and 7th harmonics | ||
| phase ‘c’ | |||
| phase ‘d’ | |||
| phase ‘e’ | |||
| Park’s Frame | pd axis | Almost equal to 0 | Mainly contains 2nd, 4th, 6th, 8th harmonics |
| pq axis | Almost an offset DC component | ||
| sd axis | Almost equal to 0 | Mainly contains 2nd, 4th, 6th, 8th and 10th harmonics | |
| sq axis | Almost an offset DC component | ||
| Homopolar | Almost equal to 0 | Mainly contains 1st, 3rd, 5th and 7th harmonics |
| Indicators | Copper Losses (W) | Torque Ripples (%) | THD (%) | |
|---|---|---|---|---|
| Working Conditions | ||||
| Healthy | No compensations | 46.65 (3.40% loss) | 28.41 | 43.23 |
| By compensations | 40.41 (2.99% loss) | 23.68 | 32.84 | |
| Single-Phase Open | No compensations | 69.93 (5.32% loss) | 42.96 | 67.28 |
| By compensations | 34.24 (2.56% loss) | 29.54 | 41.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Tang, T.; Houari, A.; Machmoum, M.; Benkhoris, M.F. An FTC Design via Multiple SOGIs with Suppression of Harmonic Disturbances for Five-Phase PMSG-Based Tidal Current Applications. J. Mar. Sci. Eng. 2021, 9, 574. https://doi.org/10.3390/jmse9060574
Liu Z, Tang T, Houari A, Machmoum M, Benkhoris MF. An FTC Design via Multiple SOGIs with Suppression of Harmonic Disturbances for Five-Phase PMSG-Based Tidal Current Applications. Journal of Marine Science and Engineering. 2021; 9(6):574. https://doi.org/10.3390/jmse9060574
Chicago/Turabian StyleLiu, Zhuo, Tianhao Tang, Azeddine Houari, Mohamed Machmoum, and Mohamed Fouad Benkhoris. 2021. "An FTC Design via Multiple SOGIs with Suppression of Harmonic Disturbances for Five-Phase PMSG-Based Tidal Current Applications" Journal of Marine Science and Engineering 9, no. 6: 574. https://doi.org/10.3390/jmse9060574
APA StyleLiu, Z., Tang, T., Houari, A., Machmoum, M., & Benkhoris, M. F. (2021). An FTC Design via Multiple SOGIs with Suppression of Harmonic Disturbances for Five-Phase PMSG-Based Tidal Current Applications. Journal of Marine Science and Engineering, 9(6), 574. https://doi.org/10.3390/jmse9060574