Review of Recent Offshore Wind Turbine Research and Optimization Methodologies in Their Design
Abstract
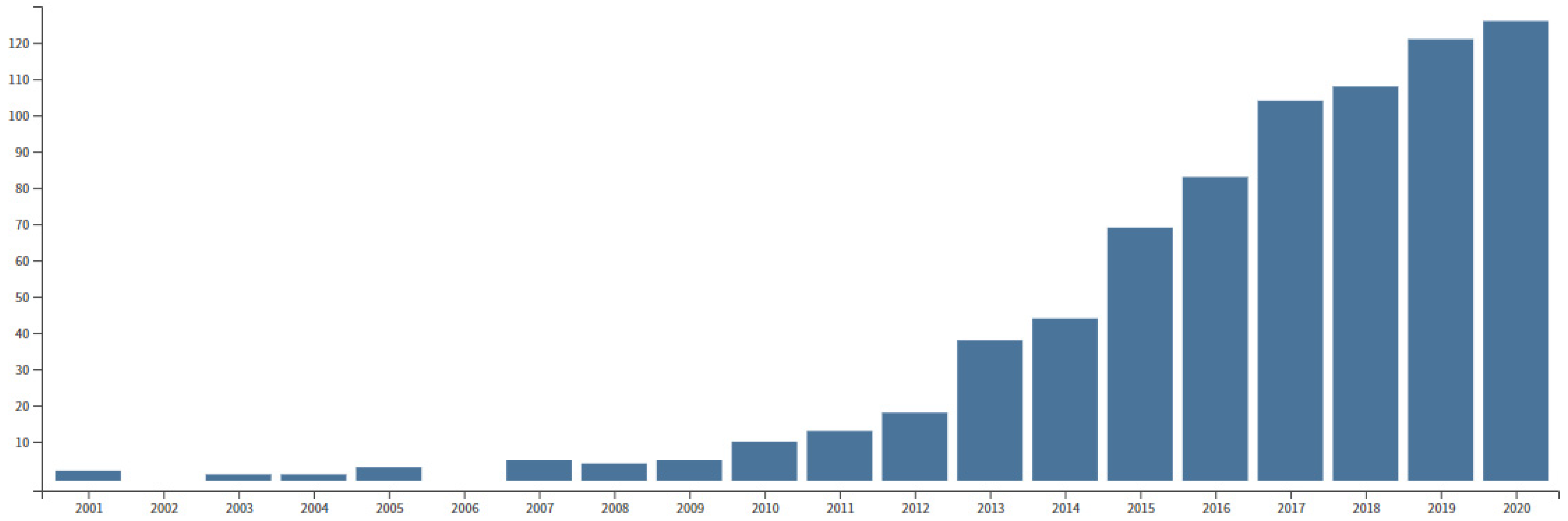
1. Introduction
2. Type of Offshore Wind Turbine
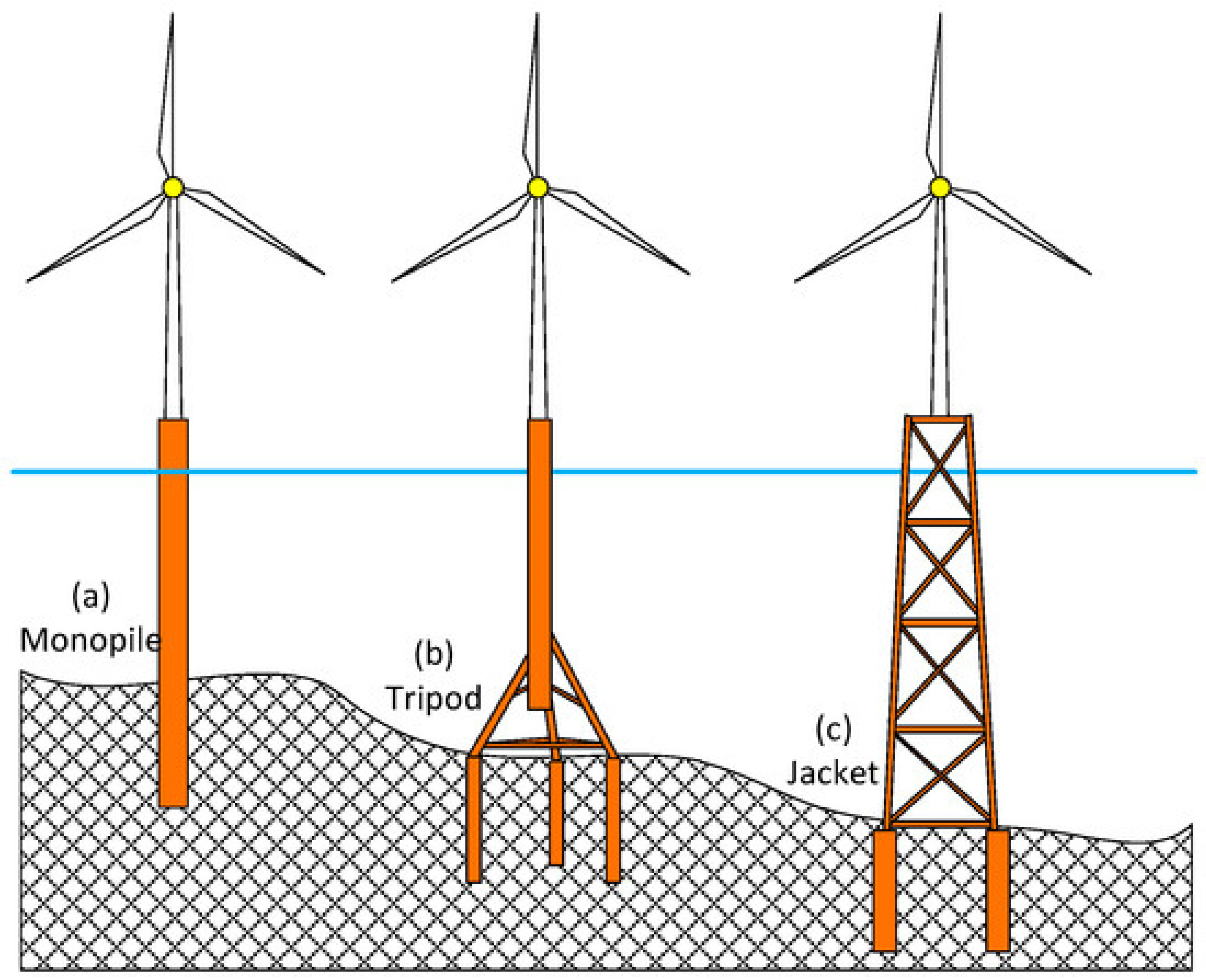
2.1. Fixed Substructure
2.1.1. Monopile Substructure
2.1.2. Tripod Substructure
2.1.3. Jacket Substructure
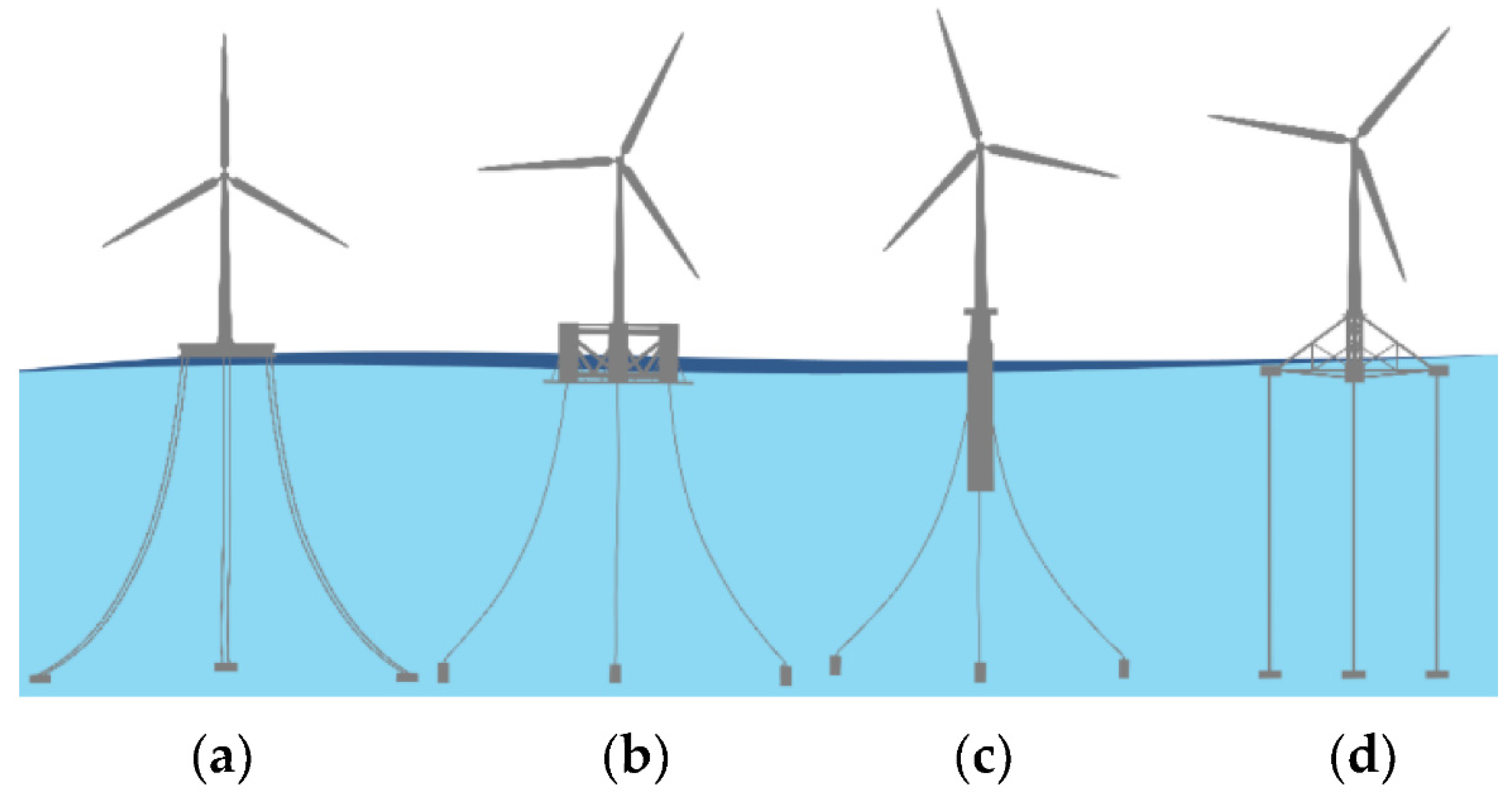
2.2. Floating Substructure
- Spar–buoy
- Semisubmersible
- Tension leg platform (TLP)
- Barge
2.2.1. Spar–Buoy Substructure
2.2.2. Semisubmersible Substructure
2.2.3. Tension Leg Platform (TLP) Substructure
2.2.4. Barge Substructure
3. Design and Optimization Approaches for Offshore Wind Turbine
3.1. Optimization Based on Static Analysis
3.2. Optimization Based on Frequency-Domain Analysis
3.3. Optimization Based on Time-Domain Analysis
4. Optimization Algorithms Used in Recent Offshore Wind Turbine Design Studies
4.1. Sequential Quadratic Programming
4.2. Genetic Algorithm
4.3. Particle Swarm Algorithm
4.4. Other Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Global Wind Energy Council. GWEC|Global Wind Report 2021; Global Wind Energy Council: Southwick, UK, 2021. [Google Scholar]
- Hansen, B. Floating Wind Turbines Expand Renewable Energy Possibilities. Civ. Eng. Mag. Arch. 2006, 76, 30. [Google Scholar] [CrossRef]
- Henderson, A.R.; Witcher, D.; Morgan, C.A. Floating Support Structures Enabling New Markets for Offshore Wind Energy. In Proceedings of the European Wind Energy Conference (EWEC), Marseille, France, 16–19 March 2009; Volume 1619. [Google Scholar]
- Wang, C.; Utsunomiya, T.; Wee, S.; Choo, Y. Research on Floating Wind Turbines: A Literature Survey. IES J. Part A Civ. Struct. Eng. 2010, 3, 267–277. [Google Scholar] [CrossRef]
- Heronemus, W. The US Energy Crisis: Some Proposed Gentle Solutions. Congr. Rec. 1972, 118, 17. [Google Scholar]
- Uzunoglu, E.; Karmakar, D.; Soares, C.G. Floating Offshore Wind Platforms. In Floating Offshore Wind Farms; Springer: Cham, Switzerland, 2016; pp. 53–76. [Google Scholar]
- Oguz, E.; Clelland, D.; Day, A.H.; Incecik, A.; López, J.A.; Sánchez, G.; Almeria, G.G. Experimental and Numerical Analysis of a TLP Floating Offshore Wind Turbine. Ocean Eng. 2018, 147, 591–605. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, X.; Li, J.; Yang, X.; Wang, H. A Review on Recent Advancements of Substructures for Offshore Wind Turbines. Energy Convers. Manag. 2018, 158, 103–119. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, X.; Yang, X.; Li, J. Feasibility Study of Offshore Wind Turbines with Hybrid Monopile Foundation Based on Centrifuge Modeling. Appl. Energy 2018, 209, 127–139. [Google Scholar] [CrossRef]
- Kaiser, M.J.; Snyder, B. Offshore Wind Energy Installation and Decommissioning Cost Estimation in the Us Outer Continental Shelf. US Dept. Inter. Bur. Ocean Energy Manag. Regul. Enforc. Herndon VA TAR 2010, 648, 18–23. [Google Scholar]
- Zhixin, W.; Chuanwen, J.; Qian, A.; Chengmin, W. The Key Technology of Offshore Wind Farm and Its New Development in China. Renew. Sustain. Energy Rev. 2009, 13, 216–222. [Google Scholar] [CrossRef]
- Fischer, T. Executive Summary–UpWind Project. WP4: Offshore Foundations and Support Structures. Available online: http://www.upwind.eu/pdf/WP4_Executive_Summary_Final.pdf (accessed on 12 December 2011).
- Junginger, M.; Agterbosch, S.; Faaij, A.; Turkenburg, W. Renewable Electricity in the Netherlands. Energy Policy 2004, 32, 1053–1073. [Google Scholar] [CrossRef]
- Saleem, Z. Alternatives and Modifications of Monopile Foundation or Its Installation Technique for Noise Mitigation; TU Delft Report; TU Delft University: Delft, The Netherlands, 2011. [Google Scholar]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A Review of Combined Wave and Offshore Wind Energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, Y.; Lu, Q.; Zhang, J. Dynamic Reliability Based Design Optimization of the Tripod Sub-Structure of Offshore Wind Turbines. Renew. Energy 2015, 78, 16–25. [Google Scholar] [CrossRef]
- Byrne, B.; Houlsby, G. Foundations for Offshore Wind Turbines. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 2909–2930. [Google Scholar] [CrossRef]
- Koh, J.; Ng, E. Downwind Offshore Wind Turbines: Opportunities, Trends and Technical Challenges. Renew. Sustain. Energy Rev. 2016, 54, 797–808. [Google Scholar] [CrossRef]
- Lozano-Minguez, E.; Kolios, A.J.; Brennan, F.P. Multi-Criteria Assessment of Offshore Wind Turbine Support Structures. Renew. Energy 2011, 36, 2831–2837. [Google Scholar] [CrossRef]
- Arshad, M.; O’Kelly, B.C. Offshore Wind-Turbine Structures: A Review. Proc. Inst. Civ. Eng. Energy 2013, 166, 139–152. [Google Scholar] [CrossRef]
- Seidel, M. Jacket Substructures for the REpower 5M Wind Turbine. In Proceedings of the Conference Proceedings European Offshore Wind, Berlin, Germany, 4–6 December 2007; pp. 1–8. [Google Scholar]
- Plodpradit, P.; Dinh, V.N.; Kim, K.-D. Tripod-Supported Offshore Wind Turbines: Modal and Coupled Analysis and a Parametric Study Using X-SEA and FAST. J. Mar. Sci. Eng. 2019, 7, 181. [Google Scholar] [CrossRef]
- Ha, K.; Kim, J.-B.; Yu, Y.; Seo, H.-S. Structural Modeling and Failure Assessment of Spar-Type Substructure for 5 MW Floating Offshore Wind Turbine under Extreme Conditions in the East Sea. Energies 2021, 14, 6571. [Google Scholar] [CrossRef]
- Roddier, D.; Cermelli, C.; Weinstein, A. WindFloat: A Floating Foundation for Offshore Wind Turbines—Part I: Design Basis and Qualification Process. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; Volume 43444, pp. 845–853. [Google Scholar]
- Jonkman, J.; Musial, W. Offshore Code Comparison Collaboration (OC3) for IEA Wind Task 23 Offshore Wind Technology and Deployment; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [Google Scholar]
- Shin, H. Others Model Test of the OC3-Hywind Floating Offshore Wind Turbine. In Proceedings of the The Twenty-First International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2011. [Google Scholar]
- Kopperstad, K.M.; Kumar, R.; Shoele, K. Aerodynamic Characterization of Barge and Spar Type Floating Offshore Wind Turbines at Different Sea States. Wind Energy 2020, 23, 2087–2112. [Google Scholar] [CrossRef]
- Meng, L.; He, Y.; Zhao, Y.; Yang, J.; Yang, H.; Han, Z.; Yu, L.; Mao, W.; Du, W. Dynamic Response of 6MW Spar Type Floating Offshore Wind Turbine by Experiment and Numerical Analyses. China Ocean Eng. 2020, 34, 608–620. [Google Scholar] [CrossRef]
- Chaviaropoulos, P.; Hansen, M.O. Investigating Three-Dimensional and Rotational Effects on Wind Turbine Blades by Means of a Quasi-3D Navier-Stokes Solver. J. Fluids Eng. 2000, 122, 330–336. [Google Scholar] [CrossRef]
- Suzuki, A.; Hansen, A. Generalized Dynamic Wake Model for YawDyn. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999; p. 41. [Google Scholar]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a Fully Coupled CFD Analysis Tool for Floating Offshore Wind Turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
- Jonkman, J.; Jonkman, B.; NWTC Information Portal (FAST V8). Last Modified 23-September-2015. 2016. Available online: https://nwtc.nrel.gov/FAST8 (accessed on 12 December 2011).
- Li, L.; Cheng, Z.; Yuan, Z.; Gao, Y. Short-Term Extreme Response and Fatigue Damage of an Integrated Offshore Renewable Energy System. Renew. Energy 2018, 126, 617–629. [Google Scholar] [CrossRef]
- Browning, J.; Jonkman, J.; Robertson, A.; Goupee, A. Calibration and Validation of a Spar-Type Floating Offshore Wind Turbine Model Using the FAST Dynamic Simulation Tool. J. Phys. Conf. Ser. 2014, 555, 012015. [Google Scholar] [CrossRef]
- Ruzzo, C.; Fiamma, V.; Collu, M.; Failla, G.; Nava, V.; Arena, F. On Intermediate-Scale Open-Sea Experiments on Floating Offshore Structures: Feasibility and Application on a Spar Support for Offshore Wind Turbines. Mar. Struct. 2018, 61, 220–237. [Google Scholar] [CrossRef]
- Duan, F.; Hu, Z.; Niedzwecki, J. Model Test Investigation of a Spar Floating Wind Turbine. Mar. Struct. 2016, 49, 76–96. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; Avossa, A.M.; Riefolo, L.; Ricciardelli, F.; Musci, E.; D’Alessandro, F.; Vicinanza, D. Dynamic Modelling of a Spar Buoy Wind Turbine. In Proceedings of the ASME 2017 36th international conference on ocean, offshore and arctic engineering, Trondheim, Norway, 25–30 June 2017; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2017. [Google Scholar]
- Bae, Y.; Kim, M.; Im, S.; Chang, I. Aero-Elastic-Control-Floater-Mooring Coupled Dynamic Analysis of Floating Offshore Wind Turbines. In Proceedings of the The Twenty-First International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in Semi-Submersible Floating Foundations Supporting Wind Turbines: A Comprehensive Review. Renew. Sustain. Energy Rev. 2016, 60, 433–449. [Google Scholar] [CrossRef]
- Van Hees, B. Study to Feasibility of and Boundary Conditions for Floating Offshore Wind Turbines (Drijfwind); TNO-Bouw: Delft, The Netherlands, 2002. [Google Scholar]
- Collu, M.; Borg, M.; Shires, A.; Brennan, F.P. FloVAWT: Progress on the Development of a Coupled Model of Dynamics for Floating Offshore Vertical Axis Wind Turbines. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2013. [Google Scholar]
- Lefebvre, S.; Collu, M. Preliminary Design of a Floating Support Structure for a 5 MW Offshore Wind Turbine. Ocean Eng. 2012, 40, 15–26. [Google Scholar] [CrossRef]
- Bossler, A. Floating Offshore Wind Foundations: Industry Consortia and Projects in the United States, Europe and Japan. Maine Int. Consult. LLC 2013, 1, 1–45. [Google Scholar]
- Karimirad, M. Floating Offshore Wind Turbines. In Offshore Energy Structures; Springer: Berlin/Heidelberg, Germany, 2014; pp. 53–76. [Google Scholar]
- Karimirad, M.; Moan, T. Extreme Dynamic Structural Response Analysis of Catenary Moored Spar Wind Turbine in Harsh Environmental Conditions. J. Offshore Mech. Arct. Eng. 2011, 133, 041103. [Google Scholar] [CrossRef]
- Homma, R.; Inoue, T.; Okawa, T.; Kayamori, Y.; Shishibori, A.; Nishimura, S. Steel Plates and Fatigue Solution for Offshore Wind Turbines in the Fukushima Floating Offshore Wind Farm Demonstration Project. Nippon. Steel Sumitomo Met. Tech. 2015, 110, 50–57. [Google Scholar]
- Huijs, F.; de Bruijn, R.; Savenije, F. Concept Design Verification of a Semi-Submersible Floating Wind Turbine Using Coupled Simulations. Energy Procedia 2014, 53, 2–12. [Google Scholar] [CrossRef]
- Bae, Y.; Kim, M.; Kim, H. Performance Changes of a Floating Offshore Wind Turbine with Broken Mooring Line. Renew. Energy 2017, 101, 364–375. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M.; Lee, J.; Kim, E.; Zhang, Z. Global Performance Analysis of 5MW WindFloat and OC4 Semi-Submersible Floating Offshore Wind Turbines (FOWT) by Numerical Simulations. In Proceedings of the the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Bae, Y.; Kim, M. Coupled Dynamic Analysis of Multiple Wind Turbines on a Large Single Floater. Ocean Eng. 2014, 92, 175–187. [Google Scholar] [CrossRef]
- Kim, H.-C.; Kim, K.-H.; Kim, M.-H.; Hong, K. Global Performance of a KRISO Semisubmersible Multiunit Floating Offshore Wind Turbine: Numerical Simulation vs. Model Test. Int. J. Offshore Polar Eng. 2017, 27, 70–81. [Google Scholar] [CrossRef]
- Jang, H.-K.; Park, S.; Kim, M.-H.; Kim, K.-H.; Hong, K. Effects of Heave Plates on the Global Performance of a Multi-Unit Floating Offshore Wind Turbine. Renew. Energy 2019, 134, 526–537. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, J.; He, Y. Preliminary Design of a Multi-Column TLP Foundation for a 5-MW Offshore Wind Turbine. Energies 2012, 5, 3874–3891. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Moan, T. Design Considerations for Tension Leg Platform Wind Turbines. Mar. Struct. 2012, 29, 89–114. [Google Scholar] [CrossRef]
- Nihei, Y.; Fujioka, H. Motion Characteristics of TLP Type Offshore Wind Turbine in Waves and Wind. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 49118, pp. 283–292. [Google Scholar]
- Bae, Y.H.; Kim, M.; Shin, Y.S. Rotor-Floater-Mooring Coupled Dynamic Analysis of Mini TLP-Type Offshore Floating Wind Turbines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 49118, pp. 491–498. [Google Scholar]
- Olondriz, J.; Elorza, I.; Jugo, J.; Alonso-Quesada, S.; Pujana-Arrese, A. An Advanced Control Technique for Floating Offshore Wind Turbines Based on More Compact Barge Platforms. Energies 2018, 11, 1187. [Google Scholar] [CrossRef]
- James, R.; Ros, M.C. Floating Offshore Wind: Market and Technology Review. Carbon Trust 2015, 439, 1–168. [Google Scholar]
- Uys, P.; Farkas, J.; Jarmai, K.; Van Tonder, F. Optimisation of a Steel Tower for a Wind Turbine Structure. Eng. Struct. 2007, 29, 1337–1342. [Google Scholar] [CrossRef]
- Chantharasenawong, C.; Jongpradist, P.; Laoharatchapruek, S. Preliminary Design of 1.5-MW Modular Wind Turbine Tower. In Proceedings of the The 2nd TSME International Conference on Mechanical Engineering, Krabi, Thailand, 14–17 December 2011; Citeseer: Princeton, NJ, USA. [Google Scholar]
- Gencturk, B.; Attar, A.; Tort, C. Optimal Design of Lattice Wind Turbine Towers. In Proceedings of the 15th world conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; pp. 24–28. [Google Scholar]
- Long, H.; Moe, G. Preliminary Design of Bottom-Fixed Lattice Offshore Wind Turbine Towers in the Fatigue Limit State by the Frequency Domain Method. J. Offshore Mech. Arct. Eng. 2012, 134, 3. [Google Scholar] [CrossRef]
- Damiani, R.R.; Song, H.; Robertson, A.N.; Jonkman, J.M. Assessing the Importance of Nonlinearities in the Development of a Substructure Model for the Wind Turbine CAE Tool FAST. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2013. [Google Scholar]
- Gentils, T.; Wang, L.; Kolios, A. Integrated Structural Optimisation of Offshore Wind Turbine Support Structures Based on Finite Element Analysis and Genetic Algorithm. Appl. Energy 2017, 199, 187–204. [Google Scholar] [CrossRef]
- Arany, L.; Bhattacharya, S.; Macdonald, J.H.; Hogan, S.J. Closed Form Solution of Eigen Frequency of Monopile Supported Offshore Wind Turbines in Deeper Waters Incorporating Stiffness of Substructure and SSI. Soil Dyn. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef]
- Thiry, A.; Rigo, P.; Buldgen, L.; Raboni, G.; Bair, F. Optimization of Monopile Offshore Wind Structures; University of Liège: Liège, Belgium, 2011. [Google Scholar]
- Van Der Tempel, J. Design of Support Structures for Offshore Wind Turbines; TU Delft: Delft, The Netherland, 2006. [Google Scholar]
- Ziegler, L.; Voormeeren, S.; Schafhirt, S.; Muskulus, M. Sensitivity of Wave Fatigue Loads on Offshore Wind Turbines under Varying Site Conditions. Energy Procedia 2015, 80, 193–200. [Google Scholar] [CrossRef]
- Dirlik, T. Application of Computers in Fatigue Analysis. Ph.D. Thesis, University of Warwick, Coventry, UK, 1985. [Google Scholar]
- Brommundt, M.; Krause, L.; Merz, K.; Muskulus, M. Mooring System Optimization for Floating Wind Turbines Using Frequency Domain Analysis. Energy Procedia 2012, 24, 289–296. [Google Scholar] [CrossRef]
- Michailides, C.; Angelides, D.C. Modeling of Energy Extraction and Behavior of a Flexible Floating Breakwater. Appl. Ocean Res. 2012, 35, 77–94. [Google Scholar] [CrossRef]
- Hall, M.; Buckham, B.; Crawford, C. Evolving Offshore Wind: A Genetic Algorithm-Based Support Structure Optimization Framework for Floating Wind Turbines. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, NY, USA, 10–14 June 2013; IEEE: New York, NY, USA; pp. 1–10. [Google Scholar]
- Yoshida, S. Wind Turbine Tower Optimization Method Using a Genetic Algorithm. Wind Eng. 2006, 30, 453–469. [Google Scholar] [CrossRef]
- Gutierrez, W.; Ruiz-Columbie, A.; Tutkun, M.; Castillo, L. Impacts of the Low-Level Jet’s Negative Wind Shear on the Wind Turbine. Wind Energy Sci. 2017, 2, 533–545. [Google Scholar] [CrossRef]
- Ashuri, T. Beyond Classical Upscaling: Integrated Aeroservoelastic Design and Optimization of Large Offshore Wind Turbines; NARCIS: The Haag, The Netherlands, 2012. [Google Scholar]
- Haghi, R.; Ashuri, T.; van der Valk, P.L.; Molenaar, D.P. Integrated Multidisciplinary Constrained Optimization of Offshore Support Structures. J. Phys. Conf. Ser. 2014, 555, 012046. [Google Scholar] [CrossRef]
- Zwick, D.; Muskulus, M.; Moe, G. Iterative Optimization Approach for the Design of Full-Height Lattice Towers for Offshore Wind Turbines. Energy Procedia 2012, 24, 297–304. [Google Scholar] [CrossRef][Green Version]
- Chew, K.H.; Ng, E.; Tai, K.; Muskulus, M.; Zwick, D. Offshore Wind Turbine Jacket Substructure: A Comparison Study between Four-Legged and Three-Legged Designs. J. Ocean Wind Energy 2014, 1, 74–81. [Google Scholar]
- Chew, K.-H.; Tai, K.; Ng, E.; Muskulus, M. Optimization of Offshore Wind Turbine Support Structures Using an Analytical Gradient-Based Method. Energy Procedia 2015, 80, 100–107. [Google Scholar] [CrossRef]
- Chew, K.-H.; Tai, K.; Ng, E.; Muskulus, M. Analytical Gradient-Based Optimization of Offshore Wind Turbine Substructures under Fatigue and Extreme Loads. Mar. Struct. 2016, 47, 23–41. [Google Scholar] [CrossRef]
- Schafhirt, S.; Zwick, D.; Muskulus, M. Reanalysis of Jacket Support Structure for Computer-Aided Optimization of Offshore Wind Turbines with a Genetic Algorithm. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014; International Society of Offshore and Polar Engineers: Mountain View, CA, USA. [Google Scholar]
- Schafhirt, S.; Page, A.; Eiksund, G.R.; Muskulus, M. Influence of Soil Parameters on the Fatigue Lifetime of Offshore Wind Turbines with Monopile Support Structure. Energy Procedia 2016, 94, 347–356. [Google Scholar] [CrossRef]
- Oest, J.; Sørensen, R.; Overgaard, L.C.T.; Lund, E. Structural Optimization with Fatigue and Ultimate Limit Constraints of Jacket Structures for Large Offshore Wind Turbines. Struct. Multidiscip. Optim. 2017, 55, 779–793. [Google Scholar] [CrossRef]
- AlHamaydeh, M.H.; Barakat, S.A.; Nassif, O.M. Optimization of Quatropod Jacket Support Structures for Offshore Wind Turbines Subject to Seismic Loads Using Genetic Algorithms. In Proceedings of the 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, COMPDYN, Crete Island, Greece, 25–27 May 2015; pp. 3505–3513. [Google Scholar]
- AlHamaydeh, M.; Barakat, S.; Nasif, O. Optimization of Support Structures for Offshore Wind Turbines Using Genetic Algorithm with Domain-Trimming. Math. Probl. Eng. 2017, 2017, 5978375. [Google Scholar] [CrossRef]
- Kaveh, A.; Sabeti, S. Optimal Design of Jacket Supporting Structures for Offshore Wind Turbines Using CBO and ECBO Algorithms. Period. Polytech. Civ. Eng. 2018, 62, 545–554. [Google Scholar] [CrossRef]
- Pasamontes, L.B.; Torres, F.G.; Zwick, D.; Schafhirt, S.; Muskulus, M. Support Structure Optimization for Offshore Wind Turbines with a Genetic Algorithm. In Proceedings of the ASME 2014 33rd Internation Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; Citeseer: Princeton, NJ, USA; pp. 1–7. [Google Scholar]
- Chen, W.-C.; Nguyen, M.-H.; Chiu, W.-H.; Chen, T.-N.; Tai, P.-H. Optimization of the Plastic Injection Molding Process Using the Taguchi Method, RSM, and Hybrid GA-PSO. Int. J. Adv. Manuf. Technol. 2016, 83, 1873–1886. [Google Scholar] [CrossRef]
- Kenway, G.; Martins, J.R. Aerostructural Shape Optimization of Wind Turbine Blades Considering Site-Specific Winds. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008; p. 6025. [Google Scholar]
- Ning, A.; Petch, D. Integrated Design of Downwind Land-Based Wind Turbines Using Analytic Gradients. Wind Energy 2016, 19, 2137–2152. [Google Scholar] [CrossRef]
- Bizzarrini, N.; Grasso, F.; Coiro, D.P. Genetic Algorithms in Wind Turbine Airfoil Design; EWEC2011; EWEA: Bruxelles, Belgium, 2011; pp. 14–17. [Google Scholar]
- Foster, N.F.; Dulikravich, G.S. Three-Dimensional Aerodynamic Shape Optimization Using Genetic and Gradient Search Algorithms. J. Spacecr. Rocket. 1997, 34, 36–42. [Google Scholar] [CrossRef]
- Vicini, A.; Quagliarella, D. Airfoil and Wing Design through Hybrid Optimization Strategies. AIAA J. 1999, 37, 634–641. [Google Scholar] [CrossRef]
- Nandigam, M.; Dhali, S.K. Optimal Design of an Offshore Wind Farm Layout. In Proceedings of the 2008 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 11–13 June 2008; IEEE: New York, NY, USA; pp. 1470–1474. [Google Scholar]
- Karimi, M.; Hall, M.; Buckham, B.; Crawford, C. A Multi-Objective Design Optimization Approach for Floating Offshore Wind Turbine Support Structures. J. Ocean Eng. Mar. Energy 2017, 3, 69–87. [Google Scholar] [CrossRef]
- Häusler, M.; Owman, F. AC or DC for Connecting Offshore Wind Farms to the Transmission Grid? In Proceedings of the International Workshop on Transmission Networks for Offshore Wind Farms, Stockholm, Sweden, 11–12 April 2002.
- Yang, J.; O’Reilly, J.; Fletcher, J.E. Redundancy Analysis of Offshore Wind Farm Collection and Transmission Systems. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; IEEE: New York, NY, USA; pp. 1–7. [Google Scholar]
- Gonzalez-Longatt, F.M.; Wall, P.; Regulski, P.; Terzija, V. Optimal Electric Network Design for a Large Offshore Wind Farm Based on a Modified Genetic Algorithm Approach. IEEE Syst. J. 2011, 6, 164–172. [Google Scholar] [CrossRef]
- Lee, K.-H.; Jun, S.-O.; Pak, K.-H.; Lee, D.-H.; Lee, K.-W.; Park, J.-P. Numerical Optimization of Site Selection for Offshore Wind Turbine Installation Using Genetic Algorithm. Curr. Appl. Phys. 2010, 10, S302–S306. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, Z.; Blaabjerg, F. Optimization of Electrical System for a Large DC Offshore Wind Farm by Genetic Algorithm. In Proceedings of the NORPIE 2004, CD-ROM, Trondheim, Norway, 14–16 June 2004; pp. 1–8. [Google Scholar]
- Zhao, M.; Chen, Z.; Hjerrild, J. Analysis of the Behaviour of Genetic Algorithm Applied in Optimization of Electrical System Design for Offshore Wind Farms. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; IEEE: New York, NY, USA; pp. 2335–2340. [Google Scholar]
- Zhao, M.; Chen, Z.; Blaabjerg, F. Optimisation of Electrical System for Offshore Wind Farms via Genetic Algorithm. IET Renew. Power Gener. 2009, 3, 205–216. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, M.; Blaabjerg, F. Application of Genetic Algorithm in Electrical System Optimization for Offshore Wind Farms. In Proceedings of the 3rd International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; IEEE: New York, NY, USA. [Google Scholar]
- Rini, D.P.; Shamsuddin, S.M.; Yuhaniz, S.S. Particle Swarm Optimization: Technique, System and Challenges. Int. J. Comput. Appl. 2011, 14, 19–26. [Google Scholar] [CrossRef]
- Liao, C.; Xi, G.; Xu, J. An Improved PSO Algorithm for Solution of Constraint Optimization Problem and Its Application. J. Eng. Thermophys. Rus 2009, 24, 256–260. [Google Scholar]
- Liao, C.; Zhao, X.; Xu, J. Blade Layers Optimization of Wind Turbines Using FAST and Improved PSO Algorithm. Renew. Energy 2012, 42, 227–233. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, A.; Yang, L.; Hu, C.; Bai, Y. Investigation on Optimization Design of Offshore Wind Turbine Blades Based on Particle Swarm Optimization. Energies 2019, 12, 1972. [Google Scholar] [CrossRef]
- Chowdhury, S.; Zhang, J.; Messac, A.; Castillo, L. Optimizing the Arrangement and the Selection of Turbines for Wind Farms Subject to Varying Wind Conditions. Renew. Energy 2013, 52, 273–282. [Google Scholar] [CrossRef]
- Häfele, J.; Rolfes, R. Approaching the Ideal Design of Jacket Substructures for Offshore Wind Turbines with a Particle Swarm Optimization Algorithm. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016; pp. 156–163. [Google Scholar]
- Tian, D.; Chen, J.; Luo, T.; Yan, X.; Deng, Y. Optimization of Supporting Structure for Offshore Wind Turbines Based on Flexible Foundation Model. Acta Energ. Sol. Sin. 2019, 40, 1185–1192. [Google Scholar]
- Wan, C.; Wang, J.; Yang, G.; Zhang, X. Optimal Micro-Siting of Wind Farms by Particle Swarm Optimization. In Proceedings of the International Conference in Swarm Intelligence, Beijing, China, 12–15 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 198–205. [Google Scholar]
- Wan, C.; Wang, J.; Yang, G.; Gu, H.; Zhang, X. Wind Farm Micro-Siting by Gaussian Particle Swarm Optimization with Local Search Strategy. Renew. Energy 2012, 48, 276–286. [Google Scholar] [CrossRef]
- Eroğlu, Y.; Seçkiner, S.U. Design of Wind Farm Layout Using Ant Colony Algorithm. Renew. Energy 2012, 44, 53–62. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Gallo-Marazuela, D.; Pastor-Sánchez, A.; Carro-Calvo, L.; Portilla-Figueras, A.; Prieto, L. Offshore Wind Farm Design with the Coral Reefs Optimization Algorithm. Renew. Energy 2014, 63, 109–115. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V.R. Colliding Bodies Optimization: A Novel Meta-Heuristic Method. Comput. Struct. 2014, 139, 18–27. [Google Scholar] [CrossRef]
- Kaveh, A.; Sabeti, S. Structural Optimization of Jacket Supporting Structures for Offshore Wind Turbines Using Colliding Bodies Optimization Algorithm. Struct. Des. Tall Spec. Build. 2018, 27, e1494. [Google Scholar] [CrossRef]
- Stieng, L.E.S.; Muskulus, M. Reliability-Based Design Optimization of Offshore Wind Turbine Support Structures Using Analytical Sensitivities and Factorized Uncertainty Modeling. Wind Energy Sci. 2020, 5, 171–198. [Google Scholar] [CrossRef]
- Willis, D.J.; Peraire, J.; White, J.K. A Combined PFFT-Multipole Tree Code, Unsteady Panel Method with Vortex Particle Wakes. Int. J. Numer. Methods Fluids 2007, 53, 1399–1422. [Google Scholar] [CrossRef]
- Li, C.; Campbell, B.K.; Liu, Y.; Yue, D.K. A Fast Multi-Layer Boundary Element Method for Direct Numerical Simulation of Sound Propagation in Shallow Water Environments. J. Comput. Phys. 2019, 392, 694–712. [Google Scholar] [CrossRef]
- Vairavamoorthy, K.; Ali, M. Pipe Index Vector: A Method to Improve Genetic-Algorithm-Based Pipe Optimization. J. Hydraul. Eng. 2005, 131, 1117–1125. [Google Scholar] [CrossRef]
- Choe, D.-E.; Kim, H.-C.; Kim, M.-H. Sequence-Based Modeling of Deep Learning with LSTM and GRU Networks for Structural Damage Detection of Floating Offshore Wind Turbine Blades. Renew. Energy 2021, 174, 218–235. [Google Scholar] [CrossRef]
| Monopile | Tripod | Jacket | |
|---|---|---|---|
| Advantage |
|
|
|
| Disadvantage |
|
|
|
| Spar-Buoy | Semisubmersible | TLP | Barge | |
|---|---|---|---|---|
| Advantage |
|
|
|
|
| Disadvantage |
|
|
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Kim, M.-H. Review of Recent Offshore Wind Turbine Research and Optimization Methodologies in Their Design. J. Mar. Sci. Eng. 2022, 10, 28. https://doi.org/10.3390/jmse10010028
Chen J, Kim M-H. Review of Recent Offshore Wind Turbine Research and Optimization Methodologies in Their Design. Journal of Marine Science and Engineering. 2022; 10(1):28. https://doi.org/10.3390/jmse10010028
Chicago/Turabian StyleChen, Jieyan, and Moo-Hyun Kim. 2022. "Review of Recent Offshore Wind Turbine Research and Optimization Methodologies in Their Design" Journal of Marine Science and Engineering 10, no. 1: 28. https://doi.org/10.3390/jmse10010028
APA StyleChen, J., & Kim, M.-H. (2022). Review of Recent Offshore Wind Turbine Research and Optimization Methodologies in Their Design. Journal of Marine Science and Engineering, 10(1), 28. https://doi.org/10.3390/jmse10010028





