Quantitative Ship Collision Frequency Estimation Models: A Review
Abstract
1. Introduction
2. Quantitative Ship Collision Frequency Estimation Models
2.1. Basic Scientific Approach to Risk Analysis in Maritime Transport
2.2. Analytical Models
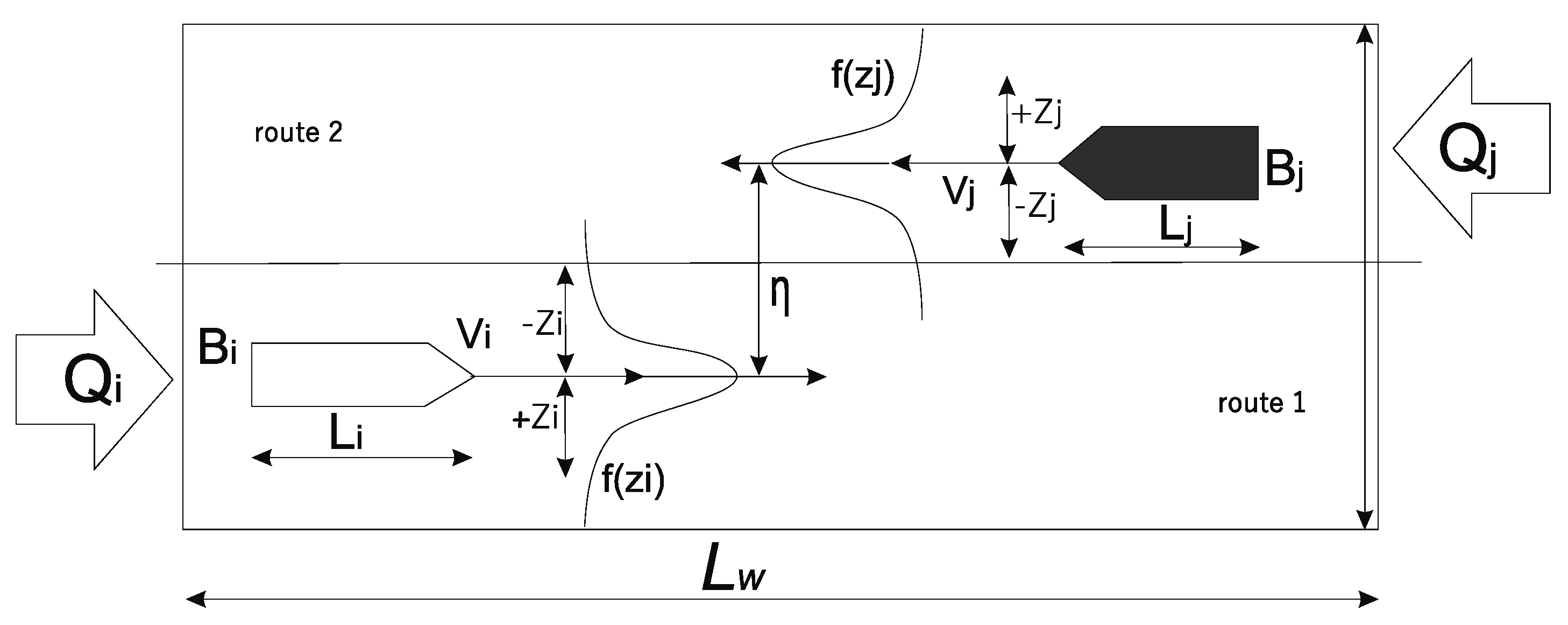
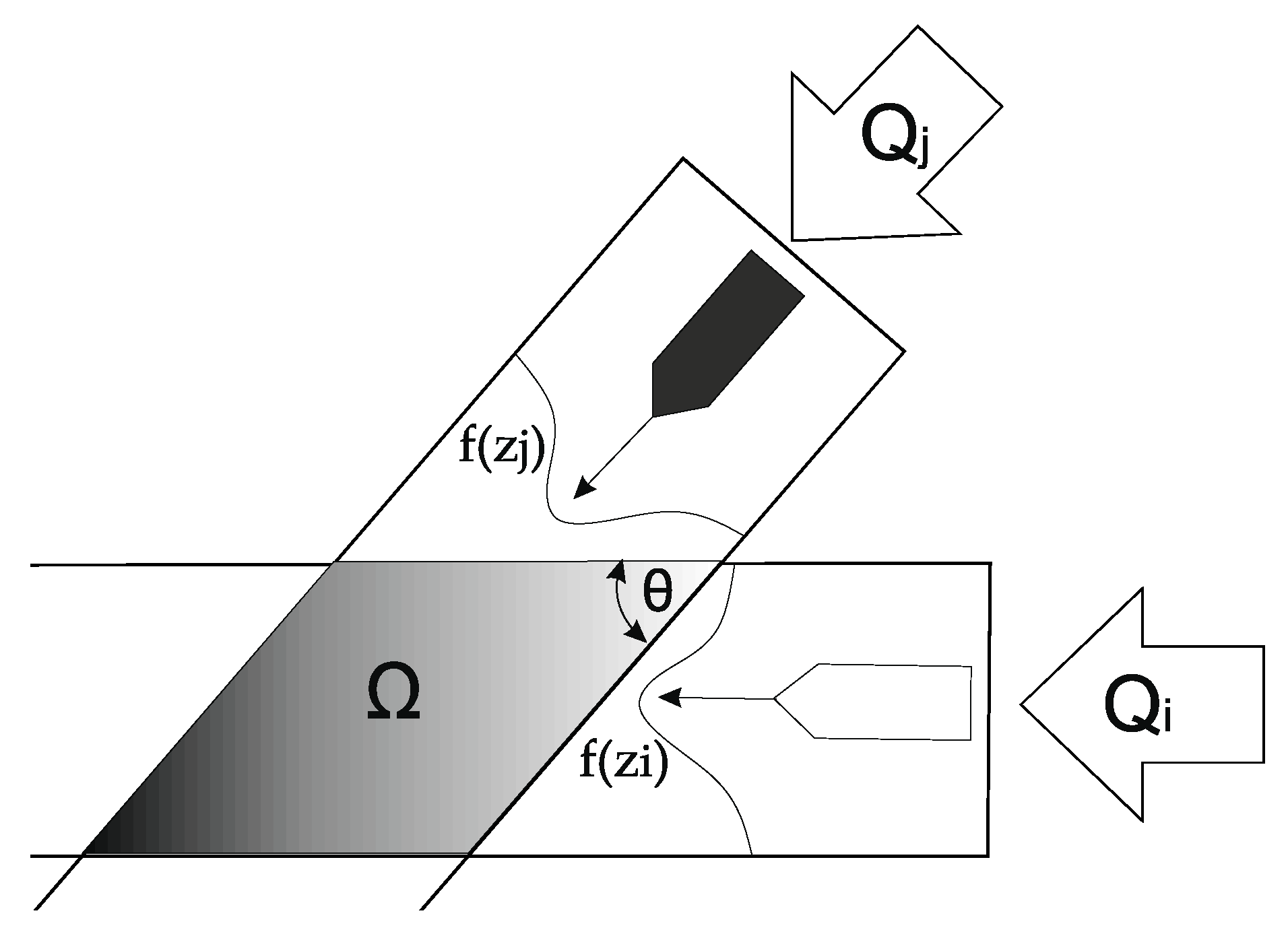
2.2.1. IWRAP Analytical Models
2.2.2. Other Analytical Models
2.3. AIS Data-Processing-Based Models
2.4. Simulation Models
2.5. Model Classification
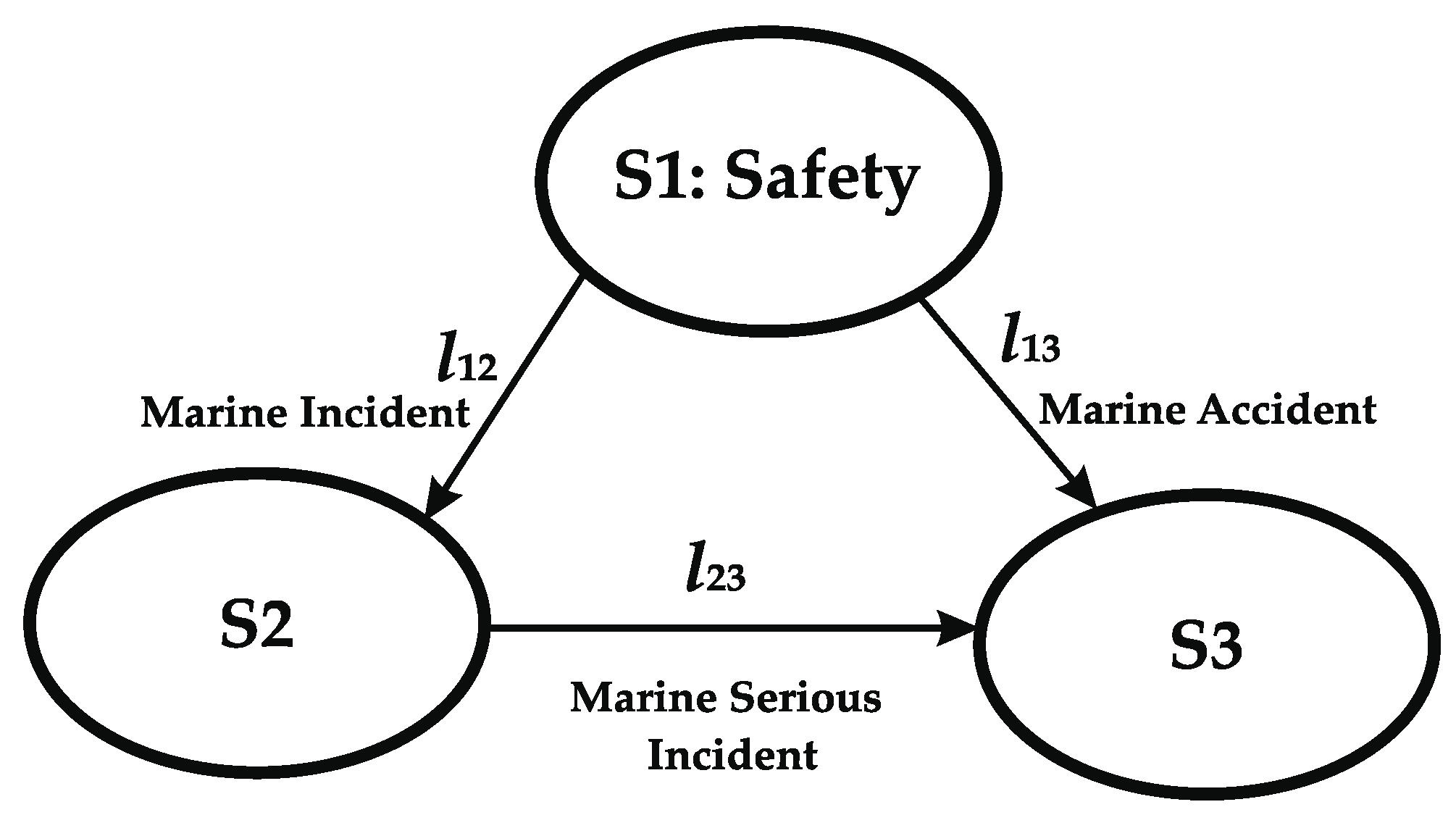
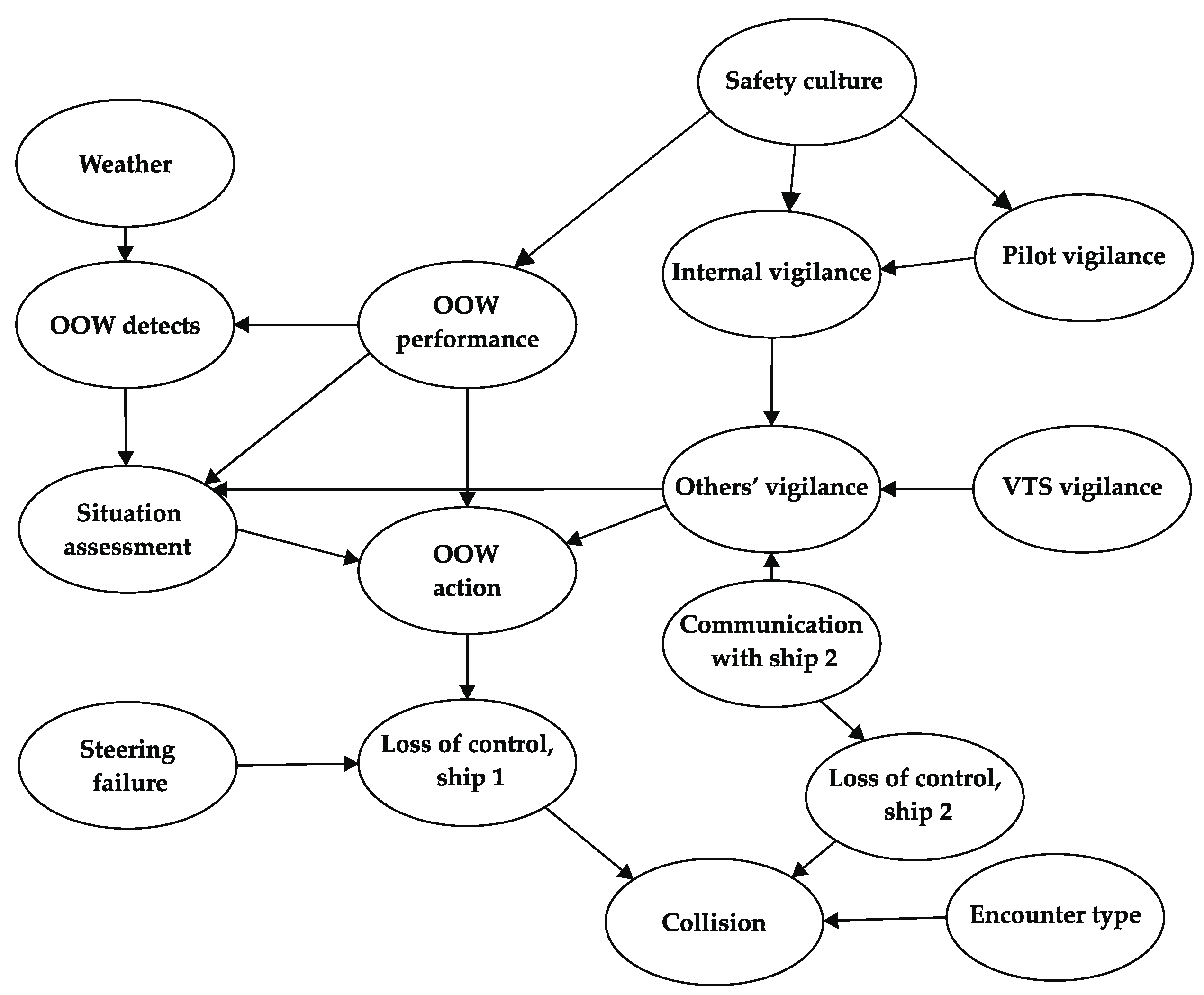
2.6. Methods for Estimating Causation Probabilities
3. Disadvantages of Existing Models and Improvement Possibilities
3.1. Disadvantages of Existing Models
- (a)
- (b)
- The aspect of uncertainty, which is part of the risk analysis, is not taken into account in most of the models used for calculating the causation probability [29], and this is particularly emphasized in the analysis of the human and organizational factors [14]. The modeling of the human factor and the lack of analysis of the uncertainty aspect have also been identified as a shortcoming in existing models within the research [76].
- (c)
- The lack of a generally accepted standard for the storage of data on maritime accidents, i.e., ship collisions with the associated detailed information, represents an issue [77]. The first problem is manifested in the fact that different models for estimating the collision frequency use different methods for detecting collision candidates [14], and the accuracy of each of these methods cannot be assessed well enough due to the lack of a standard collision database (and all the relevant details) against which the results of the model and the corresponding methods of detection of collision candidates could be compared [15]. Another potential problem arises from a possible bias in the models for calculating causation probability because such models tend to rely heavily on expert knowledge in the absence of data.
- (d)
- Most of the existing AIS data-processing-based models for estimating collision frequencies are designed for a specific navigation area, which has its own specific characteristics, and their application to other geographical navigation areas can be difficult [5].
- (e)
- Furthermore, all models for calculating causation probabilities are closely related to individual geographical navigation areas, which have their own specific properties [77]. Causation probabilities borrowed from other geographical navigation areas are often used in ship collision frequency estimation models [19,28]. This can affect the accuracy of the results, as the causation probability of one navigation area may not accurately describe the traffic situation of another navigation area.
- (f)
- Many AIS data-processing-based models and simulation models for estimating ship collision frequency use their own original methods for detecting collision candidates, do not explicitly express an estimate of the number of actual collisions and do not propose their own causation probability. The validation of such models is hindered due to the fact that it is not possible to compare the results with the actual number of collisions based on statistical historical data [48,77]. Causation probability depends on the navigation area, but also on the model, i.e., the way collision candidates are detected, so it is often not possible to use already calculated existing causation probabilities from the literature [77].
- (g)
- With regard to the detection of collision candidates, most ship collision frequency estimation models analyze two ships (a pair of ships) in a dangerous situation without considering other ships that could potentially affect the encounter of these two ships [14].
- (h)
- According to the same source [14], most AIS data-processing-based models for estimating the ship collision frequency detect collision candidates by analyzing AIS data in time intervals, which may cause an error because the time between two iterations is “ignored”. The problem is particularly emphasized in the situation of a dangerous encounter between two ships, since the kinematic status of the ships changes significantly (due to the critical situation), i.e., the criteria parameters on the basis of which the collision candidate is detected change. It follows that there is a possibility that the model may fail to detect a collision candidate due to the “ignored” time. Additionally, the direct use of AIS data assesses the risk of the current traffic situation in a navigation area, but not of a possible future hypothetical situation (change in traffic volume and structure, change in rules and regulations, etc.).
- (i)
- Analytical models for estimating ship collision frequency treat ship passages on a route (i.e., departures of ships) as a stationary Poisson process, which is often not a realistic assumption [41]. Most of the time, the number of ships passing a route varies depending on the time of day, month, etc. For example, in the Strait of Istanbul, there is a significant difference in day and night traffic [70], but this is also true for many other navigation areas.
- (j)
- Bend collision scenarios have not been adequately addressed among existing analytical models [41], including the models used in IWRAP [19]. Random sailing direction collision scenarios are also inadequately analyzed (e.g., IWRAP makes approximations to address this scenario by using head-on and crossing collision scenario to simulate random sailing direction collision scenario).
3.2. Improvement Possibilities of Existing Models
- (a)
- When developing the model, it is necessary to define which scientific approach to risk analysis will be used; this can be carried out using the methodology presented in [29].
- (b)
- The uncertainty aspect needs to be included in the models used to calculate causation probability as it improves the accuracy of the causation probability itself. The research [88] suggests the use of the “Credal Network” concept for conducting probabilistic inference with an interval, thus including the aspect of uncertainty in the model for calculating the causation probability. The research concluded that the highest degree of uncertainty is the result of individual exact probability values in the Bayesian network determined based on the collected expert knowledge, and the paper proposes a solution by introducing probability intervals (instead of single probability values). Regarding the calculation of the causation probability, it is necessary to take into account the IMO guidelines for Human Reliability Analysis (HRA), which include the analysis using the generic tools “Technique for Human Error Rate Prediction (THERP)” and “Human Error Assessment and Reduction Technique (HEART)” [76].
- (c)
- The existence of standards for the storage of ship collision information, together with collision details relevant to the development and testing of models, may help to resolve this problem. The long-term existence of such a publicly available database for at least one significant geographical navigation area would allow testing and validation of all models using a common database. In this way, comparison of results from different models is valid, as differences in results could not be attributed to the data, and the accuracy of each model’s results is measured by comparison with recorded actual collisions and associated details.
- (d)
- It is desirable to develop simulation models for estimating ship collision frequency that can be readily adapted for use in different navigation areas. Examples of computer simulation models that can be used in different navigation areas without demanding modifications are presented in [39,41]. The popularity of analytical models for estimating ship collision frequency stems from their practicality and applicability in different geographical navigation areas.
- (e)
- Although practice has shown that the use of “borrowed” causation probabilities from other navigation areas produces results of satisfactory accuracy [17], it is recommended to use the causation probability of the navigation area for which the ship collision risk is assessed.
- (f)
- For the developed AIS data-processing-based models and simulation models that estimate collision frequency, it is necessary to calculate the corresponding causation probability if the method used by a model to detect collision candidates differs from existing collision detection methods for which a calculated causation probability exists. This is also highlighted in [77].
- (g)
- The focus should be on approaches that simultaneously consider situations in which multiple dangerous encounters occur without analyzing all pairs of ships separately [14]. In other words, it is necessary to include the influence of other surrounding ships on the possibility of a collision of a pair of ships in a hazardous situation. An example of such an approach can be found in [64].
- (h)
- Instead of analyzing the data in time intervals, it is desirable to develop an approach that considers the dangerous encounter of two ships as a “process” [15]. This approach can prevent an error that occurs due to a neglected time interval in a dangerous encounter between two ships. Hypothetical scenarios can be addressed using simulation models. Alternatively, an example of the methodology from the AIS data-processing-based model which can address hypothetical scenarios to some extent is described in [52].
- (i)
- Simulation models for ship collision frequency estimation can successfully overcome this shortcoming [76].
- (j)
- Models covering bend collisions should be developed [41], as well as models that address random sailing direction collisions. Simulation models represent a suitable solution to this issue.
4. Discussion
4.1. Discussion on Recent Related Literature Reviews
4.2. General Remarks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Eleftheria, E.; Apostolos, P.; Markos, V. Statistical analysis of ship accidents and review of safety level. Saf. Sci. 2016, 85, 282–292. [Google Scholar] [CrossRef]
- 3174 Maritime Casualties and Incidents Reported in 2019. Available online: https://safety4sea.com/23073-maritime-casualties-and-incidents-reported-in-2019/ (accessed on 19 October 2020).
- Annual Overview of Marine Casualties and Incidents 2017. Available online: http://www.emsa.europa.eu/newsroom/latest-news/item/3156-annual-overview-of-marine-casualties-and-incidents-2017.html (accessed on 19 October 2020).
- Soares, C.G.; Teixeira, A.P. Risk assessment in maritime transportation. Reliab. Eng. Syst. Saf. 2001, 74, 299–309. [Google Scholar] [CrossRef]
- Ozbas, B. Safety Risk Analysis of Maritime Transportation Review of the Literature. Transp. Res. Rec. 2013, 2326, 32–38. [Google Scholar] [CrossRef]
- Vinnem, J.-E. Offshore Risk Assessment vol 2: Principles, Modelling and Applications of QRA Studies, 3rd ed.; Springer: London, UK, 2014; p. 513. ISBN 978-1-4471-5212-5. [Google Scholar] [CrossRef]
- Kristiansen, S. Maritime Transportation: Safety Management and Risk Analysis, 1st ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 2005; pp. 133–171. [Google Scholar]
- IMO. Guidelines for Formal Safety Assessment (Fsa) for Use in the Imo Rule-Making Process. 2002. Available online: http://www.safedor.org/resources/1023-MEPC392.pdf (accessed on 27 October 2020).
- Kontovas, C.A.; Psaraftis, H.N. Formal safety assessment: A critical review. Mar. Technol. SNAME News 2009, 46, 45–59. [Google Scholar] [CrossRef]
- Wang, G.; Ji, C.; Kuhala, P.; Lee, S.-G.; Marino, A.; Sirkar, J.; Suzuki, K.; Pedersen, P.T.; Vredevelt, A.W.; Yuriy, V. Collison and Grounding. In Proceedings of the 16th International Ship and Offshore Structures Congress, Southampton, UK, 20–25 August 2006; p. 57. [Google Scholar]
- Chai, T.; Weng, J.; De-qi, X. Development of a quantitative risk assessment model for ship collisions in fairways. Saf. Sci. 2017, 91, 71–83. [Google Scholar] [CrossRef]
- Pedersen, P.T. Review and application of ship collision and grounding analysis procedures. Mar. Struct. 2010, 23, 241–262. [Google Scholar] [CrossRef]
- Lušić, Z. Assessment of number of ship collisions in waterways crossing situations. NAŠE MORE 2005, 52, 185–194. [Google Scholar]
- Chen, P.; Huang, Y.; Mou, J.; van Gelder, P.H.A.J.M. Probabilistic risk analysis for ship-ship collision: State-of-the-art. Saf. Sci. 2019, 117, 108–122. [Google Scholar] [CrossRef]
- Chen, P.; Huang, Y.; Mou, J.; van Gelder, P.H.A.J.M. Ship collision candidate detection method: A velocity obstacle approach. Ocean Eng. 2018, 170, 186–198. [Google Scholar] [CrossRef]
- Fujii, Y.; Shiobara, R. The Analysis of Traffic Accidents. J. Navig. 1971, 24, 534–543. [Google Scholar] [CrossRef]
- Macduff, T. Probability of Vessel Collisions. Ocean Ind. 1974, 9, 144–148. [Google Scholar]
- Chen, P.; Mou, J.; van Gelder, P.H. Risk assessment methods for ship collision in estuarine waters using ais and historical accident data. In Proceedings of the 17th International Congress of the International Maritime Association of the mediterranean, IMAM 2017, Lisbon, Portugal, 9–11 October 2017; pp. 213–221. [Google Scholar]
- Ylitalo, J. Modelling Marine Accident Frequency. Master’s Thesis, Aalto University, Espoo, Finland, 2 February 2010. [Google Scholar]
- Du, L.; Goerlandt, F.; Kujala, P. Review and analysis of methods for assessing maritime waterway risk based on non-accident critical events detected from AIS data. Reliab. Eng. Syst. Saf. 2020, 200. [Google Scholar] [CrossRef]
- Zhang, G.; Thai, V.V. Expert elicitation and Bayesian Network modeling for shipping accidents: A literature review. Saf. Sci. 2016, 87, 53–62. [Google Scholar] [CrossRef]
- Szłapczyński, R.; Niksa-Rynkiewicz, T. A Framework of A Ship Domain-Based Near-Miss Detection Method Using Mamdani Neuro-Fuzzy Classification. Polish Marit. Res. 2018, 25, 14–21. [Google Scholar] [CrossRef]
- Lei, P.R.; Tsai, T.H.; Wen, Y.T.; Peng, W.C. A framework for discovering maritime traffic conflict from AIS network. In Proceedings of the 19th Asia-Pacific Network Operations and Management Symposium: Managing a World of Things, APNOMS 2017, Seul, Korea, 27–29 September 2017; pp. 1–6. [Google Scholar]
- Weng, J.; Xue, S. Ship collision frequency estimation in port fairways: A case study. J. Navig. 2015, 68, 602–618. [Google Scholar] [CrossRef]
- Martins, M.R.; Maturana, M.C. Human error contribution in collision and grounding of oil tankers. Risk Anal. 2010, 30, 674–698. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Jenkinson, I.; Wang, J.; Xu, D.L.; Yang, J.B. A methodology to model causal relationships on offshore safety assessment focusing on human and organizational factors. J. Safety Res. 2008, 39, 87–100. [Google Scholar] [CrossRef]
- Chauvin, C.; Lardjane, S.; Morel, G.; Clostermann, J.P.; Langard, B. Human and organisational factors in maritime accidents: Analysis of collisions at sea using the HFACS. Accid. Anal. Prev. 2013, 59, 26–37. [Google Scholar] [CrossRef] [PubMed]
- Friis-Hansen, P. Iwrap Mk Ii Working Document Basic Modelling Principles for Prediction of Collision and Grounding Frequencies. 2007. Available online: https://www.iala-aism.org/wiki/iwrap/images/2/2b/IWRAP_Theory.pdf (accessed on 15 November 2020).
- Goerlandt, F.; Montewka, J. Maritime transportation risk analysis: Review and analysis in light of some foundational issues. Reliab. Eng. Syst. Saf. 2015, 138, 115–134. [Google Scholar] [CrossRef]
- Shrader-Frechette, K. Risk and Rationality: Philosophical Foundations for Populist Reforms; University of California Press: Berkeley, CA, USA, 1992; Volume 29. [Google Scholar] [CrossRef]
- Bradbury, J.A. The Policy Implications of Differing Concepts of Risk. Sci. Technol. Human Values 1989, 14, 380–399. [Google Scholar] [CrossRef]
- Rosa, E.A. Metatheoretical foundations for post-normal risk. J. Risk Res. 1998, 1, 15–44. [Google Scholar] [CrossRef]
- IALA. Risk Management—Pawsa, Iwrap Mk2 & Simulation. 2010. Available online: https://www.iala-aism.org/product/risk-management-pawsa-iwrap-mk2-simulation/ (accessed on 22 November 2020).
- Kim, I.; Lee, H.; Lee, D. Development of a new tool for objective risk assessment and comparative analysis at coastal waters. J. Int. Marit. Safety Environ. Aff. Shipp. 2019, 2, 58–66. [Google Scholar] [CrossRef]
- Cucinotta, F.; Guglielmino, E.; Sfravara, F. Frequency of Ship Collisions in the Strait of Messina through Regulatory and Environmental Constraints Assessment. J. Navig. 2017, 70, 1002–1022. [Google Scholar] [CrossRef]
- Yoo, Y.; Kim, T.G. An improved ship collision risk evaluation method for Korea Maritime Safety Audit considering traffic flow characteristics. J. Mar. Sci. Eng. 2019, 7, 448. [Google Scholar] [CrossRef]
- Burmeister, H.-C.; Walther, L.; Jahn, C.; Toter, S.; Froese, J. Assessing the Frequency and Material Consequences of Collisions with Vessels Lying at an Anchorage in Line with IALA iWrap MkII. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2014, 8, 61–68. [Google Scholar] [CrossRef]
- Eriksson, O.F. Iwrap Mk2 Introduction Iala Waterway Risk Assessment Programme. 2018. Available online: https://portal.helcom.fi/meetings/OPENRISK%20WS%203-2018-527/MeetingDocuments/Presentaton%206.pdf (accessed on 23 November 2020).
- Lušić, Z.; Čorić, M. Models for estimating the potential number of ship collisions. J. Navig. 2015, 68, 735–749. [Google Scholar] [CrossRef]
- Pedersen, P. Collision and grounding mechanics. Danish Soc. Nav. Archit. Mar. Eng. 1995, 125–157. [Google Scholar]
- Goerlandt, F.; Kujala, P. Modeling of ship collision probability using dynamic traffic simulation. In Proceedings of the European Safety & Reliability Conference, ESREL 2010, Rhodes, Greece, 5–9 September 2010; pp. 440–447. [Google Scholar]
- Kujala, P.; Hänninen, M.; Arola, T.; Ylitalo, J. Analysis of the marine traffic safety in the Gulf of Finland. Reliab. Eng. Syst. Saf. 2009, 94, 1349–1357. [Google Scholar] [CrossRef]
- Otto, S.; Pedersen, P.T.; Samuelides, M.; Sames, P.C. Elements of risk analysis for collision and grounding of a RoRo passenger ferry. Mar. Struct. 2002, 15, 461–474. [Google Scholar] [CrossRef]
- Silveira, P.A.M.; Teixeira, A.P.; Soares, C.G. Use of AIS data to characterise marine traffic patterns and ship collision risk off the coast of Portugal. J. Navig. 2013, 66, 879–898. [Google Scholar] [CrossRef]
- COWI. Risk Analysis of Sea Traffic in the Area around Bornholm, 2008—VTT. 2008. Available online: https://www.yumpu.com/en/document/read/35601367/risk-analysis-of-sea-traffic-in-the-area-around-bornholm-2008-vtt (accessed on 28 November 2020).
- Fowler, T.G.; Sørgård, E. Modeling ship transportation risk. Risk Anal. 2000, 20. [Google Scholar] [CrossRef]
- Kaneko, F. Methods for probabilistic safety assessments of ships. J. Mar. Sci. Technol. 2002, 7, 1–16. [Google Scholar] [CrossRef]
- Montewka, J.; Hinz, T.; Kujala, P.; Matusiak, J. Probability modelling of vessel collisions. Reliab. Eng. Syst. Saf. 2010, 95, 573–589. [Google Scholar] [CrossRef]
- Curtis, R.G. A ship collision model for overtaking. J. Oper. Res. Soc. 1986, 37, 397–406. [Google Scholar] [CrossRef]
- Endoh, S. Aircraft Collision Models. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1987. [Google Scholar]
- Gil, M.; Montewka, J.; Krata, P.; Hinz, T.; Hirdaris, S. Determination of the dynamic critical maneuvering area in an encounter between two vessels: Operation with negligible environmental disruption. Ocean Eng. 2020, 213, 107709. [Google Scholar] [CrossRef]
- Rawson, A.; Brito, M. A critique of the use of domain analysis for spatial collision risk assessment. Ocean Eng. 2021, 219. [Google Scholar] [CrossRef]
- Wang, N. An intelligent spatial collision risk based on the quaternion ship domain. J. Navig. 2010, 63, 733–749. [Google Scholar] [CrossRef]
- Weng, J.; Liao, S.; Wu, B.; Yang, D. Exploring effects of ship traffic characteristics and environmental conditions on ship collision frequency. Marit. Policy Manag. 2020, 47, 523–543. [Google Scholar] [CrossRef]
- Fujii, Y.; Tanaka, K. Traffic capacity. J. Navig. 1971, 24, 543–552. [Google Scholar] [CrossRef]
- Van Westrenen, F.; Ellerbroek, J. The Effect of Traffic Complexity on the Development of Near Misses on the North Sea. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 432–440. [Google Scholar] [CrossRef]
- Van Iperen, E. Classifying Ship Encounters to Monitor Traffic Safety on the North Sea from AIS Data. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2015, 9, 51–58. [Google Scholar] [CrossRef]
- Zhang, W.; Goerlandt, F.; Montewka, J.; Kujala, P. A method for detecting possible near miss ship collisions from AIS data. Ocean Eng. 2015, 107, 60–69. [Google Scholar] [CrossRef]
- Cowi Risks of Oil and Chemical Pollution in the Baltic Sea Results and Recommendations from Helcom’s Brisk and Brisk-Ru Projects Nordic Council of Ministers. 2012. Available online: https://helcom.fi/media/publications/BRISK-BRISK-RU_SummaryPublication_spill_of_oil.pdf (accessed on 17 January 2021).
- Wu, X.; Mehta, A.L.; Zaloom, V.A.; Craig, B.N. Analysis of waterway transportation in Southeast Texas waterway based on AIS data. Ocean Eng. 2016, 121, 196–209. [Google Scholar] [CrossRef]
- Weng, J.; Meng, Q.; Qu, X. Vessel collision frequency estimation in the Singapore Strait. J. Navig. 2012, 65, 207–221. [Google Scholar] [CrossRef]
- Weng, J.; Meng, Q.; Li, S. Quantitative Risk Assessment Model for Ship Collisions in the Singapore Strait. In Proceedings of the 93rd Annual Meeting of Transportation Research Board, Washington, DC, USA, 12–16 January 2014; p. 16. [Google Scholar]
- Chen, P.; Huang, Y.; Papadimitriou, E.; Mou, J.; van Gelder, P.H.A.J.M. An improved time discretized non-linear velocity obstacle method for multi-ship encounter detection. Ocean Eng. 2020, 196. [Google Scholar] [CrossRef]
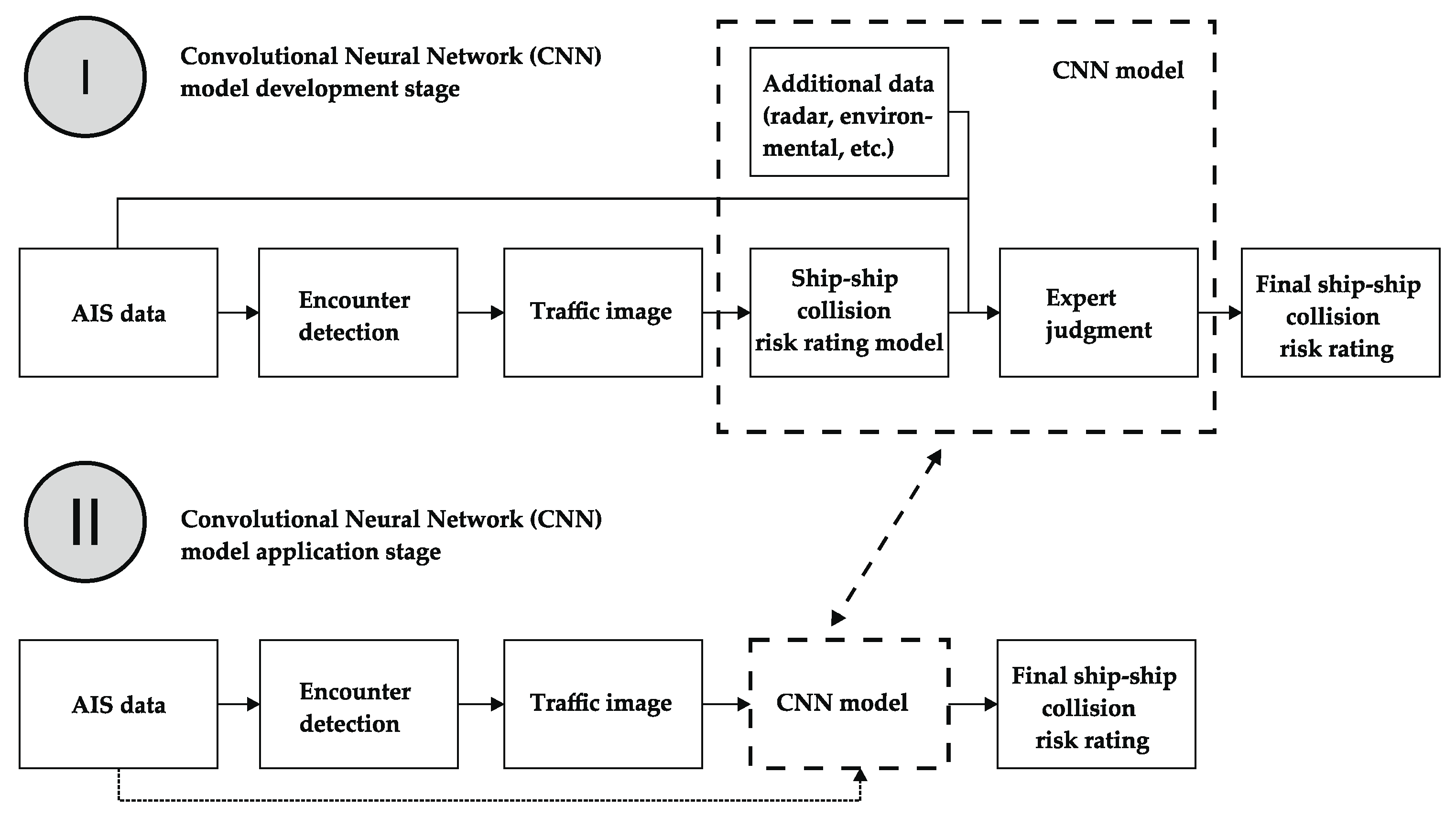
- Zhang, W.; Feng, X.; Goerlandt, F.; Liu, Q. Towards a Convolutional Neural Network model for classifying regional ship collision risk levels for waterway risk analysis. Reliab. Eng. Syst. Saf. 2020, 204. [Google Scholar] [CrossRef]
- Goerlandt, F.; Kujala, P. Traffic simulation based ship collision probability modeling. Reliab. Eng. Syst. Saf. 2011, 96. [Google Scholar] [CrossRef]
- Faghih-Roohi, S.; Xie, M.; Ng, K.M. Accident risk assessment in marine transportation via Markov modelling and Markov Chain Monte Carlo simulation. Ocean Eng. 2014, 91, 363–370. [Google Scholar] [CrossRef]
- Van Dorp, J.R.; Merrick, J.R.W.; Harrald, J.R.; Mazzuchi, T.A.; Grabowski, M. A risk management procedure for the Washington state ferries. Risk Anal. 2001, 21, 127–142. [Google Scholar] [CrossRef] [PubMed]
- Vujičić, S.; Mohović, Đ.; Mohović, R. A Model of Determining the Closest Point of Approach Between Ships on the Open Sea. Promet Traffic Transp. 2017, 29, 225–232. [Google Scholar] [CrossRef]
- Merrick, J.R.W.; Van Dorp, J.R.; Blackford, J.P.; Shaw, G.L.; Harrald, J.; Mazzuchi, T.A. A traffic density analysis of proposed ferry service expansion in San Francisco bay using a maritime simulation model. Reliab. Eng. Syst. Saf. 2003, 81, 119–132. [Google Scholar] [CrossRef]
- Ulusçu, Ö.S.; Özbaş, B.; Altiok, T.; Or, I. Risk analysis of the vessel traffic in the strait of Istanbul. Risk Anal. 2009, 29, 1454–1472. [Google Scholar] [CrossRef] [PubMed]
- Qu, X.; Meng, Q. Development and applications of a simulation model for vessels in the Singapore Straits. Expert Syst. Appl. 2012, 39, 8430–8438. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.; Soares, C. Evaluation of near-collisions in the Tagus River Estuary using a marine traffic simulation model. Zesz. Nauk. Akad. Mor. Szczec. 2015, 43, 68–78. [Google Scholar]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Simulation and analysis of maritime traffic in the tagus river estuary using AIS data. In Proceedings of the Maritime Technology and Engineering—Proceedings of MARTECH 2014: 2nd International Conference on Maritime Technology and Engineering, Lisbon, Portugal, 15–17 October 2014; pp. 185–195. [Google Scholar]
- Goerlandt, F.; Kujala, P. On the reliability and validity of ship–ship collision risk analysis in light of different perspectives on risk. Saf. Sci. 2014, 62, 348–365. [Google Scholar] [CrossRef]
- Mazaheri, A.; Montewka, J.; Kujala, P. Modeling the risk of ship grounding—a literature review from a risk management perspective. WMU J. Marit. Affairs 2014, 13, 269–297. [Google Scholar] [CrossRef]
- Li, S.; Meng, Q.; Qu, X. An Overview of Maritime Waterway Quantitative Risk Assessment Models. Risk Anal. 2012, 32, 496–512. [Google Scholar] [CrossRef]
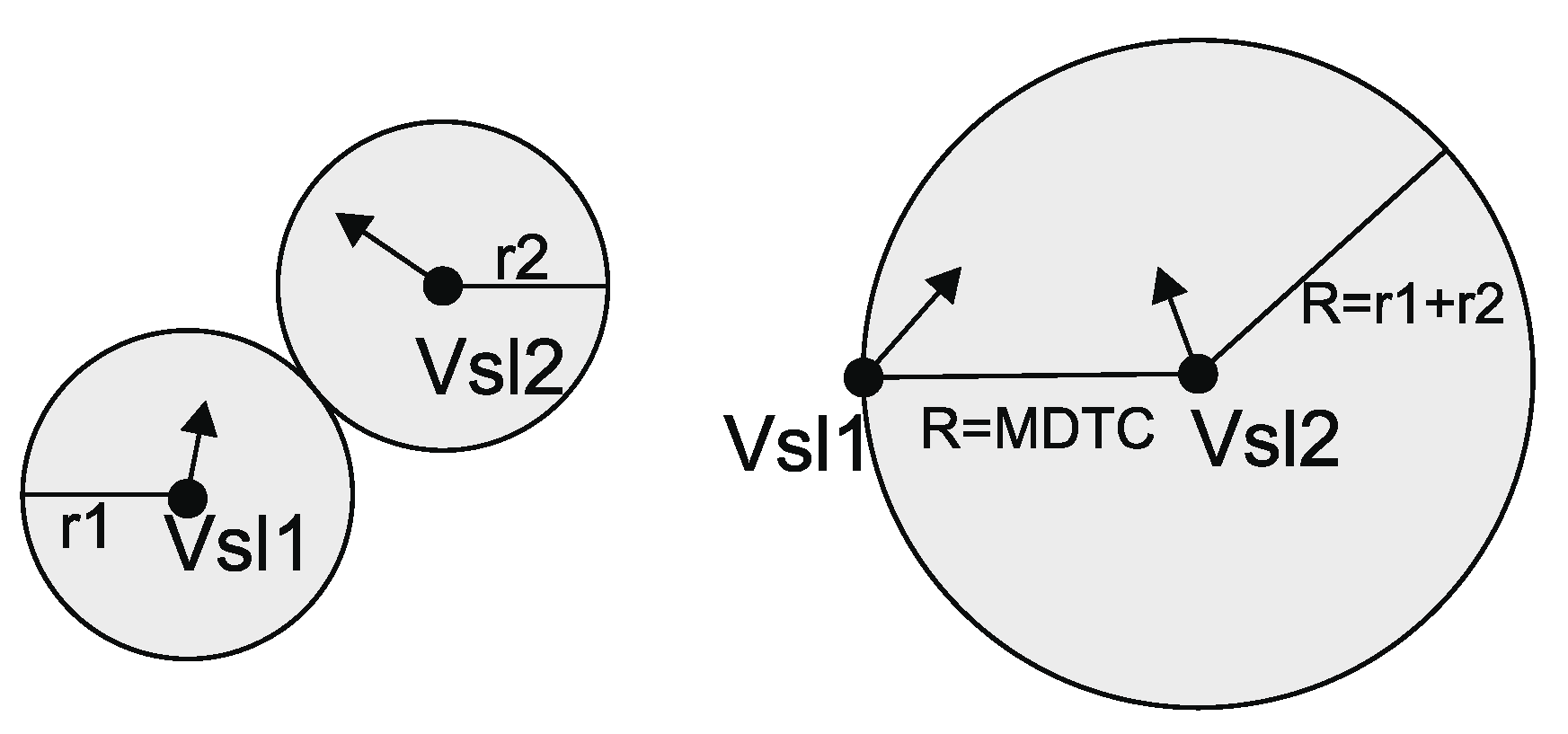
- Weintrit, A.; Neumann, T.; Montewka, J.; Goerlandt, F.; Lammi, H.; Kujala, P. A Method for Assessing a Causation Factor for a Geometrical MDTC Model for Ship-Ship Collision Probability Estimation. Methods Algorithms Navig. 2011, 5, 365–373. [Google Scholar] [CrossRef]
- IMO. Revised Guidelines for Formal Safety Assessment (Fsa) for Use in the Imo Rule-Making Process. 2018. Available online: https://wwwcdn.imo.org/localresources/en/OurWork/HumanElement/Documents/MSC-MEPC.2-Circ.12-Rev.2%20-%20Revised%20Guidelines%20For%20Formal%20Safety%20Assessment%20(Fsa)For%20Use%20In%20The%20Imo%20Rule-Making%20Proces...%20(Secretariat).pdf (accessed on 2 March 2021).
- Uğurlu, Ö.; Köse, E.; Yıldırım, U.; Yüksekyıldız, E. Marine accident analysis for collision and grounding in oil tanker using FTA method. Marit. Policy Manag. 2015, 42, 163–185. [Google Scholar] [CrossRef]
- Antão, P.; Guedes Soares, C. Fault-tree models of accident scenarios of RoPax vessels. Int. J. Autom. Comput. 2006, 3, 107–116. [Google Scholar] [CrossRef]
- Langseth, H.; Portinale, L. Bayesian networks in reliability. Reliab. Eng. Syst. Saf. 2007, 92, 92–108. [Google Scholar] [CrossRef]
- Hänninen, M.; Kujala, P. Influences of variables on ship collision probability in a Bayesian belief network model. Reliab. Eng. Syst. Saf. 2012, 102, 27–40. [Google Scholar] [CrossRef]
- Montewka, J.; Ehlers, S.; Goerlandt, F.; Hinz, T.; Tabri, K.; Kujala, P. A framework for risk assessment for maritime transportation systems—A case study for open sea collisions involving RoPax vessels. Reliab. Eng. Syst. Saf. 2014, 124, 142–157. [Google Scholar] [CrossRef]
- Martins, M.R.; Maturana, M.C. Application of Bayesian Belief networks to the human reliability analysis of an oil tanker operation focusing on collision accidents. Reliab. Eng. Syst. Saf. 2013, 110, 89–109. [Google Scholar] [CrossRef]
- Trucco, P.; Cagno, E.; Ruggeri, F.; Grande, O. A Bayesian Belief Network modelling of organisational factors in risk analysis: A case study in maritime transportation. Reliab. Eng. Syst. Saf. 2008, 93, 845–856. [Google Scholar] [CrossRef]
- Khaled, M.E.; Kawamura, Y. Application of Bayesian Belief Network to Estimate Causation Probability of Collision at Chittagong Port by Analyzing Accident Database of Bangladesh. In Proceedings of the Japan Society of Navala Architects and Ocean Engineers, Nagasaki, Japan, 20–21 November 2014; pp. 133–136. [Google Scholar]
- Kaplan, S. The words of risk analysis. Risk Anal. 1997, 17, 407–417. [Google Scholar] [CrossRef]
- Zhang, G.; Thai, V.V.; Yuen, K.F.; Loh, H.S.; Zhou, Q. Addressing the epistemic uncertainty in maritime accidents modelling using Bayesian network with interval probabilities. Saf. Sci. 2018, 102, 211–225. [Google Scholar] [CrossRef]
- Sánchez-Beaskoetxea, J.; Basterretxea-Iribar, I.; Sotés, I.; Machado, M.D.L.M.M. Human error in marine accidents: Is the crew normally to blame? Marit. Transp. Res. 2021, 2, 100016. [Google Scholar] [CrossRef]
- Hanzu-Pazara, R.; Barsan, E.; Arsenie, P.; Chiotoroiu, L.; Raicu, G. Reducing of maritime accidents caused by human factors using simulators in training process. J. Marit. Res. 2008, 5, 3–18. [Google Scholar]
- Zhang, M.; Montewka, J.; Manderbacka, T.; Kujala, P.; Hirdaris, S. A Big Data Analytics Method for Evaluation of Ship-Ship Collision Risk Reflecting Hydrometeorological Conditions. Reliab. Eng. Syst. Saf. 2021, 213, 107674. [Google Scholar] [CrossRef]
- Zhang, M.; Montewka, J.; Manderbacka, T.; Kujala, P.; Hirdaris, S. Analysis of the Grounding Avoidance Behavior of a Ro-Pax Ship in the Gulf of Finland using Big Data. In Proceedings of the 30th International Ocean and Polar Engineering Conference, Shanghai, China, 11–16 October 2020; pp. 3558–3559. [Google Scholar]

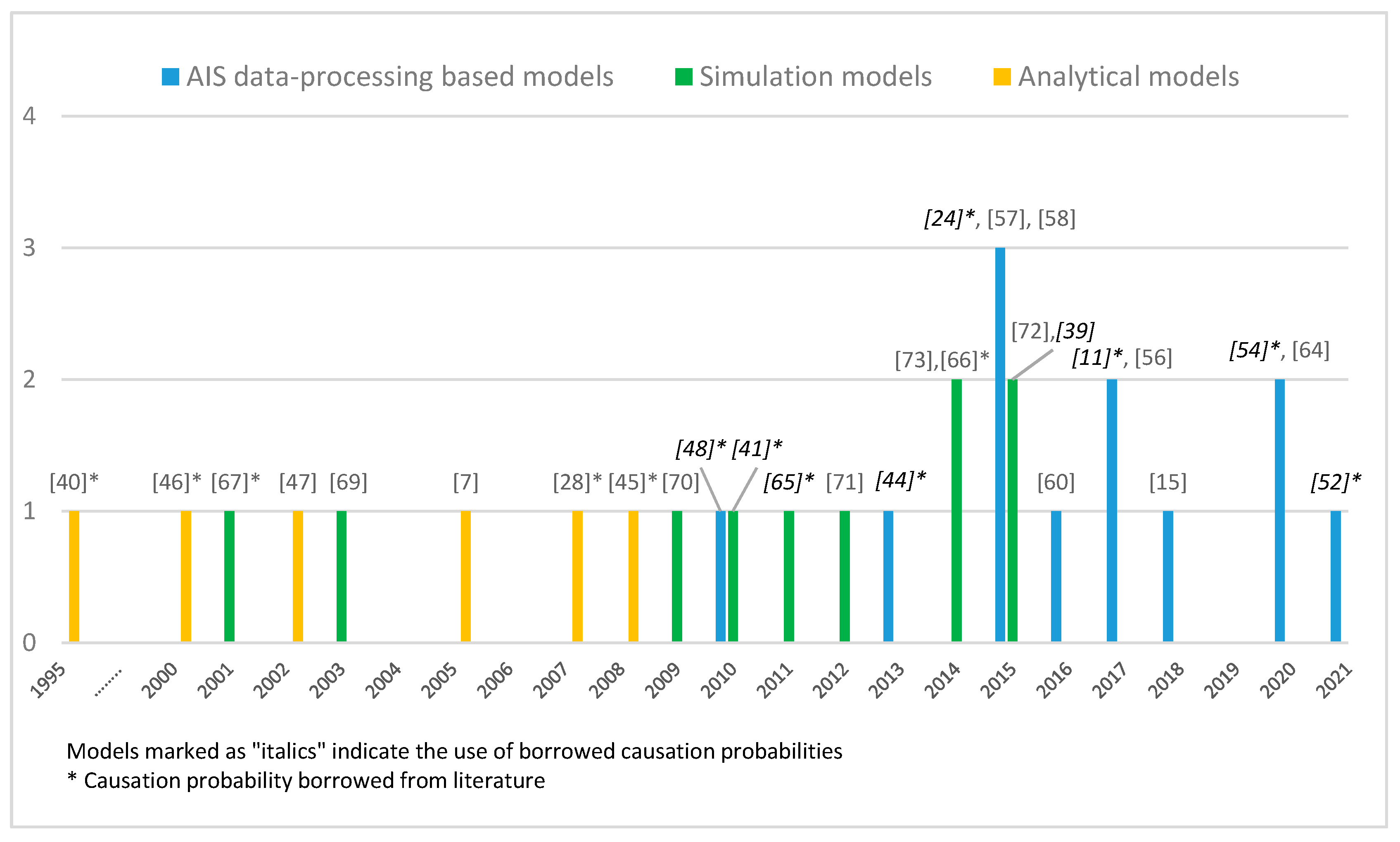
| Model Class Type | Existing Collision Candidate Detection Approaches | |||
|---|---|---|---|---|
| Safe Boundary Approach | Synthetic Indicator Approach | Non-Conventional Approaches and Approaches Emerged from Robotics and Artificial Intelligence | ||
| Ship Domain | Direct/Nearly Direct Ship–Ship Contact and Collision Diameter | |||
| AIS data-processing-based models | [48] *, [24] *, [52] *, [54] *, [11] *, [56,60] | [44] * | [57,58] | [15,64] |
| Simulation models | [72,73] | [65] *, [41] *, [39] | [67] *, [69] | [66] *, [70,71] |
| Analytical models | [7], [17] *, [28] *, [40] *, [45] *, [47] | [46] * | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čorić, M.; Mandžuka, S.; Gudelj, A.; Lušić, Z. Quantitative Ship Collision Frequency Estimation Models: A Review. J. Mar. Sci. Eng. 2021, 9, 533. https://doi.org/10.3390/jmse9050533
Čorić M, Mandžuka S, Gudelj A, Lušić Z. Quantitative Ship Collision Frequency Estimation Models: A Review. Journal of Marine Science and Engineering. 2021; 9(5):533. https://doi.org/10.3390/jmse9050533
Chicago/Turabian StyleČorić, Mirko, Sadko Mandžuka, Anita Gudelj, and Zvonimir Lušić. 2021. "Quantitative Ship Collision Frequency Estimation Models: A Review" Journal of Marine Science and Engineering 9, no. 5: 533. https://doi.org/10.3390/jmse9050533
APA StyleČorić, M., Mandžuka, S., Gudelj, A., & Lušić, Z. (2021). Quantitative Ship Collision Frequency Estimation Models: A Review. Journal of Marine Science and Engineering, 9(5), 533. https://doi.org/10.3390/jmse9050533







