Nonlinear Wave Evolution in Interaction with Currents and Viscoleastic Muds
Abstract
1. Introduction
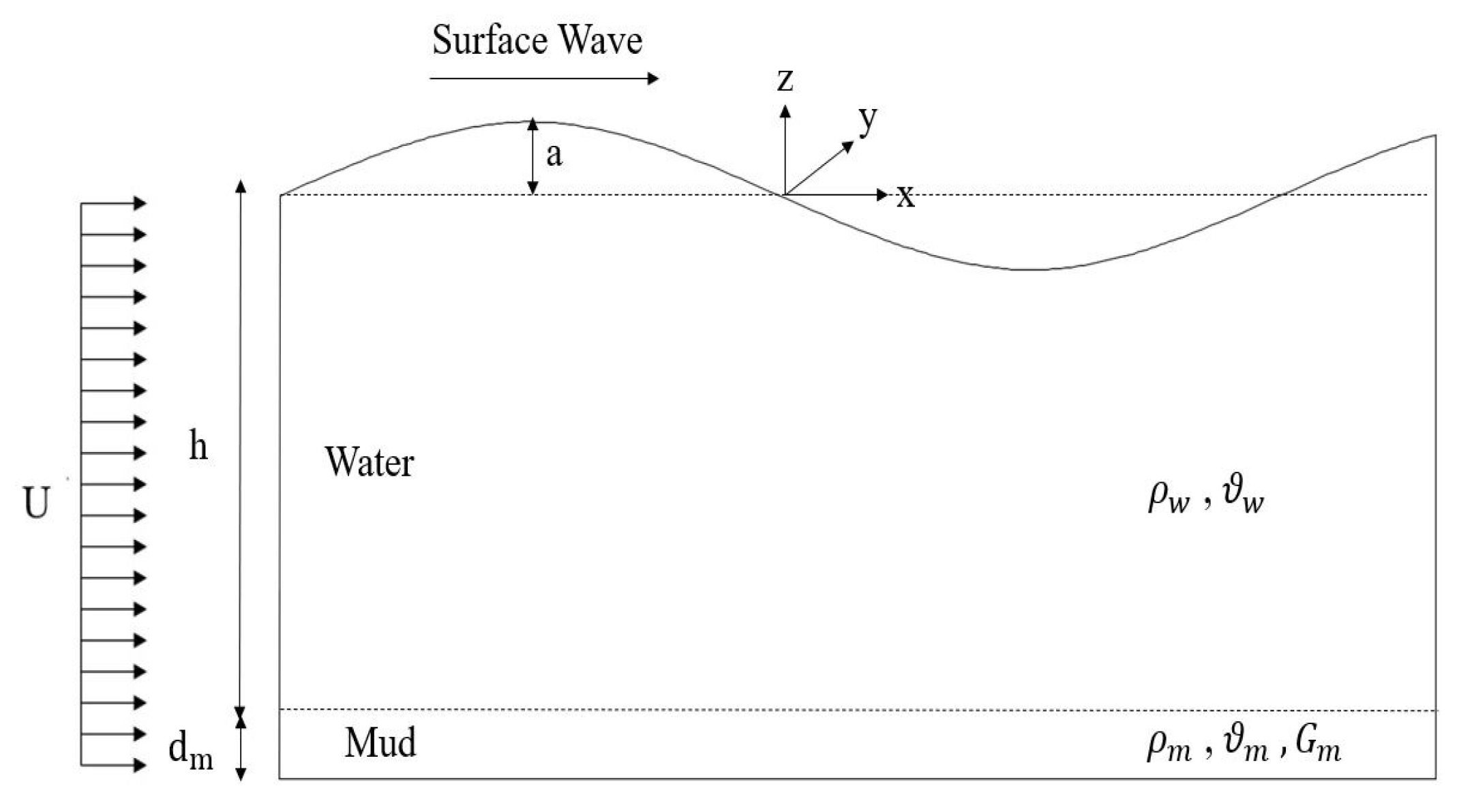
2. Numerical Model
2.1. Nonlinear Wave–Current Interaction Model
2.2. Model for Surface Wave Evolution over Viscoelastic Mud
2.2.1. Macpherson Model
2.2.2. Liu and Chan Model
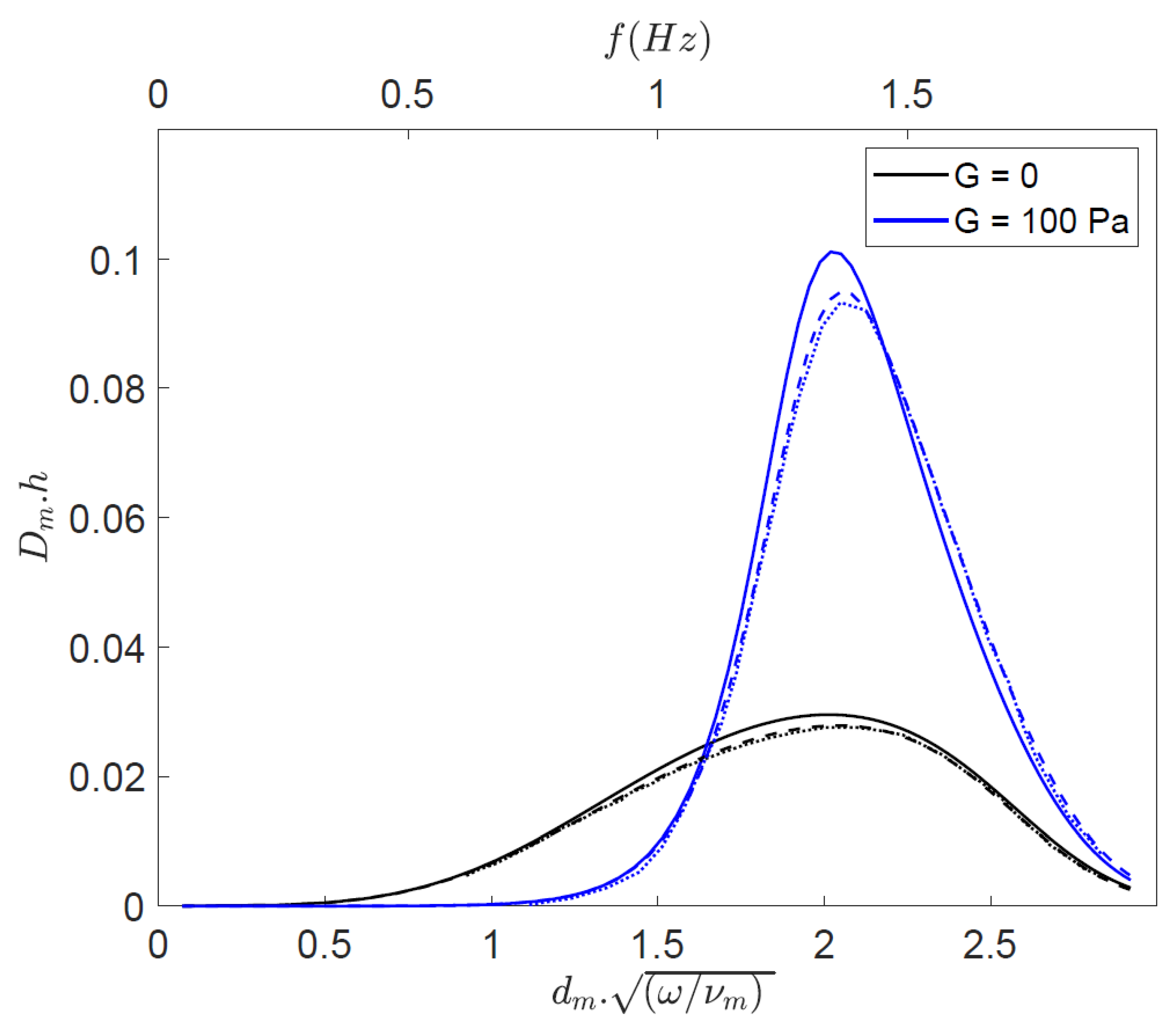
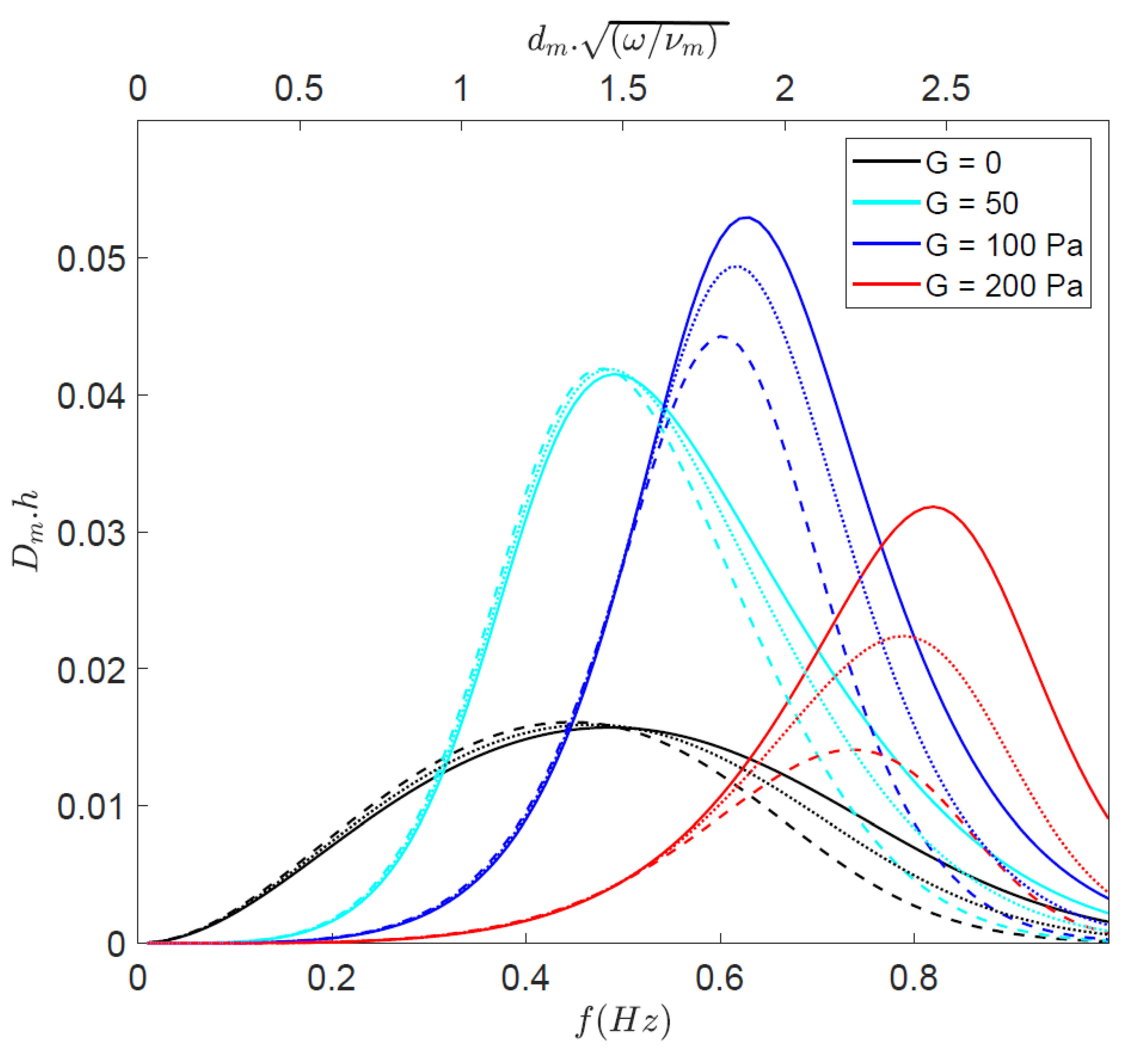
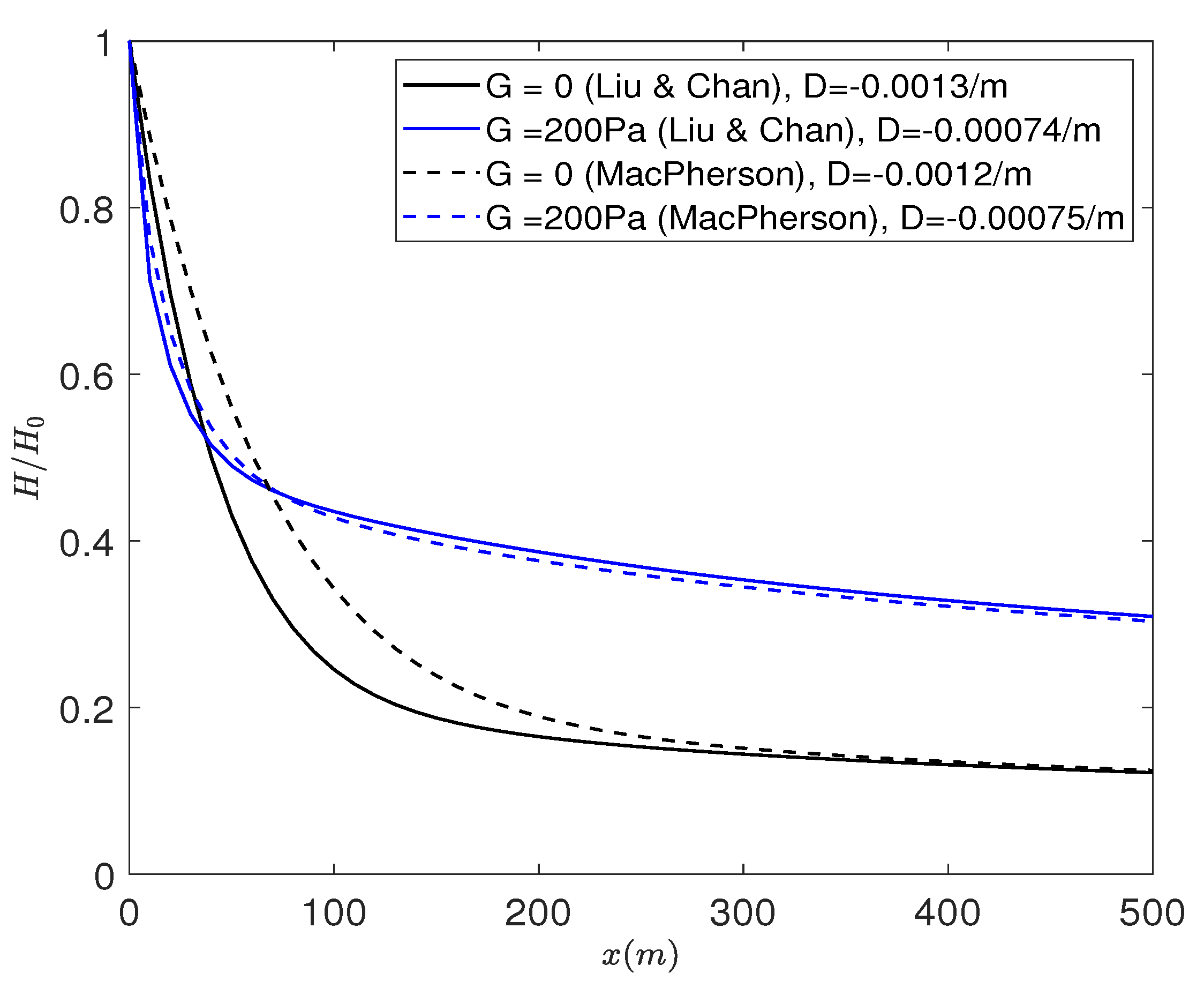
2.2.3. Comparison between Viscoelastic Mud Models
3. Model Results
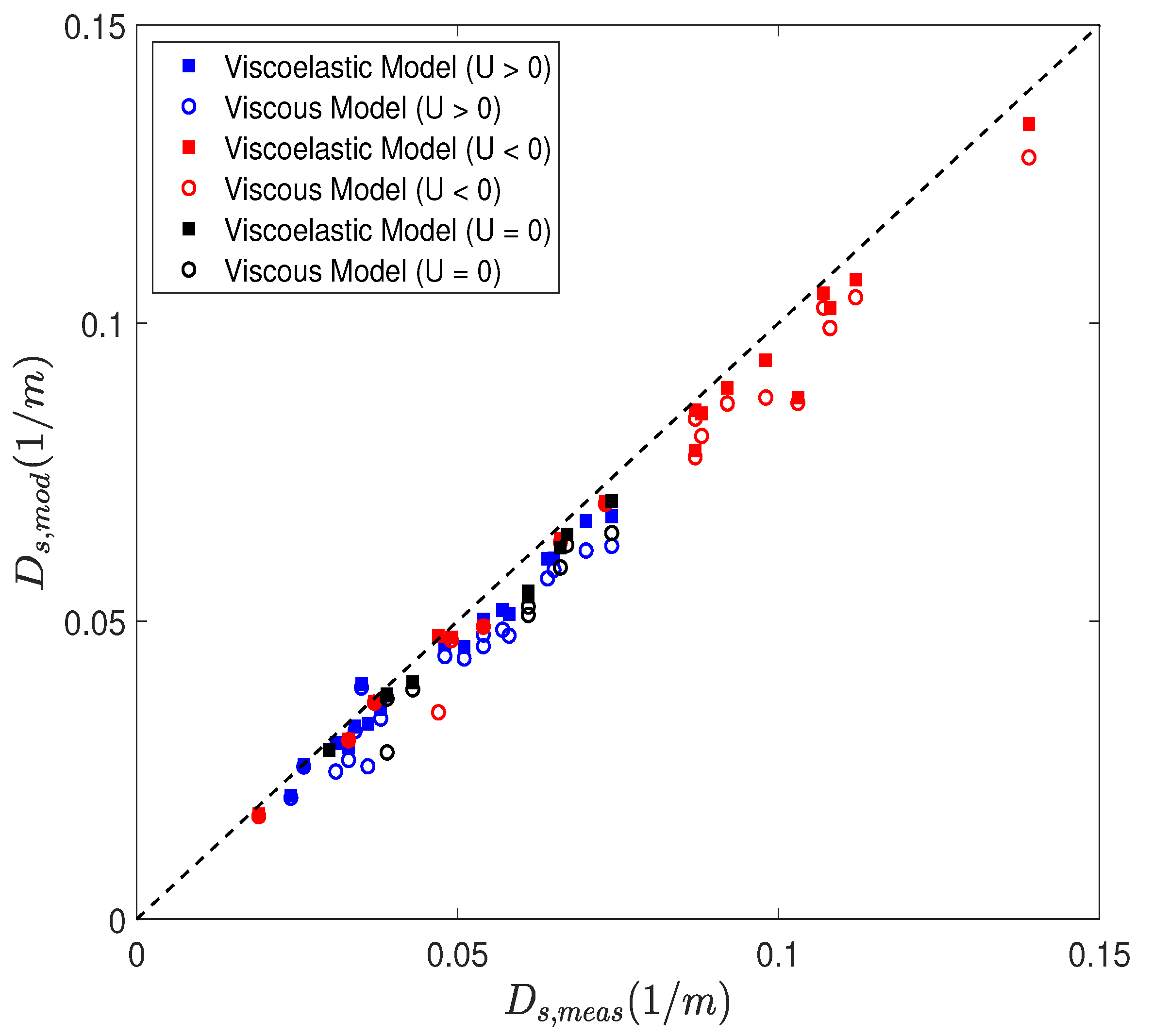
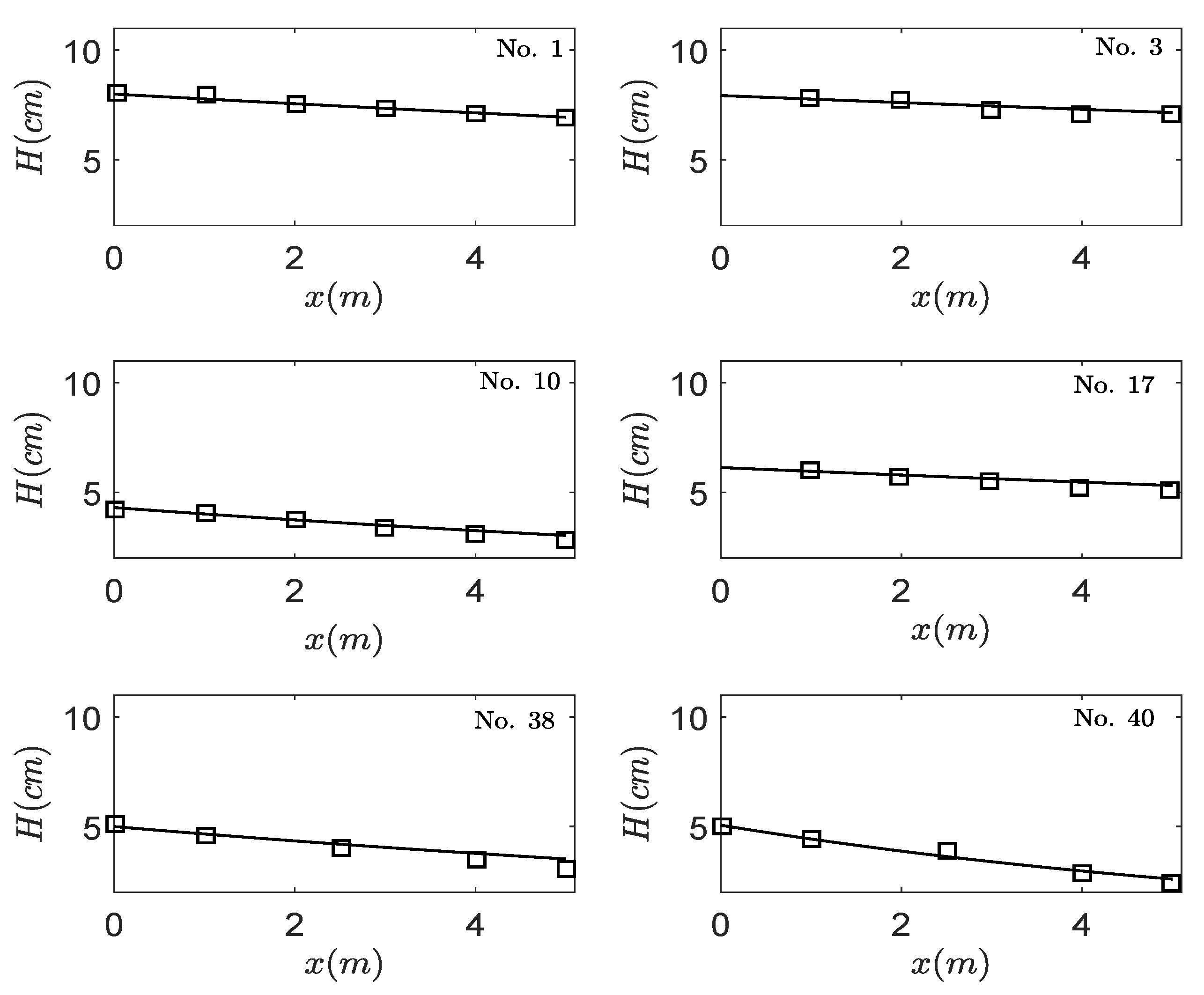
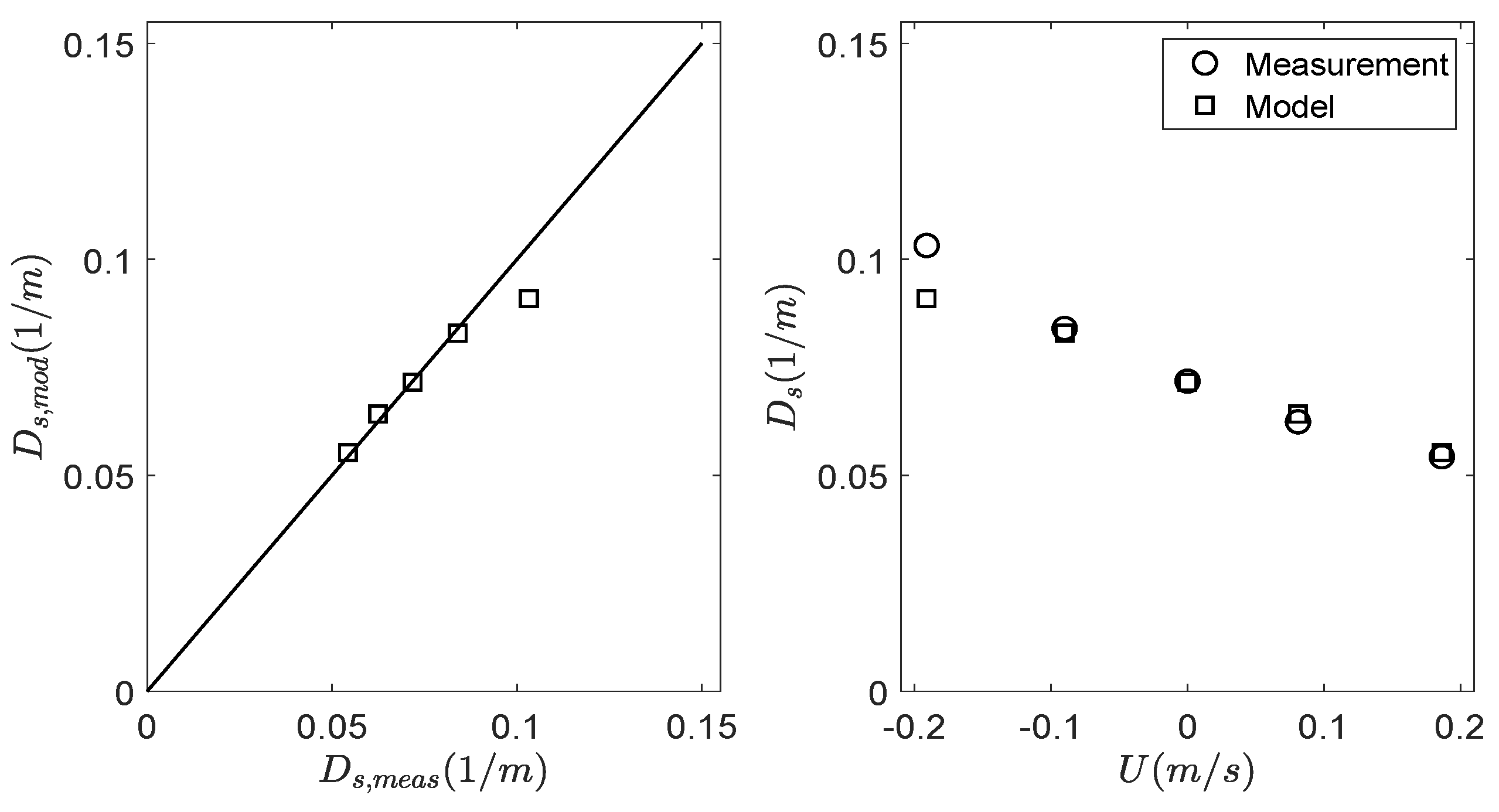
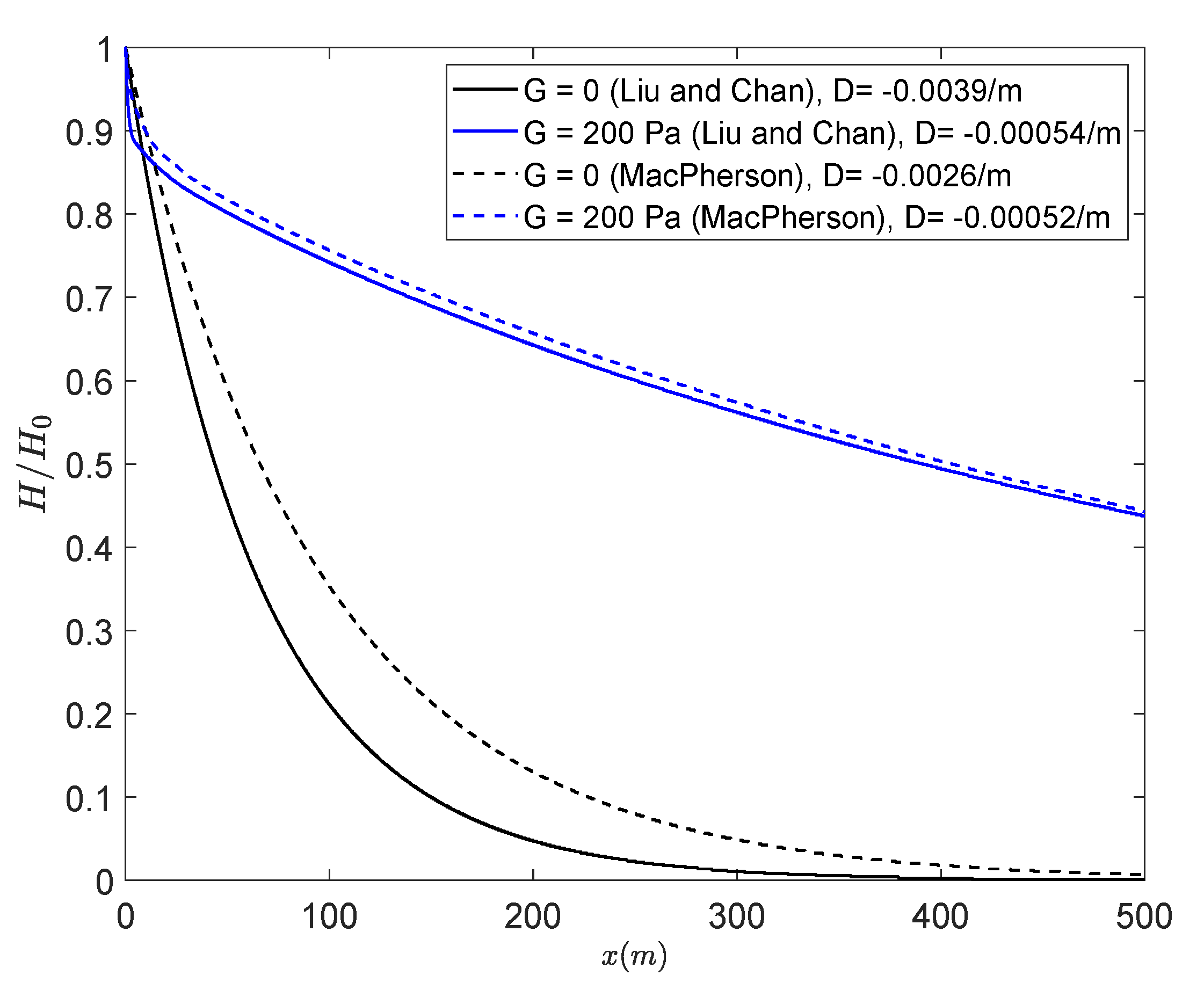
3.1. Model Validation
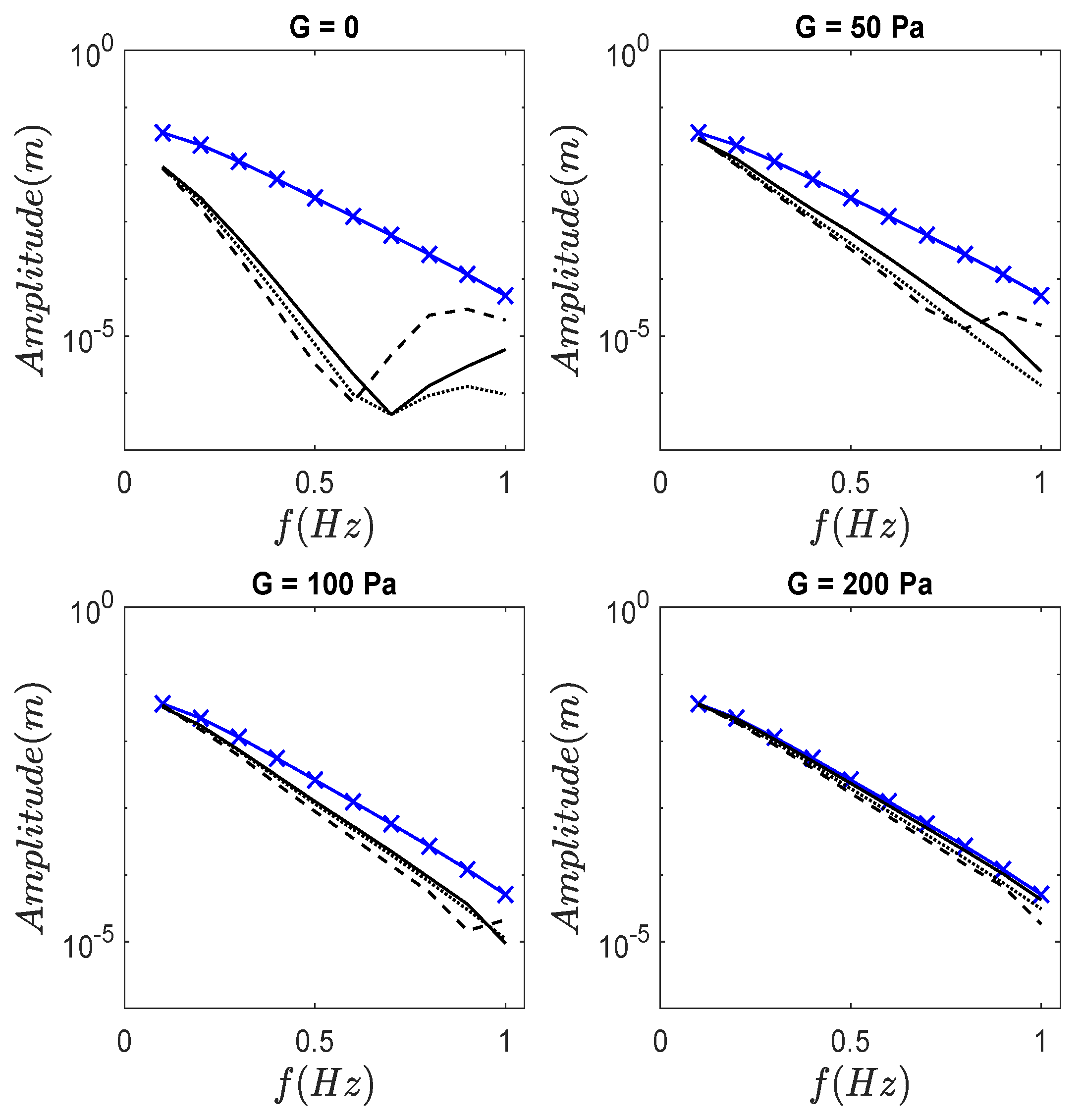
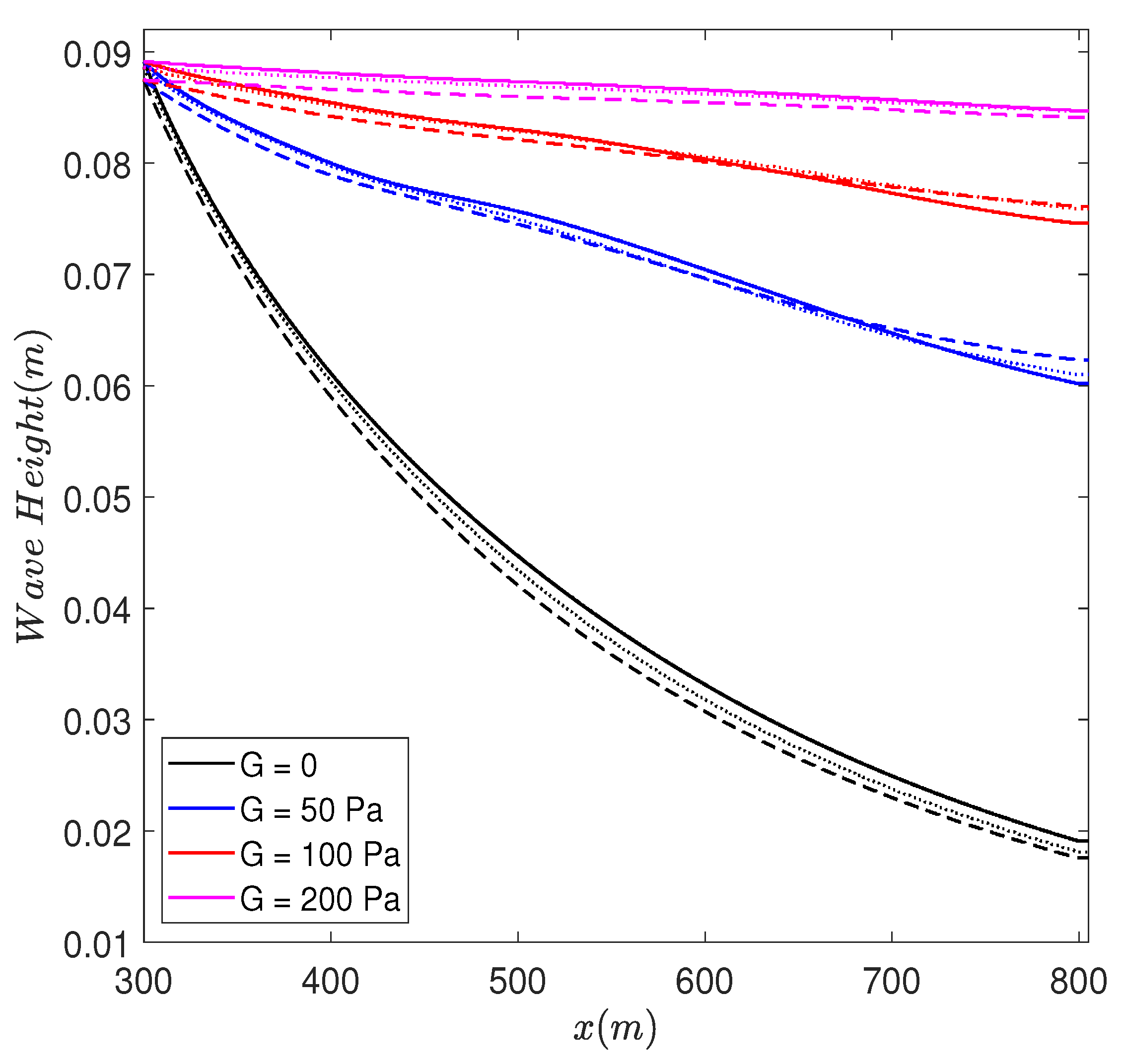
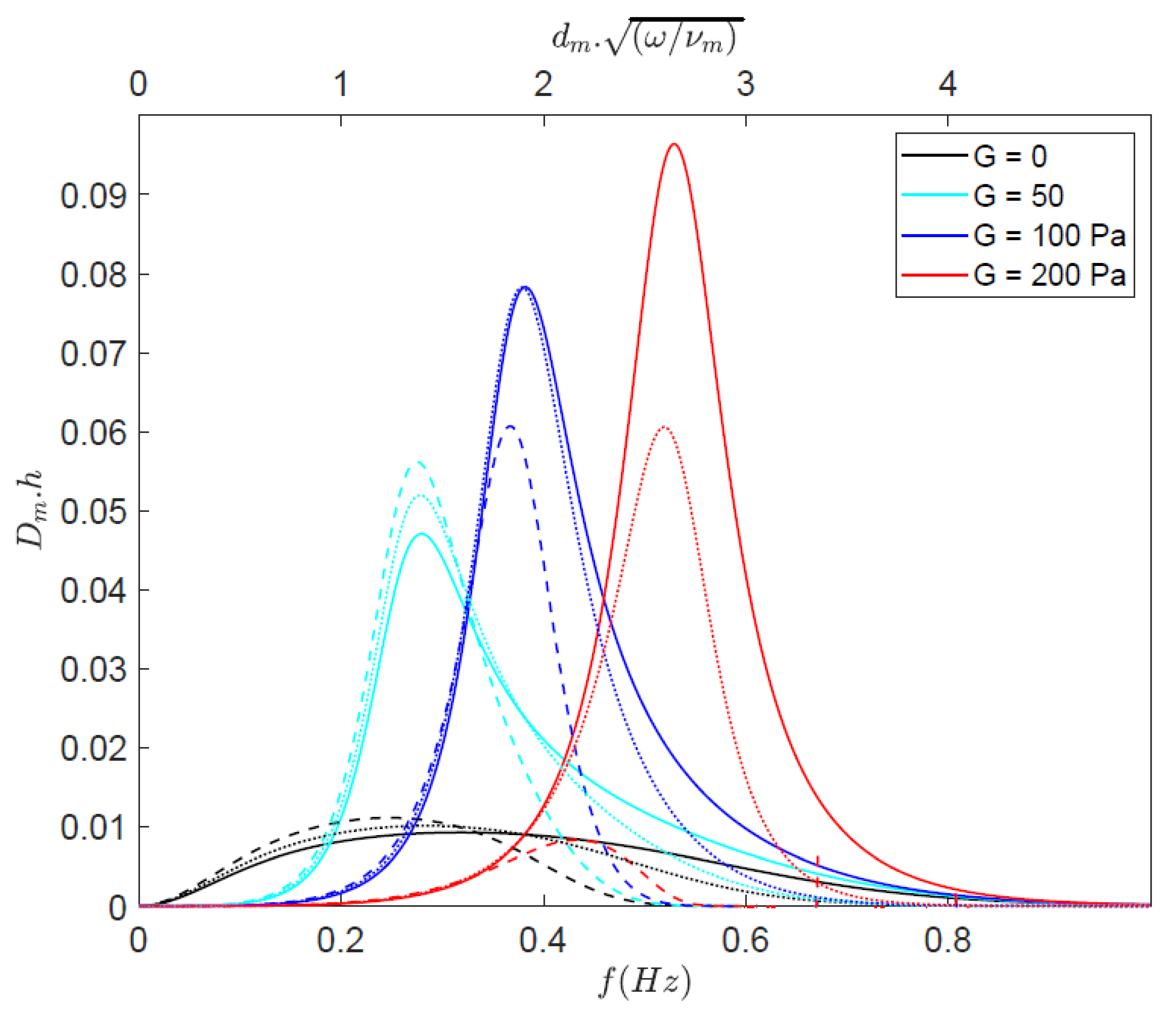
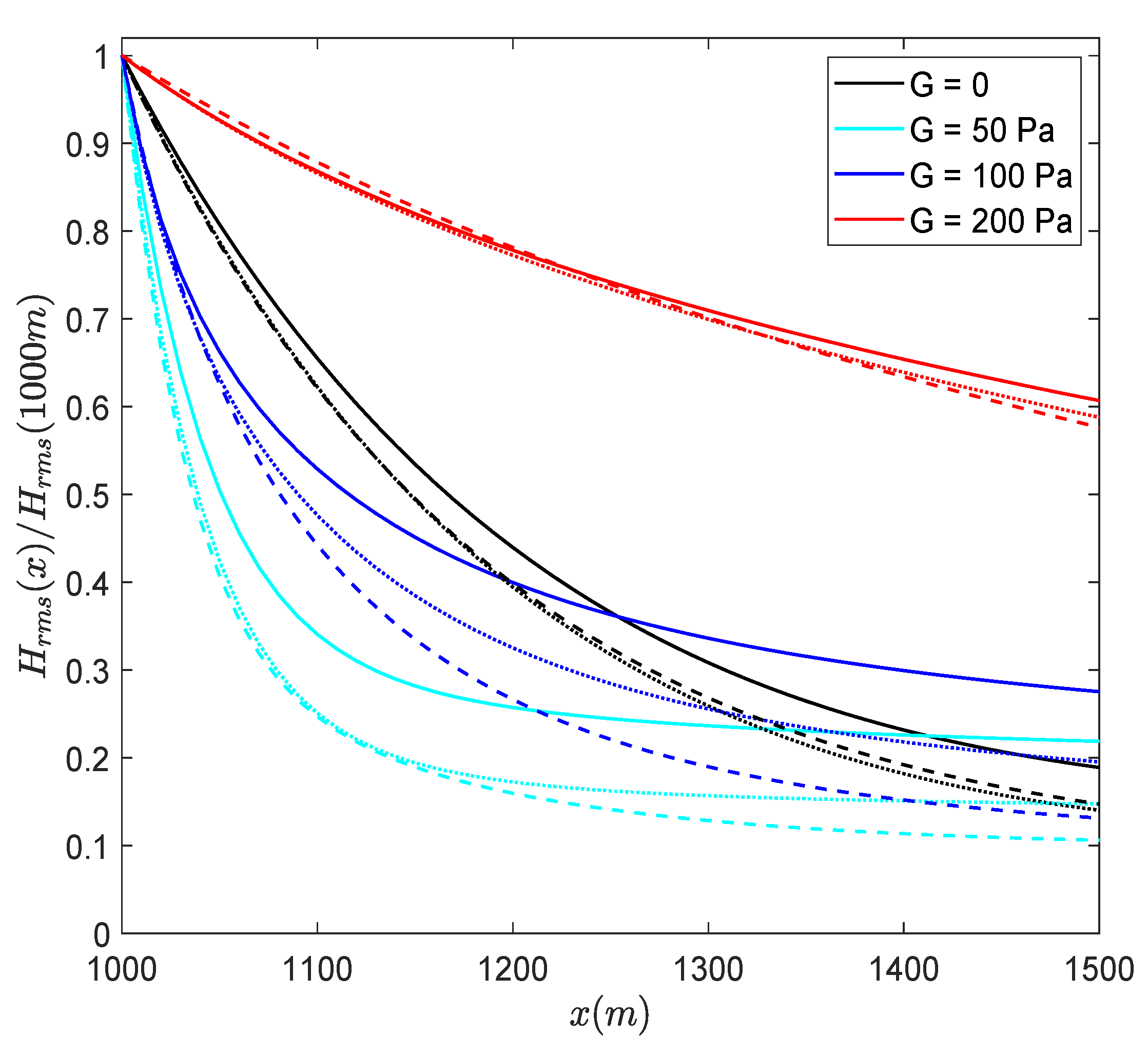
3.2. Effect of Currents on Propagation of Monochromatic Waves over Mud
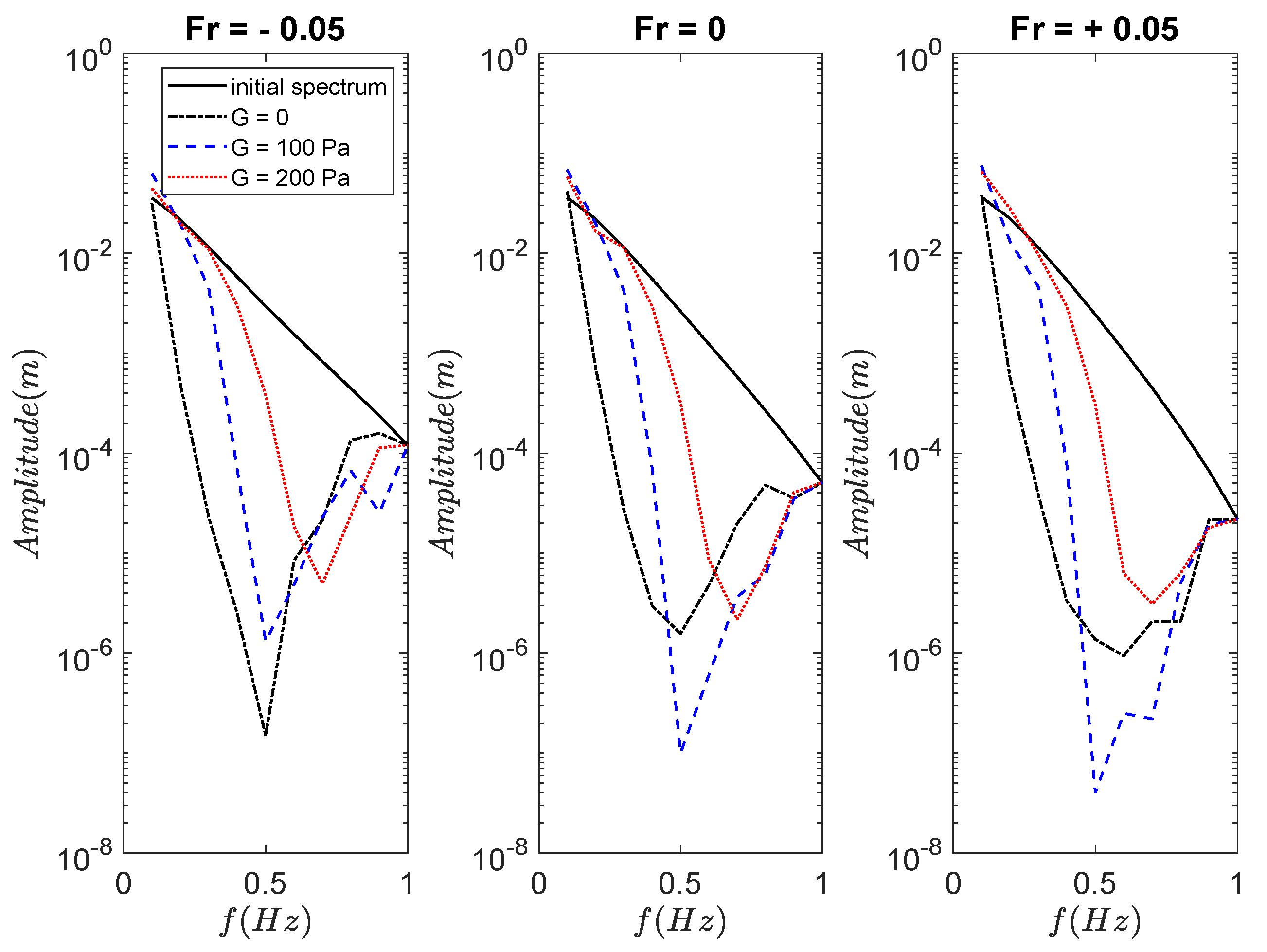
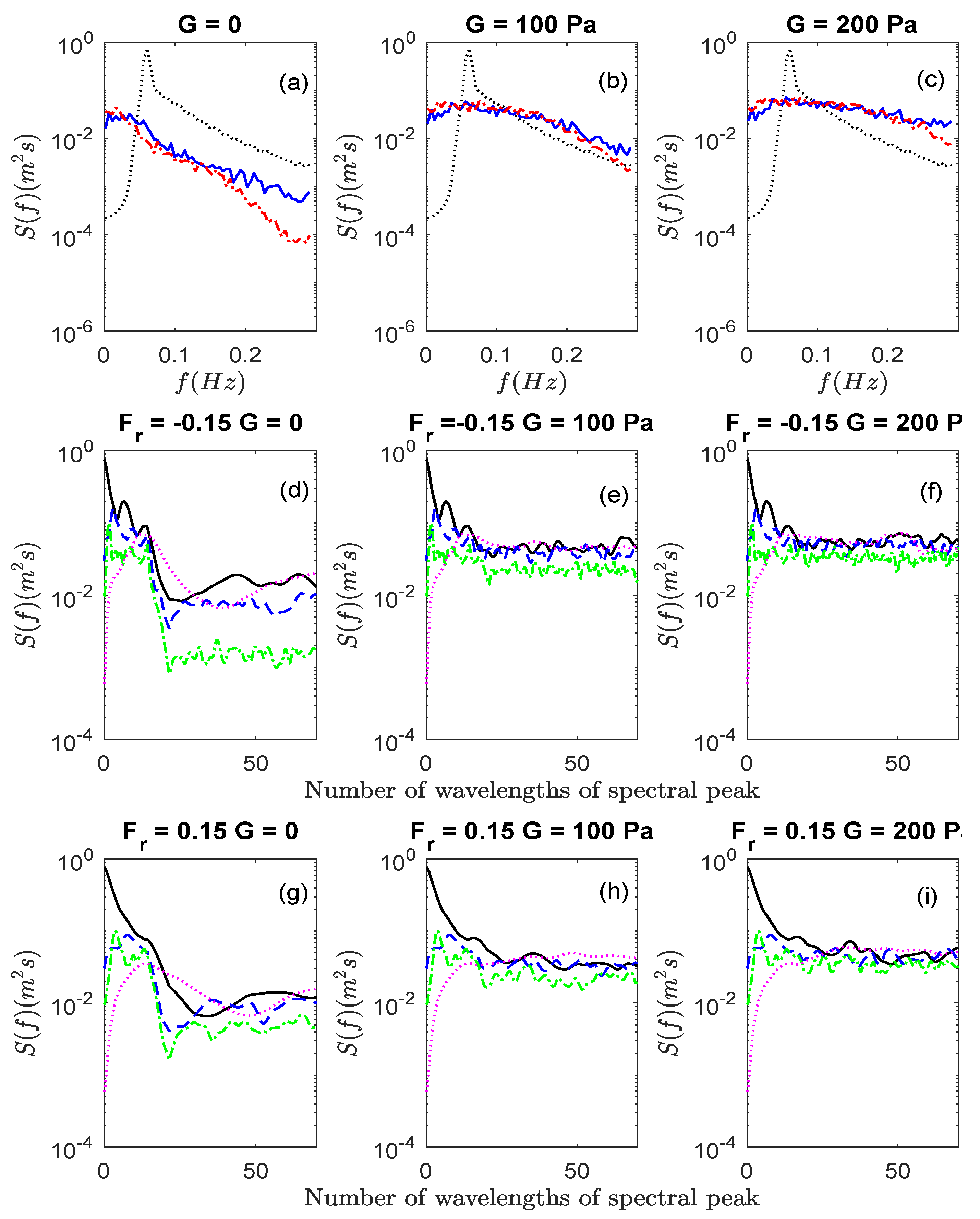
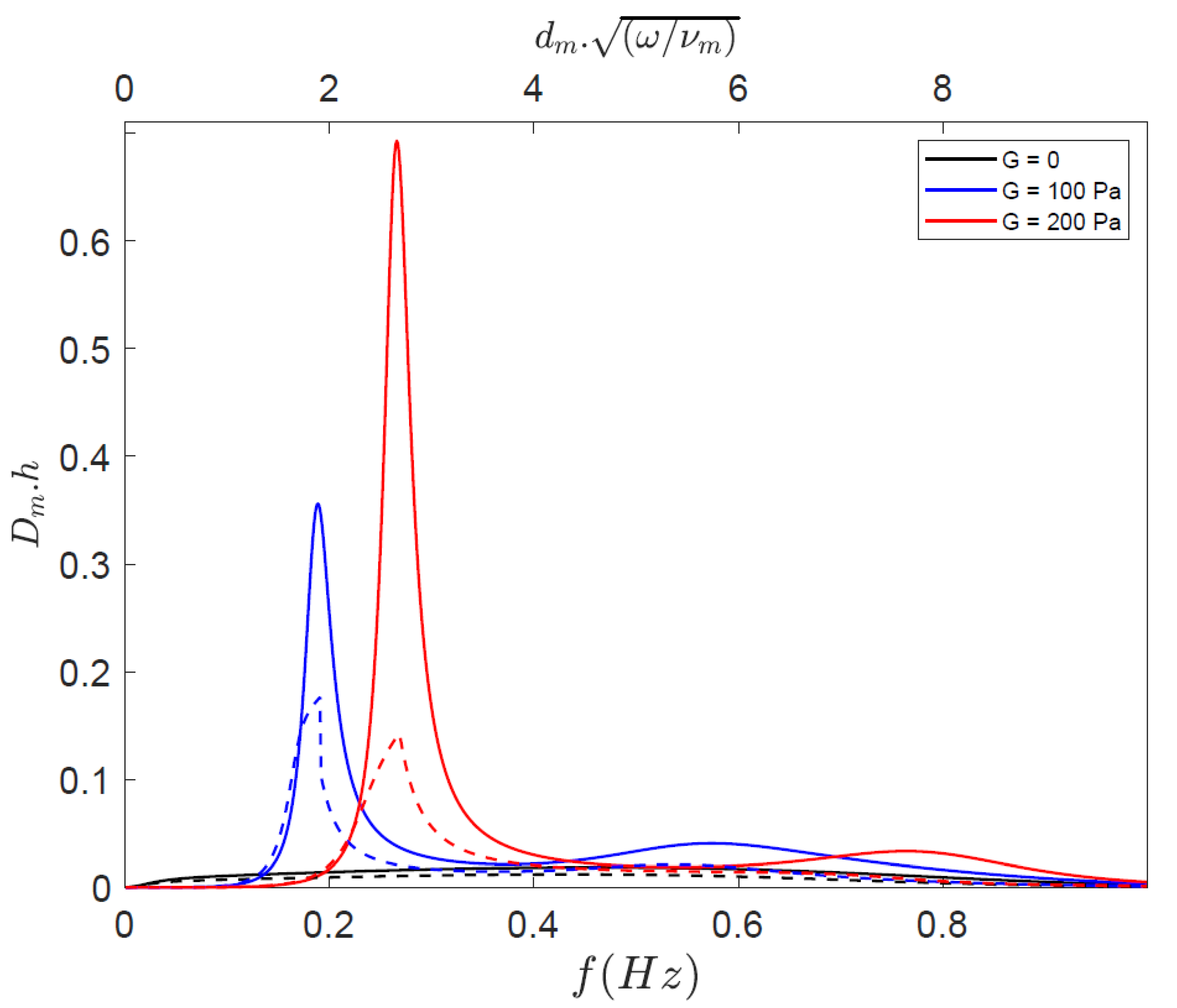
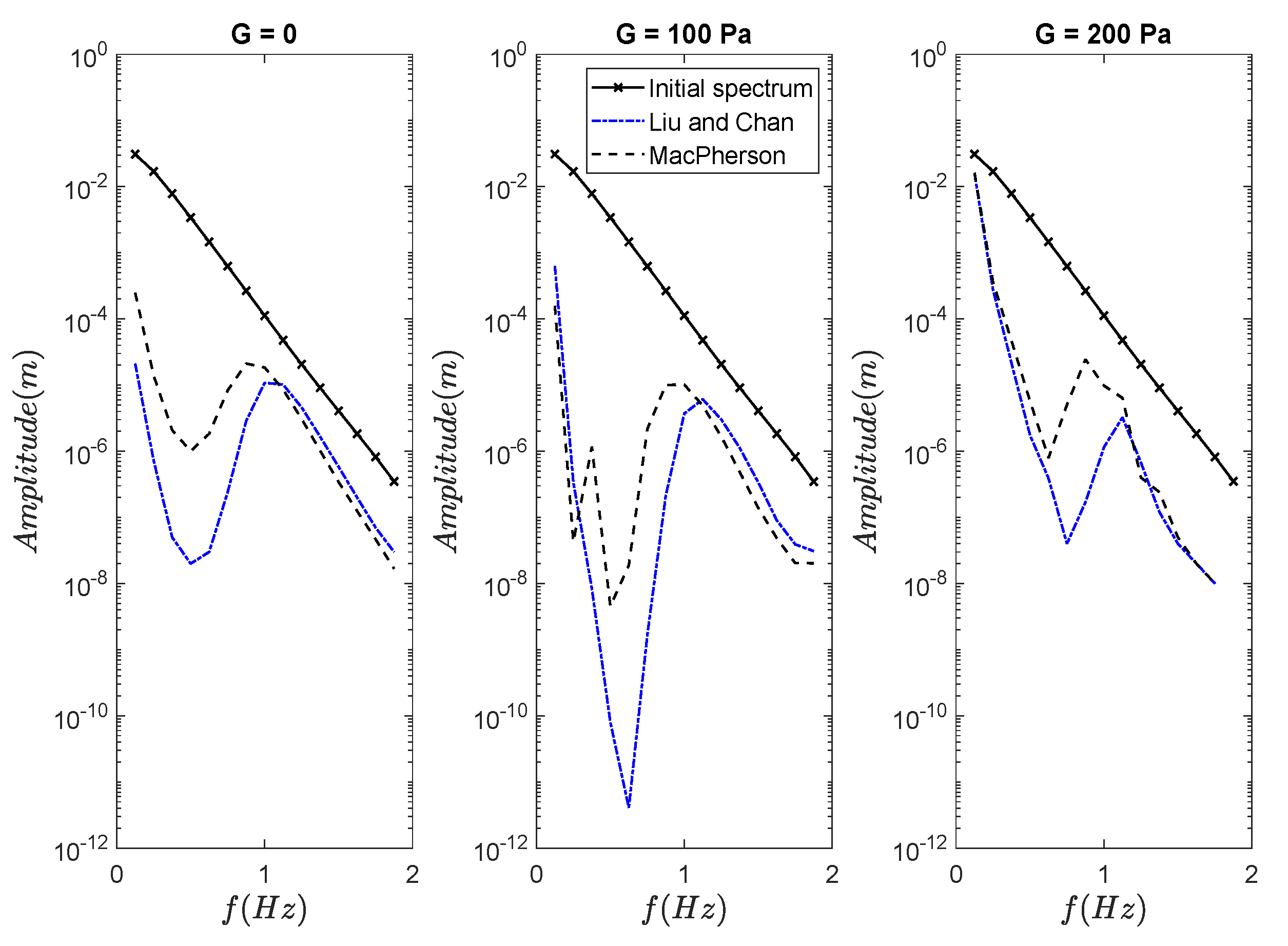
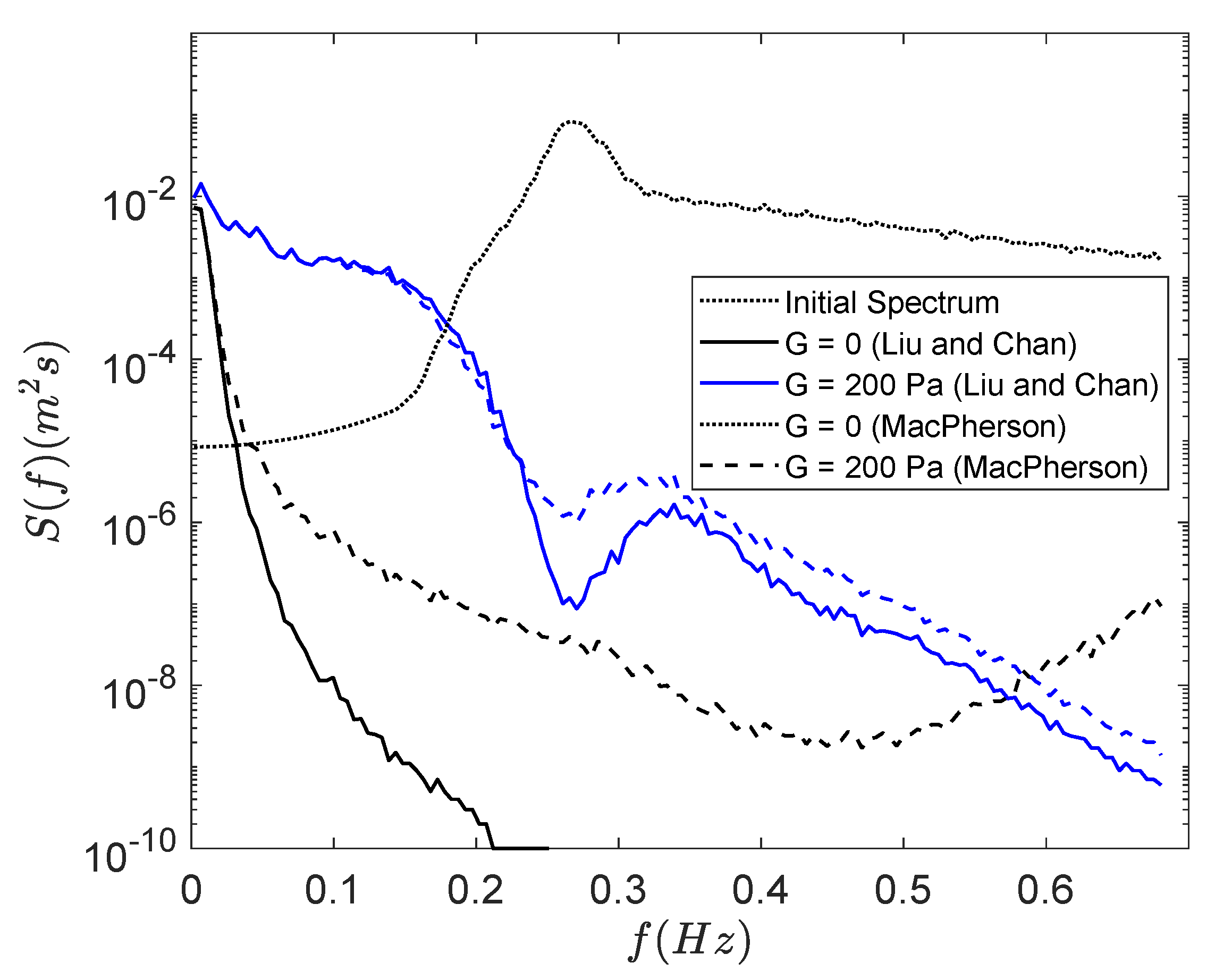
3.3. Effects of Currents on Propagation of Random Wave Spectra over Mud
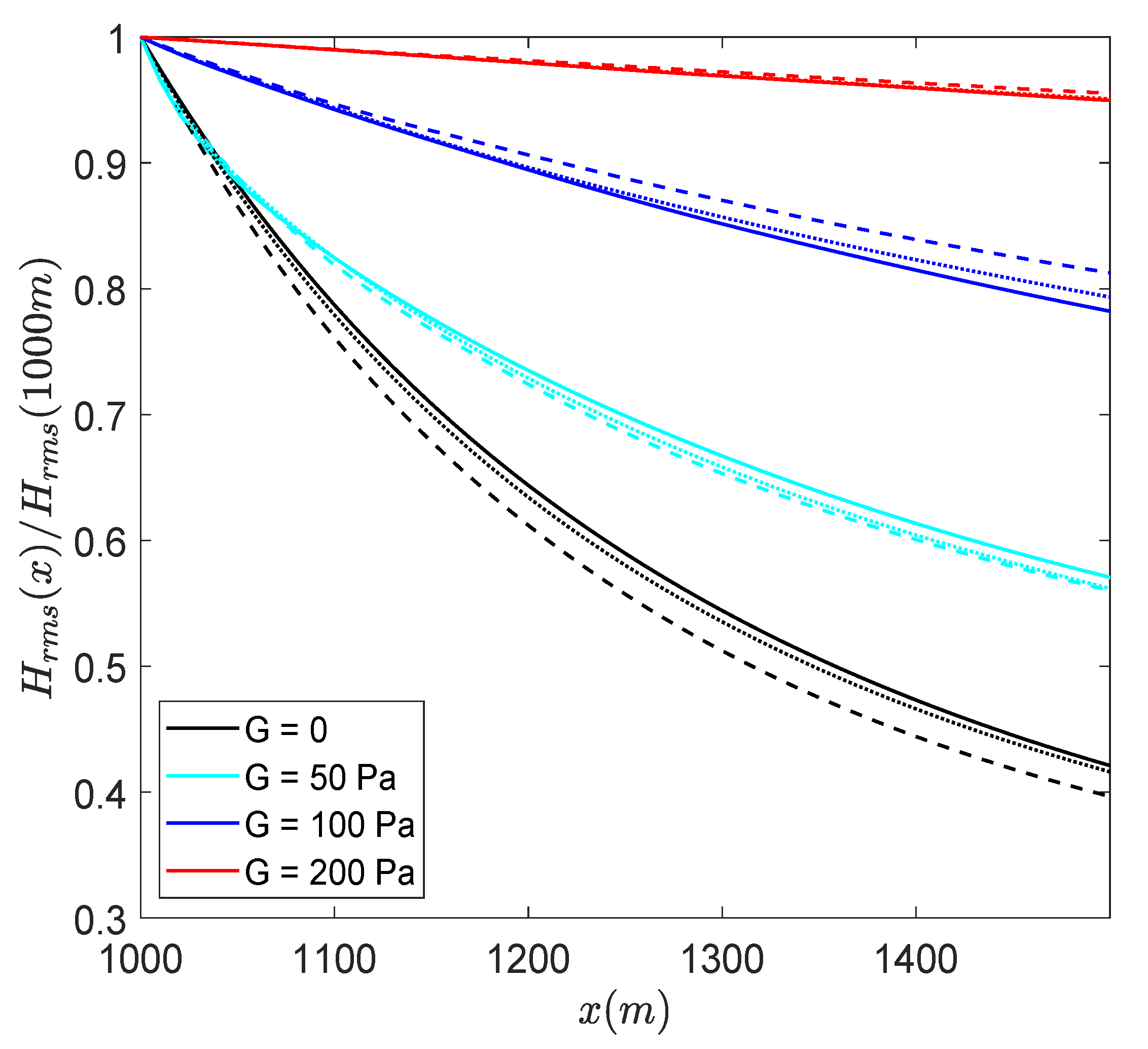
3.4. Propagation of Cnoidal and Random Wave Spectra over Mud of Arbitrary Depth
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheremet, A.; Stone, G.W. Observations of nearshore wave dissipation over muddy seabeds. J. Geophys. Res. 2003, 108, 3357–3368. [Google Scholar] [CrossRef]
- Kaihatu, J.; Sheremet, A.; Holland, K. A model for the propagation of nonlinear surface waves over viscous muds. J. Coast. Eng. 2007, 54, 752–764. [Google Scholar] [CrossRef]
- Tahvildari, N.; Kaihatu, J.M. Optimized determination of viscous mud properties using a nonlinear wave–mud interaction model. J. Atmos. Ocean. Technol. 2011, 28, 1486–1503. [Google Scholar] [CrossRef]
- Liao, Y.P.; Safak, I.; Kaihatu, J.; Sheremet, A. Nonlinear and directional effects on wave predictions over muddy bottoms: Central chenier plain coast, western louisiana shelf, usa. Ocean Dyn. 2015, 65, 1567–1581. [Google Scholar] [CrossRef]
- Safak, I.; Sheremet, A.; Davis, J.; Kaihatu, J.M. Nonlinear wave dynamics in the presence of mud-induced dissipation on atchafalaya shelf, Louisiana, USA. Coast. Eng. 2017, 130, 52–64. [Google Scholar] [CrossRef]
- Tahvildari, N.; Sharifineyestani, E. A numerical study on nonlinear surface wave evolution over viscoelastic mud. Coast. Eng. 2019, 154, 103557. [Google Scholar] [CrossRef]
- Smith, R. Giant waves. J. Fluid. Mech. 1975, 77, 417–431. [Google Scholar] [CrossRef]
- Crapper, G. Nonlinear gravity waves on steady non-uniform currents. J. Fluid. Mech. 1972, 52, 713–724. [Google Scholar] [CrossRef]
- Chawla, A.; Kirby, J. Monochromatic and random wave breaking at blocking points. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Turpin, F.M.; Benmoussa, C.; Mei, C. Effects of slowly varying depth and current on the evolution of a stokes wavepacket. J. Fluid. Mech. 1983, 132, 1–23. [Google Scholar] [CrossRef]
- Kirby, J. Higher-order approximations in the parabolic equation method for water waves. J. Geophys. Res. 1986, 91, 933–952. [Google Scholar] [CrossRef]
- Kaihatu, J. Application of a nonlinear frequency domain wave current interaction model to shallow water recurrence in random waves. J. Ocean Model. 2009, 26, 190–250. [Google Scholar] [CrossRef]
- Bretherton, F.; Garrett, C. Wavetrains in inhomogeneous moving media. Proc. R. Soc. Ser. A 1968, 302, 529–554. [Google Scholar]
- Chen, Q.; Madsen, P.; Basco, D. Current effects on nonlinear interactions of shallow-water waves. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 176–186. [Google Scholar] [CrossRef]
- Dalrymple, R.; Liu, P. Waves over soft muds: A two-layer fluid model. J. Phys. Oceanogr. 1978, 8, 1121–1131. [Google Scholar] [CrossRef]
- Ng, C.O. Water waves over a muddy bed: A two-layer stokes’ boundary layer model. Coast. Eng. 2000, 40, 221–242. [Google Scholar] [CrossRef]
- Macpherson, H. The attenuation of water waves over a non-rigid bed. J. Fluid. Mech. 1980, 97, 721–742. [Google Scholar] [CrossRef]
- Jiang, F.; Mehta, A.J. Mudbanks of the southwest coast of india iv: Mud viscoelastic properties. J. Coast. Res. 1995, 11, 918–926. [Google Scholar]
- Zhao, Z.D.; Lian, J.J.; Shi, J.Z. Interactions among waves, current, and mud: Numerical and laboratory studies. Adv. Water Resour. 2006, 29, 1731–1744. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Chan, I.C. A note on the effects of a thin visco-elastic mud layer on small amplitude water-wave propagation. Coast. Eng. 2007, 54, 233–247. [Google Scholar] [CrossRef]
- Mei, C.C.; Krotov, M.; Huang, Z.; Huhe, A. Short and long waves over a muddy seabed. J. Fluid. Mech. 2010, 643, 33–58. [Google Scholar] [CrossRef]
- Mei, C.C.; Liu, K. A bingham-plastic model for a muddy seabed under long waves. J. Geophys. Res. 1987, 92, 14581–14594. [Google Scholar] [CrossRef]
- Laigle, D.; Lachamp, P.; Naaim, M. Sph-based numerical investigation of mudflow and other complex fluid flow interactions with structures. Comput. Geosci. 2007, 11, 297–306. [Google Scholar] [CrossRef]
- Chan, I.; Liu, P. Responses of bingham-plastic muddy seabed to a surface solitary wave. J. Fluid. Mech. 2009, 618, 155–180. [Google Scholar] [CrossRef]
- Minatti, L.; Pasculli, A. Sph numerical approach in modelling 2d muddy debris flow. In Proceedings of the International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, Padova, Italy, 14–17 June 2011; pp. 467–475. [Google Scholar]
- Shakeel, A.; Kirichek, A.; Chassagne, C. Rheological analysis of natural and diluted mud suspensions. J. Non Newton. Fluid Mech. 2020, 286, 104434. [Google Scholar] [CrossRef]
- Jain, M.; Mehta, A.J. Role of basic rheological models in determination of wave attenuation over muddy seabeds. Cont. Shelf. Res. 2009, 29, 642–651. [Google Scholar] [CrossRef]
- Piedra-Cueva, I. On the response of a muddy bottom to surface water waves. J. Hydraul. Res. 1993, 31, 681–696. [Google Scholar] [CrossRef]
- Almashan, N.; Dalrymple, R. Damping of waves propagating over a muddy bottom in deep water: Experiment and theory. J. Coast. Eng. 2015, 105, 34–46. [Google Scholar] [CrossRef]
- Elgar, S.; Raubenheimer, B. Wave dissipation by muddy seafloors. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Torres-Freyermuth, A.; Hsu, T.J. On the dynamics of wave-mud interaction: A numerical study. J. Geophys. Res. Ocean 2010, 115. [Google Scholar] [CrossRef]
- Hill, D.F.; Foda, M.A. Subharmonic resonance of short internal standing waves by progressive surface waves. J. Fluid Mech. 1996, 321, 217–233. [Google Scholar] [CrossRef]
- Jamali, M.; Seymour, B.; Lawrence, G.A. Asymptotic analysis of a surfaceinterfacial wave interaction. Phys. Fluids 2003, 15, 47–55. [Google Scholar] [CrossRef]
- Tahvildari, N.; Jamali, M. Cubic nonlinear analysis of interaction between a surface wave and two interfacial waves in an open two-layer fluid. Fluid Dyn. Res. 2012, 44, 055502. [Google Scholar] [CrossRef]
- Tahvildari, N.; Kaihatu, J.M.; Saric, W.S. Generation of long subharmonic internal waves by surface waves. Ocean Model. 2016, 106, 12–26. [Google Scholar] [CrossRef]
- Hill, D.F. The Faraday resonance of interfacial waves in weakly viscous fluids. Phys. Fluids 2002, 14, 158–169. [Google Scholar] [CrossRef]
- Winterwerp, J.; De Graaff, R.; Groeneweg, J.; Luijendijk, A. Modelling of wave damping at guyana mud coast. Coast. Eng. 2007, 54, 249–261. [Google Scholar] [CrossRef]
- Kranenburg, W.; Winterwerp, J.; de Boer, G.; Cornelisse, J.; Zijlema, M. Swan-mud: Engineering model for mud-induced wave damping. J. Hydraul. Eng. 2011, 137, 959–975. [Google Scholar] [CrossRef]
- Rogers, W.; Orzech, M. Implementation and Testing of Ice and Mud Source Functions in Wavewatch III, Nrl Memorandum Report; Technical Report NRL/MR/7320-13-9462; Naval Research Laboratory: Washington, DC, USA, 2013. [Google Scholar]
- Kaihatu, J.M.; Tahvildari, N. The combined effect of wave-current interaction and mud-induced damping on nonlinear wave evolution. Ocean Model. 2012, 41, 22–34. [Google Scholar] [CrossRef]
- Kemp, P.H.; Simons, R.R. The interaction of waves and a turbulent current: Waves propagating against the current. J. Fluid Mech. 1983, 130, 73–89. [Google Scholar] [CrossRef]
- Soulsby, R.; Hamm, L.; Klopman, G.; Myrhaug, D.; Simons, R.; Thomas, G. Wave-current interaction within and outside the bottom boundary layer. Coast. Eng. 1993, 21, 41–69. [Google Scholar] [CrossRef]
- Huang, Z.; Mei, C.C. Effects of surface waves on a turbulent current over a smooth or rough seabed. J. Fluid Mech. 2003, 497, 253–287. [Google Scholar] [CrossRef]
- Tambroni, N.; Blondeaux, P.; Vittori, G. A simple model of wave–current interaction. J. Fluid Mech. 2015, 775, 328–348. [Google Scholar] [CrossRef]
- Smith, R.; Sprinks, T. Scattering of surface waves by a conical island. J. Fluid Mech. 1975, 72, 373–384. [Google Scholar] [CrossRef]
- Radder, A. On the parabolic equation method for water-wave propagation. J. Fluid Mech. 1979, 95, 159–176. [Google Scholar] [CrossRef]
- Kaihatu, J.M.; Kirby, J.T. Nonlinear transformation of waves in finite water depth. Phys. Fluids 1995, 7, 1903–1914. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. A perturbation method to solve dispersion equations for water waves over dissipative media. Coast. Eng. 2004, 51, 81–89. [Google Scholar] [CrossRef]
- Ng, C.O.; Chiu, H.S. Use of mathcad as a calculation tool for water waves over a stratified muddy bed. Coast. Eng. J. 2009, 51, 69–79. [Google Scholar] [CrossRef]
- De Wit, P.J. Liquefaction of cohesive sediments caused by waves. Oceanogr. Lit. Rev. 1996, 3, 252. [Google Scholar]
- Jiang, F.; Mehta, A.J. Mudbanks of the southwest coast of india. v: Wave attenuation. J. Coast. Res. 1996, 12, 890–897. [Google Scholar]
- Soltanpour, M.; Samsami, F. A comparative study on the rheology and wave dissipation of kaolinite and natural hendijan coast mud, the persian gulf. J. Ocean Dyn. 2011, 61, 295–309. [Google Scholar] [CrossRef]
- An, N.; Shibayama, T. Wave-current interaction with mud bed. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; pp. 2913–2927. [Google Scholar]
- Rogers, W.E.; Holland, K.T. A study of dissipation of wind-waves by mud at cassino beach, brazil: Prediction and inversion. Cont. Shelf. Res. 2009, 29, 676–690. [Google Scholar] [CrossRef]
- Kaihatu, J.M. Improvement of parabolic nonlinear dispersive wave model. J. Waterw. Port Coast. Ocean Eng. 2001, 127, 113–121. [Google Scholar] [CrossRef]
- Bouws, E.; Günther, H.; Rosenthal, W.; Vincent, C. Similarity of the wind wave spectrum in finite depth water: 1. spectral form. J. Geophys. Res. Ocean. 1985, 90, 975–986. [Google Scholar] [CrossRef]
- Ozdemir, C.E.; Hsu, T.J.; Balachandar, S. Direct numerical simulations of instability and boundary layer turbulence under a solitary wave. J. Fluid Mech. 2013, 731, 545–578. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharifineyestani, E.; Tahvildari, N. Nonlinear Wave Evolution in Interaction with Currents and Viscoleastic Muds. J. Mar. Sci. Eng. 2021, 9, 529. https://doi.org/10.3390/jmse9050529
Sharifineyestani E, Tahvildari N. Nonlinear Wave Evolution in Interaction with Currents and Viscoleastic Muds. Journal of Marine Science and Engineering. 2021; 9(5):529. https://doi.org/10.3390/jmse9050529
Chicago/Turabian StyleSharifineyestani, Elham, and Navid Tahvildari. 2021. "Nonlinear Wave Evolution in Interaction with Currents and Viscoleastic Muds" Journal of Marine Science and Engineering 9, no. 5: 529. https://doi.org/10.3390/jmse9050529
APA StyleSharifineyestani, E., & Tahvildari, N. (2021). Nonlinear Wave Evolution in Interaction with Currents and Viscoleastic Muds. Journal of Marine Science and Engineering, 9(5), 529. https://doi.org/10.3390/jmse9050529





