Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River
Abstract
1. Introduction
2. Model Description
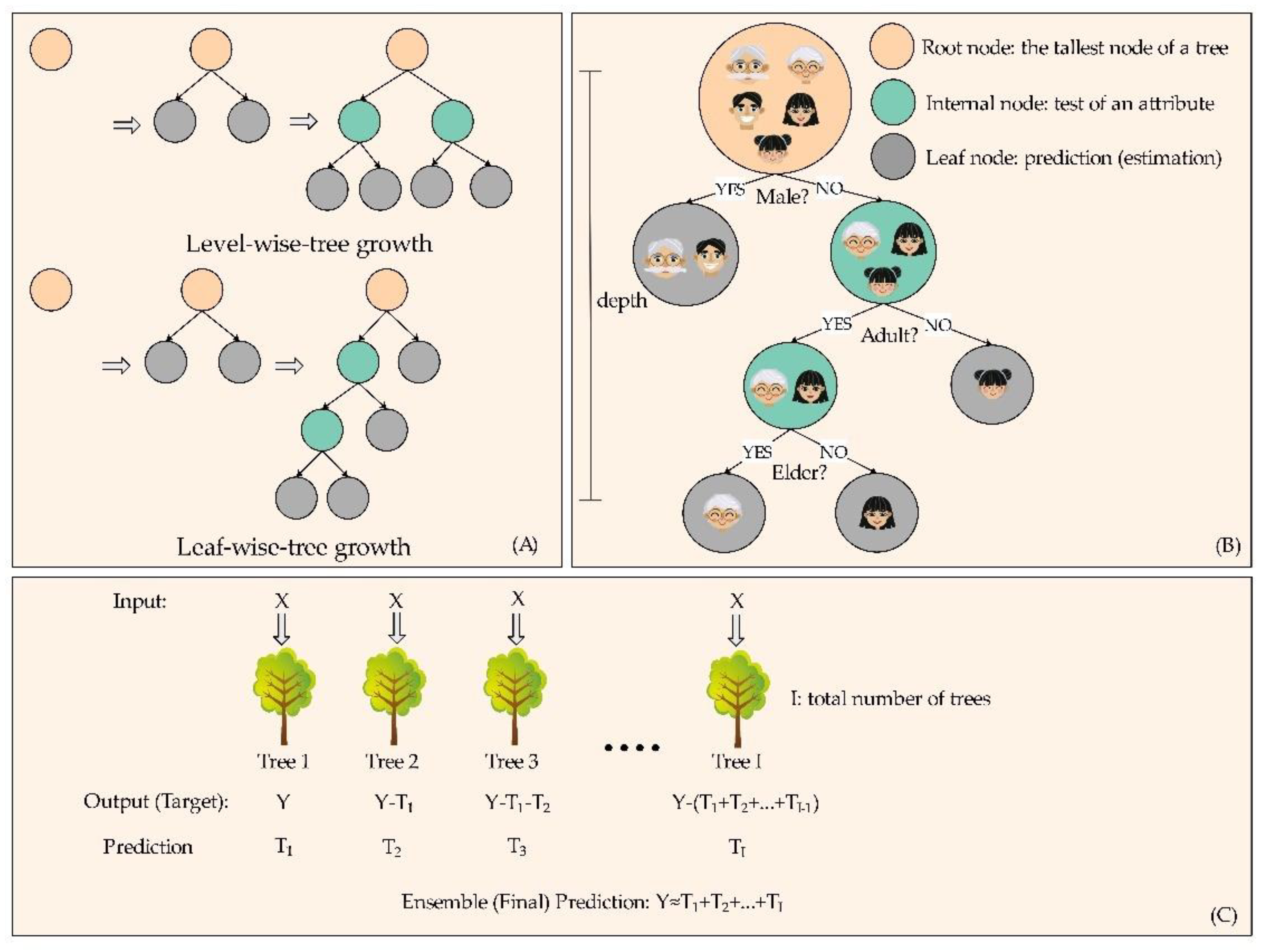
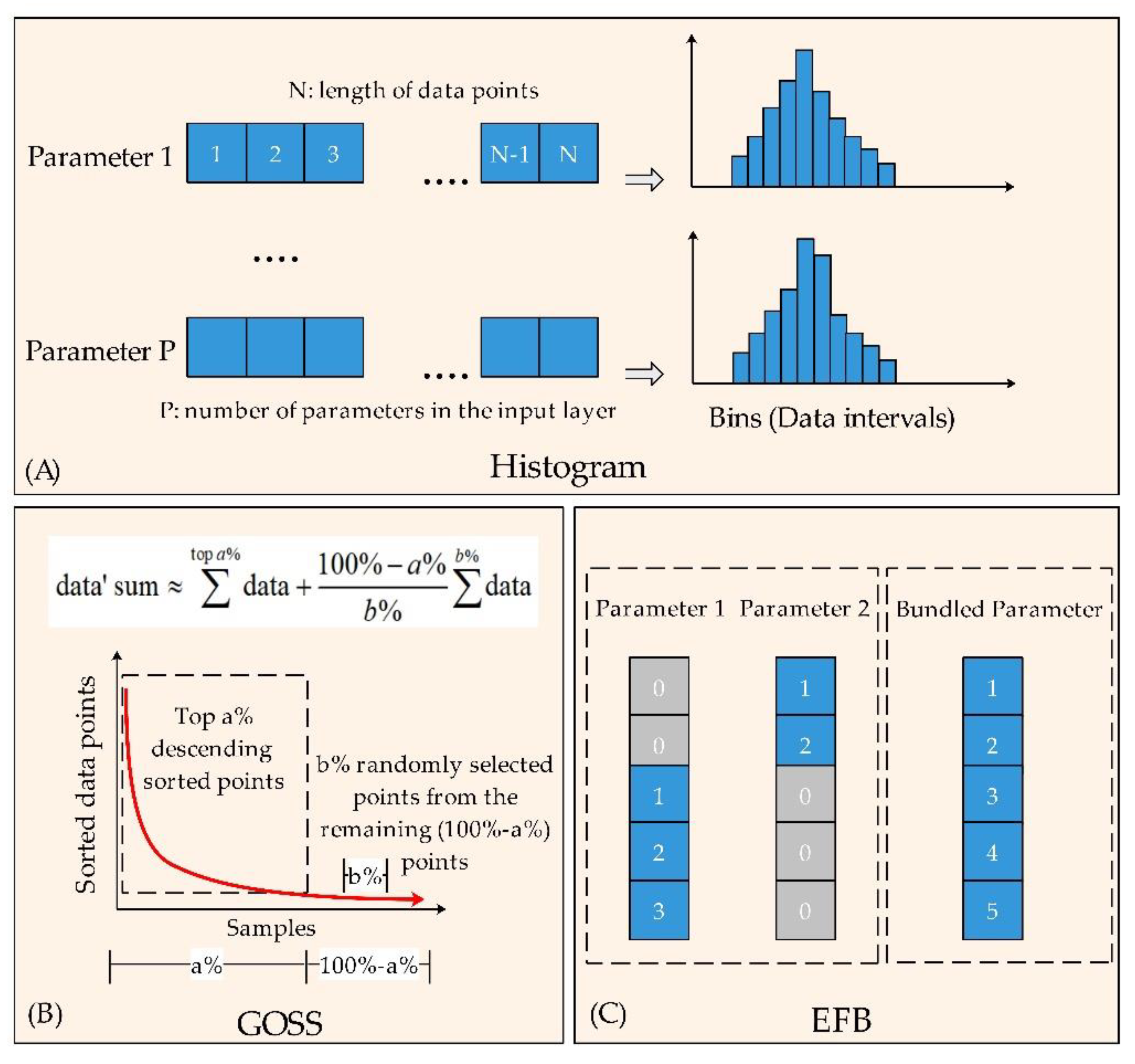
2.1. The Algorithm of the LightGBM Model
2.2. Construction of the LightGBM Model
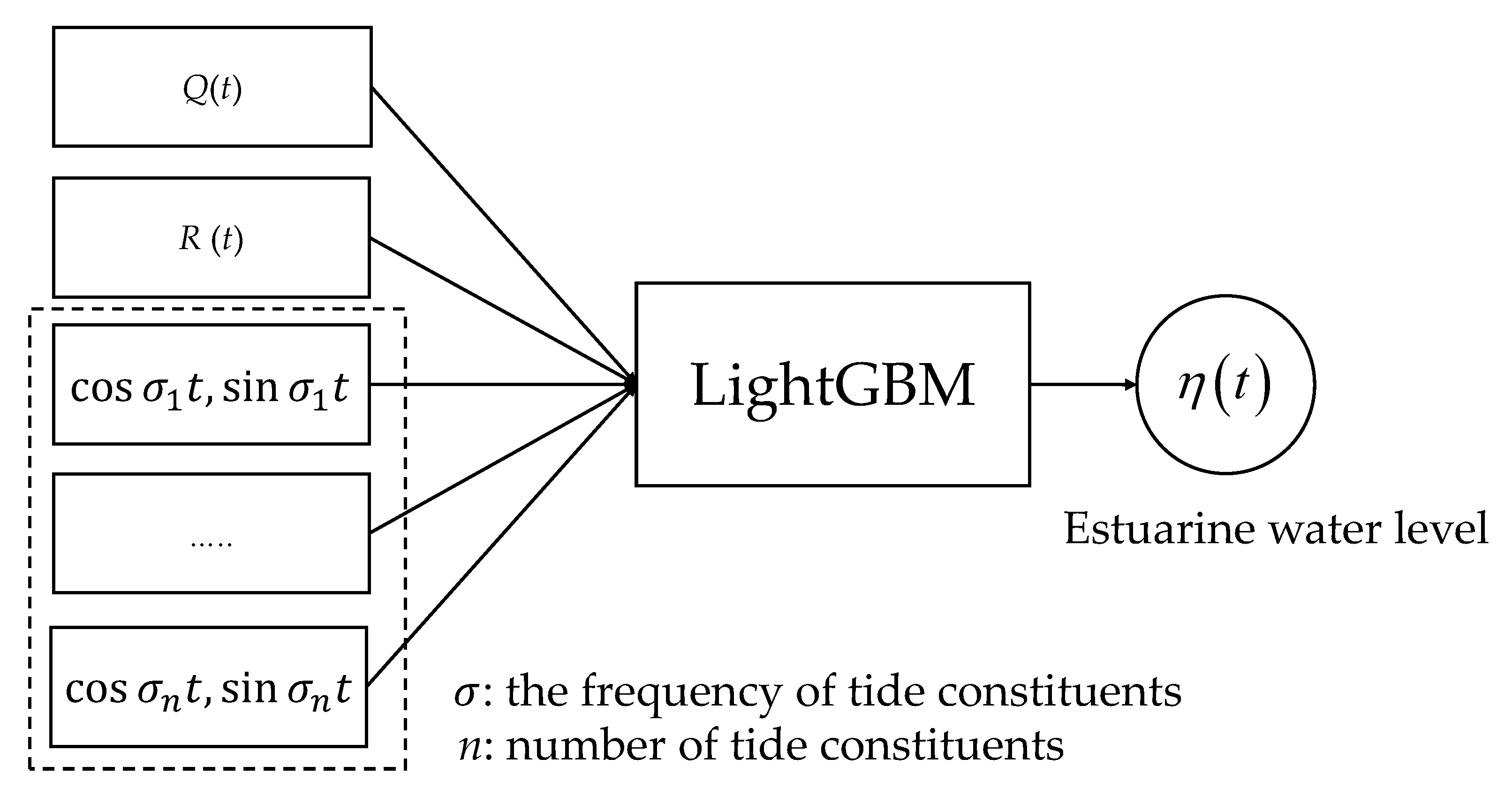
2.2.1. Input and Output Setting
2.2.2. Hyperparameters Setting
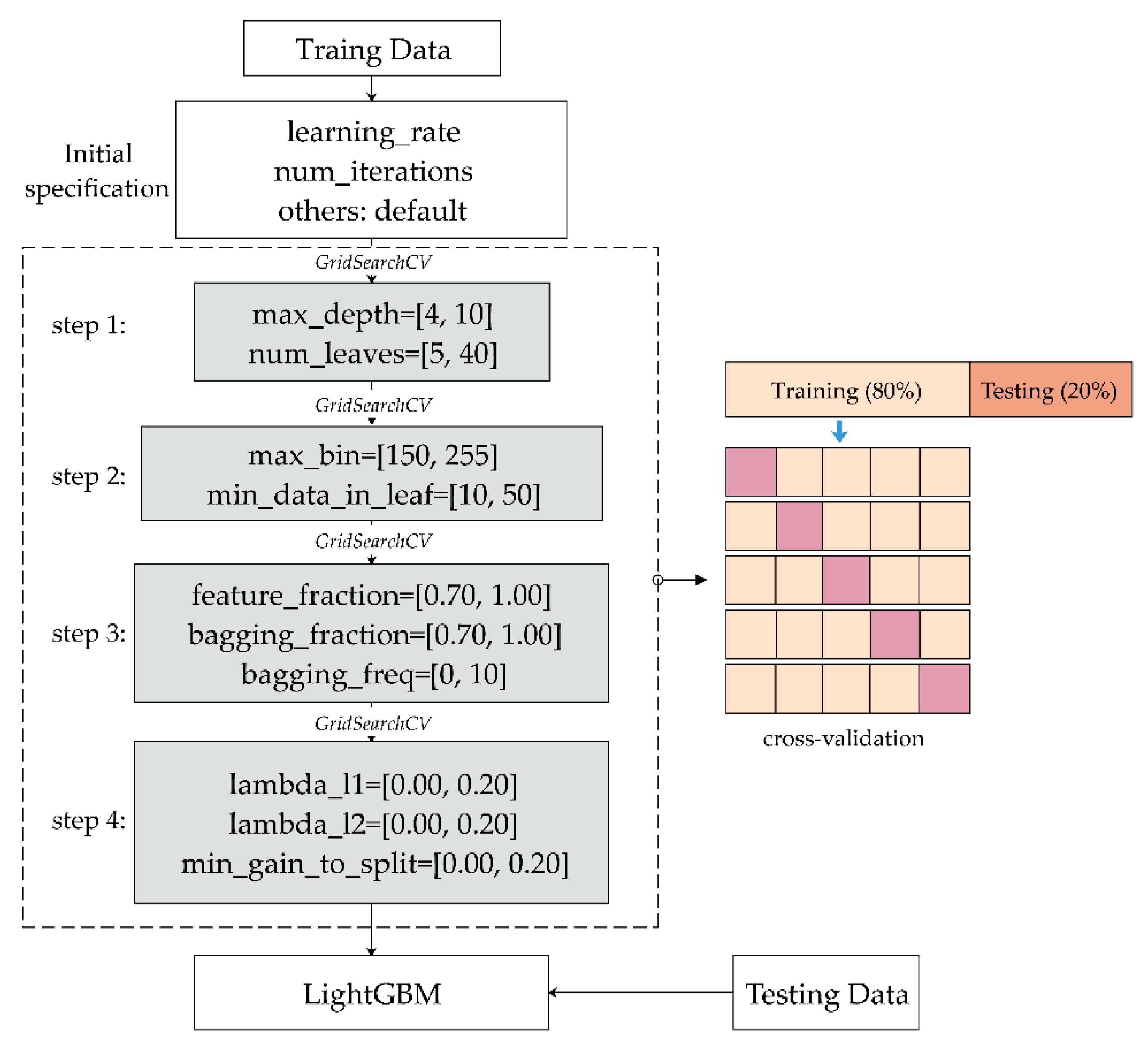
2.2.3. Optimal Hyperparameters Searching
3. Study Area & Data
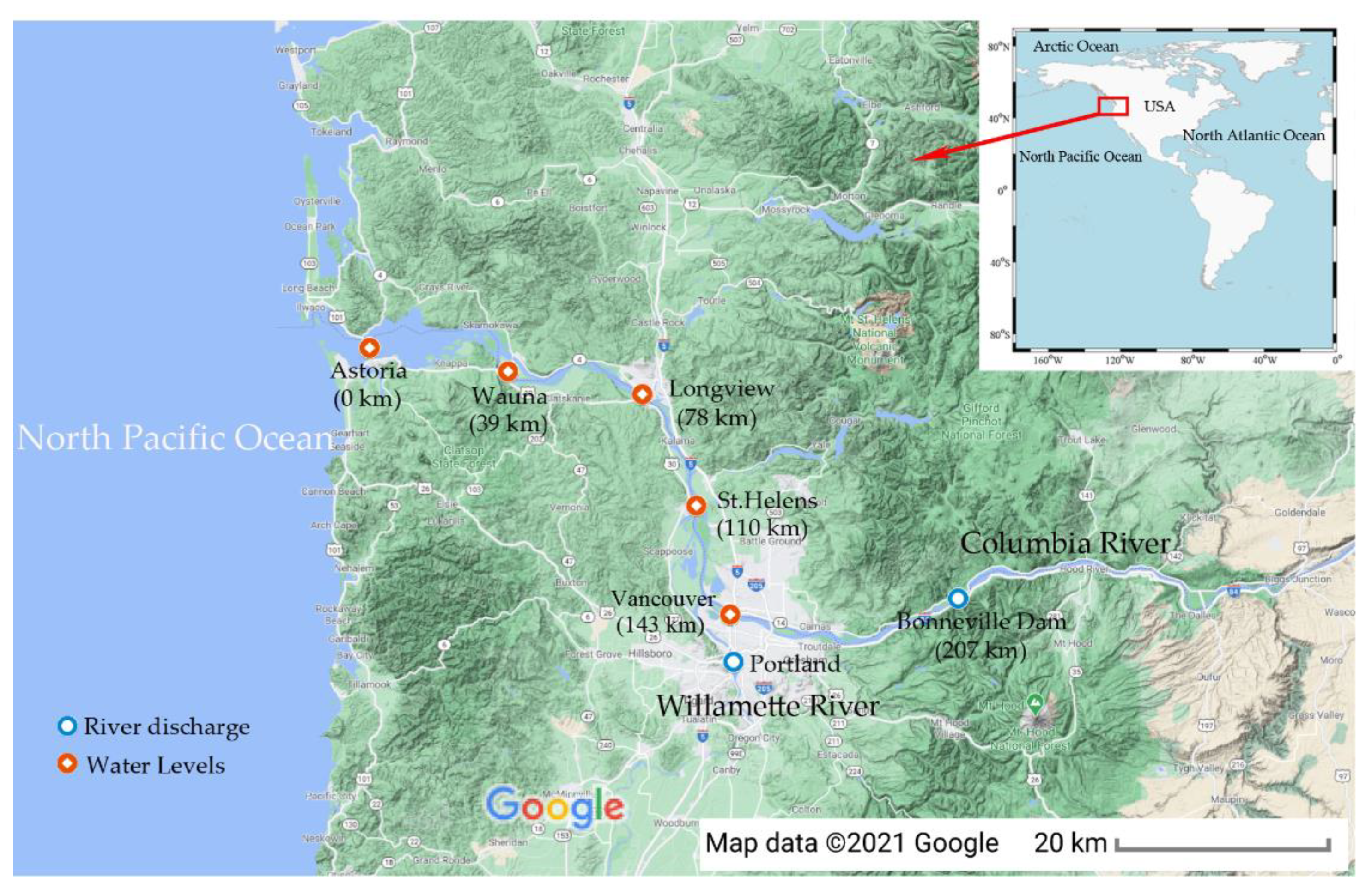
3.1. The Lower Columbia River
3.2. Data
3.3. Data Preparation
4. Model Training
5. Model Testing
6. Discussion
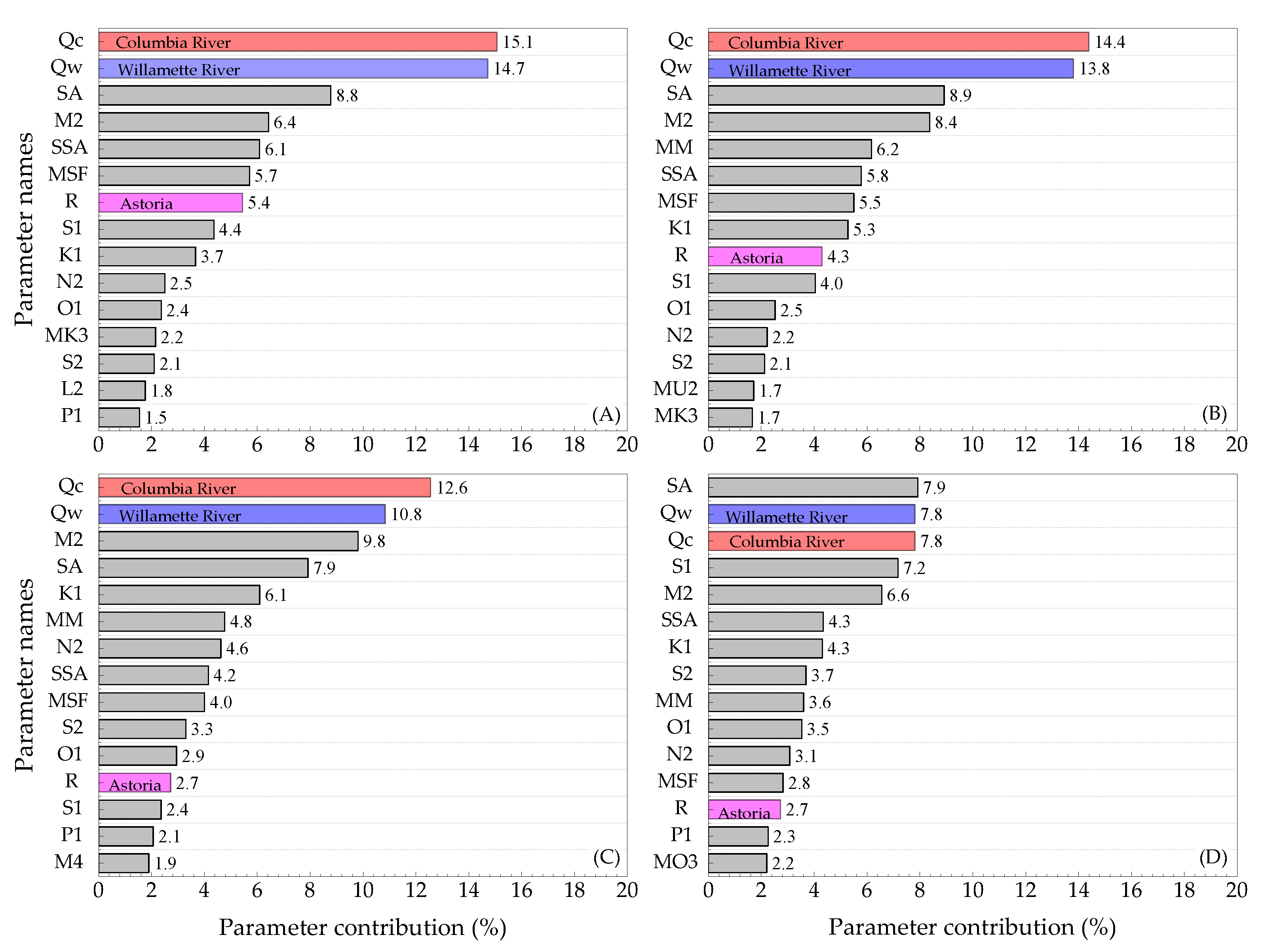
6.1. Parameter Contribution to the LightGBM Model
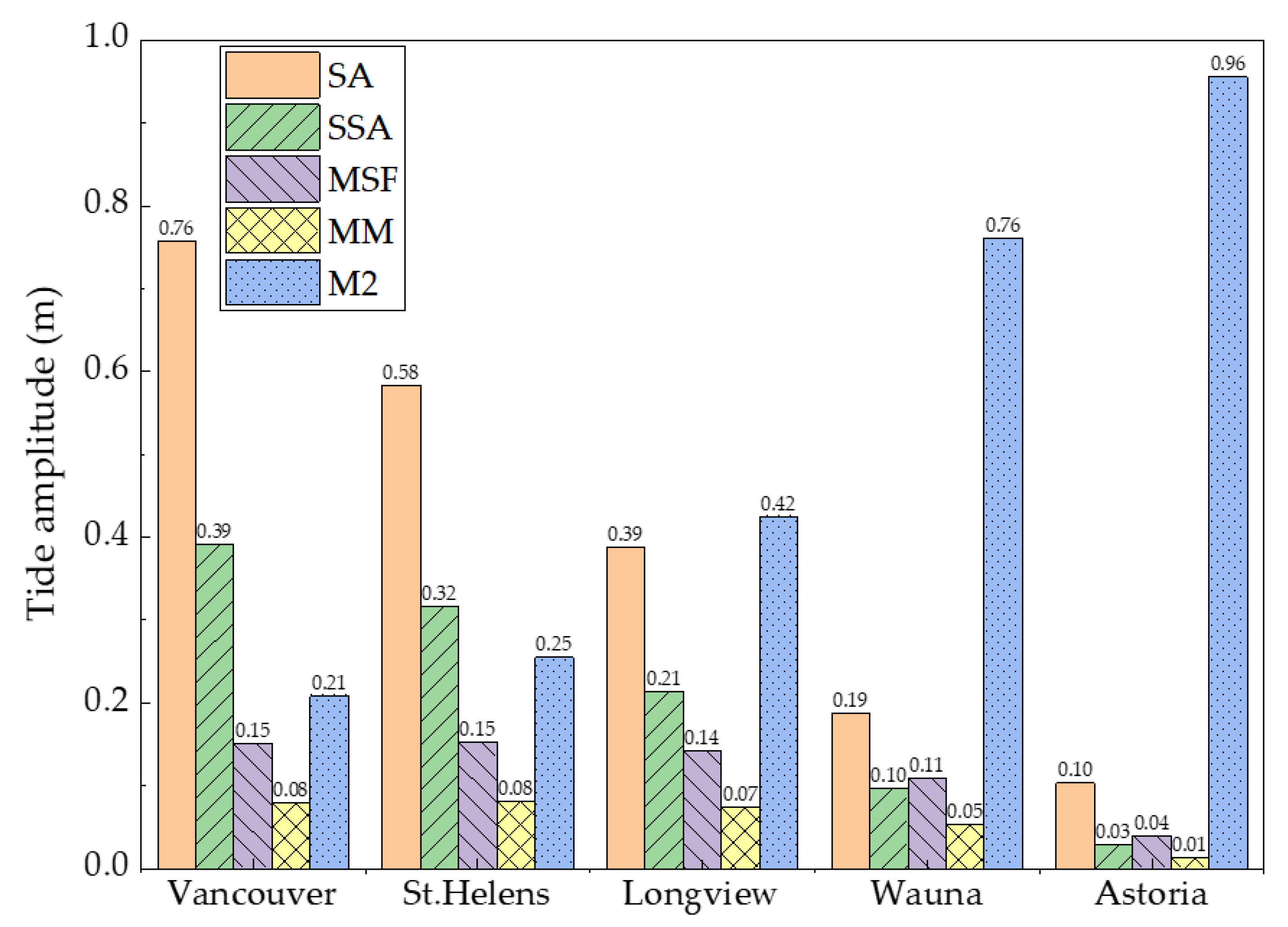
6.2. The Subtide Constituents
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Savenije, H.H.G. Prediction in ungauged estuaries: An integrated theory. Water Resour. Res. 2015, 51, 2464–2476. [Google Scholar] [CrossRef]
- Garvine, R.W. The distribution of salinity and temperature in the connecticut river estuary. J. Geophys. Res. 1975, 80, 1176–1183. [Google Scholar] [CrossRef]
- Chau, K.W. A split-step particle swarm optimization algorithm in river stage forecasting. J. Hydrol. 2007, 346, 131–135. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Gallo, M.N.; Vinzon, S.B. Generation of overtides and compound tides in Amazon estuary. Ocean Dyn. 2005, 55, 441–448. [Google Scholar] [CrossRef]
- Matte, P.; Jay, D.A.; Zaron, E.D. Adaptation of classical tidal harmonic analysis to nonstationary tides, with application to river tides. J. Atmos. Ocean. Technol. 2013, 30, 569–589. [Google Scholar] [CrossRef]
- Jay, D.A. Green’s law revisited: Tidal long-wave propagation in channels with strong topography. J. Geophys. Res. 1991, 96, 20585. [Google Scholar] [CrossRef]
- Godin, G. The propagation of tides up rivers with special considerations on the upper Saint Lawrence River. Estuar. Coast. Shelf Sci. 1999, 48, 307–324. [Google Scholar] [CrossRef]
- Pan, H.; Lv, X.; Wang, Y.; Matte, P.; Chen, H.; Jin, G. Exploration of Tidal-Fluvial interaction in the Columbia River Estuary Using S_TIDE. J. Geophys. Res. Oceans 2018, 123, 6598–6619. [Google Scholar] [CrossRef]
- Cai, H.; Yang, Q.; Zhang, Z.; Guo, X.; Liu, F.; Ou, S. Impact of river-tide dynamics on the temporal-spatial distribution of residual water level in the Pearl River channel Networks. Estuaries Coasts 2018, 41, 1885–1903. [Google Scholar] [CrossRef]
- Gan, M.; Chen, Y.; Pan, S.; Li, J.; Zhou, Z. A modified nonstationary tidal harmonic analysis model for the Yangtze estuarine tides. J. Atmos. Ocean. Technol. 2019, 36, 513–525. [Google Scholar] [CrossRef]
- Matte, P.; Secretan, Y.; Morin, J. Temporal and spatial variability of tidal-fluvial dynamics in the St. Lawrence fluvial estuary: An application of nonstationary tidal harmonic analysis. J. Geophys. Res. Oceans 2014, 119, 5724–5744. [Google Scholar] [CrossRef]
- Pan, H.D.; Guo, Z.; Wang, Y.Y.; Lv, X.Q. Application of the EMD method to river tides. J. Atmos. Ocean. Technol. 2018, 35, 809–819. [Google Scholar] [CrossRef]
- Pan, H.; Lv, X. Reconstruction of spatially continuous water levels in the Columbia River Estuary: The method of Empirical Orthogonal Function revisited. Estuar. Coast. Shelf Sci. 2019, 222, 81–90. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, Y.; Zhu, Y.; Zheng, J.; Ji, X.; Xu, Y.; Wu, Y.; Hoitink, A.J.F. Unravelling the causes of tidal asymmetry in deltas. J. Hydrol. 2018, 564, 588–604. [Google Scholar] [CrossRef]
- Chang, H.; Lin, L. Multi-point tidal prediction using artificial neural network with tide-generating forces. Coast. Eng. 2006, 53, 857–864. [Google Scholar] [CrossRef]
- Lee, T.L. Back-propagation neural network for long-term tidal predictions. Ocean Eng. 2004, 31, 225–238. [Google Scholar] [CrossRef]
- Lee, T.L.; Jeng, D.S. Application of artificial neural networks in tide-forecasting. Ocean Eng. 2002, 29, 1003–1022. [Google Scholar] [CrossRef]
- Supharatid, S. Application of a neural network model in establishing a stage–discharge relationship for a tidal river. Hydrol. Process. 2003, 17, 3085–3099. [Google Scholar] [CrossRef]
- Cox, D.T.; Tissot, P.; Michaud, P. Water level observations and short-term predictions including meteorological events for entrance of galveston bay, Texas. J. Waterw. Port Coast. Ocean Eng. 2002, 128, 21–29. [Google Scholar] [CrossRef]
- Liang, S.X.; Li, M.C.; Sun, Z.C. Prediction models for tidal level including strong meteorologic effects using a neural network. Ocean Eng. 2008, 35, 666–675. [Google Scholar] [CrossRef]
- Riazi, A. Accurate tide level estimation: A deep learning approach. Ocean Eng. 2020, 198, 107013. [Google Scholar] [CrossRef]
- Chang, F.; Chen, Y. Estuary water-stage forecasting by using radial basis function neural network. J. Hydrol. 2003, 270, 158–166. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lu, M.C.; Wei, C.C. Decision tree-based classifier combined with neural-based predictor for water-stage forecasts in a river basin during typhoons: A case study in Taiwan. Environ. Eng. Sci. 2012, 29, 108–116. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Comparison of ANN approach with 2D and 3D hydrodynamic models for simulating estuary water stage. Adv. Eng. Softw. 2012, 45, 69–79. [Google Scholar] [CrossRef]
- Yoo, H.J.; Kim, D.H.; Kwon, H.; Lee, S.O. Data driven water surface elevation forecasting model with hybrid activation function—A case study for Hangang River, South Korea. Appl. Sci. 2020, 10, 1424. [Google Scholar] [CrossRef]
- Chen, Y.P.; Gan, M.; Pan, S.Q.; Pan, H.D.; Zhu, X.; Tao, Z.J. Application of Auto-Regressive (AR) analysis to improve short-term prediction of water levels in the yangtze estuary. J. Hydrol. 2020, 590, 125386. [Google Scholar] [CrossRef]
- Zhang, Q.C.; Yang, L.T.; Chen, Z.K.; Li, P. A survey on deep learning for big data. Inf. Fusion 2018, 42, 146–157. [Google Scholar] [CrossRef]
- Sun, X.L.; Liu, M.X.; Sima, Z.Q. A novel cryptocurrency price trend forecasting model based on LightGBM. Financ. Res. Lett. 2020, 32, 101084. [Google Scholar] [CrossRef]
- Zhu, S.L.; Hrnjica, B.; Ptak, M.; Choiński, A.; Sivakumar, B. Forecasting of water level in multiple temperate lakes using machine learning models. J. Hydrol. 2020, 585, 124819. [Google Scholar] [CrossRef]
- Zhu, S.L.; Ptak, M.; Yaseen, Z.M.; Dai, J.Y.; Sivakumar, B. Forecasting surface water temperature in lakes: A comparison of approaches. J. Hydrol. 2020, 585, 124809. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Q.M.; Ma, Q.; Yu, B. LightGBM-PPI: Predicting protein-protein interactions through LightGBM with multi-information fusion. Chemom. Intell. Lab. Syst. 2019, 191, 54–64. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems; Morgan Kaufmann Publishers: San Mateo, CA, USA, 2017; pp. 3146–3154. [Google Scholar]
- Dev, V.A.; Eden, M.R. Formation lithology classification using scalable gradient boosted decision trees. Comput. Chem. Eng. 2019, 128, 392–404. [Google Scholar] [CrossRef]
- Fan, J.L.; Ma, X.; Wu, L.F.; Zhang, F.C.; Yu, X.; Zeng, W.Z. Light gradient boosting machine: An efficient soft computing model for estimating daily reference evapotranspiration with local and external meteorological data. Agric. Water Manag. 2019, 225. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Shi, X.; Wong, Y.D.; Li, M.Z.; Palanisamy, C.; Chai, C. A feature learning approach based On XGBoost for driving assessment and risk prediction. Accid. Anal. Prev. 2019, 129, 170–179. [Google Scholar] [CrossRef]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost algorithm-based prediction of concrete electrical resistivity for structural health monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- Demir-Kavuk, O.; Kamada, M.; Akutsu, T.; Knapp, E.W. Prediction Using Step-Wise L1, L2 Regularization and Feature Selection for Small Data Sets with Large Number of Features. BMC Bioinform. 2011, 12, 412. Available online: https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-12-412 (accessed on 27 April 2021). [CrossRef]
- Kukulka, T.; Jay, D.A. Impacts of Columbia River discharge on salmonid habitat: 1. A nonstationary fluvial tide model. J. Geophys. Res. Ocean. 2003, 108, 3293. [Google Scholar] [CrossRef]
- Kukulka, T.; Jay, D.A. Impacts of Columbia River discharge on salmonid habitat: 2. Changes in shallow-water habitat. J. Geophys. Res. Ocean. 2003, 108, 3294. [Google Scholar] [CrossRef]
- Jay, D.A.; Leffler, K.; Degens, S. Long-term evolution of Columbia River tides. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 182–191. [Google Scholar] [CrossRef]
- Lee, T.; Makarynskyy, O.; Shao, C. A combined harmonic analysis–artificial neural network methodology for tidal predictions. J. Coast. Res. 2007, 23, 764–770. [Google Scholar] [CrossRef]
- LightGBM’s Documentation. Available online: https://lightgbm.readthedocs.io/en/latest/ (accessed on 27 April 2021).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. Available online: https://www.jmlr.org/papers/volume13/bergstra12a/bergstra12a (accessed on 27 April 2021).
- Jay, D.A.; Flinchem, E.P. Interaction of fluctuating river flow with a barotropic tide: A demonstration of wavelet tidal analysis methods. J. Geophys. Res. 1997, 102, 5705–5720. [Google Scholar] [CrossRef]
- Pawlowicz, R. “M_Map: A Mapping Package for MATLAB”, Version 1.4m, [Computer Software]. 2020. Available online: www.eoas.ubc.ca/~rich/map.html (accessed on 27 April 2021).
- National Oceanic and Atmospheric Administration. Available online: https://www.noaa.gov/ (accessed on 27 April 2021).
- U.S. Geological Survey (USGS). Available online: https://www.usgs.gov/ (accessed on 27 April 2021).
- Murphy, A.H. Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Weather Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Guo, L.C.; Wegen, M.V.D.; Jay, D.A.; Matte, P.; Wang, Z.B.; Roelvink, D.; He, Q. River-tide dynamics: Exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary. J. Geophys. Res. Oceans 2015, 120, 3499–3521. [Google Scholar] [CrossRef]
- Guo, L.; Zhu, C.; Wu, X.; Wan, Y.; Jay, D.A.; Townend, I.; Wang, Z.B.; He, Q. Strong inland propagation of low-frequency long waves in river estuaries. Geophys. Res. Lett. 2020, 47, e2020GL089112. [Google Scholar] [CrossRef]





| Hyperparameters | Description and Usage | Type | Range | Default |
|---|---|---|---|---|
| learning_rate | Control the shrinkage rate; smaller value indicates a smaller iteration step. | double | >0.0 | 0.1 |
| num_iterations | Number of iterations (trees). | int | ≥0 | 100 |
| max_depth | Limit the max depth for a tree model. | int | case-based | |
| num_leaves | Control the maximum number of leaves of a decision tree. | int | 1–131,072 | 31 |
| max_bin | Control the max number of bins (data intervals) when the dataset of a parameter in the input layer is transformed to a histogram (Figure 2A). | int | 1–255 | 255 |
| min_data_in_leaf | Minimal number of data in one leaf. | int | ≥0 | 20 |
| feature_fraction | The proportion of the selected parameters to the total number of the parameters in the input layer. | double | 0.0–1.0 | 1.0 |
| bagging_fraction | The proportion of the selected data to the total data size. | double | 0.0–1.0 | 1.0 |
| bagging_freq | Frequency of re-sampling the data when bagging_fraction is smaller than 1.0. | int | ≥0 | 0 |
| lambda_l1 | The value of in Equation (4). | double | ≥0.0 | 0 |
| lambda_l2 | The value of in Equation (4). | double | ≥0.0 | 0 |
| min_gain_to_split | Indicating the minimal error reduction to conduct the further split; corresponding to the minimal value of Equation (16) | double | ≥0.0 | 0 |
| Hyperparameters | Stations | |||
|---|---|---|---|---|
| Wauna | Longview | St.Helens | Vancouver | |
| num_iterations | 374 | 339 | 291 | 380 |
| max_depth | 5 | 5 | 8 | 5 |
| num_leaves | 21 | 13 | 18 | 17 |
| max_bin | 165 | 190 | 195 | 194 |
| min_data_in_leaf | 17 | 16 | 23 | 19 |
| feature_fraction | 0.72 | 0.79 | 1.00 | 0.97 |
| bagging_fraction | 0.70 | 0.67 | 0.88 | 0.72 |
| bagging_freq | 1 | 6 | 8 | 4 |
| lambda_l1 | 0.016 | 0.008 | 0.000 | 0.000 |
| lambda_l2 | 0.060 | 0.100 | 0.052 | 0.138 |
| min_gain_to_split | 0.104 | 0.136 | 0.068 | 0.008 |
| Stations | LightGBM/NS_TIDE | |||
|---|---|---|---|---|
| MAE (m) | RMSE (m) | CC | SS | |
| Vancouver | 0.87/1.09 | 0.14/0.16 | 0.987/0.983 | 0.972/0.965 |
| St.Helens | 0.82/0.97 | 0.14/0.15 | 0.982/0.978 | 0.963/0.956 |
| Longview | 0.75/0.90 | 0.14/0.15 | 0.975/0.972 | 0.941/0.938 |
| Wauna | 0.72/0.82 | 0.14/0.16 | 0.977/0.975 | 0.955/0.947 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River. J. Mar. Sci. Eng. 2021, 9, 496. https://doi.org/10.3390/jmse9050496
Gan M, Pan S, Chen Y, Cheng C, Pan H, Zhu X. Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River. Journal of Marine Science and Engineering. 2021; 9(5):496. https://doi.org/10.3390/jmse9050496
Chicago/Turabian StyleGan, Min, Shunqi Pan, Yongping Chen, Chen Cheng, Haidong Pan, and Xian Zhu. 2021. "Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River" Journal of Marine Science and Engineering 9, no. 5: 496. https://doi.org/10.3390/jmse9050496
APA StyleGan, M., Pan, S., Chen, Y., Cheng, C., Pan, H., & Zhu, X. (2021). Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River. Journal of Marine Science and Engineering, 9(5), 496. https://doi.org/10.3390/jmse9050496








