Abstract
Prediction of severe natural hazards requires accurate forecasting systems. Recently, there has been a tendency towards more integrated solutions, where different components of the Earth system are coupled to explicitly represent the physical feedbacks between them. This study focuses on rapidly developing waves under extratropical storms to understand the impact of different wave source term parameterisations in the WAVEWATCH III (WWIII) model (ST4 and ST6) and coupling strategies (surface roughness closure versus surface stress closure) on the accuracy of the Met Office regional atmosphere-ocean-wave coupled research system for the north-west (NW) European shelf (UKC4). Results of a study focused on simulations during winter 2013/14 demonstrate that ST6 allows for a faster wave growth than the ST4 parameterisation but might degrade low to mid energy wave states. The difference between ST6 and ST4 in wave growth is larger for higher wind speeds and short fetches. The experiment with ST4 and roughness closure consistently under-predicts the wave growth in those locations where fetch dependence is an important factor (i.e., seas at the East (E) of Ireland and the UK for storms coming from the NW-WNW). The implementation in the wave model of ST6 physics with the stress closure coupling strategy appears to improve growth of young wind-seas, reducing bias in those locations where the storms are underestimated. The slower wave growth when using surface roughness closure seems to be related to an underestimation of the momentum transfer computed by the wave model when coupling the wind speeds. For very young to young wind seas, this can be overcome when the surface stress is computed by the atmospheric model and directly passed to the ocean.
1. Introduction
Assessment of environmental conditions and operational decision making in marine environments often requires an understanding of multiple atmospheric and ocean parameters. For environmental forecasting, there is a growing tendency to move towards more integrated modelling systems (ocean-wave, atmosphere-wave or atmosphere-ocean-wave) that are capable of more explicitly representing the physical feedbacks between system components than when components are run in isolation (e.g., [1,2,3]). Several studies demonstrate that the coupling between an atmospheric model and a wind wave model produces better estimates of the roughness lengths over the oceans [4,5,6,7,8] and, subsequently, model estimates of wind speed and significant wave height closer to observational data. Wahle et al. [6] confirmed complementary improvements in both wave and wind forecasts in coastal regions of the southern North Sea by implementing two-way coupling (with wave induced drag) between the wave and the atmosphere model. They found that significant wave height and wind speeds were reduced by approximately 8% and 3%, respectively, due to the extraction of energy and momentum from the atmosphere by the waves. Varlas et al. [3] found that coupling impacts the evolution of the overall system, with similar reductions in wind speed and wave height to those discussed by [6] and an improvement of forecast wave height and wind speed skill of up to 20% and 5%, respectively. Additionally, recent studies have demonstrated positive impacts on significant wave height prediction when surface ocean currents are accounted for (e.g., [9,10,11,12,13,14]) and in the upper-ocean dynamics when using ocean-wave coupled models (e.g., [15,16]).
Extreme events are the result of an extreme weather pattern. In the case of extratropical storms, an extreme event is characterised by very strong winds and large waves, often resulting in unusual high-water levels on the coast. All wave models struggle in extreme events as uncertainty in both storm evolution in the atmospheric forcing and source term parameterisations is high. Coupling should, in principle, improve the momentum flux at the ocean-atmosphere interface through the feedback to a more realistic surface roughness [6,17]. However, some studies have demonstrated cases where the coupling between the ocean surface and the wind might become less efficient at transferring momentum at high wind speeds [8,9,10,11,12,13,14,15,16,17,18]. Wiese et al. [8] studied the impact of two-way atmosphere-wave coupling on the lower atmosphere and found that the largest differences between the coupled and the reference model simulation occurred in areas of steep gradients in the mean sea level pressure, wind speed or temperature during storm events. They stated that significant wave height was predicted very well up to 6 m, whereas the upper tail tended to be underestimated by the coupled simulation. Lewis et al. [19] demonstrated that wave-modified surface drag had a small but positive impact on sea surface temperature; however, they found that a fully coupled atmosphere-ocean-wave simulation showed a larger bias in the wave related fields relative to the ocean-wave system, due to changes in the characteristics of the winds, with no clear improvement or even degradation in performance across the experiments during more energetic periods. Conversely, other research using fully coupled systems (ocean-atmosphere-wave) has demonstrated that despite being very sensitive to the momentum flux parameterisation, the fully coupled model was the most skilful simulation (e.g., [20]).
The exchange of momentum between the atmosphere and ocean can be achieved using wind speed-, wave age-, and/or sea state-dependent formulations (e.g., [21,22,23,24]). Most current coupling approaches include a two-way feedback in which the near-surface wind speed is passed to the wave model and information on the sea state is passed back to the atmospheric model to calculate the drag (e.g., [17]). The principle behind this ‘surface roughness closure’ coupling approach is that the best representation of form drag associated with the wave-supported stress comes from the wave model as only that system component will have knowledge of the fetch dependence and effect of currents on the wave field (i.e., the state of development of the waves; [25]). Conversely, observational studies on the exchange of momentum over the ocean have found that some wind speed-dependent formulations can match the observations well without any wave information (e.g., COARE; [23]).
Observational studies [26,27] have shown that current coupling parameterisations based on a sea state dependent drag (surface roughness closure) might not be realistic enough during periods with strong winds. Consequently, enhanced friction close to the surface might result in a negative feedback during large storms, resulting in degradation of the wind (model stress estimates that tend to be lower than the observations; e.g., [28]) and subsequently wave fields. In order to reduce extreme drag at high winds, wave models can include limiters of the roughness length (e.g., [29]) or a direct cap on the drag coefficient (e.g., [19]). This limitation avoids the effect of too much drag on the lower atmosphere and enables more realistic (stronger) winds to be forecast in the vicinity of intense storms; however, it has been demonstrated that the drag not only saturates but might tail off in high winds [23,26,30,31].
Wave model simulations can show significant sensitivity to both forcing conditions and source term formulation [32,33]. These sensitivities are even more pronounced during extreme events and might require different modelling approaches and/or source term input and dissipation parameterisations depending on the scale, nature and severity of the storms (e.g., [34,35]). Although both tropical (hurricanes or tropical storms) and extratropical (winter storms) cyclones can be described as deep low pressure systems that produce and sustain high intensity winds [36]; their origin, evolution, effect on the air-sea interface and subsequent evolution of the resultant waves are are substantially different. Indeed, waves during tropical cyclones do not always follow the local wind [27] whereas there are no major deviations during extratropical cyclones [37]. In other words, despite model errors being strongly reduced with a more realistic reproduction of the physical system components and their interaction, the storm characteristics will play a major role in the skill of the wave forecast during that event.
After the quality of the forcing, the second most important factor when modelling waves is the source term formulation [32]. The Ardhuin et al. [38] family of parameterisations for wind input and dissipation (implemented as ST4 module in WAVEWATCH III® (WWIII)) is used extensively operationally in both global and regional model configurations (e.g., Copernicus Marine Environment Monitoring Service operational ocean–wave coupled configuration with wave model specifications as per Saulter et al. [39]; NCEP Operational Global Wave Model [40] and GFSv16 wave [41]). In recent years, a new set of source terms known as ST6 [42] has been tested for both extratropical [33,43,44] and hurricane conditions [18,30,45]; proving its potential for predicting rapidly developing waves [33,34] in a variety of conditions. Although ST6 performance has been reported both in open sea (e.g., [43]) and coastal settings (e.g., [33]), its performance in a fully coupled system has not been extensively analysed.
This study focuses on rapidly developing waves in extratropical storms to investigate the sensitivity of a regional atmosphere-wave coupled system to source terms and coupling strategies. Here, we analyse the effect of momentum transfer to rapidly growing waves in both long and fetch limited conditions for km-scale simulations focused on the north-west European shelf. This energetic region provides an exceptional setting to study the effect of momentum transfer during extreme events as it is continuously affected by extratropical storms, whilst the bathymetric characteristics (deep waters of the eastern North Atlantic versus very wide and intermediate depth continental shelf seas) provide a variety of ideal “pools” for comparing different wave source code parameterisations. This paper is structured as follows. A brief description of the regional coupled model configuration is detailed in Section 2 and the methodology is shown in Section 3. Wave growth dependence to source term parameterisation using an idealised scenario is presented in Section 4. Section 5 includes results regarding model performance during the storms as well as analysis of the transfer of momentum from the atmosphere to the waves. Finally, discussion and conclusions are presented in Section 6 and Section 7, respectively.
2. The Regional Coupled Atmosphere-Ocean-Wave System (UKC4)
In recent years, scientific developments have included the introduction of coupled systems designed to reproduce the physical interactions between atmosphere, ocean and wave components. Lewis et al. [19] describe the basis of the km-scale regional coupled atmosphere-ocean-wave system used in this study. The present work uses a later revision of the modelling system, referred as UKC4 hereafter. UKC4 covers the UK and north-west European continental shelf seas (herein NW shelf; approx. 46 N–63 N, 19 W–13 E; Figure 1) and the model grid is based on a rotated pole coordinate system with the pole origin at longitude 177.5 degrees and latitude 37.5 degrees. The UKC4 fully coupled system includes two-way feedbacks represented between all model components [19]. The atmosphere component uses the Met Office Unified Model (herein UM; e.g., [46]), the shelf-seas ocean component uses Nucleus for European Models of the Ocean (NEMO ocean model; [47]) and the ocean surface waves modelled using WAVEWATCH III® (WWIII; [48]). Exchange of information between NEMO, WWIII and the UM is achieved using Ocean Atmosphere Sea Ice Soil coupling libraries version 2.0 (herein, OASIS-MCT coupler; [49]).
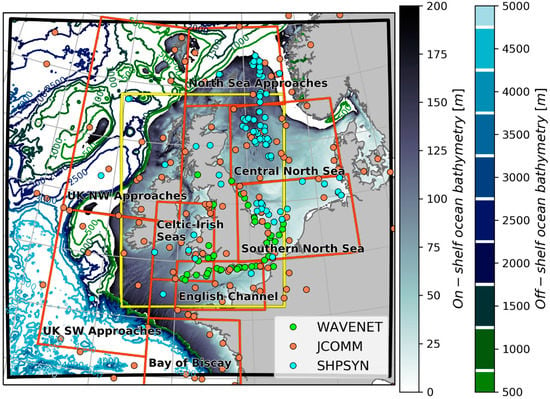
Figure 1.
North-west (NW) shelf physical context and model domain. The NW shelf domain (black boundary) includes atmosphere, ocean and wave components; the inner region (1.5 × 1.5 km) of the Met Office Unified Model (UM) atmosphere model domain is also presented (yellow boundary). In-situ observations are shown as solid dots and areas for analysis across the model domain are indicated in red. In-situ observations comprise the Joint WMO IOC Commission for Oceanography and Marine Meteorology’s operational Wave Forecast Verification Scheme (JCOMM), Ship Synop Observations at fixed platforms (SHPSYN) and UK WAVENET and Chanel Coastal Observatory (CCO) in-situ observations for coastal waters (WAVENET).
2.1. Met Office Unified Regional Atmosphere Model
The atmosphere component of UKC4 consists of the regional configuration RAL1 [50] of the Met Office Unified Model (UM). This is implicitly coupled to the Joint UK Land Environment Simulator land surface with river routing model (JULES, version 5.2; [51,52]). In common with the other UKC4 system components, the atmosphere model domain covers the northwest European region. The UM system component uses a grid with variable resolution. The grid stretches from 0.036⁰ (~4 km) to 0.0135⁰ (~1.5 km; inner domain covering UK and Ireland; yellow domain-Figure 1) and uses 70 vertical levels (model top ~40 km). The horizontal discretization of this regular grid follows Arakawa C-grid staggering [53] and the vertical discretization uses Charney-Phillips [54]. The atmospheric model grid resolution is sufficient that convection is explicitly represented rather than parameterised. Refer to Lewis et al. [17,19] for a detailed description of the UM configuration.
2.2. NEMO Regional Ocean Model
The ocean component of the UKC4 follows the Atlantic Margin Model configuration (AMM15; [55]) and uses NEMO [47] at version 3.6. The AMM15 model domain uses a rotated pole curvilinear grid of uniform ~1.5 km horizontal resolution across the entire NW shelf and overlaps in its inner part with the higher resolution region of the UM. The vertical grid uses 51 hybrid z*-s levels [56]. The model uses a non-linear free surface, an energy conserving form of the momentum advection, and a free slip lateral momentum boundary condition [57]. Turbulent viscosities and diffusivities are computed using the generic length scale scheme by Umlauf et al. [58]. The tracer equation follows a Total Variance Diminishing (TVD) advection scheme [59]. Tides are determined using 11 tidal constituents [55,57] and included both on the open boundary conditions via a Flather radiation boundary condition [60] and through the inclusion of the equilibrium tide. A detailed description of AMM15 can be found in Tonani et al. [57].
2.3. WWIII Spectral Regional Wave Model
The wave model is based on the WAVEWATCH III spectral model [48] at version 4.18, which has been modified to enable coupling exchanges [19]. The model domain covers the NW shelf and is based on a two-tier Spherical Multiple-Cell grid refinement [61] where the coarsest (open waters) cells are resolved at approximately 3 km and coastal cells with water depth less than 40 m are resolved at 1.5 km.
The current version of the wave model in UKC4 uses Ardhuin et al. [38] (ST4 package) to parameterise wind-wave interaction, whitecapping dissipation and swell dissipation. This package also includes some minor tuning adjustments for compatibility with Met Office wind forecast data [39]. The wave model also uses the surf breaking parameterisation proposed by Battjes and Janssen [62] and JONSWAP bottom friction formulation [63] to represent shallow water wave energy dissipation. These parameterisations make the UKC4-wave configuration compatible with intermediate and relatively shallow waters such as those across the NW shelf. Nonlinear wave-wave interactions are resolved using the Discrete Interaction Approximation (DIA) package [64]. Conversion from wind speed to momentum stress flux computations are included in the source term. Additionally, linear wave growth (LN1; [65]) for lower winds is also implemented.
An alternative package for the input and dissipation terms recently introduced in WWIII is the observation-based ST6 package ([30,66,67,68,69,70]). This family of parameterisations includes a wind input source with sink terms due to negative wind input, whitecapping dissipation and wave-turbulence interactions (swell dissipation). Both wind input and whitecapping formulations are based on field observations conducted at Lake George, while wave-turbulence dissipation and the negative input are based on laboratory experiments. Additionally, a parameterisation of swell decay based on field observations is also included. Section 3.2.1. provides a more detailed discussion of the ST4 and ST6 parameterisations.
3. Materials and Methods
The transfer of momentum to waves is assessed using the current research configuration of the atmosphere-ocean-wave UKC4 regional model [19]. This configuration is modified using both a different coupling strategy and an alternative parameterisation for wave input and dissipation. The coupling of momentum across the air-sea interface is analysed during the extreme events of 2013/14 winter, a period that represents a 1:60 year event for the coastlines of NW of Europe due to the extreme nature of the wave conditions [71]. Model runs encompassed the period from 30 November 2013 to 28 February 2014.
3.1. Observations and Metrics for Model Evaluation
Model experiments are evaluated using in-situ (Figure 1) and satellite altimeter wave and wind observations. In-situ data consists of floating buoys and fixed marine platforms. These include: (i) 6-hourly data from the Joint WMO-IOC Commission for Oceanography and Marine Meteorology’s operational Wave Forecast Verification Scheme [72] (hereafter referred to as the JCOMM); hourly Daily Ship Synop Observations at fixed platforms for the NW shelf (herein SHPSYN); and hourly UK WAVENET and Chanel Coastal Observatory (CCO) in-situ observations for coastal waters comprising Waverider buoys (herein simplified as WAVENET). The latter only includes measurements of wave statistics. JCOMM data have been averaged over a 4 h period (+/−2 h) around the validity time whereas no time-averaging is performed due to the potential high frequency variability introduced by tidal effects in the SHPSYN and WAVENET in-situ data. The satellite merged altimeter data (hereinafter MA data) include data from the JASON-2, CryoSat and SARAL-AltiKa missions. The altimeter significant wave heights used here were aggregated, quality controlled and corrected according to the calibration provided by CERSAT [73] and super-observed to 0.3 Hz in order to represent a scale more closely aligned with that of the in-situ observations. For a more detailed description on the observational datasets refer to Saulter [74].
Simulated values of wave and wind bulk parameters are compared against observations . Metrics for model evaluation include bias , Root Mean Square Difference and Pearson correlation coefficient , where , and n is the number of available observations.
3.2. Experimental Set-Up
3.2.1. WWIII Source Terms Parameterisations
The variance of the sea surface for irregular wind waves can be described through the two-dimensional variance density spectra that is a function of the wavenumber and the direction . Furthermore, wave propagation is described by
where is the total derivative, is the model wave action density spectrum or native WWIII wavenumber-direction spectrum (), represents the net effect of sources and sinks for the spectrum , and is the intrinsic (radian) frequency. The total source term can be defined as the combination of different physical processes that in deep water can be simplified to the wind-wave interaction term , a non-linear wave-wave interaction term and a dissipation term . Additionally, a linear input term for initial wave growth and the additional processes for shallow water (wave-bottom interactions and depth-induced breaking ) are included:
For this study we focus on the momentum budget between the atmosphere and the waves. Two different source code parameterisations for inputs to wave energy via momentum stress transferred from the atmosphere are used here: ST4 [38] and ST6 [30,42,66,67,68,69,70].
The family of parameterisations in ST4 uses a positive part of the wind input taken from WAM cycle 4 with an ad hoc reduction of the wind friction velocity (), which is implemented in order to allow a balance with a saturation-based dissipation that uses different options for a cumulative term. Hence, the ST4 parameterisation reduces the input to the waves at high wind speeds by including a tunable sheltering factor that decreases the drag coefficient at high winds as per below.
Following Janssen [75], the wind input source term in ST4 can be written as
where is the output source term that provides a linear damping of swells [75], and are the densities of air and water, is a non-dimensional growth parameter (constant), is von Karman’ constant, is a positive integration constant [38], and is a constant that controls the directional distribution of . for intermediate water depths is
where is a roughness length modified by the wave-supported stress and is a wave age tuning parameter. It is noted that although the effect of on wave growth is largely undocumented, it has a significant effect on wave growth, as it shifts the wave age of long waves. Hence is defined by
where the stress and is the height at which the wind is specified.
The reduction of in Equation (3) is obtained then by replacing it with the sheltering as
The sheltering coefficient can be used to tune the stresses limiting the wave growth at high wind speed, which would be largely overestimated for = 0. The input source term is then used to compute , expressed as
with the stress supported by shorter waves, , being a .
ST6 [30,42,66,67,68,69,70] is a new family of physics parameterisations for deep-water source and sink terms that can be implemented in WWIII. These parameterisations include a new nonlinear wind input term that accounts for dependence of the growth on wave steepness and airflow separation as well as for negative growth rate under opposing winds [30]. In addition to the basic dissipation term via wave breaking, ST6 includes a new cumulative dissipation term and a term due to production of turbulence by waves consistent with the observed decay rate of ocean swell. Following Babanin et al. [68], the input source term in ST6 is expressed as
with the spectral wave growth as
and the sheltering coefficient as
where is the wind forcing parameter and is a spectral measure of wave steepness.
where refers to the wave phase speed, is a measure of narrowness of the directional distribution at a frequency [76] calculated from the directional spectrum normalized by the maximum value of the spectrum at that frequency [70], is the radian frequency, is the wavenumber and is the scaling wind speed. follows Komen et al. [77] and Rogers et al. [70] as
At the surface, the stress can be written as the sum of the viscous and wave-supported stress . is used as a constraint of the wind input and is calculated by integration as
The closure in the total stress passed from the atmosphere is based on the 10-m wind speed alone [70] as
where the drag coefficient is taken from Hwang [78] and acts as a limit for the calculation of the wave-supported stress [30]. Hence, the flux of momentum from the atmosphere is specified by an atmospheric drag coefficient that depends only on the 10-m wind speed following the form
Furthermore, the viscous drag coefficient is parameterised using Tsagareli et al. [69].
This formulation shows a good performance for faster wave growth for young seas [30] and therefore has the potential to improve model prediction of rapidly developing waves during storm conditions common to the fetch-limited shelf seas of the NW shelf. However, this parameterisation might result in overestimation at lower wind speeds relative to Ardhuin et al. [38] when coupling with the atmospheric model, as Equation (18) is not preferred when comparing against the atmosphere-ocean bulk flux parameterisation implemented in the UM model (COARE 4.0 with cap and reduction of the drag at higher wind speeds; [23]).
A prescribed relationship to derive and is used in both source term family of parameterisations; however, the family of parameterisations used to compute this relationship differ. For ST4, implicitly depends on wind velocity and the ratio [79]. Hence, the friction velocity is calculated via a stress table where is derived as a function of and . Finally, the wind input source term is computed (Equations (3) and (7)) and updated (Equation (8)) in a source term integration loop. For ST6, u* is computed using Hwang et al. [78] based on the wind input alone (from which the limiting will be derived; Equation (16)). is then used to make a first guess estimate of (Equations (9) and (10)) as per Donelan et al. [66]. Finally, , and are used to constrain (Equation (15)) and adjust .
3.2.2. Coupling Strategies
Two different coupling strategies are tested: (i) a two-way feedback coupling strategy where a sea-state dependent surface roughness modifies the atmospheric momentum budget with wind passed from the atmospheric model to the wave model and wave feedback to the atmosphere through the Charnock coefficient (herein surface roughness closure), and (ii) a one-way strategy where no wave feedback on the atmospheric model exists but the wind stress is directly passed to the wave model (hereafter surface stress closure). Table 1 lists the coupling exchanges for the two coupling strategies that are relevant to the wave field modelling. These coupling strategies will differ in the variables exchanged between the atmosphere and wave components, depending on the WWIII physics used; i.e., ST4 versus ST6. Coupling fields passed from the atmospheric model to the wave model consist of 10-m winds (U10) for both ST4 and ST6 surface roughness closure configurations (herein named as ST4 and ST6, respectively). Atmospheric stress () is only passed in the surface stress closure set-up that is implemented using ST6 (ST6mod configuration). The latter also includes the exchange of the density of air () from the atmosphere to the wave component.

Table 1.
Coupling exchanges between the atmosphere (A) and wave (W) components relevant to wave field modelling implemented in the UK Regional Coupled Atmosphere-Ocean-Wave (UKC4) system.
Wave feedbacks on the atmosphere momentum budget for the roughness closure configuration are the modification of surface roughness throughout the Charnock coefficient which is sea state dependent. After the update of in ST4 (refer to Section 3.2.1.), an iterative calculation is performed to compute roughness length and total stress by the wave model (with an initial guess for on each of 10 iterations, with specifying a minimum possible Charnock coefficient) following
After the iteration, the roughness length is determined again from the input 10-m wind speed according to Equation (5) where , using the output wave-dependent Charnock parameter field calculated by WWIII as
The momentum roughness length is then related to the surface friction velocity in the UM atmosphere code following Charnock [80] and Smith [81] as
with the dynamic viscosity of air, , having a constant value of 1.4 × 105 ms−1 and a spatially-variable from Equation (21) that is updated and passed via OASIS3-MCT to the atmospheric model throughout the simulation.
Previous studies [26,30,31,82] have demonstrated a reduction of in high winds. Although the ST4 configuration may include a limiter on the Charnock coefficient, the parameterisation still generates a that will keep growing with wind speed (marked REG in Figure 2), albeit more slowly [18] up to the 0.003 value that corresponds to > 40 ms−1 in this scheme. The implemented through the ST6 module [78] is more consistent with previous studies of decaying for strong winds as it saturates and decreases for high winds (Equation (18) and marked ST6 in Figure 2); however, it may be excessive at lower wind speeds and is not preferred in the UM [18]. Hence, coupling is modified in order to pass the total stress () directly to the wave model. This way the preferred UM boundary layer algorithm, based on COARE 4.0, is the only drag coefficient scheme that is implemented within the coupled framework, allowing for more consistency in the stress values between system components (atmosphere and wave in this case). Additionally, direct stress transfer from the atmosphere model allows including atmospheric instability effects implicitly.
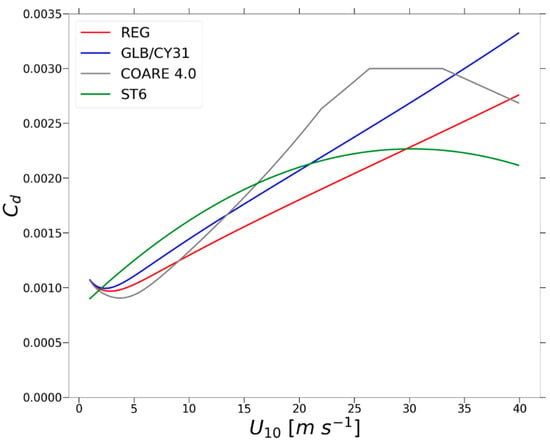
Figure 2.
Estimates of the drag coefficient () versus wind speed () for different parameterisations. The red and the blue lines correspond with model configurations (WWIII regional, REG, and global, GLB/CY31) using constant Charnock coefficients () of 0.011 and 0.018, respectively. The grey line is based on a modified version of the COARE algorithm [23] suitable for Met Office systems, COARE 4.0, where increases with wind speed up to an upper bound, hereafter it is constant. The green line is based on [80] scheme implemented in ST6 physics.
The main feature of the stress closure for ST6 coupling strategy is the modification of the coupling from the UM to WWIII to pass the atmospheric stress () and the density (). The stress is calculated in the atmospheric model independently of the sea state accounting for atmospheric stability and following a wind dependent formulation () that is consistent with a modified version of the COARE 4.0 algorithm [23]
where near-surface wind speed is expressed relative to the ocean surface current speed, , such that . Then, z0 is computed following Charnock relation [80] as per Equation (22) with based on the COARE algorithm [23] and the wind speed dependent drag coefficient calculated as
is passed to WWIII where the wind friction velocity is computed as . Several model parameterisations use constant (e.g., WWIII regional and global model configurations; Figure 2-REG and -GLB/CY31). However, in the modified COARE 4.0 boundary layer scheme (Figure 2-COARE 4.0) increases with wind speed up to an upper bound (22 ms−1), after it is constant and decreases linearly for winds above 33 ms−1 for the particular case of the UM. The cap and reduction of the drag coefficient are modifications introduced recently into global and regional operational systems at the Met Office in order to reduce excessive drag at high winds in tropical storm areas. These modifications incorporate a cap of 0.003 following Donelan [31] and a reduction to a lower value at very high wind speeds following Hsu et al. [83].
Other coupling exchanges relevant to the wave modelling include those at the wave-ocean interface. Hence, the wave model receives surface currents from the ocean model and passes significant wave height (), mean wave period, the surface Stokes drift and a wave stress to the ocean.
3.2.3. Experiments
Atmosphere-Ocean-Wave Coupled
Coupled experiments (Table 2, coupled) focus on the atmosphere-ocean-wave UKC4 coupled system with some additional modifications to the model configuration. These modifications are focused on: (i) WWIII source terms parameterisations (UKC4aow-ST4 and UKC4aow-ST6), and (ii) coupling exchanges (UKC4aow-ST6mod). UKC4aow-ST4 corresponds to the actual configuration of the regional coupled research system (refer to [84]). This configuration uses ST4 wave physics with the flux computation included in the source terms and presents the surface roughness closure coupling strategy: two-way feedback between the atmosphere and the wave model, where winds from the atmospheric model are passed to the wave model which returns the Charnock coefficient. The UKC4aow-ST6 experiment uses ST6 wave parameterisation and the same surface roughness closure coupling strategy as UKC4aow-ST4. The source term ST6 is limited using the flux parameterisation proposed by Hwang [78]. UKC4aow-ST6mod differs from UKC4aow-ST6 in the coupling strategy (i.e., exchanged variables). The former follows the surface stress closure strategy where there is no two-way feedback between the atmosphere—wave components but one-way transfer from the UM to WWIII to pass the stress () and the density () independently of the sea state. All fields are exchanged using OASIS3-MCT at a coupling frequency of one hour. Lateral boundary conditions for atmosphere and wave components are consistent across all three experiments and are provided from the relevant Met Office operational global model archive.

Table 2.
Experiments specifications.
Wave-Only
Atmosphere-ocean-wave coupled experiments are compared against uncoupled wave-only (UKW4h) control simulations (Table 2, wave-only). This set of uncoupled model runs does not include feedbacks with external model components; only hourly wind forcing read from external input files. In this study the WWIII wave-only simulations are forced by hourly UM winds from a free-running atmosphere-only UM simulation, using the same configuration as used in UKC4, interpolated to CMEMS-UK Met Office AMM15. Lateral boundary conditions are supplied from the Met Office global wave model [74] as wave spectra. Simulations were initialised from rest with a 5-day spin-up period that is discarded. As for the coupled experiments, #ST4 and #ST6 naming convention refers to the wave model source code parameterisations for inputs to wave energy () via momentum stress transferred from the atmosphere and dissipation of wave energy (), and the flux parameterisations; i.e., combination of ST4 with stress computation included in the source terms for UKW4h-ST4, and ST6 with stresses computed according to Hwang [78] for UKW4h-ST6.
3.3. Simulated Storms: Winter 2013/14 Storms
The severe winter of 2013/14 is considered the most energetic period in terms of storminess in the last 60 years across north-west Europe [71,85]. Overall, the period from mid-December 2013 to mid-February 2014 saw a succession of 12 major winter storms (Figure 3). This series of storms represents an exceptional period to study the role of wave physics and the transfer of momentum onto rapidly developing waves both on long and short fetch (i.e., fetch limited) areas such as the UK shelf seas.
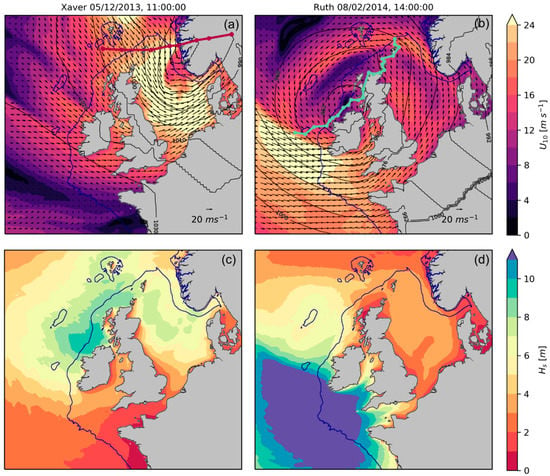
Figure 3.
Snapshots of (a,b) wind speed () and (c,d) significant wave height () during storms Xaver and Ruth. Storm snapshots for include wind direction vectors, mean sea level pressure contours and storm tracks. Winds are extracted as sea points only from WWIII system component – UKW4g-ST4 experiment. To facilitate visualization, wind vectors are plotted every 35 grid points. Pressure contours are sourced from the global pressure forcing conditions. The 200-m isobath (solid blue contour) is included to indicate the continental shelf limit.
Two extreme events affecting both the shallower shelf seas around the UK and the western approaches (off-shelf) are highlighted: the extratropical cyclone Xaver on 5–6 December 2013 and storm Ruth on 8–9 February The former generated a major storm surge affecting the North Sea and the coasts of Scotland and northern England [86,87]. Xaver formed to the south of Greenland on 4 December, and quickly developed as it moved east over Scotland towards the North Sea, intensifying further and reaching its lowest pressure over the Baltic Sea (967 hPa). Gusts exceeded 60 knots across the North and Irish Sea coasts and maximum significant wave heights exceeded 8 m. Windstorm Ruth affected the western approaches and the Irish and Celtic Seas with winds gusting at 60–70 knots and offshore waves across the SW approach reaching 12 m. The southern storm track (lowest pressure of 945 hPa) allowed storm waves to propagate into the Irish and Celtic Seas, causing very energetic wave conditions along the coast of Wales and SW England. Storm Xaver affected mainly fetch limited areas whereas the strong winds during storm Ruth mainly intensified in the western approaches after crossing the Atlantic.
4. Wave Growth Fetch Dependence: Idealised Scenarios
The aim of this section is to investigate the dependence of the wave growth on the fetch length for the different wave source term physics. An uncoupled wave model is used to run a number of idealised numerical experiments where the domain has an extension of 1015 × 515 grid cells and is discretised with a regular grid of 5 km resolution. Two idealised setups are explored: (i) deep water scenario with flat bathymetry of 1000 m depth, and (ii) intermediate water conditions with flat bathymetry of 80 m deep. The model is forced for 48 h by a constant wind speed; values are incremented over the range from 10 to 30 ms−1. Hence, dimensionless fetch limited growth and inverse wave age evolution curves are computed for both the different depth relationships (deep water and 80 m) and wind speeds. These are then compared to the theoretical wave growth relationships derived from observations by Young and Verhagen [88], hereafter YV96-1000 and YV96-80 for 1000 m and 80 m depth scenarios, respectively. We use the inverse wave age () as a diagnostic of wave development and this is defined as the ratio of the atmospheric friction velocity to the phase speed at the peak of the wave spectrum. is in the range 0.05–0.03 for waves approaching full development, attains a maximum of about 0.07 for developing seas, and tends toward large values approximately of 0.1 for very young waves [89].
Six numerical simulations (Table 3) using both idealised setups (1000 m and 80 m) are conducted. Four experiments differ only in the source term parameterisations, i.e., ST4 against ST6, and they are named as ST4-1000, ST4-80, ST6-1000 and ST6-80. The last two simulations, ST6mod-1000 and ST6mod-80, aim to mimic #ST6mod experiment. Hence, these maintain ST6 source terms, but Hwang [78] drag coefficient is substituted with the MO modified version of the COARE 4.0 algorithm [23].

Table 3.
Idealised experiments specifications.
Dimensionless wave growth () and inverse wave age () curves as a function of dimensionless fetch () for each of the constant wind speeds are presented in Figure 4. The difference in wave growth between ST4 and ST6 is greater for higher wind speeds and shorter fetches. Higher waves are generated for short fetches when using ST6 physics compared to both ST4 and YV96 relationships (Figure 4-left panels); however, ST6 growth curves are less steep than ST4 and YV96 relationships. Although this consistent ST6 behaviour for short fetches appears for all the wind speeds, differences with ST4 become smaller for longer fetches where ST4 growth is higher (Figure 4a,c,e). The implication is that for stronger winds and shorter fetches, ST6 allows faster growth of rapidly developing waves; whereas for low to moderate winds (15 ms−1) and longer fetches ( 8000–104), waves will grow less when implementing ST6 physics relative to ST4 and YV96. As expected, the short fetch fast growing waves using ST6 also correspond with more developed waves (relative to ST4 inverse wave age) for ≥ 10 ms−1 and this difference becomes more significant for stronger winds (0.19 versus 0.15 for and , respectively). It is indeed during very strong wind conditions ( = 30 ms−1), where a consistent offset between ST6 and ST4 curves is observed, with the former always representing older waves (consistent with faster prior growth). Conversely, inverse wave age ST6 and ST4 curves collapse for non-dimensional fetches of about 4000 or larger for winds up to 20 ms−1 indicating similar wave source term behaviour past those limits.
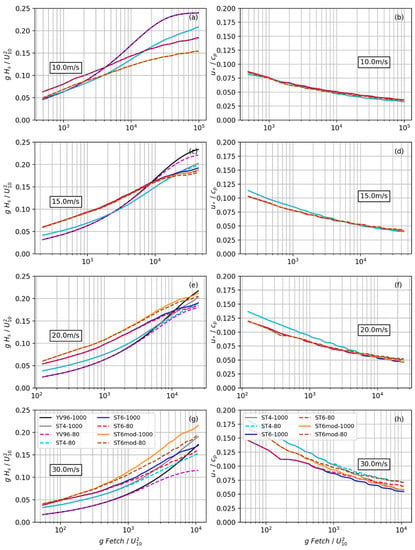
Figure 4.
(a,c,e,g) Dimensionless wave growth and (b,d,f,h) inverse wave age as a function of dimensionless fetch for constant winds from 10 to 30 ms−1 for different model configurations. Fetch limited growth and inverse wave age evolution curves include deep water and 80 m depth relationships for ST4 (ST4-1000 and ST4-80), ST6 (ST6-1000 and ST6-80) and ST6 with a modification on the drag coefficient as per Edson et al. [23] (ST6mod-1000 and ST6mod-80). The theoretical curve of Young and Verhagen [88] is presented in the fetch limited growth representation (YV96-1000 and YV96-80). Results for the different configurations correspond to 48 h model runs using a 5 km resolution grid.
We compare ST6mod-1000 and ST6mod-80 against ST4- and ST6-based idealised experiments in order to analyse the effect of the drag parameterisation: Hwang [78] versus the modified COARE 4.0 algorithm [23]. Wave growth curves for both ST6mod-1000 and ST6mod-80 match with ST6-1000 and ST6-80 up to 15 ms−1 winds whereas there is a positive offset (greater wave growth) with respect to ST4 and ST6 curves for > 20 ms−1. Indeed, although differences with ST6 based experiments are not very significant for short fetches, values of wave growth are consistently larger than with the other two configurations at any fetch. Differences between ST6 and ST6mod inverse wave age evolution curves are negligible up to of 20 ms−1. It is for strong (30 ms−1) winds and short fetches that the largest differences between configurations are observed. ST6mod-1000 and ST6mod-80 curves lie in between ST4 and ST6 configurations, with relatively younger (older) waves than ST6 (ST4). Additionally, it is noted that for long fetches (>370 km) and strong winds (>20 ms−1) during depth limited conditions (80 m experiments), ST6mod and ST4 curves collapse, indicating that the modification of the drag coefficient in ST6 produces a wave model behaviour more similar to ST4 physics.
In principle, the curves of YV96 [88] provide a best fit to observations of wind-sea-growth for each water depth, and ST4 appears to give the best overall fit against these relationships. Although based on an experiment conducted in a lake of approximately 2-m constant depth, YV96 relationships are regularly used in manual forecasting methods in different depth ranges. YV96 only exceeds ST4 and ST6 relationships for a portion of the 10 and 15 ms−1 curves (Figure 4a,c) and only exceeds ST6 for long fetches (Figure 4a,c,e). One could argue that YV96 might underpredict during short fetch conditions; conversely, this might indicate that a greater early growth phase for both ST6 and ST4 physics when winds are moderately strong (>10 ms−1) is essential in setting the underlying sea-state for the developing storm. In other words, present models might need to grow waves more quickly at short fetches during moderately strong winds (>10 ms−1) in order to be able to predict energetic conditions more accurately.
5. Results
5.1. Models Performance
Atmosphere-ocean-wave (UKC4aow#) and wave-only (UKW4h#) experiments covering three months of winter 2013/14 are compared against WAVENET, JCOMM, SHYPSYN and MA observations. Summary statistics RMSD, bias and R, for significant wave height (Hs) and wind speed (U10) are presented in Table 4. Overall, the main features are: (i) UKC4aow-ST4 shows the best skill score for the three months of hindcast of Hs, and this is very similar to UKC4aow-ST6mod; (ii) coupled models (UKC4aow#) improve wave hindcast with respect to the wave-only (UKW4h#) experiments; and (iii) there is a negative bias with respect to MA observed winds for all the experiments. Wind scores are relatively degraded in the fully coupled experiments with surface roughness closure (UKC4aow-ST4 and UKC4aow-ST6) whereas this is less obvious in UKC4aow-ST6mod, demonstrating a possible issue when introducing feedback from the wave component to the atmosphere during very energetic periods, possibly related to a too-high inferred value of Charnock’s coefficient in these energetic periods.

Table 4.
Summary statistics (root-mean-square deviation (RMSD), bias and correlation coefficient (R) for significant wave height (Hs) and wind speed (U10): UKC4aow-ST4, UKC4aow-ST6, UKC4aow-ST6mod, UKW4h-ST4 and UKW4h-ST6 versus observations of merged altimeter (MA), JCOMM, SHPSYN and WAVENET (coastal observations) over 2013-11-30 to 2014-02-28.
Hs statistics for UKWh4# allow us to analyse the sensitivity of the wave model to source term parameterisations in the absence of atmosphere–wave feedbacks. Skill results for the entire simulation period (Table 4) highlight that differences between source term parameterisation are <3% with ST6 degrading the overall model skill. Hence, UKW4h-ST6 shows the poorest performance for Hs (average bias = 0.1 m, RMSD = 0.53 m and R = 0.94; Table 4). A similar pattern is observed in UKC4aow# where, despite larger U10 biases in UKC4aow-ST4 (bias = −1.26 ms−1 respect −1.20 ms−1 for UKC4aow-ST6; Table 4), overall Hs stats are improved (around 5%) when using ST4.
Model skill is evaluated for the period of “storm-only” or “extreme period” (Figure 5 and Table 5). In this case we define an extreme period when Hs > Hs,90% (quantile of 90%) and compute the relevant skill score statistics using the match-ups in the upper 10% of data from both model and observations. In order to assess the model performance during the storms and their impact on shelf seas versus open waters, we differentiate between observations located above the 200 m isobath (on-shelf) and those below (off-shelf). When analysing model performance reproducing the upper tail of the distribution on-shelf, we see that with the exception of UKC4aow-ST4 (underpredicts, bias = −0.19 m; Table 5), all models tend to overpredict Hs,90% (bias = 0.18–0.30 m; Table 5). Additionally, there is increased variability in the system performance off-shelf: (i) UKC4aow-ST4 and wave-only with ST6 present negative bias (−0.11 to −0.15 m; Table 5) whereas UKC4aow-ST6, UKC4aow-ST6mod and wave-only with ST4 overestimate (0.11 to 0.33 m; Table 5) the waves; and (ii) values of RMSD and R indicate an overall poorer representation of the waves off-shelf by all the experiments relative to on-shelf model performance.
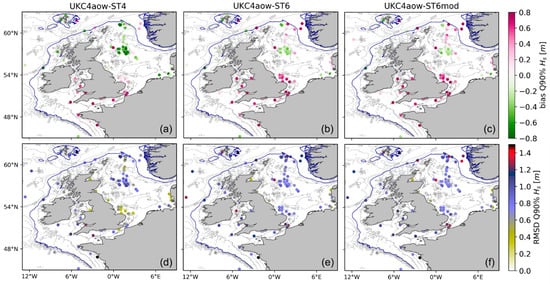
Figure 5.
Averaged significant wave height bias (a–c) and RMSD (d–f) for the quantile of 90% (Q90%) at in-situ locations for the coupled experiments (UKC4aow-ST4, UKC4ow-ST6 and UKC4aow-ST6mod). The 200-m isobath (solid blue contour) is included to indicate the continental shelf limit.

Table 5.
On-shelf and off-shelf summary statistics (root-mean-square deviation (RMSD), bias and correlation coefficient (R)) for significant wave height (Hs) and wind speed (U10) extremes, quantile of 90% (Q90%) for UKC4aow-ST4, UKC4aow-ST6, UKC4aow-ST6mod, UKW4h-ST4 and UKW4h-ST6 versus Q90 for JCOMM and SHPSYN observations over 2013-11-30 to 2014-02-28. The limit between on-shelf and off-shelf locations was the 200-m depth isobath.
The largest differences between UKC4aow# are observed on the continental shelf (Figure 5) where UKC4aow-ST4 presents overall smaller values of Hs,90% than the ST6 based experiments (e.g., larger negative biases in the central North Sea and smaller positive biases in the southern North Sea; Figure 5). For U10,90% that we observe an improvement in UKC4aow-ST6mod relative to UKC4aow-ST4 (average biases = 1.1 ms−1 and 1.3 ms−1, average R = 0.59 ms−1 and 0.57 ms−1, respectively; Table 5). These improvements are less obvious when analysing overall skill for Hs,90%. Hence, both UKC4aow-ST4 and UKC4aow-ST6mod present very broadly similar skill with minor differences: underestimation of ST4 versus overestimation of ST6mod (average bias = −0.15 m versus 0.14 m, respectively; Table 5) and increased variability by ST6mod (RMSD = 0.99 m versus 0.87 m for ST4; Table 5). Furthermore, ST6mod better reproduces Hs,90% across most of the central North Sea (average bias reduction from −0.8 m in ST4 to −0.2 m in ST6mod, Figure 5). Overestimation of the tail of the distribution at coastal locations is expected as wave breaking is tuned down from the default value (through WWIII BJALFA) when resolving shallow water physics in these systems [62]. Additionally, there are differences in observation uncertainty with location as offshore in-situ observations are collected by fixed platforms whereas coastal data come from waveriders.
In order to understand the sensitivity to the coupling and the different source term and coupling combinations during extratropical storms, the evolution of several fields at locations representing both long (Figure 6a–c and Figure 7a–c) and relatively fetch limited (Figure 6d–f and Figure 7d–f) conditions is presented for the two storms considered: Xaver (Figure 6) and Ruth (Figure 7). Fully coupled UKC4aow# experiments are compared against wave-only UKW4h-ST4 as this reference uses a similar wave model set-up to the present Met Office operational wave forecasting configuration. Diagnostic fields are Hs, U10 and inverse wave age () as an indicator of wave development.
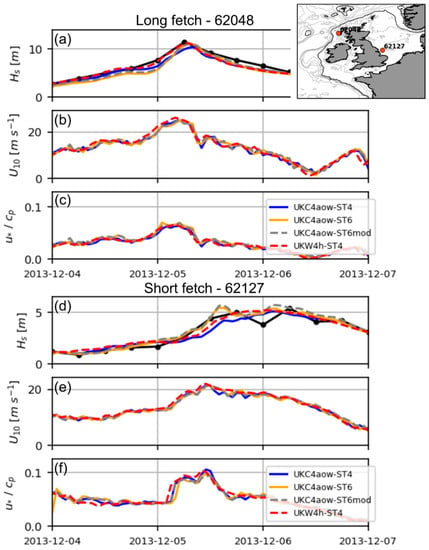
Figure 6.
Timeseries of modelled (a,d) significant wave height (Hs), (b,e) wind speed (U10) and (c,f) inverse wave age () for long (62048) and short (62127) fetch locations during storm Xaver. Observed in-situ Hs are also presented in (a,d). The exact position for the specific locations is specified in the right corner inset.
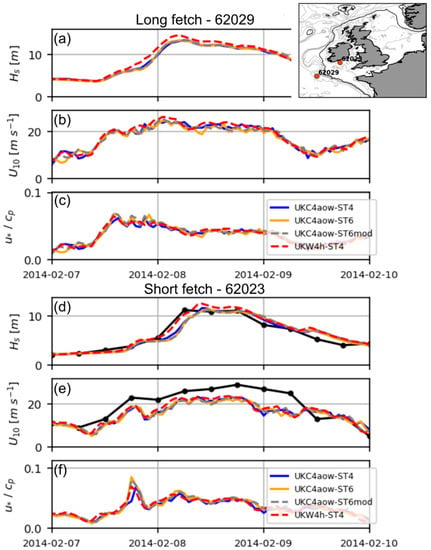
Figure 7.
Timeseries of modelled (a,d) significant wave height (Hs), (b,e) wind speed (U10), and (c,f) inverse wave age () for long (62029) and short (62023) fetch locations during storm Ruth. Observed in-situ Hs and U10 are also presented in (d) and (e), respectively. The exact position for the specific locations is specified in the right corner inset.
We analyse two long fetch locations and two locations in the lee of the land on the shelf, where the evolution of rapidly growing waves in the different experiments should be observed. As expected, UKW4h-ST4 shows slightly greater values of U10 and subsequently Hs relative to UKC4aow# in all locations given the values of in the schemes. It should be highlighted that UKW4h-ST4 U10 evolution is smoother (Figure 6b,e and Figure 7b,e) when compared with the fully coupled experiments in which U10 shorter-term variability is more evident. These short-term fluctuations also coincide with rapid changes of the sea-state dependent sea surface roughness (not shown). All UKC4aow# show similar behaviour in reproducing wave heights in long fetch locations (Figure 6a and Figure 7a). Conversely, for large rapidly developing waves in short fetch conditions, we observe that despite a very similar wind signal in all experiments, UKC4aow-ST4 does not capture wave growth accordingly (Figure 6d and Figure 7d).
UKC4aow-ST6mod seems to capture the rapid growth more successfully, increasing Hs in areas of young and very young seas ( 0.1; Figure 6f), where UKC4-aowST4 shows a significant negative bias (Figure 6d). Conversely, for more developed waves (i.e., waves approaching full development; 0.05) neither UKC4aow-ST6 nor UKC4aow-ST6mod show a reduction in the underestimation of Hs during the storm despite (Figure 6c,f and Figure 7c,f), indicative of less developed (younger) seas for ST6. It is noted that according to the idealised scenarios (Figure 4), differences in wave growth between the ST4 and ST6 physics tend to decrease significantly for longer fetches and moderate to strong winds (both curves collapse for winds of 15–20 ms−1; Figure 4d,f). Hence, the fact that the waves are more mature (averaged 0.06) during storm Ruth reduces the degree to which ST6 physics develop the waves faster than ST4 on the shelf (Figure 6c,f). Wind offset and negative sea-state related feedback (wave to ocean) are discarded as reasons for these differences, since UKW4h-ST4 seems to get the wave growth right and the #ST6mod experiment also underestimates wave growth (Figure 6a), respectively.
5.2. Sensitivity to Coupling
We use UKW4h-ST4 as a control against which to test sensitivity to coupling. The mean differences between UKC4aow-ST4 and UKW4h-ST4 represent the impact of full atmosphere-ocean-wave coupling relative to a free-running wave-only configuration. Differences are a combination of the impact of ocean-wave interactions and the effect of coupling of momentum across the air-sea interface.
Figure 8 shows mean differences of Hs, wave supported wind stress () and Charnock coefficient (α) between UKC4aow-ST4 and UKW4h-ST4 during Xaver and Ruth. The largest differences are observed in the regions affected by the storm track and on the continental shelf where, discarding the coastal locations in the lee of the land where differences are not so significant during Xaver, the UKC4aow-ST4 experiment appears to underestimate Hs relative to the wave-only simulation (Figure 8b,c). These differences are more than 0.75 m on average across wide regions (e.g., across the North Sea during Xaver and in the SW approach during Ruth) which corresponds to more than 10% of the mean field (Figure 8a). Additionally, is 0.2 N m−2 smaller in the fully coupled experiment across the North Sea (Figure 8e), and SW approaches and English Channel (Figure 8f) for Xaver and Ruth, respectively. These differences are above 20% of the total signal in some of the mentioned locations and involve around 10% of the total field across the domain (Figure 8d).
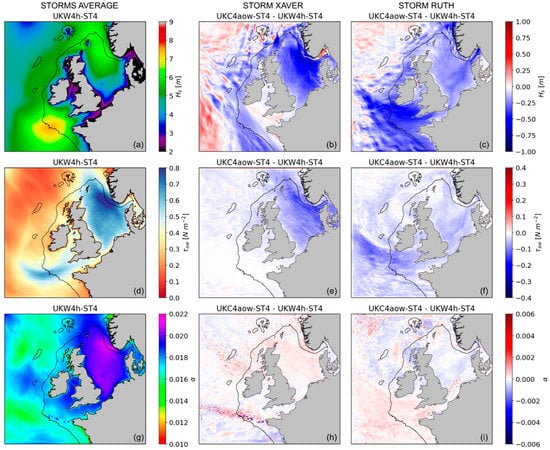
Figure 8.
Distribution of mean (a) significant wave height (Hs), (d) wave supported wind stress () and (g) Charnock coefficient (α) encompassing storms Xaver and Ruth. Difference in (b,c) Hs, (e,f) and (h,i) α between UKC4aow-ST4 and the control model run (UKW4h-ST4) for the individual storms: Xaver (mid panels) and Ruth (right panels). Mean values are computed using the two storms whereas mean differences correspond to each storm individually. The 200-m isobath (solid black contour) is included to indicate the continental shelf limit.
There is a negative feedback from the waves to the atmosphere in the coupled system, where the enhance friction during the storms (shown by larger values of Charnock coefficient in coupled mode) reduce the wind speed in excess and subsequently the wave heights. During storm Xaver, differences in the pattern of α (Figure 8h) differ from (Figure 8e) and large values of the stress do not always coincide with large values of α, also reflecting a more mature sea in UKW4h-ST4. UKC4aow-ST4 has the greatest values of α across the North Sea (Figure 8g) while smaller values (negative difference) correspond to areas with either very similar or smaller than the control (Figure 8e,h). Equally, during storm Ruth α is the largest (youngest seas) in coupled results in those areas more affected by the storm (SW approaches and English Channel), whilst α is either similar or slightly smaller across the North Sea (Figure 8f,i).
5.3. Sensitivity to Wave Source Term Parameterisation and Coupling Strategy
We analyse the sensitivity of Hs and wave supported wind stress to the wave source term physics and the modification of the coupling (Figure 9) during both storms. The largest average differences are observed in both shallow areas immediately in the lee of the land (short fetch) and along those areas more affected by the storm front (i.e., strongest winds): across the shallower shelf-seas region, more specifically in the North Sea during storm Xaver; and across the NW and SW approaches during Ruth. In these, #ST6 and #ST6mod experiments show larger Hs values than #ST4 of about 0.5 m (Figure 9a,g,h) and 0.75 m (Figure 9b) on average, which correspond to 10–15% of the mean field (Figure 8a) respectively. Differences between #ST6 and #ST6mod are of the order of 0.2 m with persistently greater values for #ST6mod across most of the domain. Results indicate that the majority of wave height differences between experiments can be explained by changes in wave physics (differences of 10%) with only around 5% due to the modification of the coupling.
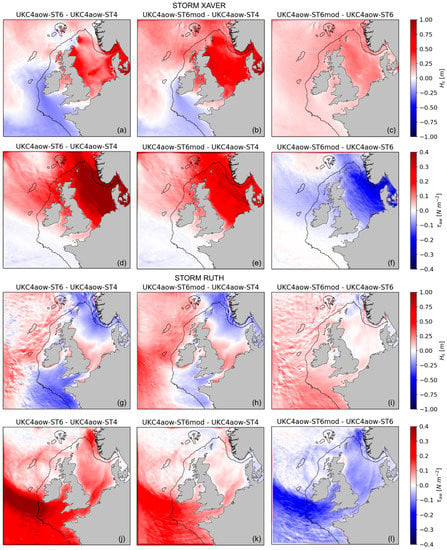
Figure 9.
Mean difference in significant wave height (Hs) and wave supported wind stress () between the coupled-ST6 physics experiments #ST6 (a,d,g,j) and #ST6mod (b,e,h,k), and the coupled-ST4 physics UKC4aow model run; and between #ST6 and #ST6mod (c,f,i,l) during storm Xaver (a–f) and storm Ruth (g–l). The 200-m isobath (solid blue contour) is included to indicate the continental shelf limit.
Wave supported stress is consistently larger in #ST6 and #ST6mod experiments (Figure 9d,e,j,k) across the entire domain, and > ; however, the stress closure strategy allows for the development of larger waves compared to the surface roughness closure (). The largest differences in relative to #ST4 are found across the North Sea and the SW approaches (Figure 9d,e,j,k) where they can represent about 40% of the total signal in some locations (Figure 8d). Hence, greater transfer of momentum does not always result in bigger waves and some areas show larger waves when using #ST4 (e.g., Bay of Biscay, Celtic Sea and the North Sea approaches during Ruth). In agreement with the idealised experiments of Section 4, this is likely to be related to either long fetch regions affected by strong winds but with a more developed sea using #ST4 and/or areas where the storm effect was weaker (low to moderate winds). It should be noted that wave growth is a balance between Sin and Sds, so these areas are likely to have more mature waves supporting less stress but also with less dissipation (i.e., waves whitecap less).
Wave height dependent sea surface roughness (z0) and wind speed relationships are presented in Figure 10a. z0 is computed following Equation (22) for #ST4 (z0-ST4) whereas for the case of #ST6mod (z0-ST6mod), instead of using z0 as function of the sea state, z0 is recalculated by the UM with α based on the COARE 4.0 algorithm as per Equation (24) [23]. This removes any possible feedback from the waves to the atmosphere when α is passed to the UM. z0-ST6mod is larger (smaller) than z0-ST4 for wind speeds above (below) 15 ms−1 (Figure 10a). This suggests that the #ST4 configuration exerts more drag on the atmosphere for low to moderate winds and slightly less drag for moderate to strong winds than the UM boundary layer scheme (COARE 4.0). The difference in surface drag between #ST4 and #ST6mod for strong winds is reduced at sheltered locations (i.e., less sensitivity between configurations for coastal areas in the lee of the land). The U10 − relationship shows that for equal moderate to strong wind speeds, #ST6 presents larger values of friction velocity (Figure 10b). This difference with #ST4 is diminished in #ST6mod (Figure 10b and blue areas in Figure 9j–l), reflecting some benefit in using wind stress directly compared to scaled U10 for those cases in which the transfer of momentum using ST6 might be overestimated (i.e., stress closure compared to roughness closure).
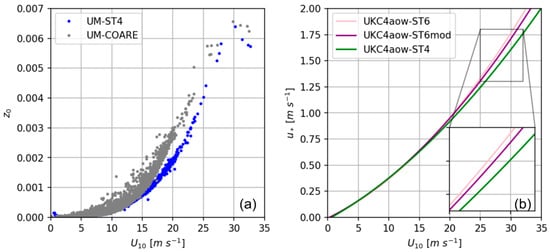
Figure 10.
(a) Wave height dependent sea-surface roughness z0 versus wind speed U10. (b) Friction velocity versus wind speed U10.
5.4. Momentum Transfer to Waves during Extremes
We analyse the effect of momentum transfer to rapidly developing waves under storm winds in fetch and duration limited conditions common to UK shelf seas. We use the ratio of momentum between the surface waves and the atmosphere () as a diagnostic for wave growth and adopt the inverse wave age () as a bulk measure of wave development. Figure 11 shows maximum values of inverse wave age and average ratio of momentum during storm Xaver and storm Ruth. We know that the smaller is, the less efficient wave growth will be. During storm Xaver, the largest (i.e., more efficient wave generation) for #ST6 and #ST6mod is observed in the North Sea (Figure 11d,e) where values of ~ 0.08–0.1 (Figure 10a). Equally, during storm Ruth, larger rates in #ST6 based systems are observed across the SW approaches (#ST6; Figure 11f,g) and also across the southern North Sea (#ST6mod; Figure 11f,h), in areas affected by the storm track and coinciding with values of inverse wave age of 0.06 (Figure 11b). Inverse wave age values corresponding to very young and young seas are where the main improvement when using ST6 with respect to ST4 is observed. It is indeed in those areas where the ratio increases when implementing #ST6mod compared to both #ST4 and #ST6 configurations, which suggests a more efficient wave growth for the former.
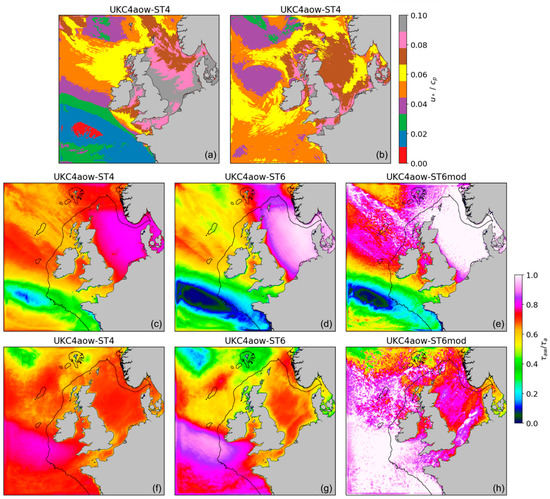
Figure 11.
(a,b) Maximum inverse wave age and (c–h) average ratio distribution during storm Xaver (c–e) and storm Ruth (f–h) for the different UKC4aow configurations. UKC4aow configurations are (c,f) #ST4, (d,g) #ST6 and (e,h) #ST6mod physics. Wave age is defined as the ratio of a characteristic wind friction velocity to the surface wave phase speed at the peak of the wave spectrum () as per Sullivan et al. [89].
The relationship between the momentum passed from atmosphere to waves () and the ratio of momentum () is presented in Figure 12. This comparison allows for an assessment of the difference in transfer of momentum between a parameterisation that takes account of the surface roughness variation directly from the waves (#ST4) and one that uses a wind-speed/stability dependent relationship (#ST6mod). As expected, there is a positive − correlation and, overall, this relationship is more scattered for smaller values of transfer of momentum to waves with greater variability for #ST4. For #ST6mod, − follows a quasi-linear relationship up to ~ 0.7 Nm−2 to remain almost constant beyond this value, indicating that beyond this limit almost all the momentum from the atmosphere goes into generating waves, so that and are approximately equal for > 0.07 (Figure 12b). Largest discrepancies between #ST4 and #ST6mod curves are observed for values of of 0.2 Nm−2 or larger (Figure 12a,b), corresponding to wave heights > 2.5 m (not shown). It is for > 0.15 Nm−2 where smaller values of for #ST4 are presented (Figure 12a). This corresponds to > 0.03–0.04 or waves approaching full development and younger. The implication is that for waves ranging from very-young to waves approaching full development, #ST6mod configuration allows greater growth. Similarly, the steepest slope of − curve for #ST6mod indicates that for smaller fluctuations in the transfer of momentum, waves can be developed more rapidly. This result is consistent with the ST6 and ST6mod growth curves obtained from the idealised scenarios.
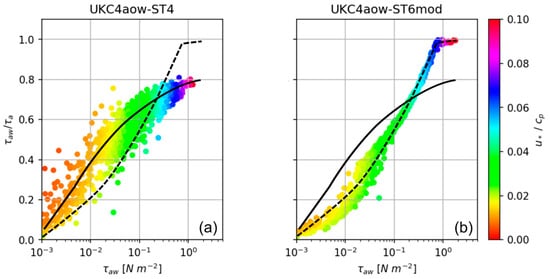
Figure 12.
Ratio of momentum atmosphere-wave versus wave supported stress . − relationships are established for (a) UKC4aow–ST4 (solid line) and (b) UKC4aow–ST6mod (dashed line). Magnitude of inverse wave age is included. Wave age is defined as the ratio of a characteristic wind friction velocity to the surface wave phase speed at the peak of the wave spectrum () as per Sullivan et al. [89].
6. Discussion
Coupled systems have improved wave model performance relative to wave-only simulations for winter 2013/14 across the north-west European shelf domain considered here. Coupling improvements (2–5% for Hs) presented are consistent with similar studies (e.g., [6,8,20]) where the positive impacts of coupled models on the prediction of significant wave height have also been demonstrated. Conversely, the wave-only systems (with wind speeds from an uncoupled atmospheric model) yield more accurate wind speeds (7% better) as coupling reduces winds excessively. These reduction rates are around 10% and in line with those presented by Varlas et al. [3] and Wahle et al. [6]. Furthermore, the change in wind speeds is consistent with the results presented by Lewis et al. [19], where the fully coupled version of UKC3 showed larger biases in some diagnostics during energetic periods. The degradation of U10 within the coupled experiments is reduced when the surface stress closure strategy is introduced (i.e., no wave feedback). This suggests some negative feedback from the wave component to the atmosphere possibly associated with excessively high Charnock coefficients during extreme events. Contrary to expectations, this degradation in the wind speed is not seen in the wave height. It is indeed the system with the ST4 and the surface roughness closure configuration (UKC4aow-ST4) where the best overall model performance among the coupled systems during the entire winter period is observed. However, the system with the modification of the coupling strategy (surface stress closure) and ST6 physics performs best when representing the upper tail of the distribution (storm only conditions) of both diagnostics. This is essentially related to the fact that ST6 based experiments present a reduction of the negative bias in Hs (12%) across the North Sea that is reflected in the overall skill for the periods of “storm-only” as well as a significant improvement (around 5%) in U10. This is in agreement with Christakos et al. [43] who found a significant improvement of wave related fields when using the ST6 formulation in this area.
The NW shelf provides an ideal setting to study the effect of momentum transfer during extreme events due to its potential for young waves in short fetches, i.e., a deviation from surface drag open-ocean formulations (e.g., [23,80]). The robustness of the experiments with the modification of the drag coefficient (UKC4aow-ST6mod and idealised ST6mod#) might suggest that this is not a major issue. However, the number of observations located in very short fetches is limited and might not be representative enough, as most observations used in the systems assessment were in relatively long fetches (intermediate waters and open ocean). Indeed, although UKC4aow-ST4 shows the best overall skill and is very similar to UKC4aow-ST6mod, the largest discrepancies are observed at the coastal locations, where results are also largely influenced by the reduced wave breaking in shallow waters, especially during the storms. Results of the idealised scenarios indicate that the modification of the drag coefficient of ST6mod produces wave model behaviour more similar to ST4 physics for more quiescent conditions whereas deviates far more strongly from ST4 at high wind speeds than ST6. It is noted that although the period of study is exceptionally energetic, overall statistics are more indicative of modal conditions (average U10 < 10 ms−1). Additionally, idealised experiments also show ST6mod behaviour close to ST4 for long fetches (>370 km) and relatively strong winds (>20 ms−1) for intermediate limited conditions such as those of the shelf seas which might partially explain the skill agreement between UKC4aow-ST4 and UKC4aow-ST6mod.
Inputs to wave energy via momentum stress transferred from the atmosphere in ST4 are based on Janssen’s theory [79] with some modifications to reduce the input at high wind speeds, while ST6 is almost entirely empirical with the flux of momentum from the atmosphere specified by Hwang [78] atmospheric drag that depends only on the 10-m wind speed. Results show that ST6 physics increases the transfer of momentum from the atmosphere to waves (maximum of 20%) in those areas closest to the storm track and characterised by stronger winds (>20 ms−1). Additionally, direct transfer to waves is relatively significant in areas of lighter winds in ST6, although in these regions the total stress is itself smaller. Often, this transfer from atmosphere to waves might be excessive, yielding a degradation of Hs (overestimation). This is in accordance with the findings of Christakos et al. [33,34] who demonstrated that ST6 captures the energy of the high frequency tail well but overestimates strongly the energy of the dominant waves. Hence, these differences in momentum transfer between source term parameterisations can be reduced (around 5%) with the modification of the coupling strategy (stress closure). The system with the surface stress closure coupling strategy and ST6 shows a reduction of the transfer from atmosphere to waves but still allows a greater ratio than the combination of ST4 and surface roughness closure in some areas. This is translated to faster wave growth in areas affected by the storm in the lee of the land (i.e., relatively short fetch) dominated by very young to young waves where wave growth is slightly underestimated by the system with ST4 physics and is better captured with ST6. Additionally, areas where wave growth is faster using ST4 coincide with long fetch regions affected by strong winds but likely supporting less stress and with less dissipation (balanced between Sin and Sds).
Ocean characteristics are driven by the stress rather than by the wind per se [90]. Therefore, passing the stress is more consistent with momentum conservation. Here, we have tested the sensitivity of the model to a two-way coupling method based on ocean surface roughness feedback from the wave model using two source term physics parameterisations. These methods improve the atmosphere model representation of ocean surface roughness; however, the closure in the system is not guaranteed as the exchange includes stability corrected wind speeds which are applied to the internal parameterisation of wind stress of the wave model rather than neutral winds (e.g., [29]), or wind stresses directly. Edson et al. [23] demonstrated that COARE 4.0, although being wind dependent, includes a good representation of the most commonly occurring moderately developed waves, and indeed, this algorithm produces similar results to drag computed sea-state dependent parameterisations (e.g., [21,22]). Our experiment UKC4aow-ST6mod with no sea-state dependent surface roughness but with closure on and accounting for stability effects is consistent with this principle. Hence, the direct comparison between surface roughness closure and surface stress closure coupling approaches shows that the ratio of momentum is slightly larger than in the other two coupled systems. This suggests that coupling the wind speeds to the wave model and allowing this to calculate the momentum transfer from the atmosphere to waves and ocean (total stress) might underestimate the transfer by a few percent. This is in line with Wiese et al. [8] and Edwards [18] who found evidence that coupling is less efficient at transferring momentum in high wind speeds (i.e., storms). We also note that when passing the winds, the wave model uses a fixed atmospheric density to compute the momentum budget. During extratropical cyclones, this density may differ slightly from the real atmospheric density implicit in the atmospheric model calculations. However, this factor becomes more important during tropical cyclones [18], where density variations can be relatively large.
7. Conclusions
Accurately replicating extreme sea-states in numerical models is a challenge. This study has investigated the effect of momentum transfer to rapidly developing waves for winds in both long and fetch limited conditions common to UK shelf seas using a km-scale atmosphere-ocean-wave regional model for 2013/14 winter. Two numerical experiments were conducted focusing on the atmosphere-wave components. The first one explored the sensitivity to two different wave source parameterisations, ST4 and ST6, using a two-way feedback coupling strategy where a sea-state dependent surface roughness modifies the atmospheric momentum budget. In the second set of simulations, the impact of the coupling strategy was assessed: surface roughness closure compared against surface stress closure.
The ST4 package with surface roughness closure coupling shows the best overall skill (5% improvement respect the other coupled systems) for the three month simulation of significant wave height, and this is very similar to the experiment with ST6 and surface stress closure discarding the coastal locations (bias = −0.12 m and −0.14 m, and RMSD of 0.54 m and 0.57 m, respectively). Additionally, all models tend to overpredict (average bias = 0.18–0.30 m) the upper tail except across the North Sea. It is across this region that the system with ST6 and surface stress closure significantly improves model skill reducing the general underprediction (bias = −0.8 m) in this area by a 12% (source term) and 17% (source term and coupling modification). For wind speed, all experiments present a negative bias (bias = −1.00–−1.26 ms−1) with respect to measured winds during the simulation period; conversely, there is a positive bias (0.97–1.98 ms−1) when representing the upper tail of the wind speed distribution. Wind speed biases in the coupled system are reduced by the ST6 and surface stress closure experiment.
Sensitivity analysis to atmosphere-wave source term parameterisations in both idealised scenarios and coupled atmosphere-ocean-wave experiments indicates that ST6 physics allows for faster wave growth (older waves) and this difference in wave growth (ST6 versus ST4) is larger for high wind speeds and short fetches. ST6 physics increases the transfer of momentum from atmosphere to waves. While this is desirable during extreme events, our results suggest that often this might lead to an excessive transfer of momentum from atmosphere to waves, with a subsequent overestimation of modal wave conditions. This overestimation can be reduced by modifying the coupling strategy. We found that combining ST6 physics with the surface stress closure coupling strategy (ST6mod) generally reduces the transfer of momentum from atmosphere to waves while still allowing greater than the systems using ST4 or ST6 with the surface roughness closure. This is true especially across areas affected by the storms at the lee of the land (i.e., relatively short fetch dominated areas), where waves are predominantly very young. The difference in ratio of momentum also suggests that passing the wind speeds to the wave model and allowing this to calculate the momentum flux from the atmosphere to waves and ocean (total stress) might underestimate the momentum transfer.
Future Work
The present effort contributes to our understanding of two important factors when predicting waves: wave source term parameterisations and atmosphere-wave coupling approaches. Further work is required to explore the possibility to include the direct stress application and closure of and a surface roughness feedback, which is indeed more consistent with momentum conservation While numerical results indicate that, overall, the configuration with ST4 and surface roughness closure might be preferable for the UK shelf seas fully coupled system; the ability of the ST6mod system to simulate more accurately large wave events suggests that passing the stress from the atmospheric model could help to reduce the underestimation of the momentum transfer when this is computed by the wave model when coupling the wind speeds. The implication is that passing the stress (and density for consistency) may help to better predict rapidly growing waves not just across shelf seas during windstorms but also in areas affected by tropical cyclones, where wave models seem to struggle the most.
Author Contributions
Conceptualization, N.G.V. and A.S.; methodology, N.G.V., A.S., J.M.E. and H.W.L.; software, N.G.V., J.M.C.S., J.M.E. and C.B.; validation, N.G.V. and A.S.; formal analysis, N.G.V.; investigation, N.G.V.; resources, N.G.V. and H.W.L.; data curation, N.G.V. and A.S.; writing—original draft preparation, N.G.V.; writing—review and editing, N.G.V., A.S., J.M.E., H.W.L., J.M.C.S., D.B. and J.S.; visualization, N.G.V. and D.B.; supervision, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Thank you to all those who have contributed to the research and development of UKC over the years.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moon, I.-J.; Ginis, I.; Hara, T. Effect of surface waves on Charnock coefficient under tropical cyclones. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Chen, S.S.; Zhao, W.; Donelan, M.A.; Tolman, H.L. Directional Wind–Wave Coupling in Fully Coupled Atmosphere–Wave–Ocean Models: Results from CBLAST-Hurricane. J. Atmos. Sci. 2013, 70, 3198–3215. [Google Scholar] [CrossRef]
- Varlas, G.; Katsafados, P.; Papadopoulos, A.; Korres, G. Implementation of a two-way coupled atmosphere-ocean wave modeling system for assessing air-sea interaction over the Mediterranean Sea. Atmos. Res. 2018, 208, 201–217. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M.; Viterbo, P. Ocean Waves and the Atmospheric Climate. J. Clim. 1996, 9, 1269–1287. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M.; Doyle, J.D.; Bidlot, J.; Hansen, B.; Isaksen, L.; Viterbo, P. Impact and feedback of ocean waves on the atmosphere. Atmos. Ocean Interact. 2002, 1, 155–197. [Google Scholar]
- Wahle, K.; Staneva, J.; Koch, W.; Fenoglio-Marc, L.; Ho-Hagemann, H.T.M.; Stanev, E.V. An atmosphere–wave regional coupled model: Improving predictions of wave heights and surface winds in the southern North Sea. Ocean Sci. 2017, 13, 289–301. [Google Scholar] [CrossRef]
- Wu, L.; Sproson, D.; Sahlée, E.; Rutgersson, A. Surface Wave Impact When Simulating Midlatitude Storm Development. J. Atmos. Ocean. Technol. 2017, 34, 233–248. [Google Scholar] [CrossRef]
- Wiese, A.; Stanev, E.; Koch, W.; Behrens, A.; Geyer, B.; Staneva, J. The Impact of the Two-Way Coupling between Wind Wave and Atmospheric Models on the Lower Atmosphere over the North Sea. Atmosphere 2019, 10, 386. [Google Scholar] [CrossRef]
- Osuna, P.; Monbaliu, J. Wave–current interaction in the Southern North Sea. J. Mar. Syst. 2004, 52, 65–87. [Google Scholar] [CrossRef]
- Hersbach, H.; Bidlot, J.-R. The relevance of ocean surface current in the ECMWF analysis and forecast system. In Proceedings of the Workshop on Ocean-Atmosphere Interactions, Reading, UK, 10–12 November 2008; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2008; pp. 61–73. [Google Scholar]
- Fan, Y.; Ginis, I.; Hara, T. The Effect of Wind–Wave–Current Interaction on Air–Sea Momentum Fluxes and Ocean Response in Tropical Cyclones. J. Phys. Oceanogr. 2009, 39, 1019–1034. [Google Scholar] [CrossRef]
- Palmer, T.; Saulter, A. Evaluating the Effects of Ocean Current Fields on a UK Regional Wave Model, Met Office Forecasting Research Technical Report 612. 2016. Available online: http://www.metoffice.gov.uk/media/pdf/j/i/FRTR_612_2016P.pdf (accessed on 2 February 2021).
- Ardhuin, F.; Gille, S.T.; Menemenlis, D.; Rocha, C.B.; Rascle, N.; Chapron, B.; Gula, J.; Molemaker, J. Small-scale open ocean currents have large effects on wind wave heights. J. Geophys. Res. Oceans 2017, 122, 4500–4517. [Google Scholar] [CrossRef]
- Valiente, N.G.; Saulter, A.; Lewis, H.W. The Effect of Different Levels of Coupling in Surface Wind Waves along the NWS during Extreme Events, Met Office Weather Science Report No 642. 2021. Available online: https://digital.nmla.metoffice.gov.uk/IO_054d5518-86af-4a24-903d-fafa0d6a2695/ (accessed on 10 March 2021).
- Lewis, H.W.; Castillo Sanchez, J.M.; Siddorn, J.; King, R.R.; Tonani, M.; Saulter, A.; Sykes, P.; Pequignet, A.-C.; Weedon, G.P.; Palmer, T.; et al. Can wave coupling improve operational regional ocean forecasts for the north-west European Shelf? Ocean Sci. 2019, 15, 669–690. [Google Scholar] [CrossRef]
- Bruciaferri, D.; Tonani, M.; Lewis, H.W.; Siddorn, J.; Saulter, A.; Castillo, J.M.; McConnell, N. The impact of ocean-wave coupling on the upper ocean circulation during storm events. Earth Space Sci. Open Arch. 2021. [Google Scholar] [CrossRef]
- Lewis, H.W.; Castillo Sanchez, J.M.; Graham, J.; Saulter, A.; Bornemann, J.; Arnold, A.; Fallmann, J.; Harris, C.; Pearson, D.; Ramsdale, S.; et al. The UKC2 regional coupled environmental prediction system. Geosci. Model Dev. 2018, 11, 1–42. [Google Scholar] [CrossRef]
- Edwards, J.M. The Momentum Budget in the Atmosphere-Ocean-Wave Coupled System; Met Office Weather Science Report; Met Office: Exeter, UK, 2020.
- Lewis, H.W.; Castillo Sanchez, J.M.; Arnold, A.; Fallmann, J.; Saulter, A.; Graham, J.; Bush, M.; Siddorn, J.; Palmer, T.; Lock, A.; et al. The UKC3 regional coupled environmental prediction system. Geosci. Model Dev. 2019, 12, 2357–2400. [Google Scholar] [CrossRef]
- Renault, L.; Chiggiato, J.; Warner, J.C.; Gomez, M.; Vizoso, G.; Tintoré, J. Coupled atmosphere-ocean-wave simulations of a storm event over the Gulf of Lion and Balearic Sea. J. Geophys. Res. Space Phys. 2012, 117, 1–25. [Google Scholar] [CrossRef]
- Smith, S.D.; Anderson, R.J.; Oost, W.A.; Kraan, C.; Maat, N.; De Cosmo, J.; Katsaros, K.B.; Davidson, K.L.; Bumke, K.; Hasse, L.; et al. Sea surface wind stress and drag coefficients: The hexos results. Boundary-Layer Meteorol. 1992, 60, 109–142. [Google Scholar] [CrossRef]
- Oost, W.; Komen, G.; Jacobs, C.; Van Oort, C. New evidence for a relation between wind stress and wave age from measurements during ASGAMAGE. Boundary-Layer Meteorol. 2002, 103, 409–438. [Google Scholar] [CrossRef]
- Edson, J.B.; Jampana, V.; Weller, R.A.; Bigorre, S.P.; Plueddemann, A.J.; Fairall, C.W.; Miller, S.D.; Mahrt, L.; Vickers, D.; Hersbach, H. On the Exchange of Momentum over the Open Ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J. On the Need to Modify the Sea Surface Roughness Formulation over Shallow Waters. J. Appl. Meteorol. Clim. 2018, 57, 1101–1110. [Google Scholar] [CrossRef]
- Donelan, M.A.; Curcic, M.; Chen, S.S.; Magnusson, A.K. Modeling waves and wind stress. J. Geophys. Res. Space Phys. 2012, 117, 1–26. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nat. Cell Biol. 2003, 422, 279–283. [Google Scholar] [CrossRef]
- Babanin, A.V.; Rogers, W.E.; De Camargo, R.; Doble, M.; Durrant, T.; Filchuk, K.; Ewans, K.; Hemer, M.; Janssen, T.; Kelly-Gerreyn, B.; et al. Waves and Swells in High Wind and Extreme Fetches, Measurements in the Southern Ocean. Front. Mar. Sci. 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Uz, B.M.; Donelan, M.A.; Hara, T.; Bock, E.J. Laboratory Studies of Wind Stress over Surface Waves. Boundary-Layer Meteorol. 2002, 102, 301–331. [Google Scholar] [CrossRef]
- ECMWF. IFS DOCUMENTATION Cy43r3—Part VII: ECMWF Wave Model Operational Implementation 11 July 2017; Series IFS Documentation; ECMWF: Reading, UK, 2017. [Google Scholar] [CrossRef]
- Zieger, S.; Babanin, A.V.; Rogers, W.E.; Young, I.R. Observation-based source terms in the third-generation wave model WAVEWATCH. Ocean Model. 2015, 96, 2–25. [Google Scholar] [CrossRef]
- Donelan, M.A. On the Decrease of the Oceanic Drag Coefficient in High Winds. J. Geophys. Res. Oceans 2018, 123, 1485–1501. [Google Scholar] [CrossRef]
- Roland, A.; Ardhuin, F. On the developments of spectral wave models: Numerics and parameterizations for the coastal ocean. Ocean Dyn. 2014, 64, 833–846. [Google Scholar] [CrossRef]
- Christakos, K.; Björkqvist, J.-V.; Tuomi, L.; Furevik, B.R.; Breivik, Ø. Modelling wave growth in narrow fetch geometries: The white-capping and wind input formulations. Ocean Model. 2021, 157, 101730. [Google Scholar] [CrossRef]
- Chalikov, D. The Parameterization of the Wave Boundary Layer. J. Phys. Oceanogr. 1995, 25, 1333–1349. [Google Scholar] [CrossRef]
- Chalikov, D.; Rainchik, S. Coupled Numerical Modelling of Wind and Waves and the Theory of the Wave Boundary Layer. Boundary-Layer Meteorol. 2011, 138, 1–41. [Google Scholar] [CrossRef]
- Domingues, R.; Kuwano-Yoshida, A.; Chardon-Maldonado, P.; Todd, R.E.; Halliwell, G.; Kim, H.-S.; Lin, I.-I.; Sato, K.; Narazaki, T.; Shay, L.K.; et al. Ocean Observations in Support of Studies and Forecasts of Tropical and Extratropical Cyclones. Front. Mar. Sci. 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Rapizo, H.; Babanin, A.V.; Schulz, E.; Hemer, M.A.; Durrant, T.H. Observation of wind-waves from a moored buoy in the Southern Ocean. Ocean Dyn. 2015, 65, 1275–1288. [Google Scholar] [CrossRef]
- Ardhuin, F.; Rogers, E.; Babanin, A.; Filipot, J.-F.; Magne, R.; Roland, A.; Collard, F. Semi-empirical dissipation source functions for wind-wave models: Part I, definition, calibration and validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Saulter, A.; Bunney, C.; Li, J.-G.; Palmer, T. Process and resolution impacts on UK coastal wave predictions from opera-tional global-regional wave models. In Proceedings of the 15th International Workshop on Wave Hindcasting and Forecasting & 6th Coastal Hazard Symposium, Liverpool, UK, 10–15 September 2017; Available online: http://www.waveworkshop.org/15thWaves/Papers/K1_WHF_SaulterEtAl_UKCoastalWave_20170913.pdf (accessed on 1 February 2021).
- Tolman, H.L.; Balasubramaniyan, B.; Burroughs, L.D.; Chalikov, D.V.; Chao, Y.Y.; Chen, H.S.; Gerald, V.M. Development and implementation of wind-generated ocean surface wave models at NCEP. Weather Forecast. 2002, 17, 311–333. [Google Scholar] [CrossRef]
- NOAA. WAVEWATCH III® Production Hindcast, Multigrid: Feb 2005 to May 2019. 2021. Available online: https://polar.ncep.noaa.gov/waves/hindcasts/prod-multi_1.php (accessed on 20 February 2021).
- Babanin, A.V.; Tsagareli, K.N.; Young, I.R.; Walker, D.J. Numerical Investigation of Spectral Evolution of Wind Waves. Part II: Dissipation Term and Evolution Tests. J. Phys. Oceanogr. 2010, 40, 667–683. [Google Scholar] [CrossRef]
- Van Vledder, G.P.; Hulst, S.T.C.; McConochie, J.D. Source term balance in a severe storm in the Southern North Sea. Ocean Dyn. 2016, 66, 1681–1697. [Google Scholar] [CrossRef]
- Christakos, K.; Furevik, B.R.; Aarnes, O.J.; Breivik, Ø.; Tuomi, L.; Byrkjedal, Ø. The importance of wind forcing in fjord wave modelling. Ocean Dyn. 2019, 70, 57–75. [Google Scholar] [CrossRef]
- Liu, Q.; Babanin, A.; Fan, Y.; Zieger, S.; Guan, C.; Moon, I.-J. Numerical simulations of ocean surface waves under hurricane conditions: Assessment of existing model performance. Ocean Model. 2017, 118, 73–93. [Google Scholar] [CrossRef]
- Brown, A.; Milton, S.; Cullen, M.; Golding, B.; Mitchell, J.F.B.; Shelly, A. Unified Modeling and Prediction of Weather and Climate: A 25-Year Journey. Bull. Am. Meteorol. Soc. 2012, 93, 1865–1877. [Google Scholar] [CrossRef]
- Madec, G. NEMO Ocean Engine; Note du Pole de Modelisation; Institut Pierre-Simon Laplace (IPSL): Guyancourt, France, 2008. [Google Scholar]
- Tolman, H.L. User Manual and System Documentation of WAVEWATCH III Version 4.18. 2014. Available online: http://polar.ncep.noaa.gov/waves/wavewatch/manual.v4.18.pdf (accessed on 28 January 2021).
- Valckle, S.; Craig, T.; Coquart, L. OASIS3-MCT User Guide; Technical Report TR/CMGC/15/38; Cerfacs: Toulouse, France, 2015. [Google Scholar]
- Bush, M.; Allen, T.; Bain, C.; Boutle, I.; Edwards, J.; Finnenkoetter, A.; Franklin, C.; Hanley, K.; Lean, H.; Lock, A.; et al. The first Met Office Unified Model–JULES Regional Atmosphere and Land configuration, RAL1. Geosci. Model Dev. 2020, 13, 1999–2029. [Google Scholar] [CrossRef]
- Best, M.J.; Pryor, M.; Clark, D.B.; Rooney, G.G.; Essery, R.L.H.; Menard, C.B.; Edwards, J.M.; Hendry, M.A.; Porson, A.; Gedney, N.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 1: Energy and water fluxes. Geosci. Model Dev. 2011, 4, 677–699. [Google Scholar] [CrossRef]
- Clark, D.B.; Mercado, L.M.; Sitch, S.; Jones, C.D.; Gedney, N.; Best, M.J.; Pryor, M.J.; Rooney, G.G.; Essery, R.L.H.; Blyth, E.M.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 2: Carbon fluxes and vegetation dynamics. Geosci. Model Dev. 2011, 4, 701–722. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model. Methods Comput. Phys. Adv. Res. Appl. 1977, 173–265. [Google Scholar] [CrossRef]
- Charney, J.G.; Phillips, N.A. Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flows. J. Meteorol. 1953, 10, 71–99. [Google Scholar] [CrossRef]
- Graham, J.A.; O’Dea, E.; Holt, J.; Polton, J.; Hewitt, H.T.; Furner, R.; Guihou, K.; Brereton, A.; Arnold, A.; Wakelin, S.; et al. AMM15: A new high-resolution NEMO configuration for operational simulation of the European north-west shelf. Geosci. Model Dev. 2018, 11, 681–696. [Google Scholar] [CrossRef]
- Siddorn, J.; Furner, R. An analytical stretching function that combines the best attributes of geopotential and terrain-following vertical coordinates. Ocean Model. 2013, 66, 1–13. [Google Scholar] [CrossRef]
- Tonani, M.; Sykes, P.; King, R.R.; McConnell, N.; Péquignet, A.-C.; O’Dea, E.; Graham, J.A.; Polton, J.; Siddorn, J. The impact of a new high-resolution ocean model on the Met Office North-West European Shelf forecasting system. Ocean Sci. 2019, 15, 1133–1158. [Google Scholar] [CrossRef]
- Umlauf, L.; Burchard, H. A generic length-scale equation for geophysical turbulence models. J. Mar. Res. 2003, 61, 235–265. [Google Scholar] [CrossRef]
- Zalesak, S.T. Fully multidimensional flux-corrected transport algorithms for fluids. J. Comput. Phys. 1979, 31, 335–362. [Google Scholar] [CrossRef]
- Flather, R.A. A tidal model of the north west European continental shelf. Mem. Société R. Sci. Liege 1976, 6, 141–164. [Google Scholar]
- Li, J.-G. Global Transport on a Spherical Multiple-Cell Grid. Mon. Weather. Rev. 2011, 139, 1536–1555. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, P. Energy loss and set-up due to breaking of random waves. Coast. Eng. 1978, 569–587. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Eake, K.; Walden, H. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP). In Deutsche Hydrograph, Zeit, Erganzung-Self Reihe, A 8(12); Deutches Hydrographisches Institut: Berlin, Germany, 1973; pp. 1–95. [Google Scholar]
- Hasselmann, S.; Hasselmann, K.; Allender, J.H.; Barnett, T.P. Computations and Parameterizations of the Nonlinear En-ergy Transfer in a Gravity-Wave Specturm. Part II: Parameterizations of the Nonlinear Energy Transfer for Application in Wave Models. J. Phys. Oceanogr. 1985, 15, 1378–1391. [Google Scholar] [CrossRef]
- Cavaleri, L.; Rizzoli, P.M. Wind wave prediction in shallow water: Theory and applications. J. Geophys. Res. Space Phys. 1981, 86, 10961–10973. [Google Scholar] [CrossRef]
- Donelan, M.A.; Babanin, A.V.; Young, I.R.; Banner, M.L. Wave-Follower Field Measurements of the Wind-Input Spectral Function. Part II: Parameterization of the Wind Input. J. Phys. Oceanogr. 2006, 36, 1672–1689. [Google Scholar] [CrossRef]
- Donelan, M.A.; Babanin, A.V.; Young, I.R.; Banner, M.L.; McCormick, C. Wave-Follower Field Measurements of the Wind-Input Spectral Function. Part I: Measurements and Calibrations. J. Atmos. Ocean. Technol. 2005, 22, 799–813. [Google Scholar] [CrossRef]
- Babanin, A.V.; Banner, M.L.; Young, I.R.; Donelan, M.A. Wave-Follower Field Measurements of the Wind-Input Spectral Function. Part III: Parameterization of the Wind-Input Enhancement due to Wave Breaking. J. Phys. Oceanogr. 2007, 37, 2764–2775. [Google Scholar] [CrossRef]
- Tsagareli, K.N.; Babanin, A.V.; Walker, D.J.; Young, I.R. Numerical Investigation of Spectral Evolution of Wind Waves. Part I: Wind-Input Source Function. J. Phys. Oceanogr. 2010, 40, 656–666. [Google Scholar] [CrossRef]
- Rogers, W.E.; Babanin, A.V.; Wang, D.W. Observation-Consistent Input and Whitecapping Dissipation in a Model for Wind-Generated Surface Waves: Description and Simple Calculations. J. Atmos. Ocean. Technol. 2012, 29, 1329–1346. [Google Scholar] [CrossRef]
- Masselink, G.; Castelle, B.; Scott, T.; Dodet, G.; Suanez, S.; Jackson, D.; Floc’H, F. Extreme wave activity during 2013/2014 winter and morphological impacts along the Atlantic coast of Europe. Geophys. Res. Lett. 2016, 43, 2135–2143. [Google Scholar] [CrossRef]
- Bidlot, J.; Wittmann, P.; Fauchon, M.; Chen, H.; Lefèvre, J.M.; Bruns, T.; Park, S. Inter-comparison of operational wave forecasting systems. In Proceedings of the 10th International Workshop on Wave Hindcasting and Forecasting and Coastal Hazard Symposium, Oahu, HI, USA, 11–16 November 2007; pp. 1–22. [Google Scholar]
- Queffeulou, P. Merged altimeter wave height data base. An update. In Proceedings of the ESA Living Planet Symposium 2013, Edinburgh, UK, 9–13 September 2013; Available online: https://ftp.space.dtu.dk/pub/Ioana/papers/s221_1quef.pdf (accessed on 10 February 2021).
- Saulter, A. QUID for NWS MFC Products—Quality Information Document, Technical Report Ref. NORTH-WESTSHELF_ANALYSIS_FORECAST_WAV_004_014. 2018. Available online: https://resources.marine.copernicus.eu/documents/QUID/CMEMS-NWS-QUID-004-014.pdf (accessed on 10 February 2021).
- Janssen, P.A.E.M. The Interaction of Ocean Waves and Wind; Cambridge University Press (CUP): Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Babanin, A.V.; Solov’yev, Y.P. Parameterization of the width of the angular distribution of wind wave energy at limited fetches. Izv. Atmos. Ocean Phys. 1987, 23, 645–651. [Google Scholar]
- Komen, G.J.; Hasselmann, K. On the Existence of a Fully Developed Wind-Sea Spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Hwang, P.A. A Note on the Ocean Surface Roughness Spectrum. J. Atmos. Ocean. Technol. 2011, 28, 436–443. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Quasi-linear Theory of Wind-Wave Generation Applied to Wave Forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Munk, W.H. Wind stress on water: An hypothesis. Q. J. R. Meteorol. Soc. 1955, 81, 639. [Google Scholar] [CrossRef]
- Smith, S.D. Coefficients for sea surface wind stress, heat flux, and wind profiles as a function of wind speed and temperature. J. Geophys. Res. Space Phys. 1988, 93, 15467–15472. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Powell, M.D.; Pietrzak, J.D. Wind and waves in extreme hurricanes. J. Geophys. Res. Space Phys. 2012, 117, 1–15. [Google Scholar] [CrossRef]
- Hsu, J.-Y.; Lien, R.-C.; D’Asaro, E.A.; Sanford, T.B. Estimates of Surface Wind Stress and Drag Coefficients in Typhoon Megi. J. Phys. Oceanogr. 2017, 47, 545–565. [Google Scholar] [CrossRef]
- Lewis, H.W.; Siddorn, J.; Castillo Sanchez, J.M.; Petch, J.; Edwards, J.M.; Smyth, T. Evaluating the impact of atmospheric forcing and air–sea coupling on near-coastal regional ocean prediction. Ocean Sci. 2019, 15, 761–778. [Google Scholar] [CrossRef]
- Matthews, T.K.; Murphy, C.; Wilby, R.L.; Harrigan, S. Stormiest winter on record for Ireland and UK. Nat. Clim. Chang. 2014, 4, 738–740. [Google Scholar] [CrossRef]
- Spencer, T.; Brooks, S.M.; Evans, B.R.; Tempest, J.A.; Möller, I. Southern North Sea storm surge event of 5 December 2013: Water levels, waves and coastal impacts. Earth-Sci. Rev. 2015, 146, 120–145. [Google Scholar] [CrossRef]
- Wadey, M.P.; Haigh, I.D.; Nicholls, R.J.; Brown, J.M.; Horsburgh, K.; Carroll, B.; Gallop, S.L.; Mason, T.; Bradshaw, E. A comparison of the 31 January–1 February 1953 and 5–6 December 2013 coastal flood events around the UK. Front. Mar. Sci. 2015, 2, 84. [Google Scholar] [CrossRef]
- Young, I.; Verhagen, L. The growth of fetch limited waves in water of finite depth. Part 1. Total energy and peak frequency. Coast. Eng. 1996, 29, 47–78. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Melville, W.K. Surface gravity wave effects in the oceanic boundary layer: Large-eddy simulation with vortex force and stochastic breakers. J. Fluid Mech. 2007, 593, 405–452. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Meissner, T.; Cerovecki, I.; Chang, P.S.; Dong, X.; De Chiara, G.; Donlon, C.; Dukhovskoy, D.S.; Elya, J.; Fore, A.; et al. Remotely Sensed Winds and Wind Stresses for Marine Forecasting and Ocean Modeling. Front. Mar. Sci. 2019, 6, 443. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).