A Review of Recent Machine Learning Advances for Forecasting Harmful Algal Blooms and Shellfish Contamination
Abstract
1. Impact of Harmful Algal Blooms (HABs) on Shellfish Safety
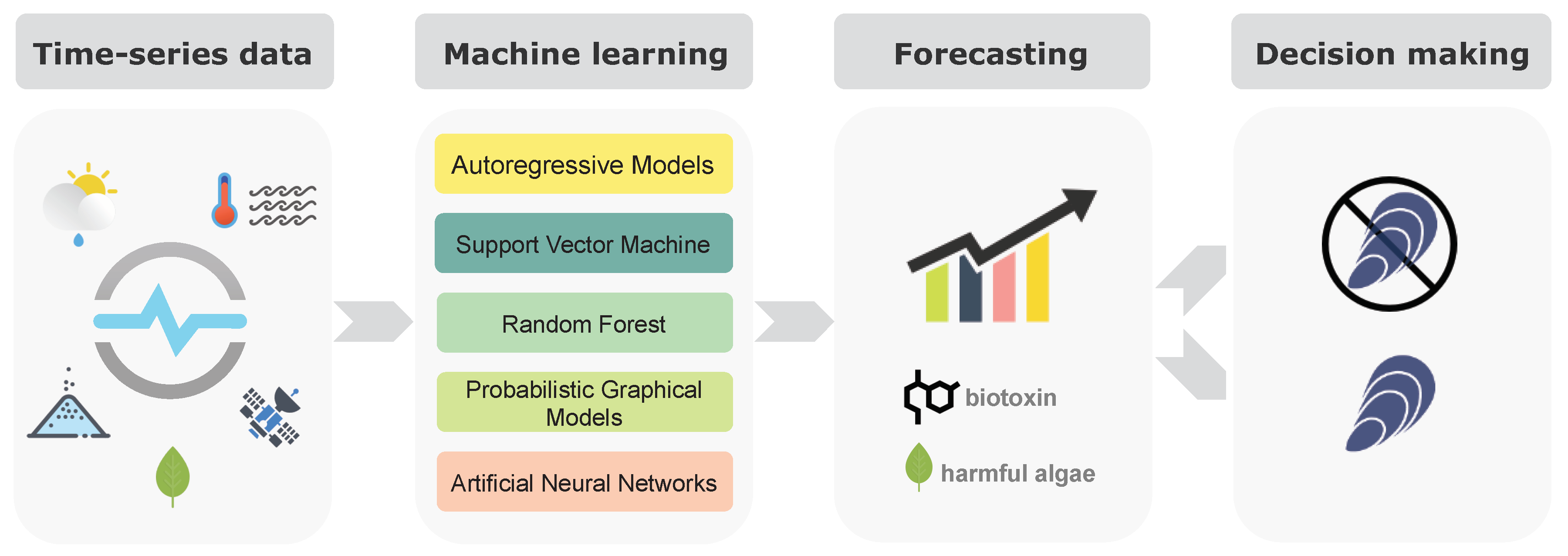
2. Forecasting HABs and Shellfish Biotoxin Contamination
3. Time-Series Forecasting Methods
3.1. Autoregressive Models
3.2. Support Vector Machine
3.3. Random Forest
3.4. Probabilistic Graphical Models
3.5. Artificial Neural Networks
3.5.1. Feed-Forward Neural Networks (FFNNs)
3.5.2. Convolutional Neural Networks (CNNs)
3.5.3. Recurrent Neural Networks (RNNs)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEW | Adaptive Exponential Weighting |
| ANN | Artificial Neural Network |
| AR | Autoregressive |
| ARIMA | Autoregressive Integrated Moving Average |
| ARMA | Autoregressive Moving Average |
| ASP | Amnesic Shellfish Poisoning |
| BN | Bayesian Network |
| CNN | Convolutional Neural Network |
| DA-RNN | Dual-stage Attention-based RNN |
| DBN | Deep Belief Network |
| DSP | Diarrhetic Shellfish Poisoning |
| FFNN | Feed-Forward Neural Network |
| HAB | Harmful Algal Bloom |
| HMM | Hidden Markov Model |
| MA | Moving Average |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| MTS | Multivariate Time Series |
| MVLR | Multivariate Linear Regression |
| LSTM | Long Short-Term Memory |
| PSP | Paralytic Shellfish Poisoning |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| SST | Sea Surface Temperature |
| SVM | Support Vector Machine |
| VAR | Vector Autoregressive |
| WNN | Wavelet Neural Network |
References
- López-Mas, L.; Claret, A.; Reinders, M.J.; Banovic, M.; Krystallis, A.; Guerrero, L. Farmed or wild fish? Segmenting European consumers based on their beliefs. Aquaculture 2021, 532, 735992. [Google Scholar] [CrossRef]
- United Nations. World Population Prospects: The 2015 Revision; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Mateus, M.; Fernandes, J.; Revilla, M.; Ferrer, L.; Villarreal, M.R.; Miller, P.; Schmidt, W.; Maguire, J.; Silva, A.; Pinto, L. Early Warning Systems for Shellfish Safety: The Pivotal Role of Computational Science. In Proceedings of the International Conference on Computational Science—ICCS 2019, Faro, Portugal, 12–14 June 2019; pp. 361–375. [Google Scholar] [CrossRef]
- Grattan, L.M.; Holobaugh, S.; Morris, J.G., Jr. Harmful Algal Blooms and Public Health. Harmful Algae 2016, 57, 2–8. [Google Scholar] [CrossRef] [PubMed]
- European Commission. Commission Regulation (EC) No 853/2004 of the European Parliament and of the Council of 29 April 2004 laying down specific hygiene rules for on the hygiene of foodstuffs. Off. J. Eur. Union L 2004, 139, 55–205. [Google Scholar]
- European Commission. Commission Regulation (EC) No 854/2004 of the European Parliament and of the Council of 29 April 2004 laying down specific rules for the organisation of official controls on products of animal origin intended for human consumption. Off. J. Eur. Union L 2004, 139, 206–320. [Google Scholar]
- Young, N.; Robin, C.; Kwiatkowska, R.; Beck, C.; Mellon, D.; Edwards, P.; Turner, J.; Nicholls, P.; Fearby, G.; Lewis, D.; et al. Outbreak of diarrhetic shellfish poisoning associated with consumption of mussels, United Kingdom, May to June 2019. Eurosurveillance 2019, 24. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, I.L.; Pelerito, A.; Ribeiro, I.; Cordeiro, R.; Núncio, M.S.; Vale, P. Paralytic shellfish poisoning due to ingestion of contaminated mussels: A 2018 case report in Caparica (Portugal). Toxicon X 2019, 4, 100017. [Google Scholar] [CrossRef] [PubMed]
- Anacleto, P.; Pedro, S.; Nunes, M.; Rosa, R.; Marques, A. Microbial composition of native and exotic clams from Tagus estuary: Effect of season and environmental parameters. Mar. Pollut. Bull. 2013, 74, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Moita, M.T.; Pazos, Y.; Rocha, C.; Nolasco, R.; Oliveira, P.B. Toward predicting Dinophysis blooms off NW Iberia: A decade of events. Harmful Algae 2016, 53, 17–32. [Google Scholar] [CrossRef]
- Aleynik, D.; Dale, A.C.; Porter, M.; Davidson, K. A high resolution hydrodynamic model system suitable for novel harmful algal bloom modelling in areas of complex coastline and topography. Harmful Algae 2016, 53, 102–117. [Google Scholar] [CrossRef] [PubMed]
- Derot, J.; Yajima, H.; Jacquet, S. Advances in forecasting harmful algal blooms using machine learning models: A case study with Planktothrix rubescens in Lake Geneva. Harmful Algae 2020, 99, 101906. [Google Scholar] [CrossRef] [PubMed]
- Harley, J.R.; Lanphier, K.; Kennedy, E.; Whitehead, C.; Bidlack, A. Random forest classification to determine environmental drivers and forecast paralytic shellfish toxins in Southeast Alaska with high temporal resolution. Harmful Algae 2020, 99, 101918. [Google Scholar] [CrossRef]
- Guallar, C.; Delgado, M.; Diogène, J.; Fernández-Tejedor, M. Artificial neural network approach to population dynamics of harmful algal blooms in Alfacs Bay (NW Mediterranean): Case studies of Karlodinium and Pseudo-nitzschia. Ecol. Model. 2016, 338, 37–50. [Google Scholar] [CrossRef]
- Shimoda, Y.; Arhonditsis, G.B. Phytoplankton functional type modelling: Running before we can walk? A critical evaluation of the current state of knowledge. Ecol. Model. 2016, 320, 29–43. [Google Scholar] [CrossRef]
- Muttil, N.; Chau, K.W. Neural network and genetic programming for modelling coastal algal blooms. Int. J. Environ. Pollut. 2006, 28, 223–238. [Google Scholar] [CrossRef]
- Huettmann, F.; Craig, E.H.; Herrick, K.A.; Baltensperger, A.P.; Humphries, G.R.W.; Lieske, D.J.; Miller, K.; Mullet, T.C.; Oppel, S.; Resendiz, C.; et al. Use of Machine Learning (ML) for Predicting and Analyzing Ecological and ’Presence Only’ Data: An Overview of Applications and a Good Outlook. In Machine Learning for Ecology and Sustainable Natural Resource Management; Humphries, G., Magness, D., Huettmann, F., Eds.; Springer: Cham, Switzerland, 2018; pp. 27–61. [Google Scholar] [CrossRef]
- Franks, P.J.S. Recent Advances in Modelling of Harmful Algal Blooms. In Global Ecology and Oceanography of Harmful Algal Blooms. Ecological Studies (Analysis and Synthesis); Glibert, P., Berdalet, E., Burford, M., Pitcher, G., Zhou, M., Eds.; Springer: Cham, Switzerland, 2018; Volume 232, pp. 359–377. [Google Scholar] [CrossRef]
- Chatfield, C. Time-Series Forecasting, 1st ed.; Chapman & Hall/CRC: London, UK, 2001. [Google Scholar]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar] [CrossRef]
- Shih, S.Y.; Sun, F.; Lee, H.Y. Temporal pattern attention for multivariate time series forecasting. Mach. Learn. 2019, 108, 1421–1441. [Google Scholar] [CrossRef]
- Hyndman, R. Measuring forecast accuracy. In Business Forecasting: Practical Problems and Solutions; Gilliland, M., Tashman, L., Sglavo, U., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2015; Chapter 3; pp. 177–184. [Google Scholar]
- Stock, J.H.; Watson, M.W. Vector Autoregressions. J. Econ. Perspect. 2001, 15, 101–115. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, revisited ed.; Holden Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Shmueli, G.; Lichtendahl, K.C. Practical Time Series Forecasting with R: A Hands-On Guide, 2nd ed.; Axelrod Schnall Publishers: Green Cove Springs, FL, USA, 2016. [Google Scholar]
- Xu, H.; Huang, Y.; Duan, Z.; Wang, X.; Feng, J.; Song, P. Multivariate Time Series Forecasting with Transfer Entropy Graph. arXiv 2020, arXiv:2005.01185. [Google Scholar]
- Chen, Q.; Guan, T.; Yun, L.; Li, R.; Recknagel, F. Online forecasting chlorophyll a concentrations by an auto-regressive integrated moving average model: Feasibilities and potentials. Harmful Algae 2015, 43, 58–65. [Google Scholar] [CrossRef]
- Qin, M.; Li, Z.; Duah, Z. Red tide time series forecasting by combining ARIMA and deep belief network. Knowl. Based Syst. 2017, 125, 39–52. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Xiao, X.; He, J.; Huang, H.; Miller, T.R.; Christakos, G.; Reichwaldt, E.S.; Ghadouani, A.; Lin, S.; Xu, X.; Shi, J. A novel single-parameter approach for forecasting algal blooms. Water Res. 2017, 108, 222–231. [Google Scholar] [CrossRef]
- Lui, G.C.; Li, W.; Leung, K.M.; Lee, J.H.; Jayawardena, A. Modelling algal blooms using vector autoregressive model with exogenous variables and long memory filter. Ecol. Model. 2007, 200, 130–138. [Google Scholar] [CrossRef]
- Ribeiro, R.; Torgo, L. A comparative study on predicting algae blooms in Douro River, Portugal. Ecol. Model. 2008, 212, 86–91. [Google Scholar] [CrossRef]
- González Vilas, L.; Spyrakos, E.; Torres Palenzuela, J.M.; Pazos, Y. Support Vector Machine-based method for predicting Pseudo-nitzschia spp. blooms in coastal waters (Galician rias, NW Spain). Prog. Oceanogr. 2014, 124, 66–77. [Google Scholar] [CrossRef]
- Li, X.; Yu, J.; Jia, Z.; Song, J. Harmful algal blooms prediction with machine learning models in Tolo Harbour. In Proceedings of the 2014 International Conference on Smart Computing, Hong Kong, China, 3–5 November 2014; pp. 245–250. [Google Scholar] [CrossRef]
- Yajima, H.; Derot, J. Application of the Random Forest model for chlorophyll-a forecasts in fresh and brackish water bodies in Japan, using multivariate long-term databases. J. Hydroinformatics 2018, 20, 206–220. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, X.; Zhang, J.; Yuan, X. A framework based on hidden Markov model with adaptative weighting for microcystin forecasting and early-warning. Decis. Support Syst. 2016, 84, 89–103. [Google Scholar] [CrossRef]
- Recknagel, F.; French, M.; Harkonen, P.; Yabunaka, K.I. Artificial neural network approach for modelling and prediction of algal blooms. Ecol. Model. 1997, 96, 11–28. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C.; Burch, M.D. Use of artificial neural networks for modelling cyanobacteria Anabaena spp. in the River Murray, South Australia. Ecol. Model. 1998, 105, 257–272. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Huang, Y.; Dickman, M.; Jayawardena, A.W. Neural network modelling of coastal algal blooms. Ecol. Model. 2003, 159, 179–201. [Google Scholar] [CrossRef]
- Recknagel, F.; Bobbin, J.; Whigham, P.; Wilson, H. Comparative application of artificial neural networks and genetic algorithms for multivariate time-series modelling of algal blooms in freshwater lakes. J. Hydroinformatics 2002, 4, 125–133. [Google Scholar] [CrossRef]
- Velo-Suárez, L.; Gutiérrez-Estrada, J. Artificial neural network approaches to one-step weekly prediction of Dinophysis acuminata blooms in Huelva (Western Andalucía, Spain). Harmful Algae 2007, 6, 361–371. [Google Scholar] [CrossRef]
- Shamshirband, S.; Nodoushan, E.J.; Adolf, J.E.; Manaf, A.A.; Mosavi, A.; Chau, K.W. Ensemble models with uncertainty analysis for multi-day ahead forecasting of chlorophyll a concentration in coastal waters. Eng. Appl. Comput. Fluid Mech. 2019, 13, 91–101. [Google Scholar] [CrossRef]
- Guo, J.; Dong, Y.; Lee, J.H. A real time data driven algal bloom risk forecast system for mariculture management. Mar. Pollut. Bull. 2020, 161, 111731. [Google Scholar] [CrossRef]
- Grasso, I.; Archer, S.D.; Burnell, C.; Tupper, B.; Rauschenber, C.; Kanwit, K.; Record, N.R. The hunt for red tides: Deep learning algorithm forecasts shellfish toxicity at site scales in coastal Maine. Ecosphere 2019, 10. [Google Scholar] [CrossRef]
- Hill, P.R.; Kumar, A.; Temimi, M.; Bull, D.R. HABNet: Machine Learning, Remote Sensing-Based Detection of Harmful Algal Blooms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3229–3239. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D. Improved Prediction of Harmful Algal Blooms in Four Major South Korea’s Rivers Using Deep Learning Models. Int. J. Environ. Res. Public Health 2018, 15, 1322. [Google Scholar] [CrossRef]
- Cho, H.; Choi, U.J.; Park, H. Deep Learning Application to Time Series Prediction of Daily Chlorophyll-a Concentration. WIT Trans. Ecol. Environ. 2018, 215, 157–163. [Google Scholar] [CrossRef]
- Cho, H.; Park, H. Merged-LSTM and multistep prediction of daily chlorophyll-a concentration for algal bloom forecast. IOP Conf. Ser. Earth Environ. Sci. 2019, 351, 012020. [Google Scholar] [CrossRef]
- Wang, X.; Xu, L. Unsteady Multi-Element Time Series Analysis and Prediction Based on Spatial-Temporal Attention and Error Forecast Fusion. Future Internet 2020, 12, 34. [Google Scholar] [CrossRef]
- Tsay, R.S. Multivariate Time Series Analysis: With R and Financial Applications, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Liong, S.Y.; Phoon, K.; Babovic, V. (Eds.) Real Time Prediction of Coastal Algal Blooms Using Artificial Neural Networks. In Proceedings of the Sixth International Conference on Hydroinformatics; World Scientific: Singapore, 2004; Volume 2. [Google Scholar]
- Gooijer, J.G.D.; Hyndman, R.J. 25 years of time series forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef]
- Gevrey, M.; Dimopoulos, I.; Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Model. 2003, 160, 249–264. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Karatzoglou, A.; Meyer, D.; Hornik, K. Support Vector Machines in R. J. Stat. Softw. 2006, 15. [Google Scholar] [CrossRef]
- Gerstner, W.; Germond, A.; Hasler, M.; Nicoud, J. (Eds.) Predicting Time Series with Support Vector Machines; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1327. [Google Scholar] [CrossRef]
- González Vilas, L.; Spyrakos, E.; Torres Palenzuela, J.M.; Estevez, M.D. Predicción de episodios de Pseudo-nitzschia spp. en las rias gallegas. In X Reuniao Ibérica de Fitoplâncton Tóxico e Biotoxinas; Instituto Nacional dos Recursos Biologicos (IPIMAR): Lisbon, Portugal, 2009; p. 7. [Google Scholar]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Huang, K.; Zheng, Z. Towards Better Forecasting by Fusing Near and Distant Future Visions. arXiv 2019, arXiv:1912.05122. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Schonlau, M.; Zou, R.Y. The random forest algorithm for statistical learning. Stata J. 2020, 20, 3–29. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Sulik, J.J.; Newlands, N.K.; Long, D.S. Encoding Dependence in Bayesian Causal Networks. Front. Environ. Sci. 2017, 4, 84. [Google Scholar] [CrossRef]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Dean, T.; Kanazawa, K. A model for reasoning about persistence and causation. Comput. Intell. 1989, 5, 142–150. [Google Scholar] [CrossRef]
- Murphy, K.; Russell, S. Dynamic Bayesian Networks: Representation, Inference and Learning; University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Liu, F.; Lu, Y.; Cai, M. A Hybrid Method With Adaptive Sub-Series Clustering and Attention-Based Stacked Residual LSTMs for Multivariate Time Series Forecasting. IEEE Access 2020, 8, 62423–62438. [Google Scholar] [CrossRef]
- Chakraborty, K.; Mehrotra, K.; Mohan, C.K.; Ranka, S. Forecasting the Behavior of Multivariate Time Series Using Neural Networks. Neural Netw. 1992, 5, 961–970. [Google Scholar] [CrossRef]
- Gamboa, J.C.B. Deep Learning for Time-Series Analysis. arXiv 2017, arXiv:1701.01887. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Cannas, B.; Fanni, A.; See, L.; Sias, G. Data preprocessing for river flow forecasting using neural networks: Wavelet transforms and data partitioning. Phys. Chem. Earth Parts A/B/C 2006, 31, 1164–1171. [Google Scholar] [CrossRef]
- Nourani, V.; Alami, M.T.; Aminfar, M.H. A combined neural-wavelet model for prediction of Ligvanchai watershed precipitation. Eng. Appl. Artif. Intell. 2009, 22, 466–472. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional Time Series Forecasting with Convolutional Neural Networks. arXiv 2018, arXiv:1703.04691. [Google Scholar]
- Koprinska, I.; Wu, D.; Wang, Z. Convolutional Neural Networks for Energy Time Series Forecasting. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time Series Forecasting With Deep Learning: A Survey. arXiv 2020, arXiv:2004.13408. [Google Scholar]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current status and future directions. Int. J. Forecast. 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Freeman, B.S.; Taylor, G.; Gharabaghi, B.; Thé, J. Forecasting air quality time series using deep learning. J. Air Waste Manag. Assoc. 2018, 68, 866–886. [Google Scholar] [CrossRef] [PubMed]
- Bowes, B.D.; Sadler, J.M.; Morsy, M.M.; Behl, M.; Goodall, J.L. Forecasting Groundwater Table in a Flood Prone Coastal City with Long Short-term Memory and Recurrent Neural Networks. Water 2019, 11, 1098. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Song, D.; Chen, H.; Cheng, W.; Jiang, G.; Cottrell, G.W. A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI-17, Melbourne, Australia, 19–25 August 2017; pp. 2627–2633. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems—Volume 2; MIT Press: Cambridge, MA, USA, 2014; pp. 3104–3112. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2016, arXiv:1409.0473. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Wallace, E.; Feng, S.; Boyd-Graber, J.L. Interpreting Neural Networks with Nearest Neighbors. arXiv 2018, arXiv:1809.02847. [Google Scholar]
- Wachter, S.; Mittelstadt, B.D.; Russell, C. Counterfactual Explanations without Opening the Black Box: Automated Decisions and the GDPR. Harv. J. Law Technol. 2017, 31, 841. [Google Scholar] [CrossRef]
| Method | Strengths | Weaknesses | Ref. |
|---|---|---|---|
| Autoregressive Models | |||
| ARIMA | Needs a small amount of data, is simple, fast, flexible, and adaptable to various types of time series. | Cannot model non-linear patterns in time series and is not applicable to multivariate cases. | [27,28,30] |
| VAR | Applicable to multivariate time series, simple and flexible. | Is prone to overfit and cannot model non-linear patterns in time series. | [31] |
| Support Vector Machine | Models non-linear data, needs a small amount of data, generalizes well, and assures a global optimal solution. | Has a high computational cost and tends to overfit when applied to high-dimensional multivariate time series. | [32,33,34] |
| Random Forest | Models non-linear data, is robust and insensitive to missing data, and its outputs are easily interpretable. | Has a high computational cost and tends to overfit when applied to high-dimensional multivariate time series. | [12,13,35] |
| Probabilistic Graphical Models | Easy to incorporate diverse data types and to specify relations between variables. Explicitly probabilistic results. | Depends on a correct manual modeling of the relations between variables. A good estimate of the joint probability distributions may require a large data set, especially with complex models. | [36] |
| Artificial Neural Networks | |||
| FFNN | Models dynamic, non-linear and noisy data, has a low computational cost, is easy to set up, self-adaptable, self-organizing, and error tolerant. | Yields instable outputs, can produce a local minimum result, has a low efficiency and slow convergence speed, the parameter tuning is difficult. | [14,16,30,34,37,38,39,40,41,42,43,44] |
| CNN | Extracts important features from the data, can work with noisy data, has a small number of trainable weights and efficient training. | The receptive field size needs to be tuned carefully to use all relevant historical information, and struggles to capture long-term dependencies in the data. | [45] |
| RNN, LSTM | Captures temporal dependencies over variable periods of time. | Has a high complexity and computational cost. | [46,47,48,49] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz, R.C.; Reis Costa, P.; Vinga, S.; Krippahl, L.; Lopes, M.B. A Review of Recent Machine Learning Advances for Forecasting Harmful Algal Blooms and Shellfish Contamination. J. Mar. Sci. Eng. 2021, 9, 283. https://doi.org/10.3390/jmse9030283
Cruz RC, Reis Costa P, Vinga S, Krippahl L, Lopes MB. A Review of Recent Machine Learning Advances for Forecasting Harmful Algal Blooms and Shellfish Contamination. Journal of Marine Science and Engineering. 2021; 9(3):283. https://doi.org/10.3390/jmse9030283
Chicago/Turabian StyleCruz, Rafaela C., Pedro Reis Costa, Susana Vinga, Ludwig Krippahl, and Marta B. Lopes. 2021. "A Review of Recent Machine Learning Advances for Forecasting Harmful Algal Blooms and Shellfish Contamination" Journal of Marine Science and Engineering 9, no. 3: 283. https://doi.org/10.3390/jmse9030283
APA StyleCruz, R. C., Reis Costa, P., Vinga, S., Krippahl, L., & Lopes, M. B. (2021). A Review of Recent Machine Learning Advances for Forecasting Harmful Algal Blooms and Shellfish Contamination. Journal of Marine Science and Engineering, 9(3), 283. https://doi.org/10.3390/jmse9030283









