Abstract
Computational Fluid Dynamics simulations of planing hulls are generally considered less reliable than simulations of displacement hulls. This is due to the flow complexity around planing hulls, especially in the bow region, where the sprays are formed. The recent and constant increasing of computational capabilities allows simulating planing hull features, with more accurate turbulence models and advanced meshing procedures. However, mesh-based approaches based on the finite volume methods have shown to be limited in capturing all the phenomena around a planing hull. As such, the focus of this study is on evaluating the ability of the Smoothed Particle Hydrodynamics mesh-less method to numerically solve the 3-D flow around a planing hull and simulate more accurately the spray structures, which is a rather challenging task to be performed with mesh-based tools. A novel application of the DualSPHysics code for simulating a planing hull resistance test has been proposed and applied to the parent hull of the Naples warped planing hull Systematic Series. The drag and the running attitudes (heave and dynamic trim angle) are computed for a wide range of Froude’s numbers and discussed concerning experimental values.
1. Introduction
Planing hulls are high-speed crafts where the hydrodynamic forces are more predominant than the hydrostatic ones. The general behavior of the planing hull is characterized by transition from displacement to planing regime passing through the transition mode, also called pre-planing regime.
Various methods are available at hand to calculate the hydrodynamic characteristics of planing hulls such as experimental, analytical, and numerical. Experimental methods (ITTC HSMV Committee report, 1999 [1]) were the first developed but require expensive facilities and measurement tools to be conducted. About the analytical methods, Savitsky [2] developed the analytical/empirical framework to evaluate the lift, drag, and dynamic trim angle based on a few input data (i.e., the hull dimensions, the deadrise angle, the longitudinal center of gravity, and the forward speed) to understand the basic hydrodynamic characteristics of the planing surface. Savitsky’s method and its developments still now represent the most widespread method to evaluate the planing hull performance in the preliminary assessments of the design stage (Blount, 2014 [3])
Over the past 20 years, researchers and designers have begun to use numerical tools based on Computational Fluid Dynamics (CFD) methods to predict the performance of the planing hulls. Generally, the computational tools are less expensive than experimental tests and more reliable than analytical/empirical methods. Hence, CFD tools are now widely used and are considered useful especially in the early-stage design phases, when understanding the behavior of the flow near and behind the hull can help designers improve the performance of high-speed planing hulls, as pointed out, for instance, by Di Caterino et al., (2018) [4].
Recently, an increased interest toward hull performance with regards to ship resistance and propulsion has been taking place in academia and industry. The main reason behind the design optimization of motorboats lies on the need to maximize fuel efficiency, with positive consequences in terms of cost-saving benefits and environmental preservation. Moreover, a pronounced interest comes from light-weight small boats in competitive sailing. A significant number of theoretical studies and experimental tests have been carried so far, for example, in Thornhill et al., (2003) [5], Begovic and Bertorello, (2012) [6], Matveev, (2014) [7], Sukas et al., (2017) [8], Jiang et al., (2016) [9], De Marco et al., (2017) [10], Niazmand Bilandi et al., (2018) [11], Tavakoli et al., (2020) [12], to name a few. Details of the study conducted in the above-mentioned papers are available in the following table (Table 1).

Table 1.
Details of the cited studies.
CFD has soon become an effective tool for revealing the hydrodynamic characteristics of high-speed marine vehicles. Several pieces of research on the topic of the planing hull performance have been carried out in the last decade using CFD tools. Among them, the most comprehensive analyses are the following:
- Fu et al., (2014) [13] showed the results from a collaborative research effort involving two different CFD codes: CFDShip-Iowa and Numerical Flow Analysis – NFA. The results were presented and discussed examining the hydrodynamic forces, moments, hull pressures, accelerations, motions, and the multi-phase free-surface flow field generated by a prismatic planing craft at high speed in calm water and waves. The comparison between numerical and experimental data for still water conditions indicated that at high Froude Number (), the dynamic trim was generally under-predicted and the resistance over-predicted.
- Kandasamy et al., (2011) [14] exposed a Verification and Validation (V&V) analysis in full scale with the Unsteady Reynolds-Averaged Navier–Stokes (URANS) code CFDShip-Iowa for two high-speed semi-planing foil-assisted catamarans. Comparing the experimental data against the full-scale simulation results, the resistance comparison error was in the range of 9.6% to 15.5% and the dynamic trim angle comparison error was in the range of −44.1% to 0.8%.
- Yousefy et al., (2013) [15] conducted a comprehensive study on the existing numerical techniques for planing craft and they used several different commercially available CFD software programs (ANSYS-FLUENT, ANSYS-CFX, CFD Ship-Iowa, ShipFlow, Tdyn, CD-Adapco Star-CCM+) to determine the flow field around a planing hull.
- Mousaviraad et al., (2015) [16] carried out a planing hull validation using the URANS code CFDShip-Iowa applied to one of the hull models of the benchmark experimental series of Fridsma, 1969 [17].
- De Luca et al., (2016) [18] showed the results of a comprehensive V&V campaign of simulations of resistance test in still water condition using the hulls of the warped planing hulls of the Naples Systematic Series. The analysis depicts, for a wide range of speed and different hull shapes, the simulation uncertainty and the comparison errors. All the simulations in this study were carried out using the CFD software Star-CCM+.
In all the above-mentioned papers the URANS method with the Volume of Fraction (VOF) approach for the air-water interface capturing is proved to be the most effective tool, in terms of accuracy and computational effort, for the planing hull performance evaluation. Furthermore, the RANS-VOF has been also found as a suitable solution for the fluid-structure interaction problem (Kocaman et al., 2020 [19]), being especially relevant when dealing with planing hulls. Indeed, the panels of high-speed planing hulls may experience severe loads and slams in still water and, of course, in rough sea conditions. Several papers discuss this topic, for instance, Volpi et al., (2017) [20]. An overview of the different approaches in the fluid-structure interaction application for the high-speed craft is available in a recent paper of Rosen et al., (2020) [21].
Different from the URANS-based software, only a few literature reports have dealt with the application of the Smoothed Particle Hydrodynamic (SPH) method to numerically model the full 3-D ship hydrodynamics. SPH is a numerical method [22], first applied to astrophysical simulations, and has presently gained momentum among the scientific community and within the industry for solving a variety of problems (see [23,24]), though only some are focused on planing hull performance. Moreover, the related carried analyses were performed around hull portions and not for the whole hull body. For instance, Landrini et al., (2012) [25] studied the free-surface bow flow around a fast and fine ship in calm water, with an emphasis on generation and evolution of the breaking and splashing bow wave. This analysis was performed using a coupled strategy of investigation. A temporal domain-decomposition strategy, which sequentially combines two Lagrangian methods, was adopted: a potential-flow solution, given by a Boundary Element Method (BEM), follows the jet evolution up to the breaking and initiates a rotational solution, provided by the SPH technique. The DDG51 vessel was used as a model for the validation. Marrone et al., (2012) [26] investigated the ship wave breaking patterns using 3D SPH simulations. Another analysis was carried out by Dashtimanesh and Gadimi, (2013) [27] that investigated, using the SPH method, the transom wave behind planing hulls. Tafuni et al., (2016) [28] investigates the bottom pressure fields and the wave elevation generated by a planing hull in finite-depth water. Additionally, the hydroelastic problem of panels and simple structures of high-speed crafts impacting on a calm water surface has been investigated in recent years using SPH codes (e.g., Brizzolara et al., 2008 [29]) and SPH coupled with finite element codes, SPH-FEM, (e.g., Campbell and Patel, 2010 [30] and Fragassa, 2019 [31]). However, no more relevant papers have been found to investigate the effectiveness of the SPH method for the entire hull simulation, especially for the high-speed craft.
The recent growth in using CFD simulations can be generally credited to the fast-growing computational capacity of entry-level solutions, which presently can balance the high demand for resources of such methods [32]. The SPH-based DualSPHysics code [33] is an open-source solver (LGPL license), developed mainly for coastal engineering applications. Specifically, the code is up to date with the newest hardware accelerator facilities, such as the general-purpose graphic processor units (GPGPUs). The solver is written in CUDA language [34] to fully exploit the potential of GPUs. Numerous functionalities have been included over the last decade to simulate fluid-driven objects to account for more realistic applications. The system can manage fluid-driven objects directly within the SPH framework, whereas the coupled Project Chrono library [35] allows dealing with a series of features for building up complex restraint systems. Many recent works have shown the viability of this approach, for example, in simulating wave energy converters [36,37,38,39], or to simulate the hydrodynamics of non-conventional vessels [40].
This work focuses on the numerical investigation, using the SPH method, of hydrodynamic performance of a typical planing hull. In particular, the parent hull of the Naples Systematic Series (NSS), also called C1 Hull, is studied. After presenting an overview of the CFD methods on the high-speed crafts performance evaluation, reporting some cases of the SPH approach, Section 2 provides details about the implementation of the SPH formulation leveraged into the code DualSPHysics. Section 3 presents the experimental setup and Section 4 goes into the numerical setup used to carry out the current study. Section 5 validates the numerical model and discusses the results of hydrodynamic characteristics such as resistance, heave, and dynamic trim angle. The validated SPH tool is used for gaining further insights about the physics of the investigated hull, focusing on the spray structures. Finally, Section 6 draws conclusions and future implications of the presented case study.
2. DualSPHysics Code
This section deals with the implemented SPH formulation which constitutes the foundation of the DualSPHysics code; important functionalities required to simulate the hull dynamics and high-speed flows are introduced as well.
2.1. SPH Method
When applied to describe fluid mechanics, the mesh-less SPH method is used to discretize a volume of fluid as a set of particles, the motion of which is dictated by the Navier–Stokes (NS) equations. These particles represent the nodal points where physical quantities (for example position, velocity, density, pressure) are approximated with an interpolation of the values of the neighboring particles on short-ranged compact support [41,42]. The technique is ideal for studying violent flows for its inherent absence of mesh distortion and can easily deal with multi-phase simulations because each particle stores its own properties. The SPH method has been used to describe a variety of free-surface flows (wave propagation over beaches, plunging breakers, impact on structures, and dambreaks [43,44,45,46,47,48,49]).
The mathematical fundamentals of the SPH method are based on the approximation of any quantities by convolution integrals. Any function F can be defined by:
where W is the kernel function [50], is the position of the point where the function is being computed, is the position of a generic computational point. This function F can be approximated by the interpolating particle contributions; a summation is performed all over the particles within the compact support of the kernel:
where a is the interpolated particle, b is a neighboring particle, m and being the mass and the density, respectively, the volume associated with the neighboring particle b, and h is the smoothing length. The kernel functions W fulfils several properties, such as positivity on the compact support, normalization, and monotonically decreasing with distance [51]. Several methodologies are available; one option is the piecewise polynomial Quintic Wendland kernel [52]:
where is a real number such that the kernel ensures the normalization property (), is the non-dimensional distance between particles, and r is the distance between a certain particle a and another particle b. In this way the Wendland kernel is used here to compute interactions of particles at a distance up to the value of .
In the Lagrangian framework, the differential form of the NS equations can be written in a discrete version using the kernel function:
where t is the time, is the velocity, P pressure, is the gravitational acceleration, is the gradient operator, the kernel function, whose value depends on the distance between a and b, with being the position of the kth particle, and c is the speed of sound.
The artificial viscosity term, , is the artificial viscosity is added in the momentum equation based on the Neumann–Richtmeyer artificial viscosity, aiming to reduce oscillations and stabilize the SPH scheme, following the work of [51]:
where with being the velocity of the kth particle, and are respectively the mean speed of sound and density, is the artificial viscosity coefficient and h guarantees a non-singular operator. It can be shown that , where is the kinematic viscosity.
In addition, a density diffusion term is implemented in DualSPHysics, which works as a high frequency numerical noise filter improving the stability of the scheme by smoothing the density. The formulation is based on the density diffusion terms introduced by Molteni and Colagrossi (2009) [53] and further developed with the name of delta-SPH by Antuono et al., (2010) and Antuono et al., (2012) [44,54]. In DualSPHysics the second term in the right-hand side of the continuity Equation (5) was proposed by Fourtakas et al., (2019) [55] as a modification of the previous cited works and the coefficient that controls the intensity of the diffusive term.
A relationship between density and pressure bonds the system of equations. DualSPHysics uses a weakly compressible SPH formulation (WCSPH) for modelling Newtonian fluids and, for such formulation, Tait’s equation of state is used to determine fluid pressure, P, from particle density.
where is the reference fluid density, is the polytropic constant. The fluid compressibility is adjusted so that c can be artificially lowered to assure reasonable values for the timesteps.
The Symplectic time integration explicit scheme [56], which is second order accurate, takes the following form, accounting for the weakly compressible formulation, for solving the position of the particle a at the step :
where , and .
The density is updated at the subsequent temporal step by means of a similar two-step strategy, which reads:
where .
As depicted in Monaghan et al., (1999) [57], a variable time stepping can be used, and considering the Courant-Friedrich-Lewy (CFL) condition, the force terms and the viscous diffusion term, it can be calculated as follows:
where is the force per unit mass.
Finally, it is important to mention that the initial condition in DualSPHysics is generated using a pre-processing tool that creates particles with an initial inter-particle of . This value also defines the resolution used in the simulations. Fluid particles and solid particles, either part of a floating object or of other solids, are then created following this initial spacing at the initial time step.
2.2. Fluid-Solid Interaction
The fluid-driven body can be easily implemented into an SPH domain. The movement of objects interacting with fluid particles in DualSPHysics is handled with different techniques. A full SPH model can deal with a rigid body by summing the total force contributions of the surrounding fluid. By assuming that a body is rigid, the net force on each boundary particle is computed according to the designated kernel function and smoothing length. Each boundary particle k experiences a force per unit mass given by:
where is the force per unit mass exerted by the fluid particle b on the boundary particle k. For the motion of a rigid body, the basic equations of rigid body dynamics can then be used:
where is the mass of the object, is the moment of inertia, is the velocity, the angular velocity, position of the particle k, and the center of mass; ∧ indicates the cross product. Equations (12) and (13) are integrated in time to predict the values of and at the beginning of the next time step. Each boundary particle within the body has a velocity given by:
Finally, the boundary particles within the rigid body are moved by integrating Equation (14) in time. This approach has been checked out by Monaghan et al., (2003) [58], which shows that linear and angular momentum are conservative properties. Validations about buoyancy-driven motion are performed in Canelas et al., 2015 [59], where DualSPHysics is tested for solid objects larger than the smallest flow scales and with various densities.
2.3. Dynamic Boundary Conditions
DualSPHysics implements the Dynamic Boundary Condition (DBC), proposed by Crespo et al., (2007) [60], as a standard method for the definition of the boundary conditions. According to this method, the set of particles that identifies the boundary region share properties that are consistent with the fluid particles, i.e., satisfying the set of Equations (4)–(6). Differently from what is done for the fluid particles, the dynamics of the boundary particles can be controlled by other system conditions, such as they can be either fixed, when they make up stationary elements, or they can move according to imposed/assigned functions. This approach is advantageous when considering that there is no special treatment to be applied for the interaction with fluid particles, and has been used for several applications.
2.4. Open Boundary Conditions
DualSPHysics includes open boundary conditions through buffer zones, which are therefore characterized as inflow/outflow areas. In principle, buffer areas are composed of several layers of particles that are mainly deployed to ensure kernel completeness, thus ensuring a safe process of adding/removing particles. Over those areas, the physical quantities (velocity, density, pressure, and surface elevation) can be either imposed or extrapolated from the adjacent fluid domain. Extrapolated velocity and density are obtained using ghost nodes in the near fluid region, where fluid quantities are computed by interpolation and applying the procedure proposed by Liu and Liu (2006) [61] to restore the lack of completeness of the kernel’s support. The complete algorithm is explained in detail by Tafuni et al., (2018) in [62]. This last work presents the first implementation of the open boundary conditions in DualSPHysics and provides a validation for the open-channel flows. Other validation for more complex channel flows can be found in Ref. [63] where a vertical slot fishway is modelled.
2.5. Coupling with Project Chrono
The DualSPHysics framework handles mechanical laws among rigid bodies via the solvers provided by Project Chrono [64]. The Project Chrono library has been implemented into the original framework, creating an integrated interface for simulating structure-structure interaction as well. The library is primarily developed to handle very large systems of 3D rigid bodies [65]. The coupling allows for arbitrarily shaped bodies to be considered, and the solver can integrate externally applied forces and torques, and the effects of kinematic-type restrictions, dynamic-type restrictions and internal collisions. For the aim of this paper, the hull motion is handled by Project Chrono.
3. Benchmark Experimental Data
3.1. Experimental Data
The experimental data reported in this paper refers to the hydrodynamic performance of the C1 hull, which is part of the Naples Systematic Series (NSS). The main dimension of the C1 hull is available in Table 2. The NSS is a systematic series of warped planing hulls and it is composed of five models, four of which are derived from the parent C1 hull, shown in Figure 1. The range of velocity tested is for between 0.5 and 1.6. For a full overview of the tested cases see De Luca et al., (2017) [66].

Table 2.
Main data of the parent hull of NSS (C1 Hull).

Figure 1.
Transversal and longitudinal sections of C1 model with the water level.
3.2. Testing Facility
The tests were performed in the towing tank at the Naval Division of the DII (Department of Industrial Engineering) of the Università Degli Studi di Napoli “Federico II” (Italy). The main dimensions of the towing tank were length 136.00 m, width 9.00 m, and depth 4.50 m. A view of the towing tank carriage is available in Figure 2a,b.

Figure 2.
Front view of the towing carriage (a) and lateral view with model and towing harm (b).
The towing force was applied horizontally at the towing point, the coordinates of which are: m in the vertical direction (z) from the hull baseline, m in the longitudinal direction (x) from the hull stern (equal to the longitudinal position of the center of buoyancy of the hull), and on the symmetry plane of the hull (). The models were tested at Reynolds Number () higher than , without turbulence stimulators, and the effects of the surge, sway, yaw, and roll were not considered. The only allowed motions are the pitch and heave. Hence, the data acquired during the tests are the hull total resistance, heave motion (also called dynamic sinkage), and the dynamic trim angle. All the measurements have been sampled at 500 Hz. Resistance, trim angle, and sinkage were analyzed in both the time and frequency domain to assure the validity of each test. Moreover, before each test, the residual waves were measured to minimize noise and to make the tests comparable among all the models. Furthermore, a specific focus was taken to keep the experimental uncertainty as small as possible, following all the International Towing Tank Conference (ITTC) recommendations and suggestions for the experimental procedures [66].
4. Numerical Setup
This section illustrates the main steps to follow to obtain the working model. The key features of this setup are the free-surface flow and the towing system. The physical tests are performed by moving the hull with a carrier at an assigned speed through still water. However, for the sake of numerical feasibility, within this numerical framework, the motion of the hull is mimicked by a free-surface flow, the velocity of which corresponds to the hull speed. Please note that this strategy represents one of the commonest approaches for the sake of numerical reproduction of experiments of this kind. As such, the degrees of freedom that the towing system deploys must differ. As opposed to the test facility, the numerical counterpart of the towing arm is fixed ( in Figure 3a). The hull is attached to a vertical (z) slider (with no friction) from its towing point ( and ), ensuring heaving motions. At this last location, a cylindrical hinge guarantees the pitch motion, thus complying with the physical model overall restrictions. For the sake of completeness, the rigid algorithms that dictate the hull’s motion are governed by the Project Chrono library, as detailed in Section 2.5.
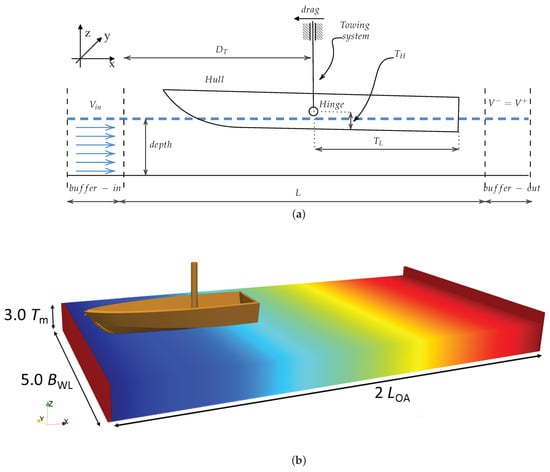
Figure 3.
(a) Schematic of the numerical domain; (b) 3-D view of the bulk of the domain.
Figure 3a depicts a schematic view of the main features of the numerical model. The free-surface current is simulated with the inlet/outlet feature (described in Section 2.4). At the left-hand side of the domain, an inlet zone is placed. The buffer (buffer-in) that controls the motion of the particles with a smoothing function that guarantees the uniform imposed velocity at the buffer threshold. On the flip side of the domain, an outlet zone takes place (buffer-out). For this side, to get an outflow consistent with the preceding area, an extrapolated method for controlling the velocity is applied, which ensures that the fluid exits undisturbed from the domain (); at the inlet and outlet zones, density is also extrapolated from the adjacent fluid domain. Moreover, for the complete definition of the open channel, the free-surface level must be defined on both sides of it. The lateral walls, which are parallel to the direction of the flow (y) are treated with periodic boundary conditions (Gómez-Gesteira et al., 2012 [67]). Figure 3a reports the quantity drag as it is computed from the system, which represents the reaction force that is experienced by the mechanical constraint handled by the Project Chrono routine.
Section 3 exposes the main geometry of the hull under study and, based on such dimensions, the numerical model takes shape. Please note that the model does not reproduce the whole bulk of the facility; an alternate, the reduced domain is used in its stead. The towing system is located at , which yields the bow of the hull 0.50 m away from the inlet to avoid the part of the current where local effects could be still in place. Therefore, L is set to twice , for this value is deemed to be sufficient for the evaluation of the three main parameters under control, i.e., the drag force, dynamic sinkage, and trim angle. To avoid any blockage effects from the lateral walls, the width of the domain is set , plus periodic boundary conditions are used to reduce the drag due to the lateral walls. For the definition of the channel depth, a proper value is defined avoiding any shallow water effect. It is proved that for this specific problem, at a depth of three times the hull maximum draft , the hull does not experience any effects from the tank bottom (Duarte et al., 2016 [68]). In the wake of this, the water depth is set to m. It is worth noticing that a sensitivity analysis was carried out on account of this aspect; it confirmed the goodness of the considered water depth. The fluid in the tank is initialized with a uniform velocity distribution, corresponding to the current velocity, and with hydrostatic pressure distribution. Finally, three different initial particle sizes are considered, namely m, so that the distances for particle interactions are m, respectively. The most refined resolution guarantees eight particles in the minimum foreseen draft (around 5 cm), according to the study proposed in Rota Roselli et al., (2018) [69]. As it turns out, such value is sufficient to accurately discretize the external features of the hull because the surface is smooth and without sudden variations.
5. Results
5.1. Hydrostatic Test
To check the correct balancing of the hull into the water in terms of forces and moments, a still water test with zero speed has been performed. Due to the granular nature of the SPH discretization, such test is also necessary before executing numerical simulations to check any inconsistency with a real case. Figure 4 depicts the results of the hydrostatic simulations performed for the hull positioned in the center of the tank (). The two in/outlet domains are disabled. This test was done for three different initial particle resolutions, namely m, and the static sinkage, static trim angle, and vertical net force are monitored.
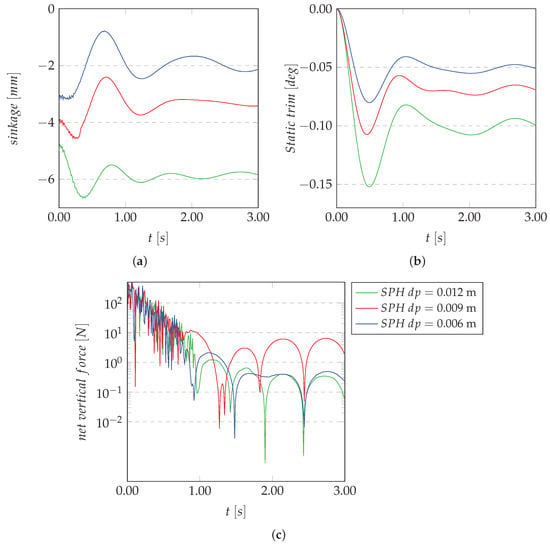
Figure 4.
Static sinkage (a), static trim angle (b), and net vertical force (c) in hydrostatic condition (still water with zero-speed flow test).
It can be seen from the charts presented in Figure 4a,b that the floating line tend to the theoretical (i.e., sinkage = 0.0 mm) one as the particle resolution decreases. The net vertical forces, as depicted in Figure 4c, demonstrate that the hull achieves equilibrium around one second of simulation. The starting points of the time series that can be observed in Figure 4a are due to the different initial lattices on which the shape of the hull is drawn, yielding a slightly different center of gravity for each resolution. In the same fashion, the misalignment between the static trim angle and the theoretical one can be explained by a small initial deviation of the center of buoyancy from the position of the towing point. Furthermore, the output of the hydrostatic analysis is applied to correct the simulation results, for the dynamic trim angle and sinkage, exposed in the next paragraph.
5.2. Total Resistance, Dynamic Trim Angle, and Sinkage
The model is herein compared with the data from the experimental campaign exposed in Section 3. The benchmark tests considered for comparison purposes are , which respectively correspond to a current velocity m/s. This speed range fully covers the pre-planing, transient, and planing regime of the C1 hull. The three resolutions used for the hydrostatic tests are considered here.
Figure 5 compares the total resistance, dynamic sinkage, and dynamic trim angle between experimental and SPH results for the three investigated resolutions. The values reported for the SPH simulations are the average values calculated from time series covering s of simulation, which are taken after one second of simulation. The cut-out is important to avoid initial transient states, in which the model adjusts itself to achieve a stable dynamic behavior. The experimental reference data are the average values calculated from time series that cover much longer time windows—depending on the length of the towing tank and the forward velocity. The values herein reported correspond to time series of 20 s for the lower bound velocity ( m/s) and of around 10 s ( m/s) for the upper bound. Please note that the shorter time windows used to average the investigated quantities, for the numerical model, do not affect the accuracy of the results due to lower variability observed in the outcomes of the simulations. The general trend depicted in Figure 5 underlines the model convergence.
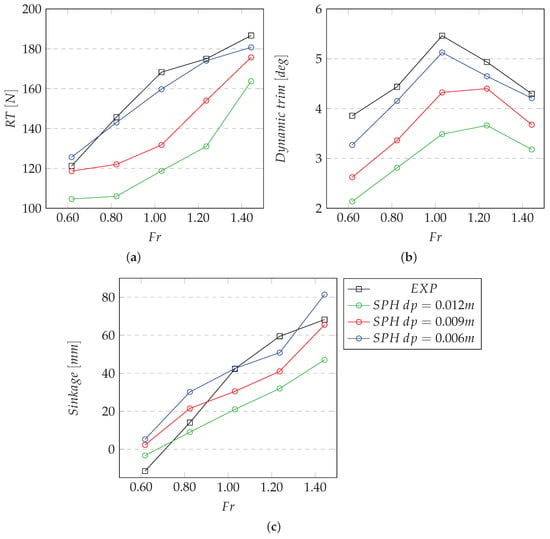
Figure 5.
Total Resistance (a), dynamic trim angle (b), and dynamic sinkage (c) comparison between experimental and SPH simulations.
Table 3 proposes the percentage discrepancies between the outcomes of the numerical method and the experimental test for the three variables under analysis, for the finest resolution m. Observing Table 3 and Figure 5, it is visible that the numerical method shows an acceptable agreement with the experimental results, though the dynamic sinkage error is high in the pre-planing regime. It is noteworthy to observe that the high percentage error for the dynamic sinkage is strictly connected to the small values of this parameter. For a more comprehensive picture about the validity of the results here exposed, it is possible to refer to the results shown in De Luca et al., 2016 [18], where the URANS CD-Adapco Star-CCM+ is used. The general trend shown in this last work is almost in line with the results obtained through the presented SPH model for the higher resolution; it is possible to recognize the same inaccuracy when dynamic trim predictions are considered. On the other hand, the good performance of the proposed numerical model for the running attitude parameters directly implies the great accuracy shown by resistance prediction; details of this point are analyzed in the next sub-paragraph.

Table 3.
Percentage comparison error between experimental and SPH and simulations with m for the three variables (total resistance, dynamic trim angle, and sinkage).
All the simulations are run on an NVIDIA© GeForce RTX 2080 Ti with 12GB of RAM and their outcomes are used to evaluate the performance of the model. Using the highest resolution ( m) a total number of 33.3 million particles are created at its initial stage; the presence of a current; however, contributes to a rate of in/out particles that is, on average, of around 40 million a second. This indeed affects the runtime, which finally amounts to 104 h (≈ 4 days) per 5.00 s of physical time - on average.
5.3. Whisker Spray
The spray region is a complex area located forward the stagnation line. According to Savitsky and Morabito (2011) [70], the stagnation line is defined as “the locus of points on the bottom along which the flow is divided into forward and aft components and on which the pressure is a maximum and is developed from bringing to rest the component of free stream velocity normal to this line”. The spray region can be divided into two different patterns: the whisker spray and the main spray. The whisker spray is a stream of small droplets of water projected out of the chine with a trajectory essentially equal to the local deadrise angle. The main spray, instead, is a cone-shaped discharge of water (continuous blister) with its apex located near the intersection of the stagnation line and the chine. The outboard trajectory of the main spray is significantly elevated compared to the whisker spray trajectory. The sprays (whisker and main) departs from the chine line and the extension is bounded by the spray edges. The spray area on the hull bottom is created as the craft moves through the water at high speeds (planing regime speeds).
In scaled models, the sprays appear as continuous sheets, while in full scale, the sheet is broken up into numerous droplets due to the effects of the surface tension that generally, for smaller scales, are relatively large compared to the inertia forces. The spray region and its features are shown in Figure 6 for the C1 hull at . The spray can account for 15% to 20% of total high-speed craft resistance. The most comprehensive experimental studies about spray are Savitsky et al., (2007) [71] and Savitsky and Morabito (2011) [70].

Figure 6.
C1 hull at , (A) Whisker spray, (B) Main spray, (C) Spray edge (red line), (D) Spray root, (E) Reflection of the spray edge.
Making a comparison of Figure 6 with a snapshot taken from the simulation at the same speed (Figure 7), it is easy to recognize the same spray structures, as highlighted in Figure 7 with a perspective view of the numerical model. The visual comparison, as exposed in this paragraph, demonstrates that the SPH model can reproduce a planing hull at high-speed, well-capturing the whisker spray area as well. This granular definition of the spray area represents a general improvement compared to what mesh-based codes can perform. It comes at a cost of an expensive computational time, which however proves to be still manageable with the right facility. Anyway, it must be underlined that as opposed to most of the mesh-based codes, the post-process is inexpensive.
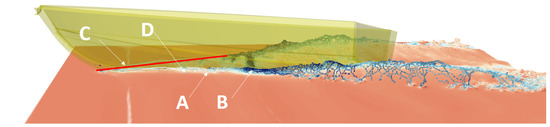
Figure 7.
C1 hull simulated at , (A) Whisker spray, (B) Main spray, (C) Spray edge (red line), (D) Spray root.
6. Conclusions
A numerical validation procedure is successfully carried out by comparing experimental and numerical results. The hydrostatic test is first presented to ensure the correct modelling of the hull’s shape with three different resolutions. The same initial inter-particle distances are used for the validation procedure, which follows the comparison of the dynamics of the hull, by considering the total resistance, sinkage, and dynamic trim angle for the five numbers, demonstrating that the model setup is viable for reproducing with accuracy the free-flow current and the towing system. The model proposed in this work has shown a good agreement with the experimental data and has provided a good level of accuracy if compared with the mesh-based approach presented in [66].
This work provides a visual analysis of the spray zone, which has no counterpart in the reference paper. The mesh-less nature of the numerical scheme herein used shows to have no shortcomings in reproducing whisker and main spray areas, while correctly simulating the solid-fluid interactions. One instant of the simulation with Fr = 1.443 is visually compared with the same area of interest in the corresponding physical test. At a glance, this comparison returns a clear and consistent overall picture, which allows identifying many features of the spray area. A whisker spray is clearly defined along with the spray root, though slightly shifted toward the aft of the hull. The main spray structures and the spray edges are also visible and in close agreement with the experimental ones. For the model can capture the whisker spray area with enough accuracy, this could be considered to be the reason for the closer estimation that the model can provide for the total resistance and dynamic trim angle.
This work lies down a groundwork on which subsequent experimental studies can be complemented by numerical analyses, in the field of naval engineering. The multiphysics solver, DualSPHysics, is employed to reproduce a test setup that is commonly used to work out the performance of planing hulls. The great versatility of the code allows building the main features of the facility with ease. For the particular case of planing hulls, where the high non-linearities of the fluid flow are critical, the Smoothed Particle Hydrodynamics method poses a good compromise between accuracy and computational effort. As has been shown through the information reported in this work, the model can achieve a sufficient degree of accuracy for the evaluation of the planing hull performance. The model setup is thoroughly reported, and it is quite straightforward to reproduce if enough knowledge about the physical tests is at hand.
The next step of this investigation will be the application of the SPH method not only to the still water resistance tests but also to the planing hull simulations in regular and irregular waves [72], to extend the engineering applications of the SPH method in the marine hydrodynamic field. Furthermore, a finer resolution will be applied to investigate the resistance of the planing hull equipped with interceptor/intruder, spray rails, and steps.
Author Contributions
Conceptualization, S.M.; methodology, B.T. and S.M.; software, J.M.D., B.T., P.R.-G. and A.J.C.C.; validation, B.T., S.M.; formal analysis, B.T. and P.R.-G., J.M.D.; investigation, S.M. and B.T.; resources, A.J.C.C. and G.V.; data curation, B.T. and S.M.; writing original draft preparation, S.M., B.T., A.J.C.C., P.R.-G., G.V.; revision, S.M., B.T., A.J.C.C., J.M.D.; visualization, S.M. and B.T.; supervision, G.V. and A.J.C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The experimental data presented in this study are openly available in https://doi.org/10.1016/j.oceaneng.2017.04.038 (accessed on 18 February 2021).
Acknowledgments
The first author of this manuscript wishes to express his gratitude to the IT support provided by Orlando Garcia-Feal, who made possible the use of the HPC system at monkey-island.uvigo.es.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BEM | Boundary Element Method |
| CCP | Cone Complementary Problem |
| CFD | Computational Fluid Dynamics |
| CFL | Courant-Friedrich-Lewy Number |
| DBC | Dynamic Boundary Condition |
| DII | Department of Industrial Engineering |
| DVI | Differential Variational Inequality |
| Fr | Froude Number |
| FVM | Finite Volume Method |
| GPU | Graphics Processing Unit |
| HSMV | High-Speed Marine Vehicle |
| ITTC | International Towing Tank Conference |
| LCB | Longitudinal position of the Center of Buoyancy |
| NFA | Numerical Flow Analysis |
| NS | Navier–Stokes |
| NSS | Naples Systematic Series |
| Re | Reynolds Number |
| (U)RANS | (Unsteady) Reynolds-Averaged Navier–Stokes |
| SPH | Smoothed Particle Hydrodynamics |
| V&V | Verification & Validation |
| VOF | Volume of Fluid |
| WCSPH | Weakly Compressible Smoothed Particle Hydrodynamics |
References
- ITTC. Model Tests of High Speed Marine Vehicles Specialist Committee. Final Report and Recommendations of the 22nd ITTC Committee. 1999. Available online: https://ittc.info/media/1510/specialist-committee-on-safety-of-high-speed-marine-vehicles.pdf (accessed on 18 February 2021).
- Savitsky, D. Hydrodynamic Design of Planing Hulls. Mar. Technol. SNAME News 1964, 1, 71–95. [Google Scholar] [CrossRef]
- Blount, D.L. Performance by Design: Hydrodynamics for High-Speed Vessels, 1st ed.; Blount, D.L., Ed.; Donald L. Blount and Associates, Inc.: Chesapeake, VA, USA, 2014. [Google Scholar]
- Di Caterino, F.; Bilandi, R.N.; Mancini, S.; Dashtimanesh, A.; De Carlini, M. A Numerical Way for a Stepped Planing Hull Design and Optimization. In Proceedings of the NAV 2018, 19th International Conference on Ship and Maritime Research, Trieste, Italy, 20–22 June 2018. [Google Scholar] [CrossRef]
- Thornhill, E.; Oldford, D.; Bose, N.; Veitch, B.; Liu, P. Planing hull performance from model tests. Int. Shipbuild. Prog. 2003, 50, 5–18. [Google Scholar]
- Begovic, E.; Bertorello, C. Resistance assessment of warped hullform. Ocean Eng. 2012, 56, 28–42. [Google Scholar] [CrossRef]
- Matveev, K.I. Hydrodynamic modeling of planing hulls with twist and negative deadrise. Ocean Eng. 2014, 82, 14–19. [Google Scholar] [CrossRef]
- Sukas, O.F.; Kinaci, O.K.; Cakici, F.; Gokce, M.K. Hydrodynamic assessment of planing hulls using overset grids. Appl. Ocean Res. 2017, 65, 35–46. [Google Scholar] [CrossRef]
- Jiang, Y.; Sun, H.; Zou, J.; Hu, A.; Yang, J. Analysis of tunnel hydrodynamic characteristics for planing trimaran by model tests and numerical simulations. Ocean Eng. 2016, 113, 101–110. [Google Scholar] [CrossRef]
- De Marco, A.; Mancini, S.; Miranda, S.; Scognamiglio, R.; Vitiello, L. Experimental and numerical hydrodynamic analysis of a stepped planing hull. Appl. Ocean Res. 2017, 64, 135–154. [Google Scholar] [CrossRef]
- Bilandi, R.; Mancini, S.; Vitiello, L.; Miranda, S.; De Carlini, M. A Validation of Symmetric 2D + T Model Based on Single-Stepped Planing Hull Towing Tank Tests. J. Mar. Sci. Eng. 2018, 6, 136. [Google Scholar] [CrossRef]
- Tavakoli, S.; Niazmand Bilandi, R.; Mancini, S.; De Luca, F.; Dashtimanesh, A. Dynamic of a planing hull in regular waves: Comparison of experimental, numerical and mathematical methods. Ocean Eng. 2020, 217, 107959. [Google Scholar] [CrossRef]
- Fu, T.; Brucker, K.; Mousaviraad, M.; Ikeda-Gilbert, C.; Lee, E.; O’Shea, T.; Wang, Z.; Stern, F.; Judge, C. An Assessment of Computational Fluid Dynamics Predictions of the Hydrodynamics of High-Speed Planing Craft in Calm Water and Waves. In Proceedings of the 30th Symposium on Naval Hydrodynamics Hobart, Tasmania, Hobart, Australia, 2–7 November 2014. [Google Scholar]
- Kandasamy, M.; Ooi, S.K.; Carrica, P.; Stern, F.; Campana, E.; Peri, D.; Osborne, P.; Cote, J.; Macdonald, N.; de Waal, N. CFD validation studies for a high-speed foil-assisted semi-planing catamaran. J. Mar. Sci. Technol. 2011, 16, 157–167. [Google Scholar] [CrossRef]
- Yousefi, R.; Shafaghat, R.; Shakeri, M. Hydrodynamic analysis techniques for high-speed planing hulls. Appl. Ocean Res. 2013, 42, 105–113. [Google Scholar] [CrossRef]
- Mousaviraad, S.M.; Wang, Z.; Stern, F. URANS studies of hydrodynamic performance and slamming loads on high-speed planing hulls in calm water and waves for deep and shallow conditions. Appl. Ocean Res. 2015, 51, 222–240. [Google Scholar] [CrossRef]
- Fridsma, G. A Systematic Study of the Rough-Water Performance of Planing Boats; Technical Report, Davidson Laboratory Report 1275; Stevens Institute of Technology Davidson Laboratory, Castle Point Station: Hoboken, NY, USA, 1969. [Google Scholar]
- De Luca, F.; Mancini, S.; Miranda, S.; Pensa, C. An Extended Verification and Validation Study of CFD Simulations for Planing Hulls. J. Ship Res. 2016, 60, 101–118. [Google Scholar] [CrossRef]
- Kocaman, S.; Güzel, H.; Evangelista, S.; Ozmen-Cagatay, H.; Viccione, G. Experimental and Numerical Analysis of a Dam-Break Flow through Different Contraction Geometries of the Channel. Water 2020, 12, 1124. [Google Scholar] [CrossRef]
- Volpi, S.; Diez, M.; Sadat-Hosseini, H.; Kim, D.H.; Stern, F.; Thodal, R.; Grenestedt, J. Composite bottom panel slamming of a fast planing hull via tightly coupled fluid-structure interaction simulations and sea trials. Ocean Eng. 2017, 143, 240–258. [Google Scholar] [CrossRef]
- Rosén, A.; Garme, K.; Razola, M.; Begovic, E. Numerical modelling of structure responses for high-speed planing craft in waves. Ocean Eng. 2020, 217, 107897. [Google Scholar] [CrossRef]
- Violeau, D.; Rogers, B. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2016, 54, 1–26. [Google Scholar] [CrossRef]
- Gotoh, H.; Khayyer, A. On the state-of-the-art of particle methods for coastal and ocean engineering. Coast. Eng. J. 2018, 60, 1–25. [Google Scholar] [CrossRef]
- Manenti, S.; Wang, D.; Domínguez, J.; Li, S.; Amicarelli, A.; Albano, R. SPH Modeling of Water-Related Natural Hazards. Water 2019, 11, 1875. [Google Scholar] [CrossRef]
- Landrini, M.; Colagrossi, A.; Greco, M.; Tulin, M. The fluid mechanics of splashing bow waves on ships: A hybrid BEM–SPH analysis. Ocean Eng. 2012, 53, 111–127. [Google Scholar] [CrossRef]
- Marrone, S.; Bouscasse, B.; Colagrossi, A.; Antuono, M. Study of ship wave breaking patterns using 3D parallel SPH simulations. Comput. Fluids 2012, 69, 54–66. [Google Scholar] [CrossRef]
- Dashtimanesh, A.; Ghadimi, P. A three-dimensional SPH model for detailed study of free surface deformation, just behind a rectangular planing hull. J. Braz. Soc. Mech. Sci. Eng. 2013, 35, 369–380. [Google Scholar] [CrossRef]
- Tafuni, A.; Sahin, I.; Hyman, M. Numerical investigation of wave elevation and bottom pressure generated by a planing hull in finite-depth water. Appl. Ocean Res. 2016, 58, 281–291. [Google Scholar] [CrossRef]
- Brizzolara, S.; Viviani, M.; Savio, L. Comparison of SPH and RANSE methods for the evaluation of impact problems in the marine field. In Proceedings of the 8th World Congress on Computational Mechanics (WCCM8), Venice, Italy, 30 June–4 July 2008. [Google Scholar]
- Campbell, J.; Patel, M. Modelling fluid–structure impact with the coupled FE-SPH approach. In Proceedings of the William Froude Conference on Advances in Theoretical and Applied Hydrodynamic, Portsmouth, UK, 24–25 November 2010; pp. 131–137. [Google Scholar]
- Fragassa, C. Engineering Design Driven by Models and Measures: The Case of a Rigid Inflatable Boat. J. Mar. Sci. Eng. 2019, 7, 6. [Google Scholar] [CrossRef]
- Altomare, C.; Viccione, G.; Tagliafierro, B.; Bovolin, V.; Domínguez, J.; Crespo, A. Free-Surface Flow Simulations with Smoothed Particle Hydrodynamics Method using High-Performance Computing. In Computational Fluid Dynamics-Basic Instruments and Applications in Science; Adela Ionescu, IntechOpen: London, UK, 2018; pp. 73–100. [Google Scholar] [CrossRef]
- Crespo, A.; Domínguez, J.; Rogers, B.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- NVIDIA; Vingelmann, P.; Fitzek, F.H. CUDA, Release: 10.2.89 [Internet]. 2020. Available online: https://developer.nvidia.com/cuda-toolkit (accessed on 18 February 2021).
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Negrut, D. Chrono: An Open Source Multi-physics Dynamics Engine. In International Conference on High Performance Computing in Science and Engineering; Springer: Cham, Switzerland, 2016; pp. 19–49. [Google Scholar] [CrossRef]
- Brito, M.; Canelas, R.; García-Feal, O.; Domínguez, J.; Crespo, A.; Ferreira, R.; Neves, M.; Teixeira, L. A numerical tool for modelling oscillating wave surge converter with nonlinear mechanical constraints. Renew. Energy 2020, 146, 2024–2043. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.; Tagliafierro, B.; Altomare, C.; Domínguez, J.M.; Gómez-Gesteira, M.; Viccione, G. Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics. Renew. Energy 2020, 162, 1763–1776. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Montuori, R.; Vayas, I.; Ropero-Giralda, P.; Crespo, A.; Domìnguez, J.; Altomare, C.; Viccione, G.; Gòmez-Gesteira, M. A new open source solver for modelling fluid-structure interaction: Case study of a point-absorber wave energy converter with a power take-off unit. In Proceedings of the 11th International Conference on Structural Dynamics, Athens, Greece, 22–24 June 2020. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.C.; Coe, R.G.; Tagliafierro, B.; Domínguez, J.M.; Bacelli, G.; Gómez-Gesteira, M. Modelling a Heaving Point-Absorber with a Closed-Loop Control System Using the DualSPHysics Code. Energies 2021, 14, 760. [Google Scholar] [CrossRef]
- Mogan, S.C.; Chen, D.; Hartwig, J.; Sahin, I.; Tafuni, A. Hydrodynamic analysis and optimization of the Titan submarine via the SPH and Finite–Volume methods. Comput. Fluids 2018, 174, 271–282. [Google Scholar] [CrossRef]
- Viccione, G.; Bovolin, V.; Carratelli, E.P. Defining and optimizing algorithms for neighbouring particle identification in SPH fluid simulations. Int. J. Numer. Methods Fluids 2008, 58, 625–638. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M.; Marongiu, J.C. Neighbour lists in smoothed particle hydrodynamics. Int. J. Numer. Methods Fluids 2011, 67, 2026–2042. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical Simulation of Interfacial Flows by Smoothed Particle Hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Pugliese Carratelli, E.; Viccione, G.; Bovolin, V. Free surface flow impact on a vertical wall: A numerical assessment. Theor. Comput. Fluid Dyn. 2016, 30, 403–414. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Falahaty, H.; Shimizu, Y. An enhanced ISPH–SPH coupled method for simulation of incompressible fluid–elastic structure interactions. Comput. Phys. Commun. 2018, 232, 139–164. [Google Scholar] [CrossRef]
- Domínguez, J.; Crespo, A.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153, 103560. [Google Scholar] [CrossRef]
- De Padova, D.; Meftah, M.; De Serio, F.; Mossa, M.; Sibilla, S. Characteristics of breaking vorticity in spilling and plunging waves investigated numerically by SPH. Environ. Fluid Mech. 2019, 1–28. [Google Scholar] [CrossRef]
- Amicarelli, A.; Manenti, S.; Albano, R.; Agate, G.; Paggi, M.; Longoni, L.; Mirauda, D.; Ziane, L.; Viccione, G.; Todeschini, S.; et al. SPHERA v.9.0.0: A Computational Fluid Dynamics research code, based on the Smoothed Particle Hydrodynamics mesh-less method. Comput. Phys. Commun. 2020, 250, 107157. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial basis functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Fourtakas, G.; Dominguez, J.M.; Vacondio, R.; Rogers, B.D. Local uniform stencil (LUST) boundary condition for arbitrary 3-D boundaries in parallel smoothed particle hydrodynamics (SPH) models. Comput. Fluids 2019, 190, 346–361. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Reich, S.; Zentrum, K.; Str, H.; Skeel, R. Integration Methods for Molecular Dynamics. In Mathematical Approaches to Biomolecular Structure and Dynamics; Springer: New York, NY, USA, 1995; Volume 82. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Cas, R.A.F.; Kos, A.M.; Hallworth, M. Gravity currents descending a ramp in a stratified tank. J. Fluid Mech. 1999, 379, 39–69. [Google Scholar] [CrossRef]
- Monaghan, J.; Kos, A.; Issa, N. Fluid Motion Generated by Impact. J. Waterw. Port Coast. Ocean Eng. 2003, 129, 250–259. [Google Scholar] [CrossRef]
- Canelas, R.B.; Domínguez, J.M.; Crespo, A.J.; Gómez-Gesteira, M.; Ferreira, R.M. A Smooth Particle Hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 2015, 78, 581–593. [Google Scholar] [CrossRef]
- Crespo, A.; Gómez-Gesteira, M.; Dalrymple, R. Boundary conditions generated by dynamic particles in SPH methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- Liu, M.; Liu, G. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Tafuni, A.; Domínguez, J.; Vacondio, R.; Crespo, A. A versatile algorithm for the treatment of open boundary conditions in Smoothed particle hydrodynamics GPU models. Comput. Methods Appl. Mech. Eng. 2018, 342. [Google Scholar] [CrossRef]
- Novak, G.; Tafuni, A.; Domínguez, J.; Četina, M.; Žagar, D. A Numerical Study of Fluid Flow in a Vertical Slot Fishway with the Smoothed Particle Hydrodynamics Method. Water 2019, 11, 1928. [Google Scholar] [CrossRef]
- Team, P.D. Chrono: An Open Source Framework for the Physics-Based Simulation of Dynamic Systems. Available online: https://github.com/projectchrono/chrono (accessed on 7 May 2020).
- Canelas, R.; Brito, M.; Feal, O.; Domínguez, J.; Crespo, A. Extending DualSPHysics with a Differential Variational Inequality: Modeling fluid-mechanism interaction. Appl. Ocean Res. 2018, 76, 88–97. [Google Scholar] [CrossRef]
- De Luca, F.; Pensa, C. The Naples warped hard chine hulls systematic series. Ocean Eng. 2017, 139, 205–236. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.; Crespo, A.; Dalrymple, R.; Narayanaswamy, M.; Dominguez, J. SPHysics – development of a free-surface fluid solver – Part 1: Theory and formulations. Comput. Geosci. 2012, 48, 289–299. [Google Scholar] [CrossRef]
- Duarte, H.; Droguett, E.; Ramos Martins, M.; Lützhöft, M.; Pereira, P.; Lloyd, J. Review of practical aspects of shallow water and bank effects. Int. J. Marit. Eng. 2016, 158, 177–186. [Google Scholar] [CrossRef]
- Rota Roselli, R.A.; Vernengo, G.; Altomare, C.; Brizzolara, S.; Bonfiglio, L.; Guercio, R. Ensuring numerical stability of wave propagation by tuning model parameters using genetic algorithms and response surface methods. Environ. Model. Softw. 2018, 103, 62–73. [Google Scholar] [CrossRef]
- Savitsky, D.; Morabito, M. Origin and Characteristics of the Spray Patterns Generated by Planing Hulls. J. Ship Prod. Des. 2011, 27, 63–83. [Google Scholar] [CrossRef]
- Savitsky, D.; DeLorme, M.; Datla, R. Inclusion of Whisker Spray Drag in Performance Prediction Method for High-Speed Planing Hulls. Mar. Technol. 2007, 44, 35–56. [Google Scholar]
- Verbrugghe, T.; Domínguez, J.; Altomare, C.; Tafuni, A.; Vacondio, R.; Troch, P.; Kortenhaus, A. Non-linear wave generation and absorption using open boundaries within DualSPHysics. Comput. Phys. Commun. 2019, 240, 46–59. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).