1. Introduction
Semantic image segmentation is the process of assigning a categorical label to each image pixel automatically. There are many critical applications that require this procedure, such as marine species detection and conservation, object localization, and scene understanding. For instance, coral detection in reef imagery is one such applications because coral reefs are struggling due to global warming and pollution. However, the quantification of coral abundance is currently completed by humans and it is a time-consuming, boring, and expensive task. For example, it takes 16 people to work for several months to analyze the abundance of corals in hundreds of images collected from one typical two-week cruise. Hence, semantic segmentation can be used to quantify the abundance of each species by counting the number of pixels belonging to that category. In recent years, this topic has been widely investigated using deep learning based methods such as SegNet [
1], Unet [
2] and fully convolutional network (FCN) [
3]. However, such models require full pixel-level annotation to train. Unfortunately, existing marine species and biomedical images data sets lack annotated labels due to the cost of pixel-level labels. In our work, humans will provide labels only for 50 pixels per image.
Figure 1 shows the sparse point-level labels in the coral images data set, where different colors represent different classes.
Semi-supervised semantic segmentation can be framed as semi-supervised image classification with sliding window patch to identify the class of the patch’s central pixel. Prior works on semi-supervised classification are divided into two main categories. The first is consistency regularization which adds a regularizer into the loss function. This term is applied to either all images or only the unlabeled samples, and designed based on the assumption that if a realistic perturbation was applied to the unlabeled data samples, the network prediction should not change significantly.
-model [
4] encourages that the distance between a network output with original input and its corresponding standard transformation (i.e., flipping, cropping) should be small. Virtual adversarial training (VAT) [
5] approximates a tiny perturbation to the corresponding input data that would most significantly affect network output, then they put consistency regularization into the objective function to penalize the difference in the network outputs for the perturbed and unperturbed samples. Methods in the second category are called pseudo labeling because they assign pseudo-labels to the unlabeled samples based on either a network trained by predictor or the similarity between labeled and unlabeled samples. The pseudo-labeled examples augment the human labels in the training process with supervised loss, such as cross entropy. Both categories use a standard loss term that is trained with supervision from labeled samples. Our method belongs to the pseudo-labeling methodology.
There are many different ways to assign pseudo-labels on unlabeled data. The simplest way to generate pseudo-labels is based on the distance from the true labels, as exemplified by our previous work [
6,
7] to generate pseudo-label using superpixels in the input images. Lee et al. [
8] was the first, to our knowledge, to use the trained network to infer pseudo-labels of unlabeled examples effectively by choosing the most confident class. Similarly, entropy minimization (EntMin) [
9] encourages the network to make “confident” predictions for all unlabeled samples. The same principle was adopted by Shi et al. [
10], where the authors further add contrastive loss to the consistency loss in the feature space, combined with a Mean Teacher approach [
11]. Blundell et al. [
12] and Kendall et al. [
13] infer the pseudo-labels using Bayesian neural network (BNN) rather than the traditional neural network. Other methods for generating pseudo-labels employ a graph model, which consider samples as nodes and find the labels of unlabeled nodes from labeled nodes. Zhu et al. [
14] proposes label prorogation and Ahmet et al. [
15] applies label propagation into a deep neural network. Carlini et al. [
16] achieves the better performance by incorporating ideas of consistency regularization, entropy minimization and Mixup operation [
17]. Recently, deep learning has been applied to coral images. Gonzalez-Rivero et al. [
18] employ convolutions neural networks in coral image patch classification, but without data augmentation. Akbari Asanjan et al. [
19] develop a deep learning model for extracting domain invariant features from multimodal remote sensing imagery to create high-resolution coral images. Modasshir et al. [
20] focus on coral images video and uses forward and backward tracking algorithms to generate labels. Our method is different from all above methods, and our pseudo-labels are inferred from a latent class distribution.
Our method focus on the feature space because the input space is high dimensional which is hard to do clustering. It is obvious that a good feature representation plays a critical role in our proposed method. To this end, we apply information maximization criterion, which maximizes the mutual information between the input and latent features, in the training process to obtain a good representation. In this paper, we use matrix-based Rényi’s
-order entropy functional proposed by Giraldo et al. [
21] to estimate the mutual information and Yu et al. [
22] extend it to multivariate condition. The main advantage of this approach is that it estimates the entropy and joint entropy directly from data without PDF estimation. This methodology is different from variational information bottleneck (VIB) [
23] and mutual information neural estimation (MINE) [
24], which either approximate the variational lower bound of mutual information or find the function to maximize the lower bound, but their accuracy in complex imagery is unclear.
The main idea of assigning pseudo-label in our method is to find the probability of the image patch given the class and assign the label to the image patch corresponding to the highest probability. To obtain the latent class distribution over the image patches, we need to fit the feature space with a statistical model. Latent Dirichlet Allocation (LDA) [
25] is a good choice, which is a three-level hierarchical Bayesian model. Each item of a collection is modeled as the mixture of topics and each topic is modeled as mixture of the codebook. To apply LDA for image processing, we regard the whole images as documents, categories as topics, and small image patches as visual words. However, traditional LDA is a ”bag-of-words” model and doesn’t consider the spatial information at all, which is essential for image processing, therefore, we add spatial information in LDA by calculating the frequency of the category around the image patches. Different from Wang et al [
26], which adds another layer between codebook and category, our method is simpler and easy to train. Motivated by active learning which allowed human in the loop to annotate data at each iteration, we also propose an iterative strategy to generate pseudo-labels. The key idea of our strategy is to use previously learned knowledge to improve the model learning by adding pseudo-labels inferred from previous knowledge.
In this paper, we propose a novel framework to generate pseudo-labels iteratively depending only on the original sparsely labels. To summarize, the contributions of this paper are as following. Firstly, we propose a simple yet effective framework to image semantic segmentation based on the sparsely point-supervision. Secondly, we modify the Latent Dirichlet allocation (LDA) by adding spatial coherence and use latent distribution as the criterion to generate pseudo-labels iteratively. Finally, we add mutual information constraint between the input and feature space to get a good representation.
The rest of this paper is organized as follows.
Section 2 provides the overview of our method and describes each part of our framework in detail.
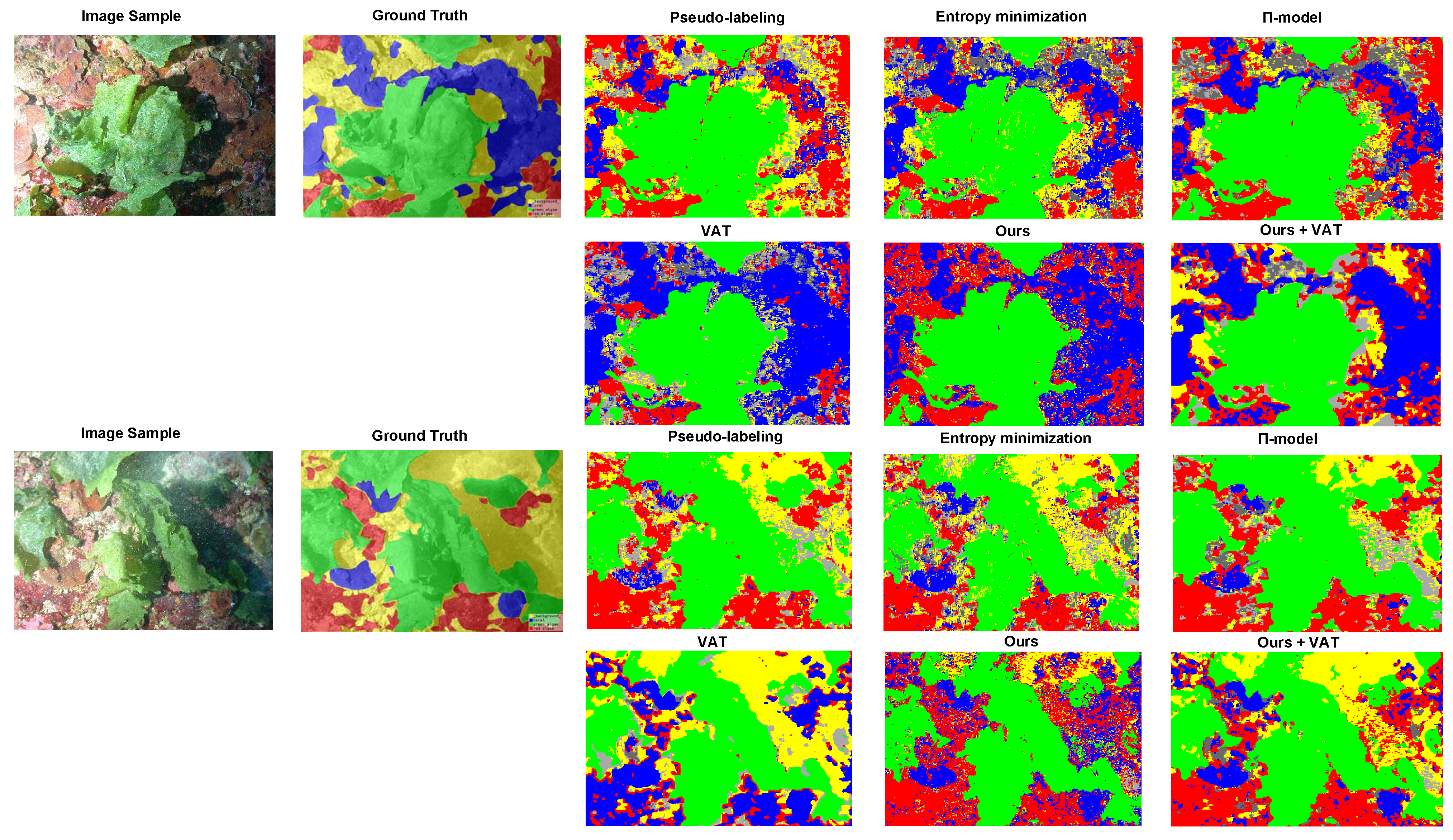
Section 3 shows the results of the proposed method in coral images dataset compared with other semi-supervised approaches, and ablation study for the impact of different components of our method. Conclusion and some future works are mentioned in
Section 4.
2. Materials and Methods
In this section, we first provide the overview of the proposed method and then formulate coral image segmentation as the semi-supervised image classification problem. Detail description for each part in
Figure 2 are also demonstrated.
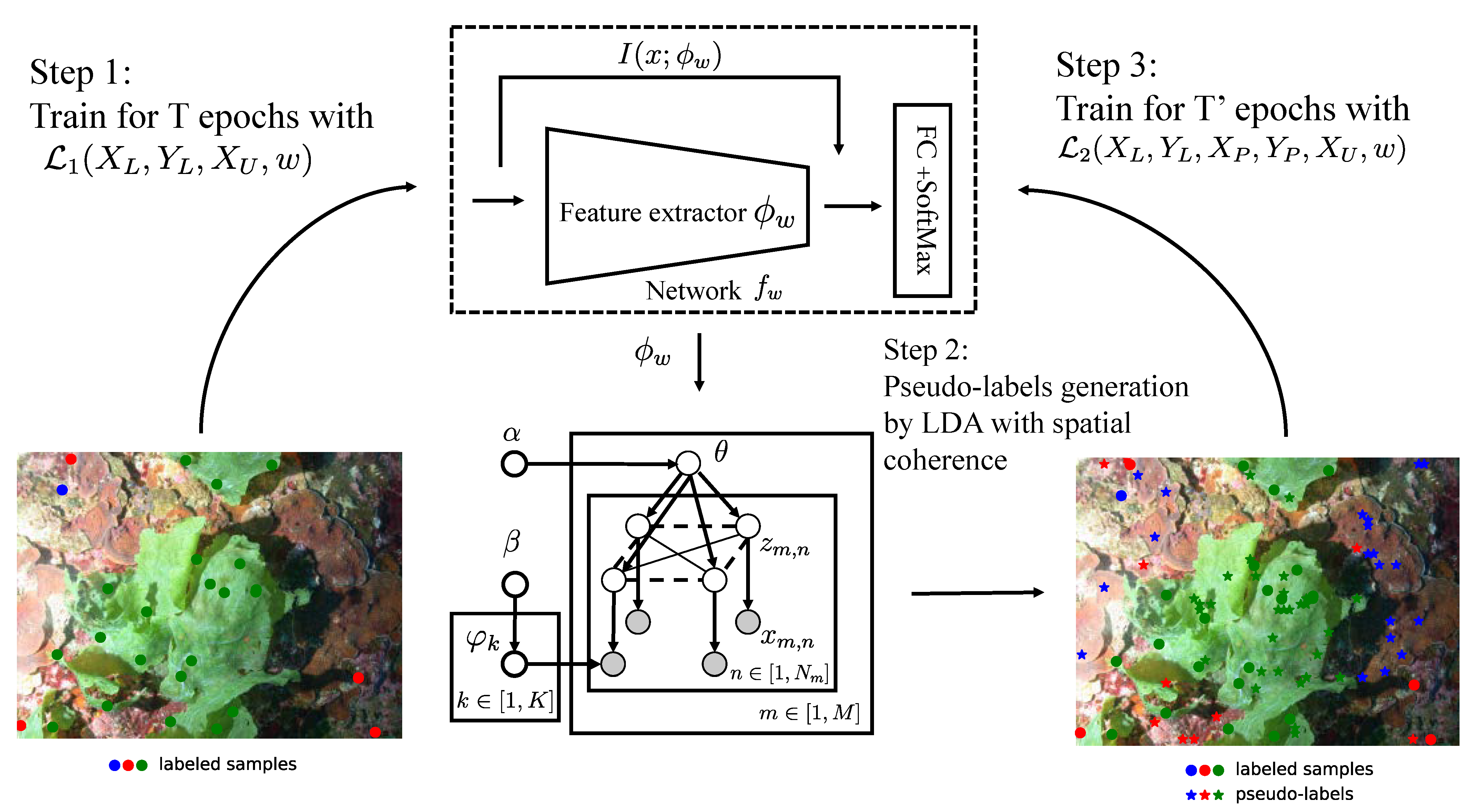
As we can see, our framework, summarized in
Figure 2, consists of three steps. Starting from a randomly initialized network. The first step is to train the network from labeled samples and mutual information constrain between input and latent features. The second step is to employ spatial coherence LDA in the embedding of the network trained in the previous step to infer the category distribution over latent features and generate pseudo-labels. The third step is to train the neural network on the entire training set, with labeled samples, pseudo-labeled samples and unlabeled samples. The pseudo-labeled samples are weighted per samples and per class.
2.1. Preliminaries
In this section, we first formulate the semi-supervised coral images segmentation and then we discuss the loss function that used in our work. For semi-supervised classification, we assume a collection of n examples with . The first l examples for denoted by are labeled by with , where is a discrete label set for c class. The remaining examples for , denoted by , are unlabeled. The goal is to use all X (image patches) and only small label size (point-supervision) to train a classifier to identify the class of unlabeled samples . In practical conditions, the number of samples in label set is much smaller than that in the unlabeled set. For our coral images dataset, there are only labeled pixels.
The neural network takes input examples from
and produce a vector of class probability. We denote it by
, where
w represents the parameters of network. Function
is the mapping from the input space to the class space. The output of the network for
ith example is
and the prediction is the index of maximum probability, which is shown in Equation (
1).
where subscript
j denotes the
j-th dimension of probability vector corresponding to the
j-th class. Basically, we need an objective function and the goal is to minimize it, which is nothing but to take the derivative of the loss function respect to the parameters
w. There are two stages for our method. First, we train a classifier with labels and mutual information constraint to get a good feature representation. Then, we generate pseudo-labeled samples via spatial LDA in the feature space extracted in the first stages and add them in the training set.
The objective function (
) for the first stage consists of two component: supervised loss(
) and mutual information constraint loss (
) shown in Equation (
2). where the minus sign is added before mutual information constraint loss because we want maximize the mutual information.
The objective function (
) for the second stage consists of three component: supervised loss (
), pseudo-label loss (
) and mutual information constraint loss (
), which is shown in Equation (
3), we bring in the pseudo-labeled samples information in loss function.
The network is trained by minimizing a supervised loss term (
) on labeled samples in
, which is shown in Equation (
4). A standard choice of
in classification is cross-entropy loss. Pseudo-label loss (
) is the second component in
, which is applied only to pseudo-labeled samples.
represents the pseudo-labels of
and
in Equation (
5) denotes the pseudo-labels for each example
for
. This label is assigned according to the latent class distribution from LDA with spatial information described in
Section 2.3.
The third component in
is the mutual information between input space and latent features space shown in Equation (
6). The reason why add such term is that we want to obtain a good representation combining not only the label information but also the input structure information. The classifier (dotted rectangle box in
Figure 1) is conceptually divided in two parts. The first part is feature extraction network
, mapping the input to a
d dimension feature vector, we denote it by
for
i-th input sample
. The second classifier part typically consists of a fully connected layer appied on the top of
followed by softmax layer.
The classifier of choice is Wide Residual Networks (WRN) [
27] which is widely used in many semi-supervised methods for image classification. It consists of an initial convolutional layer and three groups of residual blocks followed by average pooling and final fully connected layer. The main difference between WRN and ResNet [
28] is that the number of kernels is larger than that of ResNet, which achieves better representation.
2.2. Feature Extraction with Information Maximization
In order to get a good feature representation for the input samples, we require that the feature space not only contains the label information but also preserves the input sample structure as well. Therefore, we maximize the mutual information between the input space and feature space. The loss function is in Equation (
7):
The first term is the cross entropy loss between predict and true labels, the second term is mutual information between input and its corresponding features.
For completeness, we review briefly bellow the matrix-based Rényi’s -order entropy functional on positive definite matrices and how to use it for calculating mutual information. We first give the definition of entropy and joint entropy and then provide the equation to calculate the mutual information.
Definition 1. Let be a real valued positive definite kernel that is also infinitely divisible. Given , each can be a real-valued scalar or vector, and the Gram matrix computed as , a matrix-based analogue to Rényi’s α-entropy can be given by the following functional:where . A is the normalized version of K, i.e., . denotes the i-th eigenvalue of A. Definition 2. Given n pairs of samples , each sample contains two measurements and obtained from the same realization. Given positive definite kernels and , a matrix-based analogue to Rényi’s α-order joint-entropy can be defined as:where , and denotes the Hadamard product between the matrices A and B. Given Equations (
8) and (
9), the matrix-based Rényi’s
-order mutual information
in analogy of Shannon’s mutual information is given by:
Throughout this work, we use the Gaussian kernel
to obtain the Gram matrices. For each sample, we evaluate its
k (
) nearest distances and take the mean. We choose kernel width
as the average of mean values for all samples. Further information and the analytical gradient of Equation (
10) are shown in
Appendix A.
2.3. LDA with Spatial Information
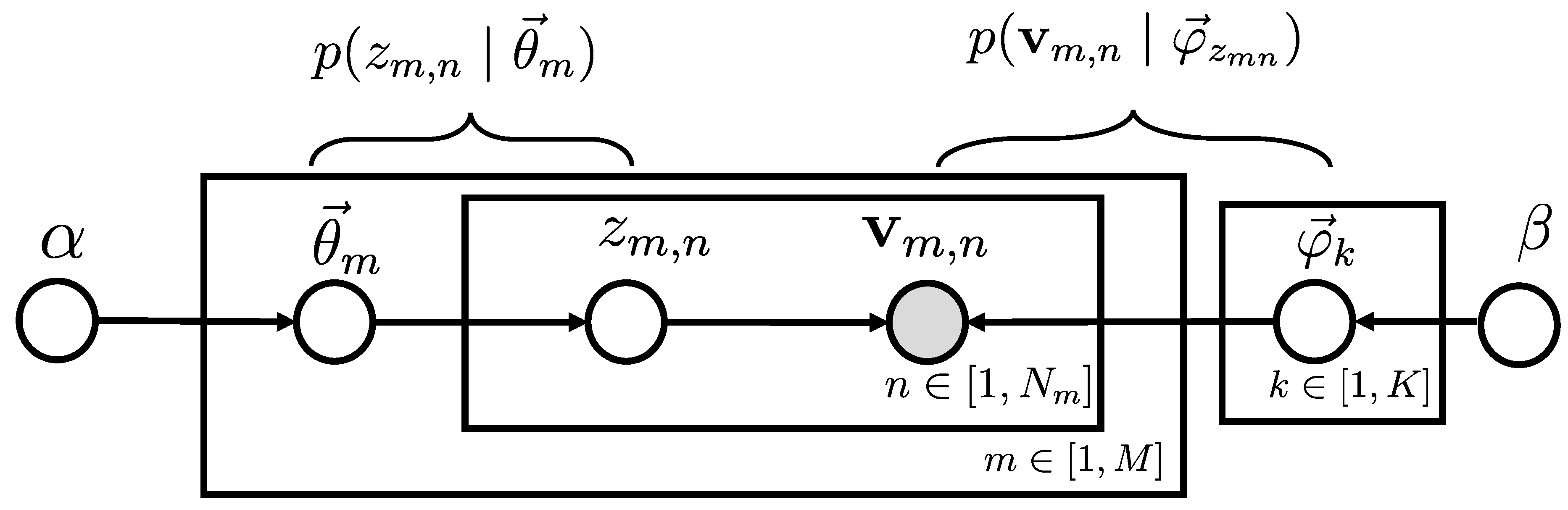
In this section, we first give a briefly introduction of traditional LDA and then we modify the LDA by adding local spatial information. LDA is one of the most popular generative models originally developed for natural language processing, which contains a three-level hierarchical structure. Recently, it has developed rapidly in the field of image processing such as image segmentation, classification and annotation. When LDA is applied to image processing, we treat the classes of objects as topics, local patches of images as words and the whole image as a document. A codebook is created by clustering all the local descriptors in the image set using K-means. Each local patch is quantized into a visual word according to the codebook. The graphical model of traditional LDA is shown in
Figure 3. There are
M images in the dataset. Each image
m has
image patches.
is the observed feature value of the local image patch
n in image
m,
denotes the hidden class for
. All the local image patches in the corpus will be clustered into K classes. Each image
m is modeled as a multinomial distribution (
) with parameter
over classes and similarly each category k is modeled as a multinomial distribution (
) with parameter
over the visual codebook, and
,
are Dirichlet prior for multinormal distribution. Equation (
11) shows the LDA model,
and
are hidden variables to be inferred. The generative process of LDA is shown in Algorithm 1.
| Algorithm 1 Generative process of LDA |
- 1:
Select the and , which are the parameters of Dirichlet distribution. - 2:
For a image m, a multinomial parameter is sampled from Dirichlet prior - 3:
For a category k, a multinomial parameter is sampled from Dirichlet prior . - 4:
For a image patch n in image m, its category is sampled from the image to category Multinomial distribution . - 5:
The features of image patch n in image m, is sampled from the category to image patch features Multinomial distribution of topic , .
|
Hidden category variable
can be sampled through a Gibbs sampling [
29] procedure which integrates out
and
. We fist randomly assign the class to each image patch and then determine the class according to Equation (
12). More details about Gibbs sampling for LDA are shown in
Appendix B.
where
is the number of visual words in the corpus with value
t assigned to category
k excluding visual word
n in document
m, and
is the number of visual words in document
m assigned to category
k excluding word
m in document
n. Equation (
12) is the product of two ratios: the probability of visual word
=
t under category
k (
) and the probability of category
k in document
m (
).
However, traditional LDA is a “bag of words” model and does not consider spatial information at all, which is essential for image processing. Therefore, we want to add spatial information in the original formulation based on the assumption that if visual words are from the same class of objects, they should also be close in space. So we group image patches which are close in space. One straightforward way is to calculate the frequency of the category in the neighborhood of the image patch and add it to the corresponding conditional category distribution. Therefore we change the category distribution term from
to
and bring the local information, which is shown in Equation (
13). The LDA graphical model with spatial coherence is shown in
Figure 4.
where
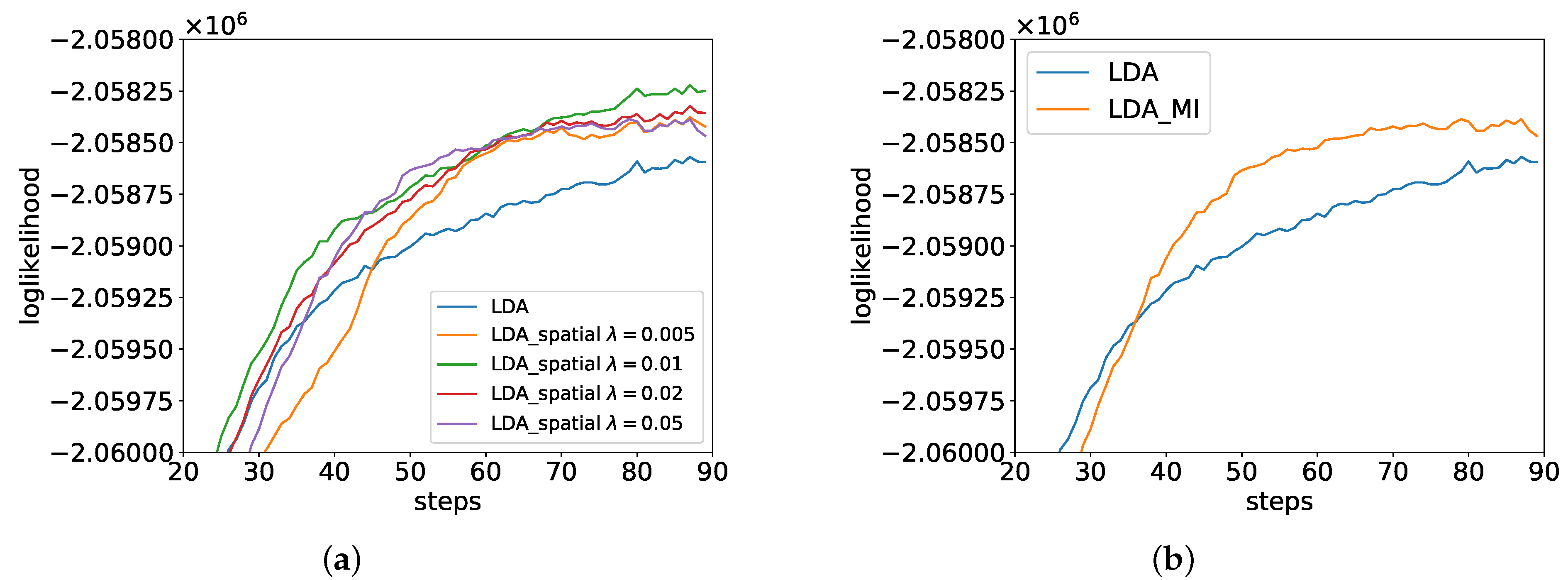
is a trade-off parameter to change the weight of the local spatial information,
represents the
i-th image patch’s category of
N neighborhoods for
. Recall that the indicator function
equals 1 if and only if
. Equation (
13) shows that the category of the image patch is more likely to belong to the neighborhood’s category than Equation (
12). In this paper, we set
denoting eight connected neighborhoods of the center image patch. The LDA generative process with spatial coherence is almost the same to original LDA (Algorithm 1), except that category
is sampled from
. Algorithm 2 demonstrates inference for parameter
and
of LDA with spatial information using Gibbs sampling.
| Algorithm 2 Gibbs sampling for LDA with spatial coherence |
- 1:
Input: image patch feature values matrix (), the number of categories K, initial category of each image patch features. - 2:
Output: and . - 3:
for each iteration T do: - 4:
for each image m do: - 5:
for each image patch n do: - 6:
Sampling category of nth image patch based on Equation ( 13). - 7:
end for - 8:
end for - 9:
end for - 10:
Estimate the and .
|
2.4. Pseudo-Label Generation
In this section, we will introduce how to generate pseudo-labels based on LDA illustrated in
Figure 5. The three heatmaps in the middle column represent higher probability over image patch codebooks in areas with coral, red algae and green algae, respectively (from top to bottom) according to the category distribution (left-hand side of
Figure 5). We annotate the pseudo-labels (star point) in the sample image at right-hand side. We calculate the distance between the pseudo-labeled samples and the original labeled samples to determine the class for each cluster.
One of the problems for generating pseudo-labels is that low-quality features extracted by the neural network at early training stages may mislead the training process into a wrong direction and such wrong information can spread to the following training process. To overcome this problem, we come up with a confidence level for each pseudo-labeled sample, which indicates how reliable the pseudo-label is. For each labeled sample
, we always set its confidence level
. For each pseudo-labeled sample
, we compute
r using Equation (
14), based on the assumption that
will be more reliable if it is located in densely populated regions.
where,
is the original labeled sample and
is the pseudo-labeled sample we generated. We adopt kernel density estimation to estimate the probability of pseudo-labeled samples within the label samples in the feature space. We use Gaussian kernel and for each sample, we evaluate its
nearest distances and take the mean. We choose the average of mean values for all samples as the kernel size
. When the pseudo-labeled samples are far away from the original labeled samples, we can get the small confidence level
r.
In addition, we also introduce the class weight (
of class
j) to deal with the issue of class imbalance.
is defined in Equation (
15), which is inversely proportional to class population.
where
denotes the number of class
j in labeled samples and
represents the number of class
j of generated pseudo-labels.
2.5. Iterative Training
After pseudo-label generation, we will train the neural network with labeled samples, pseudo-label samples and unlabeled samples together using objective function shown in Equation (
16).
As can be seen, there are three terms in Equation (
16). The first term is cross-entropy between predict of labeled samples and its corresponding true labels, the second term is cross-entropy between predict of unlabeled samples and its corresponding pseudo-labels, and the last term is mutual information between unlabeled samples and its corresponding features.
and
are the hyper-parameters to adjust the importance of them.
Given the image patch feature extraction, pseudo-labels generation and neural network training with labeled samples, pseudo-labeled samples and unlabeled samples, we plug these components into an iterative learning process. First, we train the network for
T epochs with labeled samples and mutual information constraint using Equation (
7). Second, we obtain the class distribution over feature visual words via spatial LDA. Third, we assign pseudo-labels to unlabeled image patches by selecting higher probability in class distribution. Finally, we train the network on the entire dataset using Equation (
16) for
epochs. We repeat this iterative process for
M iterations. The above steps are summarized in Algorithm 3.
| Algorithm 3 GeneratePseudo-labels iteratively via spatial LDA |
- 1:
initialize randomly - 2:
for epoch do - 3:
Optimize Equation ( 7) ▹ mini-batch optimization - 4:
for Iteration do - 5:
for do ▹ feature descriptors - 6:
▹ visual feature codebook - 7:
Equation ( 13) ▹ probability of class given unlabeled samples - 8:
for do ▹ pseudo-labels - 9:
for do Equation ( 14) ▹ confidence level - 10:
for do ▹ class weight - 11:
for epoch do - 12:
Optimize Equation ( 15) ▹ mini-batch optimization - 13:
end for - 14:
end for
|
4. Conclusions
In this paper, we propose a novel and effective framework to generate pseudo-labels iteratively only depending on sparsely labels. The results in the coral image data set from Pulley Ridge show that our approach can generate more correct pseudo-labels and help us get a better result for image segmentation against other semi-supervised method. The main advantage of generating pseudo-label iteratively is that previously learned knowledge can be incorporated to improve the model learning and final results. However, the limitation of our method is that for the under represented classes, i.e., classes that have a low percentage of the overall pixels, our method does not work well. Nevertheless, our method is a productive way to tell human experts what kind of classes should be more annotated, and which classes already have sufficient labels to yield good identification results.
Future works may follow four directions: First, we think that metric learning may quantify the uncertainty of the pseudo-labels by including distance in the input space, latent feature space and label space. Second, we want to improve the information theoretic methods to obtain more useful information besides the label information. Third, we want to change the current architecture for image patch classification to a fully convolutional network. One of the obvious weakness of the current architecture is that the network can only see the small size image patches but cannot obtain the whole image structure. Last but not least, we want to develop a graphical user interface (GUI) software to allow humans in the loop interaction to guide the annotation of more useful labels.