On the Development of a Metamodel and Design Support Excel Automation Program for Offshore Wind Farm Layout Optimization
Abstract
1. Introduction
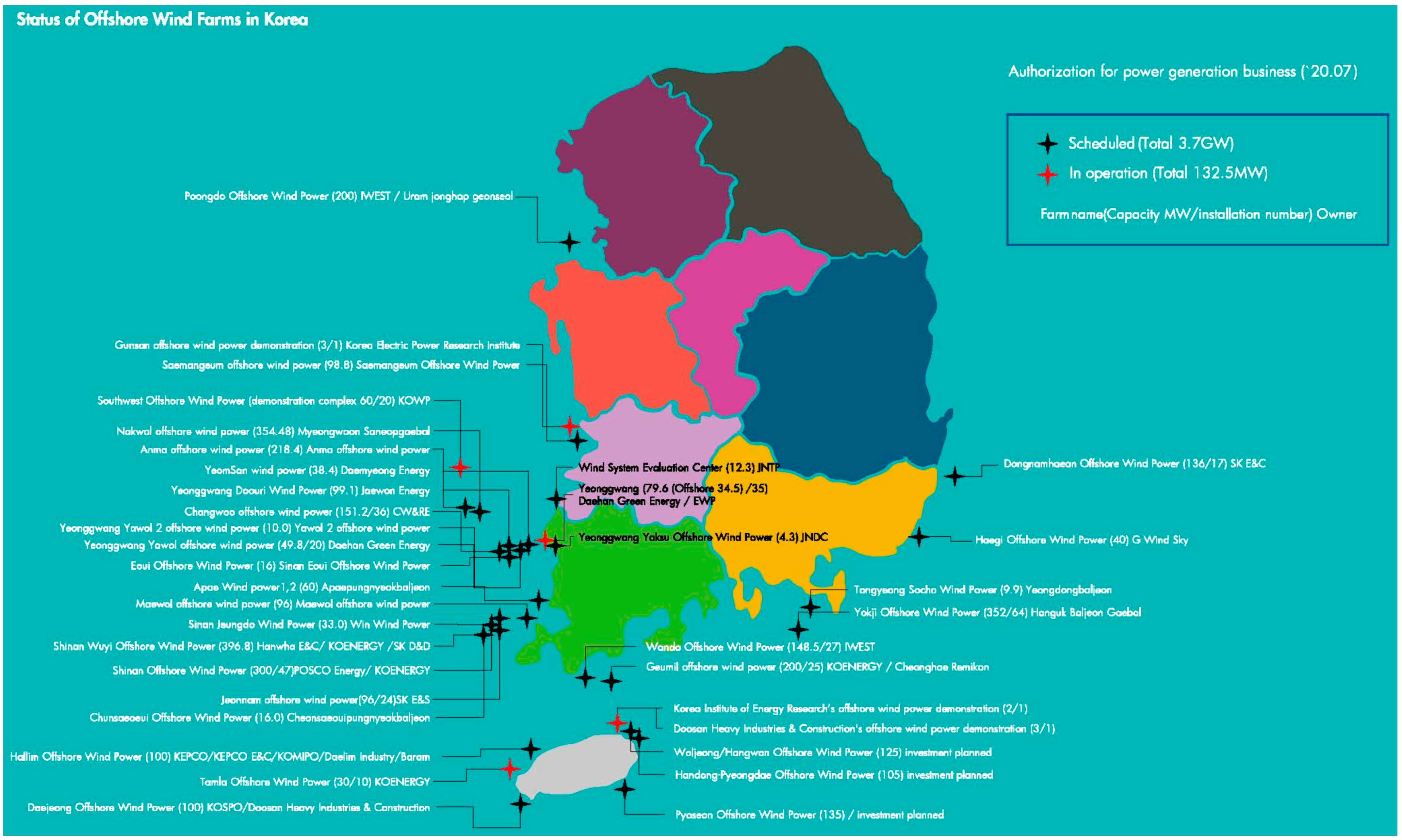
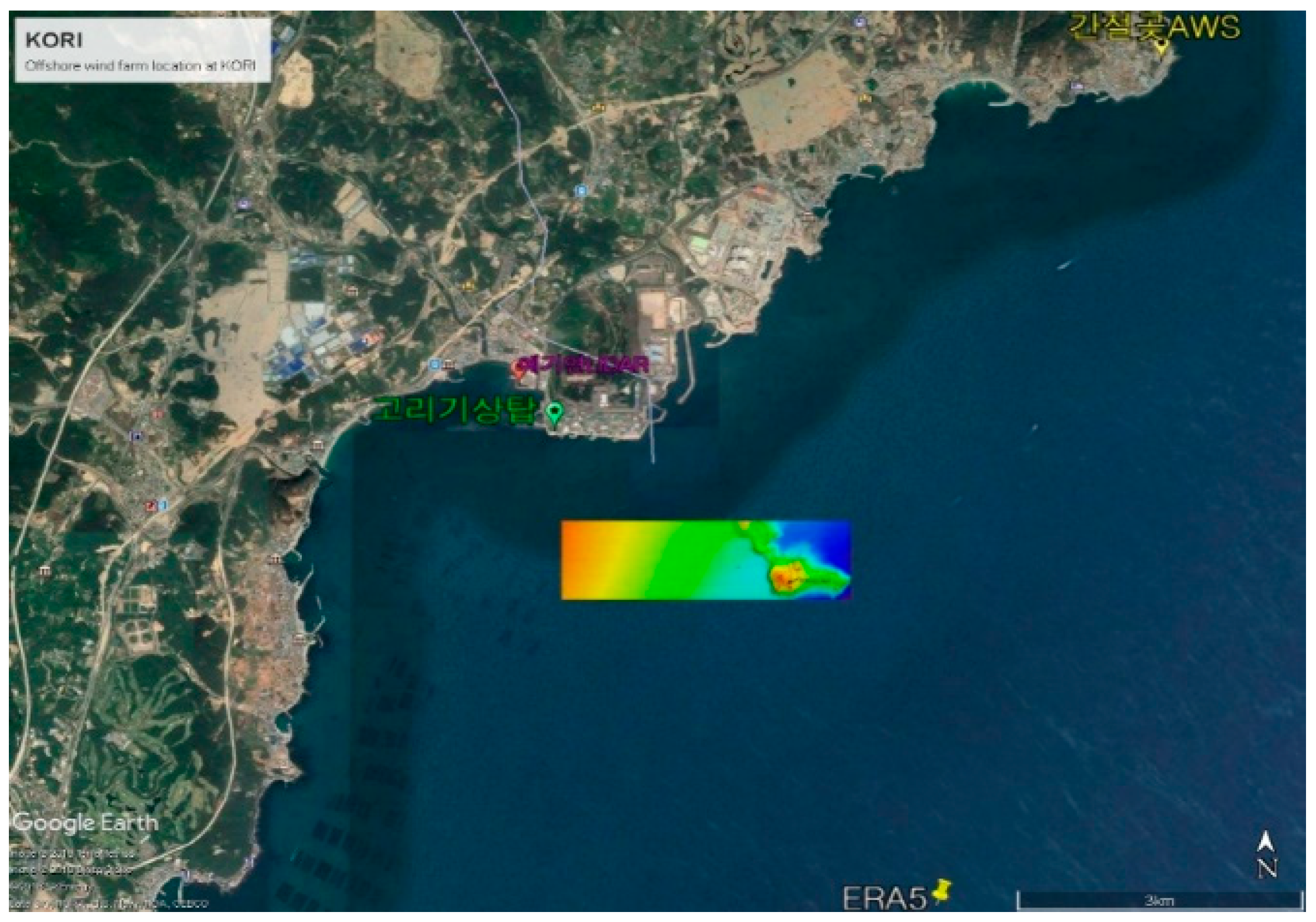
2. Offshore Site and Data
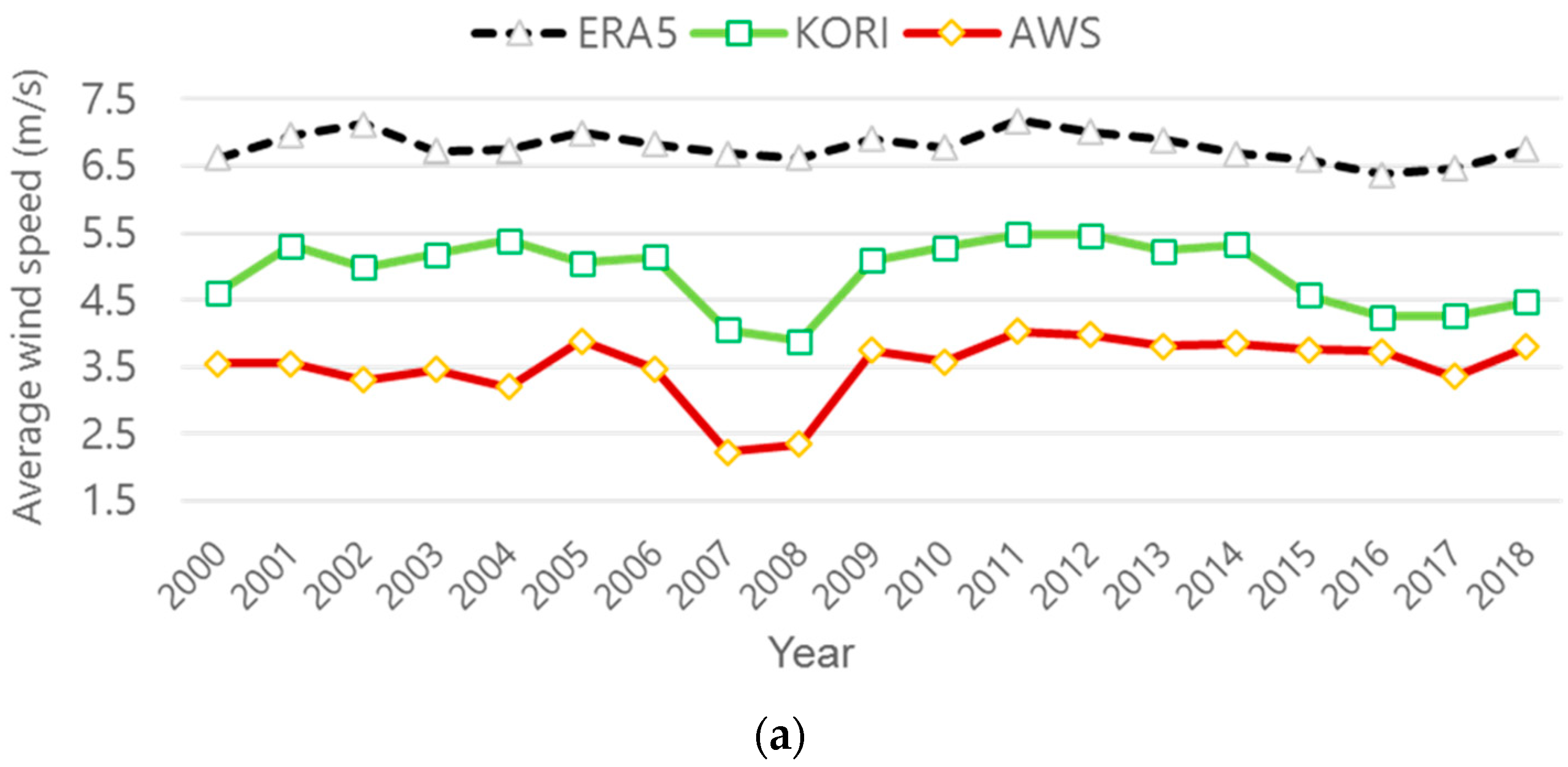
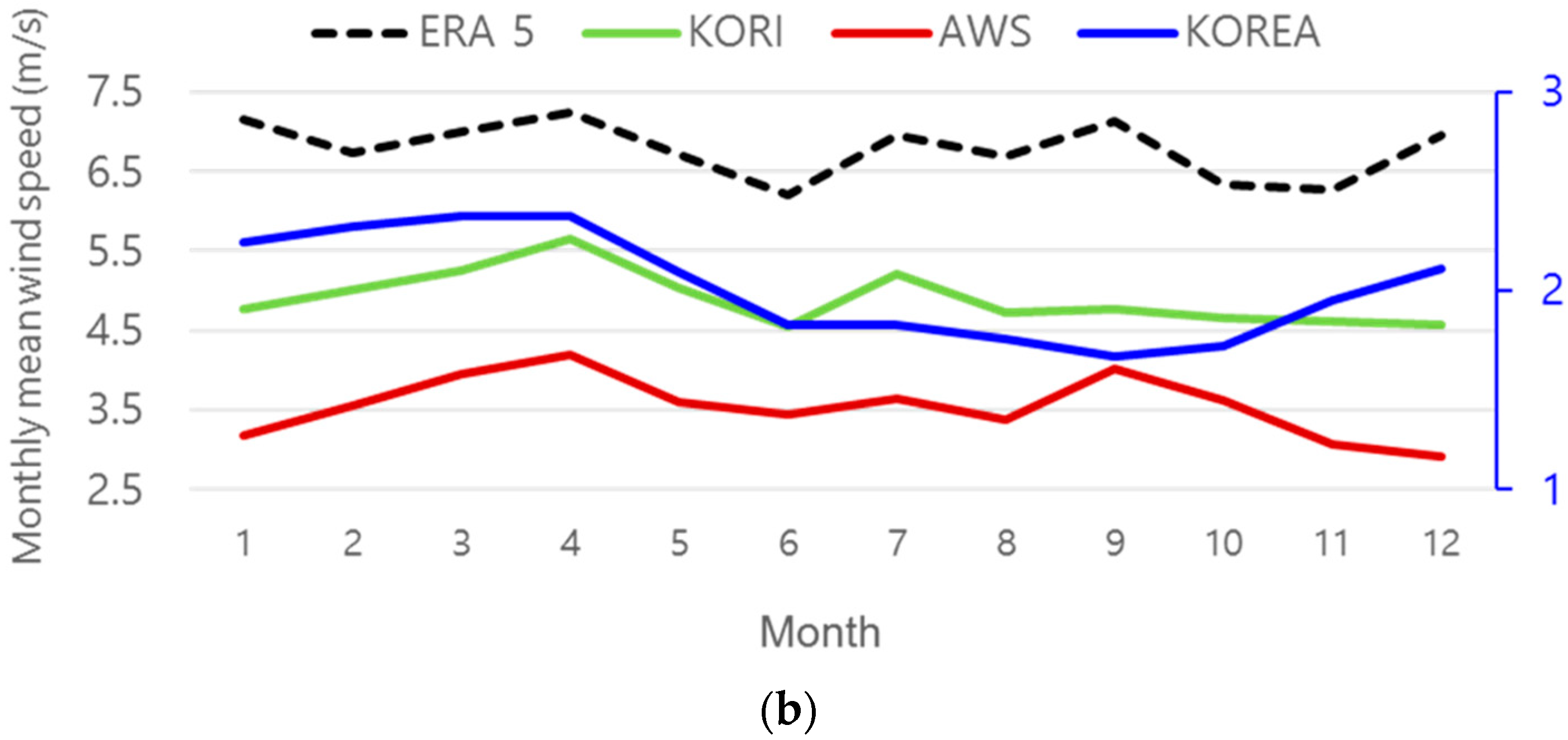
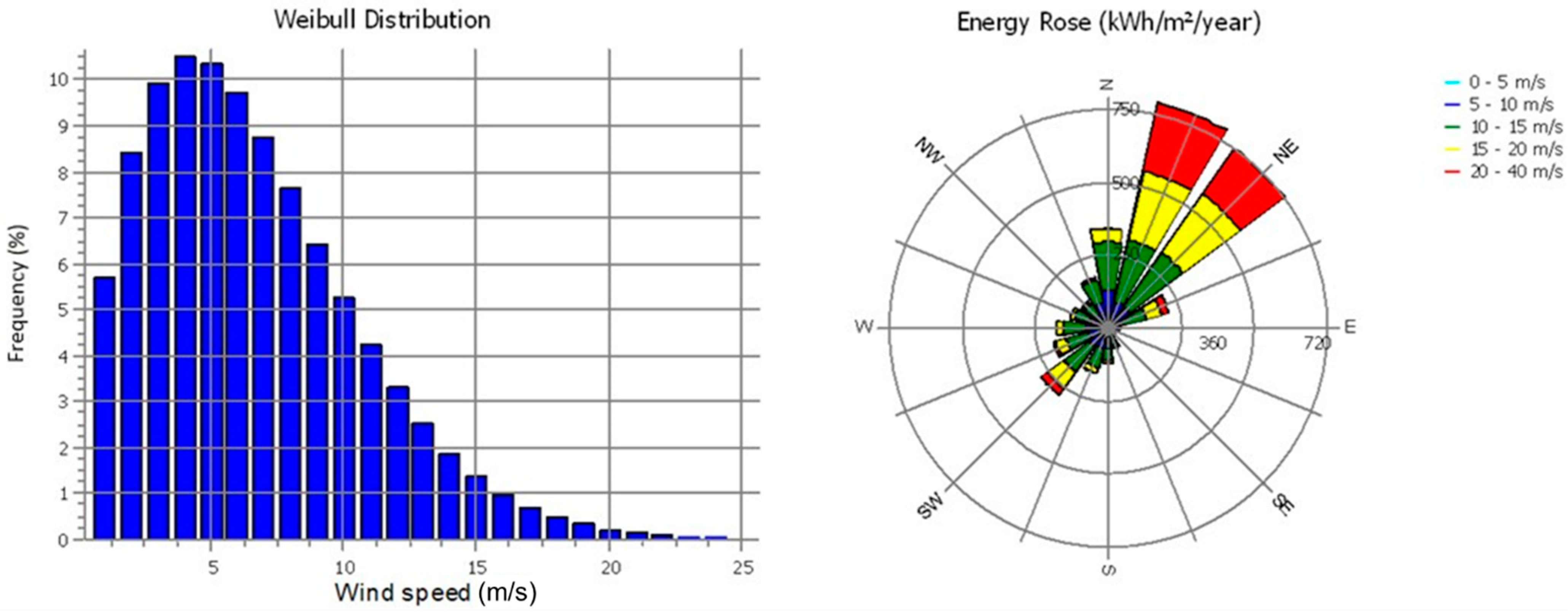
2.1. Wind Climate
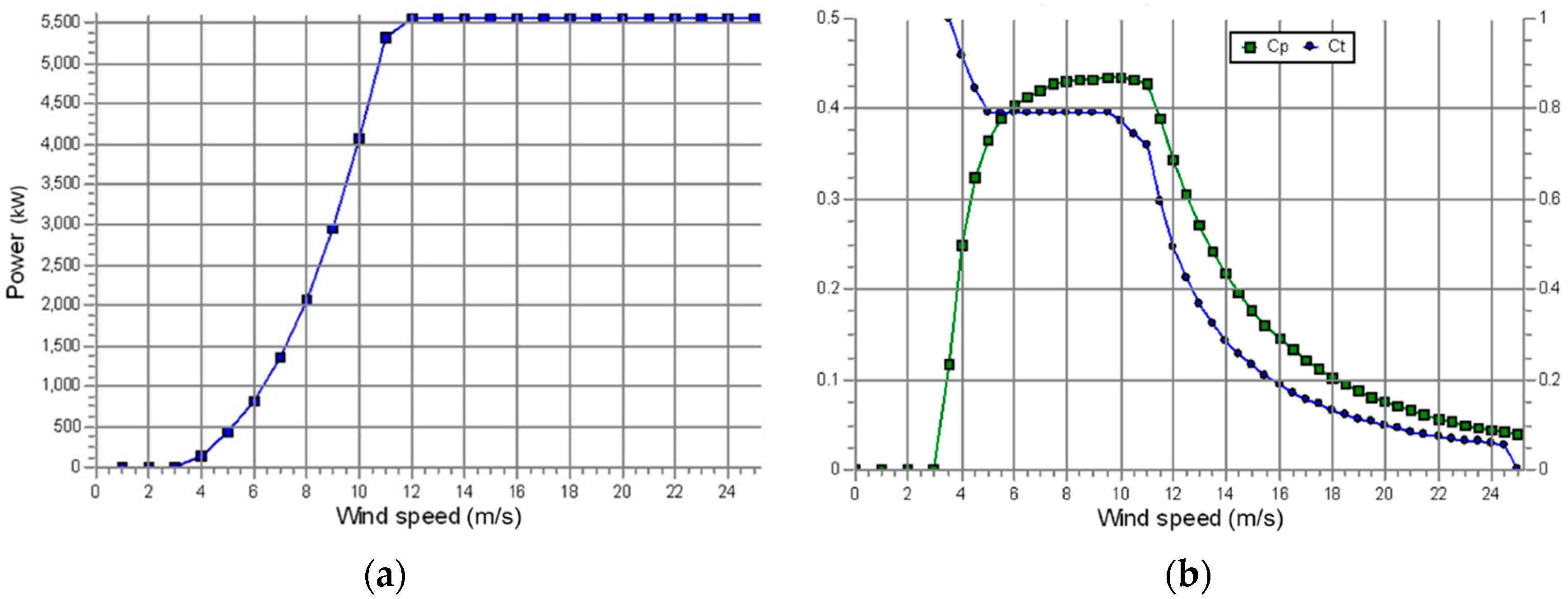
2.2. Wind Turbine Generator
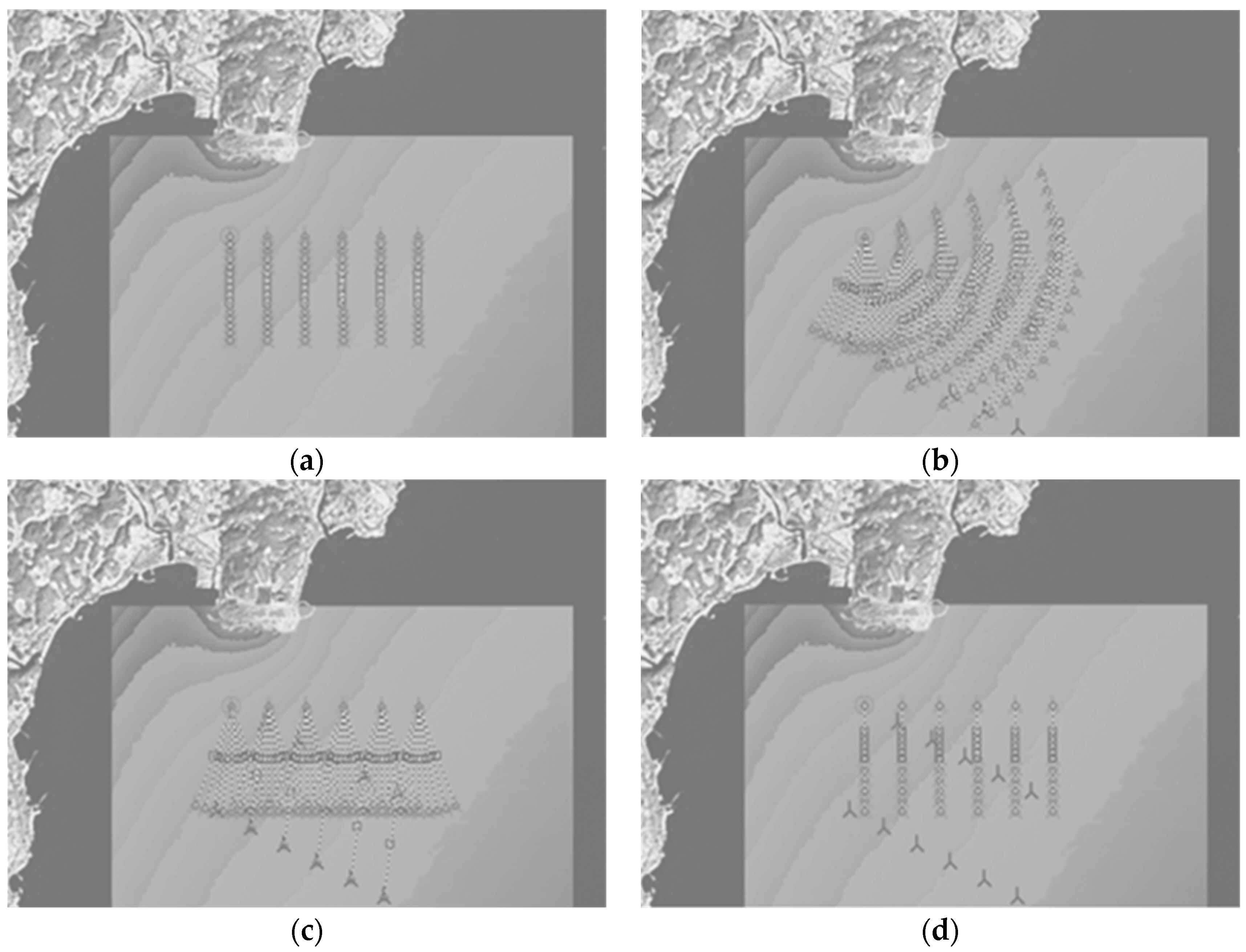
3. Wind Turbine Layout Automation
3.1. Constraints on Wind Farm Layout
- (1)
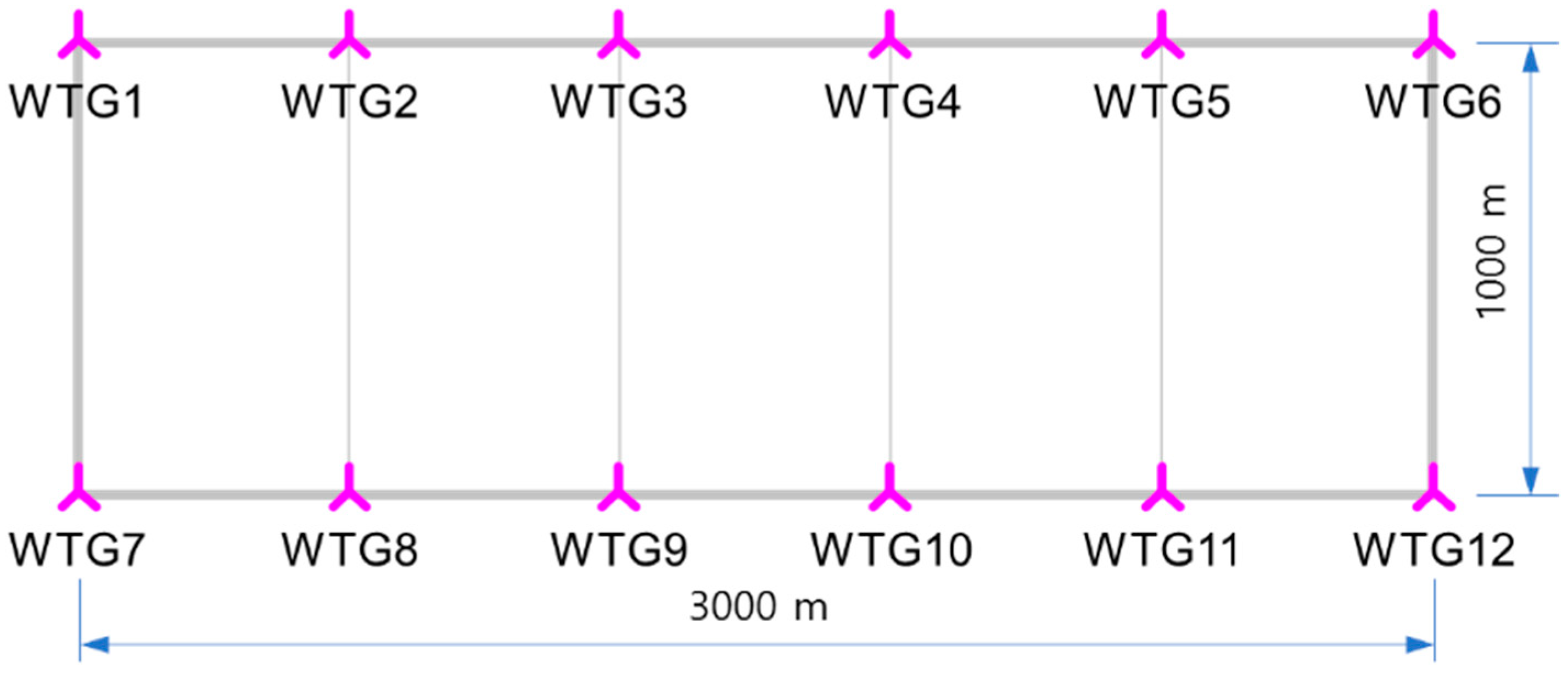
- The assumed wind-power-producing area was placed within a 3 × 1 km square shape. This assumption was useful for proving the ground research data’s effectiveness.
- (2)
- We used actual measured wind conditions as wind.
- (3)
- The turbine layout for industrial wind power areas did not consider additional practical constraints such as dynamic load, shape of the site, and cost of the model.
- (4)
- The wind turbines have identical hub heights and performance.
3.2. Defining the Design Variable and Objective Function
Maximize AEP(xi)
Minimize Wake Loss(xi)
Subject to xLower ≤ xi ≤ xUpper i = 1, 2,···, 9
| DOE (design of experiment) sampling source code for wind farm layout of Scenario 2 |
| class Program { static void writeDataFile(string fileName, DATA[ ] writeData) { StreamWriter objWriter = new StreamWriter(fileName); objWriter.Write(“index, x, y”); //objWriter.WriteLine(“index, x, y”); objWriter.WriteLine(); for (int i = 0; i < writeData.Length; i++) { objWriter.Write(writeData[i].index + “,”); objWriter.Write(writeData[i].x + “,”); objWriter.Write(writeData[i].y + “,”); objWriter.WriteLine(“ “); } objWriter.Close(); } static bool checkValue(DATA[ ] data, double x_val, double y_val, double criteria1) { bool check_value = true; for (int i = 0; i < data.Length; i++) { double delta_x = data[i].x - x_val; double delta_y = data[i].y - y_val; // double radius = Math.Sqrt(delta_x * delta_x + delta_y * delta_y); if (radius < criteria1) { check_value = false; } } // return check_value; } static void Main(string[ ] args) { if (args.Length != 7) { Console.WriteLine(“Argument must be 6 length!!!”); Console.WriteLine(“Current argument is {0}”, (int)args.Length-1); // exit Environment.Exit(-1); |
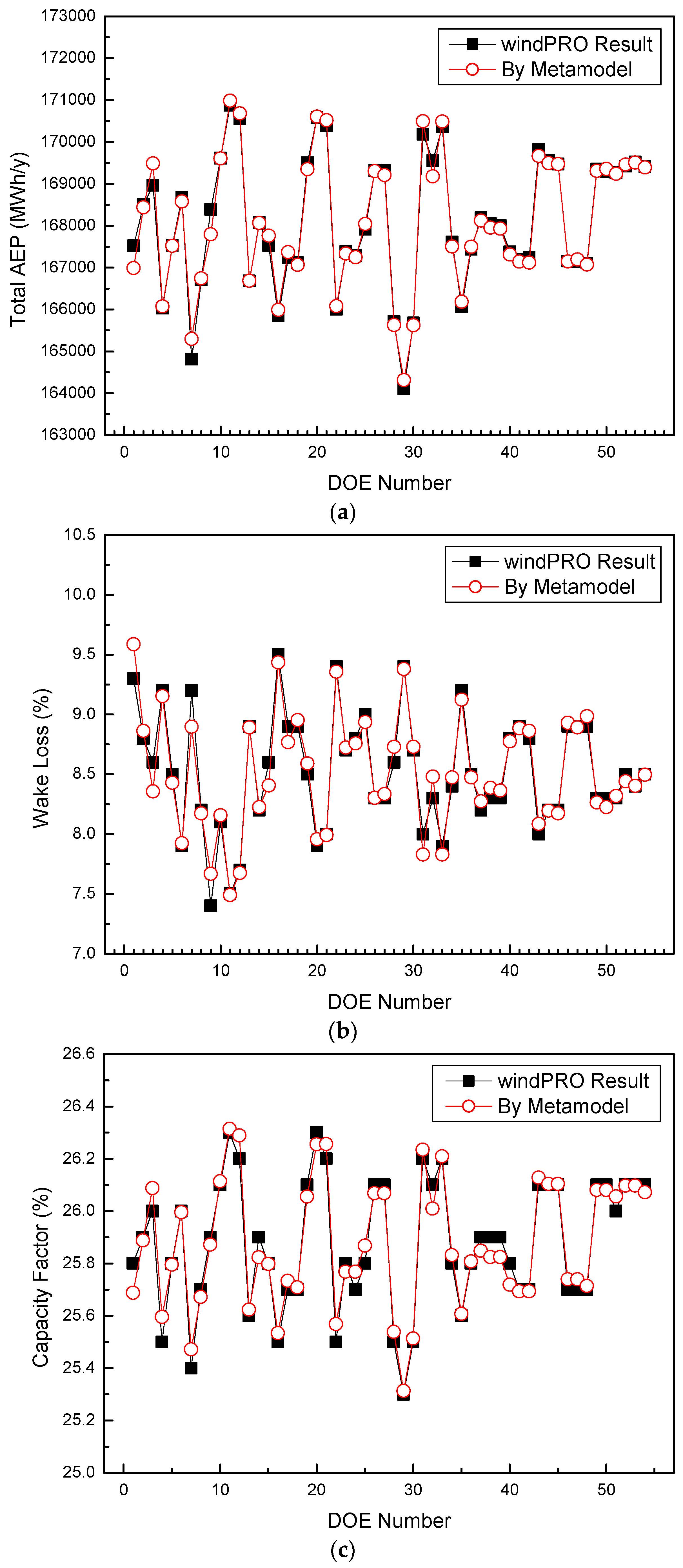
3.3. Development of the Metamodel for Wind Turbine Layout
148,220 + 17.376 × (x1) − 0.005758 × (x1)2 − 271.69 × (x2)-2.3571 × (x2)2
− 47.64 × (x3) + 0.1139 × (x3)2 + 2.737 × (x4) − 0.000852 × (x4)2 + 2.185 × (x5)
− 0.000320 × (x5)2 + 1.103 × (x6) + 0.000437 × (x6)2 + 3.856 × (x7) − 0.001398
× (x7)2 + 4.832 × (x8) − 0.001909 × (x8)2 + 3.168 × (x9) − 0.000689 × (x9)2
+ 1.4767 × (x2) × (x3)
16.7652 − 0.00446667 × (x1) + 0.0272222 × (x2) − 0.0152778 × (x3)
− 0.00142722 × (x4) − 0.00107619 × (x5) + 0.00155448 × (x6) − 0.00195342
× (x7) − 0.00227908 × (x8) − 0.00195308 × (x9) + 1.77778 × 106 × (x12)
+ 0.00111111 × (x22) + 6.94444 × 105 × (x32) + 3.94539 × 107 × (x42) + 5.63627
× 108 × (x52) − 1.46543 × 106 × (x62) + 7.32715 × 107 × (x72) + 9.01803 × 107
× (x82) + 5.63627 × 107 × (x92)
24.4237 + 0.000355556 × (x1) − 0.0216667 × (x2) − 0.00375 × (x3)
+ 0.000262763 × (x4) + 0.000325325 × (x5) + 0.000237738 × (x6)
+ 0.000262763 × (x7) + 0.0003003 × (x8) + 0.000337838 × (x9)
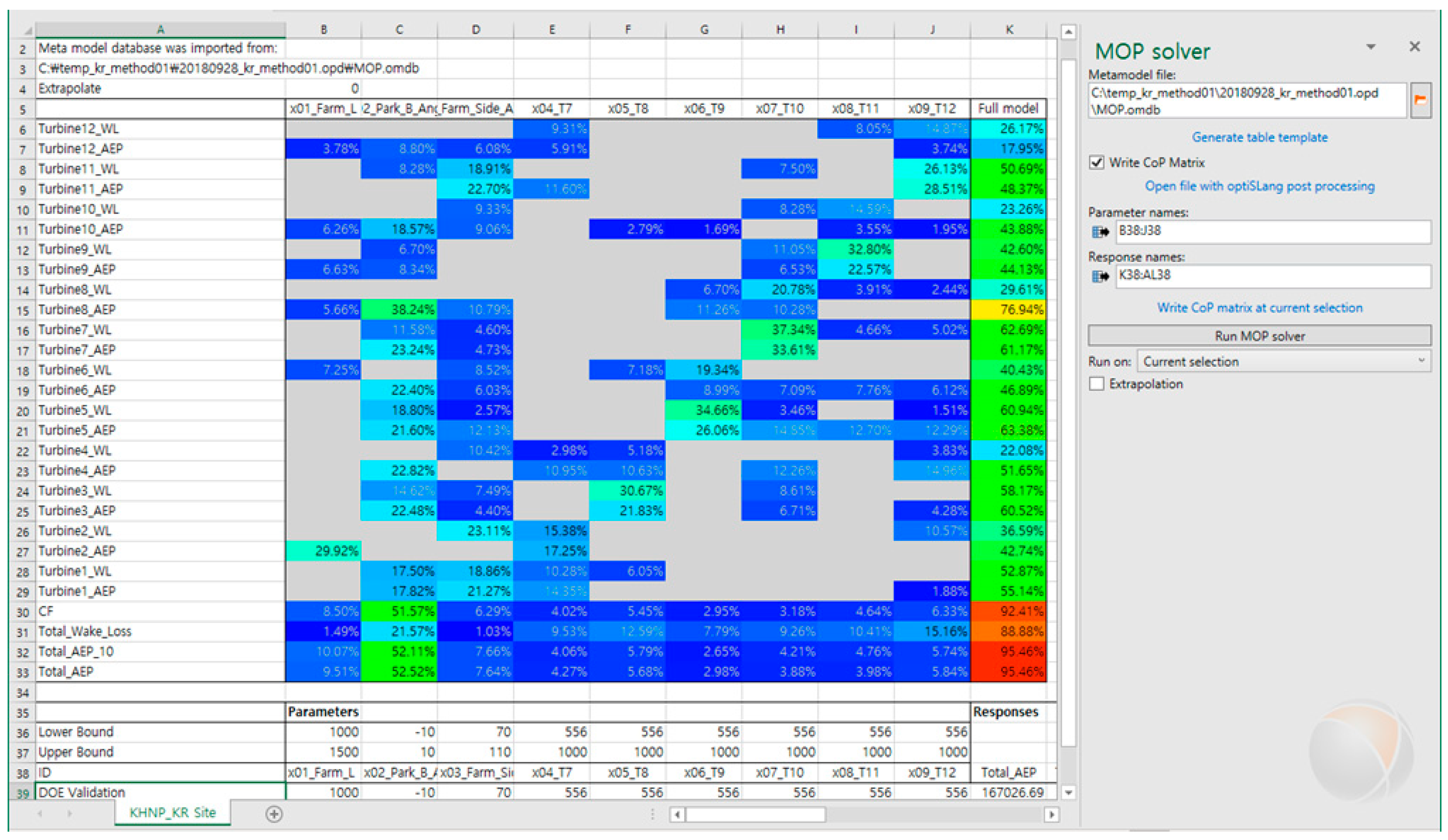
3.4. Design Support Excel Automation Program
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Gil-García, I.C.; García-Cascales, M.S.; Fernández-Guillamón, A.; Molina-García, A. Categorization and analysis of relevant factors for optimal locations in onshore and offshore wind power plants: A taxonomic review. J. Mar. Sci. Eng. 2019, 7, 391. [Google Scholar] [CrossRef]
- Global Wind Energy Council (GWEC). Global Offshore Wind Report 2020; GWEC: Brussels, Belgium, 2020; Volume 19, pp. 10–12, 63–65. [Google Scholar]
- Bui, V.-H.; Hussain, A.; Lee, W.-G.; Kim, H.-M. Multi-objective optimization for determining trade-off between output power and power fluctuations in wind farm system. Energies 2019, 12, 4242. [Google Scholar] [CrossRef]
- Christodoulou, C.A.; Vita, V.; Seritan, G.-C.; Ekonomou, L. A harmony search method for the estimation of the optimum number of wind turbines in a wind farm. Energies 2020, 13, 2777. [Google Scholar] [CrossRef]
- Al-Addous, M.; Jaradat, M.; Wellmann, A.A.J.; Al Hmidan, S. The significance of wind turbines layout optimization on the predicted farm energy yield. Atmosphere 2020, 11, 117. [Google Scholar] [CrossRef]
- Ramos, C.A.; Ramirez, D.; Jin, K.; Li, H. Factorial analysis of selected factors affecting the electricity production of onshore wind farms. Int. J. Energy Clean. Environ. 2011, 12, 67–77. [Google Scholar] [CrossRef]
- Grady, S.A.; Hussaini, M.Y.; Abdullah, M.M. Placement of wind turbines using genetic algorithms. Renew. Energy 2005, 30, 259–270. [Google Scholar] [CrossRef]
- Marmidis, G.; Lazarou, S.; Pyrgioti, E. Optimal placement of wind turbines in a wind park using Monte Carlo simulation. Renew. Energy 2008, 33, 1455–1460. [Google Scholar] [CrossRef]
- Lazarou, S.; Vita, V.; Ekonomou, L. Application of Powell’s optimization method for the optimal number of wind turbines in a wind farm. IET Sci. Meas. Technol. 2011, 5, 77–80. [Google Scholar] [CrossRef]
- Ekonomou, L.; Lazarou, S.; Chatzarakis, G.E.; Vita, V. Estimation of wind turbines optimal number and produced power in a wind farm using an artificial neural network model. Simul. Model. Pract. Theory 2012, 21, 21–25. [Google Scholar] [CrossRef]
- Yang, H.; Xie, K.; Tai, H.M.; Chai, Y. Wind farm layout optimization and its application to power system reliability analysis. IEEE Trans. Power Syst. 2015, 31, 2135–2143. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Solving the wind farm layout optimization problem using random search algorithm. Renew. Energy 2015, 78, 182–192. [Google Scholar] [CrossRef]
- Gionfra, N.; Sandou, G.; Siguerdidjane, H.; Faille, D.; Loevenbruck, P. Wind farm distributed PSO-based control for constrained power generation maximization. Renew. Energy 2019, 133, 103–117. [Google Scholar] [CrossRef]
- Hansen, K.S.; Barthelmie, R.J.; Jensen, L.E.; Sommer, A. The impact of turbulence intensity and atmospheric stability on power deficits due to wind turbine wakes at Horns Rev wind farm. Wind Energy 2012, 15, 183–196. [Google Scholar] [CrossRef]
- Andersen, P.S.; Krabbe, U.; Lundsager, P.; Petersen, H. Basismateriale for Beregning af Propelvindmøller; Risø-M-2153 (rev.); Forsøgsanlæg Risø: Roskilde, Denmark, 1980. [Google Scholar]
- Schepers, J.G. ENDOW: Validation and Improvement of ECN’s Wake Model; ECN-C-03-037; Energy Research Centre of the Netherlands ECN: Petten, The Netherlands, 2003. [Google Scholar]
- Risø National Laboratory. Guidelines for Design of Wind Turbines, DNV/Risø, 2nd ed.; Risø National Laboratory: Roskilde, Denmark, 2002. [Google Scholar]
- Available online: http://www.doosanheavy.com/download/pdf/products/energy/DHI_Wind_Power_Brochure_Eng.pdf (accessed on 1 December 2020).
- EMD International A/S. Introduction to wind turbine wake modeling and wake generated turbulence. In WindPRO/PARK; EMD International A/S: Aalborg, Denmark, 2019. [Google Scholar]
- Phadke, M. Quality Engineering Using Robust Design; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Florian, A. An efficient sampling scheme: Latin hypercube sampling. Probabilistic Eng. Mech. 1992, 279, 123–130. [Google Scholar] [CrossRef]
- Shin, J.; Baek, S.; Rhee, Y. Wind Farm Layout Optimization Using a Metamodel And Ea/Pso Algorithm In Korea Offshore. Energies 2021, 14, 146. [Google Scholar] [CrossRef]
- Dynardo GmbH. OptiSlang; Version 7.5.1; Documentation; Dynardo GmbH: Weimar, Germany, 2019. [Google Scholar]
- Simpson, T.W.; Peplinski, J.; Koch, P.N.; Allen, J.K. Metamodels for computer-based engineering design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Roos, D.; Most, T.; Unger, J.F.; Will, J. Advanced surrogate models within the robustness evaluation. In Proceedings of the Weimarer Optimierungs-und Stochastiktage 4.0, Weimar, Germany, 29–30 November 2007. [Google Scholar]
- Dynardo GmbH. optiSLang DLE (Deep Learning Extension); Dynardo GmbH: Weimar, Germany, 2019. [Google Scholar]

| Terrain Classification | Roughness Class | Roughness Length | Wake Decay Constant | Ambient Turbulence at 50 m Ax = 1.8 | Ambient Turbulence at 50 m Ax = 2.5 | Additional Detailed Description |
|---|---|---|---|---|---|---|
| Offshore water areas | 0.0 | 0.0002 | 0.040 | 0.06 | 0.08 | Oceans and large lakes. General water bodies |
| Mixed water and land | 0.5 | 0.0024 | 0.052 | 0.07 | 0.10 | Mixed water and land |
| Very open farmland | 1.0 | 0.0300 | 0.063 | 0.10 | 0.13 | No cross hedges. Scattered buildings |
| Open farmland | 1.5 | 0.0500 | 0.075 | 0.11 | 0.15 | Some buildings. Crossing hedges with an 8 m height with a distance of 1250 m apart |
| Item | Value | |
|---|---|---|
| Operational Data | Rated Power | 5560 kW |
| Class | IB | |
| Cut-in Wind Speed | 3.5 m/s | |
| Rated Wind Speed | 13 m/s | |
| Cut-out Wind Speed | 25 m/s | |
| Rotor Diameter | 140 m | |
| Extreme Survival Wind Speed | 70 m/s | |
| Blade | Length | 68 m |
| Tower | Hub Height | Site-specific |
| Design Variable | Description | Unit | Initial | Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|---|---|
| x1 | Coastline Distance | m | 1000 | 1000 | 1250 | 1500 |
| x2 | Farm Base Angle | Degree | 0 | −10 | 0 | 10 |
| x3 | Farm Side Angle | Degree | 90 | 70 | 90 | 110 |
| x4 | 1 × 1 Row Distance | m | 1000 | 556 | 778 | 1000 |
| x5 | 1 × 2 Row Distance | m | 1000 | 556 | 778 | 1000 |
| x6 | 1 × 3 Row Distance | m | 1000 | 556 | 778 | 1000 |
| x7 | 1 × 4 Row Distance | m | 1000 | 556 | 778 | 1000 |
| x8 | 1 × 5 Row Distance | m | 1000 | 556 | 778 | 1000 |
| x9 | 1 × 6 Row Distance | m | 1000 | 556 | 778 | 1000 |
| No. | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | AEP (MWh/y) | Wake Loss (%) | CF (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1000 | −10 | 70 | 556 | 556 | 556 | 556 | 556 | 556 | 167,518.2 | 9.3 | 25.8 |
| 2 | 1000 | −10 | 70 | 556 | 556 | 556 | 778 | 778 | 778 | 168,502.4 | 8.8 | 25.9 |
| ⋮ | ⋮ | ⋮ | ||||||||||
| 54 | 1500 | 0 | 70 | 778 | 1000 | 556 | 1000 | 778 | 556 | 169,410.6 | 8.5 | 26.1 |
| Metamodel Type | Response | No. Parameters | No. Coefficients | CoD | CoP |
|---|---|---|---|---|---|
| Polynomial (Box–Cox) | AEP | 9 | 10 | 0.967 | 0.955 |
| Wake Loss | 9 | 19 | 0.932 | 0.889 | |
| Capacity Factor | 9 | 10 | 0.944 | 0.924 | |
| MLS (exponential weight) | AEP | 6 | 7 | 0.864 | 0.839 |
| Wake Loss | 4 | 5 | 0.620 | 0.568 | |
| Capacity Factor | 6 | 7 | 0.836 | 0.807 | |
| Kriging (isotropic kernel) | AEP | 6 | 1 | 0.942 | 0.853 |
| Wake Loss | 6 | 1 | 0.726 | 0.852 | |
| Capacity Factor | 6 | 1 | 0.915 | 0.817 | |
| Feedforward network | AEP | 9 | 9 | 0.996 | 0.979 |
| Wake Loss | 9 | 9 | 0.912 | 0.914 | |
| Capacity Factor | 9 | 9 | 0.988 | 0.962 |
| Metamodel Type | Turbine Number | Response | No. Parameters | No. Coefficients | CoD | CoP |
|---|---|---|---|---|---|---|
| Kriging (isotropic kernel) | WTG1 | AEP | 6 | 1 | 0.804 | 0.431 |
| Polynomial (no mixed term) | Wake Loss | 2 | 5 | 0.657 | 0.587 | |
| Polynomial (with mixed terms) | WTG2 | AEP | 2 | 6 | 0.710 | 0.684 |
| Polynomial (with mixed terms) | Wake Loss | 2 | 6 | 0.827 | 0.812 | |
| Polynomial (no mixed term) | WTG3 | AEP | 3 | 7 | 0.703 | 0.674 |
| Polynomial (Box–Cox) | Wake Loss | 3 | 7 | 0.829 | 0.811 | |
| Polynomial (no mixed term) | WTG4 | AEP | 6 | 13 | 0.754 | 0.645 |
| Polynomial (no mixed term) | Wake Loss | 5 | 11 | 0.757 | 0.660 | |
| MLS (exponential weight) | WTG5 | AEP | 2 | 5 | 0.807 | 0.674 |
| MLS (exponential weight) | Wake Loss | 2 | 5 | 0.840 | 0.730 | |
| Kriging (isotropic kernel) | WTG6 | AEP | 2 | 1 | 0.792 | 0.618 |
| Polynomial (Box–Cox) | Wake Loss | 3 | 10 | 0.835 | 0.797 | |
| Kriging (isotropic kernel) | WTG7 | AEP | 4 | 1 | 0.851 | 0.685 |
| Kriging (isotropic kernel) | Wake Loss | 3 | 1 | 0.881 | 0.724 | |
| MLS (exponential weight) | WTG8 | AEP | 2 | 5 | 0.867 | 0.744 |
| MLS (exponential weight) | Wake Loss | 2 | 5 | 0.918 | 0.843 | |
| MLS (exponential weight) | WTG9 | AEP | 5 | 11 | 0.727 | 0.593 |
| Kriging (isotropic kernel) | Wake Loss | 4 | 1 | 0.966 | 0.809 | |
| Polynomial (with mixed terms) | WTG10 | AEP | 2 | 6 | 0.728 | 0.682 |
| Polynomial (with mixed terms) | Wake Loss | 2 | 6 | 0.729 | 0.682 | |
| Kriging (isotropic kernel) | WTG11 | AEP | 3 | 1 | 0.931 | 0.787 |
| Kriging (isotropic kernel) | Wake Loss | 3 | 1 | 0.957 | 0.887 | |
| Polynomial (with mixed terms) | WTG12 | AEP | 2 | 6 | 0.782 | 0.724 |
| Polynomial (with mixed terms) | Wake Loss | 2 | 6 | 0.889 | 0.861 |
| Design Variable | Sum of Squares | Degree of Freedom | F-Value | p-Value | Percentage Contribution (%) | |
|---|---|---|---|---|---|---|
| x1 | Linear | 12,848,521 | 1 | 19.56 | 0 | 20.9 |
| Quadratic | 540,417 | 1 | 14.86 | 0 | 0.1 | |
| x2 | Linear | 69,342,815 | 1 | 20.82 | 0 | 15.9 |
| Quadratic | 666,685 | 1 | 12.75 | 0.001 | 0.2 | |
| x3 | Linear | 10,607,289 | 1 | 2.56 | 0.119 | 22.3 |
| Quadratic | 24,901 | 1 | 0.48 | 0.495 | 0.1 | |
| x4 | Linear | 5,394,393 | 1 | 1.45 | 0.237 | 13.6 |
| Quadratic | 12,175 | 1 | 0.32 | 0.573 | 3.6 | |
| x5 | Linear | 7,241,302 | 1 | 0.92 | 0.343 | 2.7 |
| Quadratic | 40,476 | 1 | 0.05 | 0.832 | 1.2 | |
| x6 | Linear | 3,735,458 | 1 | 0.21 | 0.650 | 0.5 |
| Quadratic | 109,201 | 1 | 0.09 | 0.772 | 5.7 | |
| x7 | Linear | 5,010,360 | 1 | 3.40 | 0.074 | 1.6 |
| Quadratic | 56,989 | 1 | 1.09 | 0.304 | 2.2 | |
| x8 | Linear | 6,143,541 | 1 | 5.34 | 0.027 | 0.3 |
| Quadratic | 106,251 | 1 | 2.03 | 0.163 | 2.4 | |
| x9 | Linear | 7,789,495 | 1 | 2.29 | 0.139 | 1.0 |
| Quadratic | 13,849 | 1 | 0.26 | 0.610 | 0.3 | |
| x2 x3 | Interaction | 261,685 | 1 | 5.00 | 0.032 | 5.3 |
| Total | 129,945,804 | 19 | 93.48 | 100 | ||
| Design Variable | Sum of Squares | Degree of Freedom | F-Value | p-Value | Percentage Contribution (%) | |
|---|---|---|---|---|---|---|
| x1 | Linear | 0.00111 | 1 | 11.69 | 0.002 | 17.2 |
| Quadratic | 0.14815 | 1 | 11.99 | 0.001 | 1.1 | |
| x2 | Linear | 2.66778 | 1 | 6.72 | 0.014 | 17.6 |
| Quadratic | 0.14815 | 1 | 9.99 | 0.003 | 0.2 | |
| x3 | Linear | 0.11111 | 1 | 0.93 | 0.342 | 9.9 |
| Quadratic | 0.00926 | 1 | 0.62 | 0.435 | 1.6 | |
| x4 | Linear | 1.17361 | 1 | 3.46 | 0.071 | 14.7 |
| Quadratic | 0.00454 | 1 | 1.62 | 0.212 | 4.5 | |
| x5 | Linear | 1.73361 | 1 | 2.47 | 0.125 | 1.4 |
| Quadratic | 0.00009 | 1 | 0.72 | 0.402 | 1.5 | |
| x6 | Linear | 0.93444 | 1 | 0.12 | 0.726 | 0.9 |
| Quadratic | 0.06259 | 1 | 1.12 | 0.297 | 6.2 | |
| x7 | Linear | 1.17361 | 1 | 3.08 | 0.088 | 5.1 |
| Quadratic | 0.01565 | 1 | 1.05 | 0.312 | 2.4 | |
| x8 | Linear | 1.36111 | 1 | 4.19 | 0.049 | 2.4 |
| Quadratic | 0.02370 | 1 | 1.60 | 0.215 | 4.5 | |
| x9 | Linear | 2.05444 | 1 | 3.07 | 0.089 | 3.6 |
| Quadratic | 0.00926 | 1 | 0.62 | 0.435 | 0.9 | |
| x2 x3 | Interaction | 0.04481 | 1 | 3.02 | 0.091 | 4.4 |
| Total | 11.67704 | 19 | 68.08 | 100 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, J.; Baek, S.; Rhee, Y. On the Development of a Metamodel and Design Support Excel Automation Program for Offshore Wind Farm Layout Optimization. J. Mar. Sci. Eng. 2021, 9, 148. https://doi.org/10.3390/jmse9020148
Shin J, Baek S, Rhee Y. On the Development of a Metamodel and Design Support Excel Automation Program for Offshore Wind Farm Layout Optimization. Journal of Marine Science and Engineering. 2021; 9(2):148. https://doi.org/10.3390/jmse9020148
Chicago/Turabian StyleShin, Joongjin, Seokheum Baek, and Youngwoo Rhee. 2021. "On the Development of a Metamodel and Design Support Excel Automation Program for Offshore Wind Farm Layout Optimization" Journal of Marine Science and Engineering 9, no. 2: 148. https://doi.org/10.3390/jmse9020148
APA StyleShin, J., Baek, S., & Rhee, Y. (2021). On the Development of a Metamodel and Design Support Excel Automation Program for Offshore Wind Farm Layout Optimization. Journal of Marine Science and Engineering, 9(2), 148. https://doi.org/10.3390/jmse9020148





