Abstract
The numerical modeling of sediment transport under wave impact is challenging because of the complex nature of the triple wave–structure–sediment interaction. This study presents three-dimensional numerical modeling of sediment scouring due to non-breaking wave impact on a vertical seawall. The Navier–Stokes–Exner equations are approximated to calculate the full evolution of flow fields and morphodynamic responses. The bed erosion model is based on the van Rijn formulation with a mass-conservative sand-slide algorithm. The numerical solution is obtained by using a projection method and a fully implicit second-order unstructured finite-volume method in a -coordinate computational domain. This coordinate system is employed to accurately represent the free-surface elevation and sediment/water interface evolution. Experimental results of the velocity field, surface wave motion, and scour hole formation hole are used to compare and demonstrate the proposed numerical method’s capabilities to model the seawall scour.
1. Introduction
Nowadays, vertical and impermeable seawalls are still in service in many places as coastal defenses. However, these structures amplify the wave height and provoke local erosion at the toe seawall lowering the beach profile [1]. Thus, sediment scouring due to wave impacts in these structures is still an essential subject to study not only for economic issues but also for understanding physical processes and optimizing new designs. However, this phenomenon’s numerical and experimental modeling is a challenging task because of the complex nature wave, structure, and sediment bed interactions.
Several researchers have investigated the effects of vertical seawalls on beaches. Although much experimental research for vertical seawall was performed during the sixties and seventies, the number of works decreased in the following decades [2]. In recent years, some research has been conducted to improve physical understanding and the description of scouring at vertical walls [3,4,5,6]. More recently, new experiments were performed on scour erosion at the toe of a vertical seawall by Pham Van Bang et al. [7,8]. High-resolution data were obtained by employing advanced and non-intrusive measuring techniques, which combined Particle Image Velocimetry (PIV), Planar Laser-Induced Fluorescence (PLIF), and Echo-Doppler Imaging.
On the other hand, due to the problem’s complexity, only a limited number of numerical methods have been successfully proposed for the seawall scour [9,10,11,12,13,14,15,16,17]. Moreover, developing a three-dimensional (3D) model has a high computational cost. Thus, most of the methods are restricted to a two-dimensional formulation. Motivated by this, we present a 3D numerical method for solving the Navier–Stokes (N-S) equations for the hydrodynamic and the Exner equation to model morphodynamic responses.
In order to simulate sediment scouring because of wave–structure–sediment interactions, in this paper, we extend a finite volume method based on unstructured grids (UFVM) for free-surface flows, initially developed by Uh Zapata et al. [18], to include mobile beds as in [19]. The proposed numerical method can be applied for irregular domains in the horizontal, cases with free-surface, and irregular bathymetry using a -coordinate system [20]. Although several numerical models can be found using similar approaches, few 3D models combine the UFVM and transformation [21,22]. In [21], the authors only consider hydrostatic pressure and in [22], the formulation considers only an explicit first-order method. Furthermore, none of them are applied to cases with mobile beds. In this work, bed erosion is simulated by using the van Rijn model [23] and a mass-conservative sand-slide algorithm. Numerical results are also validated by using new and reliable experimental data. Previous methods considering the same formulation presented in this work cannot be found according to our best knowledge.
This work investigates seawall scour under non-breaking waves’ impacts using an original 3D approach to solve the Navier–Stokes–Exner system. This algorithm’s originality relies on the combination of the -transform, the projection method [24,25], the fully implicit second-order UFVM, and the momentum interpolation method [26]. The remainder of this paper is organized as follows. Section 2 focuses on the laboratory experiments. Section 3 presents the governing equations for the hydrodynamic and morphodynamic models. This section includes the equations in the -coordinate system. Section 4 presents a brief summary of the main components of the numerical background. In Section 5, the numerical method is evaluated by using different configurations of waves impacting the seawall. Finally, the final section includes conclusions and future work.
2. Laboratory Experiments
In this work, the data come from new experiments performed in a small plexiglass wave flume of dimension 0.3 m × 0.3 m × 9 m at the Laboratory for Hydraulic and Environment (LHE) of the Institut National de la Recherche Scientifique (INRS) in Québec, Canada [7,8] (see Figure 1). In total, 50 tests were carried out under different wave conditions, sediment size, beach configuration, and seawall. Water elevation, velocity field, and water–sediment bed interface data are available at high resolution.

Figure 1.
(a) Water/sediment bed interface monitored by the echo-Doppler a high-resolution echo-Doppler imaging device at the Laboratory for Hydraulic and Environment (LHE) of the Institut National de la Recherche Scientifique (INRS) in Québec, Canada. (b) Results of the water/sediment bed interface after some minutes.
Figure 2 shows the schematic of the wave flume used for the experimental and modeling sediment scouring due to non-breaking waves on a vertical wall. The location of the vertical wall is 7 m from the wavemaker. The domain consists of two sections: a constant water depth section and an inclined beach. The beach zone is formed for a rigid part of plexiglass with slope and an erodible sediment bed of length and slope . Non-breaking waves experiments were selected to simplify measurements.
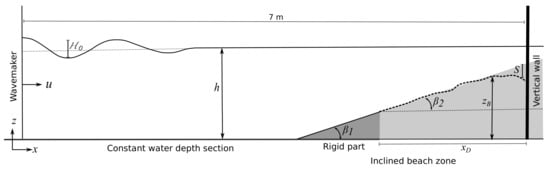
Figure 2.
The schematic of the wave flume used for the experimental and numerical modelling of sediment scouring due to non-breaking waves on a vertical wall. The figure is not to scale.
In determining the data, wave measurements are based on acoustic non-intrusive technology (General Acoustic, USS03 probes), recording the water elevation at 50 Hz in sampling frequency. Wave gauges are mounted in an independent frame, 10 cm above the wave flume. The wave height and period were recorded at eight points: Four are located at the constant water depth section (2.2 m, 3.94 m, 4.54 m, and 4.88 m away from the wavemaker), and four are located in the inclined beach (5.88 m, 6.14 m, 6.45 m, and 6.68 m away from the wavemaker). Measurements of 3D velocity fields were conducted by using the Stereo-PIV technique at 7 Hz. It is combined with small fluorescent particles and a band-pass optical filter to remove reflection on the wavy free surface or the seawall/bed interface for image processing.
The zone of interest covers an area of 15 cm × 15 cm close to the toe of the seawall. Two CCD cameras with 2048 × 2048 pixels resolution are mounted in stereoscopic mode: the pixel resolution equals 73.3 m. Finally, the water–sediment bed interface’s time evolution is monitored by using a commercial and medical high-resolution echo-Doppler imaging device (General electric, LogiQ-e) with a linear sensor (12L-RS at 12 MHz) (see Figure 1a). Bathymetry profiles are measured systematically at the centerline of the wave flume. We refer to [7,8] for more details about the laboratory experiments for obtaining data.
Numerical simulations are performed following two experimental cases: Test A and Test B. The first one corresponds to an Ottawa sand of mean diameter of m, and the second test considers perfectly rounded glass beads of mean diameter m. Table 1 details the parameters applied in these test cases, including the incoming wave height () and period (T). The wavelength (L) is estimated from water depth (h) and the dispersion equation of the linear theory by Stokes. Here, is the water depth at the vertical wall. The experimental results are presented next to the numerical simulations in Section 4.

Table 1.
Main parameters for the numerical simulations.
Following the same scaling analysis in our test conditions as the one proposed by Grasso et al. [27], we obtained, for Test A ( m), an adimensional sedimentological diameter of , settling velocity of cm/s, and friction velocity of cm/s. Thus, is twice higher than . For Test B, is close to a value eight times higher than . These numbers provide a large enough Rouse number (ratio between settling velocity to friction velocity) to neglect suspended load [23], which is also observed during the experiments.
Our testing conditions are relatively close to and cm/s in experiments by Grasso et al. [27]. By comparing their model scale to the prototype scale (Lido of Sète, France), Grasso et al. have confirmed a reduced length scale by = 10 and of time . By transposing their results on beach morphodynamic to our study on the seawall, we may upscale our model results to the prototype by a factor of 10–20 in length and 3.1–4.5 in time. More importantly, our condition corresponds to clear water scouring, a situation in which sediment transport is mainly negligible far from the seawall but is important within its vicinity.
3. Mathematical Model
The governing equations are based on a Navier–Stokes–Exner system. First, the N-S equations are solved in order to calculate the complete evolution of the flow field. Next, the Exner equation is solved to model the morphodynamic response. This paper only focuses on the bedload transport; thus, the suspended load is negligible, as discussed in the previous section.
3.1. Hydrodynamic Model
The hydrodynamic formulation is based on the N-S equations. The governing equations for the three-dimensional model in Cartesian coordinates can be written as follows:
where t is the time; is the velocity; P is the pressure; is the density; is the kinematic viscosity; is the dynamic viscosity; and is the gravitational body force. corresponds to external forces. The pressure is decomposed into a hydrostatic () and a non-hydrostatic (p) component such that . We have by definition the following:
where is the atmospheric pressure (neglected in this work), and is the free surface elevation.
3.2. Morphodynamic Model
The bed evolution is modeled by the Exner equation as follows:
where is the local bed level, and is sediment material porosity. In this work, follows the bedload transport rate given by the van Rijn model [23]:
where the specific density is given by where and are the sediment and water density, respectively. Here, represents the median grain size. The particle parameter is given by the following:
and the transport stage parameter is described as follows:
where is the bed shear stress, and is its critical value corresponding to initiation of motion at the bed.
The bed shear stress is calculated as follows:
where is the friction velocity. In this work, the friction velocity is related to the near bed flow velocity by assuming a logarithmic velocity profile near the bed [28]:
where is expressed as a function of the Nikuradse bed roughness (), with being the equivalent sand roughness, is the von Kármán constant, and is a height sufficiently close to the surface bed. In this paper is selected as the distance from the sediment bed to the the first vertical layer.
To include longitudinal and transversal sloping beds of a scour hole, we consider the modified Shields critical bed shear stress:
where is the critical bed shear stress, is the critical Shields parameter for a horizontal bed, and r is a modification factor. This last term takes into account the effect of the sloping bed. It is approximated as in the work of Roulund et al. [29]:
where is the static friction coefficient for sand, is defined as the angle of steepest descent calculated from the elevation gradient of the longitudinal bed, and is the angle between the flow-velocity vector at the top of the bedload layer and the steepest bed slope.
3.3. Sand-Slide Model
For the proposed morphodynamic model, previous studies have demonstrated that unrealistic bed-slopes may occur [19,30,31]. In particular, mesh distortion appears close to vertical walls, making numerical simulations diverge. Thus, in order to prevent the bed slope from exceeding a sediment angle of repose, , we applied a sand-slide algorithm proposed by Khosronejad et al. [30]. The bed slope is calculated for a triangular horizontal mesh by the elevation gradient between a cell-centered point and horizontal cell-centered neighbors (). If the slope angle exceeds , then the sediment particles will slide down to as follows:
where and are the bed elevations at and , respectively. Here, and are the corresponding corrections, and . Finally, bed corrections are approximated by mass conservation:
where and are the area projection of triangular cells i and j, respectively.
3.4. Equations in the -Coordinate System
Numerical simulations are performed in a wave flume with an inclined mobile beach at the end of the computational domain, as shown in Figure 3. Thus, the discretization of the N-S equations should consider water waves () and mobile bed elevation () varying the total water depth H in time and space. In order to overcome this issue, a -coordinate transformation [20] is applied to Equations (1) and (). This transformation is given by the following:
which maps the vertical coordinate into . Here, H is the total depth formed by the sum of the still depth (h) and the water surface (), as shown in Figure 3. The mobile bed is calculated as , where is a reference constant water depth. For instance, can be the water depth at the inflow boundary. As we consider bed deformations, H changes in time are due to both the water elevation and still depth. Note that the -transformation should be applied at the beginning of the simulation; otherwise, non-uniform grids in the vertical direction are required at the beach section.

Figure 3.
Physical domain and parameters used in -transformation with free surface and bed evolution in the Cartesian coordinate system.
As an initial step, Cartesian coordinates with N-S equations should be rewritten by the equivalent ones in the -coordinate system. Let us consider the transformation of partial derivatives in time:
and in space.
Thus, the derivatives of any variable can be found by using the following [32].
The equations can be simplified by using the following:
where . Thus, continuity Equation (1) can be written for three-dimensional flows in the -coordinate system as follows [18]:
where the gradient operator is given by . The momentum Equation () can be written for the -coordinate system in the following form:
where . Note that the external forces have been omitted in these equations. Finally, the governing equation for the water surface is given in term of H as follows.
This is obtained by integrating Equation (15) on .
The boundary conditions of Equations (15)–(17) are given according to the type of boundary of the computational domain. We used Neumann boundary conditions for the pressure at all edges except for the free surface where we set . For the velocity components, we consider free-slip boundary conditions for the walls and a no-slip condition for the bottom boundary. At the free surface, the following is imposed.
At the inflow boundary, the surface elevation and velocity components are specified from Stokes’ first-order waves. Thus, for the incoming wave, the surface elevation is calculated as follows:
and the velocity distribution over water depth is calculated as follows:
and , where represents the wave height. Here, is the wave frequency, and k is the wave number obtained from the linear wave dispersion relationship .
4. Numerical Method
The numerical method used in this paper extends the work presented in Uh Zapata et al. [18], where 3D hydrostatic free-surface flows are calculated by using an unstructured finite-volume method of the second order of accuracy in time and space. The present numerical technique incorporates the solution of the Exner equation as developed by Zhang et al. [19] to solve flows with mobile beds by using unstructured grids. This algorithm originality relies on the projection method, unstructured finite-volume method, and the combination between the momentum interpolation method and a flux limiter scheme for convective terms.
4.1. Projection Method
The projection method is applied to the N-S equations in -coordinates (15) and (16). Chorin and Temam [24,25] originally proposed this method to decouple the pressure and the velocity field. The projection method can be described in a two-steps technique. In the first step, an intermediate velocity, named , is obtained as follows.
In the second step, we update the velocity field at the new time step, , by using the following equation.
Here, is the computational time step, n indicates the corresponding time step, , and matrices A and B are defined as follows.
4.2. Time Integration
In this study, we proposed a time integration based on the Crank–Nicolson (C-N) method [33] in order to calculate the velocity components. One of the main advantages of this formulation is that the method is second-order accurate. Moreover, there is no time-step restriction for obtaining stable results [22]; however, it results in an implicit formulation. For instance, the intermediate velocity field in (18) is calculated as follows:
where
and the following is the case.
We remark that and need to be updated simultaneously in in roder to calculate new velocity components. This problem is overcome by including an iterative technique and performing global iterations k until converges at the new step.
4.3. Unstructured Finite Volume Discretization
The computational domain is discretized into control volumes, , of prisms with a triangular mesh in the horizontal direction. Each prism is composed of five faces: three with vertical orientation (, , and ) and two with horizontal orientation ( and ). All variables are initially calculated at the center of each prism; however, the method requires velocity components at the face centers. Moreover, variables at the vertex points are needed in the discretization. A schematic plot of the discretization is shown in Figure 4.
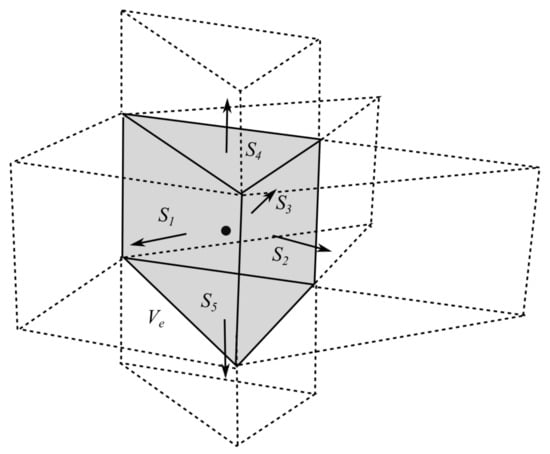
Figure 4.
Schematic plot of the control volume prism formed by an unstructured triangular grid in the horizontal and several layers in the vertical direction of the system . The five faces are denoted as ().
An unstructured finite volume method is used to approximate all equations resulting from the projection step (18)–(20) in the new coordinate system. Water elevation Equation (17) and the Exner Equation (4) are also calculated by using the same procedure. All approximations are second-order accurate in space. In order to illustrate this methodology, we present the discretization of Equation (18) in the -coordinate system. The UFVM discretization results are provided in the following equation:
where the convective and diffusive terms are given by the following:
and
respectively. Here, , v, or w. corresponds to all terms with known values of the previous time step, as described in Section 4.2. Now, we change the volume integrals into surface integral for C and D using the Green’s theorem. Thus, the resulting term is as follows:
where
and the following is the case.
Here, represents the normal vector at . Equation (22) is finally discretized with surface and volume integral approximations. One of the main challenges in any finite-volume method is the approximation of the convective terms given in (26). It is approximated by using an upwind scheme given by the following:
where indicates a value evaluated at the middle point face . On the other hand, values at the faces’ midpoints are calculated as follows:
and the following is the case:
for the vertical rectangular and horizontal triangular faces, respectively. Note that a highly accurate method is obtained because of the gradient. However, these derivatives may introduces some oscillations in the numerical simulations. In order to overcome this issue, the upwind formulation incorporates a flux limiter by using the Barth and Jesperson scheme [34]. Following [35], this flux limiter value is calculated as for all neighbors j. We refer to the work of the present authors [18,19,36,37] for more details about the UFVM for the complete set of equations.
5. Numerical Results
We have performed several numerical simulations to test the proposed method. From these simulations, we compare our results with experimental data. First, we analyze the numerical solution of the problem in terms of surface elevation and velocity field. Later, we focus on the erosion results by discussing the advantages and drawbacks of the current numerical formulation. Waves and depth configurations are chosen to agree with the corresponding experimental setup of Test A and Test B. All simulations are performed by applying the Successive-Over Relaxation solver with a tolerance of and as a relaxation parameter. This solver is run with multiple processors in parallel using a multi-coloring technique [18]. Initial conditions are set equal to zero for both surface elevation and velocity components.
5.1. Numerical Setup
The computational domain has a length of 7 m and a width of m. The still water depth is m and m for Test A and Test B, respectively. The configuration of the bottom consists of the same sections as summarized in Table 1. Note that the deep region is reduced to m in the shallowest area for Test A and reduced to m for Test B.
The domain uses structured triangular grids divided into four triangles, and each is a square of a rectangular reference grid, as shown in Figure 5. The discretization applies two different meshes, as shown in Table 2. In the case of the subdivision number in the direction, it can vary. However, is taken as a default value. It corresponds to m and m close to the seawall for Test A and B, respectively. Note that the finest resolution consists of 268,800 prisms. We can apply higher-resolution meshes; however, the simulation performance is dramatically increased for long-term simulations, even parallel codes. For instance, Mesh 2 requires 2,880,000 time steps to perform a two-hour simulation for . We remark that we are applying a temporal second-order implicit scheme; thus, this time step is enough to ensure space global error. The time step is set to s in all cases.
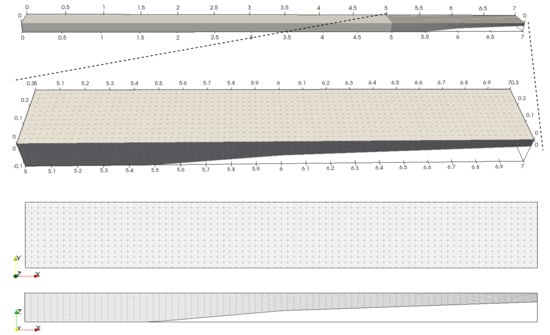
Figure 5.
Mesh example applied in the horizontal and vertical direction of the computational domain. The bottom figures corresponds to the 2D view of the selected x-y and x-z regions of the entire domain.

Table 2.
Details about the meshes used in numerical experiments.
Figure 6 shows the water elevation and velocity field’s numerical solution at four different time stages during the wave impact on the vertical seawall. We consider Test B for these simulations. Note that when the wave impinges the wall, it forms an ascending jet known as an upward deflected breaker [38]. Later, water depth near the seawall runs down during the reflecting wave formation and generates a descending vertical jet. This behavior agrees qualitatively with experimentation. It is the behavior that produces fluidized sediment at the toe and the resulting scour erosion in a long-term simulation. This simulation also evidences the 2D behavior of the problem.
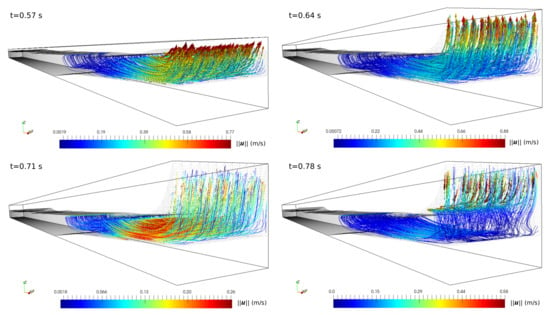
Figure 6.
Instantaneous velocity field and magnitude of the simulated wave during its impact on a vertical seawall for Test B.
5.2. Grid Convergence Study
We initially performed a grid convergence study of the water elevation to test the quality of the numerical results. We want to ensure that the mesh resolution does not influence the phenomenon description. Test B wave approximations are compared relative to higher-resolution mesh simulations. The waves are simulated over the current computational domain without sediment transport calculation. Figure 7 shows the wave surface elevations measured at the wave gauge closer to the seawall ( m). The first figure compares the results by using different vertical layers; the second one compares two different horizontal triangular mesh resolutions. Although some extra details about the secondary waves can be observed as the mesh resolution is increased, vertically or horizontally, the same wave profile is obtained for all cases.
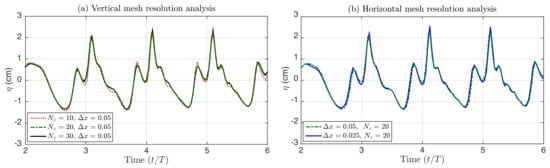
Figure 7.
Grid convergence study of the wave profile at for Test B.
5.3. Wave Elevation
Comparisons between experimental and numerical results of the water elevation are shown in Figure 8 and Figure 9. The results are measured at four of the wave gauges closest to the wall. Note that the profiles of both examples are different. Although Test A results are less accurate than Test B, the numerical model correctly reproduces wave amplitude and height. However, there are some discrepancies between experimental data and numerical solutions. These non-linear wave effects are associated with wave–wave interaction, quadratic phase coupling of waves, and infragravity waves production observed near coastlines [39,40]. Furthermore, experimental wave signals analysis [41] has shown the existence of higher-order bounded harmonics modes from gauges far from the seawall. This behavior can be observed from sharper and higher wave crests, as shown in Figure 8 and Figure 9. Furthermore, the vertical water jet and wave interaction near the seawall region deliver another degree of non-linear complexity.
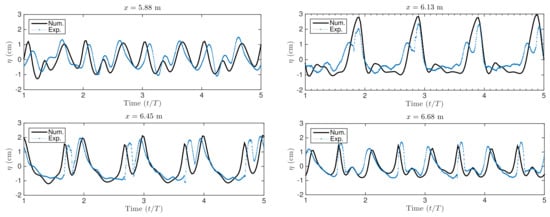
Figure 8.
Experimental and numerical results of the water elevation for Test A using Mesh 2 ( cm and cm).
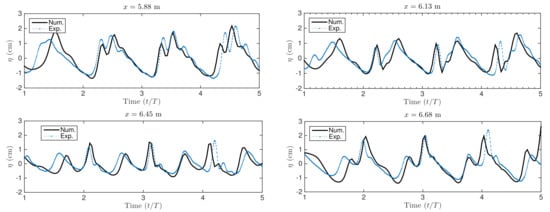
Figure 9.
Experimental and numerical results of the water elevation for Test B using Mesh 2 ( cm and cm).
Despite the discrepancies, the results show the model’s capability to simulate the main features of the complex wave hydrodynamics on a sloping bed and with reflection on the vertical seawall. These simulations are run without a mobile bed. Capturing the same wave profiles for long-time simulations becomes challenging due to the combination of incoming and reflecting waves and the velocity behavior close to the seawall.
5.4. Velocity Field
Experimental and numerical results of the flow velocity are shown in Figure 10 and Figure 11, respectively. The mesh resolution for the experimental results is cm. We present several time stages describing the field before and after the wave impacts the seawall. The results display seven frames per second corresponding to Test A and B with periods and , respectively. The velocity magnitudes are the same in all cases.
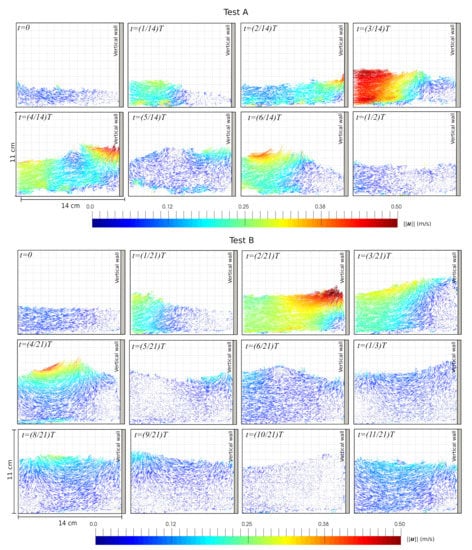
Figure 10.
Experimental results of the instantaneous velocity vector field for Test A and B.
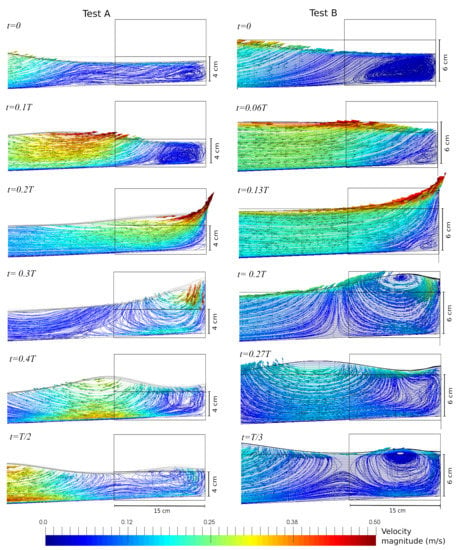
Figure 11.
Numerical results of the instantaneous velocity field for Test A and B. The box corresponds to the PIV measurement zone. The 4 cm and 6 cm legends mean the still water levels at the seawall.
The results show that the numerical results are similar to the experimental findings: complex, non-symmetric, and non-linear hydrodynamic behavior. Note the effects of the wave elevation at the wall before and after the impact. The water depth near the structure decreases when the incoming wave propagates toward the wall. The water aspired seaward, which is in the opposite direction of the incoming wave. When the wave impacts the wall, there is a significant increment in the wave height. This is because the velocity field forms an ascending jet. After the impact on the seawall, the wave is reflected and propagates backward until it is merged with the new incoming wave to repeat the cycle.
It is important to remark that the rectangular area displayed in Figure 11 for the velocity field represents less than 2% of the entire computational domain. Meshes of similar resolutions as the experimental data would require a considerable amount of computational power. For instance, we need close to 40 times the number of points of Mesh 2 to obtain the exact resolution as the experimental data (232 points for 15 cm). Although seven grid points are used in the x-direction to simulate the 15 cm employed in experimental results, we can capture the velocity field’s main features. As the experimental results, the simulations describe the ascending and descending vertical jets near the structure. Note how the numerical results provide details about the new wave’s arrival when the reflecting wave leaves the measurement zone.
5.5. Seawall Scour
This section studies sediment scouring at the inclined beach zone using the morphodynamic model based on the Exner equation and the van Rijn model. Figure 12 shows some experimental results of the echo-Doppler imaging technique relative to measuring bathymetry evolution over time for Test A and Test B.
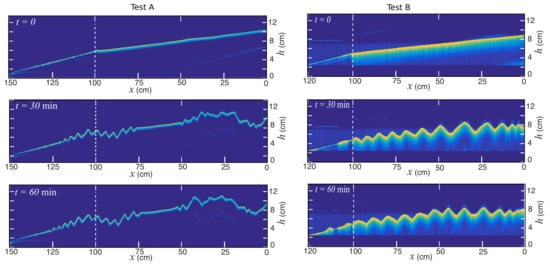
Figure 12.
Experimental results of the bathymetry evolution for Test A and B. The dash line refers to the division between the rigid and mobile bed area.
There are significant differences between Test A and Test B. As previously pointed out, Test A corresponds to the sand of m, and Test B considers perfectly rounded glass beads of m. Test B’s water–sediment interface is formed for multiple ripples and dunes that are evenly distributed in the eroded beach zone. Thus, fine resolution meshes are required to reproduce this complex structure accurately. It is important to remark that the sediment bed changes take place much slower than the flow. With the current parallel techniques [18], we can only perform long-term simulations for medium-size mesh resolutions such as Mesh 1 and Mesh 2. However, as required for Test B, high-resolution meshes are out of the scope of the present code. On the other hand, Test A seems more possible to reproduce as the number of ripples and dunes is smaller and localized in specific regions. Furthermore, Mesh 1 is sufficient for observing this test’s main features, as shown in the numerical simulations presented below. Thus, we only focus on the numerical simulation of sediment erosion of Test A.
Numerical solutions on scouring for Test A are shown in Figure 13. This figure illustrates the time evolution of the 3D scoured hole obtained by the numerical model at six time instants: initial, 5 min, 15 min, 30 min, 45 min, and 60 min. Mesh 1 is used in this simulation. For this test, the sand-slide model prescribes an angle of repose equal to 32. Following the numerical results, bathymetry shows a very rapid evolution during the first 30 min of the test with the formation of scouring and deposition zones. The development of erosion and deposition is mainly in the x-direction, as expected. The scour depth at the toe of the seawall reaches a quasi-state value of around 30 min. Thus, the profile of the beach is slowly lowered after this time. As expected, the deepest part of the main scour hole is located at the seawall’s toe.
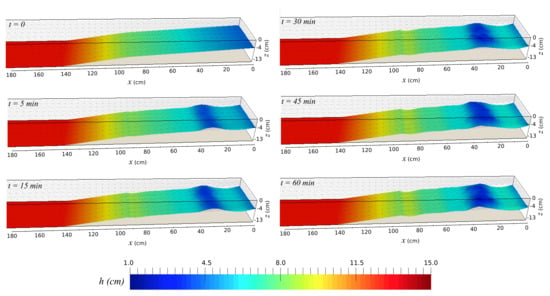
Figure 13.
Numerical results of bathymetry evolution for Test A.
Figure 14 compares the numerical results and the experimental data up to 2 h of simulation. It shows the results of the water depth (h) and the scour (S) calculated as the difference between the initial and the current water depth. As expected, the numerical results show the removal of sediments from the seawall toe with dimensions very close to experimental ones. Both numerical and experimental results confirm the steady state of the seawall scour depth around 30 min simulation. The scour hole is approximately 22 cm in width and 2.9 cm in depth. Here, the scour dimension is measured from the initial profile. These numbers are very close to the ones given by the experiments. Before the seawall-scour hole, the model correctly predicts bar characteristics (position, height, and length). In good agreement with the experimental data, a second hole is formed after the beach’s rigid part. Note that scouring downstream of the inclined apron is correctly predicted at the early stage of the simulation without any specific treatments [42].
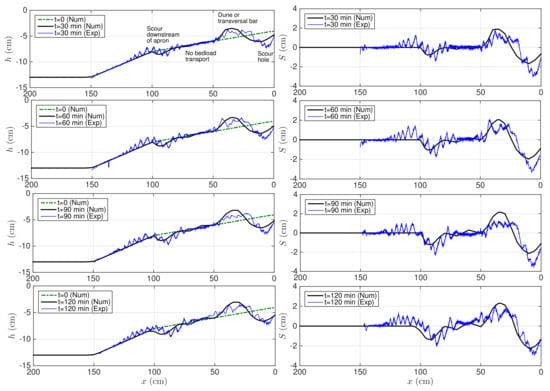
Figure 14.
Numerical and experimental results (at m) of the scour depth for Test A.
It is important to remark that the simulation can even predict the non-eroded zone between the two scour holes, as shown in Figure 14. The non-eroded area between the seawall and apron scour means that the scouring regime is of clear water type. In this case, we have globally no bedload along the beach but only near discontinuity such as the apron and seawall. Only local flow dynamic is responsible for the formation of scour holes. Once initiated, the scour hole is not filled by bedload transport from seaward. This case is the most unfavorable in terms of scour depth amplitude.
As expected, there is an absence of dunes in the numerical solution. The numerical model slightly underpredicts the maximum depth at the seawall compared to experimental data. The sand deposition before the seawall hole is also overpredicted. The discrepancy between simulation and experiment can be attributed to different reasons. For instance, we do account for neither turbulence processes nor the wave boundary layer. We also assume a simplistic formula for estimating friction velocity, which may change when ripples and bars are formed during the experiment. Despite these simplifications, the overall agreement with the experimental data is remarkable.
The secondary hole near the rigid non-erodible slope, cm, corresponds to the scour downstream of an apron, which is comprehensively detailed in Amoudry and Liu [42]. This hole is unavoidable in our experiments because of the transition from a rigid region to a sloppy beach. We remark that the fixed section is necessary to maintain the beach profile. This hole can affect the general mass conservation balance for the scour upstream of a seawall. However, the beach profile integration does not significantly differ for cm (fixed and mobile beach region). On the other hand, both the morphodynamic model and the finite-volume approach are conservative. Thus, a difference between the experimental and numerical results is expected in this region. The discrepancies between models here can also be attributed to the 3D pattern of ripples.
Finally, we remark that, as the vertical jet impinges the sediment bed, the bed could be partially liquefied or fluidized, i.e., pore pressure can equilibrate solid stress. In this study, we neglected the fluidization effect as we neither measured nor computed excess pore pressure. Moreover, fluidization effects are traditionally neglected in the bedload formula, as it needs true two-phase modeling, i.e., calculating the momentum equation for the solid phase. More studies with pore pressure measurement and a complete two-phase model are necessary for future investigations to formulate fluidization near the seawall.
6. Conclusions
This paper presents a three-dimensional numerical model to simulate the scour under wave impact on vertical seawalls. The governing equations are based on a Navier–Stokes–Exner in a -coordinate system. The numerical method is based on a fully implicit second-order unstructured finite-volume method. The numerical results demonstrate that the proposed model can simulate the hydrodynamics of the triple wave–structure–sediment interaction driving the seawall to scour processes. This study takes advantage of new and reliable experiment data to validate numerical formulations. The proposed method can model seawall scour; however, it is limited to cases with regular sediment bed deformations and non-breaking waves. More complex cases complicate the analysis with the present model as the flow is no longer tangential to the seafloor. For those tests, more complex models such as two-phase flow formulations are more suitable for application. Despite these limitations, the present numerical model provides an attractive method to obtain successful simulations of sediment erosion problems. Future investigations will be focused on developing an efficient code with more closure equations (rheological, for instance) required to capture the ripples. Furthermore, a two-phase flow extension of the present code is an ongoing process.
Author Contributions
Conceptualization, M.U.Z., D.P.V.B., and K.D.N.; methodology, M.U.Z., D.P.V.B., and K.D.N.; software, M.U.Z., D.P.V.B., and K.D.N.; validation, M.U.Z., D.P.V.B., and K.D.N.; formal analysis, M.U.Z., D.P.V.B., and K.D.N.; investigation, M.U.Z., D.P.V.B., and K.D.N.; resources, M.U.Z., D.P.V.B., and K.D.N.; writing—original draft preparation, M.U.Z., D.P.V.B., and K.D.N.; writing—review and editing, M.U.Z., D.P.V.B., and K.D.N.; visualization, M.U.Z., D.P.V.B., and K.D.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Mexican Council of Science and Technology (CONACYT) project Investigadoras e Investigadores por Mexico, the Transport Ministry of Quebec (MTQ No. R829.1) and the NSERC-Discovery program (RGPIN-2018-0677).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend special thanks to Compute Canada (contract No. 3148) for providing access to the computing facility.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hugues, S.A. Physical models and laboratory techniques in coastal engineering, In Particular Section 5.4: Vertical Wall; World Scientific: Singapore, 1993; pp. 216–222. [Google Scholar]
- Hattori, M.; Kawamata, R. Experiments on restoration of beaches backed by seawalls. Coast. Eng. Jpn. 1977, 20, 55–68. [Google Scholar] [CrossRef]
- Sutherland, J.; Obhrai, C.; Whitehouse, R.J.S.; Pearce, A. Laboratory tests of scour at a seawall. In Proceedings of the 3rd International Conference on Scour and Erosion (ICSE), Amsterdam, The Netherlands, 1–3 November 2006. [Google Scholar]
- El-Bisy, M.S. Bed changes at toe of inclined seawalls. Ocean. Eng. 2007, 34, 510–517. [Google Scholar] [CrossRef]
- Pearson, J.M. Overtopping and Toe Scour at Vertical Seawalls, Coast, Marine Structures and Breakwaters; ICE: Atlanta, GA, USA, 2010; ISBN 978-0-7277-4131-8. [Google Scholar]
- Saitoh, T.; Kobayashi, N. Wave transformation and cross-shore sediment transport on sloping beach in front of vertical wall. J. Coast. Res. 2012, 128, 354–359. [Google Scholar] [CrossRef]
- Bang, D.P.V.; Marois, L.; Roches, M.D.; Daigle, L.F.; Letellier, P. Interactions entre un Mur de Protection Cotiere et le Transport sédimentaire: Affouillements Locaux au Pied et Abaissement Global de la Plage (Progress Report No. 3, Contract R829.1, Min. Transport; Institut National de la Recherche Scientifique: Quebec City, QC, Canada, 2020. [Google Scholar]
- Marois, L.; Stolle, J.; Bang, D.P.V. Processus d’affouillement au pied d’un mur vertical de protection cotiere. J. Natl. Génie Côtier 2020, 259–266. [Google Scholar] [CrossRef]
- Dally, W.R.; Dean, R.G. Suspended sediment transport and beach profile evolution. J. Waterw. Port Coast. Ocean. Eng. 1984, 110, 15–33. [Google Scholar] [CrossRef]
- Roelvink, J.A.; Stive, M.J.F. Bar-generating cross-shore flow mechanisms on a beach. J. Geophys. Res. Ocean. 1989, 94, 4785–4800. [Google Scholar] [CrossRef]
- McDougal, W.G.; Kraus, N.C.; Ajiwibowo, H. The effects of seawalls on the beach: Part II, numerical modeling of SUPERTANK seawall tests. J. Coast. Res. 1996, 12, 702–713. [Google Scholar]
- Gislason, K.; Fredsøe, J.; Sumer, B.M. Flow under standing waves. Part 2. Scour and deposition in front of breakwaters. Coast. Eng. 2009, 56, 363–370. [Google Scholar] [CrossRef]
- Myrhaug, D.; Ong, M.C. Random wave-induced scour at the trunk section of a breakwater. Coast. Eng. 2009, 56, 688–692. [Google Scholar] [CrossRef]
- Hajivalie, F.; Yeganeh-Bakhtiary, A.; Houshanghi, H.; Gotoh, H. Euler-Lagrange model for scour in front of vertical breakwater. Appl. Ocean. Res. 2012, 34, 96–106. [Google Scholar] [CrossRef]
- Zou, Q.; Peng, Z.; Lin, P. Effects of wave breaking and beach slope on toe scour in front of a vertical seawall. Coast. Eng. Proc. 2012, 1, 122. [Google Scholar] [CrossRef]
- Ahmad, N.; Bihs, H.; Chella, M.A.; Arntsen, A. CFD modelling of Arctic coastal erosion due to breaking waves. Int. J. Offshore Polar Eng. 2019, 29, 33–41. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, N.; Bihs, H.; Myrhaug, D.; Kamath, A.; Arntsen, A. Numerical modeling of breaking wave induced seawall scour. Coast. Eng. 2019, 150, 108–120. [Google Scholar] [CrossRef]
- Zapata, M.U.; Zhang, W.; Bang, D.P.V.; Nguyen, K.D. A parallel second-order unstructured finite volume method for 3D free-surface flows using a σ-coordinate. Comput. Fluids 2019, 190, 15–29. [Google Scholar] [CrossRef]
- Zhang, W.; Zapata, M.U.; Bai, X.; Pham-Van-Bang, D.; Nguyen, K.D. Three-dimensional simulation of horseshoe vortex and local scour around a vertical cylinder using an unstructured finite-volume technique. Int. J. Sediment Res. 2020, 35, 295–306. [Google Scholar] [CrossRef]
- Phillips, N.A. A coordinate system having some special advantages for numerical forecasting. J. Meteor. 1957, 14, 184–185. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Liu, H. An unstructured Grid, Finite Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Liu, X.; Mohammadian, A.; Sedano, J.A.I. Three-dimensional modeling of non-hydrostatic free-surface flows on unstructured grids. Int. J. Numer. Meth. Fluids 2016, 82, 130–147. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sediment transport, Part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Chorin, A.J. Numerical solution of the Navier—Stokes equations. Math. Comp. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Temam, R. Sur l’approximation des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Arch. Ration. Mech. Anal. 1967, 26, 367–380. [Google Scholar] [CrossRef]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Grasso, F.; Michallet, H.; Barthélemy, E.; Certain, R. Physical modeling of intermediate cross-shore beach morphology: Transients and equilibrium states. J. Geophys. Res. Ocean. 2009, 114, C9. [Google Scholar] [CrossRef] [Green Version]
- Nikuradse, J. Laws of Flow in Rough Pipes; VDI Forschungsheft: Washington, DC, USA, 1933. [Google Scholar]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Borazjani, I.; Sotiropoulos, F. Curvilinear immersed boundary method for simulating coupled flow and bed morphodynamic interactions due to sediment transport phenomena. Adv. Water Resour. 2011, 34, 829–843. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Lin, P.; Li, C.W. A σ-coordinate three-dimensional numerical model for surface wave propagation. Int. J. Numer. Methods Fluid 2002, 38, 1045–1068. [Google Scholar] [CrossRef]
- Kim, D.; Choi, H. A second-order time-accurate finite volume method for unsteady incompressible flow on hybrid unstructured grids. J. Comput. Phys. 2000, 162, 411–428. [Google Scholar] [CrossRef]
- Barth, T.; Jespersen, D.C. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989; p. 366. [Google Scholar]
- Vidović, D.; Segal, A.; Wesseling, P. A superlinearly convergent Mach-uniform finite volume method for the Euler equations on staggered unstructured grids. J. Comput. Phys. 2006, 217, 277–294. [Google Scholar] [CrossRef]
- Zapata, M.U.; Bang, D.P.V.; Nguyen, K.D. An unstructured finite volume technique for the 3D Poisson equation on arbitrary geometry using a σ-coordinate system. Int. J. Numer. Meth. Fluids 2014, 76, 611–631. [Google Scholar] [CrossRef]
- Zhang, W.; Zapata, M.U.; Bai, X.; Bang, D.P.V.; Nguyen, K.D. An unstructured finite volume method based on the projection method combined momentum interpolation with a central scheme for three-dimensional nonhydrostatic turbulent flows. Eur. J. Mech.-B/Fluids 2020, 84, 164–185. [Google Scholar] [CrossRef]
- Oumeraci, H.; Klammer, P.; Partenscky, H.W. Classification of breaking wave loads on vertical structures. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 381–397. [Google Scholar] [CrossRef]
- Hasselmann, K.; Munk, W.; MacDonald, G. Bispectrum of Ocean Waves; Rosenblatt, M., Ed.; Time Series Analysis; JohnWiley: New York, NY, USA, 1963. [Google Scholar]
- Bertin, X.; de Bakker, A.; van Dongeren, A.; Coco, G.; André, G.; Ardhuin, F.; Bonneton, P.; Bouchette, F.; Castelle, B.; Crawford, W.C.; et al. Infragravity waves: From driving mechanisms to impacts. Earth Sci. Rev. 2018, 177, 774–799. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.-Y.; Huang, C.-J. Decomposition of incident and reflected higher harmonic waves using four wave gauges. Coast. Eng. 2004, 51, 395–406. [Google Scholar] [CrossRef]
- Amoudry, L.O.; Liu, P.L.-F. Two-dimensional, two-phase granular sediment transport model with applications to scouring downstream of an apron. Coast. Eng. 2009, 56, 693–702. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).