Abstract
The pollution problems of water resources have affected the ecology of the Earth, especially the ecological environment of the oceans. In order to find a cheaper and cleaner organic wastewater treatment method and explore the effect of geometrical parameters and external parameters of self-excited oscillation on cavitation performance, apply it in engineering stably and efficiently, this study took the cavitation effect of self-excited oscillating cavitation jet nozzle as the research target and simulated the geometrical parameters and external parameters of the nozzle. The primary and secondary relationship of the effect of all parameters on cavitation performance was summarized by analyzing the correlation and partial correlation of each parameter. Subsequently, principal component analysis (PCA) was conducted to build a mathematical model of self-excited oscillating cavitation jet nozzle suitable for multiphase transport. As revealed from the results, the contribution rate of parameters to vapor volume fraction followed the order of CLD > d1 > Cd21 > CDd2 > Pin. The ratio of outlet diameter to inlet diameter (Cd21) of the self-excited oscillating cavitation jet nozzle significantly impacted the volume fraction of cavitation vapor (VOF) due to the change of particle diameter, while the influence of other design parameters on VOF was not significant with the change of particle diameter. The larger the content of solid particles, the less the VOF would be impacted by the design parameters. Under the solid particle content of 10% and the particle diameter of 0.2 mm, an independent working point was obtained. In addition, after experimental verification, it was found that the slope of experimental fitting was basically the identical to the corresponding coefficient of parameters in the model. This model and the self-excited nozzle with good cavitation performance provide a theoretical basis for solving the problem of water pollution.
1. Introduction
Numerous issues have been caused in the wake of the rapid development of industry and agriculture. Considerable organic wastewater has been discharged during the production process, which contains many toxic and harmful substances with complex structures that are difficult to degrade efficiently [1] and eventually affect the ecology of the oceans. If organic wastewater fails to be treated effectively and timely, water pollution will be triggered, thereby causing teratogenic, carcinogenic and mutagenic hazards to organisms and human bodies [2]. In the treatment of industrial wastewater, conventional biological treatment and physical and chemical treatment face several problems (e.g., long cycle times, low efficiency and secondary pollution) [3]. Accordingly, novel methods to degrade and treat high-concentration refractory industrial and agricultural wastewater are urgently required. Hydraulic cavitation is considered a promising technology that can be applied in numerous fields for its advantages of simple structure, low cost and environmental friendliness [4,5,6,7,8].
Over the past two decades, a novel self-excited oscillating cavitation jet has been developed for degrading refractory industrial wastewater. Cavitation jets generated by self-excited resonance exhibit high intensity pressure oscillations and large-structure separating vortex rings, thereby endowing them with greater cavitation capacity than ordinary jets under atmospheric pressure and confining pressure conditions. Thus, cavitation jets can significantly damage pollutants, showing promising applications [9,10]. It is noteworthy that in the practical process of industrial wastewater treatment, the liquid medium generally covers tiny solid particles, which pertains to the category of multiphase mixing transport condition. Solid particles will increase the number of gas nuclei in the liquid, thereby further increasing the possibility of cavitation.
Scholars worldwide have found that the concentration [11], size and shape [12] of various particles significantly impact cavitation erosion. However, in the complex field of pollutant degradation, how to strengthen the cavitation of self-excited oscillation to improve the degradation effect remains to be explored. Moreover, the relationship between geometrical parameters of self-excited oscillation, external parameters and cavitation performance remains unclear, and each parameter has insignificant contribution to cavitation performance. Therefore, to examine the cavitation effect of the self-excited oscillation nozzle under various parameters and build the mathematical model, it is particularly important to clarify the relationship between the parameters of self-excited oscillation and cavitation performance, which can provide theoretical prediction for the application of cavitation degradation technology. Remarkable achievements have been currently made in the study of parameters affecting the performance exhibited by self-excited oscillating cavitation jet. Li [13,14] analyzed and derived the natural frequency of the resonant cavity of the organ tube by using the principles of transient flow and hydroacoustics, built the design mode, and found through experimental verification that the diameter and length of the resonant cavity were important factors affecting the resonance of the resonant fluid. Li et al. studied the effects of internal surface roughness [15], inlet diameter [16] and outlet angle [17] on cavitation erosion characteristics of immersed cavitation jet nozzle from two aspects of erosion strength and erosion efficiency.
To study the effect of structural parameters of the self-excited oscillating cavitation jet nozzle on the flow field of the internal cavitation jet, Qi [18] et al. established a double-chamber self-excited oscillating cavitation jet nozzle using the series method for numerical simulation and obtained the influence law of the inlet flow Reynolds number, the length ratio of the front and rear chambers, and the cavity diameter ratio of the cavitation jet. Yang et al. [19] studied the effect of structural parameters on natural frequency characteristics of self-excited oscillating pulse jet by using numerical simulation. It was found that the frequency characteristic of the self-excited oscillating cavitation jet nozzle was nonlinear and resonant by establishing the similar grid theory. It was also found that the length and diameter of the cavity and the lower nozzle of the device had great influence on the self-excitation frequency. Tang et al. [20] analyzed the effect of pump source pulsation on oscillation characteristics of self-excited oscillating cavitation jet nozzle. They found that when the natural frequency of the self-excited oscillating cavitation nozzle was greater than or equal to the incoming flow pulsation frequency, the oscillation and erosion effect of the jet were improved. Besides, experimental data shows that the optimum cavity length of the self-excited oscillating cavitation jet nozzle matches the peak pressure of the pulsed jet. Gao et al. [21,22,23] studied the effect of the structural parameters of self-excited oscillating cavitation jet nozzles on the suction performance exhibited by underwater self-excited oscillating cavitation jet nozzle, as well as the effect of suction volume on structural parameters of self-excited oscillating cavitation jet nozzle. The mean square deviation, peak value of pulsating pressure and time mean pressure of impulse pulsating pressure test data were obtained with the area ratio of upper and lower nozzles, cavity length to lower nozzle area ratio and cavity diameter to cavity length ratio, whereas the formation mechanism of negative pressure pulsation was not clearly analyzed. Li et al. [24] used the scaled self-excited oscillating cavitation nozzle to perform experiments and revealed the effect of different inlet pressures on the evolution of cavitation clouds by means of high-speed photography. They found that the cavitation cloud varies periodically, which covers four different stages of cavitation initiation, development, shedding and collapse, and it reaches the maximum area, width and density of the cavitation cloud during shedding. Lu [25], Ge [26] and Li et al. [27] used theoretical analysis and experimental study to show that the oscillation frequency of self-excited oscillating cavitation nozzle device could reach 200–1000 Hz through design. It was found that the length of cavitation cloud was determined by the target distance, and the factors affecting the rock fragmentation ability of high-pressure water jet included cavitation conditions as well as the characteristics of the material under cavitation erosion. Li et al. [28] studied the relationship between jet characteristics and internal surface roughness of the organ tube self-excited oscillating cavitation jet nozzle by using experimental methods. Based on the experimental results and the energy conservation theorem, a mathematical model was built for the relationship between the peak value of pressure pulsation in the jet axis and inlet pressure, surface roughness and target distance. Lu et al. [25] enriched the impact stress wave and cavitation effect breakage theory of self-excited oscillating cavitation jet by studying the hydrodynamic characteristics of self-excited oscillating cavitation jet nozzle.
Given the mentioned research, scholars have primarily studied the working principle of self-excited oscillation and the effect of structural parameters on self-excited frequency. At present, the contribution of each parameter to cavitation performance have been rarely studied. In this study, the cavitation effect of the self-excited oscillating cavitation jet nozzle was studied, and the inlet pressure and structural parameters of the nozzle were numerically simulated. By analyzing and summarizing the primary and secondary relationship of the effect of each factor on cavitation performance, the cavitation theory was improved. At the same time, the mathematical model between the geometrical parameters of self-excited oscillation, inlet pressure and cavitation performance was built. This model can apply self-excited oscillation cavitation in the field of wastewater degradation, which will protect water resources and marine ecology better.
2. Simulation and Experiment
2.1. Model Selection
There are many design parameters of self-excited oscillating cavitation jet nozzle (e.g., inlet diameter, cavity diameter, cavity length, outlet diameter, diffusion angle, inlet pressure). If the orthogonal array method is used, the test efficiency will be lower, and the test accuracy and effect will be worse. At the same time, the level of the optimal Latin hypercube design factor is limited by the corresponding algorithm to ensure that the selected sample points have good representativeness in the whole design space. Therefore, this study selected the optimal Latin hypercube design method. It is based on the random Latin square method by improving the uniformity, which makes the design results more accurate and real.
The three-phase flow analyzed in this study is complicated. In the process of CFD simulation, a mixture model was selected. The mixture model has the advantages of high accuracy, small resource occupancy and fast calculation, which meets the requirements of cavitation characteristics calculation in the cavitation jet flow field. The application range of the mixture model is very wide, including various flow forms (e.g., low load particle flow and bubble flow, sedimentation and cyclone separator). The diffusion, pulsation and interfacial transfer characteristics of two phases were considered in the mixture model, and the flow field was expressed by the mixture characteristic parameter equation. The mixed two-phase momentum equation was solved, is expressed in Equation (1):
where the is the drift speed in the k-th term, is the density of the mixture, is velocity of the mixture, is volume force.
The expression form of slip velocity in two-phase, expressed in Equation (2):
The drift velocity of vapor is combined by Equations (1) and (2), as Equation (3):
The vapor volume fraction equation is shown in Equation (4):
2.2. Parameter Determination
The geometric model of the self-excited oscillating cavitation jet nozzle is shown in Figure 1. The inlet diameter of the cavity mainly composed of the self-excited oscillating cavitation jet nozzle is d1, the outlet diameter of the self-excited oscillating cavitation jet nozzle is d2, the diameter of the cavity is D, the length of the cavity is L, and the impact angle of the cavity is α. To facilitate the analysis and summary of regularity, the subsequent simulation analysis adopted the dimensionless form, and the specific value range is listed in Table 1.
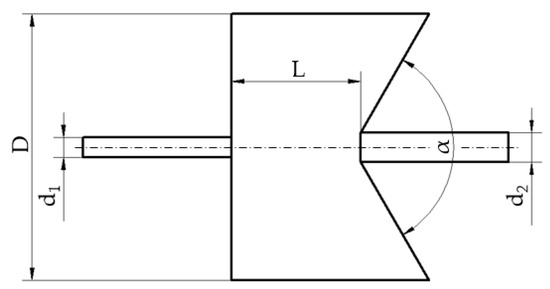
Figure 1.
Geometrical structure diagram of self-excited oscillation cavitation jet nozzle.

Table 1.
Design variables and their value ranges.
According to the parameters in Figure 1 and Table 1, the structured grids were divided by ICEM, and the grid independence was tested by using multiple groups of grids increasing by 20% until the outlet velocity no longer changes significantly. The final selected number of grids exceeds 730,000. The grids are shown in Figure 2.
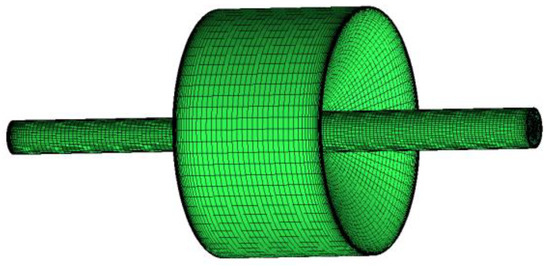
Figure 2.
Grids of self-excited oscillating cavitation jet nozzles.
To be specific, the design variable d1 is the inlet diameter of self-excited oscillation cavitating jet nozzle, Cd21 is the ratio of the outlet diameter d2 of self-excited oscillation cavitating jet nozzle to the inlet diameter d1, CLD is the ratio of the self-excited oscillation cavitating jet nozzle cavity length L and the cavity diameter D, CDd2 is the ratio of cavity diameter D and the self-excited oscillation cavitating jet nozzle outlet diameter d2, Pin is the inlet pressure of the self-excited oscillating cavitation jet nozzle. According to the grids shown in Figure 2, the optimized Latin square design of the self-excited oscillating nozzle was carried out using CFD simulation method, and the optimized parameter matrix of the self-excited oscillating cavitation jet nozzle was obtained (Table 2).

Table 2.
Optimization Latin square design matrix of a self-excited oscillating cavitation jet nozzle.
2.3. Criteria
2.3.1. Simulation Criteria
The optimization design of self-excited oscillating cavitation jet nozzle adopted the disciplinary analysis method of constructing approximate model to reduce the calculation time and cost. The purpose of the optimization was to make the nozzle structure parameters and inlet pressure of the self-excited oscillating cavitation jet to achieve the best cavitation performance. The optimization objective was to maximize the volume fraction of vapor. The optimization model is as follows: the objective function is max VOF. The output variable VOF was used to measure the volume of vapor contained in the nozzle of self-excited oscillating cavitation jet, reflecting the degree of cavitation. When the local pressure inside the nozzle of the self-excited oscillating cavitation jet was lower than the saturated vapor pressure, the vapor core in the liquid would grow into cavitation. After cavitation initiation, the vapor nuclei would first develop into vacuoles in the low-pressure region of the cavity and flow to a specific high-pressure region. Shrinkage collapsed due to the imbalance of internal and external pressure difference. In this process, VOF was in a dynamic process of change. However, in a certain fixed stage of cavitation (e.g., the development stage of cavitation), VOF reflected the degree of cavitation inside the nozzle of the self-excited oscillating cavitation jet.
2.3.2. Experiment Criteria
During the experiment, the cavitation effect of nozzle was evaluated by using erosion mass loss to represent cavitation performance, based on fixed target distance and specified cavitation time. Erosion intensity could be evaluated by sample mass loss. The mass loss of the respective sample was determined before and after each test by weighing an electronic balance (Model: BSA224SCW, Sartorius, Göttingen, Germany) with a resolution of 0.1 mg. The mass loss rate was calculated according to Equation (5) below:
where, w denotes the mass loss rate of cavitation specimen, m0 represents the mass of specimen before cavitation erosion, and m expresses the mass of specimen after cavitation.
2.4. Experimental Materials and Devices
The test bench was built in the laboratory of National Research Center of Pumps at Jiangsu University. Figure 3 is a schematic diagram of the degradation test rig of self-excited oscillating cavitation jet nozzle (1 plunger pump; 2 pump pressure gauge; 3 pressure regulating relief valve; 4 electromagnetic flowmeter; 5 pressure gauge; 6. self-excited oscillation cavitation jet nozzle; 7 jet platform; 8 tank; 9 filter; 10 valve). A model KEFC-P-25G6-CNTNL7 intelligent electromagnetic flowmeter with a diameter of DN25, error ± 0.5% made by Shanghai Kent (Shanghai, China) was selected as the flowmeter. During installation, the distance between the straight pipe section in front of the flowmeter should be no less than 10 × 25 mm, and the distance between the straight pipe section in back of the flowmeter should be no less than 5 × 25 mm, so as to ensure the accuracy of the flowmeter measurement process. The nozzles of self-excited oscillating cavitation jet were numbered as shown in Figure 4, where #1–3 and #4–6 could be combined with each other because they adopted the same cavity diameter structure, respectively.
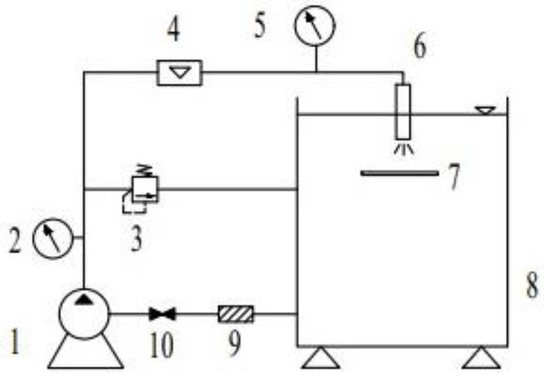
Figure 3.
Schematic diagram of self-excited oscillation cavitation jet nozzle test bench.

Figure 4.
Photo of self-excited oscillation cavitation jet nozzles.
3. Results and Discussion
3.1. Simulation Results of Self-Excited Oscillating Cavitation Jet Nozzle
To examine the effect of solid particle diameter and solid particle percentage in the nozzle medium of self-excited oscillating cavitation jet nozzle on the cavitation performance exhibited by the nozzle, this study selected 5%, 10% and 20% solid particles in the medium, and the solid particle diameter in the medium containing 5% solid particles was 0.1 mm, 0.2 mm and 0.3 mm, respectively. In the medium containing 10% and 20% solid particles, the diameter of solid particles was 0.1 mm and 0.2 mm, respectively. Based on the automatic optimization platform built by Isight, the optimization Latin square combination (Table 1) of the design parameters of 30 groups of different self-excited oscillating cavitation jet nozzles was simulated in this study under the above three solid particle percentages and different solid particle diameters. The calculation results are shown in Table 3.

Table 3.
Cavitation vapor volume fraction of self-excited oscillating cavitation jet nozzle corresponding to different medium parameters (solid particle content and solid particle diameter) and design parameters.
According to Table 3, the relationship diagram of cavitation vapor volume fraction of self-excited oscillating cavitation jet nozzle corresponding to different medium parameters and design parameters was drawn, as shown in Figure 5 and Figure 6.
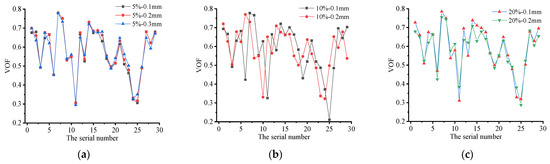
Figure 5.
Vapor volume fractions of self-excited oscillation cavitation jet nozzles corresponding to different particle contents. (a) Solid particle content 5%; (b) Solid particle content 10%; (c) Solid particle content 20%.
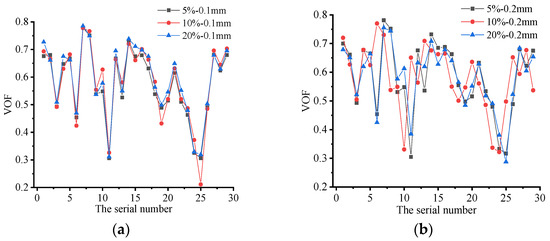
Figure 6.
Vapor volume fractions of self-oscillating cavitation jet nozzles corresponding to different particle diameters. (a) Solid particle diameter 0.1 mm; (b) Solid particle diameter 0.2 mm.
According to Figure 5, with the identical solid particle content and the increase of particle diameter, the variation trend of the volume fraction of cavitation vapor in the self-excited oscillating cavitation jet nozzle with different structural parameters was basically the consistent. However, in Figure 5b, the volume fraction of cavitation vapor in the self-excited oscillating cavitation jet nozzle changed more significantly. As indicated from Figure 5a, when the content of solid particles was 5%, the vapor volume fraction of the self-excited oscillating cavitation jet nozzle increased gradually with the increase in the particle diameter, whereas the increase was not obvious, and the change trend was nearly consistent. According to Figure 5b, when the content of solid particles was 10%, the vapor volume fraction of the self-excited oscillating cavitation jet nozzle increased gradually with the increase in the particle diameter, and the variation trend was obvious. As indicated from Figure 5c, when the content of solid particles was 20%, the vapor volume fraction of the self-excited oscillating cavitation jet nozzle decreased first and then increased with the increase in the particle diameter. As revealed from the figure, different combinations of solid particle diameter and solid particle content exerted different influences on the cavitation of the self-excited oscillating cavitation jet nozzle, and the identical combination of design parameters exerted different influences on the cavitation of the self-excited oscillating cavitation jet nozzle under different media conditions.
Figure 6 shows that when the diameter of solid particles was 0.1 mm, the vapor volume fraction of the self-excited oscillating cavitation jet nozzle increased gradually with the increase in the content of solid particles, whereas the increase was insignificant, and the change trend was nearly unchanged. When the diameter of solid particles was 0.2 mm, with the increase in the content of solid particles, the vapor volume fraction of the self-excited oscillating cavitation jet nozzle increased first and then decreased, and the variation trend was obvious. As revealed from Figure 6b, when the diameter of solid particles was 0.1 mm, and the content of solid particles reached 20%, the cavitation effect of the nozzle of self-excited oscillating cavitation jet was high.
3.2. Correlation Analysis of Structural Parameters
Data should be standardized before multiple regression analysis. Since each variable represented different physical attributes, and its order of magnitude and dimension were different, the regression equation could not be directly constructed. Besides, when analyzing the constructed regression equation, some extremely high values would cause unreliable analysis results. The standardized regression coefficient was calculated as follows:
where the terms Sx and Sy are the standard deviations of x and y, respectively
The relationship between variables (independent and dependent) could be expressed by a correlation coefficient, reflecting the degree of connection between variables. Correlation coefficient between variables refers to one of the indicators of collinearity between diagnostic variables. The correlation coefficient matrix composed of the five structural parameters simulated and calculated in this study and the vapor volume fraction is shown in Table 4. According to Table 4, the ratio of nozzle outlet diameter to inlet diameter and inlet pressure of the self-excited oscillating cavitation jet nozzle was positively correlated with the volume fraction of the vapor, and the inlet pressure was positively correlated with the volume fraction of the vapor. The other design parameters were negatively correlated with the vapor volume fraction. To be specific, the correlation coefficient of the respective design parameter to the volume of steam was CLD > d1 > Cd21 > CDd2 > Pin. Therefore it was therefore indicated that the ratio of cavity length to cavity diameter and inlet diameter more significantly impacted the volume fraction of the vapor body, while the ratio of cavity diameter to outlet diameter and inlet pressure exerted a smaller effect on the volume fraction of the vapor.

Table 4.
Correlation coefficient between nozzle design parameters and cavitation index.
As revealed from Table 4, the correlation between different design parameters was different. The ratio of nozzle outlet diameter to inlet diameter was positively correlated with inlet pressure, whereas it was negatively correlated with other design parameters. The ratio of cavity length to cavity diameter and that of cavity diameter to outlet diameter were positively correlated with inlet pressure, whereas they were negatively correlated with other design parameters. The ratio of cavity diameter to outlet diameter and that of outlet diameter to inlet diameter were negatively correlated, while they were positively correlated with other design parameters. The ratio of inlet diameter and cavity diameter to outlet diameter was positively correlated, while it was negatively correlated with other design parameters. The inlet pressure was negatively correlated with the inlet diameter and other design parameters.
3.3. Partial Correlation Analysis of Solid Particles
The design parameters of the self-excited oscillating cavitation jet nozzle exerted a direct influence on the cavitation index, while having different degrees of influence on each other. According to Table 5, with the identical content of solid particles in the medium, the respective design parameter of the self-excited oscillating cavitation jet nozzle exerted different influences on the vapor volume fraction under different particle diameters, which demonstrated that different particle diameters also impact the cavitation performance exhibited by the self-excited oscillating cavitation jet nozzle.

Table 5.
Partial correlation coefficients between nozzle design parameters and vapor volume fraction of self-excited oscillating cavitation jet in different media.
Under the content of solid particles of 5%, the partial correlation coefficient between the ratio of the outlet diameter to the inlet diameter of the self-excited oscillating cavitation jet nozzle and the volume fraction of steam decreased from −0.701 to −0.328 gradually with the increase of the diameter of solid particles. When the content of solid particles was 10%, the partial correlation coefficient between the ratio of the inlet diameter to the outlet diameter of the self-excited oscillating cavitation jet nozzle and the vapor volume fraction decreased from −0.599 to −0.329. When the content of solid particles was 20%, the partial correlation coefficient increased from −0.492 to −0.576.
It was therefore revealed that when the content of solid particles was low, the effect of the ratio of the outlet diameter to the inlet diameter of the self-excited oscillating cavitation jet nozzle on the vapor volume fraction decreased with the increase in the particle diameter. However, when the content of solid particles was large, the effect of the ratio of nozzle outlet diameter to inlet diameter on vapor volume fraction increased with the increase in the particle diameter. Moreover, the ratio of cavity length to cavity diameter, the ratio of cavity diameter to outlet diameter, inlet diameter and inlet pressure all varied with the increase of particle diameter when the solid particle content was 5%, whereas these variations were insignificant.
It was demonstrated that the effect of other design parameters on vapor volume fraction with particle diameter was not obvious, except for the ratio of inlet diameter to outlet diameter of self-excited oscillating cavitation jet nozzle. When the content of solid particles was 10%, the effect of the ratio of cavity diameter to outlet diameter on vapor volume fraction increased from −0.036 to −0.163. When the solid particle content was 20%, the ratio of cavity diameter to outlet diameter did not significantly impact the process of stepwise regression analysis. As concluded from the analysis, the ratio of cavity diameter to outlet diameter slightly impacted the vapor volume fraction with the increase of solid particle content. The other design parameters slightly impacted the vapor volume fraction with the increase in the particle diameter when the content was 10%.
Under the identical particle diameter and three different solid particle content percentages, the partial correlation coefficient between the ratio of the outlet diameter to the inlet diameter of the self-excitation oscillating cavitation jet nozzle and the volume fraction of the vapor decreased from −0.701 to −0.492, which revealed that with the increase in the solid particle content, the ratio of outlet diameter to inlet diameter of self-excited oscillating cavitation jet nozzle exerted less influence on the vapor volume fraction. The partial correlation coefficients of the other design parameters were reduced, but not obviously under the same particle diameter and three different solid particle contents. The partial correlation coefficient was the maximum when the particle diameter was 0.1 mm or 0.2 mm and the solid particle content was 5%, which indicated that the larger the solid particle content, the less influence the design parameters would exert on the vapor volume fraction.
Table 6 indicates that a stepwise linear regression method was adopted to determine the coefficient under different solid particle contents and different particle diameters. Only when the content was 5% and the particle diameter was 0.1 mm and 0.2 mm, the coefficient was above 0.9, while the residual diameter coefficient was small. It was therefore suggested that the linear equation established by stepwise regression between design parameters and vapor volume fraction exhibited high accuracy. However, the determination coefficients were not above 0.9 under other conditions, whereas they were close to each other.

Table 6.
Determination coefficients of nozzle design parameters and vapor volume fraction and residual diameter coefficients of self-excited oscillating cavitation jet nozzle in different media.
3.4. Construction of Mathematical Model under Multiphase Transport
Through stepwise regression analysis, the linear regression equation of the design parameters of the self-excited oscillating cavitation jet nozzle under different medium parameters was obtained, as expressed in Equation (7), where VOFi denotes the vapor volume fraction under different media conditions (i = 1, 2 and 3 represents the particle diameter of 0.1 mm, 0.2 mm and 0.3 mm when the solid particle content was 5%, respectively; i = 4 and 5 expresses the particle diameters of 0.1 mm and 0.2 mm when the solid particle content was 10%, respectively; i = 6 and 7 represents the particle diameters of 0.1 mm and 0.2 mm when the solid particle content was 20%, respectively):
To comprehensively consider the effect of design parameters on the cavitation performance exhibited by self-excited oscillating cavitation jet nozzle under different solid particle contents and particle diameters, principal component analysis (PCA) was conducted to clarify the effect of design parameters on the cavitation index. In this study, the vapor volume fraction of the self-excited oscillating cavitation jet nozzle calculated in Table 3 under different medium parameters was selected as the original data for PCA. PCA was performed by exploiting the function of multivariate analysis in data processing method. The analysis results comprised the correlation matrix, eigenvalue and eigenvector of the correlation matrix between the original data.
Table 7 lists the phase relationship between vapor volume fractions of self-excited oscillating cavitation jet nozzles under different medium parameters. As revealed from the Table 7, the correlation coefficient between the volume fraction of steam under 10% solid particle content and 0.2 mm particle diameter was relatively small, and the correlation coefficient between the volume fraction of steam under other medium parameters was especially significant. It was therefore demonstrated that medium parameters with solid particle content of 10% and particle diameter of 0.2 mm were independent operating points. At this point, the influence of design parameters on cavitation index of self-excited oscillating cavitation jet nozzle was inconsistent with that of other medium parameters. Furthermore, the effect of design parameters on cavitation index of self-excited oscillating cavitation jet nozzle would be regulated with the change of medium parameters.

Table 7.
Correlation coefficients between design parameters and vapor volume fraction of self-excited oscillating cavitation jet nozzle in different media.
Table 8 lists the eigenvalues calculated by correlation matrix of vapor volume fraction under different medium parameters, i.e., contribution rate and accumulative contribution percentage of components. As suggested from Table 8, the characteristic value of the first principal component was 6.3582, the contribution rate took up 90%, while other characteristic values were relatively small, and the contributing rate was relatively low. Accordingly, the selection of the first principal component could fully account for the vapor volume fraction under different medium parameters. The feature vectors of the respective component factor are listed in Table 8.

Table 8.
Characteristic values of different principal components.
Given the feature vector of the first major component calculated in Table 9, the mathematical model of the new parameter variable is expressed as:

Table 9.
Eigenvectors of different factors.
In Equation (8), VOFnew denotes a new parameter variable generated according to the vapor volume fraction under different medium parameters, capable of describing the change of vapor volume fraction under different medium parameters.
Substituting each VOFi in Equation (7) for (I = 1,2,3, … 7) into Equation (8) yields:
Equation (9) expresses the change of VOF under the multiphase transport conditions.
3.5. Model Validation
In this study, the mass loss rate of specimens was adopted to characterize cavitation performance by using fixed target distance (15 mm) and cavitation time (2 h). On that basis, the accuracy of the model was verified by using the mathematical model of the volume fraction of cavitation vapor under the condition of multiphase transport. In the process of cavitation, when the pressure dropped to the saturated vapor pressure, the vapor core developed into cavitation, and the VOF inside the self-excited oscillating cavitation jet nozzle increases. VOF could reflect the degree of cavitation in the self-excited oscillating cavitation jet nozzle. When the cavitation flowed to the high-pressure area, the collapse was attributed to the imbalance of internal and external pressure difference. Cavitation collapse led to mass loss of specimens. Accordingly, the mass loss rate could also imply the degree of cavitation in the self-excited oscillating cavitation jet nozzle. Figure 7 presents the mass loss rate of specimens changing with geometric parameters. Figure 8 illustrates the mass loss rate of specimens changing with geometric parameters.

Figure 7.
Picture of cavitation jet experiment and results. (a) Picture of cavitation jet experiment; (b) Picture of experimental results.
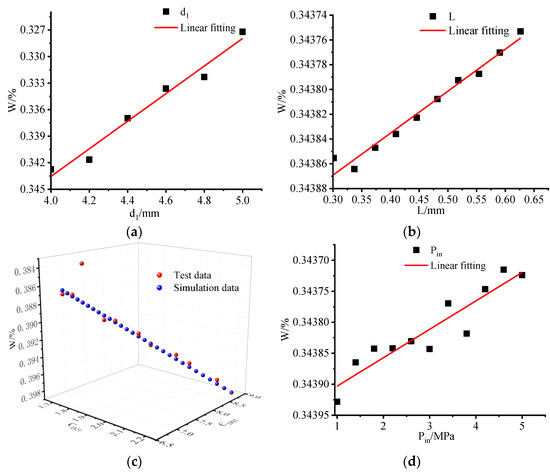
Figure 8.
Mass loss rate of specimen varies with geometric parameters and external parameters. (a) The mass loss rate changes with d1; (b) The mass loss rate changes with L; (c) The mass loss rate changes with d2; (d) The mass loss rate changes with Pin.
The mass loss rate under the respective parameter could be determined experimentally, and the slope could be determined by fitting the synthetic curve, as summarized in Table 10 below.

Table 10.
Comparison of the simulation results of test data and model parameters.
According to Table 10, the fitting correlation coefficient was close to 1, thereby indicating that the curve fitting was appropriate. The slope of test fitting was basically identical to the corresponding coefficient of parameters in the model. It was therefore suggested that the model was reasonable, and the model could predict the cavitation performance exhibited by the self-excited oscillating cavitation jet nozzle under the multiphase transport.
4. Conclusions
In this study, stepwise regression analysis was conducted to build the mathematical model of parameter variables by adopting the linear regression equation of the optimized structure parameters of the self-excited oscillating cavitation jet nozzle under different medium parameters. On that basis, the influence of the structural parameters and external parameters of the cavitation jet nozzle on the cavitation performance was examined. The following conclusions are drawn:
- (1)
- When the content of solid particles was 5% and 10%, VOF increases with the increase in the particle diameter. When the content of solid particles was 20%, VOF decreases first and then increases with the increase in the particle diameter;
- (2)
- Cavitation performance of self-excited oscillating cavitation jet nozzle is affected by design parameters. Under the identical particle diameter, the larger the content of solid particles, the less the effect of design parameters will exert on VOF;
- (3)
- The correlation analysis of the respective design parameter revealed that its influence on vapor volume fraction was CLD > d1 > Cd21 > CDd2 > Pin;
- (4)
- The effect of Cd21 on VOF is obvious with particle diameter, while the influence of other design parameters on VOF is insignificant with particle diameter;
- (5)
- When the solid particle content was 10% and the particle diameter was 0.2 mm, an independent operating point would be generated. At this point, VOF was slightly correlated with VOF in other media;
- (6)
- A novel VOFnew with different medium parameters is determined, which could express the variation of vapor volume fraction under different medium parameters and imply the contribution rate of the respective parameter to cavitation performance. It has been verified experimentally that the slope of test fitting is basically identical to the corresponding coefficient of parameters in the model, and the model could be reasonable.
Author Contributions
Conceptualization, X.W. and W.X.; methodology, F.Z. and Y.Z.; software, F.Z.; validation, G.Z.; formal analysis, W.X.; investigation, F.Z. and H.Z.; resources, X.W.; data curation, F.Z.; writing—original draft preparation, F.Z.; writing—review and editing, W.X.; visualization, G.Z.; supervision, F.Z.; project administration, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
Key R&D programs of Anhui Province of China (201904a05020070); Research on Key Technologies of High-efficiency Wastewater Harmless Treatment and Purification Equipment (GY2020015); Jiangsu Agricultural Science and Technology Innovation Fund (CX(21)3078).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| PCA | Principal component analysis |
| CLD | Ratio of the self-excited oscillation cavitating jet nozzle cavity length L and the cavity diameter D |
| d1 | Inlet diameter |
| Cd21 | Ratio of outlet diameter to inlet diameter |
| CDd2 | Ratio of cavity diameter D and the self-excited oscillation cavitating jet nozzle outlet diameter d2 |
| Pin | Inlet pressure |
| VOF | Volume fraction of cavitation vapor |
| d2 | Outlet diameter |
| Drift speed in the kth term | |
| Density of the mixture | |
| Velocity of the mixture | |
| Volume force | |
| D | Diameter of the cavity |
| L | Length of the cavity |
| α | Impact angle of the cavity |
| w | Mass loss rate of cavitation specimen |
| m0 | Mass of specimen before cavitation erosion |
| m | Mass of specimen after cavitation erosion |
| r(X,VOF) | Partial correlation coefficient between parameter X and vapor volume fraction |
| VOFi | Vapor volume fraction under different media conditions |
| VOFnew | A new mathematical model of vapor volume fraction |
References
- Peng, Z.; Liu, X.J.; Zhang, W.; Zeng, Z.T.; Liu, Z.F.; Zhang, C.; Liu, Y.; Shao, B.B.; Liang, Q.H.; Tang, W.W.; et al. Advances in the application, toxicity and degradation of carbon nanomaterials in environment: A review. Environ. Int. 2020, 134, 105298. [Google Scholar] [CrossRef]
- Zhang, X. Study on treatment of phenolic wastewater by microbial degradation. Fresenius Environ. Bull. 2020, 29, 129–1133. [Google Scholar]
- An, H.X.; Li, X.M.; Yang, Q.; Wang, D.B.; Xie, T.; Zhao, J.W.; Xu, Q.X.; Chen, F.; Zhong, Y.; Yuan, Y.J.; et al. The behavior of melamine in biological wastewater treatment system. J. Hazard. Mater. 2017, 322, 445–453. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, S.; Ji, H. Mechanism of rock breaking by pick assisted with water jet of different modes. J. Mech. Sci. Technol. 2015, 29, 5359–5368. [Google Scholar] [CrossRef]
- Huang, L.; Kinnell, P.; Shipway, P.H. Removal of heat-formed coating from a titanium alloy using high pressure waterjet: Influence of machining parameters on surface texture and residual stress. J. Mater. Process. Technol. 2015, 223, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Careddu, N.; Akkoyun, O. An investigation on the efficiency of water-jet technology for graffiti cleaning. J. Cult. Herit. 2016, 19, 426–434. [Google Scholar] [CrossRef]
- Jiang, H.; Du, C.; Dong, J. Investigation of rock cutting dust formation and suppression using water jets during mining. Powder Technol. 2017, 307, 99–108. [Google Scholar] [CrossRef]
- Den Dunnen, S.; Dankelman, J.; Kerkhoffs, G.M.; Tuijthof, G. Colliding jets provide depth control for water jetting in bone tissue. J. Mech. Behav. Biomed. Mater. 2017, 72, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Li, G.; Wang, Z.M.; Hou, F.S. New jet theory and prospects of application in drilling engineering. In Proceedings of the 13th World Petroleum Congress, Buenos Aires, Argentina, 20–25 October 2021; pp. 397–405. [Google Scholar]
- Johnson, V.E.J.; Chahine, G.L.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S.; Giacchino, G.J. The development of structured cavitating jet for deep hole bits. SPE 1982, 11060, 1–8. [Google Scholar]
- Peng, C.; Tian, S.C.; Li, G.S.; Wei, M.H. Enhancement of cavitation intensity and erosion ability of submerged cavitation jet by adding micro-particles. Ocean Eng. 2020, 209, 107516. [Google Scholar] [CrossRef]
- Xu, W.L.; Zhang, Y.L.; Luo, J.; Arong; Zhang, Q.; Zhai, Y.W. The impact of particles on the collapse characteristics of cavitation bubbles. Ocean Eng. 2017, 131, 15–24. [Google Scholar] [CrossRef]
- Gensheng, L.; Zhonghou, S. Experimental study on pressure pulsation of self-resonating cavitating water jet. J. Univ. Pet. 1996, 5, 35–39. [Google Scholar]
- Li, G.S.; Shen, H.Z.; Zhou, C.S.; Zhang, D.B.; Yi, C. An experimental study on impact pressure characteristics of self-resonant cavitating jets. J. Hydrodyn. 2003, 18, 570–575. [Google Scholar]
- Li, D.; Kang, Y.; Wang, X.; Ding, X.L.; Fang, Z.L. Effects of nozzle inner surface roughness on the cavitation erosion characteristics of high speed submerged jets. Exp. Therm. Fluid Sci. 2016, 74, 444–452. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Ding, X.; Ding, X.L.; Wang, X.C.; Liu, W.C. Effects of feeding pipe diameter on the performance of a jet-driven Helmholtz oscillator generating pulsed waterjets. J. Mech. Sci. Technol. 2017, 31, 1203–1212. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z.; Yuan, M.; Fan, Q.; Wang, X.C. Effects of nozzle exit angle on the pressure characteristics of SRWJs used for deep-hole drilling. Appl. Sci. 2019, 9, 155. [Google Scholar] [CrossRef] [Green Version]
- Qi, M.; Wang, L.F.; Chen, Q.G.; Zhao, J.L.; Ju, Y.H.; Fu, Q.Q. Numerical simulation of cavitating jet in dual chamber self-oscillation pulse nozzle. J. Drain. Irrig. Mach. Eng. 2020, 38, 457–461. [Google Scholar]
- Yang, L.; Li, X.H.; Wang, J.S.; Lu, Y.Y. The natural frequency of self-oscillating pulsed jet with structural parameters effect of characteristics. Fluid Mach. 2001, 2, 26–28. [Google Scholar]
- Tang, C.L.; Hu, D.; Pei, J.H. Experimental research on dynamic characteristics of the self-excited oscillation pulsed water jet. Water Conserv. Hydropower Technol. 2006, 12, 71–74. [Google Scholar]
- Gao, C.C.; Xie, K.Y.; Liu, X.Y.; Hu, Y.Z.; Ma, W.L. Numerical simulation and experiment on flow fields in underwater self-excited pulse jet device. J. Drain. Irrig. Mach. Eng. 2016, 34, 220–226. [Google Scholar]
- Gao, C.C.; Hu, Y.Z.; Liu, X.Y.; Xie, K.Y.; Ma, W.L.; Wang, M.F. Experimental study on suction performance of underwater self-excited pulse jet self-excited oscillation cavitation jet nozzle. South North Water Transf. Water Conserv. Technol. 2016, 1, 109–113. [Google Scholar]
- Gao, C.C.; Hu, Y.W.; Li, H.; Ma, W.L. Statistical analysis of effects of structural parameters on characteristics of underwater self-excited pulse jet. J. Drain. Irrig. Mach. Eng. 2018, 36, 327–333. [Google Scholar]
- Li, W.; Zhang, W.Q.; Shi, W.D.; Yang, Y.F.; Cao, W.D. Experimental study on cavitation cloud evolution of self-excited oscillating cavitation jet nozzle. J. Drain. Irrig. Mach. Eng. 2020, 38, 547–552. [Google Scholar]
- Lu, Y.Y.; Zhang, S.; Liu, Y.; Lu, Z.H.; Jiang, L.Y. Analysis on stress wave effect during the process of rock breaking by pulsed jet. J. Chongqing Univ. 2012, 35, 117–124. [Google Scholar]
- Lu, Y.Y.; Ge, Z.L.; Li, X.H.; Shen, D.F.; Kang, Y.; Chen, J.F. Numerical analysis of cavitation development and collapse process. J. China Univ. Min. Technol. 2009, 4, 582–585. [Google Scholar]
- Li, X.H.; Zhao, Y.; Lu, Y.Y.; Kang, Y. Mechanism of self-excited oscillation jet to improve permeability of soft coal seam. J. Liaoning Tech. Univ. 2009, S1, 202–205. [Google Scholar]
- Li, D.; Kang, Y.; Ding, X.L.; Wang, X.C.; Fang, Z.L. Effects of Nozzle Inner Surface Roughness on the Performance of Self-resonating Cavitating Waterjets under Different Ambient Pressures. J. Mech. Eng. 2017, 63, 92–102. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).