A New Scheme of Adaptive Covariance Inflation for Ensemble Filtering Data Assimilation
Abstract
:1. Introduction
2. Methodology
2.1. EAKF Assimilation Method
2.2. Adaptive Inflation Algorithm
2.2.1. Basic Inflation Theory
2.2.2. The New Inflation Scheme
Prior Probability
Likelihood Function
Posterior Probability
Algorithm Implementation
- Without abandoning the Gaussian framework, the t distribution of the likelihood function and the distribution of the prior probabilities are used, assuming that their Gaussian distributions are available, and their product outputs are Gaussian priors when assimilating the next observation.
- The prior inflation factor is used before each variable assimilation step, and the posterior inflation factor is used after it.
- Localization is not considered in this paper, and since the state space and the observation space are consistent, .
- The rate parameter is calculated by the mean and variance of the prior inflation factor.
- The innovation statistic as well as its variance are calculated. Then, the ratio of the gamma function is calculated by the special method proposed in this paper to obtain the values of and .
- Finally, the quadratic equation containing , , and is solved to obtain the updated inflation factor . The new is the prior inflation factor when assimilating the next observation.
3. 5VCCM Experiments
3.1. The Model
3.2. Experiment Design
3.3. Result Analysis
3.3.1. Inflation Scheme Comparison
Imperfect Model
- Prior inflation scheme
- Posterior inflation scheme
Perfect Model
3.3.2. The Inflation Effect
4. MOCBM Experiments
4.1. The Model
4.2. The Build-Biased Model
4.3. Experimental Design
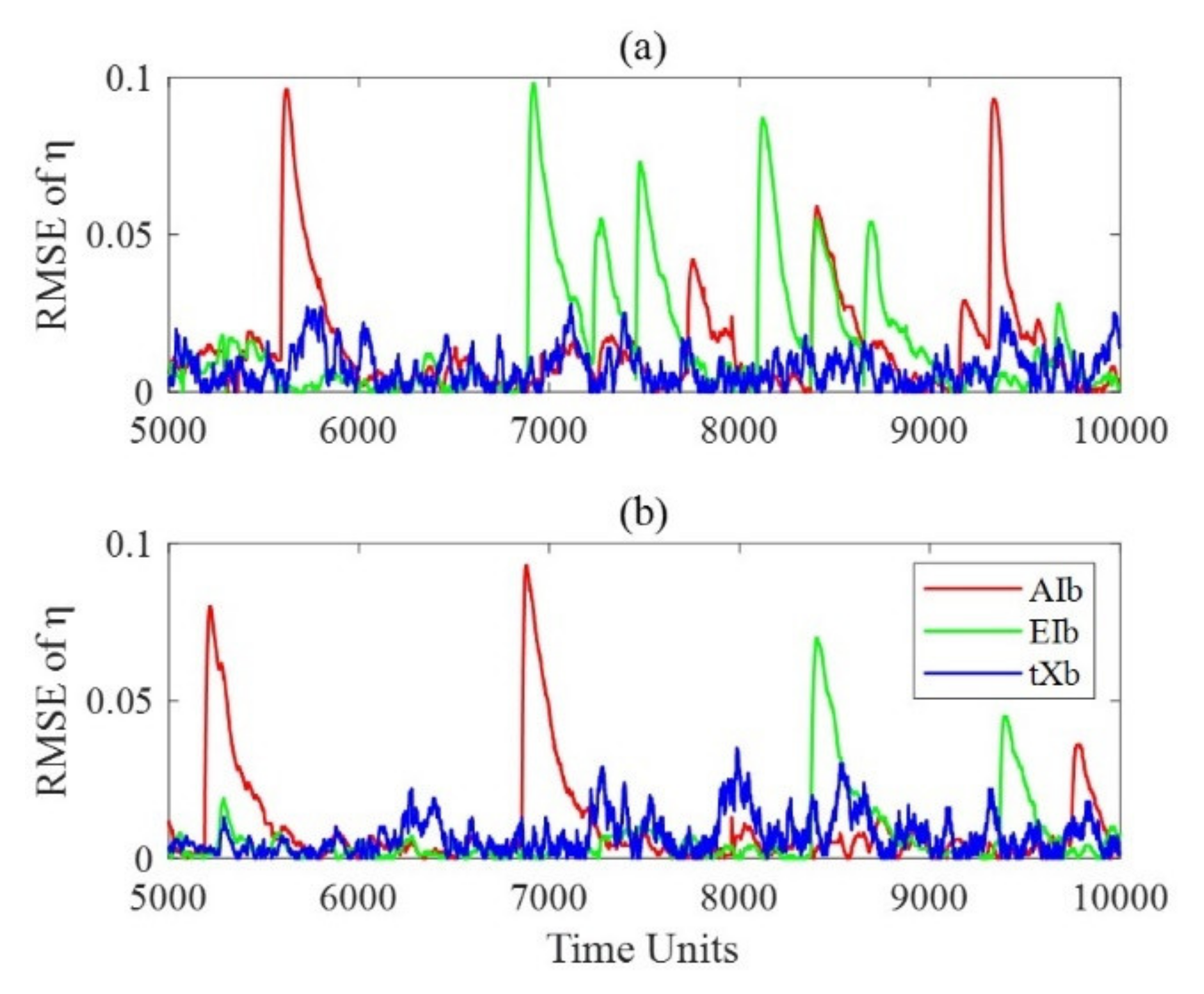
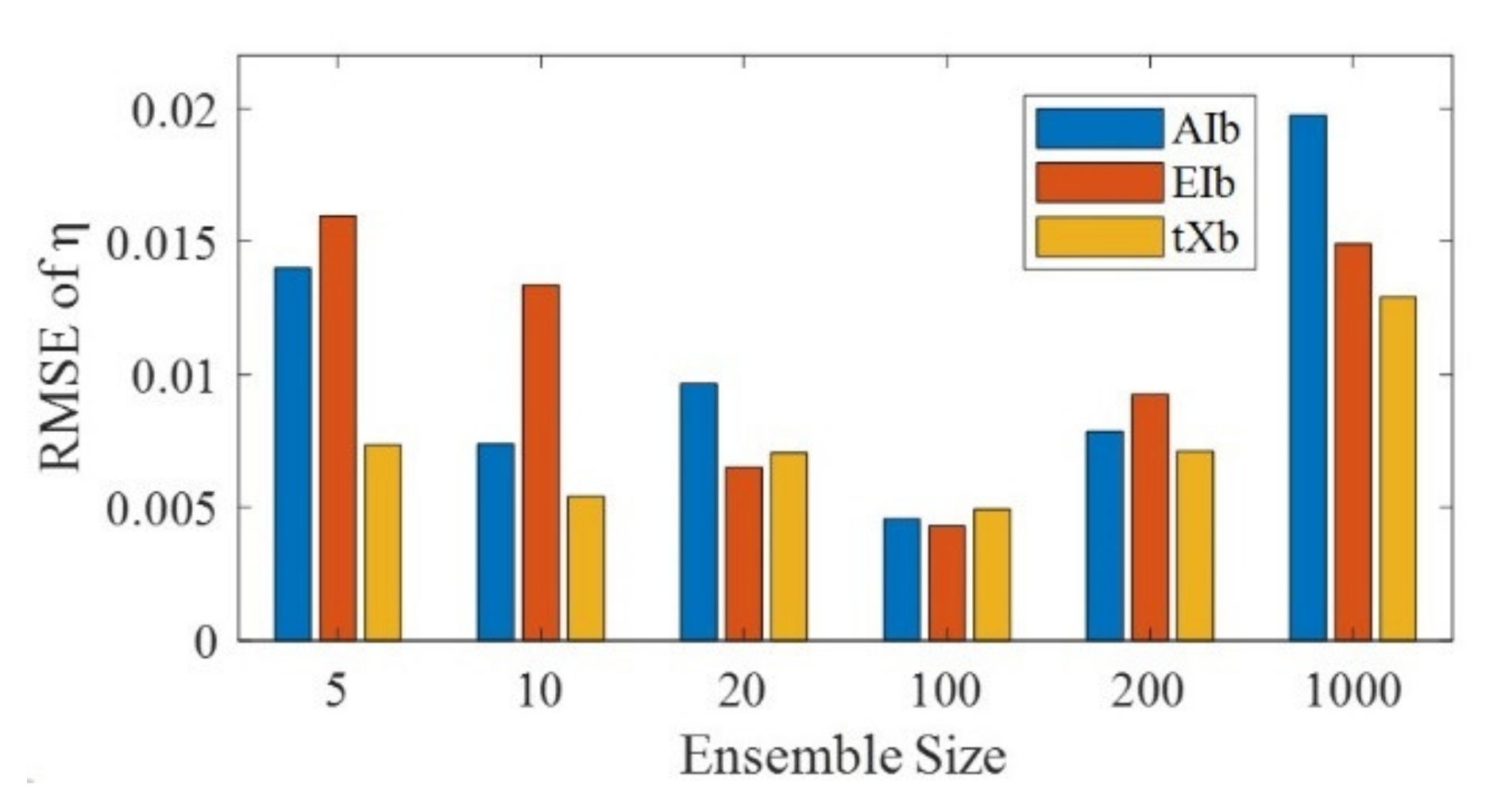
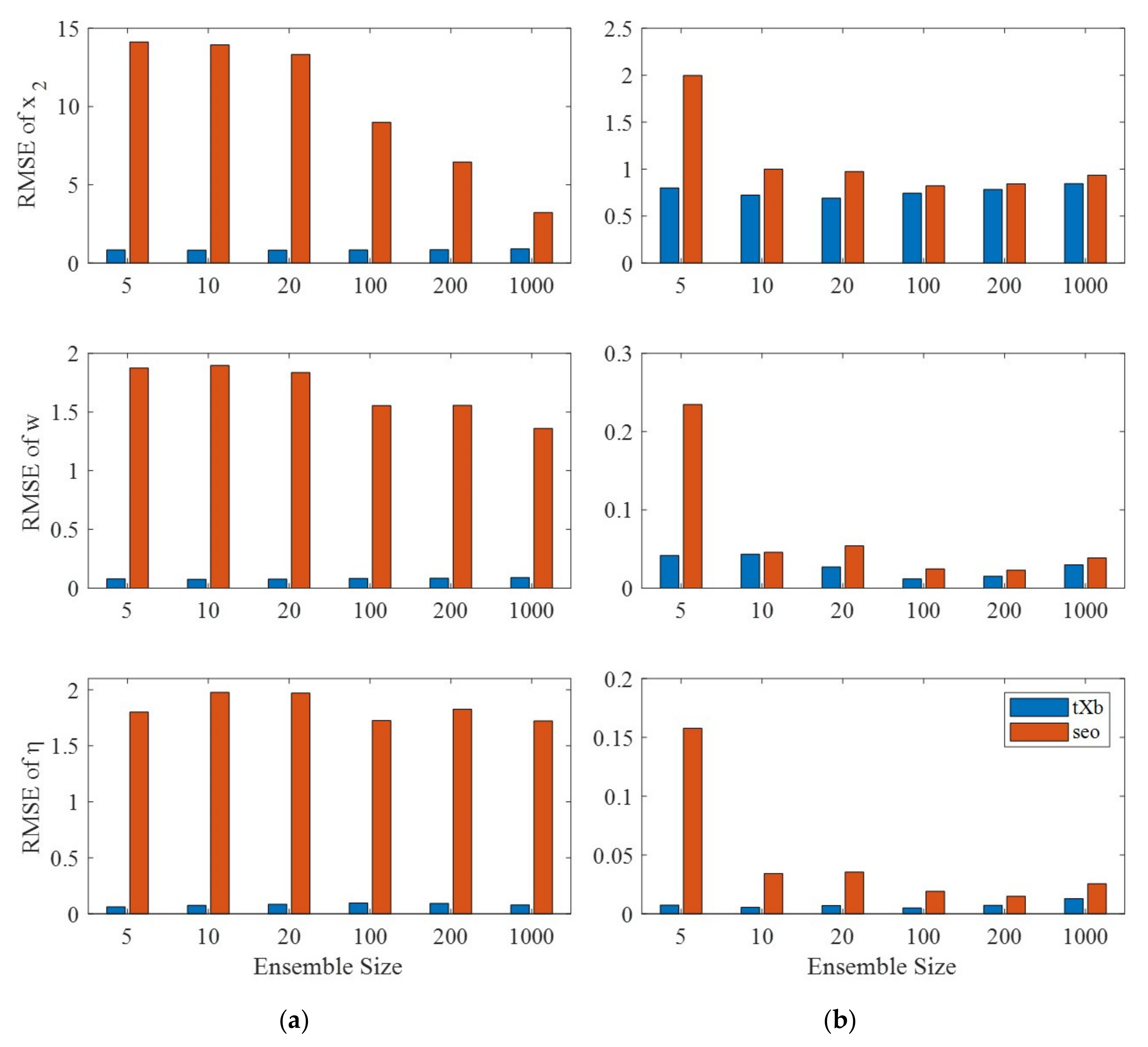
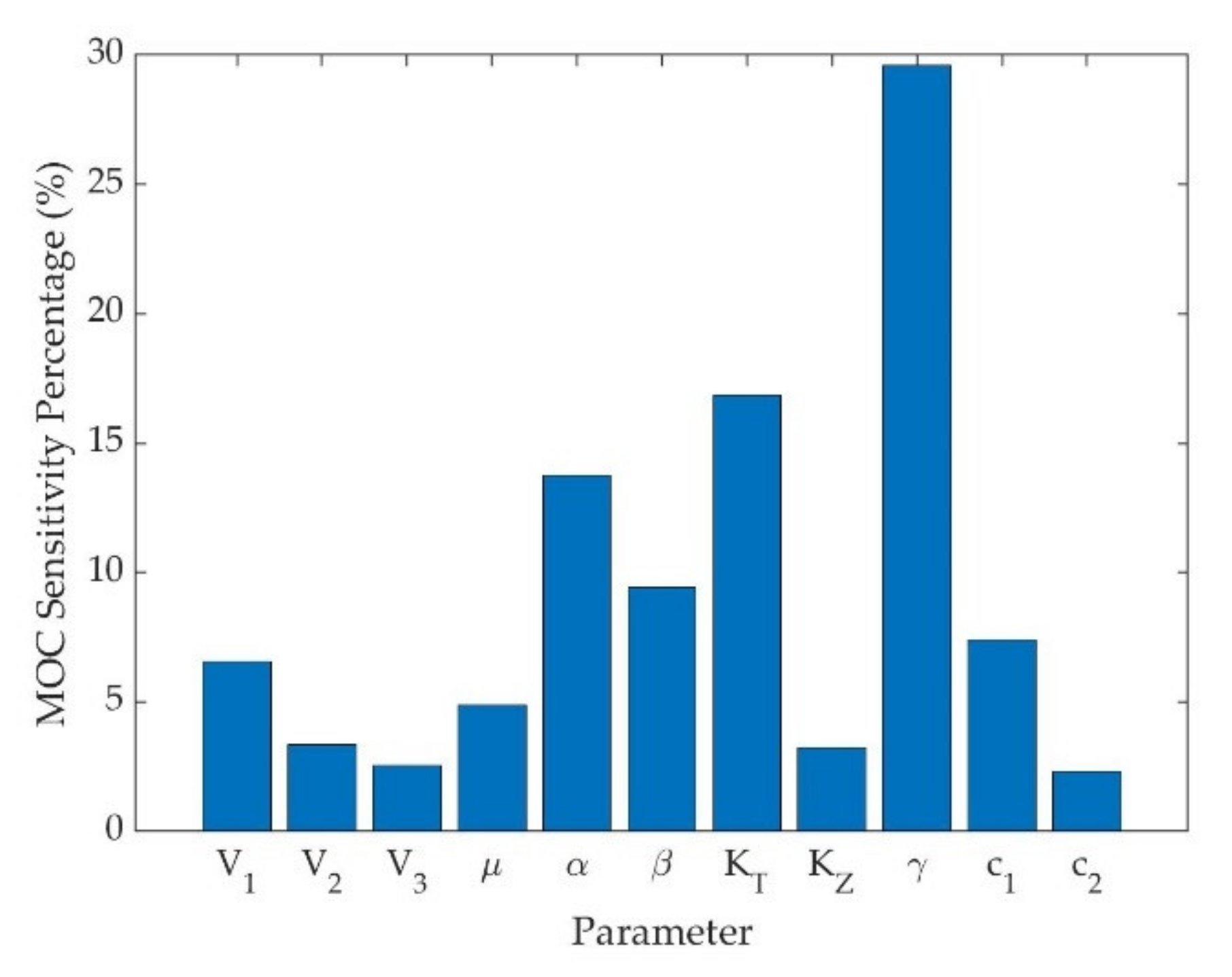
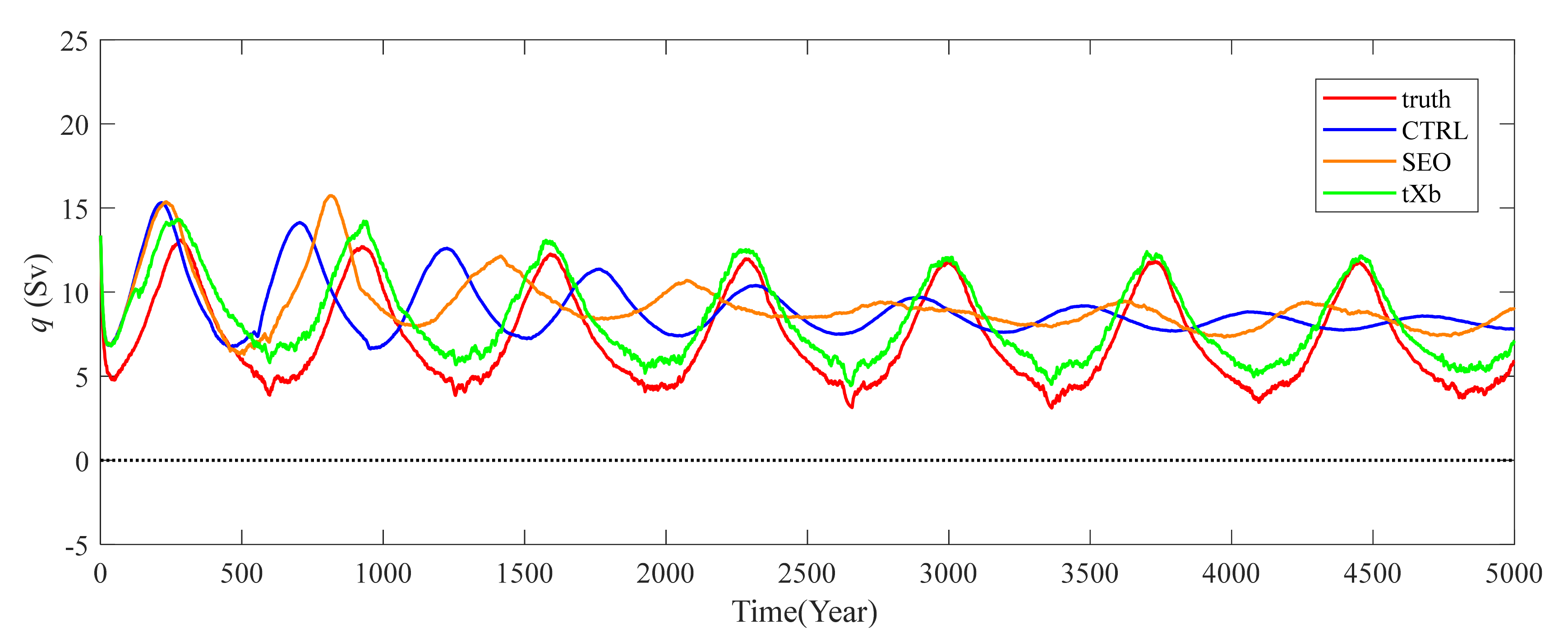
4.4. Result Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Definition |
|---|---|
| AIa | Adaptive posterior inflation |
| AIb | Adaptive prior inflation |
| CTRL | Control experiment |
| CGCM | Coupled general circulation model |
| EAKF | Ensemble adjustment Kalman filter |
| EIa | Enhanced posterior inflation |
| EIb | Enhanced prior inflation |
| EnKF | Ensemble Kalman filter |
| ETKF | Ensemble transform Kalman filter |
| MOCBM | North Atlantic meridional overturning circulation box model |
| RTPP | Relaxation-to-prior-perturbation |
| RTPS | Relaxation-to-prior-spread |
| SEO | State estimation only experiment |
| tXa | posterior inflation |
| tXb | prior inflation |
| 5VCCM | Five-variable coupled climate model |
Appendix B
References
- Daley, R. Atmospheric data analysis; Cambridge University Press: Cambridge, UK, 1991; p. 457. [Google Scholar]
- Kalnay, E. Atmospheric modeling, data assimilation, and predictability; Cambridge University Press: New York, NY, USA, 2003; p. 341. [Google Scholar]
- Zhang, S.; Liu, Z.; Rosati, A.; Delworth, T. A study of enhancive parameter correction with coupled data assimilation for climate estimation and prediction using a simple coupled model. Tellus A Dynamic Meteorol. Oceanogr. 2012, 64. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. Data assimilation: The ensemble Kalman filter, 2nd ed.; Springer: New York, NY, USA, 2009; p. 307. [Google Scholar]
- Anderson, J.L.; Anderson, S.L. A Monte Carlo Implementation of the Nonlinear Filtering Problem to Produce Ensemble Assimilations and Forecasts. Mon. Weather Rev. 1999, 127, 2741–2758. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Snyder, C. Distance-Dependent Filtering of Background Error Covariance Estimates in an Ensemble Kalman Filter. Mon. Weather Rev. 2001, 129, 2776–2790. [Google Scholar] [CrossRef] [Green Version]
- Pham, D.T.; Verron, J.; Roubaud, M.C. A singular evolutive extended Kalman filter for data assimilation in oceanography. J. Marine Syst. 1998, 16, 323–340. [Google Scholar] [CrossRef]
- Mitchell, H.L.; Houtekamer, P.L. An adaptive ensemble Kalman filter. Mon. Weather Rev. 2000, 128, 416–433. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Zheng, X.G.; Zhang, S.P.; Wu, G.C.; Dai, Y.J.; Li, Y. Maximum likelihood estimation of inflation factors on error covariance matrices for ensemble Kalman filter assimilation. Q. J. Roy. Meteor. Soc. 2012, 138, 263–273. [Google Scholar] [CrossRef]
- Anderson, J.L. An Ensemble Adjustment Kalman Filter for Data Assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef] [Green Version]
- Nerger, L. On Serial Observation Processing in Localized Ensemble Kalman Filters. Mon. Weather Rev. 2015, 143, 1554–1567. [Google Scholar] [CrossRef] [Green Version]
- Whitaker, J.S.; Hamill, T.M. Evaluating Methods to Account for System Errors in Ensemble Data Assimilation. Mon. Weather Rev. 2012, 140, 3078–3089. [Google Scholar] [CrossRef]
- Anderson, J.L. An adaptive covariance inflation error correction algorithm for ensemble filters. Tellus A Dynamic Meteorol. Oceanogr. 2007, 59, 210–224. [Google Scholar] [CrossRef]
- Anderson, J.L. Spatially and temporally varying adaptive covariance inflation for ensemble filters. Tellus A Dynamic Meteorol. Oceanogr. 2009, 61, 72–83. [Google Scholar] [CrossRef]
- Wang, X.; Bishop, C.H. A Comparison of Breeding and Ensemble Transform Kalman Filter Ensemble Forecast Schemes. J. Atmos. Sci. 2003, 60, 1140–1158. [Google Scholar] [CrossRef]
- Li, H.; Kalnay, E.; Miyoshi, T. Simultaneous estimation of covariance inflation and observation errors within an ensemble Kalman filter. Q. J. Roy. Meteor. Soc. 2009, 135, 523–533. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, T. The Gaussian Approach to Adaptive Covariance Inflation and Its Implementation with the Local Ensemble Transform Kalman Filter. Mon. Weather Rev. 2011, 139, 1519–1535. [Google Scholar] [CrossRef]
- Lien, G.; Miyoshi, T.; Kalnay, E. Assimilation of TRMM Multisatellite Precipitation Analysis with a Low-Resolution NCEP Global Forecast System. Mon. Weather Rev. 2016, 144, 643–661. [Google Scholar] [CrossRef]
- Miyoshi, T.; Kunii, M. Using AIRS retrievals in the WRF-LETKF system to improve regional numerical weather prediction. Tellus A Dynamic Meteorol. Oceanogr. 2012, 64. [Google Scholar] [CrossRef] [Green Version]
- Terasaki, K.; Sawada, M.; Miyoshi, T. Local Ensemble Transform Kalman Filter Experiments with the Nonhydrostatic Icosahedral Atmospheric Model NICAM. Sola 2015, 11, 23–26. [Google Scholar] [CrossRef] [Green Version]
- Yoshimura, K.; Miyoshi, T.; Kanamitsu, M. Observation system simulation experiments using water vapor isotope information. J. Geophys. Res. Atmos. 2014, 119, 7842–7862. [Google Scholar] [CrossRef]
- Zheng, X. An adaptive estimation of forecast error covariance parameters for Kalman filtering data assimilation. Adv. Atmos. Sci. 2009, 26, 154–160. [Google Scholar] [CrossRef]
- Zhang, F.; Snyder, C.; Sun, J. Impacts of Initial Estimate and Observation Availability on Convective-Scale Data Assimilation with an Ensemble Kalman Filter. Mon. Weather Rev. 2004, 132, 1238–1253. [Google Scholar] [CrossRef]
- Ying, Y.; Zhang, F. An adaptive covariance relaxation method for ensemble data assimilation. Q. J. Roy. Meteor. Soc. 2015, 141, 2898–2906. [Google Scholar] [CrossRef]
- Kotsuki, S.; Ota, Y.; Miyoshi, T. Adaptive covariance relaxation methods for ensemble data assimilation: Experiments in the real atmosphere. Q. J. Roy. Meteor. Soc. 2017, 143, 2001–2015. [Google Scholar] [CrossRef] [Green Version]
- Desroziers, G.; Berre, L.; Chapnik, B.; Poli, P. Diagnosis of observation, background and analysis-error statistics in observation space. Q. J. Roy. Meteor. Soc. 2005, 131, 3385–3396. [Google Scholar] [CrossRef]
- Brankart, J.M.; Cosme, E.; Testut, C.E.; Brasseur, P.; Verron, J. Efficient Adaptive Error Parameterizations for Square Root or Ensemble Kalman Filters: Application to the Control of Ocean Mesoscale Signals. Mon. Weather Rev. 2010, 138, 932–950. [Google Scholar] [CrossRef]
- El Gharamti, M. Enhanced Adaptive Inflation Algorithm for Ensemble Filters. Mon. Weather Rev. 2018, 146, 623–640. [Google Scholar] [CrossRef]
- El Gharamti, M.; Raeder, K.; Anderson, J.; Wang, X. Comparing Adaptive Prior and Posterior Inflation for Ensemble Filters Using an Atmospheric General Circulation Model. Mon. Weather Rev. 2019, 147, 2535–2553. [Google Scholar] [CrossRef]
- Raanes, P.N.; Bocquet, M.; Carrassi, A. Adaptive covariance inflation in the ensemble Kalman filter by Gaussian scale mixtures. Q. J. Roy. Meteor. Soc. 2019, 145, 53–75. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.L. A Local Least Squares Framework for Ensemble Filtering. Mon. Weather Rev. 2003, 131, 634–642. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Anderson, J.L. Impact of spatially and temporally varying estimates of error covariance on assimilation in a simple atmospheric model. Tellus A Dynamic Meteorol. Oceanogr. 2003, 55, 126–147. [Google Scholar] [CrossRef]
- Zhang, S.; Harrison, M.J.; Rosati, A.; Wittenberg, A. System design and evaluation of coupled ensemble data assimilation for global oceanic climate studies. Mon. Weather Rev. 2007, 135, 3541–3564. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S. A Study of Impacts of Coupled Model Initial Shocks and State–Parameter Optimization on Climate Predictions Using a Simple Pycnocline Prediction Model. J. Clim. 2011, 24, 6210–6226. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S. Impact of observation-optimized model parameters on decadal predictions: Simulation with a simple pycnocline prediction model. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Zhang, X.; Zhang, S.; Wu, X.; Liu, Z. Mitigation of coupled model biases induced by dynamical core misfitting through parameter optimization: Simulation with a simple pycnocline prediction model. Nonlinear Proc. Geoph. 2014, 21, 357–366. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Gnanadesikan, A. A Simple Predictive Model for the Structure of the Oceanic Pycnocline. Science 1999, 283, 2077–2079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asselin, R. Frequency Filter for Time Integrations. Mon. Weather Rev. 1972, 100, 487–490. [Google Scholar] [CrossRef]
- Robert, A. The integration of a spectral model of the atmosphere by the implicit method. In Proceedings of the WMO/IUGG Symposium on NWP, Japan Meteorological Society, Tokyo, Japan, 1969; pp. 19–24. [Google Scholar]
- Zhao, Y.; Deng, X.; Zhang, S.; Liu, Z.; Liu, C. Sensitivity determined simultaneous estimation of multiple parameters in coupled models: Part I—based on single model component sensitivities. Clim. Dynam. 2019, 53, 5349–5373. [Google Scholar] [CrossRef]
- Roebber, P.J. Climate variability in a low-order coupled atmosphere-ocean model. Tellus A 1995, 47, 473–494. [Google Scholar] [CrossRef]
- Tardif, R.; Hakim, G.J.; Snyder, C. Coupled atmosphere-ocean data assimilation experiments with a low-order climate model. Clim. Dynam. 2014, 43, 1631–1643. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Irregularity: A fundamental property of the atmosphere. Tellus A 1984, 36A, 98–110. [Google Scholar] [CrossRef]
- Lorenz, E.N. Can chaos and intransitivity lead to interannual variability? Tellus A 1990, 42, 378–389. [Google Scholar] [CrossRef]
- Stommel, H. Thermohaline Convection with Two Stable Regimes of Flow. Tellus B 1961, 13, 224–230. [Google Scholar] [CrossRef]
- Stone, P.H.; Yao, M. Development of a Two-Dimensional Zonally Averaged Statistical-Dynamical Model. Part III: The Parameterization of the Eddy Fluxes of Heat and Moisture. J. Clim. 1990, 3, 726–740. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, S.; Shen, Y.; Guan, Y.; Deng, X. A Study of Capturing AMOC Regime Transition through Observation-Constrained Model Parameters. Nonlinear Proc. Geoph. 2021, 5, 1–29. [Google Scholar] [CrossRef]
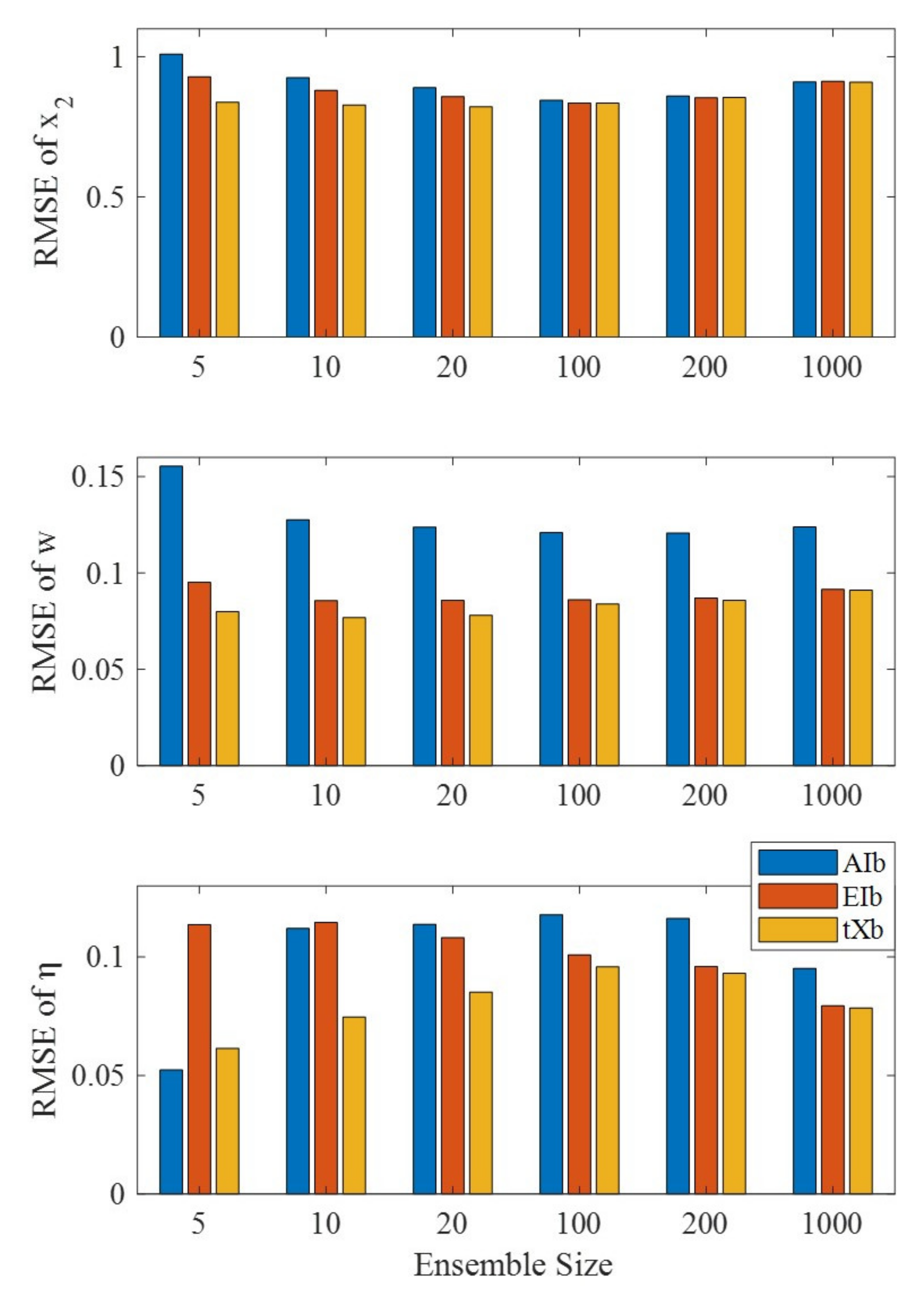
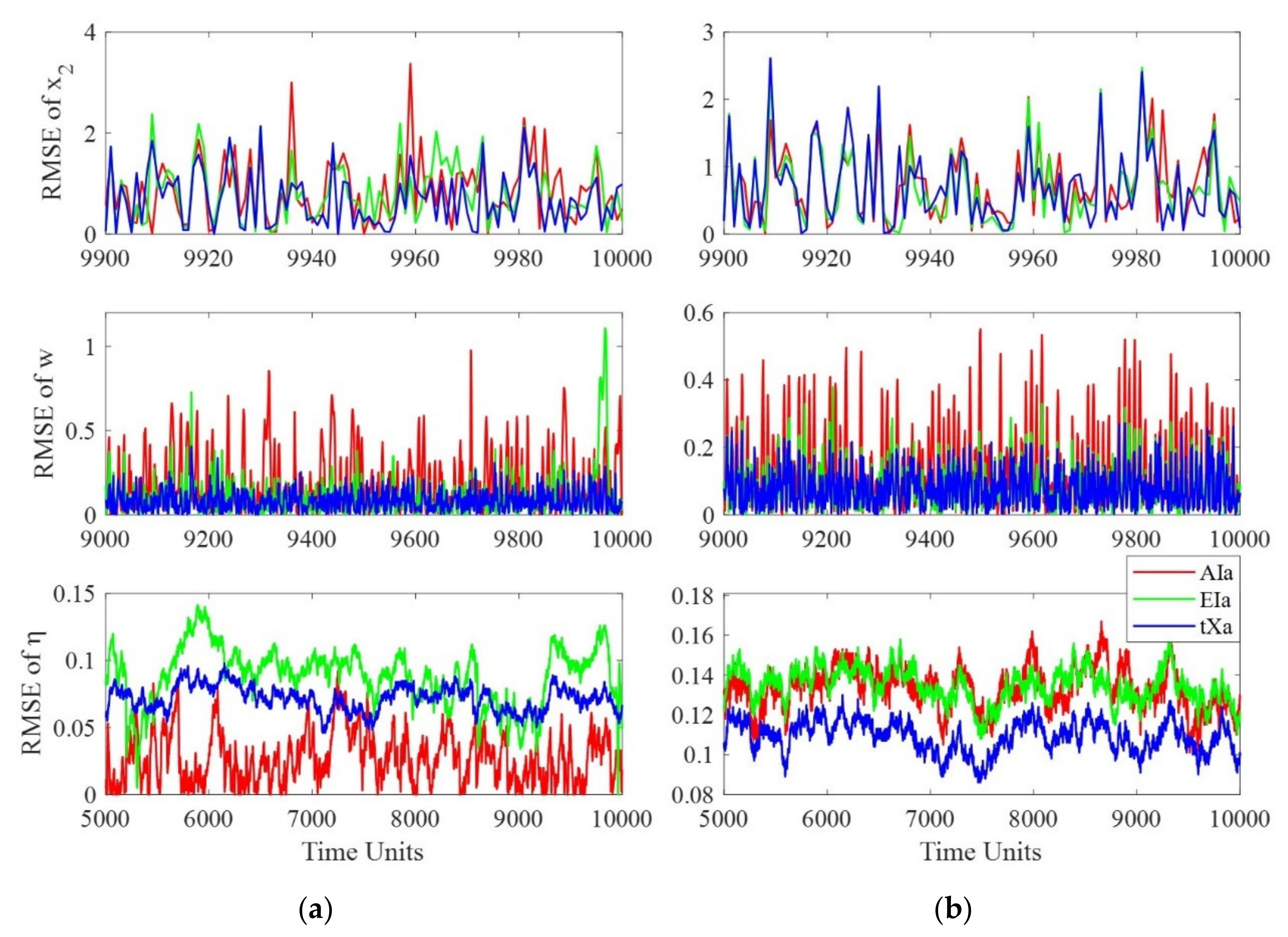
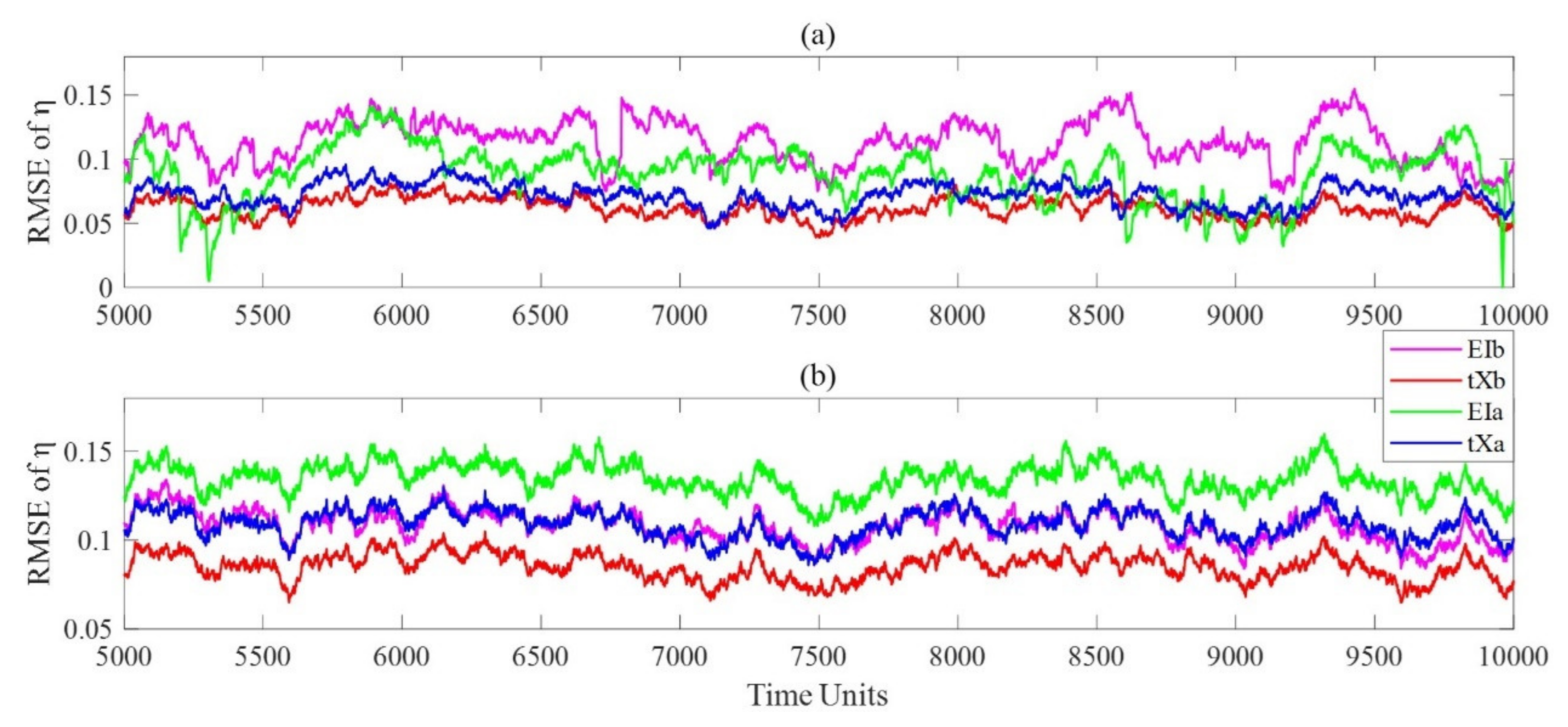
| Ensemble Size | AIb | EIb | tXb |
|---|---|---|---|
| 5 | 1.6875 s | 1.9531 s | 1.9218 s |
| 20 | 5.2031 s | 5.4218 s | 5.4531 s |
| 100 | 23.4531 s | 23.6875 s | 23.9218 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, A.; Zhang, L.; Zhang, X.; Zhang, S.; Liu, Z.; Liu, C.; Zhang, A. A New Scheme of Adaptive Covariance Inflation for Ensemble Filtering Data Assimilation. J. Mar. Sci. Eng. 2021, 9, 1054. https://doi.org/10.3390/jmse9101054
Su A, Zhang L, Zhang X, Zhang S, Liu Z, Liu C, Zhang A. A New Scheme of Adaptive Covariance Inflation for Ensemble Filtering Data Assimilation. Journal of Marine Science and Engineering. 2021; 9(10):1054. https://doi.org/10.3390/jmse9101054
Chicago/Turabian StyleSu, Ang, Liang Zhang, Xuefeng Zhang, Shaoqing Zhang, Zhao Liu, Caili Liu, and Anmin Zhang. 2021. "A New Scheme of Adaptive Covariance Inflation for Ensemble Filtering Data Assimilation" Journal of Marine Science and Engineering 9, no. 10: 1054. https://doi.org/10.3390/jmse9101054
APA StyleSu, A., Zhang, L., Zhang, X., Zhang, S., Liu, Z., Liu, C., & Zhang, A. (2021). A New Scheme of Adaptive Covariance Inflation for Ensemble Filtering Data Assimilation. Journal of Marine Science and Engineering, 9(10), 1054. https://doi.org/10.3390/jmse9101054







