Development of Depth-Limited Wave Boundary Layers over a Smooth Bottom
Abstract
1. Introduction
2. Theoretical Considerations
2.1. Criterion Modified from the Rough-Turbulent Formula by Tanaka
2.2. Criterion Modified from the Rough-Turbulent Formula by Kajiura
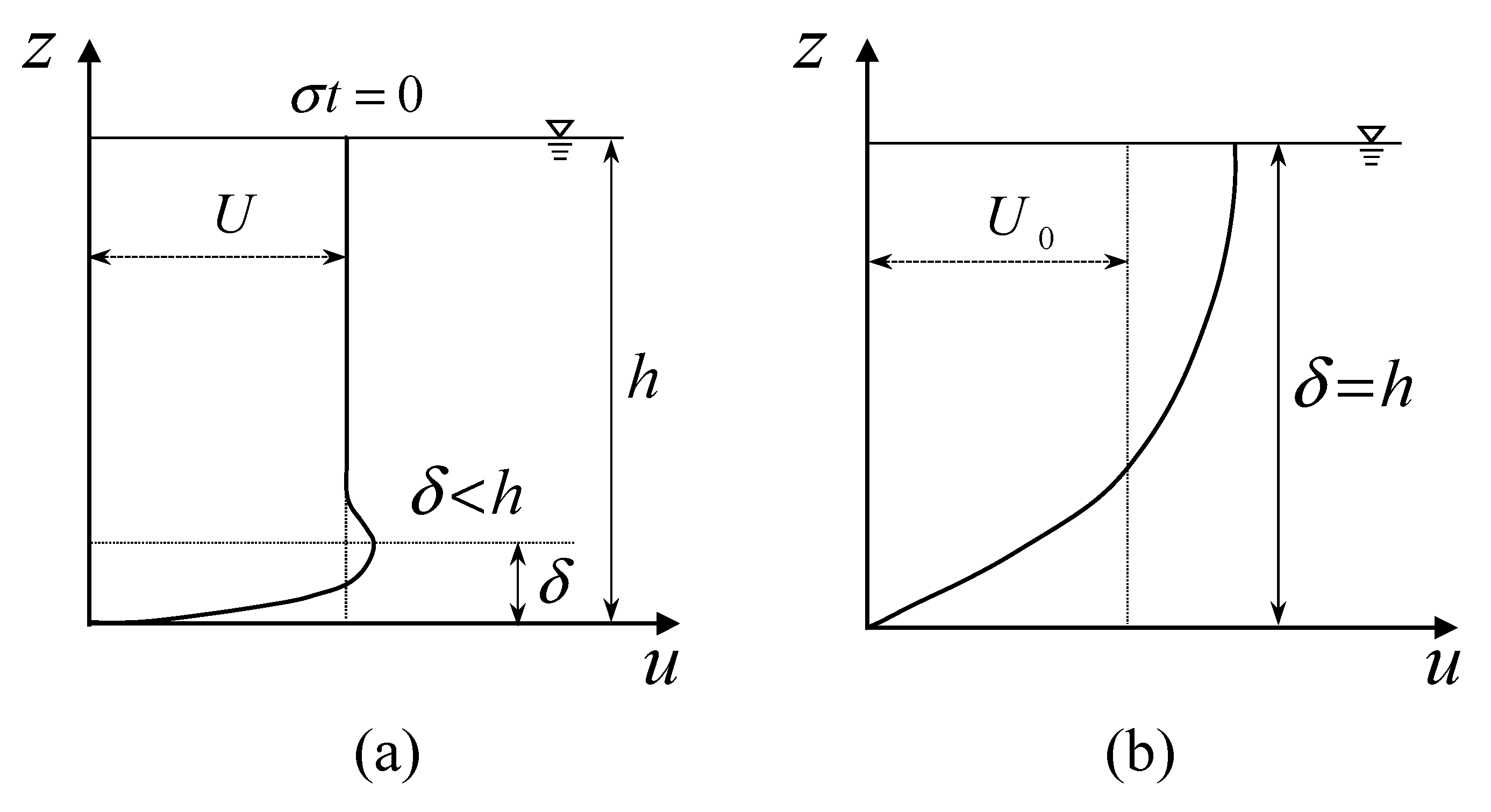
2.3. Criterion in Terms of Boundary Layer Thickness
2.4. Criterion in Terms of Friction Factor
3. Data Collection and Numerical Analysis Using the k-ω Model
3.1. Data Collection
3.2. Numerical Analysis Using a Turbulence Model
4. Results and Discussion
4.1. Numerical Results Using the k-ω Model
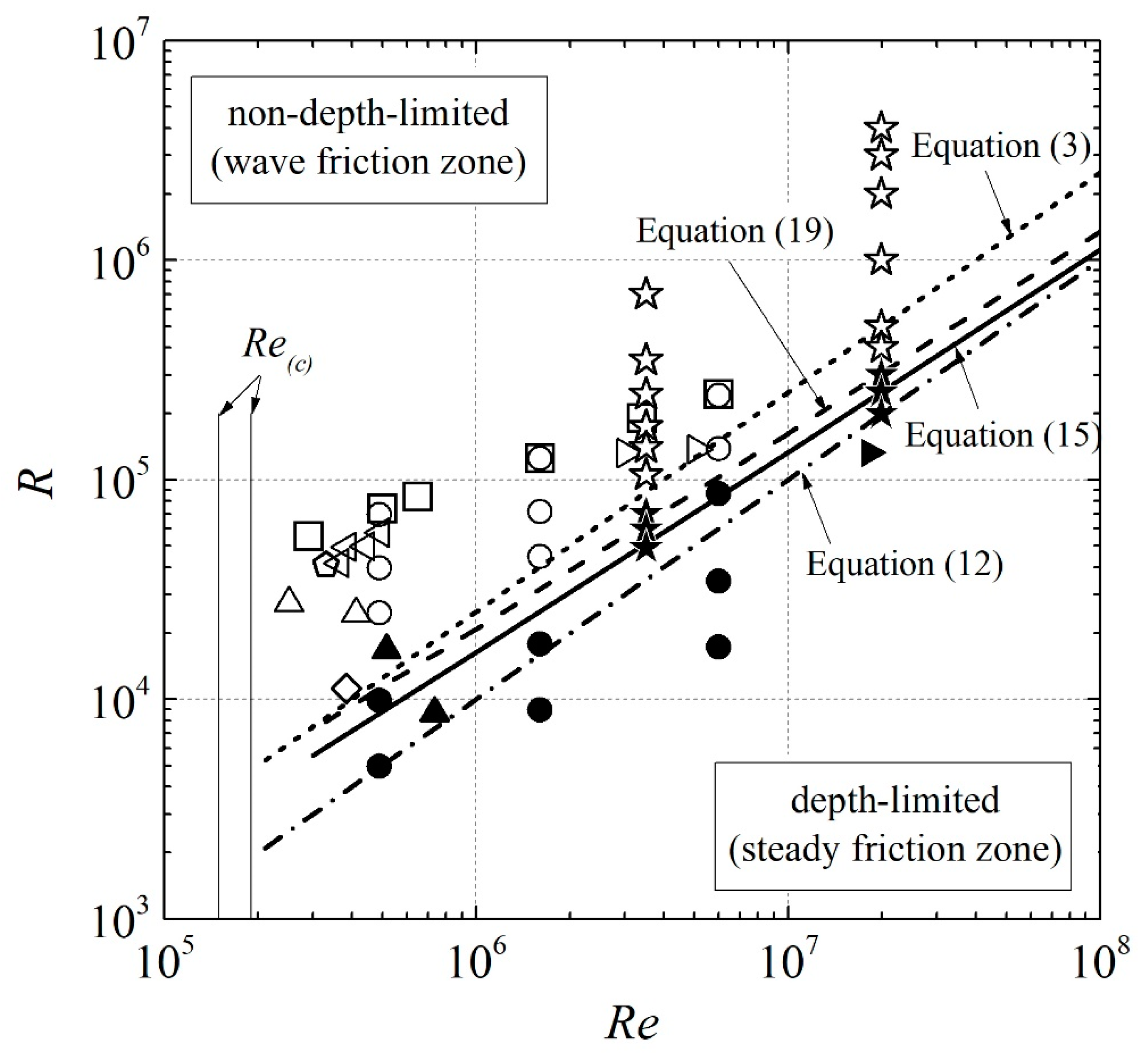
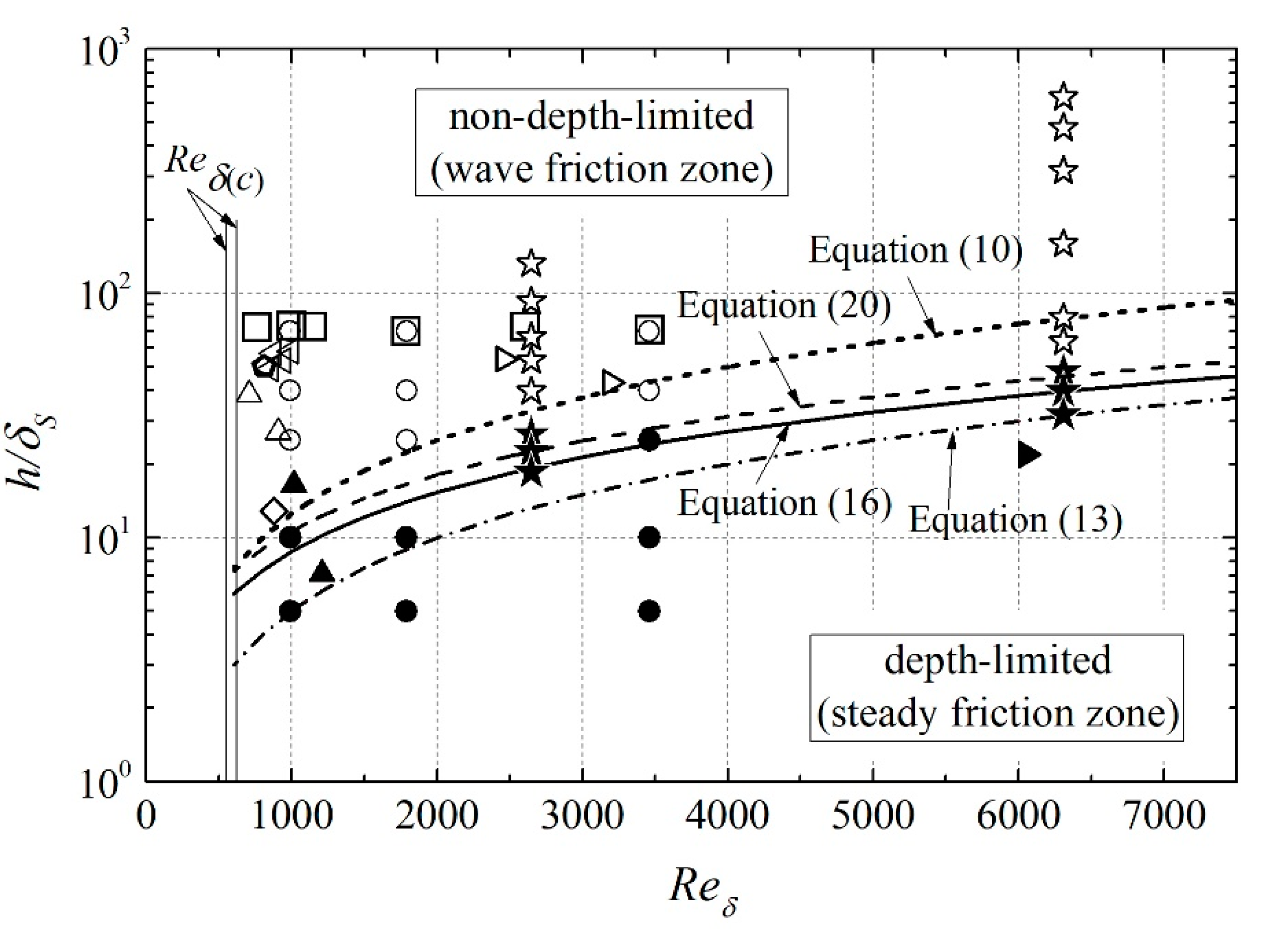
4.2. Validation of Proposed Criteria by Using the Collected Data and k-ω Model Computations
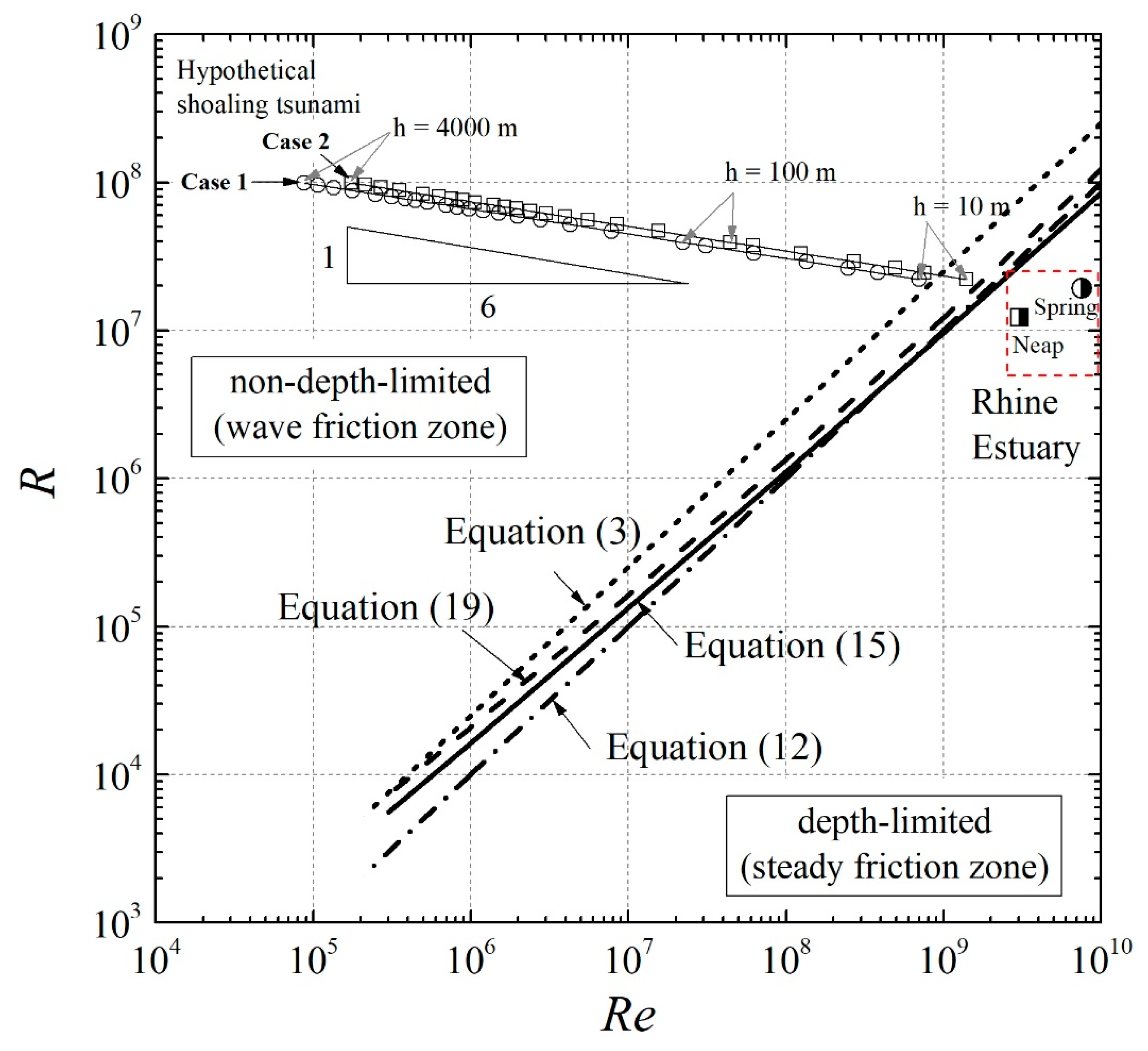
4.3. Application to the Rhine Estuary
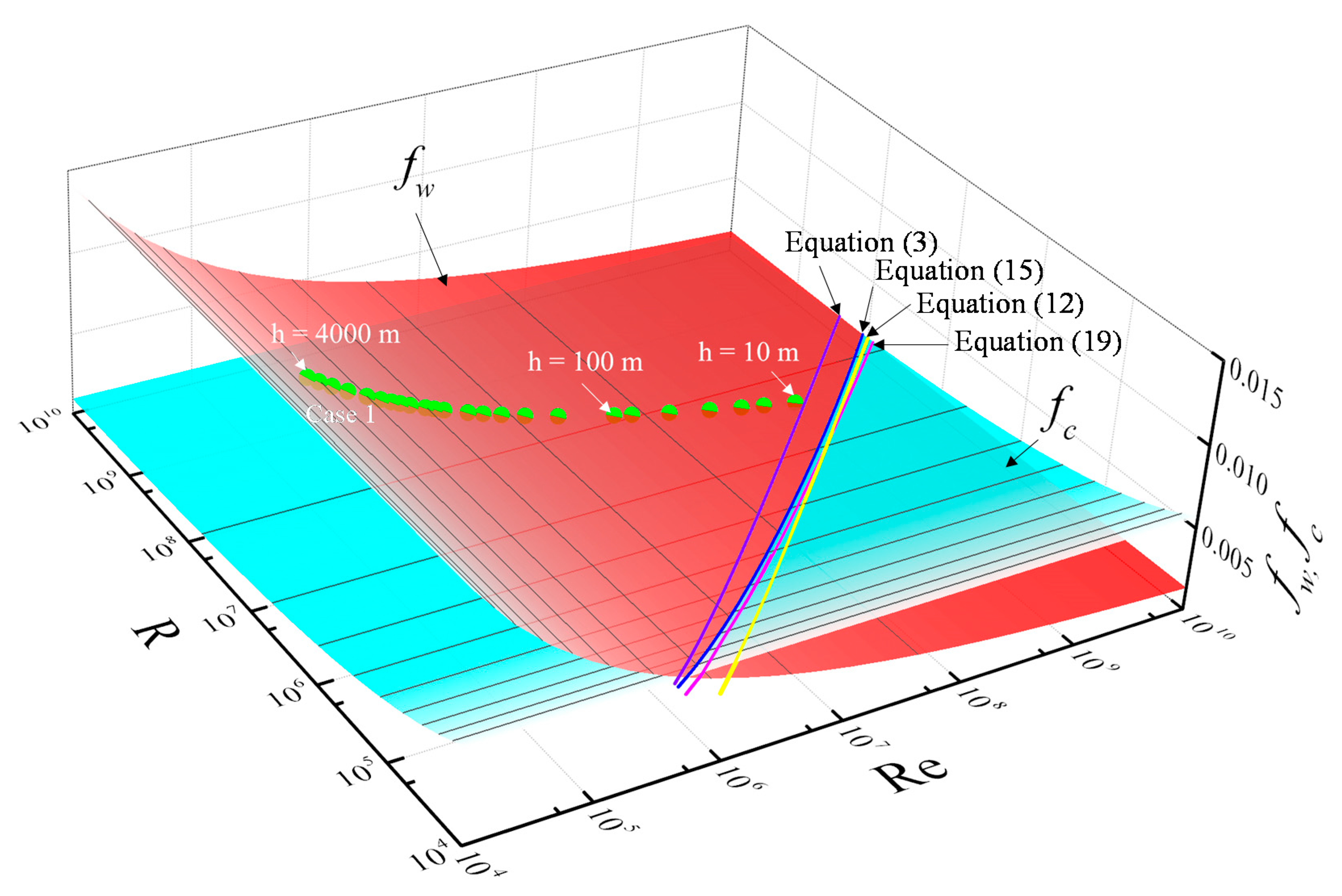
4.4. Demarcation in Terms of and
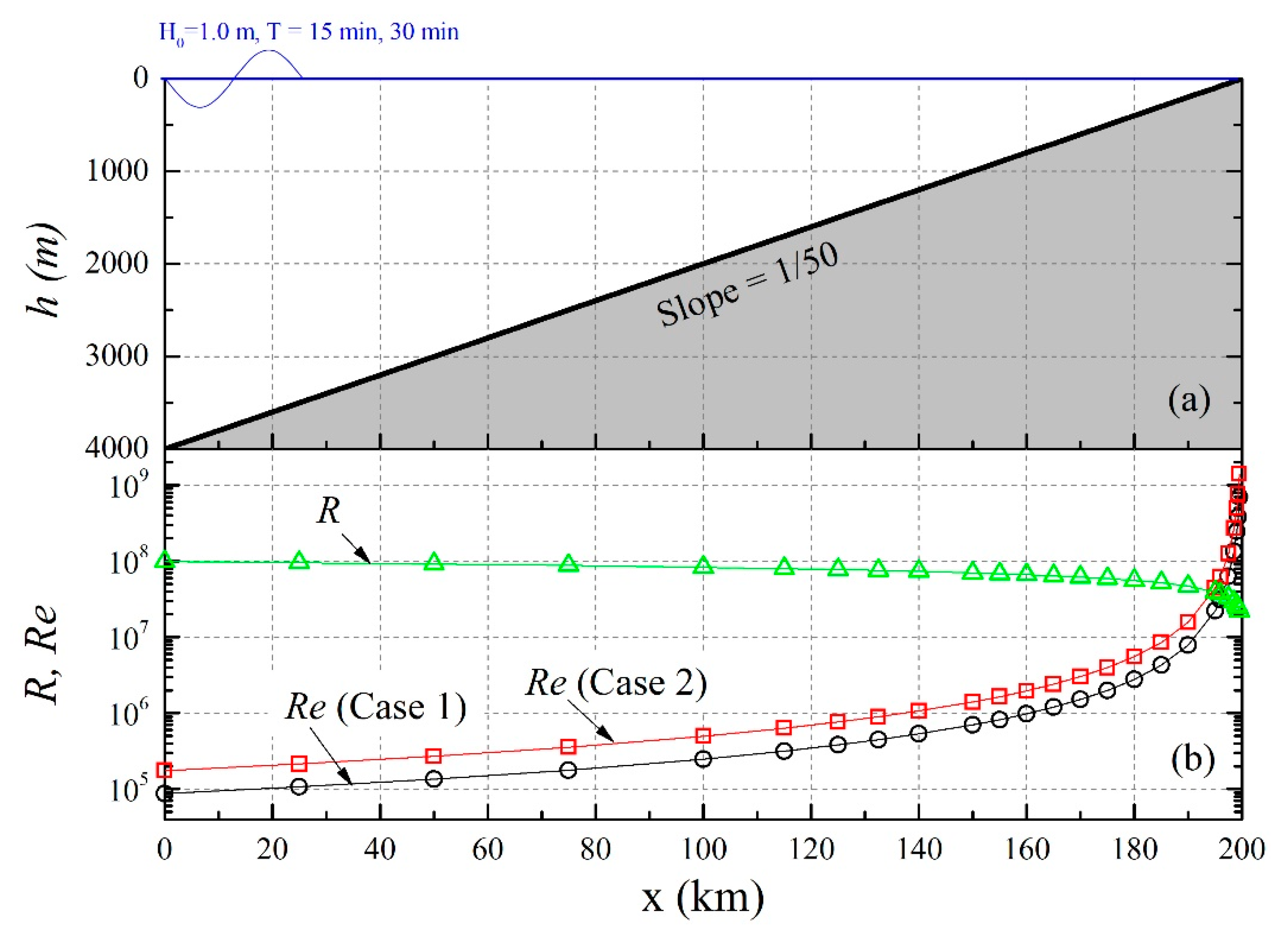
4.5. Application to a Hypothetical Shoaling Tsunami
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schlichting, H. Boundary Layer Theory, 9th ed.; Springer: Berlin/Heidelberg, Germany, 1979; 805p. [Google Scholar]
- Jonsson, I.G. Measurements in the turbulent wave boundary layer. In Proceedings of the 10th IAHR Congress, London, UK, 1–5 September 1963; pp. 85–92. [Google Scholar]
- Carstens, M.R.; Neilson, F.M. Evolution of a duned bed under oscillatory flow. J. Geophys. Res. 1967, 72, 3053–3059. [Google Scholar] [CrossRef]
- Chan, K.W.; Baird, M.H.I.; Round, G.F. Behavior of beds of dense particles in a horizontally oscillating liquid. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 330, 537–559. [Google Scholar]
- Lofquist, K.E.B. An Effect of Permeability on Sand Transport by Waves; CERC TM-62. U. S. Army Corps of Engineers; Coastal Engineering Research Center: Vicksburg, MS, USA, 1975; 74p. [Google Scholar]
- Hulsbergen, C.H.; Bosman, J.J. A closely responding, versatile wave tunnel. In Proceedings of the 17th Coastal Engineers Conference, Sydney, Australia, 23–28 March 1980; ASCE: New York, NY, USA, 1980; pp. 310–317. [Google Scholar]
- Horikawa, K.; Watanabe, A.; Katori, S. Sediment transport under sheet flow condition. In Proceedings of the 18th Coastal Engineers Conference, Cape Town, South Africa, 14–19 November 1982; ASCE: New York, NY, USA, 1982; pp. 1335–1352. [Google Scholar]
- King, D.B.; Powell, J.D.; Seymour, R.J. A new oscillatory flow tunnel for use in sediment transport experiments. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 1559–1570. [Google Scholar]
- Gonzalez-Rodriguez, D.; Madsen, O.S. Boundary-layer hydrodynamics and bedload sediment transport in oscillating water tunnels. J. Fluid Mech. 2011, 667, 48–84. [Google Scholar] [CrossRef][Green Version]
- Van der A, D.A.; O’Donoghue, T.; Davies, A.G.; Ribberink, J.S. Experimental study of the turbulent boundary layer in acceleration-skewed oscillatory flow. J. Fluid Mech. 2011, 684, 251–283. [Google Scholar] [CrossRef]
- Dedow, H.R.A. A pulsating water tunnel for research in reversing flow. Houille Blanche 1966, 7, 837–841. [Google Scholar] [CrossRef]
- Riedel, H.P.; Kamphuis, J.W.; Brebner, A. Measurement of bed shear stress under waves. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; ASCE: New York, NY, USA, 1972; pp. 587–603. [Google Scholar]
- Jonsson, I.G. Wave boundary layers and friction factors. In Proceedings of the 10th International Conference on Engineers Conference, Tokyo, Japan, 5–8 September 1966; ASCE: New York, NY, USA, 1966; pp. 127–148. [Google Scholar]
- Jonsson, I.G. A new approach to oscillatory rough turbulent boundary layers. Ocean Eng. 1980, 7, 109–152. [Google Scholar] [CrossRef]
- Sleath, J.F.L. Turbulent oscillatory flow over rough beds. J. Fluid Mech. 1987, 82, 369–409. [Google Scholar] [CrossRef]
- Jensen, B.L.; Sumer, B.M.; Fredsøe, J. Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 1989, 206, 265–297. [Google Scholar] [CrossRef]
- Yuan, J.; Madsen, O.S. Experimental study of turbulent oscillatory boundary layers in an oscillating water tunnel. Coast. Eng. 2014, 89, 63–84. [Google Scholar] [CrossRef]
- Tinh, N.X.; Tanaka, H. Study on boundary layer development and bottom shear stress beneath a tsunami. Coast. Eng. J. 2019, 61, 574–589. [Google Scholar] [CrossRef]
- Lacy, J.R.; Rubin, D.M.; Buscombe, D. Currents, drag, and sediment transport induced by a tsunami. J. Geophys. Res. 2012, 117, C9. [Google Scholar] [CrossRef]
- Sana, A.; Tanaka, H. Full-range equation for wave boundary layer thickness. Coast. Eng. 2007, 54, 639–642. [Google Scholar] [CrossRef]
- Sana, A.; Tanaka, H. Corrigendum to “Full-range equation for wave boundary layer thickness” [Coast. Eng. 54 (2007) 639–642]. Coast. Eng. 2019, 152, 103516. [Google Scholar] [CrossRef]
- Tanaka, H.; Tinh, N.X.; Sana, A. Transitional behavior of flow regime in shoaling tsunami boundary layers. J. Mar. Sci. Eng. 2020, 8, 700. [Google Scholar] [CrossRef]
- Tanaka, H.; Tinh, N.X.; Sana, A. Improvement of the full-range equation for wave boundary layer thickness. J. Mar. Sci. Eng. 2020, 8, 573. [Google Scholar] [CrossRef]
- Yalin, M.S.; Russell, R.C.H. Shear stresses due to long waves. J. Hyd. Res. 1966, 4, 55–98. [Google Scholar] [CrossRef]
- Knight, D.W.; Ridgway, M.A. Velocity distributions in unsteady open channel flow with different boundary roughness. In Proceedings of the 17th of IAHR Congress, Baden, Germany, 15–19 August 1977; pp. 437–444. [Google Scholar]
- Chen, D.; Chen, C.; Tang, F.E.; Stansby, P.; Li, M. Boundary layer structure of oscillatory open-channel shallow flows over smooth and rough beds. Exp. Fluids 2007, 42, 719–736. [Google Scholar] [CrossRef]
- Larsen, B.E.; Arbøll, L.K.; Kristoffersen, S.F.; Carstensen, S.; Fuhrman, D.R. Experimental study of tsunami-induced scour around a monopile foundation. Coast. Eng. 2018, 138, 9–21. [Google Scholar] [CrossRef]
- Celik, I.; Rodi, W. Calculation of wave-induced turbulent flows in estuaries. Ocean Eng. 1985, 12, 531–542. [Google Scholar] [CrossRef]
- Johns, B. On the vertical structure of tidal flow in river estuaries. Geophys. J. R. Astr. Soc. 1966, 12, 103–110. [Google Scholar] [CrossRef]
- Li, M.; Sanford, L.; Chao, S.Y. Effects of time dependence in unstratified tidal boundary layers: Results from large eddy simulations. Estuar. Coast. Shelf Sci. 2005, 62, 193–204. [Google Scholar] [CrossRef]
- Williams, I.A.; Fuhrman, D.R. Numerical simulation of tsunami-scale wave boundary layers. Coast. Eng. 2016, 110, 17–31. [Google Scholar] [CrossRef]
- Kaptein, S.J.; Duran-Matute, M.; Roman, F.; Armenio, V.; Clercx, H.J.H. Effect of the water depth on oscillatory flows over a flat plate: From the intermittent towards the fully turbulent regime. Environ. Fluid Mech. 2019, 19, 1167–1184. [Google Scholar] [CrossRef]
- Tanaka, H.; Sana, A.; Kawamura, I.; Yamaji, H. Depth-limited oscillatory boundary layers on a rough bottom. Coast. Eng. Jap. 1999, 41, 85–105. [Google Scholar] [CrossRef]
- Kajiura, K. On the bottom friction in an oscillatory current. Bull. Earthq. Res. Inst. 1964, 42, 147–174. [Google Scholar]
- Tanaka, H. An explicit expression of friction coefficient for a wave-current coexistent motion. Coast. Eng. Jpn. 1992, 35, 83–91. [Google Scholar] [CrossRef]
- Tanaka, H.; Thu, A. Full-range equation of friction coefficient and phase difference in a wave-current boundary layer. Coast. Eng. 1994, 22, 237–254. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. Full-scale CFD simulation of tsunamis. Part 2: Boundary layers and bed shear stresses. Coast. Eng. 2019, 151, 42–57. [Google Scholar] [CrossRef]
- Hayashi, T.; Ohashi, M. A dynamical and visual study on the oscillatory turbulent boundary layer. In Turbulent Shear Flows 3; Springer: Berlin/Heidelberg, Germany, 1982; pp. 18–33. [Google Scholar]
- Hino, M.; Kashiwayanagi, M.; Nakayama, A.; Hara, T. Experiments on the turbulence characteristics and the structure of a reciprocating flow. J. Fluid Mech. 1983, 131, 363–400. [Google Scholar] [CrossRef]
- Sawamoto, M.; Sato, E. The structure of oscillatory turbulent boundary layer over rough bed. Coast. Eng. Jpn. 1991, 34, 1–14. [Google Scholar] [CrossRef]
- Proudman, J. Dynamical Oceanography; Methuen: London, UK, 1953; 409p. [Google Scholar]
- Bakker, W.T. Sand concentration in an oscillatory flow. In Proceedings of the 14th International Conference on Coastal Engineering, Copenhagen, Denmark, 24–28 June 1974; ASCE: New York, NY, USA, 1974; pp. 1129–1148. [Google Scholar]
- Sheng, Y.P. A turbulent transport model of coastal processes. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 2380–2396. [Google Scholar]
- Brørs, B.; Eidsvik, K.J. Oscillatory boundary layer flows modelled with dynamic Reynolds stress turbulence closure. Cont. Shelf Res. 1994, 14, 1455–1475. [Google Scholar] [CrossRef]
- Hanjalić, K.; Jakirlić, S.; Hadžić, I. Computation of oscillating turbulent flows at transitional Re-numbers. In Turbulent Shear Flows 9; Durst, F., Kasagi, N., Launder, B.E., Schmidt, F.W., Suzuki, K., Whitelaw, J.W., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 323–342. [Google Scholar]
- Justesen, P.; Fredsøe, J. Distribution of turbulence and suspended sediment in the wave boundary layer. Prog. Rep. 1985, 62, 61–67. [Google Scholar]
- Tanaka, H.; Sana, A. Numerical Study on Transition to Turbulence in a Wave Boundary Layer. In Sediment Transport Mechanisms in Coastal Environments and Rivers; World Scientific: Singapore, 1994; pp. 14–25. [Google Scholar]
- Foti, E.; Scandura, P. A low Reynolds number k–ε model validated for oscillatory flows over smooth and rough wall. Coast. Eng. 2004, 51, 173–184. [Google Scholar] [CrossRef]
- Sana, A.; Tanaka, H. Review of k-ε model to analyze oscillatory boundary layers. J. Hydr. Eng. 2000, 126, 701–710. [Google Scholar] [CrossRef]
- Tanaka, H. Turbulence structure and bed friction under waves and current interacted motion. In Proceedings of the 3rd International Symposium on River Sedimentation, Jackson, MS, USA, 31 March–4 April 1986; University of Mississippi: Oxford, MS, USA, 1986; pp. 334–343. [Google Scholar]
- Justesen, P. Prediction of turbulent oscillatory flow over rough beds. Coast. Eng. 1988, 12, 257–284. [Google Scholar] [CrossRef]
- Sana, A.; Ghumman, A.R.; Tanaka, H. Modeling of a rough-wall oscillatory boundary layer using two-equation turbulence models. J. Hydr. Eng. 2009, 135, 60–65. [Google Scholar] [CrossRef]
- Spalart, P.R.; Baldwin, B.S. Direct Simulation of a Turbulent Oscillating Boundary Layer; NASA Tech. Memorandum 89460; Ames Research Center: Moffett Field, CA, USA, 1987.
- Vittori, G.; Verzicco, R. Direct simulation of transition in an oscillatory boundary layer. J. Fluid Mech. 1998, 371, 207–232. [Google Scholar] [CrossRef]
- Sumer, M.B.; Fuhrman, D.R. Turbulence in Coastal and Civil Engineering; World Scientific: Singapore, 2020; 758p. [Google Scholar]
- Tanaka, H.; Tinh, N.X. Numerical study on sea bottom boundary layer and bed shear stress under tsunami. In Proceedings of the 29th International Ocean and Polar Engineering Conference (ISOPE), Honolulu, HI, USA, 16–21 June 2019; pp. 3189–3195. [Google Scholar]
- Tanaka, H.; Shuto, N. Friction laws and flow regimes under wave and current motion. J. Hydr. Res. 1984, 22, 245–261. [Google Scholar] [CrossRef]
- Van der Giessen, A.; De Ruijter, W.; Borst, J. Three-dimensional current structure in the Dutch coastal zone. Neth. J. Sea Res. 1990, 25, 45–55. [Google Scholar] [CrossRef]

| Authors | Boundary Layer Classification (*) | |||||
|---|---|---|---|---|---|---|
| Kaptein et al. [32] | 990 | 5 | 4.90 × 105 | 4.95 × 103 |  | |
| 990 | 10 | 4.90 × 105 | 9.90 × 103 |  | ||
| 990 | 25 | 4.90 × 105 | 2.48 × 104 |  | ||
| 990 | 40 | 4.90 × 105 | 3.96 × 104 |  | ||
| 990 | 70 | 4.90 × 105 | 6.93 × 104 |  | ||
| 1790 | 5 | 1.60 × 106 | 8.95 × 103 |  | ||
| 1790 | 10 | 1.60 × 106 | 1.79 × 104 |  | ||
| 1790 | 25 | 1.60 × 106 | 4.48 × 104 |  | ||
| 1790 | 40 | 1.60 × 106 | 7.16 × 104 |  | ||
| 1790 | 70 | 1.60 × 106 | 1.25 × 105 |  | ||
| 3460 | 5 | 5.99 × 106 | 1.73 × 104 |  | ||
| 3460 | 10 | 5.99 × 106 | 3.46 × 104 |  | ||
| 3460 | 25 | 5.99 × 106 | 8.65 × 104 |  | ||
| 3460 | 40 | 5.99 × 106 | 1.38 × 105 |  | ||
| 3460 | 70 | 5.99 × 106 | 2.42 × 105 |  | ||
| Knight and Ridgway [25] | Exp. 1 | 707 | 38.6 | 2.51 × 105 | 2.74 × 104 | △ |
| 2 | 907 | 27.0 | 4.13 × 105 | 2.46 × 104 | △ | |
| 3 | 1015 | 16.5 | 5.16 × 105 | 1.67 × 104 | ▲ | |
| 4 | 1209 | 7.1 | 7.36 × 105 | 8.67 × 103 | ▲ | |
| Larsen et al. [27] | Case 10 | 2457 | 53.8 | 3.02 × 106 | 1.32 × 105 | ▷ |
| 11 | 3191 | 43.2 | 5.09 × 106 | 1.37 × 105 | ▷ | |
| 12 | 6051 | 21.9 | 1.83 × 107 | 1.32 × 105 | ▶ | |
| Hayashi and Ohashi [38] | Case 1 | 872 | 56.8 | 3.87 × 105 | 4.95 × 104 | ◁ |
| 2 | 995 | 57.7 | 4.95 × 105 | 5.74 × 104 | ◁ | |
| 3 | 939 | 53.0 | 4.44 × 105 | 4.98 × 104 | ◁ | |
| 4 | 854 | 48.9 | 3.65 × 105 | 4.18 × 104 | ◁ | |
| Hino et al. [39] | - | 876 | 12.8 | 3.84 × 105 | 1.13 × 104 | ◇ |
| Jensen et al. [16] | Test 5 | 761 | 72.6 | 2.9 × 105 | 5.5 × 104 |  |
| 6 | 1000 | 73.7 | 5.0 × 105 | 7.4 × 104 |  | |
| 7 | 1140 | 73.2 | 6.5 × 105 | 8.4 × 104 |  | |
| 8 | 1789 | 70.0 | 1.6 × 106 | 1.3 × 105 |  | |
| 9 | 2608 | 73.0 | 3.4 × 106 | 1.9 × 105 |  | |
| 10 | 3464 | 70.9 | 6.0 × 106 | 2.5 × 105 |  | |
| Sawamoto and Sato [40] | Case 2 | 812 | 50.2 | 3.30 × 106 | 5.71 × 104 |  |
| Numerical Cases | Boundary Layer Classification (*) | ||||
|---|---|---|---|---|---|
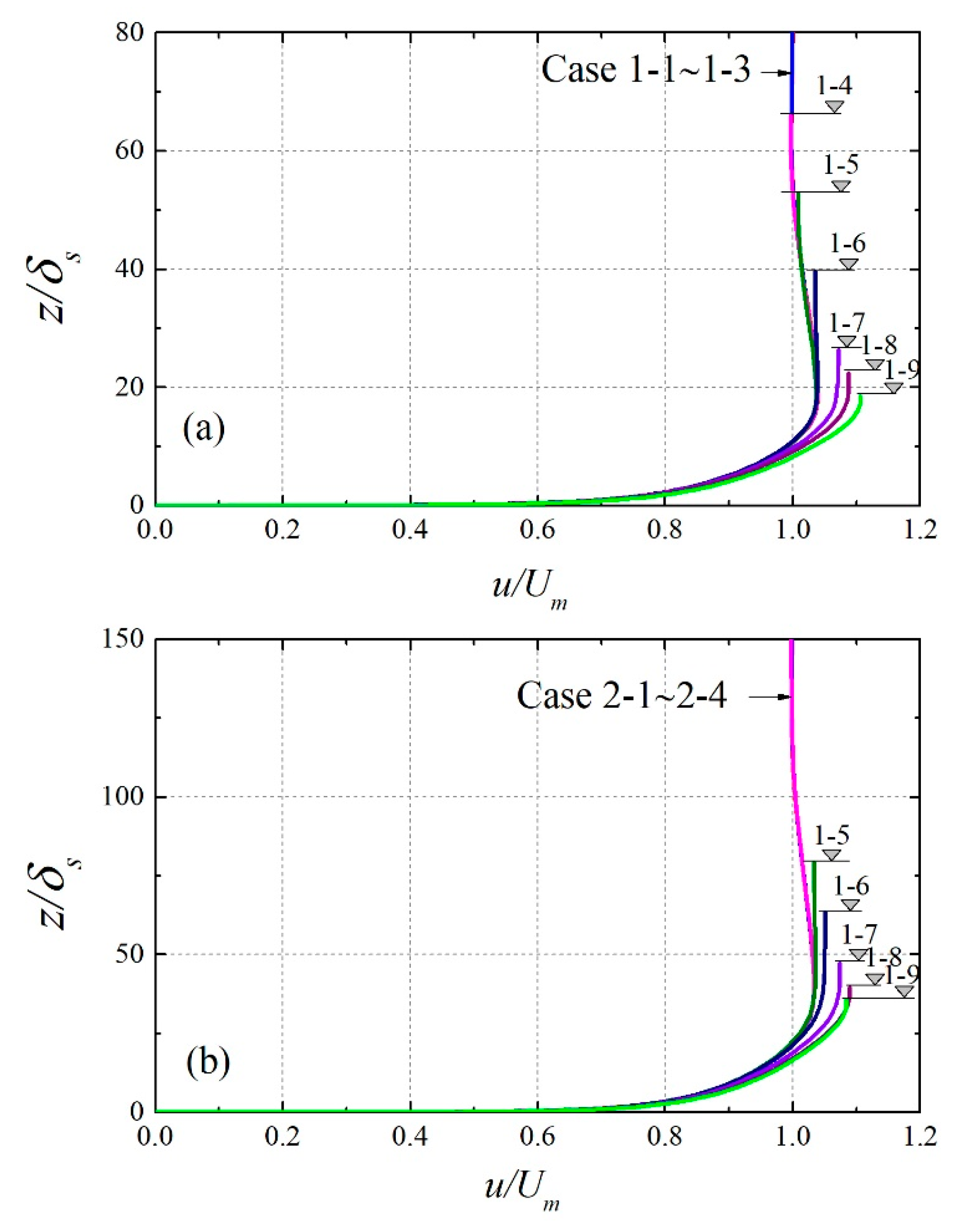
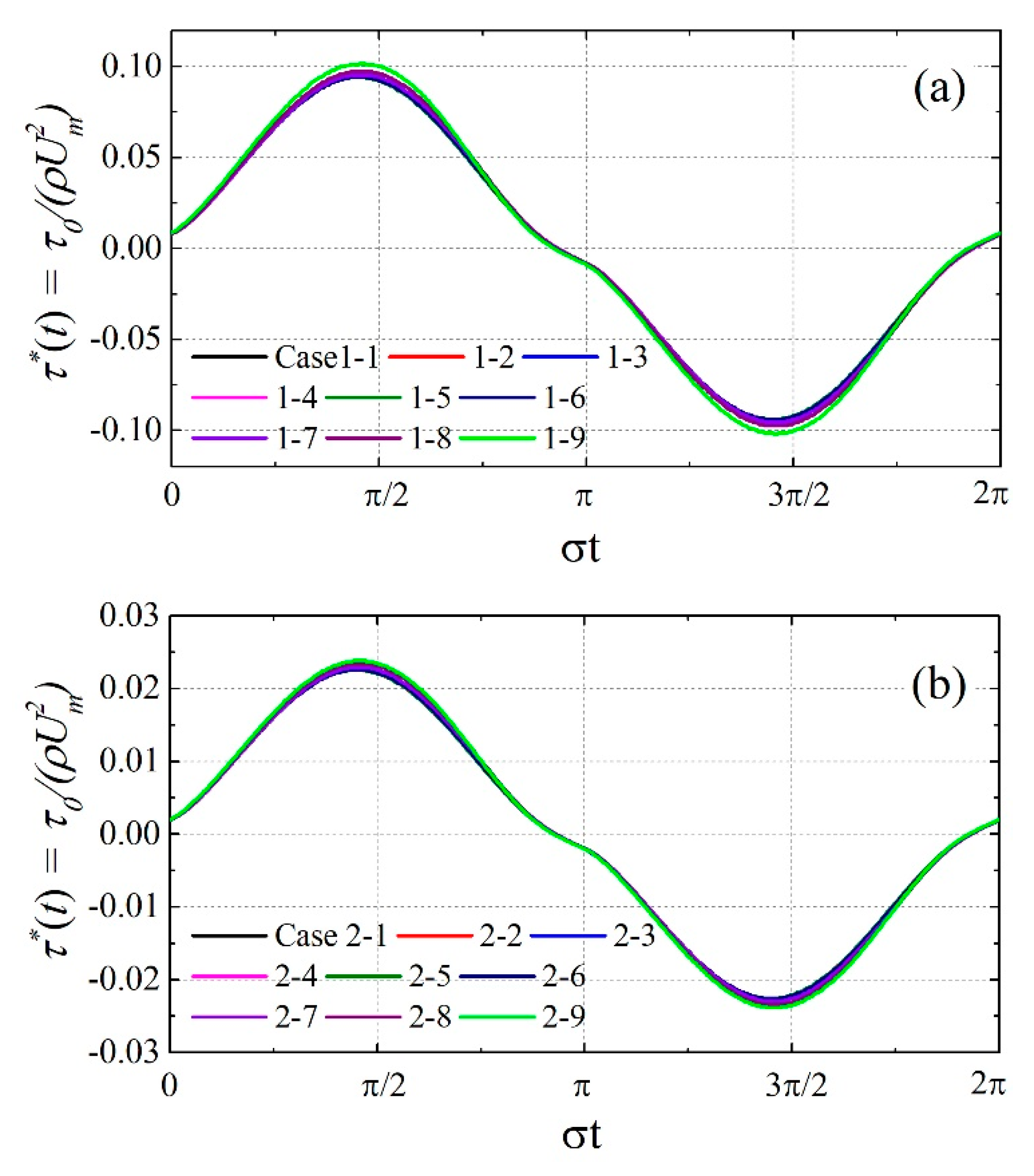
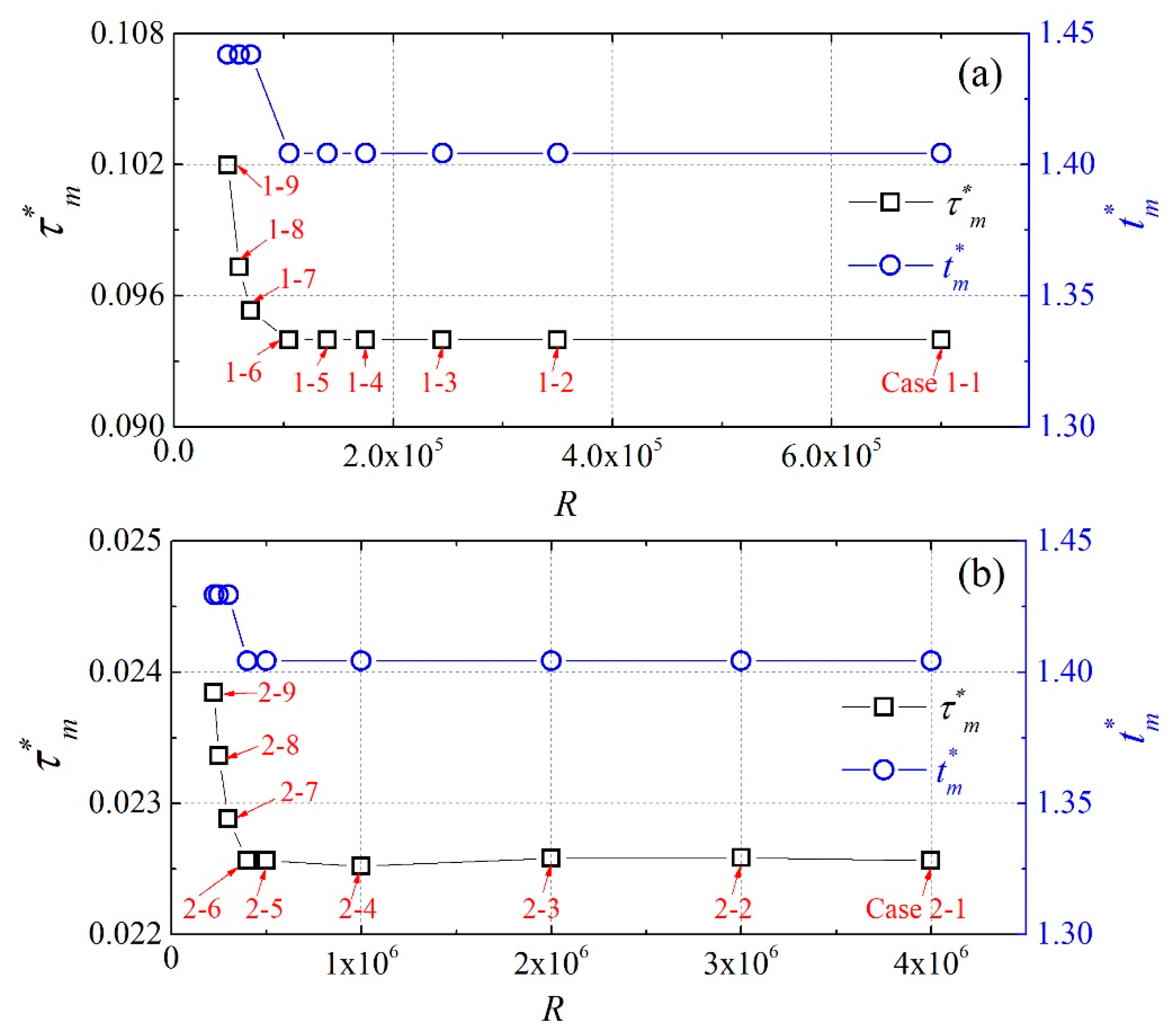
| Case 1-1 | 2649 | 264 | 3.51 × 106 | 7.00 × 105 | ☆ |
| 1-2 | 2649 | 132 | 3.51 × 106 | 3.50 × 105 | ☆ |
| 1-3 | 2649 | 92 | 3.51 × 106 | 2.45 × 105 | ☆ |
| 1-4 | 2649 | 66 | 3.51 × 106 | 1.75 × 105 | ☆ |
| 1-5 | 2649 | 53 | 3.51 × 106 | 1.40 × 105 | ☆ |
| 1-6 | 2649 | 40 | 3.51 × 106 | 1.05 × 105 | ★ |
| 1-7 | 2649 | 26 | 3.51 × 106 | 7.00 × 104 | ★ |
| 1-8 | 2649 | 22 | 3.51 × 106 | 5.95 × 104 | ★ |
| 1-9 | 2649 | 18 | 3.51 × 106 | 4.90 × 104 | ★ |
| Case 2-1 | 6308 | 634 | 1.99 × 107 | 4.00 × 106 | ☆ |
| 2-2 | 6308 | 476 | 1.99 × 107 | 3.00 × 106 | ☆ |
| 2-3 | 6308 | 317 | 1.99 × 107 | 2.00 × 106 | ☆ |
| 2-4 | 6308 | 159 | 1.99 × 107 | 1.00 × 106 | ☆ |
| 2-5 | 6308 | 79 | 1.99 × 107 | 5.00 × 105 | ☆ |
| 2-6 | 6308 | 63 | 1.99 × 107 | 4.00 × 105 | ☆ |
| 2-7 | 6308 | 48 | 1.99 × 107 | 3.00 × 105 | ★ |
| 2-8 | 6308 | 40 | 1.99 × 107 | 2.50 × 105 | ★ |
| 2-9 | 6308 | 36 | 1.99 × 107 | 2.25 × 105 | ★ |
| (m/s) | (m) | ||||
|---|---|---|---|---|---|
| Neap tide | 0.7 | 3.06 × 109 | 1.23 × 107 | 44.9 | 2.25 |
| Spring tide | 1.1 | 7.55 × 109 | 1.92 × 107 | 67.4 | 3.37 |
| Case 1 | Case 2 | |
|---|---|---|
| Depth of the source | 4000 m | 4000 m |
| Tsunami height at the source | 1 m | 1 m |
| Tsunami period at the source | 15 min | 30 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanaka, H.; Tinh, N.X.; Yu, X.; Liu, G. Development of Depth-Limited Wave Boundary Layers over a Smooth Bottom. J. Mar. Sci. Eng. 2021, 9, 27. https://doi.org/10.3390/jmse9010027
Tanaka H, Tinh NX, Yu X, Liu G. Development of Depth-Limited Wave Boundary Layers over a Smooth Bottom. Journal of Marine Science and Engineering. 2021; 9(1):27. https://doi.org/10.3390/jmse9010027
Chicago/Turabian StyleTanaka, Hitoshi, Nguyen Xuan Tinh, Xiping Yu, and Guangwei Liu. 2021. "Development of Depth-Limited Wave Boundary Layers over a Smooth Bottom" Journal of Marine Science and Engineering 9, no. 1: 27. https://doi.org/10.3390/jmse9010027
APA StyleTanaka, H., Tinh, N. X., Yu, X., & Liu, G. (2021). Development of Depth-Limited Wave Boundary Layers over a Smooth Bottom. Journal of Marine Science and Engineering, 9(1), 27. https://doi.org/10.3390/jmse9010027