Numerical Study of an Oscillating-Wing Wingmill for Ocean Current Energy Harvesting: Fluid-Solid-Body Interaction with Feedback Control
Abstract
1. Introduction
2. Problem Statement
The Feedback Loop
3. Numerical Simulations
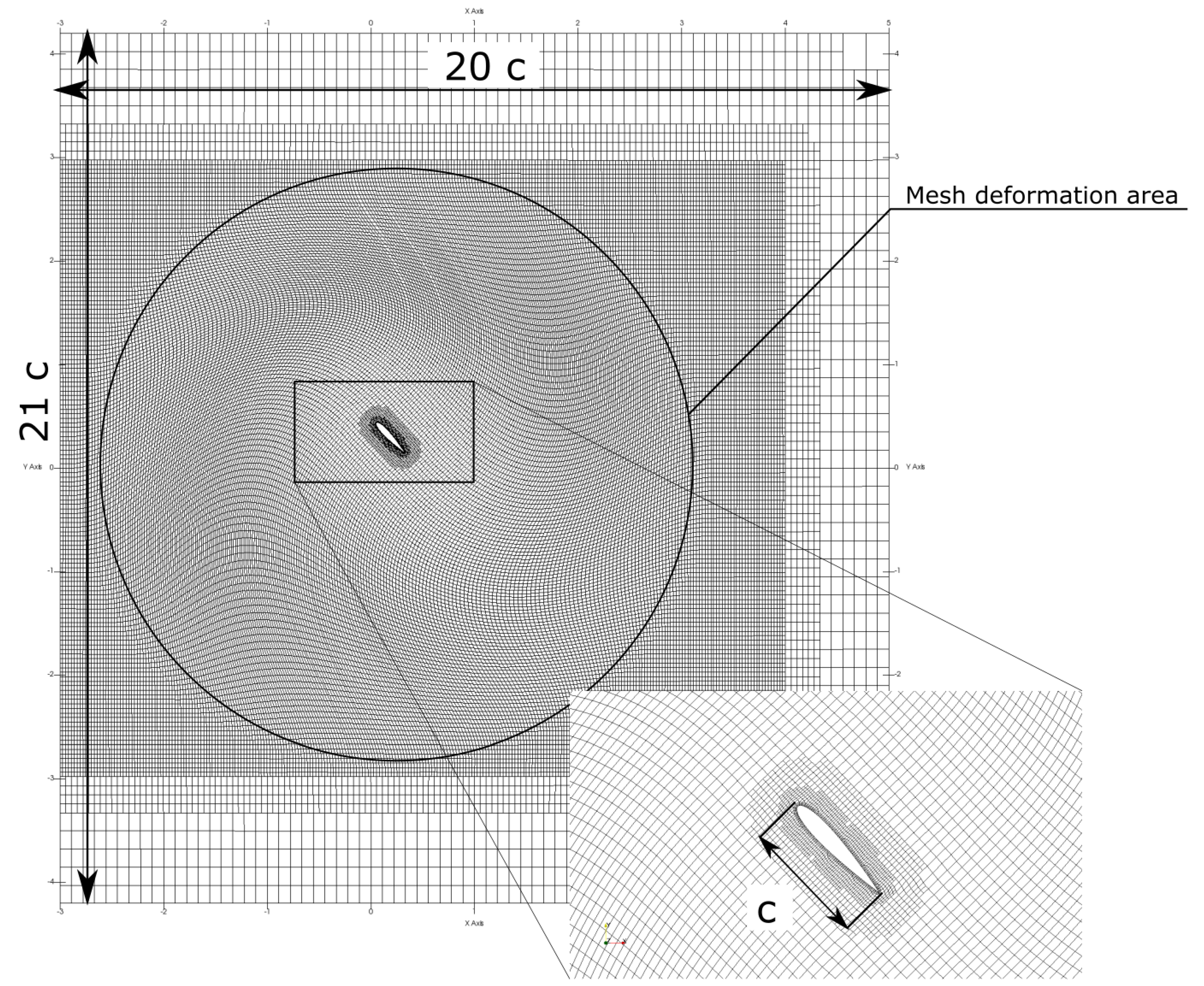
3.1. The Mesh
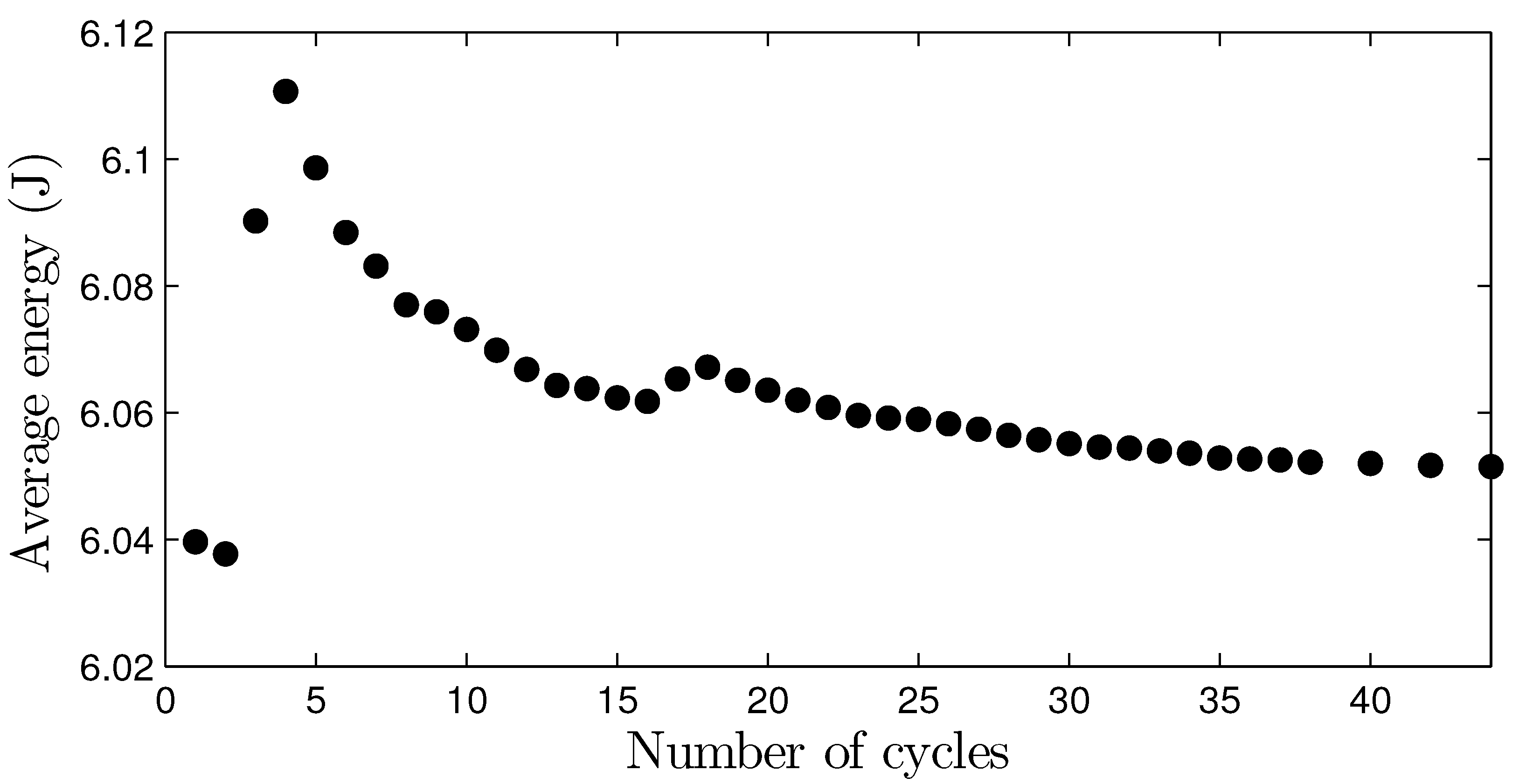
3.2. Mesh Validation
3.3. Control Scheme
3.4. Limitations
4. Dimensionless Parameters
- The efficiency
- The Reynolds number
- Dimensionless heaving
- Inertia 1
- Inertia 2 (rotational)
- Dimensionless damping ratio
- Dimensionless gain
- Strouhal number
- Density ratio between the fluid and solid body
Reynolds Number and Turbulence
5. Results
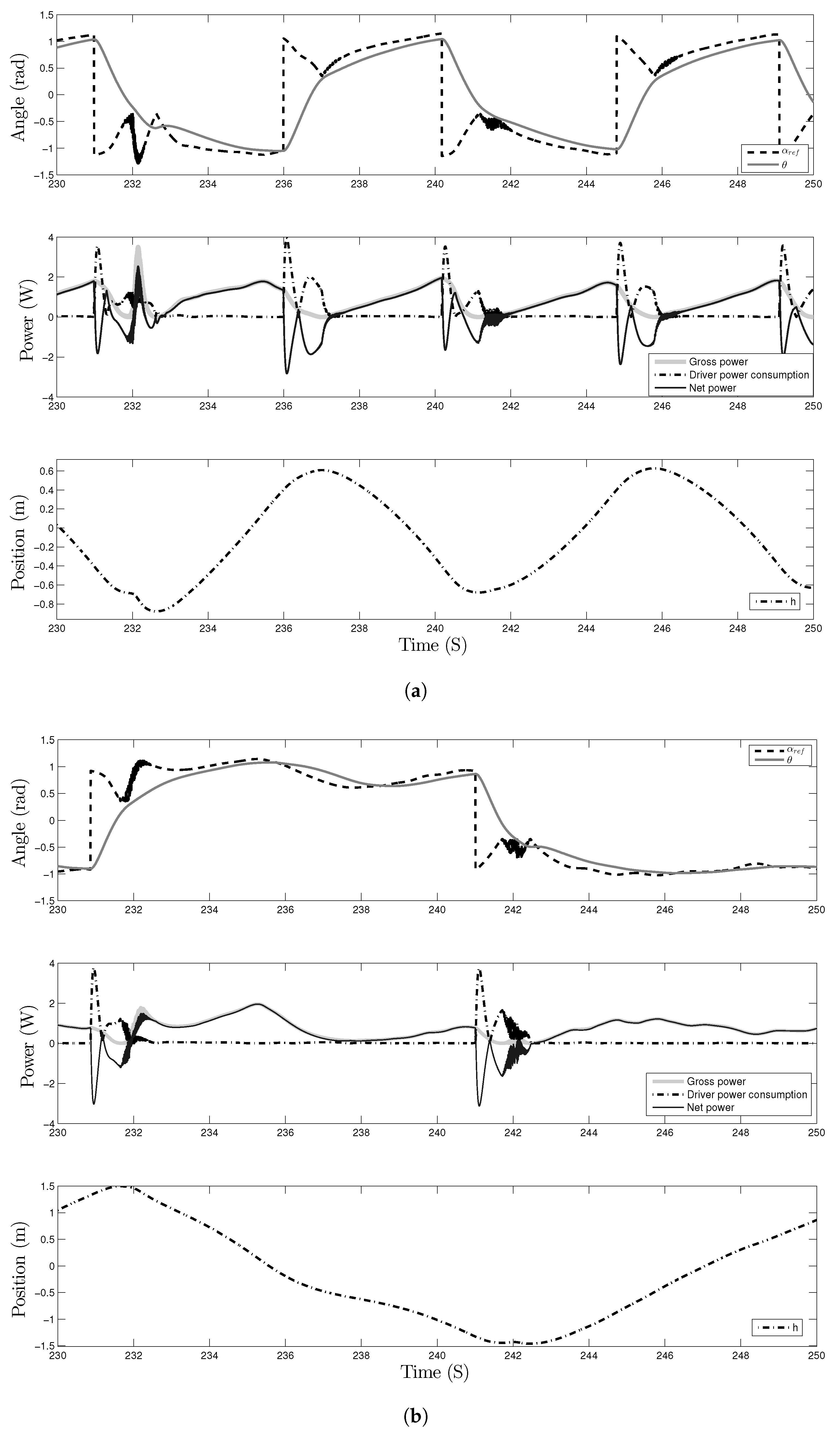
5.1. Effects of the Closed-Loop Control
- A noisy high frequency oscillation can occur on the reference signal for shortly after the foil has changed direction. This is an effect of the control action; since the dynamic angle depends on , the latter derivative amplifies small oscillations that are caused by the control torque. Even if the torque is applied at the center of mass, linear and angular motions are coupled by hydrodynamic forces, so a sudden torque may cause a small jump in . This effect is only observable when the heaving speed is close to zero (and it can be avoided while using a properly tuned PI controller; this added complexity is out of the scope of the present report).
- The control effort (energy spent in the control action) may be very important in the vicinity of . The net power could be substantially increased if this energy could be spared (following the sign change in the reference angle). Three possible ways of doing so would be: (a) a passive mechanism that turns the airfoil once the threshold is reached, (b) instead of pitching of the whole airfoil, set an aileron near the trailing edge, so the pitching effort decreases substantially, (c) to saturate the controller output to limit the spent energy (this would have consequences on the response time), and (d) to implement a control strategy that can be proved to be optimal in the sense of net power extraction. Of course, some of these suggestions may be combined in order to increase the efficiency.
- The power curve shows a maximum before reaching the time where the new is assigned. This should not happen if the lift coefficient was that of a static polar for the airfoil (maximum). The power should not decay until the controller sets a new reference ( is reached). Even if the reference angle was chosen, such as to have maximum static lift, the actual lift is not parallel to the y axis, multiplying, by , where . This causes the lift to decrease whenever the heaving speed becomes comparable to U. When this happens, a plot of the factor versus power (not presented here for brevity) shows that the maximum power coincides with the cosine crest. This correlation is clear when , as and the power that is extracted from the damping is proportional to . This is a very important consideration, because this is a limit to the velocity (and power) that can be extracted while using oscillating foils whose motion is constrained to the y axis.
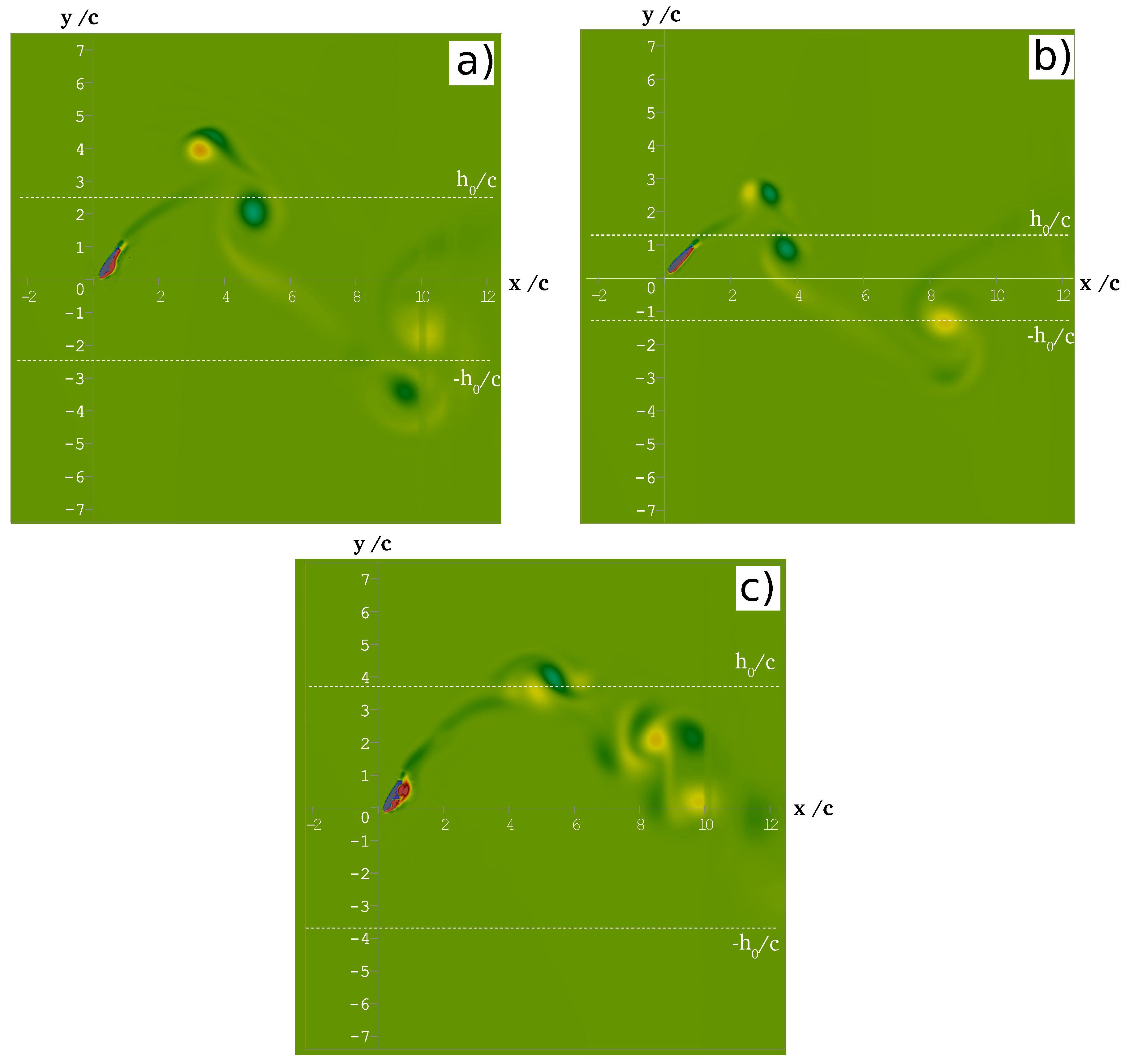
- Dynamic stall: even though the reference angle was chosen to be below the maximum lift (5% smaller) in order to avoid stall, a more detailed inspection of the boundary layer separation and vortices detachment made clear that unsteady stall is taking place for some cases. Figure 6 shows the vorticity of the velocity field for three cases () at different times and : (a) for , , the boundary layer remains attached to the foil, with the exception of a small perturbation (incipient eddy) forming near the leading edge lower surface. This eddy will eventually detach from the trailing edge. One can observe that a pair of counter-rotating vortices detached from the foil when it switched direction in the vicinity of ; (b) for , the boundary layer clearly stays attached to the foil, and the only remnant eddies are again forming a vortex pair, close to the turning point ; however, in (c), there is dynamic stall (, , ). The image shows the airfoil heaving downwards (halfway towards ). There is an alternating sign vortex street left from the previous cycle. There is clear detachment of the boundary layer in the lower surface of the airfoil. The time t corresponds to the horizontal axis shown in Figure 5. The exact nature of the dynamic stall, in our case, is out of the scope of this work; however, the reader may refer to [47,53,54] for a comprehensive characterization of the phenomenon. Moreover, we observed that, whenever the controller overshoots ( crosses ), there is a detachment of eddies and oscillations in , so dynamic stall may, in some cases, be caused by the control action itself (if that is the case, the optimal control problem is further complicated).
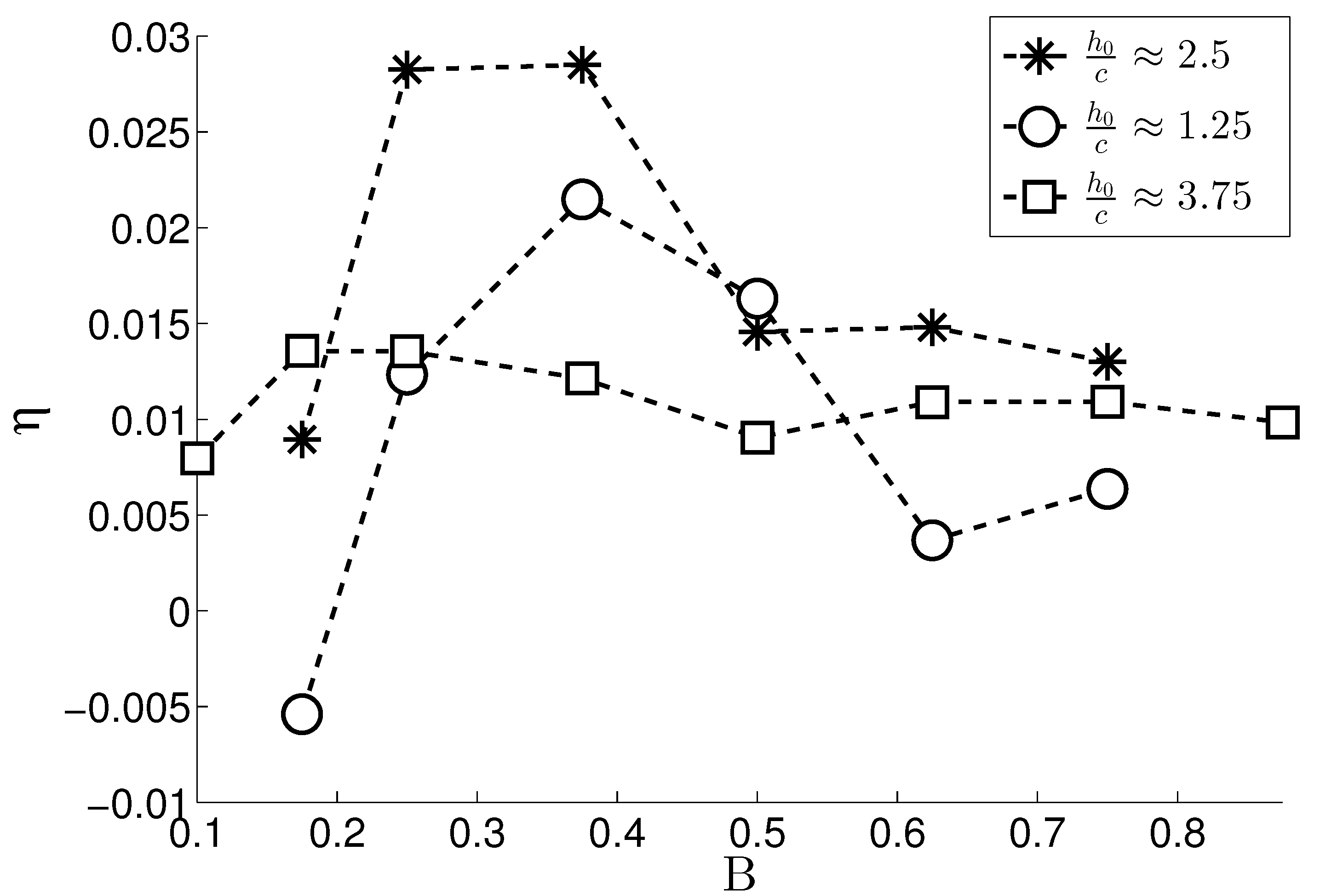
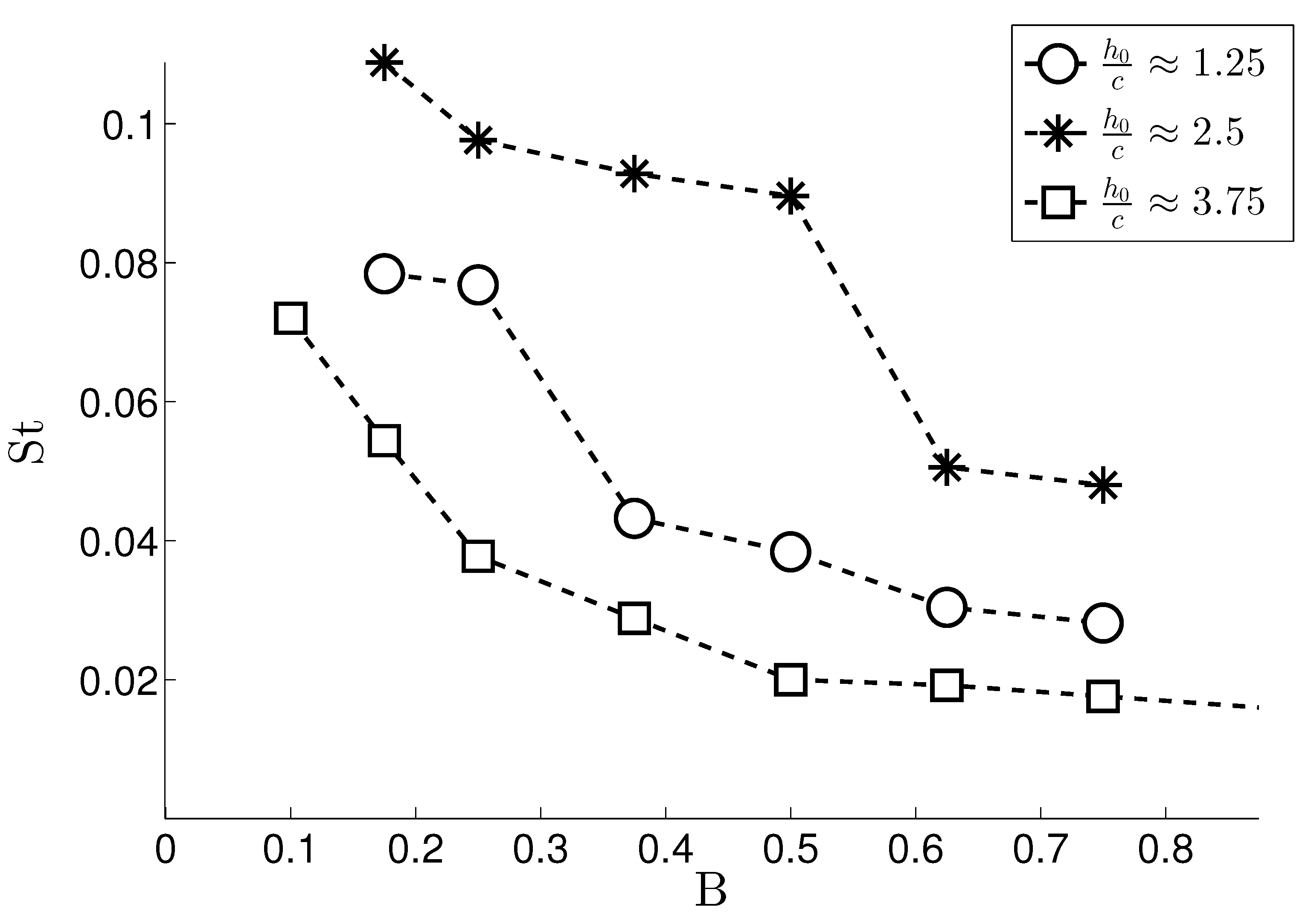
5.2. Effect of B on the Efficiency
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tables and Figures
| Authors | Year | AR | Type | Foil | ||
|---|---|---|---|---|---|---|
| Kinsey and Dumas | 2012 | 2D | Prescribed & tandem | NACA0015 | 0.63 | |
| Platzer et al. | 2010 | 2D | Fully Passive prescribed y tandem | NACA0014 | 0.54 | |
| Ashraf et al. | 2011 | 2D | Prescribed & tandem | NACA0014 | 0.54 | |
| Young et al. | 2013 | 2D | Fully passive | NACA0012 | – | 0.41 |
| Campobasso et al. | 2013 | 2D | Prescribed | NACA0015 | – | 0.40 |
| Le et al. | 2013 | 2D | Prescribed | Biomimetic | 0.39 | |
| Ashraf et al. | 2009 | 2D | Prescribed | NACA0012 | 1100 | 0.38 |
| Shimizu et al. | 2008 | 2D | Semi-passive open-loop | NACA0012 | 0.35 | |
| This study | 2019 | Semi-passive closed-loop | NACA0015 | 0.12 |
| Authors | Year | Type | Foil | ||
|---|---|---|---|---|---|
| Kinsey et al. | 2011 | Fully passive | NACA0015 | 5 × | 0.4 |
| Kinsey and Dumas | 2010 | Fully passive | NACA0015 | 5 × | 0.4 |
| Simpson et al. | 2009 | Prescribed | NACA0012 | 1.38 × | 0.32 |
| Huxham et al | 2012 | Semi-passive | NACA0015 | 4.5 × | 0.24 |
| Lindsey, Jones et al. | 2003 | Fully passive | NACA0014 | 2.2 × | 0.23 |
| McKinney and DeLaurier | 1981 | Fully passive | NACA0012 | 8.5 ×–1.1 × | 0.17 |
| Name | Number of Cells | Initial-Final-Refinement Level | Average Energy (J) |
|---|---|---|---|
| M1 | 18,040 | 3-4-1 | |
| M2 | 47,440 | 3-4-3 | |
| M3 | 290,326 | 4-4-1 | |
| M4 | 291,286 | 4-4-3 | |
| M5 | 322,606 | 4-5-3 |
| ID | B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.03 | 2.5 | 0.0937 | 0.0437 | 0.25 | 0.175 | |||
| 2 | 9.03 | 2.5 | 0.0937 | 0.0625 | 0.25 | 0.25 | |||
| 3 | 10.97 | 2.5 | 0.0937 | 0.0937 | 0.25 | 0.375 | |||
| 4 | 7.17 | 2.5 | 0.0937 | 0.1250 | 0.25 | 0.5 | |||
| 5 | 6.29 | 2.5 | 0.0937 | 0.1562 | 0.25 | 0.625 | |||
| 6 | 5.61 | 2.5 | 0.0937 | 0.1875 | 0.25 | 0.75 | |||
| 7 | 2.25 | 1.25 | 0.0937 | 0.0437 | 0.25 | 0.175 | |||
| 8 | 6.62 | 1.25 | 0.0937 | 0.0625 | 0.25 | 0.25 | |||
| 9 | 6.86 | 1.25 | 0.0937 | 0.0937 | 0.25 | 0.375 | |||
| 10 | 7.38 | 1.25 | 0.0937 | 0.1250 | 0.25 | 0.5 | |||
| 11 | 7.32 | 1.25 | 0.0937 | 0.1562 | 0.25 | 0.625 | |||
| 12 | 6.62 | 1.25 | 0.0937 | 0.1875 | 0.25 | 0.75 | |||
| 13 | 2.39 | 3.75 | 0.0937 | 0.0250 | 0.25 | 0.1 | |||
| 14 | 3.75 | 3.75 | 0.0937 | 0.0437 | 0.25 | 0.175 | |||
| 15 | 3.40 | 3.75 | 0.0937 | 0.0625 | 0.25 | 0.25 | |||
| 16 | 2.91 | 3.75 | 0.0937 | 0.0937 | 0.25 | 0.375 | |||
| 17 | 2.66 | 3.75 | 0.0937 | 0.1250 | 0.25 | 0.5 | |||
| 18 | 2.54 | 3.75 | 0.0937 | 0.1562 | 0.25 | 0.625 | |||
| 19 | 1.74 | 3.75 | 0.0937 | 0.1875 | 0.25 | 0.75 | |||
| 20 | 1.46 | 3.75 | 0.0937 | 0.2187 | 0.25 | 0.875 | |||
| 1 | 0.009 | 2.5 | 0.0937 | 0.0437 | 0.25 | 0.175 | |||
| 2 | 0.028 | 2.5 | 0.0937 | 0.0625 | 0.25 | 0.25 | |||
| 3 | 0.016 | 2.5 | 0.0937 | 0.0937 | 0.25 | 0.375 | |||
| 4 | 0.015 | 2.5 | 0.0937 | 0.1250 | 0.25 | 0.5 | |||
| 5 | 0.028 | 2.5 | 0.0937 | 0.1562 | 0.25 | 0.625 | |||
| 6 | 0.024 | 2.5 | 0.0937 | 0.1875 | 0.25 | 0.75 | |||
| 7 | -0.005 | 1.25 | 0.0937 | 0.0437 | 0.25 | 0.175 | |||
| 8 | 0.012 | 1.25 | 0.0937 | 0.0625 | 0.25 | 0.25 | |||
| 9 | 0.021 | 1.25 | 0.0937 | 0.0937 | 0.25 | 0.375 | |||
| 10 | 0.016 | 1.25 | 0.0937 | 0.1250 | 0.25 | 0.5 | |||
| 11 | 0.004 | 1.25 | 0.0937 | 0.1562 | 0.25 | 0.625 | |||
| 12 | 0.006 | 1.25 | 0.0937 | 0.1875 | 0.25 | 0.75 | |||
| 13 | 0.008 | 3.75 | 0.0937 | 0.0250 | 0.25 | 0.1 | |||
| 14 | 0.013 | 3.75 | 0.0937 | 0.0437 | 0.25 | 0.175 | |||
| 15 | 0.014 | 3.75 | 0.0937 | 0.0625 | 0.25 | 0.25 | |||
| 16 | 0.012 | 3.75 | 0.0937 | 0.0937 | 0.25 | 0.375 | |||
| 17 | 0.009 | 3.75 | 0.0937 | 0.1250 | 0.25 | 0.5 | |||
| 18 | 0.011 | 3.75 | 0.0937 | 0.1562 | 0.25 | 0.625 | |||
| 19 | 0.011 | 3.75 | 0.0937 | 0.1875 | 0.25 | 0.75 | |||
| 20 | 0.010 | 3.75 | 0.0937 | 0.2187 | 0.25 | 0.875 |
| Unused Energy | Net Harnessed Energy | Control Energy Consumption | |
|---|---|---|---|
| 2.5 | 83.8% | 10.6% | 5.7% |
| 1.25 | 87.3% | 6.9% | 5.8% |
| 3.75 | 95.9% | 3.2% | 0.9% |
References
- Bahaj, A.S. Generating electricity from the oceans. Renew. Sustain. Energy Rev. 2011, 15, 3399–3416. [Google Scholar] [CrossRef]
- Da Rosa, A.V. Fundamentals of Renewable Energy Processes; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Rourke, F.O.; Boyle, F.; Reynolds, A. Marine current energy devices: Current status and possible future applications in Ireland. Renew. Sustain. Energy Rev. 2010, 14, 1026–1036. [Google Scholar] [CrossRef]
- Rourke, F.O.; Boyle, F.; Reynolds, A. Tidal energy update 2009. Appl. Energy 2010, 87, 398–409. [Google Scholar] [CrossRef]
- McKinney, W.; DeLaurier, J. Wingmill: An oscillating-wing windmill. J. Energy 1981, 5, 109–115. [Google Scholar] [CrossRef]
- Zhu, Q. Optimal frequency for flow energy harvesting of a flapping foil. J. Fluid Mech. 2011, 675, 495–517. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Testing and analysis of an oscillating hydrofoils turbine concept. In Proceedings of the ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting collocated with 8th International Conference on Nanochannels, Microchannels, and Minichannels; American Society of Mechanical Engineers: New York, NY, USA, 2010; pp. 9–22. [Google Scholar]
- Kinsey, T.; Dumas, G.; Lalande, G.; Ruel, J.; Mehut, A.; Viarouge, P.; Lemay, J.; Jean, Y. Prototype testing of a hydrokinetic turbine based on oscillating hydrofoils. Renew. Energy 2011, 36, 1710–1718. [Google Scholar] [CrossRef]
- Simpson, B.J.; Hover, F.S.; Triantafyllou, M.S. Experiments in direct energy extraction through flapping foils. In Proceedings of the Eighteenth International Offshore and Polar Engineering Conference, Vancouver, BC, Canada, 6–11 July 2008; International Society of Offshore and Polar Engineers: Cupertino, CA, USA, 2008. [Google Scholar]
- Simpson, B.J.; Licht, S.; Hover, F.S.; Triantafyllou, M.S. Energy extraction through flapping foils. In Proceedings of the ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; American Society of Mechanical Engineers: New York, NY, USA, 2008; pp. 389–395. [Google Scholar]
- The Engineering Business Limited Ltd. Research and Development of A 150 kw Tidal Stream Generator. T/06/00211/00/REP, Department of Trade and Industry Crown Copyright 2002. Available online: https://archive.uea.ac.uk/~e680/energy/energy_links/renewables/stingray0.pdf (accessed on 18 December 2020).
- The Engineering Business Limited Ltd. Stingray Tidal Stream Energy Device—Phase 2, T/06/00218/00/REP. The Engineering Business Ltd.: Stocksfield, UK, 2003. Available online: https://archive.uea.ac.uk/~e680/energy/energy_links/renewables/stingray_part1.pdf (accessed on 18 December 2020).
- The Engineering Business Limited Ltd. Stingray Tidal Stream Energy Device—Phase 3, T/06/00230/00/REP, Department of Trade and Industry Crown Copyright 2005. Available online: https://tethys.pnnl.gov/sites/default/files/publications/Stingray_Tidal_Stream_Energy_Device.pdf (accessed on 18 December 2020).
- Young, J.; Lai, J.C.; Platzer, M.F. A review of progress and challenges in flapping foil power generation. Prog. Aerosp. Sci. 2014, 67, 2–28. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhu, Q. A review on flow energy harvesters based on flapping foils. J. Fluids Struct. 2014, 46, 174–191. [Google Scholar] [CrossRef]
- Huxham, G.; Cochard, S.; Patterson, J. Experimental parametric investigation of an oscillating hydrofoil tidal stream energy converter. In Proceedings of the 18th Australasian Fluid Mechanics Conference AFMC, Launceston, Tasmania, Australia, 3–7 December 2012. [Google Scholar]
- Jones, K.D.; Lindsey, K.; Platzer, M. An Investigation of the Fluid-Structure Interaction in an Oscillating-Wing Micro-Hydropower Generator; WIT Press: Southampton, UK, 2003. [Google Scholar]
- Ashraf, M.; Young, J.S.; Lai, J.; Platzer, M. Numerical analysis of an oscillating-wing wind and hydropower generator. AIAA J. 2011, 49, 1374–1386. [Google Scholar] [CrossRef]
- Shimizu, E.; Isogai, K.; Obayashi, S. Multiobjective design study of a flapping wing power generator. J. Fluids Eng. 2008, 130, 021104. [Google Scholar] [CrossRef]
- Zhu, Q.; Peng, Z. Mode coupling and flow energy harvesting by a flapping foil. Phys. Fluids 2009, 21, 033601. [Google Scholar] [CrossRef]
- Koutsogiannakis, P.E.; Filippas, E.S.; Belibassakis, K.A. A Study of Multi-Component Oscillating-Foil Hydrokinetic Turbines with a GPU-Accelerated Boundary Element Method. J. Mar. Sci. Eng. 2019, 7, 424. [Google Scholar] [CrossRef]
- Maeda, D.; Morishita, E. Numerical Simulation for Feedback Control of Airfoil Oscillation in Incompressible Flow. Trans. Jpn. Soc. Aeronaut. Space Sci. 2006, 49, 117–124. [Google Scholar] [CrossRef]
- Mandre, S.; Breuer, K.; Strom, B.; Miller, M.; Franck, J.; Kim, D. Kinetic Energy Harvesting Using Cyber-Physical Systems. US 2014/0203558 A1. 2014. Available online: https://bit.ly/34Pazy7 (accessed on 18 December 2020).
- Anderson, J.D. Fundamentals of Aerodynamics; Mc. Graw Hill: New York, NY, USA, 1991. [Google Scholar]
- Abbot, I.H.; Von Doenhoff, A.E. Theory of Wing Sections; Dover: New York, NY, USA, 1959. [Google Scholar]
- Kinsey, T.; Dumas, G. Optimal tandem configuration for oscillating-foils hydrokinetic turbine. J. Fluids Eng. 2012, 134, 031103. [Google Scholar] [CrossRef]
- Greenshields, C.J. OpenFOAM User Guide; OpenFOAM Foundation Ltd.: London, UK, 2018; Available online: https://usermanual.wiki/Document/OpenFOAMUserGuideV6.37159236/html (accessed on 18 December 2020).
- Greenshields, C.J. Programmers Guide; OpenFOAM Foundation Ltd.: London, UK, 2015; Volume 27. [Google Scholar]
- Issa, R. Solution of the Implicitly Discretized Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1985, 62, 40–65. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flow. Ph.D. Thesis, Department of Mechanical Engineering, Imperial College of Science, Technology, and Medicine, London, UK, 1996. [Google Scholar]
- Chow, J.H.; Ng, E. Strongly coupled partitioned six degree-of-freedom rigid body motion solver with Aitken’s dynamic under-relaxation. Int. J. Nav. Archit. Ocean. Eng. 2016, 8, 320–329. [Google Scholar] [CrossRef][Green Version]
- Baker, T.J. Mesh deformation and modification for time dependent problems. Int. J. Numer. Methods Fluids 2003, 43, 747–768. [Google Scholar] [CrossRef]
- Dwight, R.P. Robust mesh deformation using the linear elasticity equations. In Computational Fluid Dynamics 2006; Springer: Berlin/Heidelberg, Germany, 2009; pp. 401–406. [Google Scholar]
- BOS, F.M. Numerical Simulations of Flapping Foil and Wing Aerodynamics: Mesh Deformation Using Radial Basis Functions. Master’s Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2010. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The finite volume method in computational fluid dynamics. In An Advanced Introduction with OpenFOAM and Matlab; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–8. [Google Scholar]
- Jasak, H.; Tukovic, Z. Automatic mesh motion for the unstructured finite volume method. Trans. FAMENA 2006, 30, 1–20. [Google Scholar]
- Ekedahl, E. 6-DOF VOF-solver without Damping in OpenFOAM. In Project Work for the Ph.D. Course “CFD with Open Source Software”; Chalmers University of Technology: Gothenburg, Sweden, 2008. [Google Scholar]
- Amiraslanpour, M.; Ghazanfarian, J.; Razavi, S.E. Drag suppression for 2D oscillating cylinder with various arrangement of splitters at Re=100: A high-amplitude study with OpenFOAM. J. Wind. Eng. Ind. Aerodyn. 2017, 164, 128–137. [Google Scholar] [CrossRef]
- Radtke, L.; Larena-Avellaneda, A.; Debus, E.S.; Düster, A. Convergence acceleration for partitioned simulations of the fluid-structure interaction in arteries. Comput. Mech. 2016, 57, 901–920. [Google Scholar] [CrossRef]
- Kotsur, O.; Scheglov, G.; Leyland, P. Verification of modelling of fluid structure interaction (FSI) problems based on experimental research of bluff body oscillations in fluids. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014; pp. 7–12. [Google Scholar]
- Dunbar, A.J.; Craven, B.A.; Paterson, E.G. Development and validation of a tightly coupled CFD/6-DOF solver for simulating floating offshore wind turbine platforms. Ocean. Eng. 2015, 110, 98–105. [Google Scholar] [CrossRef]
- Jacobs, E.N.; Sherman, A. Airfoil section characteristics as affected by variations of the Reynolds number. NACA Rep. 1937, 586, 227–264. [Google Scholar]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; Technical Report; Sandia National Labs.: Albuquerque, NM, USA, 1981. [Google Scholar]
- An, X.; Williams, D.R.; Eldredge, J.D.; Colonius, T. Lift Coefficient Estimation for a Rapidly Pitching Airfoil. arXiv 2020, arXiv:2005.01870. [Google Scholar]
- Ghoreyshi, M.; Cummings, R.M. Challenges in the aerodynamics modeling of an oscillating and translating airfoil at large incidence angles. Aerosp. Sci. Technol. 2013, 28, 176–190. [Google Scholar] [CrossRef]
- Yousefi K., R.A. Determination of the Critical Reynolds Number for Flow over Symmetric NACA Airfoils. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; Volume 2018, pp. 8–12. [Google Scholar]
- Mueller, T.J. The influence of laminar separation and transition on low Reynolds number airfoil hysteresis. J. Aircr. 1985, 22, 763–770. [Google Scholar] [CrossRef]
- Mueller, T.J.; DeLaurier, J.D. Aerodynamics of small vehicles. Annu. Rev. Fluid Mech. 2003, 35, 89–111. [Google Scholar] [CrossRef]
- Menter, F. Zonal two equation kw turbulence models for aerodynamic flows. In Proceedings of the 23rd fluid dynamics, plasmadynamics, and lasers conference AIAA, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Lu, K.; Xie, Y.; Zhang, D. Nonsinusoidal motion effects on energy extraction performance of a flapping foil. Renew. Energy 2014, 64, 283–293. [Google Scholar] [CrossRef]
- Ericsson, L.; Reding, J. Fluid dynamics of unsteady separated flow. Part II. Lifting surfaces. Prog. Aerosp. Sci. 1987, 24, 249–356. [Google Scholar] [CrossRef]
- Digavalli, S. Dynamic Stall of NACA 0012 Airfoil in Laminar Flow. Ph.D. Thesis, MIT, Cambridge, MA, USA, 1993. [Google Scholar]
- Garcia, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Faller, W.E.; Schreck, S.J. Unsteady fluid mechanics applications of neural networks. J. Aircr. 1997, 34, 48–55. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balam-Tamayo, D.; Málaga, C.; Figueroa-Espinoza, B. Numerical Study of an Oscillating-Wing Wingmill for Ocean Current Energy Harvesting: Fluid-Solid-Body Interaction with Feedback Control. J. Mar. Sci. Eng. 2021, 9, 23. https://doi.org/10.3390/jmse9010023
Balam-Tamayo D, Málaga C, Figueroa-Espinoza B. Numerical Study of an Oscillating-Wing Wingmill for Ocean Current Energy Harvesting: Fluid-Solid-Body Interaction with Feedback Control. Journal of Marine Science and Engineering. 2021; 9(1):23. https://doi.org/10.3390/jmse9010023
Chicago/Turabian StyleBalam-Tamayo, David, Carlos Málaga, and Bernardo Figueroa-Espinoza. 2021. "Numerical Study of an Oscillating-Wing Wingmill for Ocean Current Energy Harvesting: Fluid-Solid-Body Interaction with Feedback Control" Journal of Marine Science and Engineering 9, no. 1: 23. https://doi.org/10.3390/jmse9010023
APA StyleBalam-Tamayo, D., Málaga, C., & Figueroa-Espinoza, B. (2021). Numerical Study of an Oscillating-Wing Wingmill for Ocean Current Energy Harvesting: Fluid-Solid-Body Interaction with Feedback Control. Journal of Marine Science and Engineering, 9(1), 23. https://doi.org/10.3390/jmse9010023





