Abstract
Concerns about the potential environmental impacts of geophysical surveys using air gun sources, coupled with advances in geophysical surveying technology and data processing, are driving research and development of commercially viable alternative technologies such as marine vibroseis (MV). MV systems produce controllable acoustic signals through volume displacement of water using a vibrating plate or shell. MV sources generally produce lower acoustic pressure and reduced bandwidth (spectral content) compared to air gun sources, but to be effective sources for geophysical surveys they typically produce longer duration signals with short inter-signal periods. Few studies have evaluated the potential effects of MV system use on marine fauna. In this desktop study, potential acoustic exposure of marine mammals was estimated for MV and air gun arrays by modeling the source signal, sound propagation, and animal movement in representative survey scenarios. In the scenarios, few marine mammals could be expected to be exposed to potentially injurious sound levels for either source type, but fewer were predicted for MV arrays than air gun arrays. The estimated number of marine mammals exposed to sound levels associated with behavioral disturbance depended on the selection of evaluation criteria. More behavioral disturbance was predicted for MV arrays compared to air gun arrays using a single threshold sound pressure level (SPL), while the opposite result was found when using frequency-weighted sound fields and a multiple-step, probabilistic, threshold function.
1. Introduction
Compressed air sources, commonly referred to as seismic air guns, are the most common marine geophysical survey sound source for oil and gas exploration [1] and are also used for construction siting and studying subsea geomorphology. Substantial technological and geophysical data processing advancements, combined with concerns about potential effects of seismic air gun sources on marine fauna, are driving a resurgence in research and commercial development of alternate technologies. Vibroseis technology, used extensively on land, has been investigated for marine use since the 1970s, but it had limited success until recently.
Marine vibroseis (MV) systems produce controllable acoustic signals through volume displacement of water using a vibrating plate or shell that, unlike air guns, produce broadband acoustic signals when an ejected air bubble collapses in water. The output signals of MV are often narrowband tones or swept frequency signals, but they can be tuned to produce a variety of waveforms (e.g., pseudorandom noise, upsweeps, and downsweeps). Compared to air gun signals, MV signals are generally lower in zero-to-peak sound pressure level (PK) and root-mean-square sound pressure level (SPL), and they have reduced bandwidth [2,3,4]. To obtain enough return of acoustic energy for seismic data processing, MV signals are typically longer waveforms with shorter inter-signal intervals than air guns.
This study builds on previous modeling assessments of MV sources [5], comparing signal characteristics and estimated sound exposures to assess the potential effects on marine mammals using MV versus air gun sources. Here, modeled results for a generic MV array configuration are compared to a realistic operational air gun array, in three acoustically different hydrocarbon-producing basins. Except where otherwise indicated, acoustical terminology follows ISO 18405:2017 [3]. Underwater acoustic metrics used in this study are listed in Table 1.

Table 1.
List of underwater acoustic metrics. dB: decibel; µPa: micropascal.
2. Methods
2.1. Scenarios
Marine geophysical surveys are performed globally in widely different ocean environments where differing biota may be present. To address this variability, three survey environments were defined (Table 2) based on water depth regimes, the likely occurrence of oil and gas exploration, and the presence of marine mammals: a Transition Zone offshore Indonesia (10–25 m), a Shallow Water area in the northern North Sea (110–130 m), and a Deep Water area in the Gulf of Mexico (>1000 m). In each study area, the source array, survey design, and month were selected from the most common survey parameters and operational seasons. In total, four scenarios were evaluated: one in the Transition Zone, two in the Shallow Water area, and one in the Deep Water area (Table 2).

Table 2.
Summary list of scenarios.
MV and air gun arrays were configured to produce a similar broadband energy source level (ESL) in the vertical direction: 223 dB re 1 µPa2·s m2 per sweep for the MV array and 218–233 dB re µPa2·s m2 per pulse for the air gun array. Two survey patterns were evaluated: a tight-spaced (100 m) pattern and a wide-spaced (500 m) pattern. A tow speed of 2.3 m/s (4.5 knots) and acquisition spacing of 25 m was used for all surveys.
2.2. Comparison
To compare potential effects on marine mammals from sounds produced by MV and air guns, we compared the characteristics of modeled received signals and estimated marine mammal exposure to injury and disturbance thresholds. The received signal characteristics studied were PK, sound exposure level (SEL), pulse duration, duty cycle, and the time and frequency domain representations of the received signal. To calculate the received pulse duration, the SPL was calculated using a 0.125 s sliding window and compared to the estimated ambient level in each region (see Section 2.3.2. and Section 2.3.4). The duty cycle was defined as the percentage of time when the received signal was more than 6 dB above ambient level (see Section 2.3.4).
The probability of detecting and discriminating a signal in the presence of noise increases as a signal becomes louder relative to the noise [6]. The signal-to-noise ratio (SNR) is often used in signal detection theory to estimate when a signal can be reliably detected. While humans can detect speech in noise when the signal is about the same level as the noise (SNR ≈ 0 dB), many factors contribute to this performance such as signal redundancy and the direction of the signal compared to the direction of the noise (e.g., [7]). Given that in this study we did not know the amount of redundant information in the signal nor did we know the direction of the signal relative to the noise, we assumed that reliable detection would occur when the signal had a sound pressure level 6 dB higher than the ambient noise. The critical ratio level is the difference between the SPL of a barely audible pure tone in the presence of a continuous noise of constant spectral density and the spectral density level (SDL) for that noise [3]; it depends on frequency and duration of the signal. In other words, it is the minimal ratio between a signal and noise levels at which the signal can be perceived. For marine mammals, the critical ratio level is ~10 to 35 dB re 1 Hz [8]. The chosen SNR threshold of 6 dB, for a noise bandwidth of 25 kHz, corresponds to a ratio of 50 dB re 1 Hz, which exceeds the largest critical ratio level for marine mammals, indicating that the chosen SNR threshold is conservative. In cases where detection requires a greater SNR (e.g., the signal is relatively new or non-redundant, or the direction of the signal is the same as that of the noise), the reported pulse duration and duty cycle would be overestimates. In cases where animals could detect signals closer to ambient levels (i.e., for smaller SNR), the reported values would be underestimates.
These received signal characteristics were compared at multiple distances from the sources. This comparison highlights the differences between the air gun array impulsive sounds (typically <<1 s) and the MV array non-impulsive sounds (>>1 s) [9,10]. Impulsive and non-impulsive sounds affect marine life differently, especially in terms of their potential to cause injury [9,11]. Thus, the inherent difference between the sources required the application of different criteria when predicting and comparing their potential effect on marine mammals. The relative novelty of the MV technology and lack of research on its effect on marine mammals means, however, that no effect criteria or guidelines are specific to this type of seismic source. The comparison of received signal characteristics may be useful in the development of MV-specific effect criteria.
Estimated marine mammal exposure to injury and disturbance thresholds were also compared. These exposure estimates were calculated using an agent-based model (see Section 2.3.5) and the current effect criteria that are most likely to be applied, based on the best available science today.
The injury criteria recommended by Southall et al. [12] and the US National Marine Fisheries Service (NMFS) [13] were used to calculate exposure estimates. They are the most commonly used criteria for estimating the potential for injury to exposure to air gun sounds, and both criteria provide acoustic thresholds for the onset of permanent threshold shift (PTS) for impulsive (air gun array) and non-impulsive (MV array) sounds. They recommend using dual criteria for assessing exposures to potentially injurious sound levels: a frequency-weighted SEL metric, which accumulates over a set exposure duration (i.e., 24 h), and a PK metric, which is a measure of acute exposure to high-amplitude sounds. These criteria also divide marine mammals into functional hearing groups (low-, high-, and very high-frequency cetaceans, phocids, and otariids [12]), each with different threshold levels and weighting functions applied to the sound field to account for the hearing sensitivity as a function of frequency for the hearing group. The auditory weighting functions associated with the Southall et al. [12] set of criteria are similar to those recommended by the NMFS [13], only the name of the hearing groups differ. Here, the NMFS [13] names have been used; Table 3 shows the PTS onset thresholds used in this study.

Table 3.
Summary of PTS onset acoustic thresholds from NMFS [13]. Lpk, flat: unweighted zero-to-peak sound pressure level referenced to 1 µPa; LE: frequency-weighted sound exposure level accumulated over a 24 h period referenced to 1 µPa2·s; the subscript associated with LE thresholds indicates the designated hearing group and the associated frequency-weighting function.
Despite numerous studies on behavioral responses of marine mammals to sound, there is little consensus among the scientific community on the most appropriate approach for assessing noise as an impact producing factor. Behavioral responses to sound are highly variable and depend on the context in which a sound is received. Many factors may contribute to the likelihood of a response in addition to the received sound level [9,14]. Here, two different criteria were used to evaluate potential behavioral disturbance. The first set of criteria involves thresholds of unweighted SPL as currently used by NMFS [15]: 160 dB re 1 µPa for impulsive sounds and 120 dB re 1 µPa for non-impulsive sounds. These thresholds have been used for many years by NMFS and other agencies around the world to assess behavioral impacts from various sound-producing offshore projects (seismic or other). Alternative methods to these simplistic thresholds that are based on observations of mysticetes alone [16,17,18,19], have been proposed (e.g., [14,20]). Alternative criteria used in this study include frequency-weighted SPL step functions proposed by Wood et al. [21] for impulsive sounds, and frequency-weighted SPL values adopted by the US Department of the Navy (DoN) [22] for non-impulsive sounds. These criteria associate a series of increasing sound level thresholds with increasing probability of behavioral response. The DoN criterion uses a smooth continuous function, adapted from Feller [23]. We discretized the DoN function at 10%, 50% and 90% probabilities of response, corresponding to the Wood et al. [21] step functions, giving weighted SPL of 155, 165, and 180 dB re 1 µPa, respectively.
2.3. Computation
2.3.1. Sources Levels
Marine Vibroseis (MV)
Few measured output signals from marine vibrators were publicly available at the time of this study; none showed spectral levels at more than ~100 Hz. The MV array layout and synthetic source waveform [3] in this study were based on publicly available information for General Dynamic’s CoHerent Acoustic Modulation Projector (CHAMP) system [24]. This system consists of three strings of six identical vibrators units (18 elements in total) towed at 6 m depth (Figure 1). It was designed to produce signals at frequencies between 5 and 100 Hz and includes an adaptive, in-line, compensation filter that uses acceleration data at the piston assembly for gain control (along with other controller technology) to reduce sound levels at frequencies outside the desired frequency band [25].
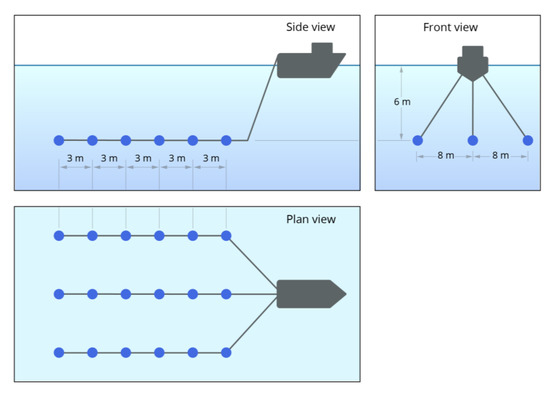
Figure 1.
Illustration of MV layout B. Port and starboard arrays are assumed to be identical.
In general, three signal types are possible from MV elements: linear frequency sweeps, logarithmic frequency sweeps [26], and pseudorandom noise (PRN) [27,28,29,30,31]. Here, we studied the most common signal type, a linear frequency upsweep, with specifications within the Marine Vibrator Joint Industry Project (MVJIP) guidelines [32,33]. This input signal is defined as:
where df/dt is positive (upsweep), fo is the starting frequency, and A(t) is the amplitude of the signal. The synthetic signal is a 5 s linear upsweep from 5 to 100 Hz, with a 10 dB amplitude ramp up from 5 to 10 Hz and cosine taper of 0.1 s at the start and end of the signal to reduce transients produced in real systems during abrupt signal changes. Harmonics will arise from distortion of signals in marine vibrator systems, but their nature is not empirically characterized. Harmonics were added to the synthetic MV signal based on the progression of a damped harmonic oscillator whose amplitude decreased linearly with time and exponentially with harmonic order. For this study, the amplitude of the source waveform of one MV element was set to 5 kPa (zero-to-peak source level (SLPK) [34] of 194 dB re 1 µPa m), resulting in an energy source spectral density level (ESSL) [35] of 178 dB re 1 µPa2·s m2/Hz from 10 to 100 Hz. Harmonics were assumed to be at least 20 dB below the main signal spectral level for frequencies ≤150 Hz (i.e., with an ESSL of 158 dB re 1 µPa2·s/Hz at 5 Hz, decreasing linearly with time and exponentially with harmonic order) and at least 40 dB less than the main signal spectral level for frequencies ≥150 Hz, as prescribed by the MVJIP guidelines [32,33].
The array source waveform was modeled by summing the contributions of the 18 individual MV elements using linear superposition of signals from individual vibrator elements. While the signal parameters were well informed by industry experts involved in developing the technology, the modeled output signals have not been compared to measured MV signals. Mutual impedance (the load on one piston due to the pressure waveform from the other elements in the array) may be important for some arrays [36,37,38]. This physical effect is not currently implemented in the MV source waveform model because of the lack of available output signal measurements that would allow proper benchmarking of the model. The studied MV array synthetic sound waveforms and ESSL are presented in Figure 2; the corresponding ESSL is shown for two frequency ranges (1 Hz to 25 kHz; Figure 2, left). The array signal outputs (source levels) are summarized in Table 4.
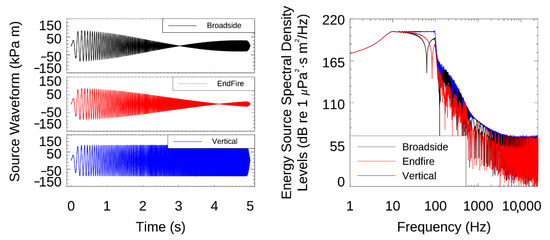
Figure 2.
MV array 5–100 Hz linear upsweep (left) source waveform and (right) energy source spectral density levels (ESSL) for broadside (perpendicular to tow direction), endfire (directly aft of the array), and vertical directions. The ESSL is shown on two frequency scales (1 Hz to 25 kHz). Tow depth 6 m.

Table 4.
Marine vibroseis source levels. SLPK: zero-to-peak source level [34]; SL: source level [3]; ESL: energy source level [3].
Air Gun Arrays
Seismic air gun arrays comprise individual air guns with different air chamber volumes. Air gun arrays are configured to generate a desired dominant low-frequency beam pattern by placement of the individual air guns. Two hypothetical air gun arrays were modeled in this study: a relatively small volume, 12,290 cm3 (750 in3) array operating in the Transition Zone (scenario 1), and a larger 67,680 cm3 (4130 in3) array operating in the Shallow Water and Deep Water areas (scenarios 2–4). The smaller volume array consisted of one triangular cluster towed at 6 m depth (at the cluster center; Figure 3). The cluster was made of three identical 4100 cm3 (250 in3) air guns with a 0.9 m spacing separation between elements. The larger volume array consisted of 31 elements on three strings, towed at 6 m depth (Figure 4), with individual volumes ranging from 660 to 4100 cm3 (40 to 250 in3). In each array, the air guns simultaneously released compressed air pulses at a firing pressure (chamber pressure relative to atmospheric pressure) of 13.8 MPa (2000 lbf/in2).
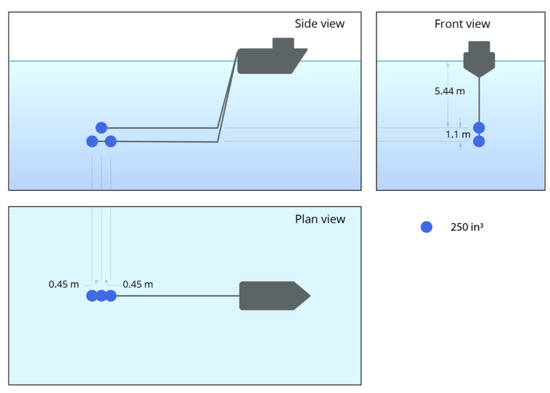
Figure 3.
A 750 in3 air gun array.
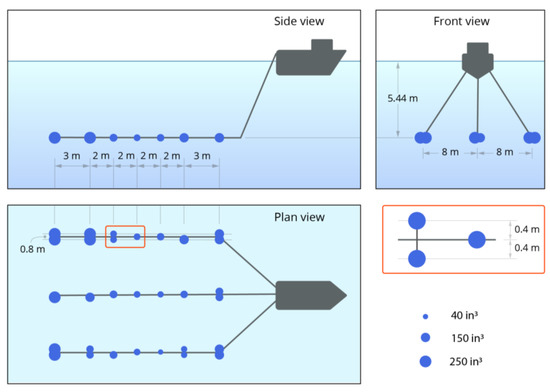
Figure 4.
A 4130 in3 air gun array.
The source waveforms of the air gun arrays were predicted using JASCO’s Air gun Array Source Model (AASM) [39], which is based on the physics of oscillation and radiation of air gun bubbles [40]. Physical effects accounted for in the simulation include pressure interactions between air gun array elements, port throttling, bubble damping, and generator-injector element [41,42,43]. The high-frequency module of AASM uses a stochastic simulation to predict the sound emissions of individual elements above 800 Hz using a multivariate statistical model. A global optimization algorithm tunes free parameters in the model to a large library of air gun source waveforms. AASM has been tuned to fit a large library of high-quality, air gun source, waveform data [44].
The horizontal source waveforms and corresponding ESSL for each air gun array were computed at frequencies up to 25 kHz (Figure 5; Table 5). Figure 5 (right) presents the ESSL over the same frequency range (1 Hz to 25 kHz) as for the MV array results (Figure 2); levels above 2 kHz decreased at an average rate of 23 dB per decade. The source waveforms consisted of a strong primary peak related to the initial pulse followed by a series of pulses associated with bubble oscillations. Most acoustic energy was produced at frequencies below 500 Hz, and the spectra showed peaks and nulls resulting from interactions between the array elements (Figure 5 right).
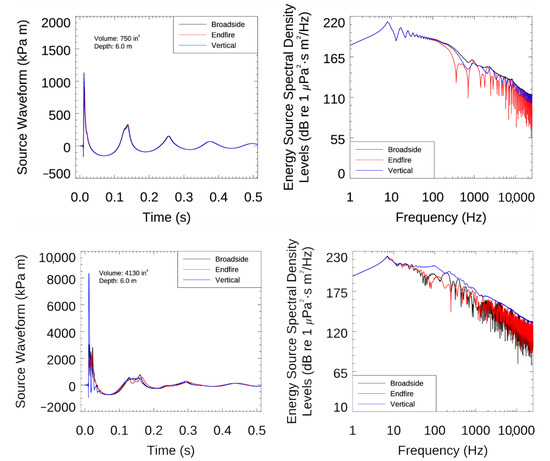
Figure 5.
(Top) 12,290 cm3 (750 in3) and (bottom) 676,780 cm3 (4130 in3) air gun array (left) source waveform and (right) energy source spectral density levels (ESSL) for broadside (perpendicular to tow direction), endfire (directly aft of the array), and vertical directions. The ESSL is shown on two frequency scales (1 Hz to 25 kHz). Surface ghost effects are not included in the presented source waveform and spectra.

Table 5.
Air Gun array source levels. SLPK: zero-to-peak source level [34]; SL: source level [3]; ESL: energy source level [3].
2.3.2. Sound Propagation
Sound Propagation Models
Sound propagation was modeled using JASCO’s Marine Operations Noise Model (MONM), which combines a wide-angle parabolic equation model [45,46,47,48] and a ray-tracing model [49], and JASCO’s Full Waveform Range-dependent Acoustic Model (FWRAM; [50]). Both models have been extensively validated with experimental data from several underwater acoustic measurement programs [48,51,52,53,54,55,56,57,58]. MONM and FWRAM incorporate the following site-specific environmental properties: a bathymetric grid of the modeled area, underwater sound speed as a function of depth, and a geoacoustic profile based on the overall stratified composition of the seafloor. The models account for the reflection loss at the seabed, which results from partial conversion of incident compressional waves to shear waves at the seabed and sub-bottom interfaces, and they include wave attenuations in all layers.
Per-pulse SEL sound fields over the frequency range 4 Hz–25 kHz, in decidecade frequency bands, were predicted using MONM. (A decidecade is one tenth of a decade. One tenth of a decade is approximately equal to one third of an octave. For this reason, a decidecade is sometimes incorrectly referred to as a “one-third octave”.) Three-dimensional (3-D) acoustic fields were modeled by computing the propagation loss along 36 two-dimensional (2-D) vertical planes radiating from the source with a 10° angular step and adding the directional source levels (presented in Section 2.3.1). The full-wave modeling approach (FWRAM) was used to calculate time-domain waveforms along eight radials to then calculate a range-dependent conversion factor. This factor was applied to convert the predicted sound fields in terms of per-pulse SEL to SPL. Sound fields in terms of PK were calculated directly from the time-domain waveforms. All sound fields were modeled to a distance of up to 30 km in the Transition Zone and 50 km in the Shallow Water and Deep Water areas. The computation range step decreased from 30 to 1 m with increasing frequency. The output field was sampled at depths spanning the entire water column, with step sizes ranging from 1 to 100 m, increasing with depth.
Environmental Parameters
To address the variability in ocean environments where geophysical surveys are performed, three sound propagation environments were modeled (Table 2). Profiles of geoacoustic properties characterizing each survey area (Table 6) were developed using an empirical relationship between the sediments physical and acoustic properties [59,60]. The area-specific sediment properties (i.e., grain sizes and sediment porosity) were gathered from publicly available borehole data and borehole logs. The seabed in the Transition Zone (Java Sea) consisted of young sediments made of sand and muddy swamp deposits, reaching a thickness of ~20 m [61]. This surficial sediment layer overlaid claystone with sandstone, conglomerates, and limestone [62]. The Shallow Water area (Northern North Sea) was modeled with a hard to very hard sandy clay layer, 700 m thick [63]. The Deep Water area (Gulf of Mexico) was modeled with a layer of unconsolidated sediments at least several hundred meters thick [64].

Table 6.
Estimated geoacoustic properties of the sub-bottom sediments as a function of depth below the seafloor. P wave: compressional wave; S wave: shear wave.
One representative sound speed profile in each area was derived from the US Naval Oceanographic Office’s Generalized Digital Environmental Model (GDEM) V 3.0 [65,66]. Monthly averaged temperature–salinity profiles were converted to sound speed profiles as described by Coppens [67]. The final profiles represent the monthly climatic conditions in the water column.
In the Transition Zone, the sound speed profile for July was used, representing a time of the year suitable climate wise (June to August) for geophysical surveys for oil and gas exploration (known as seismic surveys) and the most suitable for long-distance propagation. In the Shallow Water area, the profile for August was assumed to best represent a time of the year suitable climate wise for survey operations. In the Deep Water area, the profile for February was used, representing the time of the year most suitable for long-distance propagation, due to the weak surface sound channel to a depth of 100 m, a strong downward refracting environment to 800 m depth, and a weak upward refracting environment below that depth. Figure 6 presents the profiles associated with each survey area.
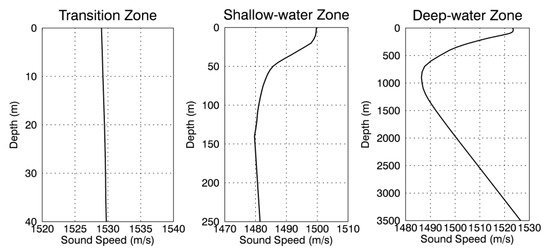
Figure 6.
Sound speed profile for (left) July in the Transition Zone, (middle) August in Shallow Water, and (right) February in Deep Water.
Ambient Sound Levels
Ambient spectral levels (Figure 7) were estimated based on published data near the modeled areas or in similar environments. Broadband levels were used to compute the received signal duration and duty cycle (as defined in Section 2.2 and Section 2.3.3) and spectral levels (integrated over the period of the modeled received signal) were compared to the modeled received spectral levels (presented in Section 3.1).
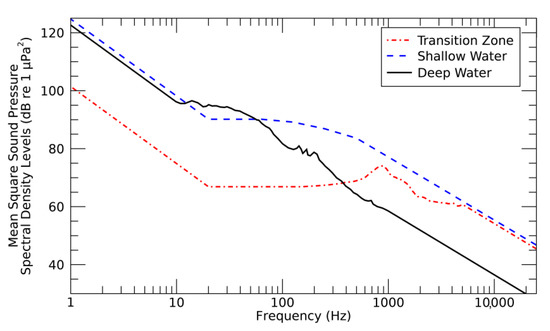
Figure 7.
Estimated ambient sound spectral density levels in the survey areas (Transition Zone, Shallow Water, and Deep Water).
Published data on ambient sound levels in the Java Sea were inadequate for this study; representative ambient levels in the Transition Zone area were based on measurements from the shallow waters of the southwestern Bay of Bengal [68]. The measured levels during the transition period between monsoon seasons were used to derive spectral levels at frequencies between 150 and 5000 Hz. For frequencies 20–150 Hz, the spectral levels were assumed to be equal to the level at 150 Hz. Ambient levels measured in four decidecade frequency bands, centered at 63, 125, 250, and 500 Hz [69,70], were used to estimate spectral levels for the Shallow Water survey area. The spectral levels were interpolated between 56 and 560 Hz based on the published decidecade-band SPL values. For frequencies 20–56 Hz, the levels were assumed to be equal to the level at 56 Hz. Ambient spectral levels measured at the Green Canyon monitoring station between 10 and 1000 Hz [71] were used for the Deep Water survey area. In all areas, the spectral levels were extrapolated below 20 Hz by assuming an 8 dB per decade increase with decreasing frequency, and above the maximum available spectral level, assuming a 22 dB per decades decrease with increasing frequency [72].
2.3.3. Surveys Characteristics
In all scenarios, both sources were simulated with a 2.3 m/s (4.5 knots) tow speed and emitting one pulse every 25 m along the survey lines. Therefore, the duty cycle of the MV array was 45% (5 s sweep every 11 s) and the duty cycle of the air gun array was <9%. Marine animal exposure was calculated over a 24 h of survey and averaged over 7 days (Section 2.3.5). To do so, per-pulse sound fields were computed at three locations in each survey area, with different water depths, and transposed geographically along the survey lines to simulate a moving source. Because of the low variability in water depth within the Shallow Water survey area (North Sea), the per-pulse sound field was calculated at one location, in the center of the survey area. Two survey types were modeled: tight surveys (scenarios 1 and 2; Table 2) and wide surveys (scenarios 3 and 4; Table 2). The adjacent lines in the tight survey were surveyed consecutively using half “dog-bone” turns. A “racetrack” pattern was used for the wide survey with half-circle turns with a radius of 2500 m (5 survey lines). For both survey types, the arrays were fully active during the turns (as opposed to using one mitigation element or ramp up).
2.3.4. Received Signal Characteristics
PK, SEL, duration of the signal, duty cycle, and time and frequency domain representations of the received signal were calculated as a function of distance from the sources from the synthetic pulses modeled by FWRAM. Broadband SPL (4 Hz to 25 kHz) was calculated over a 0.125 s sliding time window (as an approximate integration time of the mammalian ear [73], which is believed to be similar for land and aquatic mammals [74,75]). The time interval over which the SPL exceeded the estimated broadband (5–25,000 Hz) ambient level by more than 6 dB was used as a proxy for the audible duration of the signal. This approach was not species specific; it did not consider frequency-dependent hearing sensitivities of various species. The duty cycle was defined as the percentage of time, over a time interval common to all sources, when the broadband SPL of the received signal was more than 6 dB above ambient level; a common period of 11 s was chosen.
The per-pulse sound field modeled at the center location of each survey area was used to calculate the received signal characteristics. The signal characteristics were sampled at up to 10 distances between 50 m and 50 km from the source along one representative azimuth.
2.3.5. Agent-Based Model
The acoustic effects criteria (Section 2.2) indicate the lowest received sound levels that could result in injury or behavioral disturbance. To use the criteria in a realistic context, the sound levels received by animals must be estimated considering the time-evolving distance of animals relative to a source. An agent-based model was used to predict the probability that animals could be exposed to sound levels exceeding sound threshold criteria. In this approach, simulated animals (animats) moving in a realistic way are used to sample the sound fields. The combined received levels of many animats generates a probability density function (PDF) predicting animal exposure in the evolving sound field. This repeated random sampling (Monte Carlo method) yields an estimate of the probability that animals are exposed above effects thresholds.
The JASCO Animal Simulation Model Including Noise Exposure (JASMINE) used in this study is based on the open-source Marine Mammal Movement and Behavior Model (3MB) [76], one of several animal movement models [76,77,78], and is integrated with MONM and FWRAM acoustic propagation models (Section 2.3.2). JASMINE includes survey source track inputs and allows animats to change behavioral states based on time and space dependent variables, such as received sound level history.
JASMINE’s behavioral input parameters include travel rate and direction, dive details and surface intervals. Animats were randomly seeded within the simulated environment at an animat density of 0.5 km−2. The simulation area for potential behavioral responses was limited in this analysis to a maximum distance of 30 km from the simulated survey tracks in the Transition Zone (scenario 1) and 50 km in other areas (scenarios 2–4). Seven-day simulations were modeled for each scenario (Section 2.3.3) to achieve multiple examples of exposures and to mimic the approximate scale of the animal movement data [76]. The average number of exposures above threshold levels per 24 h period was calculated over the duration of the simulation. The thresholds used (discussed in Section 2.2) were based on the recommendation by NMFS [13].
To obtain the number of real-world animals predicted to be exposed to levels at or exceeding threshold values, the output PDF was scaled by the ratio of the estimated real-world density to simulation density. Each survey area contains more than 20 species of marine mammals. We selected a representative species from each functional hearing group (as recommended by Southall et al. [12] and NMFS [13]) in each area. Other behaviorally sensitive species were added to represent different behavioral categories, such as Cuvier’s beaked whales in the Deep Water survey area. The species considered are listed in Table 7.

Table 7.
Representative species used in exposure models for each survey area, classified by hearing group, as defined by NMFS [13].
Density estimates in Indonesia (Transition Zone) were from a variety of sources, including best estimates for humpback whale using habitat-based models [79]. Bottlenose dolphin density estimates were from Kreb and Budiono [80], finless porpoise density estimates were based on Shirakihara et al. [81], and sea turtle density estimates were best estimates from Reyne et al. [82]. Density estimates for most marine mammal species in the North Sea were obtained from Hammond et al. [83], with the assumption that densities were constant across seasons. Harbor seal density estimates were from the US Navy OPAREA Density Estimate NODE; NODE; [84] model. The marine mammal density data used in this assessment for the Gulf of Mexico region were from the Duke University Marine Geospatial Ecological Laboratory model [85]. The sources of animal density information in Indonesia are limited relative to the compiled data and models for the Gulf of Mexico [85], so their uncertainties were higher. Because the same marine mammal and sea turtle densities were used in each area, the same level of uncertainty relating to animal density was expected for both source types.
3. Results
3.1. Signal Characteristics with Distance
The received signal characteristics were compared to highlight the differences between the air gun array impulsive sounds and the MV array non-impulsive sounds. The modeled sound fields were sampled at 10 distances along one direction in each survey area; the direction was selected to be representative of the entire (360°) field. At each sampling distance, the PK, SEL, duration of the signal, and duty cycle were calculated as the maximum broadband (4 Hz to 25 kHz) value over all modeled depths. The results are presented in Figure 8.
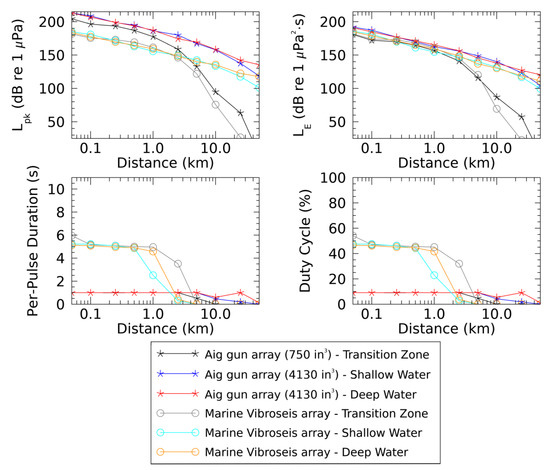
Figure 8.
Received peak sound pressure levels (Lpk; top left), sound exposure levels (LE; top right), pulse duration (bottom left) and duty cycle (bottom right) as a function of distance. LE, pulse duration and percentage of quiet time are calculated over a common time interval of 11 s.
Because of propagation loss effects, the difference in received PK (Figure 8, top left) between MV and air gun sounds decreased somewhat as the distance from the sources increased. Our results indicated, however, that large differences in PK remained over several kilometers in all modeled environments. In the Transition Zone, PK values remained at least 10 dB greater for the air gun array (black line; Figure 8) than the MV array (grey line; Figure 8), up to 30 km (maximum modeled distance). In the Shallow Water and Deep Water environments, the air gun array PK values (blue and red lines; Figure 8) remained at least 20 and 17 dB greater than those for the MV sources (cyan and yellow lines; Figure 8), respectively, up to 50 km (maximum modeled distance).
Because MV arrays have lower source levels (SL; compare Table 4 and Table 5), the sweeps produced must have a longer duration to result in a signal with similar SEL as air gun array pulses (Figure 8, top right and bottom left). The longer duration means shorter periods of quiet time between MV sweeps than between air gun pulses (~55% quiet time per period (the complement of duty cycle) for MV array at less than 1 km, compared to 90% for air gun array; see bottom right plot in Figure 8). However, because the SL for the MV array was lower than for the air gun arrays, its received SPL decreased below detectable levels (considered here as 6 dB above ambient levels) at a shorter distance. In the studied environments, this resulted in the signal duration for the MV array becoming shorter than that of the air gun array, and the duty cycle becoming shorter, between 2 and 5 km from the sources.
Figure 9 presents the received signals as sound pressure (left) and spectral density levels (right). For conciseness, only the results in the Shallow Water area, sampled in approximately the middle of the water column (50 m), are presented here; results were similar for all scenarios. The dash line on the spectral density levels plots represent the ambient levels integrated over the same period as the modeled received signal (10 s for the MV array and 1 s for the air gun array). Note that the same scale was used to present the sources spectral density levels (left), but different scales had to be used to present the sound pressure (right).
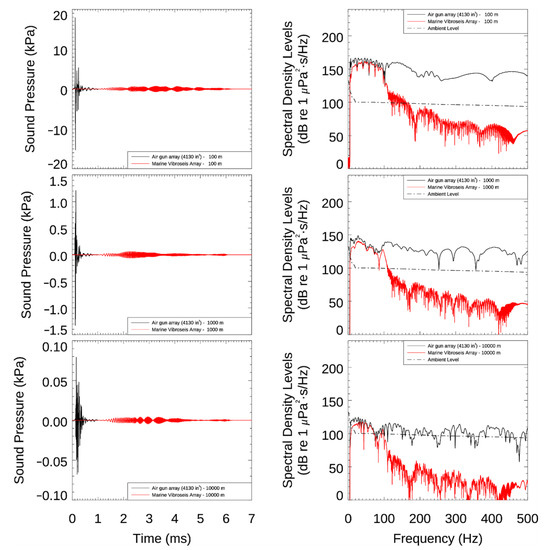
Figure 9.
MV array (red) and 4130 in3 air gun (black). Sound pressure (left) and energy spectral density levels (right) received at three sampling locations: 100 m (top), 1000 m (middle), and 10 km (bottom). The ambient level (dashed lines, right) was based on the integration period of 10 s. Results are shown along the tow direction (0°) at a depth of 50 m in the Shallow Water area (scenario 2; Table 2).
Figure 9 shows that at all modeled distances both sources produced similar spectral levels below 100 Hz, while the spectral levels at higher frequencies were much higher for the air gun array. Here, results show MV sound above 200 Hz was below ambient levels at distances as short as 100 m, while spectral levels for the air gun array in the same frequency band remained above ambient levels for several (>10) kilometers.
Per-pulse frequency-weighted SEL sound fields over the frequency range 4 Hz–25 kHz (in decidecade frequency bands) were predicted using MONM and then input to JASMINE. Figure 10 presents an example of received frequency-weighted SEL for the MV array (left) and the air gun array (right), at 1000 m from the arrays in the middle of the water column (50 m; scenario 2). This example illustrates the effect of frequency weighting on the received sound field, following the NMFS guidance [13].
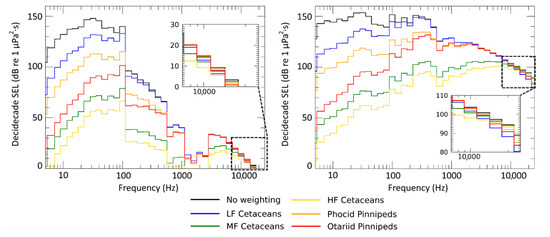
Figure 10.
Example of received frequency-weighted sound exposure levels (SEL) in decidecade bands for the MV array (left) and the air gun array (right). Results are shown at a distance of 1000 m from the arrays, along the tow direction (0°), at a depth of 50 m in the Shallow Water area (scenario 2; Table 2). The frequency weighting was applied according to the designated NMFS [13] hearing group and the associated frequency-weighting functions.
3.2. Exposure Estimates from Agent-Based Model
The agent-based model was used to estimate marine mammal exposure to injury and behavioral thresholds for each scenario. The mean number of marine mammals exposed to sound levels above injury thresholds based on NMFS guidelines [13] due to MV and air gun sounds are presented in Table 8. The mean number of marine mammals exposed to sound levels above behavioral thresholds based on frequency-weighted step functions and on single unweighted values (discussed in Section 2.2) are shown in Table 9.

Table 8.
Mean number of marine mammals expected to be exposed to sound levels at or above injury thresholds during a 24 h survey period. Peak sound pressure level (PK) and sound exposure level (SEL) thresholds based on NMFS [13]. SEL sound fields were frequency-weighted and accumulated over a 24 h survey period according to the NMFS guidelines [13].

Table 9.
Mean number of marine mammals expected to be exposed to sound levels at or above behavioral thresholds during a 24 h survey period. Step function thresholds are based on DoN [22] for MV array and Wood et al. [21] for the air gun arrays; single-value thresholds are based on NMFS [86].
Although the ESL of MV and air gun sounds were similar, applying the frequency-weighting functions and the SEL-based injury criteria resulted in fewer predicted exposures to levels at or above injury thresholds from the MV array than the air gun array (Table 8) because the MV energy is concentrated at lower frequencies than the air gun array (Figure 10). In this study, however, SEL for both sources quickly decreased to below injury thresholds, such that few marine mammals were predicted to be exposed to injurious acoustic levels in any of the scenarios (Table 8).
Increasing the width between survey lines (scenarios 2 and 3; Table 2), increased the area ensonified at or above the injury thresholds for air gun array sounds. This resulted in a small increase (≤0.7) in the number of marine mammals potentially exposed to injurious acoustic levels from the air gun array. The variation in the survey line spacing did not affect the results for the MV array.
A change in behavioral criteria resulted in the reversal of conclusions regarding which source was likely to cause more behavioral disturbance. Results showed a higher number of animals exposed to acoustic levels at or above the regulatory-defined thresholds for behavioral response (single unweighted values) when exposed to MV sounds compared to air gun sounds. In contrast, when frequency-weighted step functions were used, a higher number of animals were predicted to be exposed to sound levels resulting in behavioral responses when exposed to air gun sounds versus MV sounds.
4. Discussion
From a biological point of view, one advantage of MV arrays is their lower SLPK; MV arrays are expected to have a lower potential than air gun arrays to cause onset of permanent or temporary threshold shift in marine mammals or to cause mortality and injury in fish and other animals. In the current study, SLPK values for the air gun arrays were 21 to 39 dB higher than for the MV array (see Table 5). Our results indicated that a large difference in PK persist over several kilometers (>30 km). Thus, the likelihood of injury due to high PK values was much lower for an MV array than for an air gun array.
To acquire the desired geophysical data, a certain level of energy must be produced by the seismic source. Therefore, for similar SEL and lower PK levels, the MV array must produce a much longer signal than the air gun array. The longer duration means there is less opportunity for “dip-listening” between MV sounds than between air gun pulses. This would appear to be a clear advantage of air guns over MVs in terms of a lower risk of masking effects, but the lower SPL of MV array sounds means the distances within which this masking may occur (considered here as the maximum distance where per-pulse duration was greater than zero) is shorter than for air guns (~5 km for the MV array versus 10 to 50 km for the air gun arrays, for the modeled scenarios). Additionally, if the harmonic content of MV array sounds above ~100 Hz is kept low (i.e., the MV array follows the specifications required by the MVJIP), then potential masking of mid- and high-frequency cetaceans may be negligible and greatly reduced for low-frequency cetaceans.
Responses to disturbance include a variety of effects, ranging from subtle to conspicuous changes in behavior, movement, and displacement. Available detailed data on reactions of marine mammals to air gun sounds (and other anthropogenic sounds) are limited to relatively few species and situations (see reviews in [9,87,88,89,90,91,92]). Behavioral reactions to sound are highly variable and context specific, and they may differ for species, state of maturity, experience, current activity, reproductive state, time of day, and many other factors [9,87,90,91,93,94].
Given the many uncertainties in predicting behavioral responses in marine mammals, it is common practice to assume that behavioral responses will occur if an animal is within a predicted distance, as is done with the single-value criteria currently used by NMFS [86]. Even though MV arrays have lower source amplitudes, the distances to the estimated behavioral response SPL isopleths are longer than for the MV arrays. Therefore, when these single-step threshold criteria were used in exposure modeling simulations, results showed a higher number of animals exposed to MV sounds than air gun sound (Table 9). This was due to the substantially lower NMFS SPL threshold for non-impulsive sounds compared to that for impulsive sounds (120 vs. 160 dB re 1 μPa). It is therefore imperative to either have clear rules for determining the impulsiveness of the sound produced or to develop criteria that do not depend so critically on this distinction. While the duration of a signal at its source has historically been used to separate sources into two groups (impulsive vs. non-impulsive), other metrics such as kurtosis [95], crest factor, and the Harris impulse factor are being proposed to quantify the impulsiveness of ocean sounds [10].
As an alternative to the single-value criteria currently used by NMFS [86], animal exposure to sound potentially resulting in behavioral disturbance was calculated using weighted sound fields to account for the hearing range of the animals, and a 2- or 3-step (depending on the species and activity group) probability of response to impulsive sounds, as proposed by Wood et al. [21], or a continuous probability of response function, for non-impulsive sounds, as used by DoN [22]; the two probability of response functions are similar. Because of the effect of frequency weighting, distances to behavioral disturbance thresholds are much shorter for MV sounds than air gun sounds. Therefore, exposure modeling using the graded probability thresholds resulted in a smaller estimated number of exposures to the MV array than the air gun array (Table 9).
The reversal of conclusions regarding which source was likely to cause more behavioral disturbance depending on the assessment criteria used was notable, although perhaps not surprising given the differences in the criteria (with vs. without frequency weighting; step function vs. single value; difference in thresholds for impulsive vs. non-impulsive sound). If the graded probability of response functions [21,22] better reflects actual behavioral responses when frequency-weighting functions are applied, then MV arrays may elicit substantially fewer behavioral disturbances than air gun arrays. However, the variability in observed behavioral response to anthropogenic sounds [9] and the importance of context [90] means that we do not know how animals might respond to sounds from MV arrays.
Because MV is a new technology still largely under development, there are no data available documenting injury or behavioral responses of marine mammals to sounds produced by this source. Some naval sonar sources produce sounds of similar durations but at somewhat higher frequencies (100–500 Hz for low-frequency active sonar, 1–8 kHz for mid-frequency active sonar). A recent review of behavioral responses to naval sonar source (from 1–8 kHz) shows similarly high levels of variability among species and individuals as observed for other sources [91]. Systematic well-controlled studies of animal responses to MV sounds are necessary before the relative behavioral responses from MV and air gun sources can be meaningfully compared.
5. Conclusions
The goal of this study was to quantify the potential effects of MV array sounds by comparing the signal characteristics and estimate marine mammal exposures associated with geophysical surveys conducted using MV arrays versus air gun arrays. Various survey designs scenarios were selected to allow meaningful comparisons among representative survey operations in three different environmental settings. Because of the difference in signal type (impulsive versus non-impulsive), different acoustic thresholds were necessarily applied for each seismic source, complicating the comparison. Nonetheless, the results of this study provide important insights into the relative potential for the two sources to cause injury and behavioral disturbance.
The lower source amplitudes of MV array sounds mean that they are less likely than air gun arrays to exceed the currently prescribed marine mammal injury thresholds based on PK levels. For arrays with similar energy source levels (ESL), the frequency weighting used in estimating distances to injurious thresholds for most marine mammal hearing groups has a greater filtering effect on the sound field of the MV than the air gun array. This is due to differences in acoustic energy propagating at frequencies outside the main frequency band of interest for seismic surveys; the spectral levels for the MV array are expected to be much lower than that of the air gun array above 100 to 200 Hz. Therefore, MV arrays with well-suppressed harmonics are expected to exceed the studied SEL injury thresholds at shorter distances than air gun arrays with similar ESL. However, sounds from air gun arrays typically decrease to below current injurious thresholds at relatively short distances (tens of meters in this study, depending on the hearing group). None of the scenarios in this modeling study, regardless of source, resulted in more than 25 regulatory-defined injurious exposures (Table 8).
The single-step unweighted SPL thresholds currently used by NMFS [13] resulted in higher estimates of behavioral effects from MV arrays than air gun arrays, primarily as a result of the lower SPL threshold (120 dB re 1 μPa) used for non-impulsive sounds. Because it is unlikely that sounds outside of the hearing range of an animal will result in behavioral response, it can be argued that frequency weighting should be applied and that a more statistical approach should be used when assessing behavioral effects on marine mammals. When the frequency-weighted and multiple-step functions proposed by Wood et al. [21] and DoN [22] were used, the modeled air gun arrays are predicted to cause more behavioral disturbance than the MV array. This is primarily caused by the higher frequency-weighted source pressure levels of air gun arrays resulting in longer distances to nearly equivalent behavioral response threshold levels for the two source types.
Author Contributions
Conceptualization: D.S.I., D.G.Z., R.H.B. and C.D.P.; Formal analysis: M.-N.R.M., D.S.I. and D.G.Z.; Funding acquisition: C.D.P.; Investigation: M.-N.R.M. and R.H.B.; Methodology: M.-N.R.M., D.S.I., D.G.Z. and R.H.B.; Project administration: C.D.P.; Resources: C.D.P.; Software: M.-N.R.M.; Validation: D.G.Z.; Visualization: M.-N.R.M. and D.G.Z.; Writing—original draft: M.-N.R.M., D.S.I., D.G.Z. and and C.D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the E&P Sound and Marine Life Joint Industry Programme (SML JIP).
Acknowledgments
Thanks to Kirsty Speirs and Andrew Feltham with Total, and Michael Jenkerson with ExxonMobil, for their invaluable guidance and information on the various source configurations used in the modeling. Several modelers and scientists contributed to this work, including Z. Alavizadeh, J. Christian, S. Denes, T.J. Deveau, H. Frouin-Mouy, V. Moulton, G. Warner, J. Richardson, M.A. Ainsley, K. Lucke, and D.E. Hannay.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parkes, G.E.; Hatton, L. The Marine Seismic Source, 1st ed.; Springer Science & Business Media: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Carroll, P. A note on synthetic vibroseis sweep generation. Can. J. Explor. Geophys. 1971, 7, 80–82. [Google Scholar]
- International Organization for Standardization. Underwater Acoustics—Terminology; ISO 18405:2017; ISO: Geneva, Switzerland, 2017; p. 51. [Google Scholar]
- Spence, J.H. Seismic survey noise under examination. In Offshore: World Trends and Technology for Offshore Oil and Gas Operations; Endeavor Business Media LCC.: Nashville, TN, USA, 2009; Volume 69. [Google Scholar]
- LGL. Environmental Assessment of Marine Vibroseis; Report for the Joint Industry Programme on E&P Sound and Marine Life; LGL: King City, CA, USA; Marine Acoustics Inc.: Middletown, RI, USA, 2011; p. 207. [Google Scholar]
- Green, D.M.; Swets, J.A. Signal Detection Theory and Psychophysics; Krieger: Huntington, WV, USA, 1974. [Google Scholar]
- Moore, B.C.J. An Introduction to the Psychology of Hearing, 6th ed.; Emerald Group Publishing: Bingley, UK, 2012. [Google Scholar]
- Erbe, C.; Reichmuth, C.; Cunningham, K.; Lucke, K.; Dooling, R. Communication Masking in Marine Mammals: A Review and Research Strategy. Mar. Pollut. Bull. 2016, 103, 15–38. [Google Scholar] [CrossRef]
- Southall, B.L.; Bowles, A.E.; Ellison, W.T.; Finneran, J.J.; Gentry, R.L.; Greene, C.R., Jr.; Kastak, D.; Ketten, D.R.; Miller, J.H.; Nachtigall, P.E.; et al. Marine Mammal Noise Exposure Criteria: Initial Scientific Recommendations. Aquat. Mamm. 2007, 33, 411–521. [Google Scholar] [CrossRef]
- Martin, S.B.; Lucke, K.; Barclay, D.R. Techniques for Distinguishing between Impulsive and Non-Impulsive Sound in the Context of Regulating Sound Exposure for Marine Mammals. J. Acoust. Soc. Am. 2020, 147, 2159–2176. [Google Scholar] [CrossRef]
- Popper, A.N.; Hawkins, A.D.; Fay, R.R.; Mann, D.A.; Bartol, S.; Carlson, T.J.; Coombs, S.; Ellison, W.T.; Gentry, R.L.; Halvorsen, M.B.; et al. Sound Exposure Guidelines for Fishes and Sea Turtles: A Technical Report Prepared by ANSI-Accredited Standards Committee S3/SC1 and Registered with ANSI; ASA S3/SC1.4 TR-2014; ASA Press: Washington, DC, USA; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Southall, B.L.; Finneran, J.J.; Reichmuth, C.J.; Nachtigall, P.E.; Ketten, D.R.; Bowles, A.E.; Ellison, W.T.; Nowacek, D.P.; Tyack, P.L. Marine Mammal Noise Exposure Criteria: Updated Scientific Recommendations for Residual Hearing Effects. Aquat. Mamm. 2019, 45, 125–232. [Google Scholar] [CrossRef]
- National Marine Fisheries Service. 2018 Revision to: Technical Guidance for Assessing the Effects of Anthropogenic Sound on Marine Mammal Hearing (Version 2.0): Underwater Thresholds for Onset of Permanent and Temporary Threshold Shifts; US Department of Commerce: Washington, DC, USA; NOAA: Washington, DC, USA, 2018; p. 167. [Google Scholar]
- Ellison, W.T.; Frankel, A.S. A common sense approach to source metrics. In The Effects of Noise on Aquatic Life; Popper, A.N., Hawkins, A.D., Eds.; Springer: New York, NY, USA, 2012; pp. 433–438. [Google Scholar]
- National Oceanic and Atmospheric Administration. Notice of Public Scoping and Intent to Prepare an Environmental Impact Statement; NOAA: Washington, DC, USA, 2005. [Google Scholar]
- Malme, C.I.; Miles, P.R.; Clark, C.W.; Tyack, P.L.; Bird, J.E. Investigations of the Potential Effects of Underwater Noise from Petroleum Industry Activities on Migrating Gray Whale Behavior. Phase II: January 1984 migration; US Department of the Interior. Minerals Management Service: Cambridge, MA, USA, 1984. [Google Scholar]
- Richardson, W.J.; Würsig, B.; Greene, C.R., Jr. Reactions of bowhead whales, Balaena mysticetus, to drilling and dredging noise in the Canadian Beaufort Sea. Mar. Environ. Res. 1990, 29, 135–160. [Google Scholar] [CrossRef]
- Richardson, W.J.; Würsig, B.; Greene, C.R., Jr. Reactions of bowhead whales, Balaena mysticetus, to seismic exploration in the Canadian Beaufort Sea. J. Acoust. Soc. Am. 1986, 79, 1117–1128. [Google Scholar] [CrossRef]
- Malme, C.I.; Miles, P.R.; Clark, C.W.; Tyack, P.L.; Bird, J.E. Investigations of the Potential Effects of Underwater Noise from Petroleum Industry Activities on Migrating Gray Whale Behavior; US Department of the Interior: Washington, DC, USA; Minerals Management Service: Cambridge, MA, USA, 1983. [Google Scholar]
- Nedwell, J.R.; Turnpenny, A.W.; Lovell, J.; Parvin, S.J.; Workman, R.; Spinks, J.A.L.; Howell, D. A Validation of the dBht as a Measure of the Behavioural and Auditory Effects of Underwater Noise; Department for Business, Enterprise and Regulatory Reform: London, UK, 2007; p. 74. [Google Scholar]
- Wood, J.D.; Southall, B.L.; Tollit, D.J. PG&E offshore 3-D Seismic Survey Project Environmental Impact Report–Marine Mammal Technical Draft Report; SMRU Ltd.: St Andrews, UK, 2012; p. 121. [Google Scholar]
- Department of the Navy (US). Final Supplemental Environmental Impact Statement/Supplemental Overseas Environmental Impact Statement for Surveillance Towed Array Sensor System Low Frequency Active (SURTASS LFA) Sonar; Department of the Navy: Washington, DC, USA, 2012. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1968; Volume 1. [Google Scholar]
- McConnell, J.A.; Berkman, E.F.; Murray, B.S.; Abraham, B.M. Coherent Sound Source for Marine Seismic Surveys. U.S. Patent 9,625,598, 18 April 2017. [Google Scholar]
- McConnell, J.A.; Berkman, E.F.; Murray, B.S.; Abraham, B.M.; Roy, D.A. Coherent Sound Source for Marine Seismic Surveys. U.S. Patent 9,562,982, 18 April 2017. [Google Scholar]
- Tellier, N.; Ollivrin, G. Low-frequency Vibroseis: Current achievements and the road ahead? First Break 2019, 37, 49–54. [Google Scholar] [CrossRef]
- Sallas, J.; Gibson, J.; Maxwell, P.; Lin, F. Pseudorandom sweeps for simultaneous sourcing and low-frequency generation. Lead. Edge 2011, 30, 1162–1172. [Google Scholar] [CrossRef]
- Scholtz, P. Pseudo-random sweeps for built-up area seismic surveys. Lead. Edge 2013, 32, 276–282. [Google Scholar] [CrossRef]
- Dean, T. Establishing the limits of vibrator performance-experiments with pseudorandom sweeps. In SEG Technical Program Expanded Abstracts 2012; Society of Exploration Geophysicists: Tulsa, OK, USA, 2012; pp. 1–5. [Google Scholar]
- Dean, T. The use of pseudorandom sweeps for vibroseis surveys. Geophys. Prospect. 2014, 62, 50–74. [Google Scholar] [CrossRef]
- Dean, T.; Tulett, J.; Lane, D. The use of pseudorandom sweeps for vibroseis acquisition. First Break 2017, 35, 107–112. [Google Scholar]
- Feltham, A.; Girard, M.; Jenkerson, M.; Nechayuk, V.; Griswold, S.; Henderson, N.; Johnson, G. The Marine Vibrator Joint Industry Project: Four years on. Explor. Geophys. 2017, 49, 675–687. [Google Scholar] [CrossRef]
- Schostak, B.; Jenkerson, M. The Marine Vibrator Joint Industry Project. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2015; pp. 4961–4962. [Google Scholar]
- Ainslie, M.A. Principles of Sonar Performance Modeling; Praxis Books; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ainslie, M.A.; de Jong, C.A.F.; Martin, S.B.; Miksis-Olds, J.L.; Warren, J.D.; Heaney, K.D.; Hillis, C.A.; MacGillivray, A.O. ADEON Project Dictionary: Terminology Standard; JASCO: Oklahoma City, OK, USA, 2020. [Google Scholar]
- Sallas, J.; Teyssandier, B. Vibrator Source Array Load-Balancing Method and System. U.S. Patent 9482765, 1 November 2016. [Google Scholar]
- Teyssandier, B.; Sallas, J.J. The shape of things to come—Development and testing of a new marine vibrator source. Lead. Edge 2019, 38, 680–690. [Google Scholar] [CrossRef]
- Scandrett, C.L.; Baker, S.R. Pritchard’s Approximation in Array Modeling; Naval Postgraduate School: Monterey, CA, USA, 1999. [Google Scholar]
- MacGillivray, A.O. An Acoustic Modelling Study of Seismic Airgun Noise in Queen Charlotte Basin; University of Victoria: Victoria, BC, Canada, 2006; p. 98. [Google Scholar]
- Ziolkowski, A.M. A method for calculating the output pressure waveform from an air gun. Geophys. J. Int. 1970, 21, 137–161. [Google Scholar] [CrossRef]
- Dragoset, W.H. A comprehensive method for evaluating the design of airguns and airgun arrays. In Proceedings of the 16th Annual Offshore Technology Conference, Houston, TX, USA, 7–9 May 1984; pp. 75–84. [Google Scholar]
- Laws, R.M.; Hatton, L.; Haartsen, M. Computer modeling of clustered airguns. First Break 1990, 8, 331–338. [Google Scholar] [CrossRef]
- Landro, M. Modeling of GI gun signatures. Geophys. Prospect. 1992, 40, 721–747. [Google Scholar] [CrossRef]
- Mattsson, A.; Jenkerson, M. Single Airgun and Cluster Measurement Project. In Joint Industry Programme (JIP) on Exploration and Production Sound and Marine Life Proramme Review; International Association of Oil and Gas Producers: Houston, TX, USA, 2008. [Google Scholar]
- Zhang, Z.Y.; Tindle, C.T. Improved equivalent fluid approximations for a low shear speed ocean bottom. J. Acoust. Soc. Am. 1995, 98, 3391–3396. [Google Scholar] [CrossRef]
- Collins, M.D.; Cederberg, R.J.; King, D.B.; Chin-Bing, S. Comparison of algorithms for solving parabolic wave equations. J. Acoust. Soc. Am. 1996, 100, 178–182. [Google Scholar] [CrossRef]
- Collins, M.D. A split-step Padé solution for the parabolic equation method. J. Acoust. Soc. Am. 1993, 93, 1736–1742. [Google Scholar] [CrossRef]
- Hannay, D.E.; Racca, R.G. Acoustic Model Validation; JASCO Research Ltd.: Oklahoma City, OK, USA, 2005; p. 34. [Google Scholar]
- Porter, M.B.; Liu, Y.C. Finite-element ray tracing. In Proceedings of the International Conference on Theoretical and Computational, Manchester, UK, 13–16 December 1994; pp. 947–956. [Google Scholar]
- MacGillivray, A.O.; Chapman, N.R. Modeling underwater sound propagation from an airgun array using the parabolic equation method. Can. Acoust. 2012, 40, 19–25. [Google Scholar] [CrossRef][Green Version]
- Aerts, L.A.M.; Blees, M.; Blackwell, S.B.; Greene, C.R., Jr.; Kim, K.H.; Hannay, D.E.; Austin, M.E. Marine Mammal Monitoring and Mitigation during BP Liberty OBC Seismic Survey in Foggy Island Bay, Beaufort Sea, July-August 2008: 90-Day Report; NOAA: Washington, DC, USA, 2008; p. 199. [Google Scholar]
- Funk, D.W.; Hannay, D.E.; Ireland, D.S.; Rodrigues, R.; Koski, W.R. Marine Mammal Monitoring and Mitigation during Open Water Seismic Exploration by Shell Offshore Inc. in the Chukchi and Beaufort Seas, July–November 2007: 90-Day Report; NOAA: Washington, DC, USA, 2008; p. 218. [Google Scholar]
- Funk, D.W.; Hannay, D.E.; Ireland, D.S.; Rodrigues, R.; Koski, W.R. Marine Mammal Monitoring and Mitigation during Open Water Seismic Exploration by Shell Offshore Inc. in the Chukchi and Beaufort Seas, July–October 2008: 90-Day Report; NOAA: Washington, DC, USA, 2009; p. 277. [Google Scholar]
- O’Neill, C.; Leary, D.; McCrodan, A. Sound Source Verification. In Marine Mammal Monitoring and Mitigation during open water seismic exploration by Statoil USA E&P Inc. in the Chukchi Sea, August-October 2010: 90-Day Report; Blees, M.K., Ed.; LGL Report P1119; NOAA: Washington, DC, USA, 2010; pp. 1–34. [Google Scholar]
- Warner, G.A.; Erbe, C.; Hannay, D.E. Underwater Sound Measurements. In Marine Mammal Monitoring and Mitigation during Open Water Shallow Hazards and Site Clearance Surveys by Shell Offshore Inc. in the Alaskan Chukchi Sea, July-October 2009: 90-Day Report; Reiser, C.M., Ed.; NOAA: Washington, DC, USA, 2010; pp. 1–54. [Google Scholar]
- Racca, R.G.; Rutenko, A.N.; Bröker, K.; Gailey, G. Model Based Sound Level Estimation and in-Field Adjustment for Real-Time Mitigation of Behavioural Impacts from a Seismic Survey and Post-Event Evaluation of Sound Exposure for Individual Whales; Acoustics: Fremantle, Australia, 2012. [Google Scholar]
- Racca, R.G.; Rutenko, A.N.; Bröker, K.; Austin, M.E. A Line in the Water—Design and Enactment of a Closed Loop, Model Based Sound Level Boundary Estimation Strategy for Mitigation of Behavioural Impacts from a Seismic Survey. In Proceedings of the 11th European Conference on Underwater Acoustics, Edinburgh, UK, 2–6 July 2012. [Google Scholar]
- Martin, B.; Bröker, K.; Matthews, M.-N.R.; MacDonnell, J.T.; Bailey, L. Comparison of measured and modeled air-gun array sound levels in Baffin Bay, West Greenland. In Proceedings of the OceanNoise, Barcelona, Spain, 11–15 May 2015. [Google Scholar]
- Hamilton, E.L. Geoacoustic modeling of the sea floor. J. Acoust. Soc. Am. 1980, 68, 1313–1340. [Google Scholar] [CrossRef]
- Buckingham, M.J. Compressional and Shear Wave Properties of Marine Sediments: Comparisons between Theory and data. J. Acoust. Soc. Am. 2005, 117, 137–152. [Google Scholar] [CrossRef] [PubMed]
- Hanebuth, T.J.J.; Voris, H.K.; Yokoyama, Y.; Saito, Y.; Okuno, J. Formation and fate of sedimentary depocentres on Southeast Asia’s Sunda Shelf over the past sea-level cycle and biogeographic implications. Earth-Sci. Rev. 2011, 104, 92–110. [Google Scholar] [CrossRef]
- Bishop, M.G. Petroleum Systems of the Northwest Java Province, Java and offshore Southeast Sumatra, Indonesia, in Open-File Report; US Department of the Interior: Washington, DC, USA; US Geological Survey: Reston, VA, USA, 2000; p. 31. [Google Scholar]
- [NPD] Oljedirektoratet–Norwegian Petroleum Directorate. The NPD’s Fact-pages-Hordaland Group. 2011. Available online: http://www.npd.no/engelsk/cwi/pbl/en/su/all/67.htm (accessed on 21 December 2020).
- Shipboard Scientific Party. Site 96, Leg 619. In Deep Sea Drilling Projects Initial Reports; US Government Printing Office: Washington, DC, USA, 1987. [Google Scholar]
- Teague, W.J.; Carron, M.J.; Hogan, P.J. A comparison between the Generalized Digital Environmental Model and Levitus climatologies. J. Geophys. Res. 1990, 95, 7167–7183. [Google Scholar] [CrossRef]
- Carnes, M.R. Description and Evaluation of GDEM-V 3.0; MS. NRL Memorandum Report 7330-09-9165; US Naval Research Laboratory, Stennis Space Center: New Orleans, MS, USA, 2009; p. 21. [Google Scholar]
- Coppens, A.B. Simple equations for the speed of sound in Neptunian waters. J. Acoust. Soc. Am. 1981, 69, 862–863. [Google Scholar] [CrossRef]
- Mahanty, M.M.; Sanjana, M.C.; Latha, G.; Raguraman, G. An Investigation on the Fluctuation and Variability of Ambient Noise in Shallow Waters of South West Bay of Bengal; National Institute of Science Communication and Information Resources: New Delhi, India, 2014; Volume 43, pp. 747–753. [Google Scholar]
- International Electrotechnical Commission. IEC 61260-1:2014 Electroacoustics—Octave-Band and Fractional-Octave-Band Filters—Part 1: Specifications; IEC: London, UK, 2014; p. 88. [Google Scholar]
- Merchant, N.D.; Brookes, K.L.; Faulkner, R.C.; Bicknell, A.W.J.; Godley, B.J.; Witt, M.J. Underwater noise levels in UK waters. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef]
- Wiggins, S.M.; Hall, J.M.; Thayre, B.J.; Hildebrand, J.A. Gulf of Mexico low-frequency ocean soundscape impacted by airguns. J. Acoust. Soc. Am. 2016, 140, 176–183. [Google Scholar] [CrossRef]
- Urick, R.J. Principles of Underwater Sound, 3rd ed.; McGraw-Hill: New York, NY, USA; London, UK, 1983; p. 423. [Google Scholar]
- Martin, B.; MacDonnell, J.T.; Bröker, K. Cumulative sound exposure levels—Insights from seismic survey measurements. J. Acoust. Soc. Am. 2017, 141, 3603. [Google Scholar] [CrossRef]
- Plomp, R.; Bouman, M.A. Relation between Hearing Threshold and Duration for Tone Pulses. J. Acoust. Soc. Am. 1959, 31, 749–758. [Google Scholar] [CrossRef]
- MacGillivray, A.O.; Racca, R.G.; Li, Z. Marine mammal audibility of selected shallow-water survey sources. J. Acoust. Soc. Am. 2014, 135, EL35–EL40. [Google Scholar] [CrossRef] [PubMed]
- Houser, D.S. A method for modeling marine mammal movement and behavior for environmental impact assessment. IEEE J. Ocean. Eng. 2006, 31, 76–81. [Google Scholar] [CrossRef]
- Ellison, W.T.; Clark, C.W.; Bishop, G.C. Potential use of surface reverberation by bowhead whales, Balaena mysticetus, in under-ice navigation: Preliminary considerations. In Report of the International Whaling Commission; International Whaling Commission: Cambridge, UK, 1987; pp. 329–332. [Google Scholar]
- Frankel, A.S.; Ellison, W.T.; Buchanan, J. Application of the acoustic integration model (AIM) to predict and minimize environmental impacts. In OCEANS’02 MTS/IEEE; IEEE: Biloxi, MI, USA, 2002; pp. 1438–1443. [Google Scholar]
- Kaschner, K.; Rius-Barile, J.; Kesner-Reyes, K.; Garilao, C.; Kullander, S.O.; Rees, T.; Froese, R. AquaMaps: Predicted Range Maps for Aquatic Species; World Wide Web Electronic Publication. 2016. Available online: www.aquamaps.org (accessed on 21 December 2020).
- Kreb, D. Cetacean diversity and habitat preferences in tropical waters of East Kalimantan, Indonesia. Raffles Bull. Zool. 2005, 53, 149–155. [Google Scholar]
- Shirakihara, K.; Shirakihara, M.; Yamamoto, Y. Distribution and abundance of finless porpoise in the Inland Sea of Japan. Mar. Biol. 2007, 150, 1025–1032. [Google Scholar] [CrossRef]
- Reyne, M.; Webster, I.; Huggins, A. A Preliminary Study on the Sea Turtle Density in Mauritius. Mar. Turt. Newsl. 2017, 152, 5–8. [Google Scholar]
- Hammond, P.S.; Macleod, K.; Berggren, P.; Borchers, D.L.; Burt, L.; Cañadas, A.; Desportes, G.; Donovan, G.P.; Gilles, A.; Gillespie, D. Cetacean abundance and distribution in European Atlantic shelf waters to inform conservation and management. Biol. Conserv. 2013, 164, 107–122. [Google Scholar] [CrossRef]
- [DoN] Department of the Navy (US). Navy OPAREA Density Estimate (NODE) for the Gulf of Mexico; Contract #N62470-02 D-9997, CTO 0030; Department of the Navy: Washington, DC, USA, 2007. [Google Scholar]
- Roberts, J.J.; Best, B.D.; Mannocci, L.; Fujioka, E.; Halpin, P.N.; Palka, D.L.; Garrison, L.P.; Mullin, K.D.; Cole, T.V.N.; Khan, C.B.; et al. Habitat-based cetacean density models for the U.S. Atlantic and Gulf of Mexico. Sci. Rep. 2016, 6, 22615. [Google Scholar] [CrossRef]
- [NOAA] National Oceanic and Atmospheric Administration (US). Notice of Public Scoping and Intent to Prepare an Environmental Impact Statement. Fed. Regist. 2005, 70, 1871–1875. [Google Scholar]
- Richardson, W.J.; Greene, C.R., Jr.; Malme, C.I.; Thomson, D.H. Marine Mammals and Noise; Academic Press: San Diego, CA, USA, 1995; p. 576. [Google Scholar]
- Gordon, J.; Gillespie, D.; Potter, J.R.; Frantzis, A.; Simmonds, M.P.; Swift, R.; Thompson, D. A Review of the Effects of Seismic Surveys on Marine Mammals. Mar. Technol. Soc. J. 2003, 37, 16–34. [Google Scholar] [CrossRef]
- Nowacek, D.P.; Thorne, L.H.; Johnston, D.W.; Tyack, P.L. Responses of cetaceans to anthropogenic noise. Mammal Rev. 2007, 37, 81–115. [Google Scholar] [CrossRef]
- Ellison, W.T.; Southall, B.L.; Clark, C.W.; Frankel, A.S. A New Context-Based Approach to Assess Marine Mammal Behavioral Responses to Anthropogenic Sounds. Conserv. Biol. 2012, 26, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Southall, B.L.; Nowaceck, D.P.; Miller, P.J.O.; Tyack, P.L. Experimental field studies to measure behavioral responses of cetaceans to sonar. Endanger. Species Res. 2016, 31, 293–315. [Google Scholar] [CrossRef]
- Dunlop, R.A.; Noad, M.J.; McCauley, R.D.; Scott-Hayward, L.; Kniest, E.; Slade, R.; Paton, D.; Cato, D.H. Determining the behavioural dose–response relationship of marine mammals to air gun noise and source proximity. J. Exp. Biol. 2017, 220, 2878–2886. [Google Scholar] [CrossRef] [PubMed]
- Wartzok, D.; Popper, A.N.; Gordon, J.; Merrill, J. Factors affecting the responses of marine mammals to acoustic disturbance. Mar. Technol. Soc. J. 2003, 37, 6–15. [Google Scholar] [CrossRef]
- Weilgart, L.S. A Brief Review of Known Effects of Noise on Marine Mammals. Int. J. Comp. Psychol. 2007, 20, 159–168. [Google Scholar]
- Müller, R.A.J.; von Benda-Beckmann, A.M.; Halvorsen, M.B.; Ainslie, M.A. Application of kurtosis to underwater sound. J. Acoust. Soc. Am. 2020, 148, 780–792. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).