Improvement of the Full-Range Equation for Wave Boundary Layer Thickness
Abstract
:1. Introduction
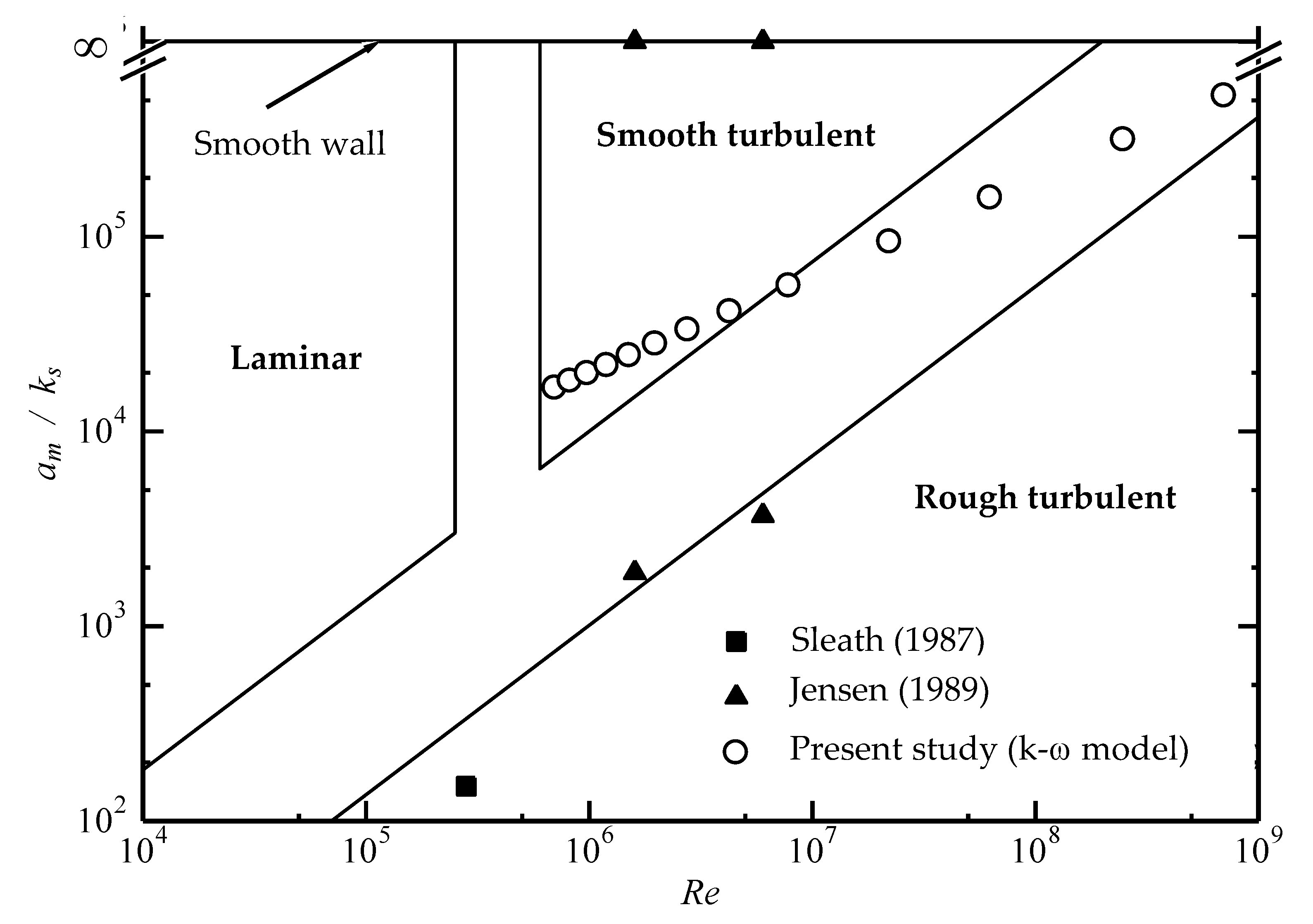
2. Comparison of Existing Formulae
- Smooth turbulent
- Rough turbulent
3. Proposal of New Formulae for Turbulent Flow
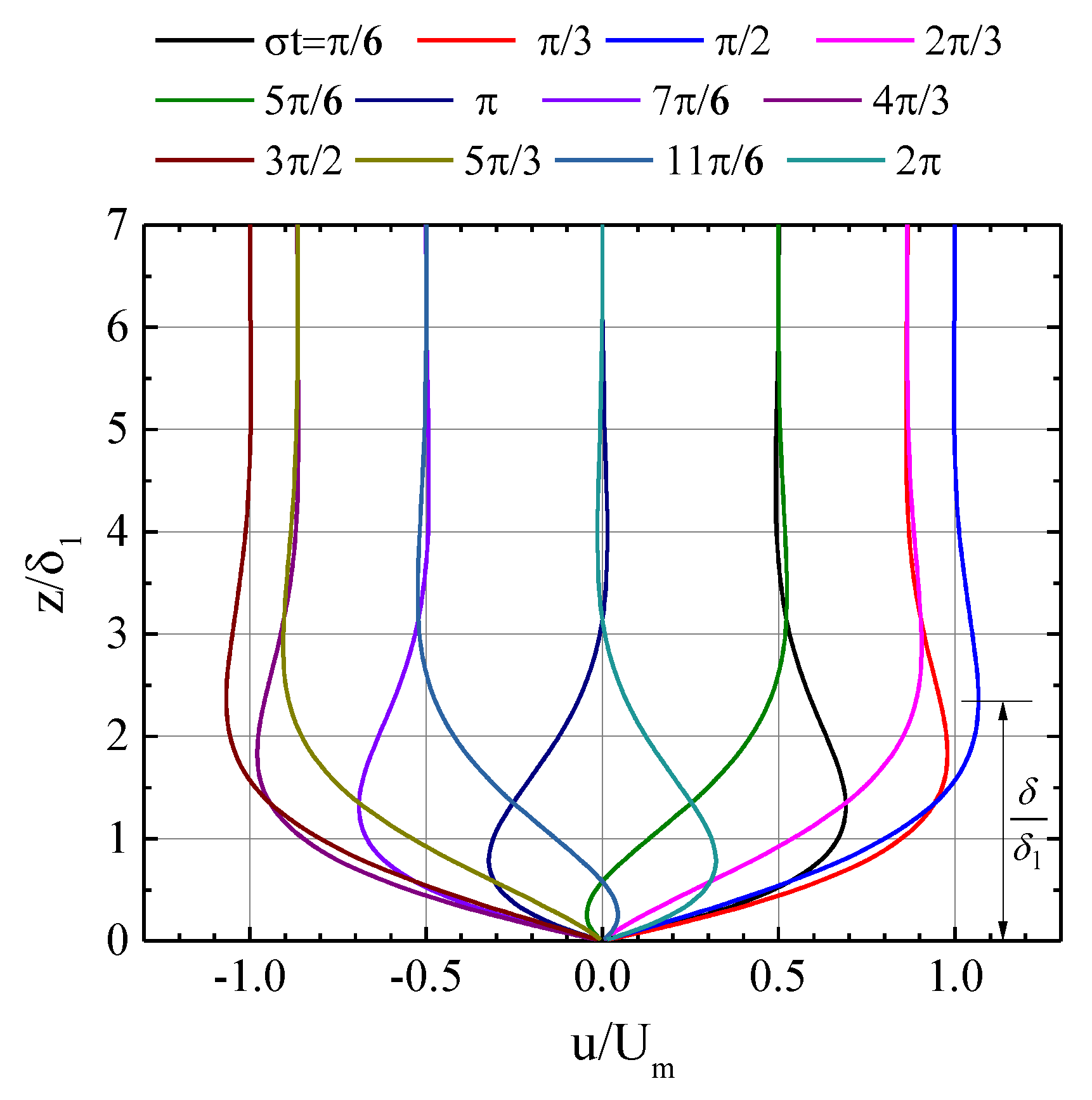
3.1. Theoretical Consideration
3.2. Proposal of New Calculation Formulas for Each Flow Regime
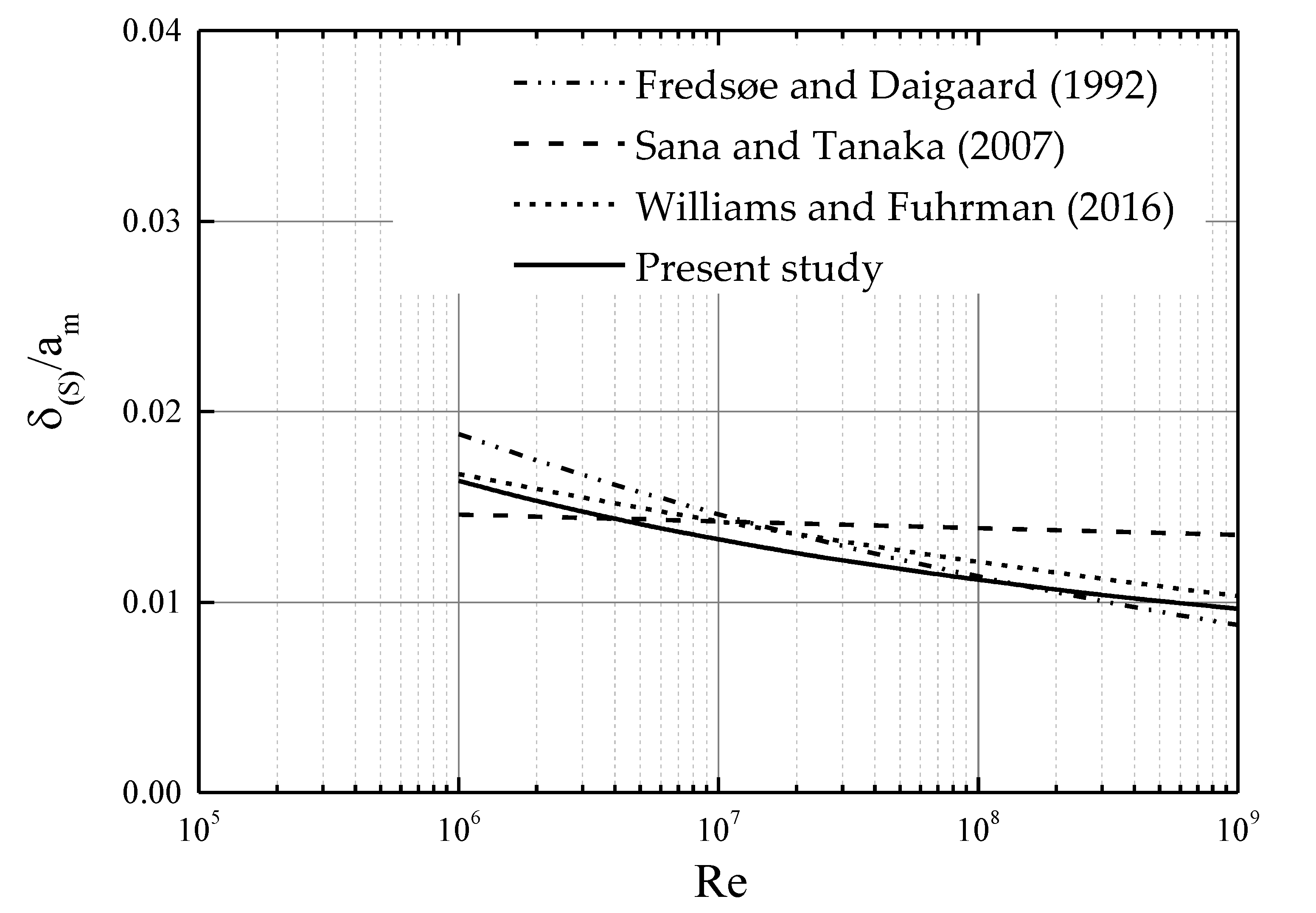
3.3. Full-Range Equation
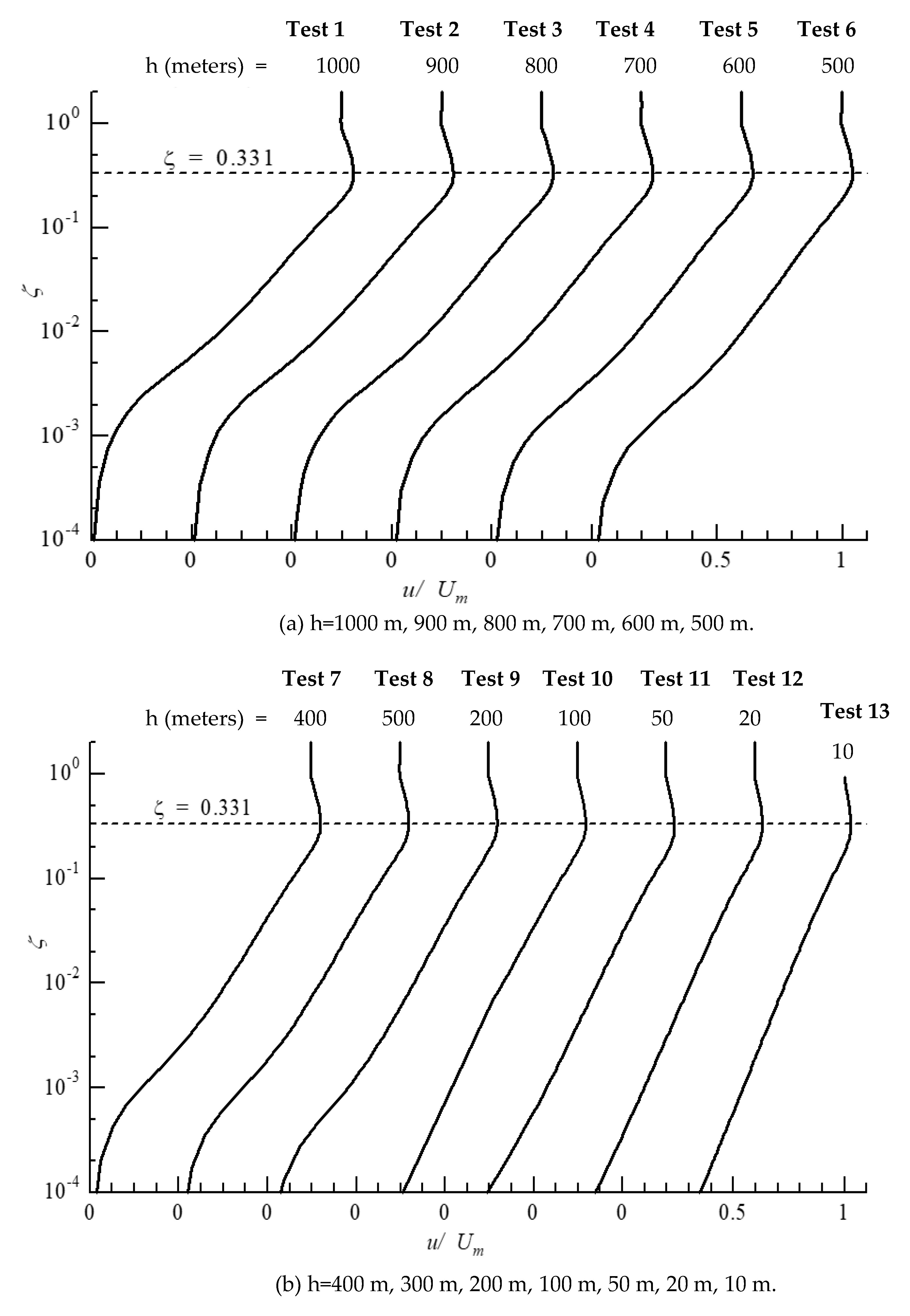
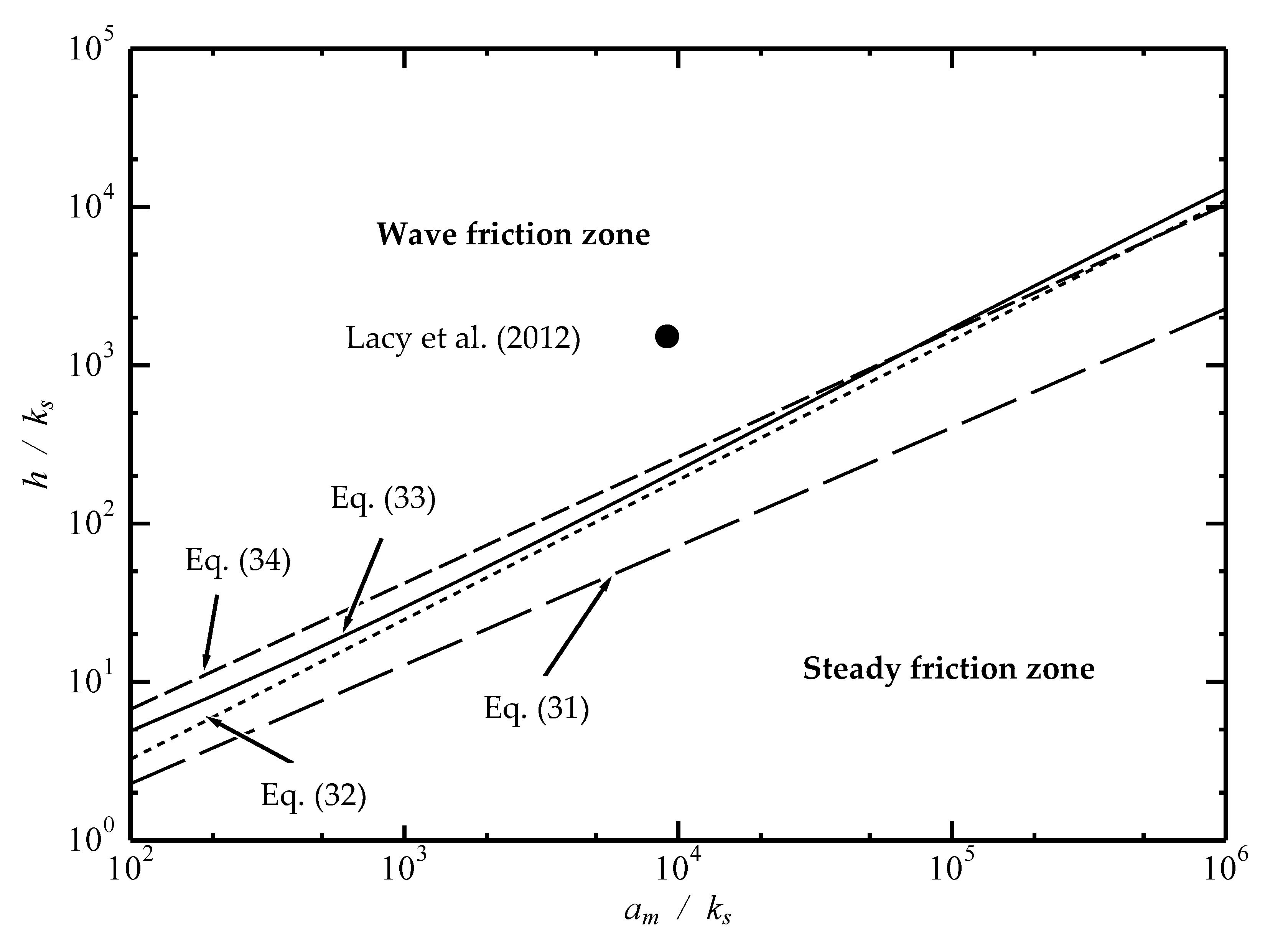
4. Application of the New Formula to Demarcation of Friction Law under Tsunami
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tanaka, H.; Tinh, N.X.; Umeda, M.; Hirao, R.; Pradjoko, E.; Mano, A.; Udo, K. Coastal and Estuarine Morphology Changes Induced by the 2011 Great East Japan Earthquake Tsunami. Coast. Eng. J. 2012, 54, 1250010. [Google Scholar] [CrossRef]
- Tanaka, H.; Adityawan, M.B.; Mano, A. Morphological changes at the Nanakita River mouth after the Great East Japan Tsunami of 2011. Coast. Eng. 2014, 86, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Sugawara, D.; Takahashi, T.; Imamura, F. Sediment Transport Due to the 2011 Tohoku-Oki Tsunami at Sendai: Results from Numerical Modeling. Mar. Geol. 2014, 358, 18–37. [Google Scholar] [CrossRef]
- Yamashita, K.; Sugawara, D.; Takahashi, T.; Imamura, F.; Saito, Y.; Imato, Y.; Kai, T. Numerical Simulations of Large-scale Sediment Transport Caused by the 2011 Tohoku Earthquake Tsunami in Hirota Bay, Southern Sanriku Coast. Coast. Eng. J. 2016, 58, 1640015. [Google Scholar] [CrossRef] [Green Version]
- Williams, I.A.; Fuhrman, D.R. Numerical simulation of tsunami-scale wave boundary layers. Coast. Eng. 2016, 110, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Lacy, J.R.; Rubin, D.M.; Buscombe, D. Currents, drag, and sediment transport induced by a tsunami. J. Geophys. Res. 2012, 117, C9. [Google Scholar] [CrossRef]
- Tinh, N.X.; Tanaka, H. Study on boundary layer development and bottom shear stress beneath a tsunami. Coast. Eng. J. 2019, 61, 574–589. [Google Scholar] [CrossRef]
- Sleath, J.F.L. Turbulent oscillatory flow over rough beds. J. Fluid Mech. 1987, 82, 369–409. [Google Scholar] [CrossRef]
- Jensen, B.L.; Sumer, B.M.; Fredsøe, J. Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 1989, 206, 265–297. [Google Scholar] [CrossRef] [Green Version]
- Fredsøe, J.; Deigaard, R. Mechanics of Coastal Sediment Transport; World Scientific: Singapore, 1992; 369p. [Google Scholar]
- Sana, A.; Tanaka, H. Full-range equation for wave boundary layer thickness. Coast. Eng. 2007, 54, 639–642. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 9th ed.; Springer: Berlin/Heidelberg, Germany, 1979; 805p. [Google Scholar]
- Lundgren, H.; Sorensen, T. A pulsating water tunnel. In Proceedings of the 6th International Conference on Coast. Eng., Gainesville, FL, USA, 29 January 1957; pp. 356–358. [Google Scholar]
- Kamphuis, J.W. Friction factor under oscillatory waves. J. Waterw. Port Coast. Ocean Eng. 1975, 101, 135–144. [Google Scholar]
- Jonsson, I.G.; Carlsen, N.A. Experimental and theoretical investigation in an oscillatory turbulent boundary layer. J. Hydr. Res. 1976, 14, 45–60. [Google Scholar] [CrossRef]
- Jonsson, I.G. Wave boundary Layers and Friction Factors. In Proceedings of the 10th International Conference on Coast. Eng., Tokyo, Japan, 5–8 September 1966; ASCE: New York, NY, USA, 1966; pp. 127–148. [Google Scholar]
- Tanaka, H.; Sana, A. Characteristics of turbulent boundary layers over a rough bed under saw-tooth waves and its application to sediment transport. Coast. Eng. 2008, 55, 1102–1112. [Google Scholar]
- Yuan, J.; Madsen, O.S. Experimental study of turbulent oscillatory boundary layers in an oscillating water tunnel. Coast. Eng. 2014, 89, 63–84. [Google Scholar] [CrossRef]
- Tanaka, H.; Sana, A. Numerical study on Transition to Turbulence in a Wave Boundary Layer. In Sediment Transport Mechanisms in Coastal Environments and Rivers; World Scientific: Singapore, 1994; pp. 14–25. [Google Scholar]
- Tanaka, H.; Thu, A. Full-range equation of friction coefficient and phase difference in a wave-current boundary layer. Coast. Eng. 1994, 22, 237–254. [Google Scholar] [CrossRef]
- Jonsson, I.G. A new approach to oscillatory rough turbulent boundary layers. Ocean Eng. 1980, 7, 109–152. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fuhrman, D.R. Turbulence in Coastal and Civil Engineering; World Scientific: Singapore, 2020; 758p. [Google Scholar]
- Carslaw, H.; Jaeger, J. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Larson, M.; Hanson, H.; Kraus, N.C. Analytical Solutions of the One-Line Model of Shoreline Change, Technical Report CERC-87-15; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1987; 72p.
- Larson, M.; Hanson, H.; Kraus, N.C. Analytical solution of one-line model for shoreline change near coastal structures. J. Waterw. Port Coast. Ocean Eng. 1997, 123, 180–191. [Google Scholar] [CrossRef]
- Kajiura, K. A model of the bottom boundary layer in water waves. Bullet. Earthq. Res. Inst. 1968, 46, 75–123. [Google Scholar]
- Tanaka, H.; Shuto, N. Friction laws and flow regimes under wave and current motion. J. Hydr. Res. 1984, 22, 245–261. [Google Scholar] [CrossRef]
- Grant, W.D.; Madsen, O.S. Combined wave and current interaction with a rough bottom. J. Geophys. Res. 1979, 84, 1797–1808. [Google Scholar] [CrossRef]
- Tanaka, H. Bottom boundary layer under nonlinear wave motion. J. Waterw. Port Coast. Ocean Eng. 1989, 115, 40–57. [Google Scholar] [CrossRef]
- Jensen, B.L. Experimental Investigation of Turbulent Oscillatory Boundary Layers; Series Paper; Technical University of Denmark: Kgs. Lyngby, Denmark, 1989; Volume 45, 157p. [Google Scholar]
- Sana, A.; Ghumman, A.R.; Tanaka, H. Modeling of a rough-wall oscillatory boundary layer using two-equation turbulence models. J. Hydr. Eng. 2009, 135, 60–65. [Google Scholar] [CrossRef]
- Tanaka, H.; Tinh, N.X. Numerical Study on Sea Bottom Boundary Layer and Bed Shear Stress under Tsunami. In Proceedings of the 29th International Ocean and Polar Engineering Conference (ISOPE), Honolulu, HI, USA, 16–21 June 2019; pp. 3189–3195. [Google Scholar]
- Tanaka, H. An explicit expression of friction coefficient for a wave-current coexistent motion. Coast. Eng. Jap. 1992, 35, 83–91. [Google Scholar] [CrossRef]
- Van der A, D.A.; O’Donoghue, T.; Davies, A.G.; Ribberink, J.S. Experimental study of the turbulent boundary layer in acceleration-skewed oscillatory flow. J. Fluid Mech. 2011, 684, 251–283. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Wang, D. An experimental investigation of acceleration-skewed oscillatory flow over vortex ripples. J. Geophys. Res. Oceans 2019, 124, 9620–9643. [Google Scholar] [CrossRef]
- Tanaka, H.; Sana, A.; Kawamura, I.; Yamaji, H. Depth-limited Oscillatory Boundary Layers on a Rough Bottom. Coastal Eng. J. 1999, 41, 85–105. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. Full-scale CFD simulation of tsunamis. Part 1: Model validation and run-up. Coast. Eng. 2019, 151, 22–41. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. Full-scale CFD simulation of tsunamis. Part 2: Boundary layers and bed shear stresses. Coast. Eng. 2019, 151, 42–57. [Google Scholar] [CrossRef]

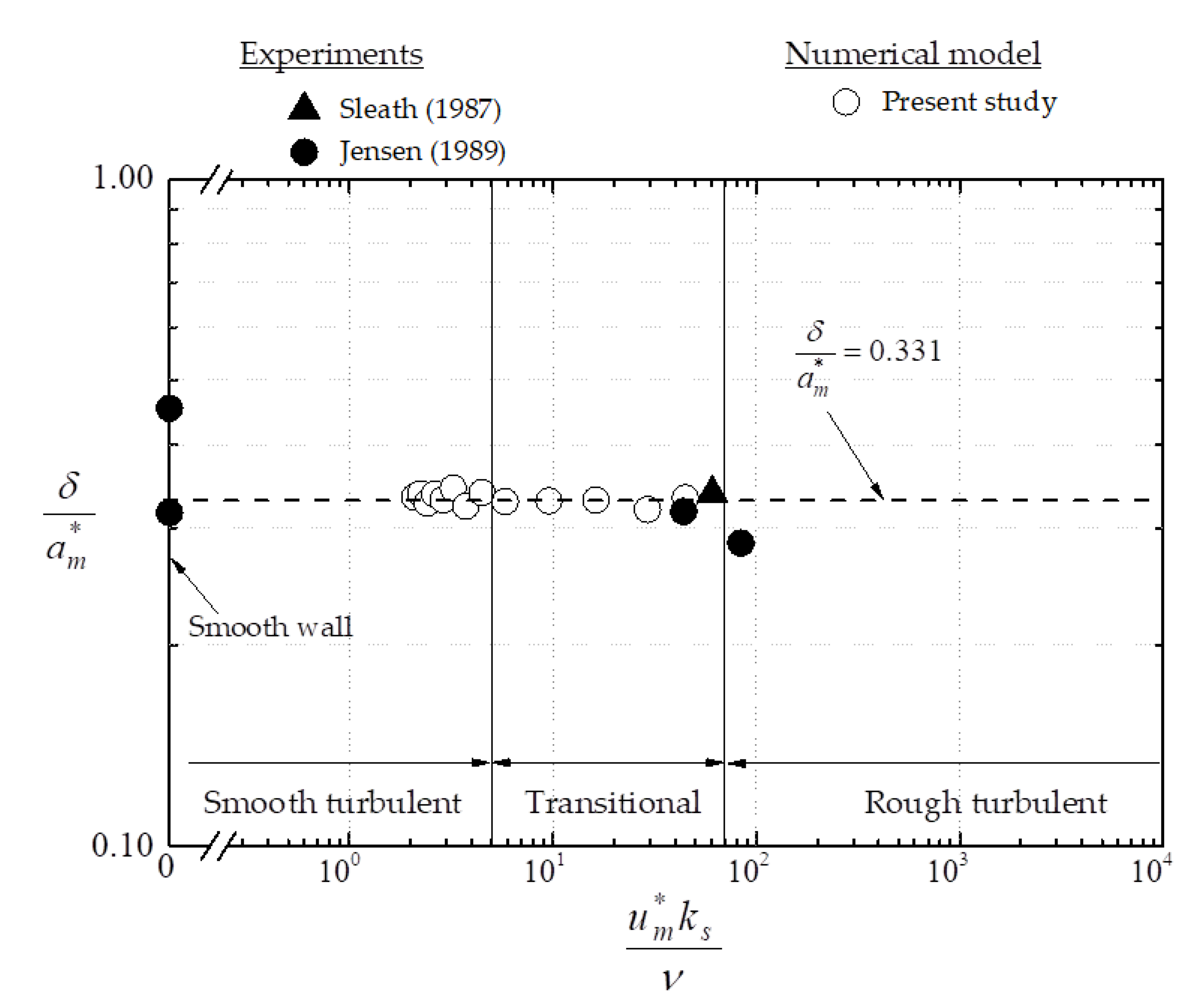

| Data Source | Test No. | (s) | (m/s) | (mm) | ||
|---|---|---|---|---|---|---|
| Experiment (Sleath [8], 1987) | 3 | 4.54 | 0.686 | 3.26 | 151 | 2.81 × 105 |
| Experiment (Jensen [30], 1989) | 8 | 9.72 | 1.02 | 0.0 | (smooth) | 1.6 × 106 |
| 10 | 9.72 | 2.00 | 0.0 | (smooth) | 6.0 × 106 | |
| 12 | 9.72 | 1.02 | 0.84 | 1.88 × 103 | 1.6 × 106 | |
| 13 | 9.72 | 2.00 | 0.84 | 3.70 × 103 | 6.0 × 106 | |
| k- model computation | 1 | 900 | 0.070 | 0.60 | 1.67 × 104 | 7.02 × 105 |
| 2 | 900 | 0.076 | 0.60 | 1.81 × 104 | 8.22 × 105 | |
| 3 | 900 | 0.083 | 0.60 | 1.98 × 104 | 9.81 × 105 | |
| 4 | 900 | 0.091 | 0.60 | 2.18 × 104 | 1.20 × 106 | |
| 5 | 900 | 0.10 | 0.60 | 2.45 × 104 | 1.51 × 106 | |
| 6 | 900 | 0.12 | 0.60 | 2.81 × 104 | 1.98 × 106 | |
| 7 | 900 | 0.14 | 0.60 | 3.32 × 104 | 2.77 × 106 | |
| 8 | 900 | 0.17 | 0.60 | 4.12 × 104 | 4.27 × 106 | |
| 9 | 900 | 0.23 | 0.60 | 5.59 × 104 | 7.85 × 106 | |
| 10 | 900 | 0.39 | 0.60 | 9.40 × 104 | 2.22 × 107 | |
| 11 | 900 | 0.66 | 0.60 | 1.58 × 105 | 6.28 × 107 | |
| 12 | 900 | 1.32 | 0.60 | 3.14 × 105 | 2.48 × 108 | |
| 13 | 900 | 2.21 | 0.60 | 5.28 × 105 | 7.02 × 108 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanaka, H.; Tinh, N.X.; Sana, A. Improvement of the Full-Range Equation for Wave Boundary Layer Thickness. J. Mar. Sci. Eng. 2020, 8, 573. https://doi.org/10.3390/jmse8080573
Tanaka H, Tinh NX, Sana A. Improvement of the Full-Range Equation for Wave Boundary Layer Thickness. Journal of Marine Science and Engineering. 2020; 8(8):573. https://doi.org/10.3390/jmse8080573
Chicago/Turabian StyleTanaka, Hitoshi, Nguyen Xuan Tinh, and Ahmad Sana. 2020. "Improvement of the Full-Range Equation for Wave Boundary Layer Thickness" Journal of Marine Science and Engineering 8, no. 8: 573. https://doi.org/10.3390/jmse8080573
APA StyleTanaka, H., Tinh, N. X., & Sana, A. (2020). Improvement of the Full-Range Equation for Wave Boundary Layer Thickness. Journal of Marine Science and Engineering, 8(8), 573. https://doi.org/10.3390/jmse8080573








