A New Algorithm to Estimate Diffuse Attenuation Coefficient from Secchi Disk Depth
Abstract
:1. Introduction
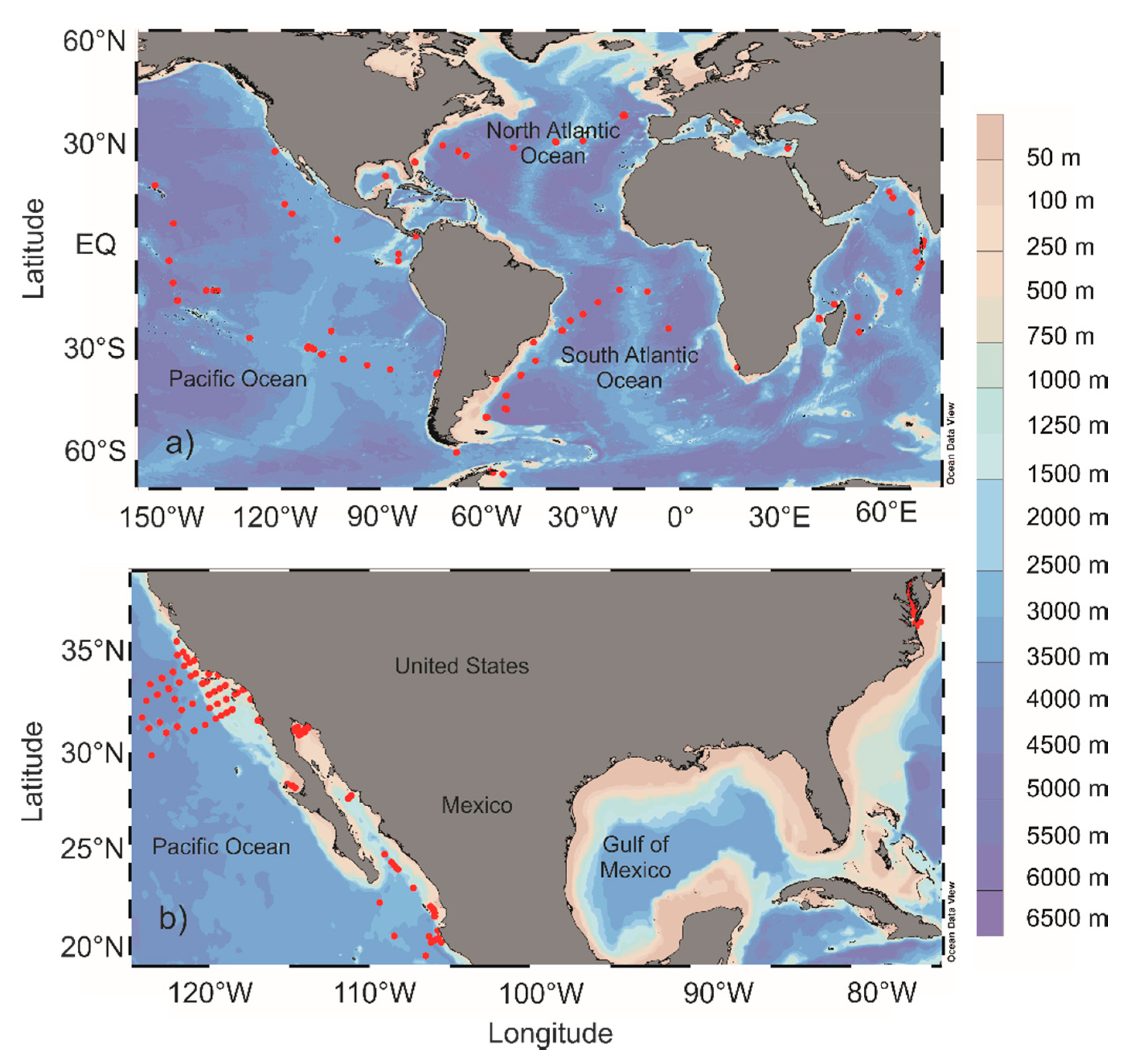
2. Materials and Methods
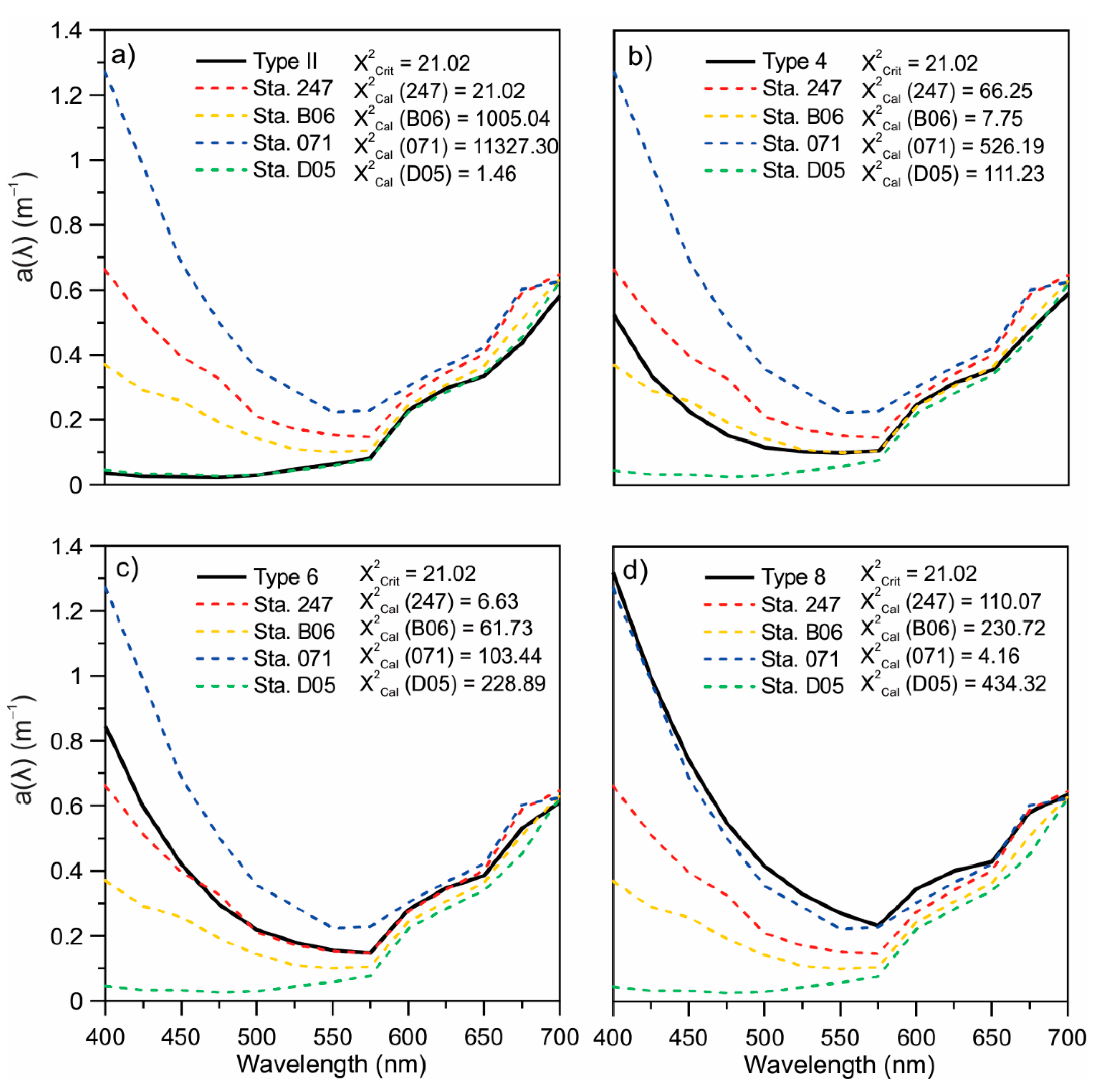
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011; p. 649. [Google Scholar]
- Frouin, R.; Ramon, D.; Boss, E.; Jolivet, D.; Compiègne, M.; Tan, J.; Bouma, H.; Jackso, T.; Franz, B.; Platt, T.; et al. Satellite Radiation Products for Ocean Biology and Biogeochemistry: Needs, State-of-the-Art, Gaps, Development Priorities, and Opportunities. Front. Mar. Sci. 2018, 5, 3. [Google Scholar] [CrossRef] [Green Version]
- Platt, T.; Denman, K.L.; Jassby, A.D. Modeling the Productivity of Phytoplankton, in the Sea: Ideas and Observations on Progress in the Study of the Seas; Goldberg, E.D., Ed.; John Wiley: New York, NY, USA, 1977; pp. 807–856. [Google Scholar]
- Falkowski, P.G.; Raven, J.A. Aquatic Photosynthesis; Blackwell Science: Malden, MA, USA, 1997; p. 375. [Google Scholar]
- Antoine, D.; Babin, M.; Berthon, J.; Bricaud, A.; Gentili, B.; Loisel, H.; Maritorena, S.; Stramski, D. Shedding Light on the Sea: André Morel’s Legacy to Optical Oceanography. Annu. Rev. Mar. Sci. 2014, 6, 1–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Secchi, A. Schreiben des Herrn Prof. Secchi, Directors der Sternwarte des Collegio Romano, an den Herausgeber. Astron. Nachr. 1866, 68, 63. [Google Scholar] [CrossRef] [Green Version]
- Wernard, M.R. On the history of the Secchi Disk. J. Eur. Opt. Soc.-Rapid 2010, 5, 100135. [Google Scholar] [CrossRef] [Green Version]
- Davies-Colley, R.J.; Vant, W.N.; Smith, D.G. Colour and Clarity of Natural Waters. Science and Management of Optical Water Quality; Ellis-Horwood: New York, NY, USA, 1993; p. 310. [Google Scholar]
- Poole, H.H.; Atkins, W.R.G. Photo-Electric Measurements of Submarine Illumination throughout the Year. J. Mar. Biol Assoc. UK 1929, 16, 297–324. [Google Scholar] [CrossRef] [Green Version]
- Preisendorfer, R.W. Secchi disk science: Visual optics of natural waters. Limnol. Oceanogr. 1986, 31, 909–926. [Google Scholar] [CrossRef] [Green Version]
- Lund-Hansen, L.C. Diffuse Attenuation Coefficients Kd(PAR) at the Estuarine North Sea–Baltic Sea Transition: Time-Series, Partitioning, Absorption, and Scattering. Estua Coast. Shelf Sci. 2004, 61, 251–259. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption Spectrum (380–700 nm) of Pure Water. II. Integrating Cavity Measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An Optical Classification of Coastal and Oceanic Waters Based on the Specific Spectral Absorption Curves of Phytoplankton Pigments, Dissolved Organic Matter, and Other Particulate Materials. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- Santamaría-del-Ángel, E.; Millán-Núñez, R.; González-Silvera, A.; Cajal-Medrano, R. Producción Primaria Fitoplanctónicas. En Manuales del cuerpo Académico de Ecología del Fitoplancton de la Facultad de Ciencias Marinas de la Universidad Autónoma de Baja California; Series White Papers POPEYE 41 p; Universidad Autónoma de Baja California, Facultad de Ciencias Marinas: Ensenada, Mexico, 2005. [Google Scholar] [CrossRef]
- Holmes, R.W. The Secchi disk in turbid coastal waters. Limnol. Oceanogr. 1970, 15, 688–694. [Google Scholar] [CrossRef]
- Megard, R.O.; Berman, T. Effects of algae on the Secchi transparency of the southeastern Mediterranean Sea. Limnol. Oceanogr. 1989, 34, 1640–1655. [Google Scholar] [CrossRef]
- Montes-Hugo, M.A.; Álvarez-Borrego, S. Empirical relations to estimate PAR attenuation in San Quintín Bay, using Secchi depth and sighting range. Cienc Mar. 2005, 31, 685–695. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Du, K.; Wei, J. Resolving the Long-Standing Puzzles about the Observed Secchi Depth Relationships. Limnol. Oceanogr. 2018, 63, 2321–2336. [Google Scholar] [CrossRef]
- Harvey, E.T.; Walve, J.; Andersson, A.; Karlson, B.; Kratzer, S. The effect of optical properties on Secchi depth and implications for eutrophication management. Front. Mar. Sci. 2019, 5, 496. [Google Scholar] [CrossRef] [Green Version]
- Steinmetz, H.; Staudinger, M.; Balch, W.M. Analyzing the Effects of Coccolithophore Concentration on the Relationship between Vertical Absorption Coefficient and Secchi Disk Depth. Student Showcase. 2019. Available online: https://scholarworks.umass.edu/sustainableumass_studentshowcase/26 (accessed on 10 June 2020).
- Gallegos, C.L.; Werdell, P.J.; McClain, C.R. Longterm changes in light scattering in Chesapeake Bay inferred from Secchi depth, light attenuation, and remote sensing measurements. J. Geophys. Res. 2011, 116, C00H08. [Google Scholar] [CrossRef]
- Barbosa, A.; Domingues, R. Effects of Nutrient and Light Enrichment on Phytoplankton Growth. In Practical Experiments Guide for Ecohydrology; Chícharo, L., Wagner, I., Chicharo, M., Lapinska, M., Zalewski, M., Eds.; UNESCO: Venice, Italy, 2009; pp. 27–30. [Google Scholar]
- Lee, Z.; Shang, S.; Hu, C.; Du, K.; Weidemann, A.; Hou, W.; Lin, J.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef] [Green Version]
- IOCCG. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications. In Reports of the International Ocean Colour Coordinating Group No. 5; Lee, Z.P., Ed.; IOCCG: Dartmouth, NS, Canada, 2006; p. 126. [Google Scholar]
- Mobley, C.D.; Sundman, L.K. HydroLight 5.2 User’s Guide; Sequoia Scientific: Seattle, WA, USA, 2013. [Google Scholar]
- Padial, A.A.; Thomaz, S.M. Prediction of the light attenuation coefficient through the Secchi disk depth: Empirical modeling in two large Neotropical ecosystems. Limnology 2008, 9, 143–151. [Google Scholar] [CrossRef]
- Ficek, D.; Zapadka, T. Variability of bio-optical parameters in Lake Jasień Północny and Lake Jasień Południowy. Limnol. Rev. 2010, 10, 67–76. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, X.; Yin, Y.; Wang, M.; Qin, B. Predicting the light attenuation coefficient through Secchi disk depth and beam attenuation coefficient in a large, shallow, freshwater lake. Hydrobiologia 2012, 693, 29–37. [Google Scholar] [CrossRef]
- Jerlov, N.G. Optical Oceanography; American Elsevier Publishing Company Incorporation: New York, NY, USA, 1968; p. 194. [Google Scholar]
- Solonenko, M.G.; Mobley, C.D. Inherent optical properties of Jerlov water types. Appl. Opt. 2015, 54, 5392–5401. [Google Scholar] [CrossRef]
- Tara Oceans Consortium, Coordinators; Tara Oceans Expedition. Environmental Context of All Samples from the Tara Oceans Expedition (2009–2013), about Mesoscale Features; PANGAEA: Bremerhaven, Germany, 2016. [Google Scholar] [CrossRef]
- Werdell, P.J.; Bailey, S.W. An improved bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Steyerberg, E.W. Validation of Prediction Models. In Clinical Prediction Models. Statistics for Biology and Health, 2nd ed.; Springer: Cham, Germany, 2019; pp. 329–344. [Google Scholar]
- IOCCG. Synergy between Ocean Colour and Biogeochemical/Ecosystem Models 2020; IOCCG Report Series, No. 19; Dutkiewicz, S., Ed.; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2020. [Google Scholar] [CrossRef]
- Xu, W.; Chen, W.; Liang, Y. Feasibility Study on the Least Square Method for Fitting Non-Gaussian Noise Data. Phys. A Stat. Mech. Appl. 2017, 492, 1917–1930. [Google Scholar] [CrossRef] [Green Version]
- Ocean Color Data. Available online: https://oceandata.sci.gsfc.nasa.gov/ (accessed on 5 July 2020).
- Kahru, M.; Kudela, R.M.; Anderson, C.R.; Mitchell, B.G. Optimized merger of ocean chlorophyll algorithms of MODIS-Aqua and VIIRS. IEEE Geosci. Remote Sens. 2015, 12, 11. [Google Scholar] [CrossRef] [Green Version]
- Kahru, M.; Di Lorenzo, E.; Manzano-Sarabia, M.; Mitchell, B.G. Spatial and temporal statistics of sea surface temperature and chlorophyll fronts in the California Current. J. Plankton Res. 2012, 34, 749–760. [Google Scholar] [CrossRef] [Green Version]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Wilcoxon, F.; Katti, S.K.; Wilcox, R.A. Critical Values and Probability Levels for the Wilcoxon Rank Sum Test and the Signed Rank Test; American Cyanamid Co., & Lederle Lab.: Pearl River, NY, USA, 1963. [Google Scholar]
- Wilcoxon, F.; Katti, S.K.; Wilcox, R.A. Critical Values and Probability Levels for the Wilcoxon Rank Sum Test and the Wilcoxon Signed Rank Test. In Selected Tables in Mathematical Statistics; Amer Mathematical Society: Providence, RI, USA, 1970; Volume 1, pp. 171–259. [Google Scholar]
- Mitchell, B.G.; Bricaud, A.; Carder, K.; Cleveland, J.; Ferrari, G.M.; Gould, R.; Kahru, M.; Kishino, M.; Maske, H.; Moisan, T.; et al. Determination of Spectral Absorption Coefficients of Particles, Dissolved Material and Phytoplankton for Discrete Water Samples. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Revision 2; Fargion, G.S., Mueller, J.L., McClain, C.R., Eds.; Goddard Space Flight Space Center: Greenbelt, MD, USA, 2000; pp. 125–153. [Google Scholar]
- Mueller, J.L.; Austin, R.W. Ocean Optics Protocols for SeaWIFS Validation; Revision 1; SeaWiFS Technical Report Series; Hooker, S.B., Firestone, E.R., Acker, J.G., Mueller, J.L., Austin, R.W., Eds.; Goddard Space Flight Space Center: Greenbelt, MD, USA, 1995; p. 25.
- Zar, J.H. Biostatistical Analysis, 5th ed.; Prentice-Hall: New Jersey, NJ, USA, 2010; p. 944. [Google Scholar]
- Koenings, J.P.; Edmundson, J.A. Secchi disk and photometer estimates of light regimes in Alaskan lakes: Effects of yellow color and turbidity. Limnol. Oceanogr. 1991, 36, 91–105. [Google Scholar] [CrossRef]
- Lugo-Fernández, A.; Gravois, M.; Montgomery, T. Analysis of Secchi depths and light attenuation coefficients in the Louisiana-Texas shelf, northern Gulf of Mexico. Gulf Mex. Sci. 2008, 26, 14–27. [Google Scholar] [CrossRef] [Green Version]
- Santamaría-del-Ángel, E.; Millán-Núñez, R.; Soto, I.; González-Silvera, A.; Wolny, J.; Cerdeira-Estrada, S.; Cajal-Medrano, R.; Muller-Karger, F.; Padilla-Rosas, Y.X.S.; Mercado-Santana, A.; et al. Phytoplankton Blooms: New Initiative Using Marine Optics as a Basis for Monitoring Programs. In Coastal Ecosystems: Experiences and Recommendations for Environmental Monitoring Programs; Nova Science Publisher: New York, NY, USA, 2015; Chapter 4. [Google Scholar]
- Aguilar-Maldonado, J.A.; Santamaría-del-Ángel, E.; González-Silvera, A.; Cervantes-Rosas, O.; López, L.M.; Gutiérrez-Magness, A.; Cerdeira-Estrada, S.; Sebastiá-Frasquet, M.T. Identification of Phytoplankton Blooms under the Index of Inherent Optical Properties (IOP Index) in Optically Complex Waters. Water 2018, 10, 129. [Google Scholar] [CrossRef] [Green Version]
- Austin, R.W.; Petzold, T.J. The Determination of the Diffuse Attenuation Coefficient of Sea Water Using the Coastal Zone Color Scanner. In Oceanography from Space; Springer: Boston, MA, USA, 1981; pp. 239–256. [Google Scholar]
- Hicks, B.J.; Stichbury, G.A.; Brabyn, L.K.; Allan, M.G.; Ashraf, S. Hindcasting water clarity from Landsat satellite images of unmonitored shallow lakes in the Waikato region, New Zealand. Environ. Monit. Assess. 2013, 185, 7245–7261. [Google Scholar] [CrossRef]
- Butt, M.J.; Nazeer, M. Landsat ETM+ Secchi Disc Transparency (SDT) retrievals for Rawal Lake, Pakistan. Adv. Space Res. 2015, 56, 1428–1440. [Google Scholar] [CrossRef]
- Rodrigues, T.; Alcântara, E.; Watanabe, F.; Imai, N. Retrieval of Secchi disk depth from a reservoir using a semi-analytical scheme. Remote Sens. Environ. 2017, 198, 213–228. [Google Scholar] [CrossRef] [Green Version]
- Leite, H.R.; de Oliveira, F.A.; Drago, D.; Muraro, A.; Teixeira, L.F.; Hainosz, F.S.; Prochnow, R.M.; Quicu, S.T.; Nascimento, C. Natural effects on remote sensing of water quality parameters data: A case study on available algorithms at the Jupia Reservoir, Brazil. In Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions; International Society for Optics and Photonics: Washington, DC, USA, 2019; Volume 11150, p. 1115006. [Google Scholar]
- Nouchi, V.; Kutser, T.; Wüest, A.; Müller, B.; Odermatt, D.; Baracchini, T.; Bouffard, D. Resolving biogeochemical processes in lakes using remote sensing. Aquat. Sci. 2019, 81, 27. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.H.; Yang, C.S.; Ouchi, K. Validation of the semi-analytical algorithm for estimating vertical underwater visibility using MODIS data in the waters around Korea. Korean J. Remote Sens. 2013, 29, 601–610. [Google Scholar] [CrossRef] [Green Version]
- Tyler, J.E. The Secchi Disk. Limnol. Oceanogr. 1968, 13, 1–6. [Google Scholar] [CrossRef]
- Doron, M.; Babin, M.; Mangin, A.; Hembise, O. Estimation of light concentration, and horizontal and vertical visibility in oceanic and coastal waters from surface reflectance. J. Geophys. Res. 2007, 112, C06003. [Google Scholar] [CrossRef] [Green Version]
- Doron, M.; Babin, M.; Hembise, O.; Mangin, A.; Garnesson, P. Ocean transparency from space: Validation of algorithm estimating Secchi depth using MERIS, MODIS and SeaWiFS data. Remote Sens. Environ. 2011, 115, 2986–3001. [Google Scholar] [CrossRef]
- Betancur-Turizo, S.P.; González-Silvera, A.G.; Santamaría-Del-Ángel, E.; Millán-Núñez, R.; Millán-Núñez, E.; García-Nava, H.; Godínez, V.M.; Sánchez-Velasco, L. Variability in the Light Absorption Coefficient by Phytoplankton, Non-Algal Particles and Colored Dissolved Organic Matter in the Northern Gulf of California. Open J. Mar. Sci. 2018, 8, 20–37. [Google Scholar] [CrossRef] [Green Version]
- Jiang, D.; Matsushita, B.; Setiawan, F.; Vundo, A. An improved algorithm for estimating the Secchi disk depth from remote sensing data based on the new underwater visibility theory. ISPRS J. Photogramm. 2019, 152, 13–23. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, C.; Li, J.; Zhang, F.; Wang, S. Secchi Disk Depth Estimation from China’s New Generation of GF-5 Hyperspectral Observations Using a Semi-Analytical Scheme. Remote Sens. 2020, 12, 1849. [Google Scholar] [CrossRef]
- Arabi, B.; Salama, M.S.; Pitarch, J.; Verhoef, W. Integration of in-situ and multi-sensor satellite observations for long-term water quality monitoring in coastal areas. Remote Sens. Environ. 2020, 239, 111632. [Google Scholar] [CrossRef]
- Djavidnia, S.; Ott, M.; Seeyave, S. (Eds.) Oceans and Society: Blue Planet; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2014. [Google Scholar]

| Reference | Equation | MAE | RMSD | BIAS | MPI | |
|---|---|---|---|---|---|---|
| Poole and Atkins [9] | 1.9–35 | 0.182 | 0.285 | 0.217 | 0.104 | |
| Poole and Atkins [9] Holmes [15] | 1.9–35 2–12 | 0.125 | 0.273 | 0.120 | 0.416 | |
| Megard and Berman [16] | 6–46 | 0.142 | 0.285 | 0.118 | 0.229 | |
| Lee et al. [18] | All intervals | 0.134 | 0.285 | 0.078 | 0.354 | |
| Montes-Hugo and Álvarez-Borrego [17] | 1–12 | 0.141 | 0.359 | −0.013 | 0.250 | |
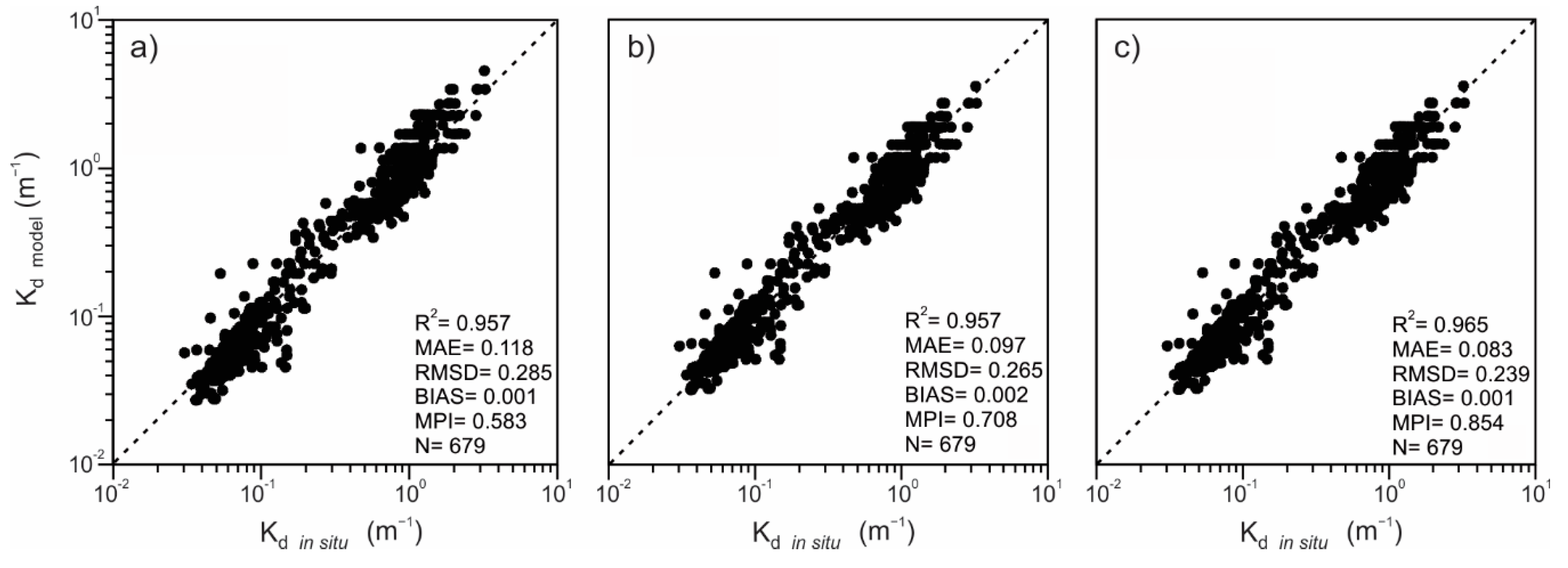
| Model a | All intervals | 0.118 | 0.285 | 0.003 | 0.583 | |
| Model b | All intervals | 0.097 | 0.265 | 0.002 | 0.708 | |
| Model c | Equations (15)–(17) | <2.20 Transition zone ≥5.37 | 0.083 | 0.239 | 0.001 | 0.854 |
| Reference | Equation | MAE | RMSD | BIAS | MPI | |
|---|---|---|---|---|---|---|
| Poole and Atkins [9] | 1.9–35 | 0.041 | 0.073 | −0.028 | 0.074 | |
| Poole and Atkins [9] Holmes [15] | 1.9–35 2–12 | 0.034 | 0.063 | −0.006 | 0.460 | |
| Megard and Berman [16] | 6–46 | 0.032 | 0.063 | −0.011 | 0.425 | |
| Lee et al. [18] | All intervals | 0.031 | 0.062 | −0.005 | 0.740 | |
| Montes-Hugo and Álvarez-Borrego [17] | 1–12 | 0.034 | 0.003 | 0.021 | 0.425 | |
| Model a | All intervals | 0.029 | 0.063 | 0.007 | 0.592 | |
| Model b | All intervals | 0.032 | 0.072 | 0.009 | 0.388 | |
| Model c | Equations (15)–(17) | <2.20 | 0.026 | 0.062 | 0.005 | 0.814 |
| satellite model (490) | Standard SeaDAS product | Transition zone ≥5.37 | 0.079 | 0.187 | 0.015 | 0.074 |
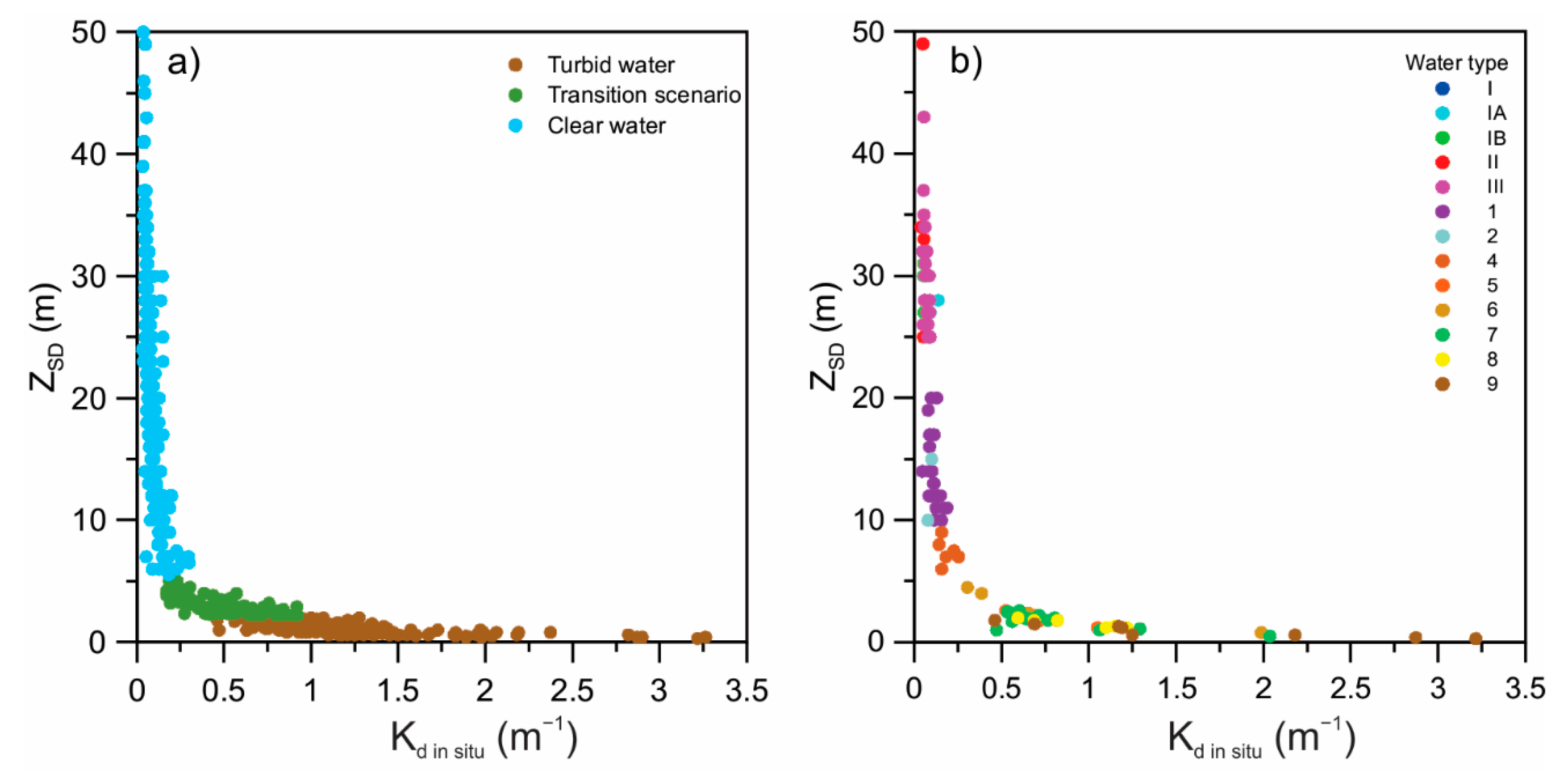
| Descriptors | Oceanic | Coastal | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
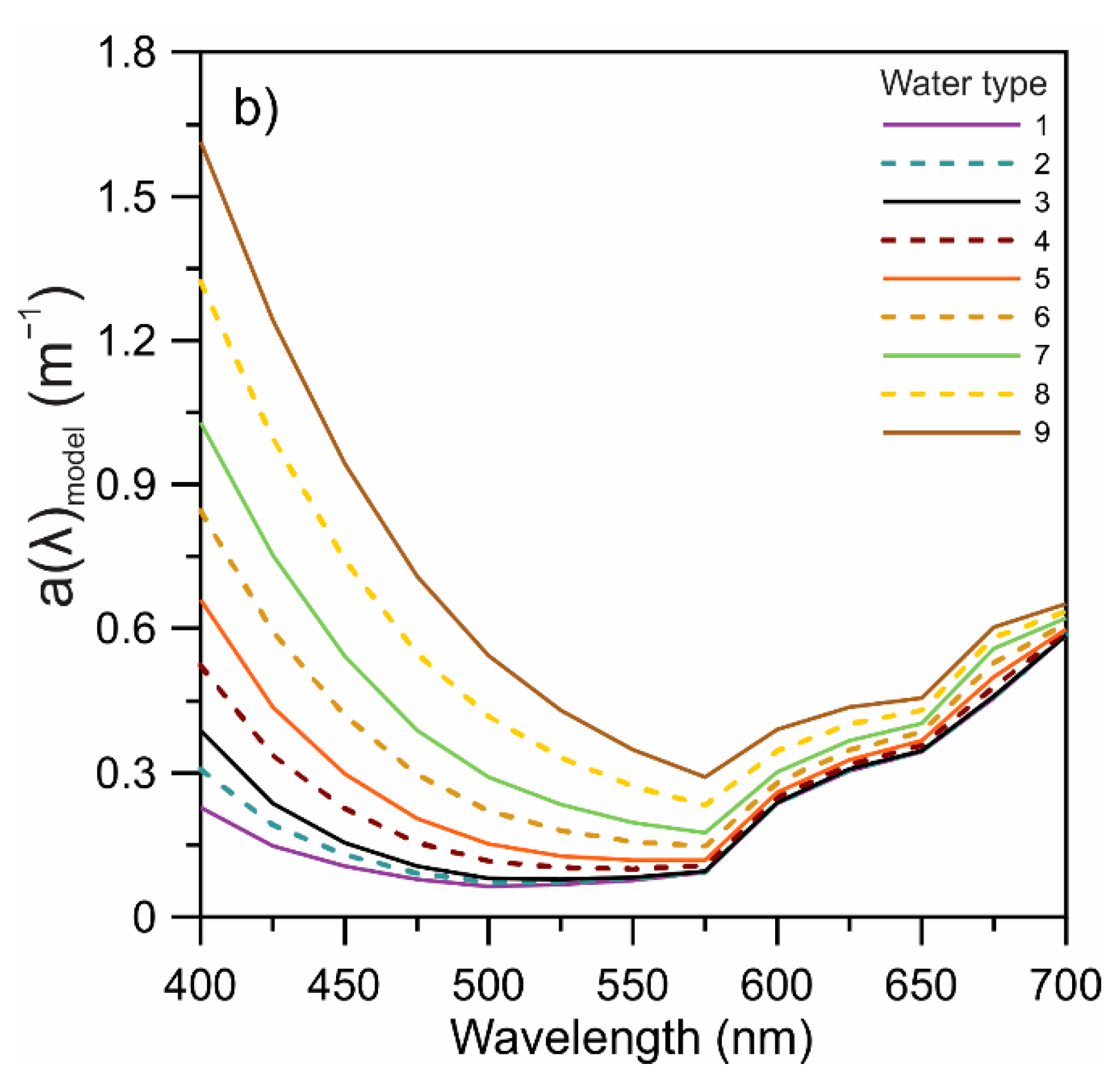
| Water Type | I | IA | IB | II | III | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| N | 2 | 4 | 4 | 8 | 26 | 21 | 2 | - | 6 | 5 | 7 | 14 | 6 | 8 |
| Water Type | Model | Equation | MAE | RMSD | BIAS |
|---|---|---|---|---|---|
| Oceanic group | Model c Model oceanic | Equations (15)–(17) | 0.016 0.550 | 0.018 0.020 | 0.016 0.055 |
| Coastal group | Model c Model coastal | Equations (15)–(17) | 0.149 0.346 | 0.260 0.469 | 0.037 −0.343 |
| III | Model c Model III | Equations (15)–(17) | 0.011 0.027 | 0.009 0.010 | 0.011 0.027 |
| 1 | Model c Model 1 | Equations (15)–(17) | 0.021 0.027 | 0.027 0.027 | 0.016 0.025 |
| 7 | Model c Model 7 | Equations (15)–(17) | 0.051 0.105 | 0.053 0.074 | −0.032 0.105 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo-Ramírez, A.; Santamaría-del-Ángel, E.; González-Silvera, A.; Frouin, R.; Sebastiá-Frasquet, M.-T.; Tan, J.; Lopez-Calderon, J.; Sánchez-Velasco, L.; Enríquez-Paredes, L. A New Algorithm to Estimate Diffuse Attenuation Coefficient from Secchi Disk Depth. J. Mar. Sci. Eng. 2020, 8, 558. https://doi.org/10.3390/jmse8080558
Castillo-Ramírez A, Santamaría-del-Ángel E, González-Silvera A, Frouin R, Sebastiá-Frasquet M-T, Tan J, Lopez-Calderon J, Sánchez-Velasco L, Enríquez-Paredes L. A New Algorithm to Estimate Diffuse Attenuation Coefficient from Secchi Disk Depth. Journal of Marine Science and Engineering. 2020; 8(8):558. https://doi.org/10.3390/jmse8080558
Chicago/Turabian StyleCastillo-Ramírez, Alejandra, Eduardo Santamaría-del-Ángel, Adriana González-Silvera, Robert Frouin, María-Teresa Sebastiá-Frasquet, Jing Tan, Jorge Lopez-Calderon, Laura Sánchez-Velasco, and Luis Enríquez-Paredes. 2020. "A New Algorithm to Estimate Diffuse Attenuation Coefficient from Secchi Disk Depth" Journal of Marine Science and Engineering 8, no. 8: 558. https://doi.org/10.3390/jmse8080558
APA StyleCastillo-Ramírez, A., Santamaría-del-Ángel, E., González-Silvera, A., Frouin, R., Sebastiá-Frasquet, M.-T., Tan, J., Lopez-Calderon, J., Sánchez-Velasco, L., & Enríquez-Paredes, L. (2020). A New Algorithm to Estimate Diffuse Attenuation Coefficient from Secchi Disk Depth. Journal of Marine Science and Engineering, 8(8), 558. https://doi.org/10.3390/jmse8080558









