Effect of a Coccolithophore Bloom on the Underwater Light Field and the Albedo of the Water Column
Abstract
1. Introduction
2. Materials and Methods
2.1. Field and Satellite Data for Modeling
2.2. Calculation Method
2.3. Input Parameters for the Modeling
3. Results Obtained
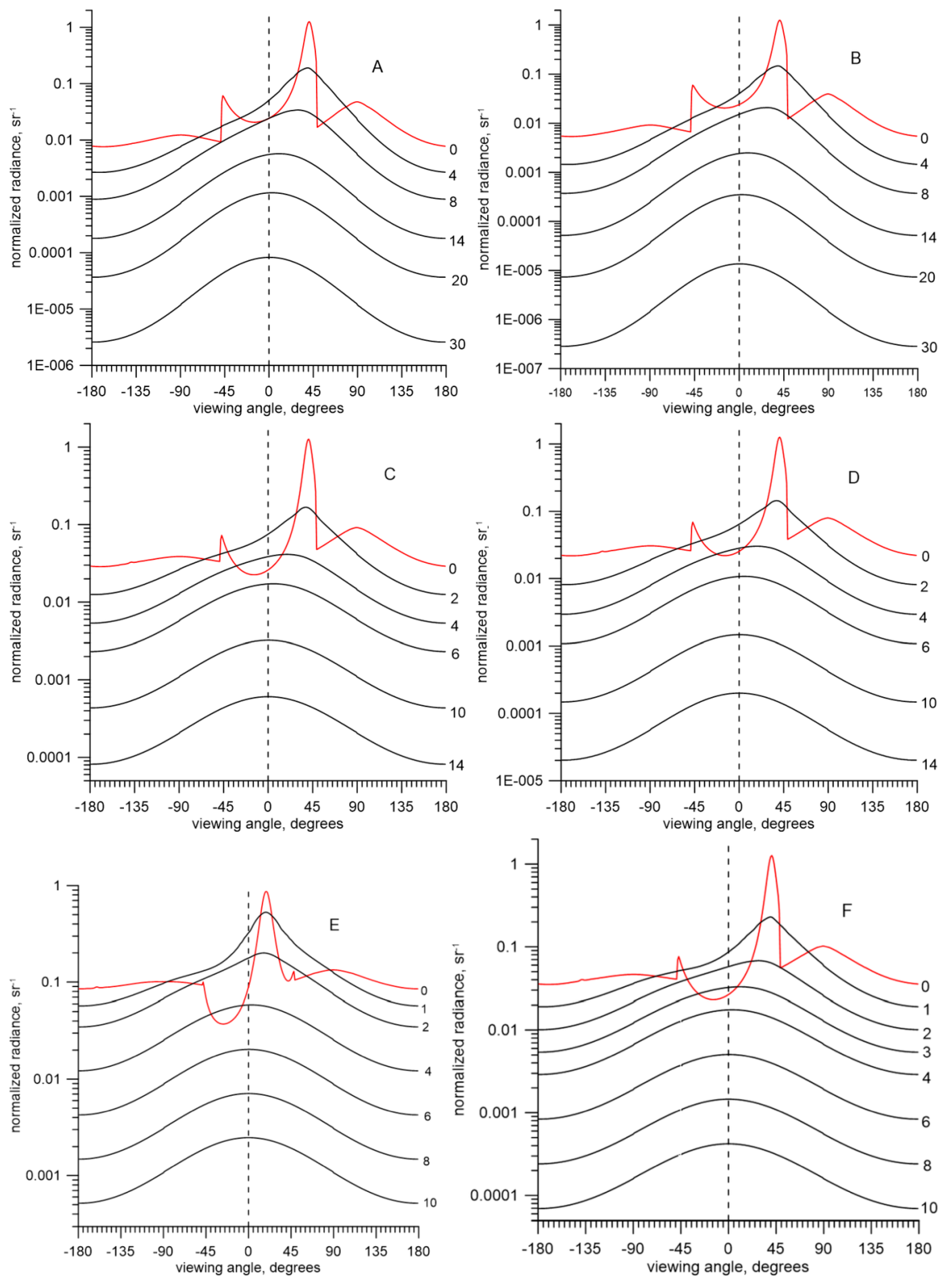
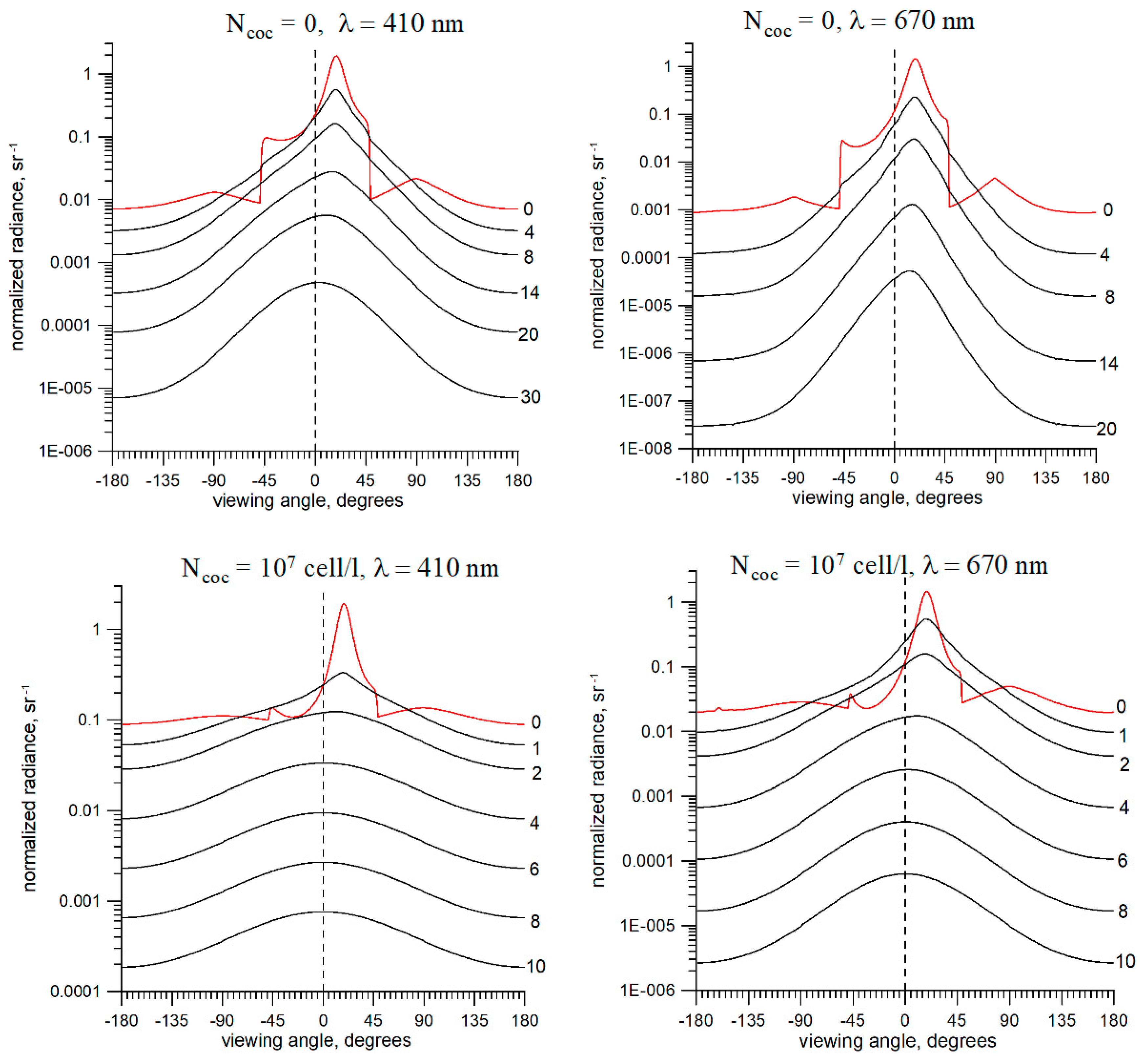
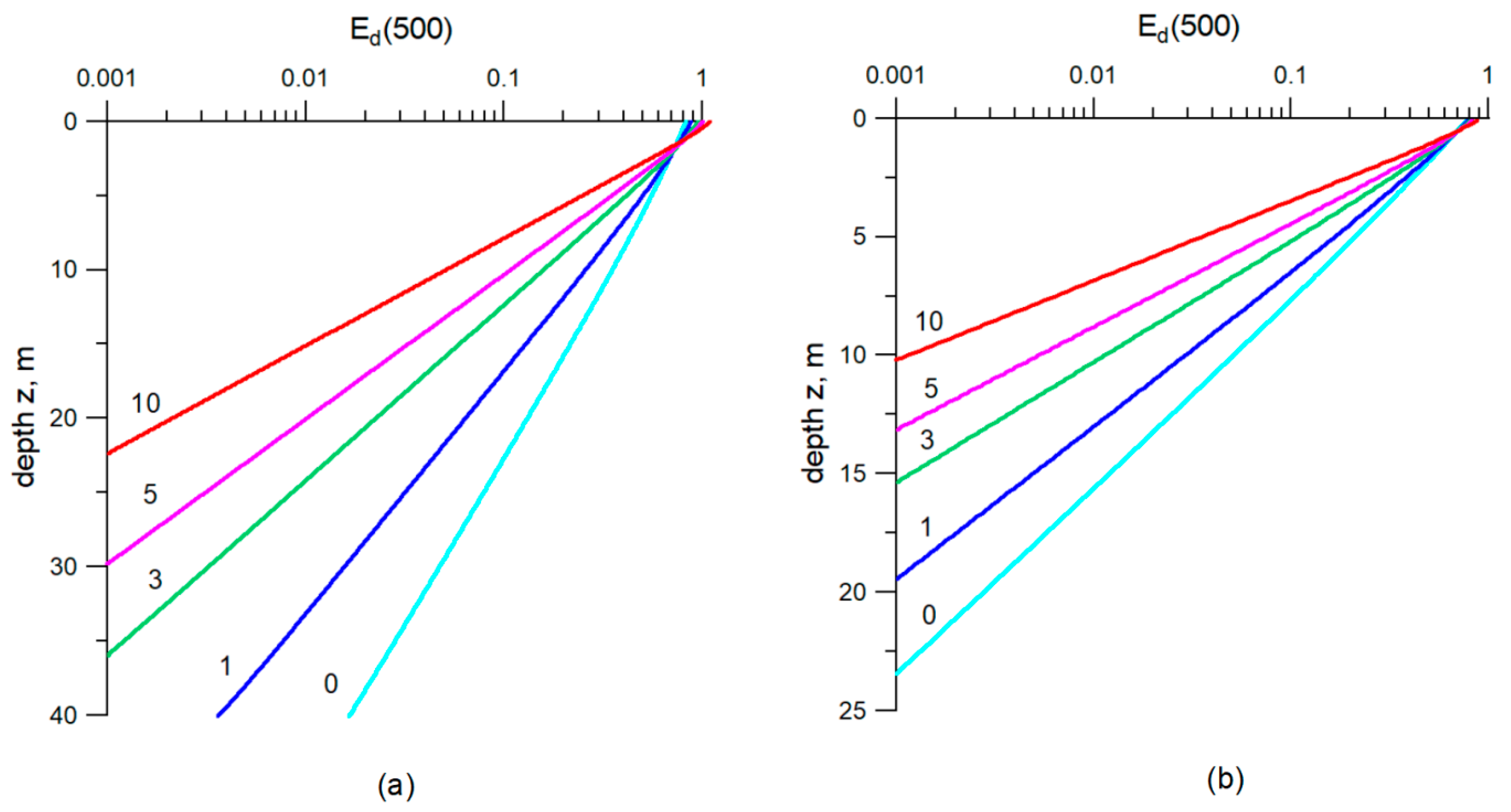
3.1. Effect of the Coccolithophore Bloom on the Underwater Light Field
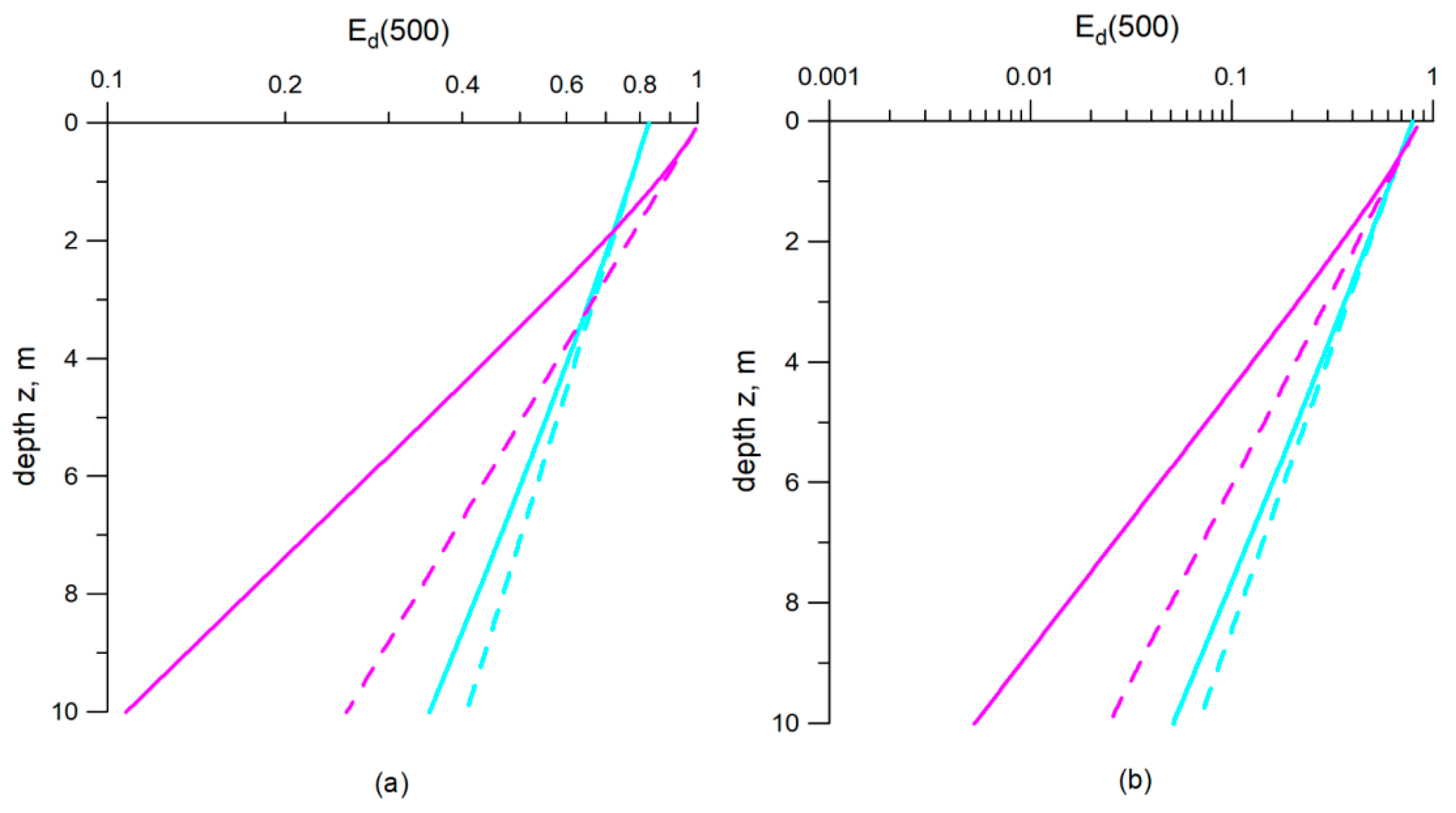
3.2. Coccolithophore Bloom Impact on the Water Radiance Reflectance
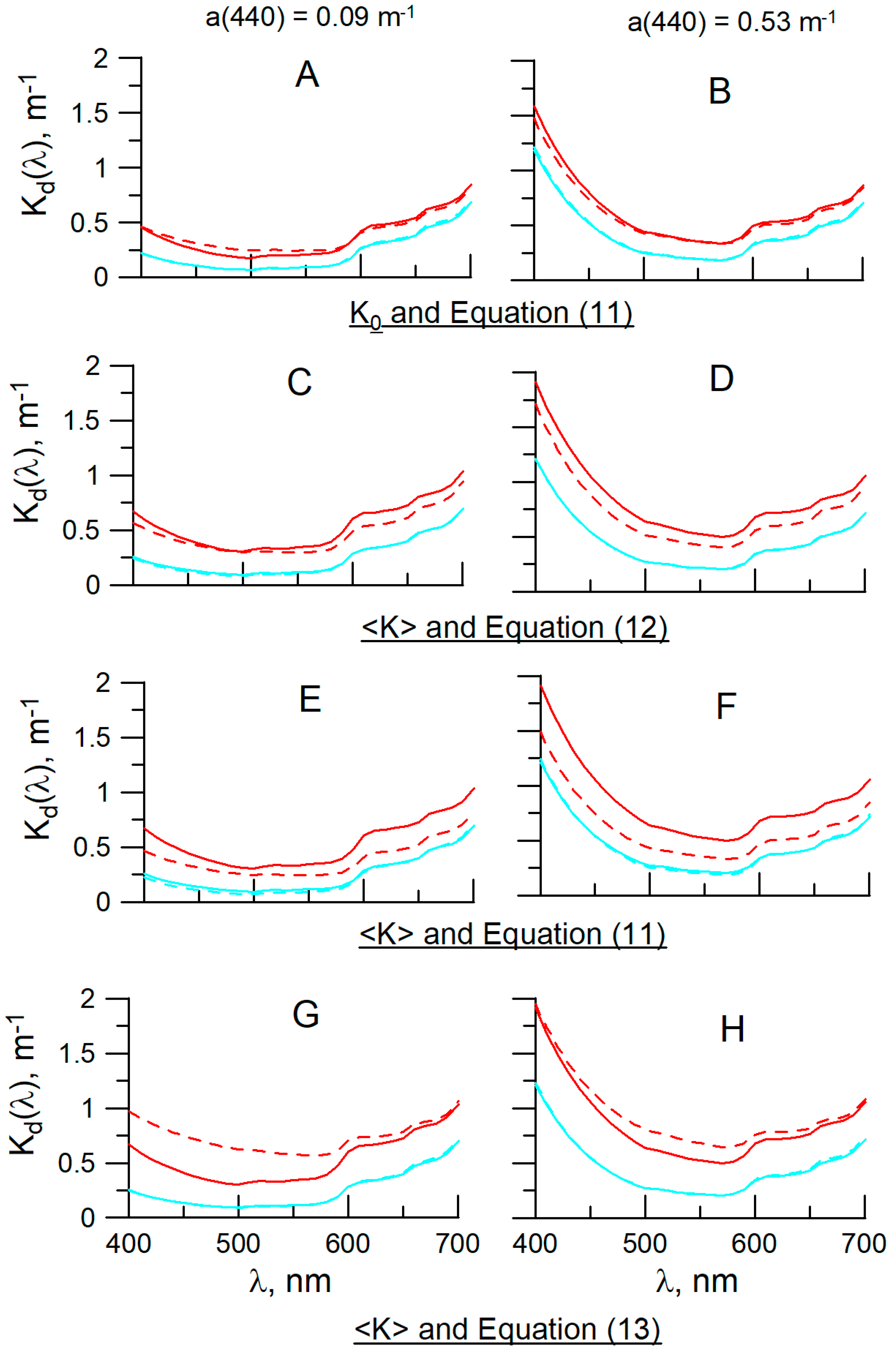
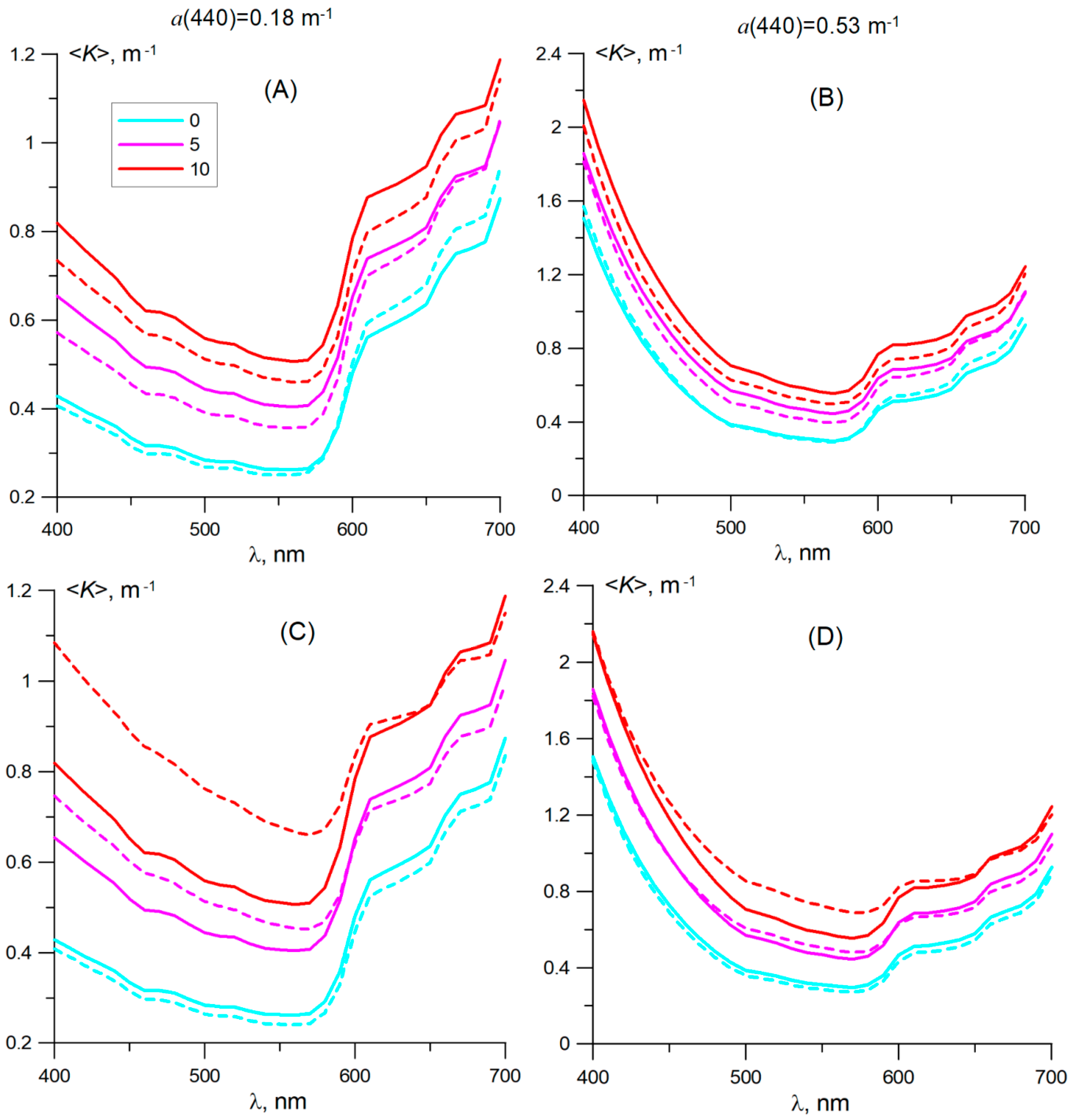
3.3. Coccolithophore Impact on the Diffuse Attenuation Coefficient
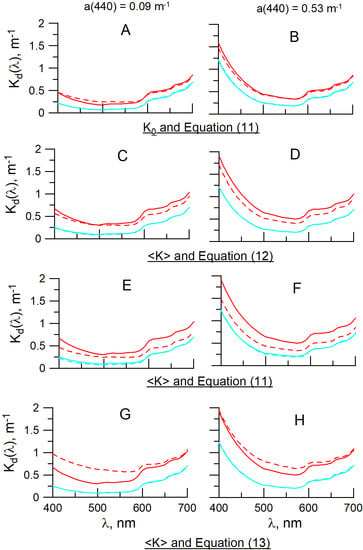
4. Influence of the Coccolithophore Blooms on the Accuracy of the Approximate Formulas
4.1. Water Radiance Reflectance
4.2. Diffuse Attenuation Coefficient
5. Discussion and Conclusions
5.1. Comments to the Calculation Methods
5.2. Set of the Input Parameters
5.3. Asymptotic Regime
5.4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thierstein, H.R.; Young, J.R. Coccolithophores—From Molecular Processes to Global Impact; Springer: Berlin, Germany, 2004. [Google Scholar]
- Kopelevich, O.V.; Burenkov, V.I.; Ershova, S.V.; Sheberstov, S.V.; Evdoshenko, M.A. Application of SeaWiFS data for studying variability of bio-optical characteristics in the Barents, Black and Caspian Seas. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2004, 51, 1063–1091. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Burenkov, V.I.; Sheberstov, S.V. Case Studies of optical remote sensing in the Barents Sea, Black Sea, and Caspian Sea. In Remote Sensing of the European Seas; Springer: Dordrecht, Holland, 2008; pp. 53–66. [Google Scholar]
- Kopelevich, O.V.; Burenkov, V.I.; Sheberstov, S.V.; Vazyulya, S.V.; Kravchishina, M.D.; Pautova, L.; Silkin, V.A.; Artemiev, V.A.; Grigoriev, V. Satellite monitoring of coccolithophore blooms in the Black Sea from ocean color data. Remote Sens. Environ. 2014, 146, 113–123. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Artemiev, V.A. Comparison of biooptical characteristics of the Baltic, Norwegian, and Barents Seas: Summer 2016 (Cruise 65 of the R/V Akademik Mstislav Keldysh). Oceanology 2017, 57, 340–342. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Vazyulya, S.V.; Grigoriev, A.V.; Khrapko, A.N.; Sheberstov, S.V.; Sahling, I.V. Penetration of visible solar radiation in waters of the Barents sea depending on cloudiness and coccolithophore blooms. Oceanology 2017, 57, 402–409. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2017; OOO «VASh FORMAT»: Moscow, Russia, 2018. [Google Scholar]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Electronic Atlas. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2018. Available online: http://optics.ocean.ru/ (accessed on 12 May 2020).
- Jerlov, N.G. Marine Optics; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Voss, K.J. Electro-optic camera system for measurement of the underwater radiance distribution. Opt. Eng. 1989, 28, 283241. [Google Scholar] [CrossRef]
- Timofeeva, V.A. Optics of turbid water. In Optical Aspects of Oceanography; Jerlov, N.G., Nielsen, E.S., Eds.; Academic Press: London, UK, 1974; pp. 177–219. [Google Scholar]
- Gershun, A. Light Field; ONTI NKTP: Moscow, Soviet Union, 1936. [Google Scholar]
- Gordon, H.R. Physical Principles of Ocean Color Remote Sensing. Available online: https://ioccg.org/wp-content/uploads/2019/11/gordon_book_nov_20_2019.pdf (accessed on 12 May 2020).
- Jerlov, N.G. Optical Oceanography; Elsevier: New York, NY, USA, 1968. [Google Scholar]
- Ivanoff, A. Introduction a L’oceanographie; Librairie Vuibert: Paris, France, 1975. [Google Scholar]
- Ivanov, A.P. Phyzical Background of Hydrooptics; Nauka i technika: Minsk, Soviet Union, 1975. [Google Scholar]
- Preizendorfer, R. Hydrologic Optics; NOAA: Honolulu, HI, USA, 1976.
- Dolin, L.S.; Levin, I.M. Handbook of the Theory of Underwater Vision; Gidrometeoizdat: Leningrad, Soviet Union, 1991. [Google Scholar]
- Monin, A. Ocean Optics; Nauka: Moscow, Soviet Union, 1983. [Google Scholar]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Plass, G.N.; Kattawar, G.W. Monte Carlo calculations of radiative transfer in the earth’s atmosphere–ocean system. 1. Flux in the atmosphere and ocean. J. Phys. Oceanogr. 1972, 2, 139–145. [Google Scholar] [CrossRef]
- Jin, Z.; Stamnes, K. Radiative transfer in nonuniformly refracting layered media: Atmosphere-ocean system. Appl. Opt. 1994, 33, 431–442. [Google Scholar] [CrossRef]
- Sheberstov, S.V.; Nabiullina, M.V.; Lukyanova, E.A. Numerical modeling of radiative transfer in ocean-atmosphere system with wind-roughened surface. In Proceedings of the II International Conference «Current Problems in Optics of Natural Waters», St. Petersburg, Russia, 8–12 September 2003; pp. 90–95. [Google Scholar]
- Mobley, C.D.; Sundman, L.K. Hydrolight 5.2, Ecolight 5.2, Users Guide. Available online: http://www.sequoiasci.com/wp-content/uploads/2013/07/HE52UsersGuide.pdf (accessed on 12 May 2020).
- Smyth, T.J.; Moore, G.F.; Groom, S.B.; Land, P.E.; Tyrrell, T. Optical modeling and measurements of a coccolithophore bloom. Appl. Opt. 2002, 41, 7679–7688. [Google Scholar] [CrossRef]
- McKee, D.; Cunningham, A.; Craig, S. Semi-empirical correction algorithm for AC-9 measurements in a coccolithophore bloom. Appl. Opt. 2003, 42, 4369–4374. [Google Scholar] [CrossRef]
- Tyrrel, T.; Holligan, P.M.; Mobley, C. Optical impacts of oceanic coccoblooms. J. Geophys. Res. Atmos. 1999, 104, 3223–3242. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Kopelevich, O.V.; Sahling, I.V.; Artemiev, V.A.; Pautova, L.A.; Lange, E.K.; Kravchishina, M.D. Biooptical characteristics of the surface layer of the Baltic, Norwegian, and Barents seas in summer 2014–2016 from shipboard and satellite data. Oceanology 2017, 57, 410–418. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Sheberstov, S.V.; Kopelevich, O.V.; Zaytseva, A.F.; Pogosyan, S.I. Measuring the sea water absorption factor using integrating sphere. Light Eng. 2018, 26, 120–126. [Google Scholar] [CrossRef]
- Yushmanova, A.V.; Kopelevich, O.V.; Vazyulya, S.V.; Sahling, I.V. Inter-annual variability of the seawater light absorption in surface layer of the northeastern Black Sea in connection with hydrometeorological factors. J. Mar. Sci. Eng. 2019, 7, 326. [Google Scholar] [CrossRef]
- Plass, G.N.; Kattawar, G.W.; Catchings, F.E. Matrix operator theory of radiative transfer. 1: Rayleigh scattering. Appl. Opt. 1973, 12, 314–329. [Google Scholar] [CrossRef]
- Bates, D.R. Rayleigh scattering by air. Planet. Space Sci. 1984, 32, 785–790. [Google Scholar] [CrossRef]
- Gordon, H.R.; Castaño, D.J. Aerosol analysis with Coastal Zone Color Scanner. A simple method for including multiple scattering effects. Appl. Opt. 1989, 28, 1320–1326. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Surface-roughness considerations for atmospheric correction of ocean color sensors. I: The rayleigh-scattering component. Appl. Opt. 1992, 32, 4247–4260. [Google Scholar] [CrossRef]
- Nakajima, T.; Tanaka, M. Effect of wind-generated waves on the transfer of solar radiation in the atmosphere-ocean system. J. Quant. Spectrosc. Radiat. Transf. 1983, 29, 521–537. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover Publications: New York, NY, USA, 1960. [Google Scholar]
- Stamnes, K.; Swanson, R.A. A new look at the discrete ordinate method for radiative transfer calculations in anisotropically scattering atmospheres. J. Atmos. Sci. 1981, 38, 387–398. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.-C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef]
- Kopelevich, O.V. Application of data on seawater light scattering for the study of marine particles: A selective review focusing on Russian literature. Geo Mar. Lett. 2012, 32, 183–193. [Google Scholar] [CrossRef]
- Kopelevich, O.V. Low-parameter model of seawater optical properties. In Ocean Optics, Vol. 1: Physical Ocean Optics; Monin, A.S., Ed.; Nauka Pub., Nauka: Moscow, Russia, 1983; Volume 1, pp. 208–234. [Google Scholar]
- Levin, I.M.; Kopelevich, O.V. Correlations between the Inherent Hydrooptical Characteristics in the spectral range close to 550 nm. Oceanology 2007, 47, 344–348. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Lutsarev, S.V.; Rodionov, V.V. Spectral absorption by “yellow substance” of ocean waters. Oceanology 1989, 29, 409–414. [Google Scholar]
- Kopelevich, O.V.; Burenkov, V.I.; Vazyulya, S.V.; Sheberstov, S.V. Problems of detection of coccolithophore blooms from satellite data. Mod. Probl. Remote Sens. Earth Space 2012, 9, 241–250. [Google Scholar]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. I. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Burenkov, V.I.; Sheberstov, S.V.; Artemiev, V.A.; Taskaev, V.R. Estimation of measurement error of the seawater beam attenuation coefficient in turbid water of Arctic seas. Light Eng. 2019, 27, 103–111. [Google Scholar] [CrossRef]
- Gordon, H.R.; Du, T. Light scattering by nonspherical particles: Application to coccoliths detached from Emiliania huxleyi. Limnol. Oceanogr. 2001, 46, 1438–1454. [Google Scholar] [CrossRef]
- Gordon, H.R. Light scattering and absorption by randomly-oriented cylinders: Dependence on aspect ratio for refractive indices applicable for marine particles. Opt. Express 2011, 19, 4673–4691. [Google Scholar] [CrossRef]
- Zhai, P.-W.; Hu, Y.; Trepte, C.R.; Winker, D.M.; Josset, D.B.; Lucker, P.L.; Kattawar, G.W. Inherent optical properties of the coccolithophore: Emiliania huxleyi. Opt. Express 2013, 21, 17625–17638. [Google Scholar] [CrossRef]
- Reynolds, R.A.; Stramski, D.; Neukermans, G. Optical backscattering by particles in Arctic seawater and relationships to particle mass concentration, size distribution, and bulk composition. Limnol. Oceanogr. 2016, 61, 1869–1890. [Google Scholar] [CrossRef]
- Voss, K.J.; Balch, W.M.; Kilpatrick, K.A. Scattering and attenuation properties of emiliania huxleyi cells and their detached coccoliths. Limnol. Oceanogr. 1998, 43, 870–876. [Google Scholar] [CrossRef]
- Balch, W.M. The ecology, biogeochemistry, and optical properties of coccolithophores. Annu. Rev. Mar. Sci. 2018, 10, 71–98. [Google Scholar] [CrossRef]
- Algorithm Descriptions. Available online: https://oceancolor.gsfc.nasa.gov/atbd/ (accessed on 16 May 2020).
- Gordon, H.R. Can the Lambert-Beer law be applied to the diffuse attenuation coefficient of ocean water? Limnol. Oceanogr. 1989, 34, 1389–1409. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. Bidirectional aspects. Appl. Opt. 1993, 32, 6864–6879. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D.; Gentili, B.; Gordon, H.R.; Jin, Z.; Kattawar, G.W.; Morel, A.; Reinersman, P.; Stamnes, K.; Stavn, R.H. Comparison of numerical models for computing underwater light fields. Appl. Opt. 1993, 32, 7484–7504. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. Space Phys. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Lee, Z.-P.; Du, K.-P.; Arnone, R. A model for the diffuse attenuation coefficient of downwelling irradiance. J. Geophys. Res. 2005, 110, 02016. [Google Scholar] [CrossRef]
- von Dassow, P.; Engh, G.; Iglesias-Rodrıguez, M.D.; Gittins, J.R. Calcification state of coccolithophores can be assessed by light scatter depolarization measurements with flow cytometry. J. Plankton Res. 2012, 34, 1011–1027. [Google Scholar] [CrossRef]
- Fournier, G.; Neukermans, G. An analytical model for light backscattering by coccoliths and coccospheres of Emiliania huxleyi. Opt. Express 2017, 25, 14996. [Google Scholar] [CrossRef] [PubMed]
- Hovland, E.K.; Hancke, K.; Alver, M.O.; Drinkwater, K.; Høkedal, J.; Johnsen, G.; Moline, M.; Sakshaug, E. Optical impact of an emiliania huxleyi bloom in the frontal region of the Barents Sea. J. Mar. Syst. 2014, 130, 228–240. [Google Scholar] [CrossRef]
- Poulton, A.J.; Young, J.R.; Bates, N.R.; Balch, W.M. Biometry of detached emiliania huxleyi coccoliths along the Patagonian Shelf. Mar. Ecol. Prog. Ser. 2011, 443, 1–17. [Google Scholar] [CrossRef]
- Dolin, L.S. Propagation of a narrow beam of light in a medium with strongly anisotropic scattering. Radiophys. Quantum Electron. 1967, 9, 40–47. [Google Scholar] [CrossRef]

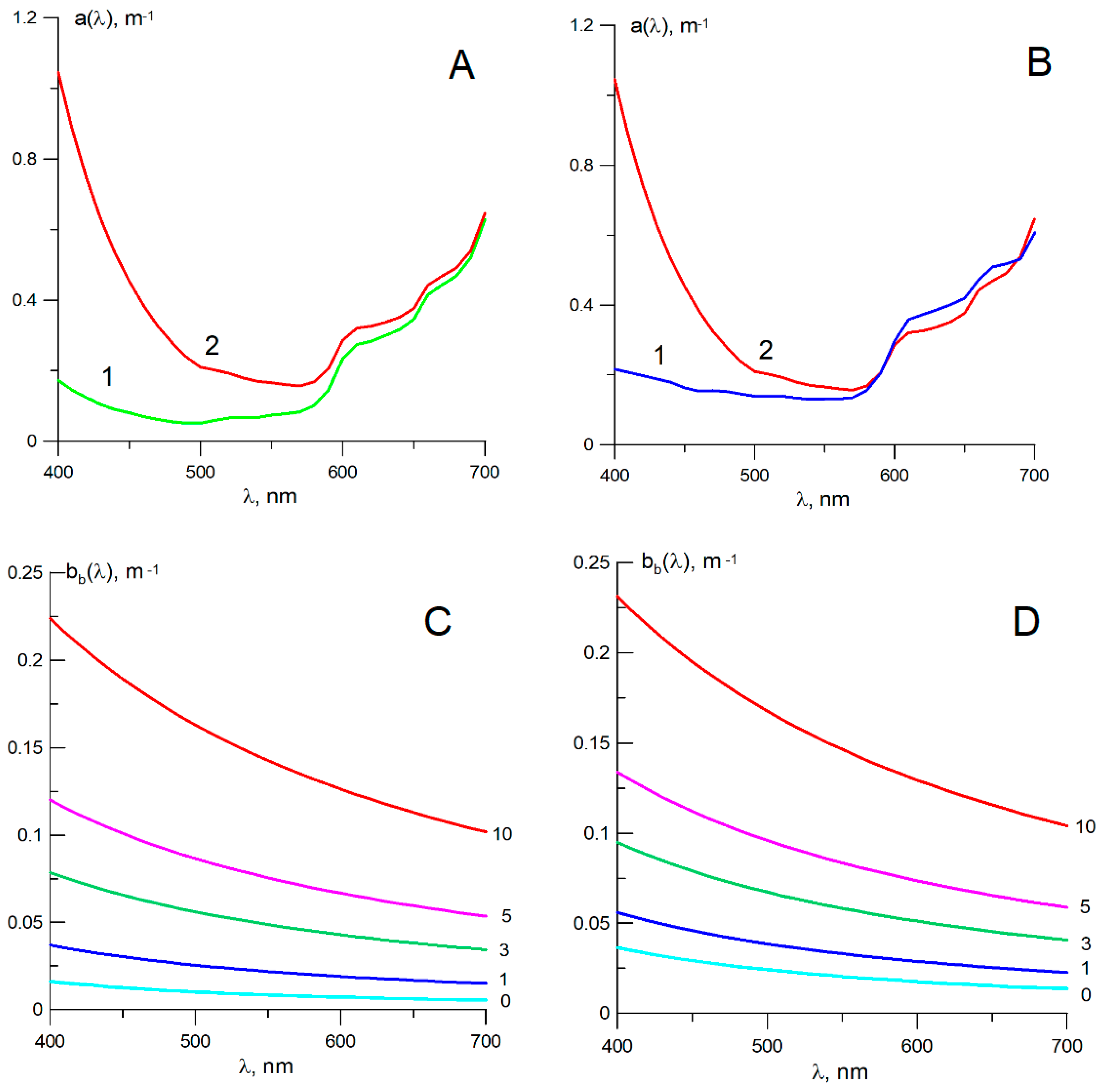








| Seawater Optical Parameters | absorption coefficients: seawater—a(λ), filtrate—af(λ), |
| CDOM—ag(λ) = af(λ)−aw(λ), particulate—ap(λ); | |
| Beam attenuation coefficient—c(530); | |
| Scattering coefficient—b(530) = c(530)−a(530); | |
| Backscattering coefficient—bb(λ) from ρ(λ); | |
| b(λ), β(λ), P(λ)—using model [40,41,42,43] | |
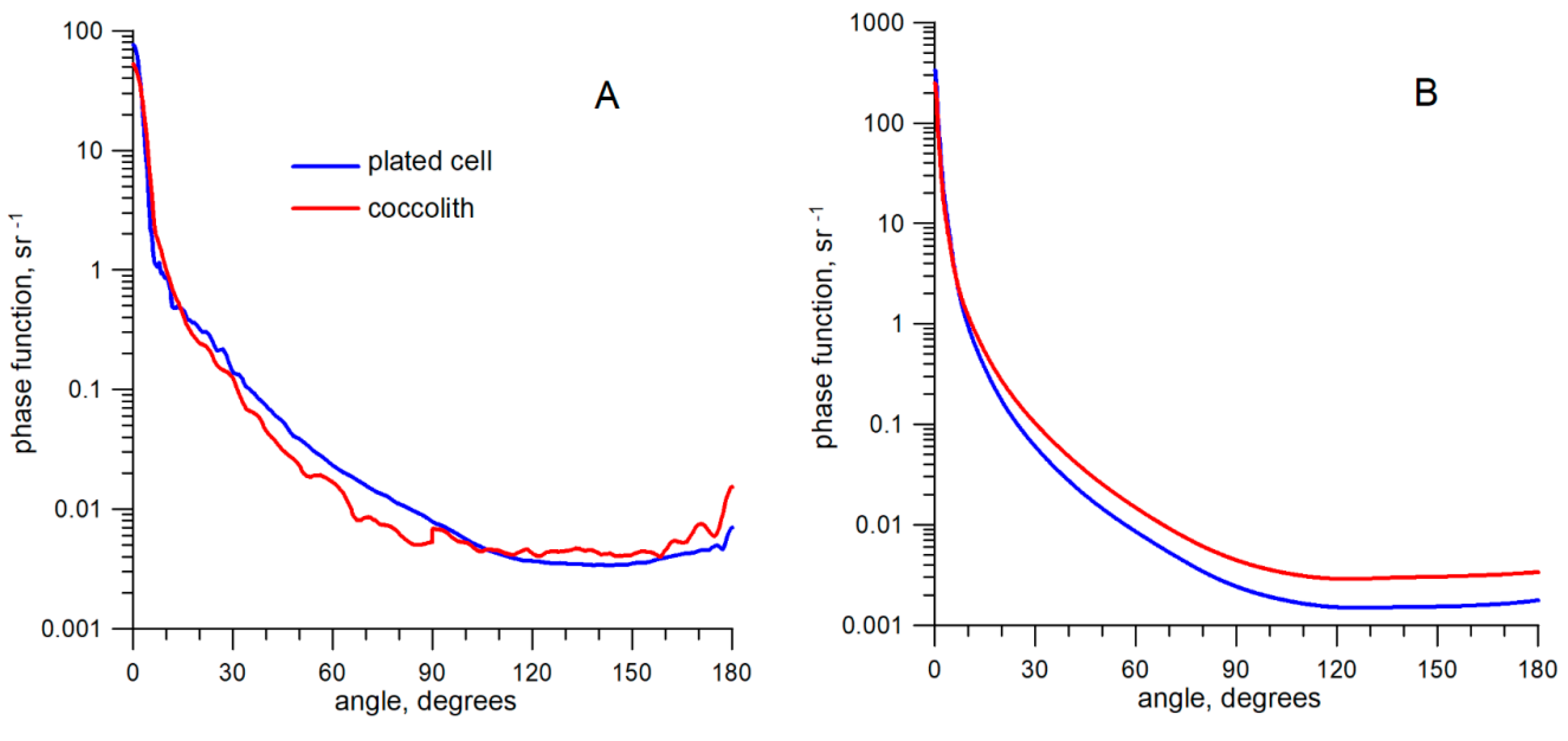
| Coccolithophore Parameters | plated cell and coccolith concentration Ncoc and Nlith—from direct determination or by setting for model; |
| Optical characteristics—from [4,44]. | |
| Non-coccolithophore Parameters | particle scattering coefficients bp(λ), βp(λ), Pp(λ)—using model [40,41,42,43]; |
| absorption coefficient from ICAM measurements as a(λ)−aw(λ) or by setting for model; |
| Input Parameters | Optical Characteristics | |||||||
|---|---|---|---|---|---|---|---|---|
| Ncoc | a(440) | b(440) | ω0(440) | b(555) | bb(555) | ω0(555) | <cos> | |
| Black Sea | ||||||||
| 0 | 0.09 | 0.60 | 0.87 | 0.48 | 0.008 | 0.864 | 0.017 | 0.922 |
| 0 | 0.53 | 0.60 | 0.531 | 0.48 | 0.008 | 0.748 | 0.017 | 0.922 |
| 5 | 0.09 | 3.82 | 0.977 | 2.81 | 0.075 | 0.974 | 0.027 | 0.895 |
| 5 | 0.53 | 3.78 | 0.877 | 2.81 | 0.075 | 0.945 | 0.027 | 0.895 |
| 10 | 0.09 | 6.83 | 0.987 | 5.13 | 0.141 | 0.985 | 0.027 | 0.892 |
| 10 | 0.53 | 6.93 | 0.929 | 5.13 | 0.141 | 0.969 | 0.027 | 0.892 |
| Barents Sea | ||||||||
| 0 | 0.18 | 2.55 | 0.934 | 2.18 | 0.02 | 0.943 | 0.0091 | 0.949 |
| 0 | 0.53 | 2.53 | 0.827 | 2.18 | 0.02 | 0.93 | 0.0091 | 0.949 |
| 5 | 0.18 | 5.63 | 0.969 | 4.37 | 0.082 | 0.971 | 0.0188 | 0.918 |
| 5 | 0.53 | 5.56 | 0.913 | 4.37 | 0.082 | 0.964 | 0.0188 | 0.918 |
| 10 | 0.18 | 8.39 | 0.979 | 6.56 | 0.145 | 0.985 | 0.0221 | 0.908 |
| 10 | 0.53 | 8.61 | 0.942 | 6.56 | 0.145 | 0.975 | 0.0221 | 0.908 |
| Black Sea | |||||||||||||
| Ncoc = 5 × 106 cell/L, a(440) = 0.09 m−1 | Ncoc = 5 × 106 cell/L, a(440) = 0.53 m−1 | ||||||||||||
| z, m | −90 | −45 | 0 | 45 | 90 | k * | z, m | −90 | −45 | 0 | 45 | 90 | k |
| 4 | 0.910 | 1.491 | 2.366 | 1.949 | 1 | - | 4 | 0.867 | 2.023 | 4.033 | 2.881 | 1 | |
| 6 | 0.967 | 1.680 | 2.301 | 1.844 | 1 | 0.281 | 6 | 0.946 | 2.366 | 3.975 | 2.708 | 1 | 0.485 |
| 10 | 0.996 | 1.777 | 2.292 | 1.795 | 1 | 0.264 | 10 | 0.993 | 2.570 | 3.986 | 2.616 | 1 | 0.471 |
| 14 | 1.000 | 1.788 | 2.293 | 1.790 | 1 | 0.260 | 14 | 0.999 | 2.598 | 3.993 | 2.604 | 1 | 0.467 |
| Ncoc = 107 cell/L, a(440) = 0.09 m−1 | Ncoc = 107 cell/L, a(440) = 0.53 m−1 | ||||||||||||
| z, m | −90 | −45 | 0 | 45 | 90 | k | z, m | −90 | −45 | 0 | 45 | 90 | k |
| 4 | 0.990 | 1.499 | 1.831 | 1.547 | 1 | - | 4 | 0.981 | 1.956 | 2.746 | 2.057 | 1 | |
| 6 | 0.999 | 1.527 | 1.830 | 1.532 | 1 | 0.350 | 6 | 0.998 | 2.015 | 2.748 | 2.029 | 1 | 0.608 |
| 8 | 1.000 | 1.530 | 1.830 | 1.531 | 1 | 0.348 | 8 | 1.000 | 2.023 | 2.750 | 2.025 | 1 | 0.605 |
| 10 | 1.000 | 1.530 | 1.831 | 1.530 | 1 | 0.349 | 10 | 1.000 | 2.024 | 2.750 | 2.024 | 1 | 0.605 |
| Barents Sea | |||||||||||||
| Ncoc = 5 × 106 cell/L, a(440) = 0.18 m−1 | Ncoc = 5 × 106 cell/L, a(440) = 0.53 m−1 | ||||||||||||
| z, m | −90 | −45 | 0 | 45 | 90 | k | z, m | −90 | −45 | 0 | 45 | 90 | k |
| 4 | 0.886 | 1.756 | 2.685 | 2.376 | 1 | - | 4 | 0.872 | 1.936 | 3.156 | 2.691 | 1 | |
| 6 | 0.969 | 2.029 | 2.904 | 2.194 | 1 | 0.406 | 6 | 0.964 | 2.268 | 3.446 | 2.475 | 1 | 0.485 |
| 10 | 0,996 | 1,777 | 2,292 | 1,795 | 1 | 0.417 | 10 | 0.997 | 2.399 | 3.529 | 2.414 | 1 | 0.497 |
| 14 | 1.000 | 1.788 | 2.293 | 1.790 | 1 | 0.418 | 14 | 1.000 | 2.409 | 3.534 | 2.410 | 1 | 0.499 |
| Ncoc = 107 cell/L, a(440) = 0.18 m−1 | Ncoc = 107 cell/L, a(440) = 0.53 m−1 | ||||||||||||
| z, m | −90 | -45 | 0 | 45 | 90 | k | z, m | −90 | −45 | 0 | 45 | 90 | k |
| 4 | 0.977 | 1.755 | 2.290 | 1.824 | 1 | - | 4 | 0.983 | 0.983 | 2.618 | 2.006 | 1 | |
| 6 | 0.999 | 1.796 | 2.311 | 1.803 | 1 | 0.525 | 6 | 0.998 | 0.998 | 2.647 | 1.980 | 1 | 0.621 |
| 8 | 1.000 | 1.800 | 2.313 | 1.801 | 1 | 0.526 | 8 | 1.000 | 1.000 | 2.649 | 1.977 | 1 | 0.620 |
| 10 | 1.000 | 1.801 | 2.313 | 1.801 | 1 | 0.526 | 10 | 1.000 | 1.000 | 2.649 | 1.976 | 1 | 0.623 |
| Ncoc, 106 cell/L | 0 | 1 | 3 | 5 | 10 |
|---|---|---|---|---|---|
| Black Sea, a(440) = 0.09 m−1, θ0 = 25° | 1.9 | 1.7 | 1.5 | 1.4 | 1.3 |
| Black Sea, a(440) = 0.53 m−1, θ0 = 25° | 0.87 | 0.82 | 0.82 | 0.83 | 0.86 |
| Barents Sea, a(440) = 0.18 m−1, θ0 = 60° | 1.10 | 1.08 | 1.06 | 1.05 | 1.04 |
| Barents Sea, a(440) = 0.53 m−1, θ0 = 60° | 0.82 | 0.81 | 0.82 | 0.84 | 0.82 |
| Ncoc, 106 cell/L | 0 | 5 | 10 | 0 | 5 | 10 |
|---|---|---|---|---|---|---|
| Illumination Conditions | Black Sea, a(440) = 0.09 m−1 | Black Sea, a(440) = 0.53 m−1 | ||||
| Clear Sky,θ0 = 25° | >40 | 20.8 | 15.6 | 16.3 | 9.2 | 7.1 |
| Clear Sky,θ0 = 60° | >40 | 20.2 | 15.2 | 14.4 | 8.7 | 6.8 |
| Overcast | >40 | 20.5 | 15.5 | 15.6 | 9.0 | 7.0 |
| Illumination Conditions | Barents Sea, a(440) = 0.18 m−1 | Barents Sea, a(440) = 0.53 m−1 | ||||
| Clear Sky,θ0 = 25° | 17.5 | 10.8 | 8.5 | 13.1 | 8.5 | 6.8 |
| Clear Sky,θ0 = 60° | 16.3 | 10.4 | 8.3 | 12.1 | 8.1 | 6.5 |
| Overcast | 17.0 | 10.6 | 8.4 | 12.7 | 8.4 | 6.7 |
| Ncoc, 106 cell/L | 0 | 5 | 10 | 0 | 5 | 10 |
|---|---|---|---|---|---|---|
| Illumination Conditions | Black Sea, a(440) = 0.09 m−1 | Black Sea, a(440) = 0.53 m−1 | ||||
| Clear Sky, θ0 = 25° | 0.094 | 0.224 | 0.304 | 0.272 | 0.487 | 0.639 |
| Clear Sky, θ0 = 60° | 0.105 | 0.236 | 0.317 | 0.317 | 0.532 | 0.684 |
| Overcast | 0.098 | 0.228 | 0.309 | 0.288 | 0.503 | 0.656 |
| Illumination Conditions | Barents Sea, a(440) = 0.18 m−1 | Barents Sea, a(440) = 0.53 m−1 | ||||
| Clear Sky, θ0 = 25° | 0.252 | 0.411 | 0.525 | 0.335 | 0.520 | 0.661 |
| Clear Sky, θ0 = 60° | 0.284 | 0.444 | 0.558 | 0.385 | 0.569 | 0.705 |
| Overcast | 0.263 | 0.423 | 0.538 | 0.354 | 0.538 | 0.675 |
| Ncoc, 106 Cells/L | θ0, ° | Absolute Formula Errors | Relative Formula Errors | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (7) | (8) | (9) | (10) | (7) | (8) | (9) | (10) | ||
| 0 (0.17) | 25 | −0.004 | −0.004 | −0.005 | −0.004 | −6% | −6% | −8% | −6% |
| 60 | −0.008 | −0.008 | −0.010 | −0.009 | −12% | −12% | −14% | −13% | |
| 1 (0.34) | 25 | 0.002 | 0.001 | −0.017 | −0.007 | 1% | 1% | −12% | −5% |
| 60 | −0.004 | −0.005 | −0.023 | −0.013 | −3% | −3% | −15% | −8% | |
| 3 (0.53) | 25 | 0.064 | 0.014 | −0.035 | −0.004 | 24% | 5% | −13% | −2% |
| 60 | 0.059 | 0.009 | −0.039 | −0.009 | 22% | 4% | −15% | −3% | |
| 5 (0.63) | 25 | 0.17 | 0.021 | −0.049 | −0.003 | 49% | 6% | −14% | −1% |
| 60 | 0.16 | 0.018 | −0.052 | −0.006 | 48% | 5% | −15% | −2% | |
| 10 (0.77) | 25 | 0.50 | 0.020 | −0.080 | −0.011 | 109% | 4% | −18% | −2% |
| 60 | 0.50 | 0.021 | −0.079 | −0.009 | 109% | 5% | −17% | −2% | |
| a(440) | 0.09 | 0.53 | ||||||
|---|---|---|---|---|---|---|---|---|
| θ0 | 25 | 60 | 25 | 60 | ||||
| λ, nm | (13) | (12) | (11) | (13) | (13) | (12) | (11) | (13) |
| Ncoc = 0 | ||||||||
| 400 | −0.004 | −0.010 | −0.032 | −0.002 | 0.018 | −0.008 | 0.032 | 0.039 |
| 450 | −0.002 | −0.012 | −0.029 | −0.004 | 0.006 | −0.001 | −0.007 | −0.001 |
| 500 | −0.001 | −0.012 | −0.024 | −0.003 | 0.000 | −0.001 | −0.019 | −0.009 |
| 550 | −0.003 | −0.007 | −0.021 | −0.007 | −0.001 | 0.000 | −0.017 | −0.010 |
| 600 | 0.004 | 0.004 | −0.011 | −0.010 | 0.007 | 0.004 | −0.007 | −0.010 |
| 650 | 0.011 | 0.005 | −0.001 | −0.010 | 0.013 | 0.004 | 0.001 | −0.010 |
| 700 | 0.029 | 0.001 | 0.017 | −0.009 | 0.030 | 0.001 | 0.018 | −0.009 |
| Ncoc = 5 | ||||||||
| 400 | 0.11 | −0.09 | −0.16 | 0.11 | −0.001 | −0.08 | −0.22 | 0.01 |
| 450 | 0.13 | −0.05 | −0.10 | 0.13 | 0.02 | −0.09 | −0.19 | 0.01 |
| 500 | 0.13 | −0.03 | −0.07 | 0.13 | 0.05 | −0.08 | −0.15 | 0.04 |
| 550 | 0.09 | −0.05 | −0.08 | 0.09 | 0.05 | −0.07 | −0.12 | 0.04 |
| 600 | 0.03 | −0.07 | −0.13 | 0.01 | 0.02 | −0.07 | −0.13 | 0.002 |
| 650 | 0.01 | −0.05 | −0.12 | −0.01 | 0.01 | −0.05 | −0.12 | −0.01 |
| 700 | 0.02 | −0.03 | −0.11 | −0.03 | 0.02 | −0.03 | −0.11 | −0.03 |
| Ncoc = 10 | ||||||||
| 400 | 0.30 | −0.11 | −0.20 | 0.30 | 0.04 | −0.20 | −0.43 | 0.05 |
| 450 | 0.33 | −0.03 | −0.10 | 0.33 | 0.11 | −0.17 | −0.31 | 0.10 |
| 500 | 0.32 | −0.004 | −0.06 | 0.31 | 0.16 | −0.12 | −0.21 | 0.16 |
| 550 | 0.23 | −0.04 | −0.10 | 0.23 | 0.15 | −0.10 | −0.18 | 0.14 |
| 600 | 0.10 | −0.11 | −0.19 | 0.08 | 0.08 | −0.12 | −0.21 | 0.06 |
| 650 | 0.06 | −0.11 | −0.21 | 0.03 | 0.05 | −0.11 | −0.21 | 0.02 |
| 700 | 0.03 | −0.09 | −0.21 | -0.02 | 0.03 | −0.09 | −0.21 | −0.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopelevich, O.; Sheberstov, S.; Vazyulya, S. Effect of a Coccolithophore Bloom on the Underwater Light Field and the Albedo of the Water Column. J. Mar. Sci. Eng. 2020, 8, 456. https://doi.org/10.3390/jmse8060456
Kopelevich O, Sheberstov S, Vazyulya S. Effect of a Coccolithophore Bloom on the Underwater Light Field and the Albedo of the Water Column. Journal of Marine Science and Engineering. 2020; 8(6):456. https://doi.org/10.3390/jmse8060456
Chicago/Turabian StyleKopelevich, Oleg, Sergey Sheberstov, and Svetlana Vazyulya. 2020. "Effect of a Coccolithophore Bloom on the Underwater Light Field and the Albedo of the Water Column" Journal of Marine Science and Engineering 8, no. 6: 456. https://doi.org/10.3390/jmse8060456
APA StyleKopelevich, O., Sheberstov, S., & Vazyulya, S. (2020). Effect of a Coccolithophore Bloom on the Underwater Light Field and the Albedo of the Water Column. Journal of Marine Science and Engineering, 8(6), 456. https://doi.org/10.3390/jmse8060456