Numerical Prediction of Welding Distortion Considering Gravity Force on General Ship Grillage Structure by Elastic Finite Element Method Using Inherent Strain
Abstract
:1. Introduction
2. Elastic FEM Using Inherent Strain
2.1. Basic Concept of Inherent Strain and Inherent Displacment
2.2. Caculation of Inherent Deforatmion and Inherent Strain
- Transverse Shrinkage
- Angular Deformation
- Longitudinal Shrinkage (Contraction Force)where
- is the angular deformation at a welding length of 200 mm;
- is the welding length compensation coefficient for lateral shrinkage;
- is the welding length compensation coefficient for angular deformation;
- is the vertical contraction force;
- is the welding length [mm];
- is Poisson’s ratio;
- is the net heat input [J/mm];
- is the plate thickness [mm];
- is [J/mm3];
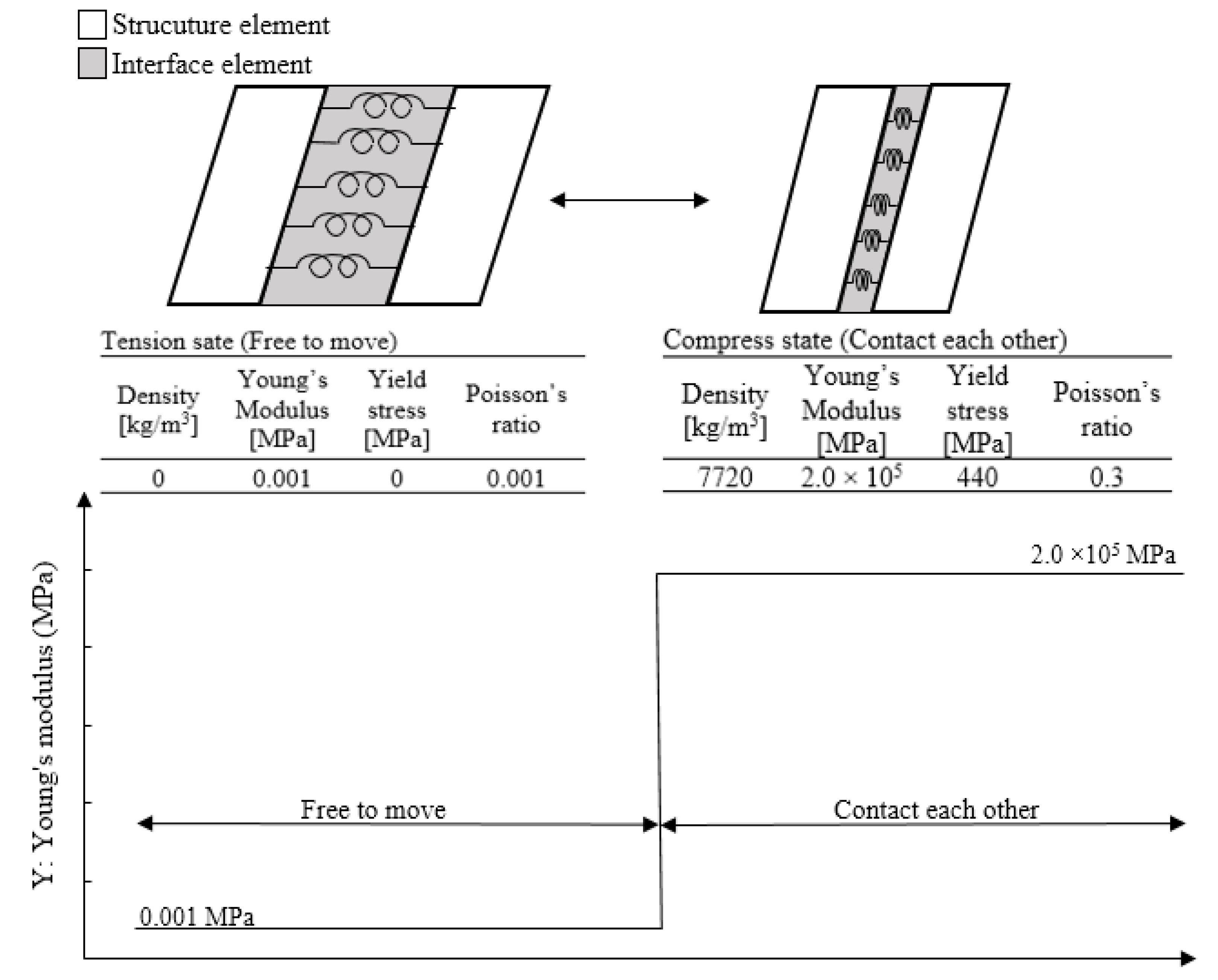
2.3. Interface Element Method
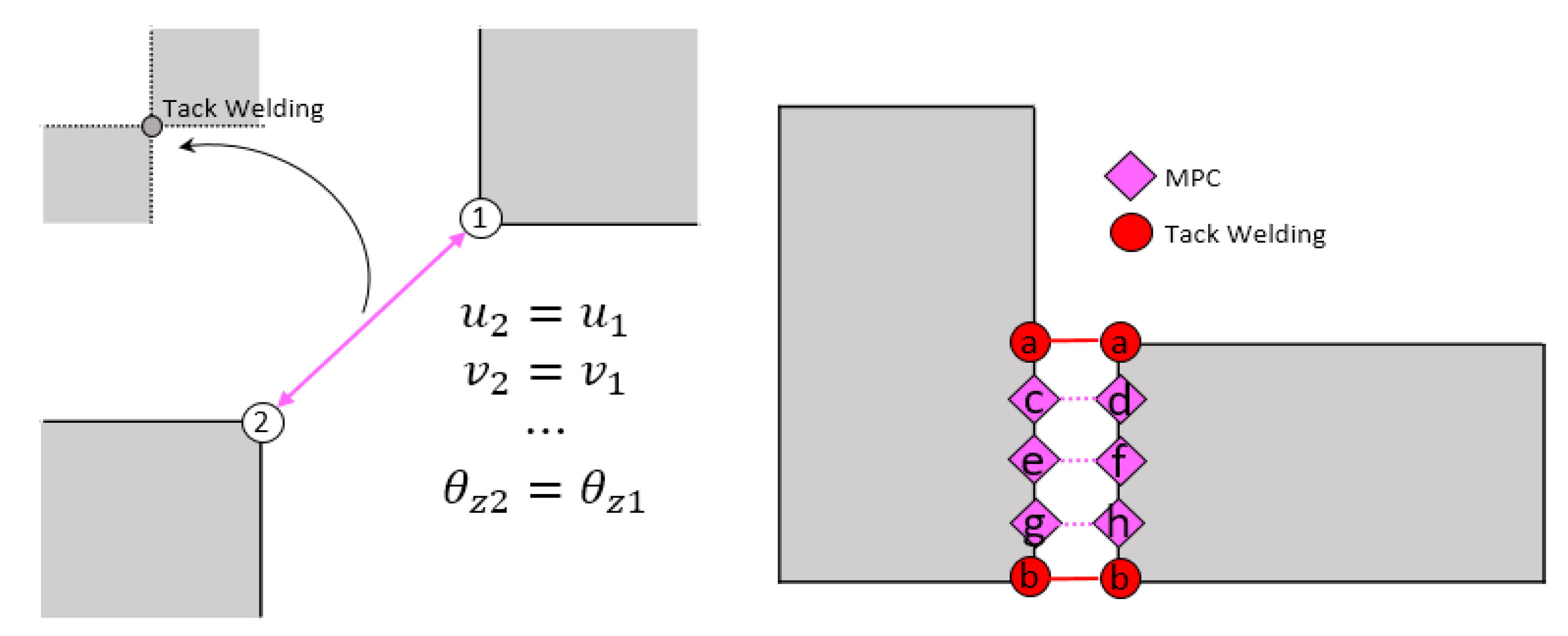
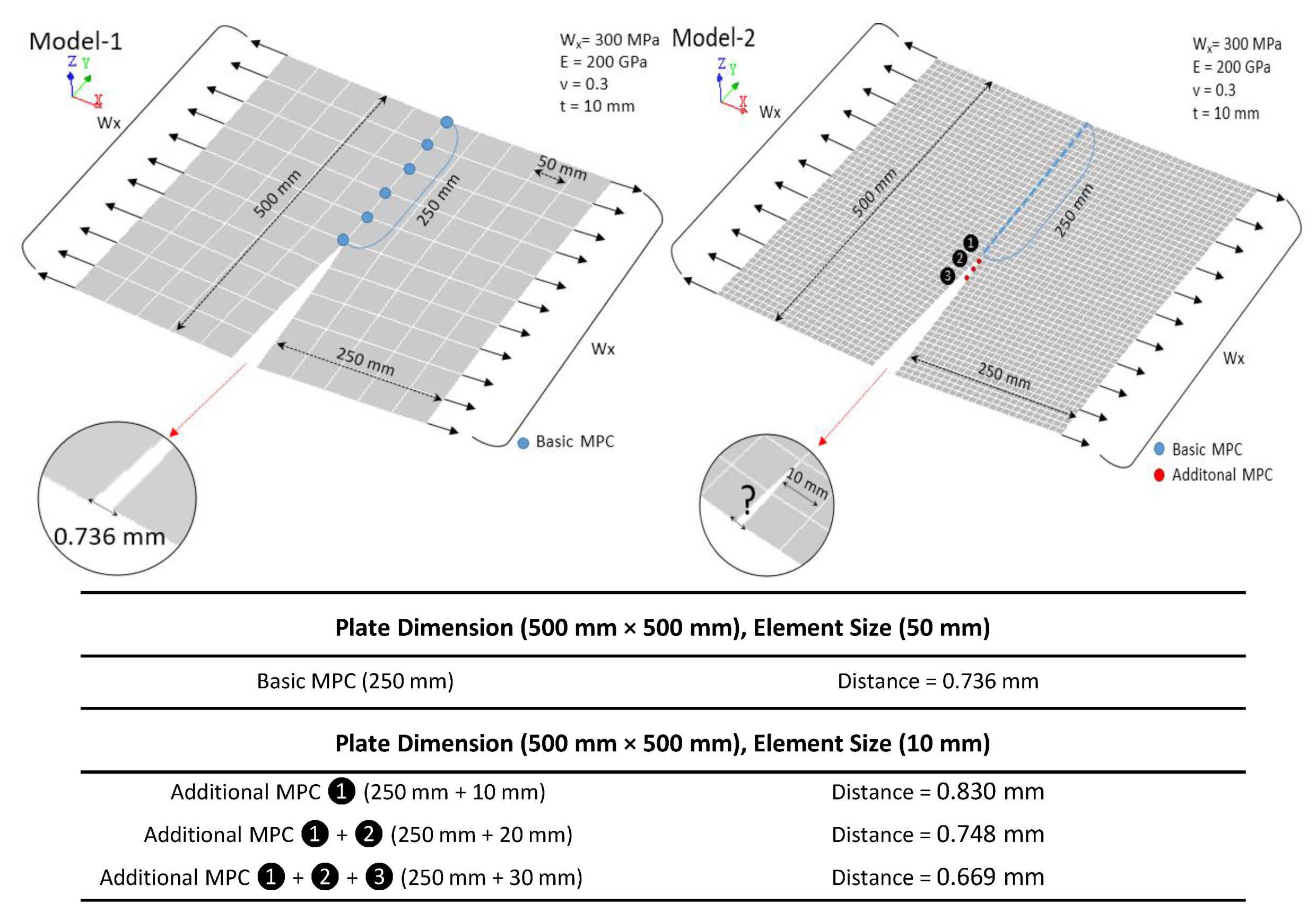
2.4. Multipoint Constraint Function
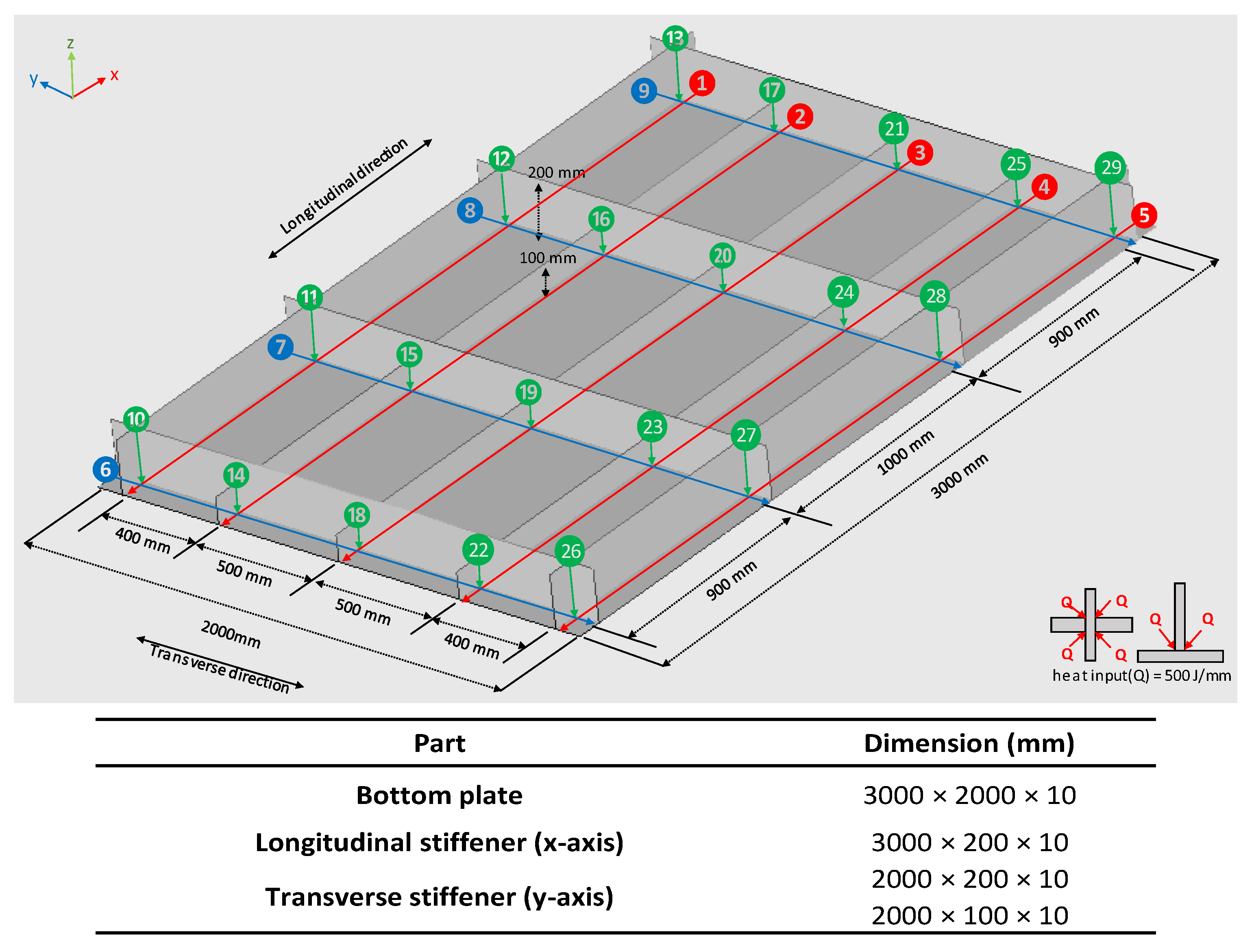
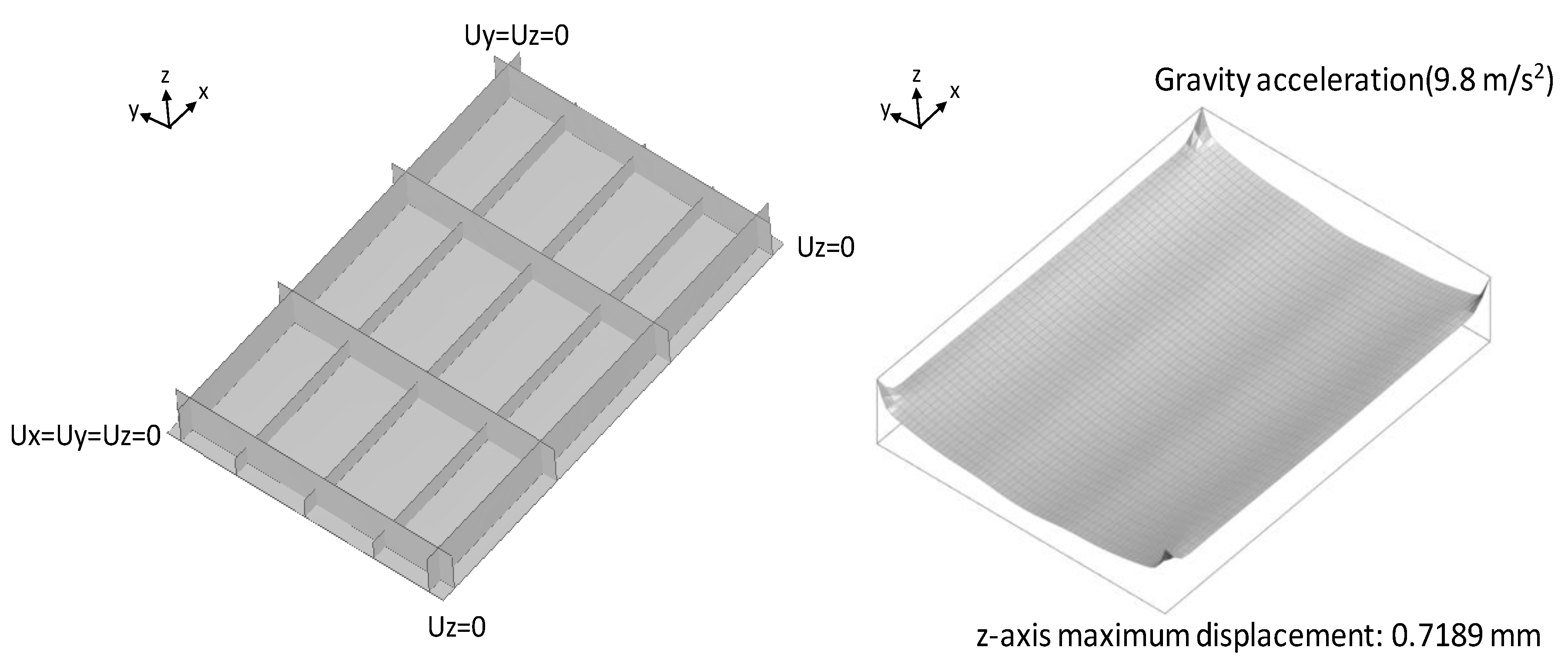
3. Analysis Model
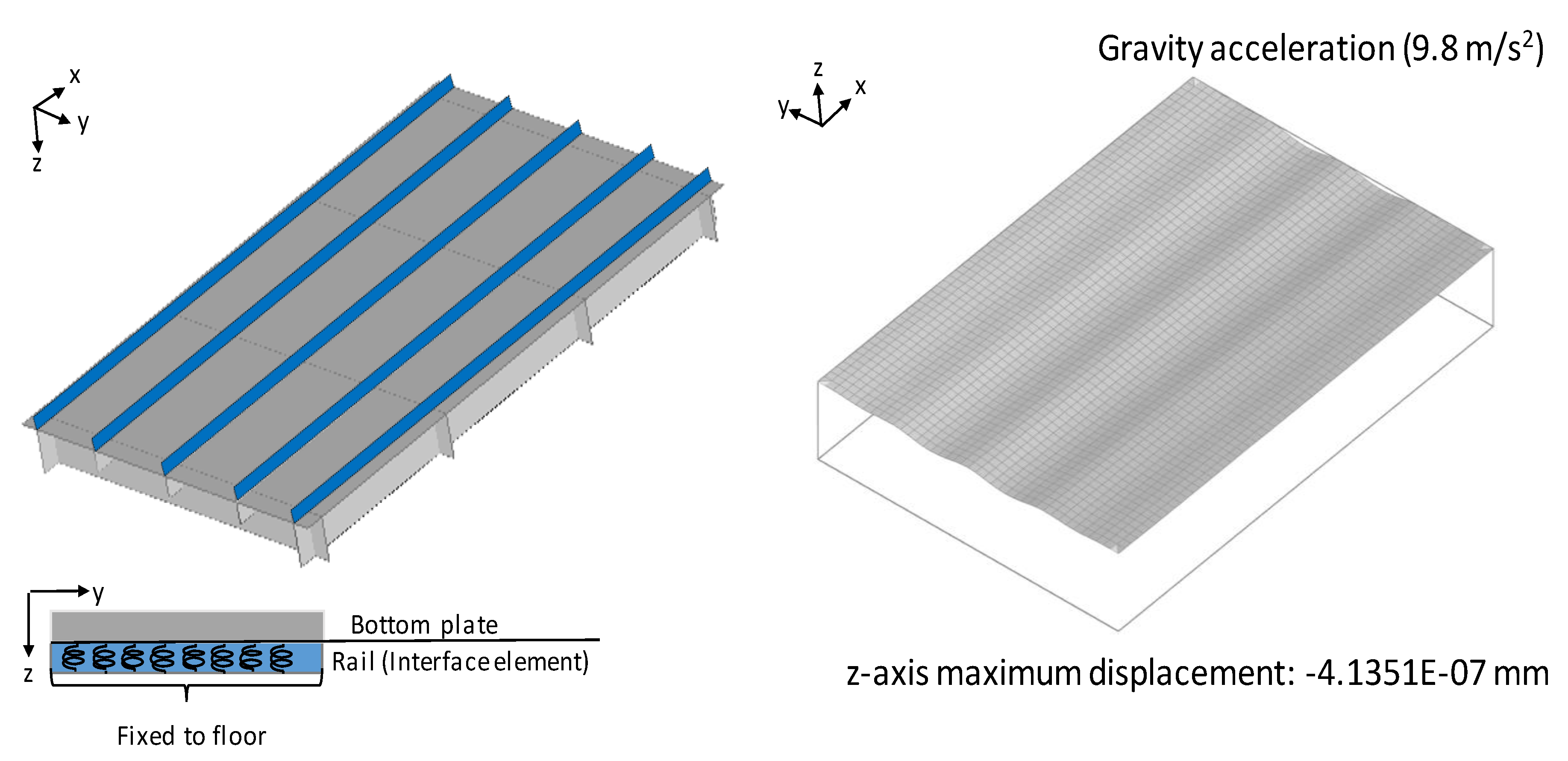
4. Boundary Condition of the Rails Considering the Gravity Force
5. Effect of the Gravity Force under the Rail Boundary Condition on Welding Sequence
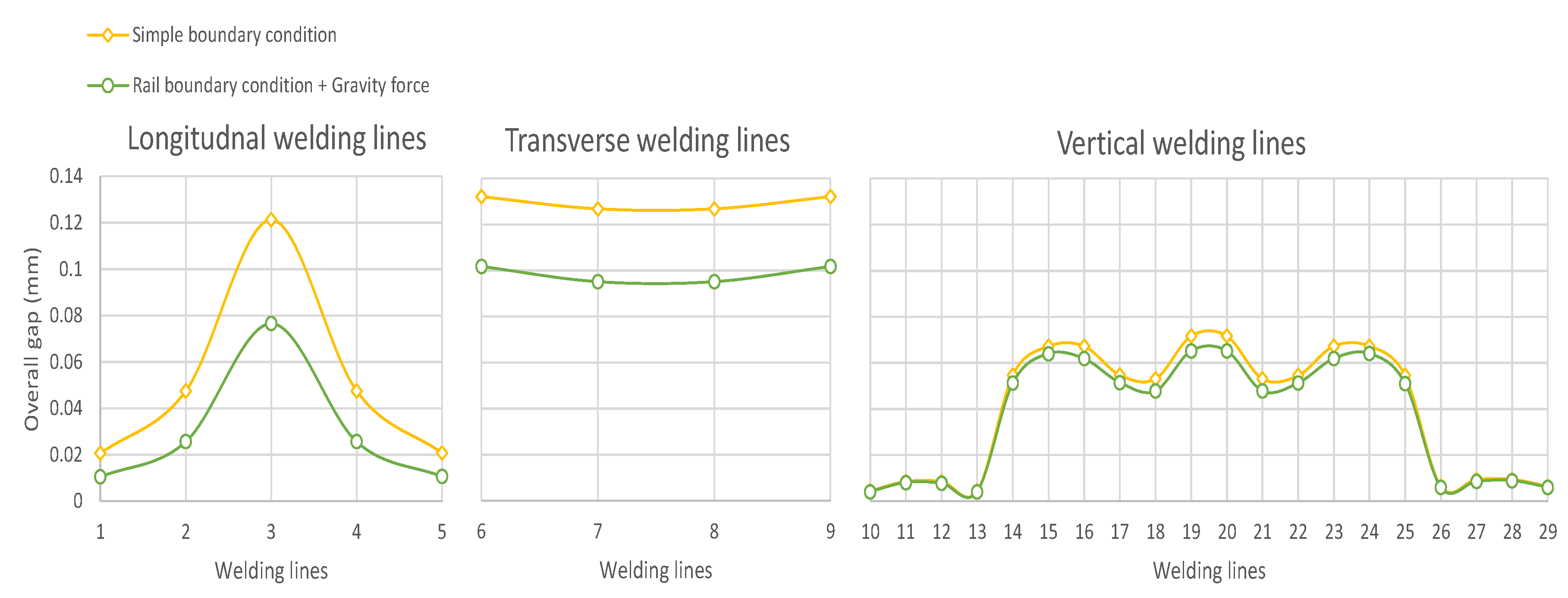
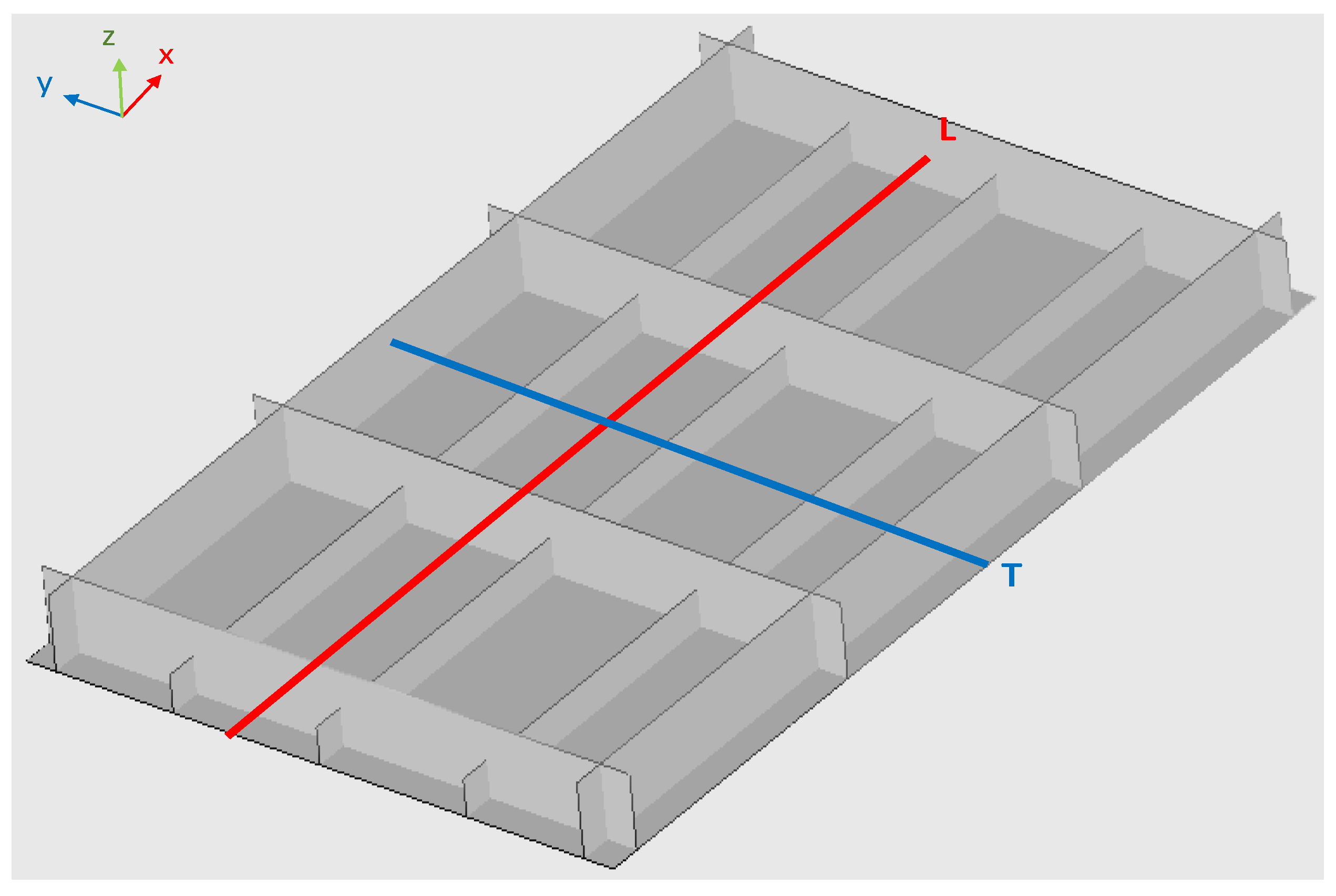
5.1. Effect of Each Welding Line on the Bottom Plate
5.2. Welding Sequence
5.3. Result and Discussion of Effect of Gravity Force Under the Rail Boundary Condition on Welding Sequence
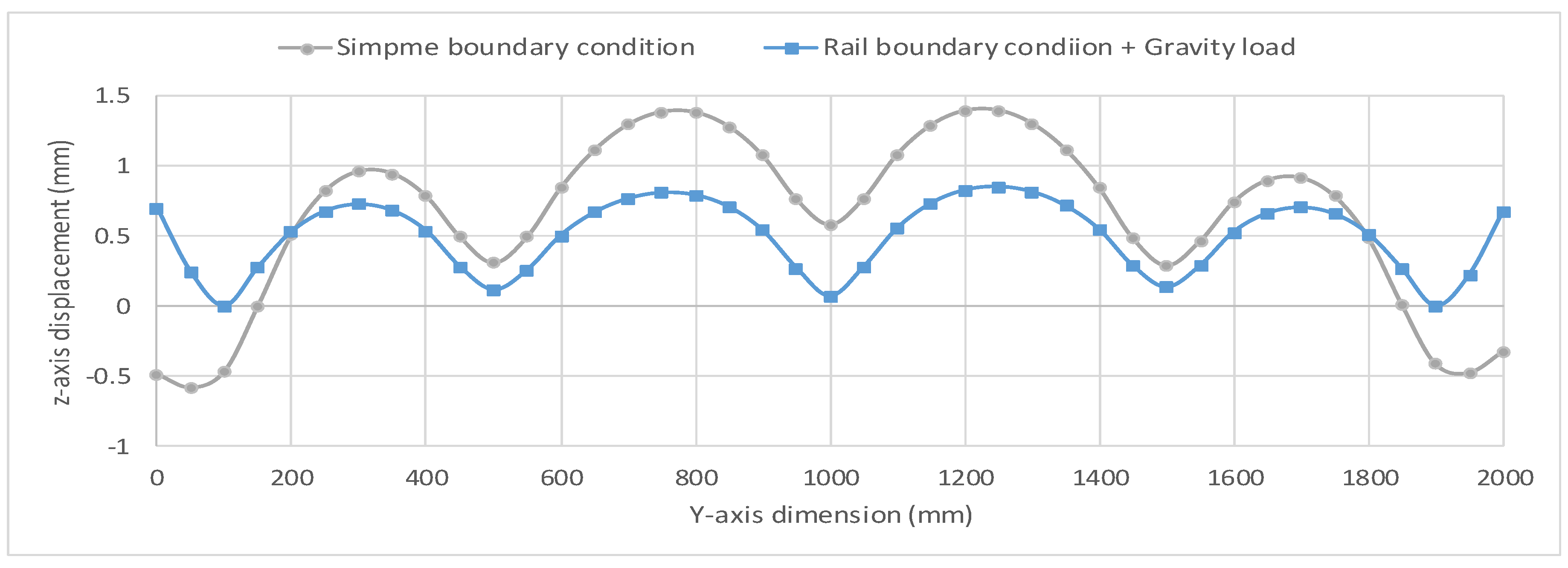
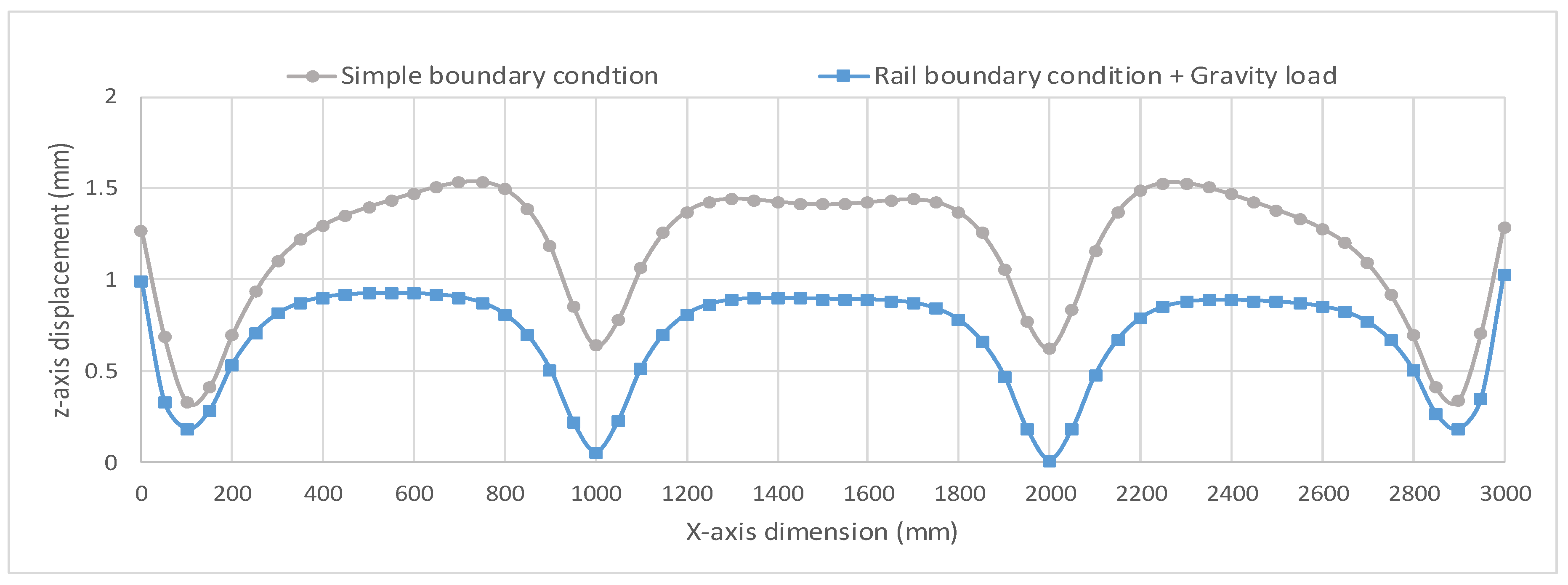
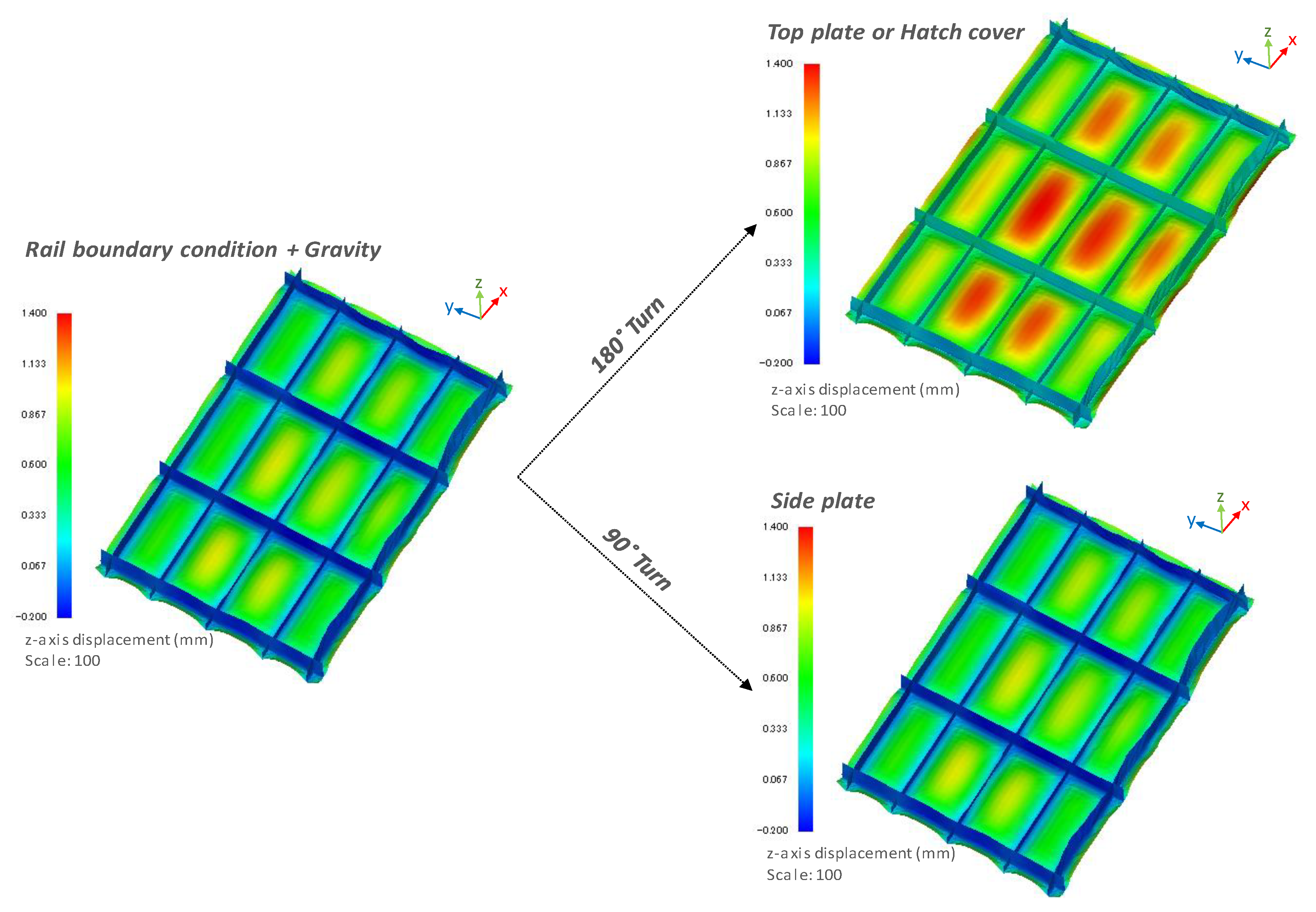
6. Effect of the Change in Gravity Direction on the Numerical Prediction of Welding Displacements
Results and Discussion of Effect of Change in Gravity Direction on the Numerical Prediction of Welding Displacements
7. Conclusions
- (1)
- Although the bottom plate and rails touch each other under the gravity force while processing the welding sequence under the rail boundary condition, these considerably constraint the structure, and therefore, significantly mitigate the welding displacement without additional clamps for the restriction of its movement. In other words, the numerical prediction of welding displacements without precisely reflecting the real work environment would lead to enormous errors in heavy industries.
- (2)
- In the rail boundary condition under the effect of the gravity force, the optimal welding sequence is to weld first vertically for improving the stiffness of the structure and then horizontally. It is preferable to begin the horizontal welding lines, which generate a direct heat effect on the bottom plate, as late as possible. Moreover, welding the transverse lines before the longitudinal lines is preferred for minimizing welding displacements. The conclusion is the same as that in the previous study of D. Woo et al. (2019), which was validated according to the result of the simple boundary condition.
- (3)
- The change in direction of the gravity force according to the design plan has significant effects on the change in the distribution of welding displacements. Without consideration of these effects, the prediction of the additional production cost for the revision work could involve a substantial error. Thus, in the numerical prediction of welding displacements in the welding process, consideration of the change in direction of the gravity force with respect the structure is technically essential.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ueda, Y.; Yuan, M.G.; Mochizuki, M.; Umezawa, S.; Enomoto, K. Experimental verification of a method for prediction of welding residual stresses in T joints using inherent strains 4th report: Method for prediction using source of residual stress. Weld. Int. 1993, 11, 327–333. [Google Scholar] [CrossRef]
- Luo, Y.; Murakawa, H.; Ueda, Y. Prediction of welding deformation and residual stress by elastic FEM based on inherent strain (Report I). Trans. JWRI 1997, 182, 783–793. [Google Scholar]
- Deng, D.; Murakawa, H.; Ueda, Y. Theoretical prediction of welding distortion considering positioning and gap between parts. Int. J. Offshore Polar Eng. 2004, 30, 89–96. [Google Scholar]
- Deng, D.; Murakawa, H.; Liang, W. Numerical simulation of welding distortion in large structures. Comput. Methods Appl. Mech. Eng. 2007, 196, 4613–4627. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Prediction of welding distortion and residual stress in a thin plate butt-welded joint. Comput. Mater. Sci. 2008, 43, 353–365. [Google Scholar] [CrossRef]
- Ueda, Y.; Yuan, M.G. Prediction of residual stresses in butt welded plates using inherent strains. J. Eng. Mater. Technol. 2008, 115, 417–423. [Google Scholar] [CrossRef]
- Shadkam, S.; Ranjbarnodeh, E.; Iranmanesh, M. Effect of sequence and stiffener shape on welding distortion of stiffened panel. J. Constr. Steel Res. 2018, 149, 41–52. [Google Scholar] [CrossRef]
- Liang, W.; Deng, D. Influences of heat input, welding sequence and external restraint on twisting distortion in an asymmetrical curved stiffened panel. Adv. Eng. Softw. 2018, 115, 439–451. [Google Scholar] [CrossRef]
- Woo, D.; Kitamura, M.; Takezawa, A. Method to systemically order welding sequence to efficiently mitigate welding displacement of a general ship grillage structure. Ships Offshore Struct. 2019. [Google Scholar] [CrossRef]
- Woo, D.; Kitamura, M.; Takezawa, A. Systematic method for positioning clamps and strongbacks based on their influence on welding displacements. Ocean Eng. 2020, 202. [Google Scholar] [CrossRef]
- Murakawa, H.; Deng, D.; Ma, N.; Wang, J. Applications of inherent strain and interface element to simulation of welding deformation in thin plate structures. Comput. Mater. Sci. 2012, 51, 43–52. [Google Scholar] [CrossRef]
- Japan Shipbuilding Research Association. Japan Shipbuilding Research Association Research Subcommittee: Research on Advanced Machine Accuracy Management Technology (Total Joint Report); SR237; Japan Shipbuilding Research Association: Tokyo, Japan, 2000; pp. 65–75. [Google Scholar]
- Kunihiko, S.; Terasaki, T. Effect of welding conditions on residual stresses distributions in welded structures materials. J. JAPAN Weld. Soc. 1976, 45, 150–156. [Google Scholar]
- White, J.D.; Leggatt, R.H.; Dwight, J.B. Weld shrinkage prediction. Weld. Met. Fabr. 1980, 9, 587–596. [Google Scholar]
- PEMA Welding Automation Company. Available online: https://pemamek.com/case/seaspans-vancouver-shipyard-selects-pema-welding-automation-solutions/ (accessed on 15 June 2019).
- Abe, R. A study on the accuracy control and measurement of hull structure using 3D Measurement Technique. Ph.D. Thesis, Hiroshima University, Hiroshima, Japan, March 2017. [Google Scholar]







| Current [A] | Voltage [V] | Travel Speed [mm/s] | Heat Efficiency | Net Heat [J/mm2] |
|---|---|---|---|---|
| 230 | 23 | 5 | 0.77 | 500 |
| Density [kg/m3] | Young’s Modulus [MPa] | Specific Heat [J/kg/°C] | Yield Stress [MPa] | Poisson’s Ratio |
|---|---|---|---|---|
| 7720 | 2.0 × 105 | 659.4 | 440 | 0.3 |
| Sequence | Welding Sequence Preference | Welding Sequence | ||||
|---|---|---|---|---|---|---|
| Category A | A-1 | Horizontal | H | Vertical | H | 6→9→7→8→3→2→4→5→1→20→19→24→23→15→16→14→ 17→22→25→18→21→27→28→11→12→26→29→10→13 |
| A-2 | H | L | 6→9→7→8→3→2→4→5→1→10→13→26→29→11→12→27→ 28→18→21→22→25→14→17→15→16→23→24→19→20 | |||
| A-3 | L | H | 1→5→4→2→3→7→8→6→9→20→19→24→23→15→16→14→ 17→22→25→18→21→27→28→11→12→26→29→10→13 | |||
| A-4 | L | L | 1→5→4→2→3→7→8→6→9→10→13→26→29→11→12→27→ 28→18→21→22→25→14→17→15→16→23→24→19→20 | |||
| A-5 | Vertical | H | Horizontal | H | 20→19→24→23→15→16→14→17→22→25→18→21→27→28→11→12→26→29→10→13→6→9→7→8→3→2→4→5→1 | |
| A-6 | H | L | 20→19→24→23→15→16→14→17→22→25→18→21→27→28→11→12→26→29→10→13→1→5→4→2→3→7→8→6→9 | |||
| A-7 | L | H | 10→13→26→29→11→12→27→28→18→21→22→25→14→17→15→16→23→24→19→20→6→9→7→8→3→2→4→5→1 | |||
| A-8 | L | L | 10→13→26→29→11→12→27→28→18→21→22→25→14→17→15→16→23→24→19→20→1→5→4→2→3→7→8→6→9 | |||
| Sequence | Welding Sequence Preferences | Welding Sequence | ||||||
|---|---|---|---|---|---|---|---|---|
| Category B | B-1 | Vertical | H | Longitudinal | H | Transverse | H | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→3→2→4→5→1→6→9→7→8 |
| B-2 | H | H | L | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→3→2→4→5→1→7→8→6→9 | ||||
| B-3 | H | L | H | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→1→5→4→2→3→6→9→7→8 | ||||
| B-4 | H | L | L | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→1→5→4→2→3→7→8→6→9 | ||||
| B-5 | L | H | H | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→3→2→4→5→1→6→9→7→8 | ||||
| B-6 | L | H | L | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→3→2→4→5→1→7→8→6→9 | ||||
| B-7 | L | L | H | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→1→5→4→2→3→6→9→7→8 | ||||
| B-8 | L | L | L | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→1→5→4→2→3→7→8→6→9 | ||||
| B-9 | Vertical | H | Transverse | H | Longitudinal | H | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→6→9→7→8→3→2→4→5→1 | |
| B-10 | H | H | L | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→6→9→7→8→1→5→4→2→3 | ||||
| B-11 | H | L | H | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→7→8→6→9→3→2→4→5→1 | ||||
| B-12 | H | L | L | 13→10→26→29→12→11→27→28→18→21→25→14→22→17→16→23→15→24→19→20→7→8→6→9→1→5→4→2→3 | ||||
| B-13 | L | H | H | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→6→9→7→8→3→2→4→5→1 | ||||
| B-14 | L | H | L | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→6→9→7→8→1→5→4→2→3 | ||||
| B-15 | L | L | H | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→7→8→6→9→3→2→4→5→1 | ||||
| B-16 | L | L | L | 19→20→24→15→23→16→17→22→14→25→18→21→28→27→11→12→29→26→10→13→7→8→6→9→3→2→4→5→1 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, D.; Kitamura, M. Numerical Prediction of Welding Distortion Considering Gravity Force on General Ship Grillage Structure by Elastic Finite Element Method Using Inherent Strain. J. Mar. Sci. Eng. 2020, 8, 454. https://doi.org/10.3390/jmse8060454
Woo D, Kitamura M. Numerical Prediction of Welding Distortion Considering Gravity Force on General Ship Grillage Structure by Elastic Finite Element Method Using Inherent Strain. Journal of Marine Science and Engineering. 2020; 8(6):454. https://doi.org/10.3390/jmse8060454
Chicago/Turabian StyleWoo, Donghan, and Mitsuru Kitamura. 2020. "Numerical Prediction of Welding Distortion Considering Gravity Force on General Ship Grillage Structure by Elastic Finite Element Method Using Inherent Strain" Journal of Marine Science and Engineering 8, no. 6: 454. https://doi.org/10.3390/jmse8060454
APA StyleWoo, D., & Kitamura, M. (2020). Numerical Prediction of Welding Distortion Considering Gravity Force on General Ship Grillage Structure by Elastic Finite Element Method Using Inherent Strain. Journal of Marine Science and Engineering, 8(6), 454. https://doi.org/10.3390/jmse8060454





