Abstract
The aim of coastal structures for the defense from erosion is to modify the hydrodynamic fields that would naturally occur with the wave motion, to produce zones of sedimentation of solid material, and to combat the recession of the coastline. T-head groin-shaped structures are among the most adopted in coastal engineering. The assessment of the effectiveness of such structures requires hydrodynamic study of the interaction between wave motion and the structure. Hydrodynamic phenomena induced by the interaction between wave motion and T-head groin structures have three-dimensionality features. The aim of the paper is to propose a new three-dimensional numerical model for the simulation of the hydrodynamic fields induced by the interaction between wave fields and coastal structures. The proposed model is designed to represent complex morphologies as well as coastal structures inside the domain. The numerical scheme solves the three-dimensional Navier–Stokes equations in a contravariant formulation, on a time-dependent coordinate system, in which the vertical coordinate varies over time to follow the free-surface elevation. The main innovative element of the paper consists in the proposal of a new numerical scheme that makes it possible to simulate flows around structures with sharp-cornered geometries. The proposed numerical model is validated against a well-known experimental test-case consisting in a wave train approaching a beach (non-parallel with the wave front), with the presence of a T-head groin structure. A detailed comparison between numerical and experimental results is shown.
1. Introduction
Coastal defense structures are aimed at modifying the free-surface elevation and velocity fields produced during wave events, in a way to damp the wave energy and to prevent the nearshore wave-induced currents transporting the suspended solid material offshore. T-head groin-shaped coastal structures are one of the most used types of structures that are able to induce the sedimentation of solid material near the shore, by physically blocking the long-shore currents that transport the sediment (see [1,2] for details of these structures). Therefore, the study of the hydrodynamics around T-head groin-shaped structures is essential to properly design them, with the purpose of obtaining the desired response in terms of hydrodynamic fields and the morphological modifications of the coastline.
As recalled by [3,4,5], coastal currents and hydrodynamic phenomena related to the interaction of waves and coastlines have a three-dimensional structure that can be locally important. One of the most important aforementioned three-dimensional phenomena is the undertow current [6], i.e., a circulation in the vertical plane consisting in offshore-directed velocities near the bed and onshore-directed velocities near the free surface. The importance of these near-bed current velocities relies on their substantial impact on the morphology modification. Furthermore, the presence of coastal structures can induce vortices and velocity fields with a significant vertical component, which can cause local phenomena of erosion and scour around the structures.
The study of the interaction between waves and coastal structures can be carried out by means of numerical models. Models that are based on the nonlinear shallow water equations (NSWEs) [7,8] or Boussinesq equations [9,10,11] represent the velocity fields exclusively in terms of horizontal components that can be depth-averaged (NSWE-type models) or defined at a given depth (Boussinesq-type models). In particular, in Boussinesq-type models, the vertical distribution of the horizontal velocity field is taken into account by means of a Taylor series expansion of the velocity. In order to allow NSWE-type or Boussinesq-type models to adequately represent undertow currents, correction procedures of the horizontal velocity fields are necessary [12]; in any case, the vertical components of the velocity are not represented and the corrections of the horizontal velocities are effective for wave fronts parallel to the coastline and simple coastal morphologies. Furthermore, with NSWE-type or Boussinesq-type models, it is not possible to represent the fully three-dimensional structures of the hydrodynamic fields induced by the interaction between the wave and structure.
In order to overcome the limitations imposed by models based on depth-averaged equations, a number of recent models have been devised to solve the three-dimensional Navier–Stokes (NS) equations [13,14,15]. In the solution of NS equations in the context of free-surface flows, the tracking of the free-surface is a challenging issue. A number of models [16,17,18,19] solved this issue by adopting the so-called volume of fluid (VOF) technique [20]. Several numerical models available in the literature employ the VOF technique, as it is a robust and stable one; OpenFOAM® [18] and IHFOAM® [21] (a model derived from OpenFOAM® specifically designed for coastal and ocean hydrodynamics) are among the most popular numerical models in which the VOF technique is implemented. With this technique, a correct assignment of pressure and kinematic boundary conditions at the free surface is difficult, because the vertical fluxes can arbitrarily cross the computational cell. Some recent models are based on a particular coordinate transformation, called sigma coordinate transformation [22,23,24], by means of which the Cartesian vertical coordinate is transformed into a moving vertical coordinate in order to follow the free surface. Hence, at every instant, the free surface is always located at the upper boundary of the computational grid and pressure boundary conditions can be correctly assigned at it. Cannata et al. [25] solved an integral form of NS equations with a shock-capturing scheme over a boundary-conforming moving grid; this allows the models to properly treat the free-surface boundary, as well as to precisely take into account lateral boundaries in complex geometries.
All the above-described numerical models fall under the general class of models in which the free-surface elevation is represented by means of a function of horizontal coordinates and time, so that at a given position in the horizontal plane and in time, a single value of the free-surface elevation is allowed. This approach does not make it possible to directly simulate a wave front that curls over, forming a tube. This limitation is currently overcome by smoothed particle hydrodynamics (SPH) meshless-type models [26,27], in which the position of the water particles that belong to the free surface is tracked one by one, by means of a Lagrangian approach. The main drawback of SPH models is that they are computationally very expensive, so their use is limited to cases in which the spatial scales are lower than the typical scales of a coastal engineering problem.
Three-dimensional models with shock-capturing schemes that employ a vertical coordinate transformation to follow the free surface allow the wave front to be directly simulated up to the point at which the wave front inclination overcomes the vertical direction inclination. After that, the successive wave breaking and particles’ turbulent mixing phase is represented with a moving vertical front. This vertical front is treated as a discontinuity in the water depth and in the product between it and the flow velocity and no criterion is needed to set the breaking location and features [24,25]. With these shock-capturing schemes, non-plunging breakers can be directly simulated while plunging breakers are represented by means of a moving discontinuity in the solution.
Cannata et al. [28] recently proposed a three-dimensional non-hydrostatic model that solves an integral form of NS equations in contravariant formulation, on a time-dependent curvilinear coordinate system. In models by [28,29], the time dependence of the curvilinear coordinate system is related to the free surface movement, following the above-mentioned approach. The model proposed by [28], thanks to the use of boundary conforming grids, is suitable for complex geometries that are present in coastal regions, but it is not indicated to represent domains in which structures with a sharp-cornered geometry are present. In fact, in the model, the possibility to introduce internal boundary conditions is not considered. One of the most used strategies in order to represent internal boundary conditions in computational domains, alternative to the use of boundary conforming grids, is the immersed boundary (IB) method [30,31], by means of which a structure can be treated as a virtual body inside the computational domain. In particular, Roman et al. [32] proposed an implementation of the IB method into the context of curvilinear grids. With the use of a boundary conforming grid, the IB method is not necessary to impose internal boundaries, since the computational grid can be chosen so that the coordinate lines follow the boundaries of the structures.
In this work, we propose a novel numerical scheme for the solution of the integral contravariant form of the NS equations presented in [28]. In the proposed numerical scheme, a two-steps predictor-corrector method is employed: In the predictor step, the governing equations are solved with the hydrostatic pressure assumption; in the corrector step, a correction of the hydrodynamic field is made, by means of the solution of a Poisson-like equation. Differently from the numerical scheme presented by Cannata et al. [28], the proposed numerical scheme allows the representation of three-dimensional velocity fields around sharp-cornered coastal structures. In particular, we implement a proper strategy for the imposition of boundary conditions in the numerical solution of the Poisson-like equation. By doing so, the proposed three-dimensional non-hydrostatic numerical model is able to reproduce internal objects inside the computational domain. Furthermore, we adopt a novel procedure to assign the dynamic pressure boundary conditions at the free-surface. The proposed model is used to numerically simulate the wave field and the wave-induced three-dimensional velocity fields produced by the interaction between random wave trains and a T-head groin-shaped sharp-cornered structure. The numerical results are compared against experimental measurements by [33].
The paper is structured as follows: In Section 2, we describe the model equations; in Section 3, we present the numerical model; in Section 4, the numerical results obtained by the proposed model are compared with the experimental measurements by [33]; and in Section 5, we present the conclusion of the study.
2. Governing Equations
The main feature of the proposed three-dimensional numerical model relies on the fact that the physical domain occupied by the free-surface flow is described by moving curvilinear coordinates defined by a time-dependent coordinate transformation. The physical domain is divided into grid cells bounded by curvilinear coordinate surfaces that move with a velocity different from the fluid velocity; the free-surface coincides with a moving coordinate surface. By means of a time-dependent coordinate transformation, the irregular and time-varying physical domain is transformed into a regular and fixed computational domain, in which the upper boundary represents the free surface. In the proposed integral form of the governing equations, the calculation cells, which have a time-varying geometry, are used as control volumes. Consequently, control volumes, whose boundary surfaces move with a velocity that is different from the fluid velocity, must be defined in the time-dependent curvilinear coordinate system.
Let us consider a coordinate transformation , from a system of Cartesian coordinates to a system of moving curvilinear coordinates , with . Let be the covariant base vectors and the contravariant base vectors. The metric tensor is , with . The Jacobian of the transformation is given by:
The velocity vector of the moving curvilinear coordinates, expressed in the Cartesian coordinate system, is:
where represents the time derivative of the position vector that represents a point that is defined by fixed curvilinear coordinates. As demonstrated by [28], the contravariant component of the velocity vector is given by:
In the curvilinear coordinate system, the integral contravariant expression of the continuity equation for a control volume that coincides with a material fluid volume with a surface , at time , which moves with a velocity different from the fluid velocity , is:
where is the density of the fluid and is the covariant outward normal vector component.
Let be a constant and parallel vector field. This vector field is represented in the Cartesian coordinate system by constant and uniform components and in the curvilinear coordinate system by constant and space-varying (not uniform) covariant components, . Indeed, since the base vectors of the curvilinear coordinate system vary from point to point, the values of vector components , which are relative to those base vectors, must vary from point to point to represent the same physical direction at every point. From a general point of view, to express the momentum conservation law in an integral form, the rate of change of the momentum of a material volume and the total net force must be projected in a physical direction. As stated by [28], let us define a parallel vector field , which is normal to the coordinate line on which the coordinate is constant at point :
For the sake of brevity, we indicate and . The integral form of the momentum conservation equation projected in the physical direction defined by the vector field , reads:
where are the contravariant components of the stress tensor and is the external body force per unit mass vector. The stress tensor can be expressed in the form , where is the pressure, is the dynamic viscosity, and are the contravariant components of the strain rate tensor ( is the deviatoric part of the viscous stress tensor). Let us consider as a volume element defined by surface elements bounded by curves lying on the coordinate lines. We define the volume element in the physical space as:
and the volume element in the transformed space as:
It is possible to see that the volume element defined in Equation (7) is time dependent while the one defined in Equation (8) is not. Similarly, we define the surface element in the physical space as , which is time dependent, and the surface element in the transformed space as , which is constant over time. By doing so, Equation (6) can be rewritten as [28]:
where and indicate the contour surfaces of the volume on which is constant and which are located at the larger and the smaller value of , respectively. Here, the indices , , and are cyclic.
By adopting the same control volume, , the integral contravariant continuity of Equation (4) can be rewritten as:
Let at the horizontal reference plane defined by the still free surface. Let the water depth be , where is the still water depth and is the free-surface elevation. Let the bottom elevation with respect to the horizontal reference plane be . Let us indicate by the acceleration due to gravity and let us split the pressure into a hydrostatic part, , and a dynamic one, . In order to represent the bottom and surface geometry and to correctly assign the pressure and kinematic conditions at the bottom and at the free surface, we introduce the following transformation from Cartesian to curvilinear coordinates, in which coordinates vary in time in order to follow the free-surface movements [28]:
Under the transformation (Equation (11)), the components of vector are:
This coordinate transformation basically maps the time-varying coordinates of the physical domain into a fixed coordinate system , where spans from to . Let , where indicates the vertical unit vector and × indicates the vector product. As stated by [28], the Jacobian of the transformation can be written in the form . This makes it possible to write the integral contravariant momentum equation expressed by Equation (9) in a three-dimensional conservative form, in which the conserved variables are given by the cell-averaged product between the water depth and the three contravariant components of the velocity with . To this end, let us define the following cell-averaged values in the transformed space:
where is the horizontal surface element in the transformed space.
By recalling that is not time dependent, by dividing by , and by recalling Equation (13), Equation (9), expressed in the time-dependent coordinate system defined in Equation (11), becomes:
In order to take into account turbulence, the deviatoric part of the viscous stress tensor is replaced by the turbulent stress tensor, , in which is the eddy viscosity and it is estimated by a Smagorinsky sub-grid model.
Let us integrate the continuity Equation (10) over a vertical water column, between the bottom and the free surface, which is bounded by coordinate surfaces. In the transformed space defined by Equation (11), recalling Equation (14), the integral of Equation (10) over the vertical water column reads:
in which and indicate the contour lines of the surface element on which is constant and which are located at the larger and the smaller value of , respectively. Equation (16) represents the governing equation that predicts the free-surface motion.
Equations (15) and (16) represent the expression of the three-dimensional motion equations as a function of the and variables in the coordinate system . The numerical integration of the abovementioned equations allows the fully dispersive wave-propagation simulation.
3. The Numerical Scheme
Equations (15) and (16) are solved by means of a numerical scheme based on the one proposed by [28]. In particular, in order to simulate hydrodynamic fields in the presence of internal objects, in the model presented in this paper, a new numerical procedure for the solution of the Poisson-like equation is proposed. The numerical scheme proposed by [28] consists in a combined finite-volume and finite-difference scheme with a Godunov-type method, and it is briefly described as follows.
A two-stage second-order Runge–Kutta method [34] is used in the advancing of the solution. Starting from the values of and , which are related to the time level , the numerical method aims to calculate the values and , related to the time level . Let:
In Equation (17), the superscripts (0RK), (1RK), and (2RK) indicate values obtained at the end of every Runge–Kutta step, while superscripts and indicate the intermediate value obtained by the predictor-corrector procedure to be described. At each stage of the Runge–Kutta method, the predictor fields are calculated as follows:
where indicates the discretization of the right-hand side of Equation (15), in which the term related to the dynamic pressure gradient is neglected and indicates the discretization of the right-hand side of Equation (16). and are calculated by solving local Riemann problems at cell interfaces. Neglect of the dynamic pressure gradient term leads to a predictor velocity field, , which is not divergence free. In order to obtain a divergence-free velocity field, we add a corrector field to the predictor field :
where:
where is a scalar field that is obtained by solving the integral contravariant formulation of a Poisson-like equation:
Equation (21) is discretized by means of a finite volume scheme at a control volume, , centered at the center of the calculation cells upper faces, in which the pressure is defined:
The right-hand side of Equation (22) represents the discretization of the opposite of the divergence of the predictor velocity field. In order to overcome the check-board solution issue [35], Cannata et al. [28] computed the contravariant velocity components defined at the lateral faces from the values obtained by the Riemann solver. By means of this strategy, the pressure–velocity decoupling problems are avoided and the shock-capturing property of the scheme is extended to the corrector step. It must be noted that the terms that appear on the left-hand side of Equation (22) represent the contravariant corrector velocity components:
The corrector velocities , , , , , and are discretized to solve Equation (26), in order to obtain the following set of equations, where the matrix of coefficients has 19 non-null diagonals:
where the term on the right-hand side represents the divergence (changed in sign) of the predictor velocity field. See [28] for the 19 coefficients and for more details about the numerical model.
3.1. Boundary Conditions
3.1.1. Internal Boundary Conditions
Cannata et al. [28] adopted a procedure based on ghost cells for the boundary conditions. In particular, on the closed boundaries, a null derivative in the normal direction is assigned for the free surface elevation and a null flux is imposed through the boundary. The lateral boundary condition of the Poisson-like equation is obtained by imposing the derivative as null in the direction normal to the boundary.
Unfortunately, the procedure proposed by [28] cannot be used for internal boundaries. In fact, in the corner cells of the internal object, it would be necessary to impose two different conditions for a single ghost calculation cell. Let us consider by way of example the case in which in the calculation cells , , and (with ), an internal object is defined (see Figure 1). The calculation cell is a ghost cell and the internal boundary is defined on the cells’ interfaces defined between and and between and . In order to define an internal closed boundary with the procedure proposed by [28], in the calculation cell defined in , a value of has to be computed, in a way to have simultaneously.
and:
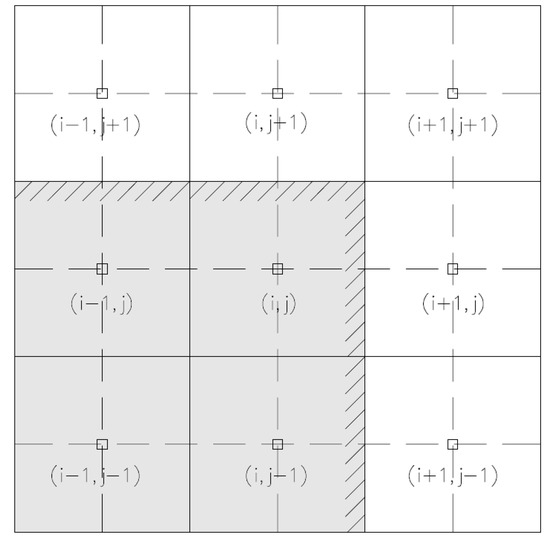
Figure 1.
Cell stencil for an internal boundary defined by the cell interfaces between the calculation cells and and between the calculation cells and , with . Grey cells represent internal objects.
These two conditions (Equations (25) and (26)) cannot be satisfied simultaneously, hence a single value of that satisfies both Equations (25) and (26) cannot be generally computed. For this reason, in the present work, an alternative strategy is proposed for the definition of the internal closed boundaries. Firstly, in the calculation cell interfaces in which the internal closed boundary is defined, the corrective velocities, i.e., the components of the gradient of , which are normal to the interfaces, are explicitly set to zero. Furthermore, the derivatives of Equation (22) are discretized in a way that does not involve the values of belonging to calculation cells in which the internal object is defined.
In order to better explain the two aforementioned conditions, let us consider by way of example the case shown in Figure 2. The calculation cells in which the internal object is defined are and , with . The internal boundary is hence defined over the calculation cell interfaces between and , between and , and between and , with . In particular, for the case shown in Figure 2, regarding the solution of Equation (22), in the calculation cell , the following corrective velocity components will be set to zero:
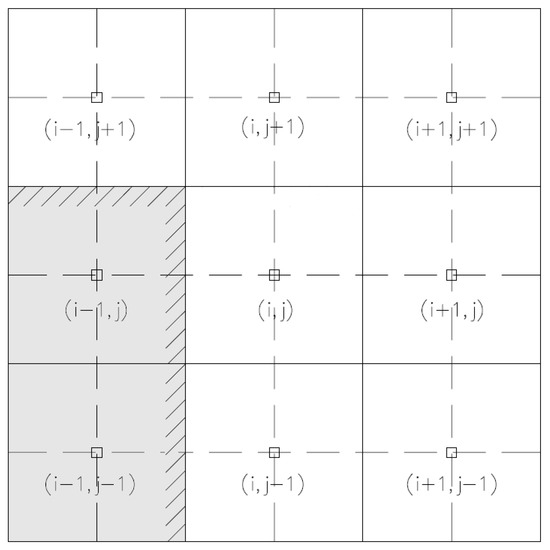
Figure 2.
Cell stencil for an internal boundary defined by the cell interfaces between the calculation cells and , between the calculation cells and , and between the calculation cells and , with . Grey cells represent internal objects.
So, in Equation (22) the following conditions are imposed:
Furthermore, in the example shown in Figure 2, the following derivatives:
if discretized with a symmetric scheme would involve respectively and ; for this reason, we use an asymmetric discretization of the derivatives Equations (31) and (32) that would involve the calculation cell if discretized symmetrically. The derivative Equation (31) is discretized by means of a composition of two asymmetric derivatives:
The derivative Equation (32) is discretized by means of a composition of an asymmetric derivative and a symmetric derivative:
By discretizing the other derivatives that are involved in Equation (22) by means of the procedure proposed by [28], the 19 coefficients of Equation (24) for the specific case of Figure 2 can be computed as follows:
Generally speaking, in the discretization of Equation (22), the corrective velocities related to calculation cells’ interfaces in which an internal boundary is defined are set to zero. Furthermore, the derivatives that would involve a grid node in which the internal object is defined are discretized asymmetrically in a way as not to involve these grid nodes.
3.1.2. Free-Surface Boundary Conditions
In the proposed model, the free-surface boundary conditions are imposed in order to take into account that, at the free surface, the normal stresses can be different from zero. Let us express with the physical contravariant components of the generic tensor . At the free surface, the external and internal normal stresses per unit density are, respectively:
where is the atmospheric pressure.
must be equal to because of continuity of the normal stresses, so that:
Recalling that the turbulent stress tensor is related to the strain rate tensor, , Equation (37) becomes:
Equation (38) is used for the calculation of the dynamic pressure at the free-surface, i.e., at the upper face of the top calculation cell.
4. Results and Discussion
In order to validate the proposed three-dimensional nonhydrostatic numerical model, we reproduced an experimental laboratory test. The test is named T3C1 and it is described in the data report “LSTF Experiments Transport by Waves and Currents & Tombolo Development Behind Headland Structures” [33] and was used as a benchmark test for numerical hydrodynamic and morphodynamic models by several authors [4,36]. The test was originally carried out on a natural beach, with a T-head groin, with a head section parallel to the shore, 4 m long and located 4 m offshore with respect to the shoreline. The T-head groin was constructed by [33] as a rubble-mound structure, with a core built with concrete blocks and the porous external layer built with riprap stones. With the proposed numerical model, it is not possible to represent porous boundaries, so the T-head groin is numerically represented by a non-porous object, with no-slip boundary conditions at its surface. In the experimental test by [33], velocity measurements were taken at approximately two-thirds of the water depth with respect to the free surface, to have a reasonable representation of the depth-averaged velocity. A random wave train was generated, with a 0.26 m significant wave height, 1.5 s period, and an incoming wave angle of 10° with respect to the shoreline; the deep water level is 0.7 m. The experimental test was aimed to produce waves with a non-zero angle with respect to the shoreline; this causes cross-shore and long-shore currents to be produced. As reported by Gravens and Wang [33], spilling breaking wave conditions were reached in the experimental test.
In order to numerically reproduce the test carried out by [33], we extend the strategy proposed by Gallerano et al. [4] in the context of a two-dimensional Boussinesq for the computational domain, to our three-dimensional model. The plan view of the computational domain is shown in Figure 3. The red line represents the border of the laboratory basin of the experimental test by [33], the bathymetry of 0.7 m represents the line that divides the deep water region (with constant water depth) and the shallow water region, with decreasing water depth. The wave trains are generated at the north boundary in Figure 3. As stated by [4], at the east and west boundaries, the bathymetric lines are perpendicular to the boundary lines: The random wave fronts stay orthogonal to the boundaries over time, so that an open boundary (with null derivative of velocities and free-surface elevation) can be easily imposed. A simple wet-dry technique is used to simulate the shoreline position (see [37]). The T-head groin structure is sufficiently far from the computational boundaries, so that the experimental test is numerically reproduced with good approximation. The number of cells is , with 8 vertical layers. Random wave trains are numerically reproduced by means of the Jonswap spectrum, with a spectral enhancement factor of γ = 3.3. The mean values are calculated in the time interval 60–120 s.
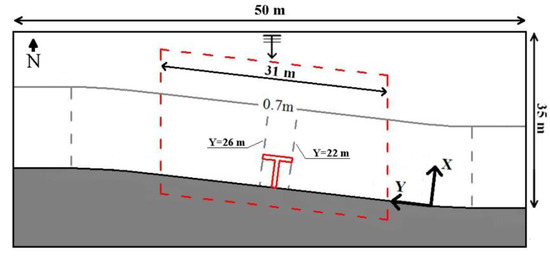
Figure 3.
Plan view of the computational domain. Dashed line: domain used in the experimental test.
Figure 4 shows an instantaneous free-surface elevation field at time t = 100 s reproduced with the proposed model. The wave transformation from deep to shallow water can be deducted from Figure 4. The wave height decreases when approaching to the shoreline, thanks to the wave breaking. Furthermore, it can be noted that the effect of the structure over the wave train, in terms of diffraction and reflection, is evident.
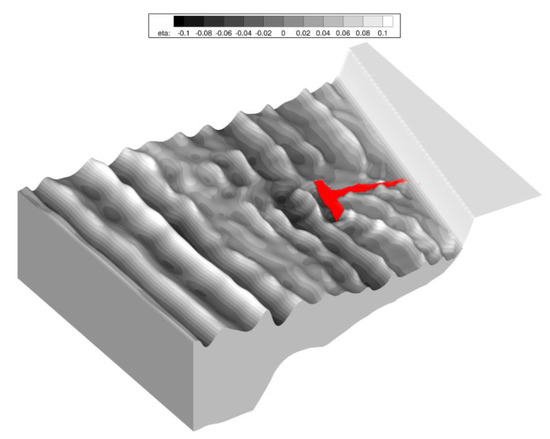
Figure 4.
Plan view of the free surface elevation field at time .
Figure 5 shows a comparison between the time-averaged and depth-averaged velocity field obtained by the numerical simulation, and the experimental results obtained by [33]. From Figure 5, it can be noted that in the zone between and and between and , the recirculation pattern close to the structure is well rendered by the numerical model. The simulated velocity field is overall in good agreement with the measured field, even if the magnitude of the field is slightly underestimated by the numerical model in the zone between and .
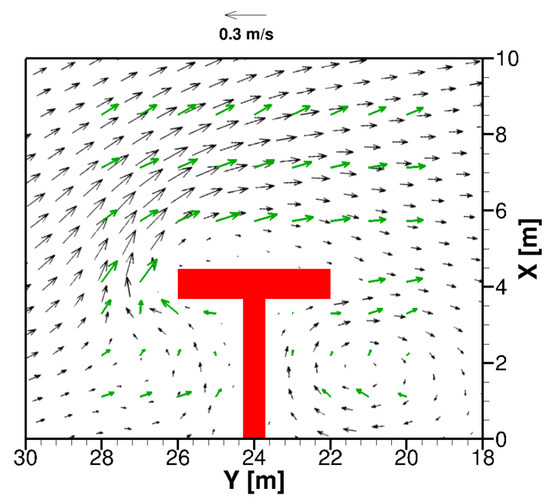
Figure 5.
Time-averaged and depth-averaged velocity field. Calculated by the proposed model (black vectors) and measured by [33] (green vectors).
In Figure 6, Figure 7 and Figure 8, three plan views of the time-averaged velocity fields are shown. Figure 6 shows the plan view of the time-averaged velocity field near the bed, at a relative position from the free surface of ( is the bed elevation with respect to the still free surface); Figure 7 shows the plan view of the time-averaged velocity field at a relative position from the free surface of ; and Figure 8 shows the plan view of the time-averaged velocity field near the free-surface, at a relative position from the free surface of . From the comparison between Figure 5 and Figure 6, it can be noted that near the bed the currents are more offshore oriented, while from the comparison between Figure 5 and Figure 8 it can be noted that near the free surface the currents are more onshore oriented. The offshore-oriented near-bed velocity field represented in Figure 6 can be related to an offshore-oriented undertow current. From Figure 6, Figure 7 and Figure 8, it can be seen that the recirculation pattern located in the zone between and and between and preserves its structure over the depth.
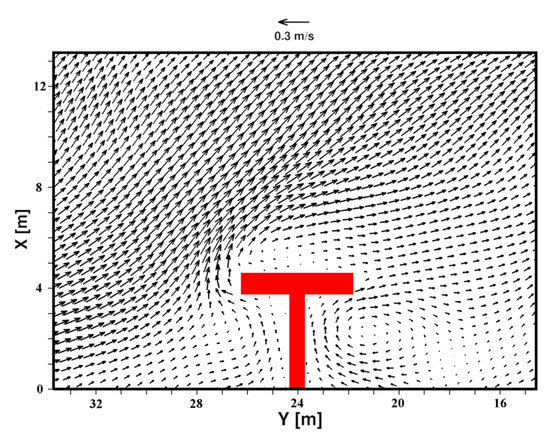
Figure 6.
Plan view of the time-averaged velocity field. Near the bed, at a relative position from the free surface of .
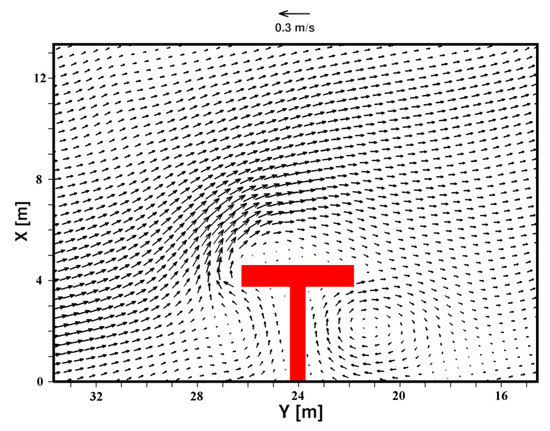
Figure 7.
Plan view of the time-averaged velocity field. At a relative position from the free surface .
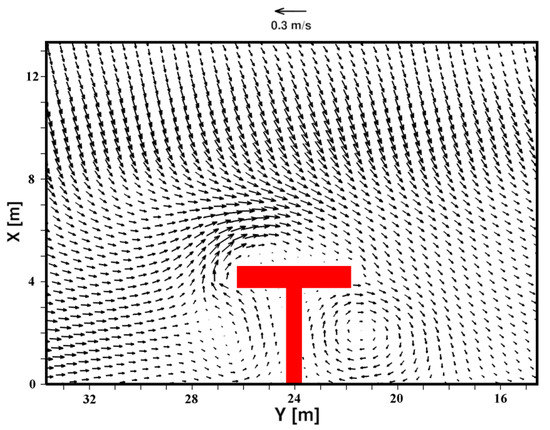
Figure 8.
Plan view of the time-averaged velocity field. Near the free surface, at a relative position from the free surface .
In Figure 9, the significant wave height computed by the proposed numerical model is compared against the experimental results obtained by Gravens and Wang [33]. The results are shown at two different sections, (Figure 9a) and (Figure 9b). From Figure 9, it can be seen that the decay of the wave height due to the wave breaking is well rendered by the numerical model. From Figure 9a, it can be seen that the numerical model slightly overestimates the significant wave height in the zone between and while the agreement outside this zone is very good. Moreover, from Figure 9b, a good agreement can be noted between the numerical and experimental results, with a slight overestimation of the significant wave height in the zone between and .
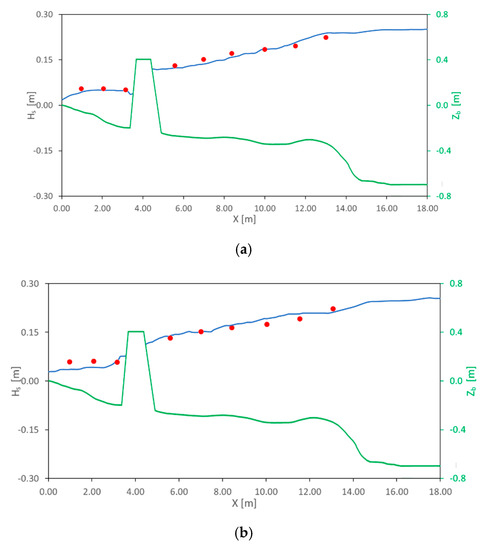
Figure 9.
Significant wave height at (a) and (b). Blue line: results obtained by the proposed model. Red circles: experimental results obtained by Gravens and Wang [33]. Green line: bottom elevation.
Figure 10 shows the comparison between the long-shore currents computed by the proposed model and those experimentally measured by Gravens and Wang [33], at two different sections, (Figure 10a) and (Figure 10b). The results are shown in terms of the depth-averaged velocity (dashed line) and in terms of velocities at different relative positions from the free surface , , , . The depth-averaged velocity resulting from the numerical simulation is shown to be in good agreement with the experimental measurements. From Figure 10b, it can be seen that at , the long-shore current magnitude is slightly underestimated by the proposed model in the zone between the shoreline and the structure, and slightly overestimated in the offshore zone, close to the structure. Slight differences between the numerical and experimental results, in terms of long-shore currents, are mainly visible close to the structure, in particular for section . This can be related to the fact that in the numerical model, the rubble-mound structure is represented as an impermeable object.
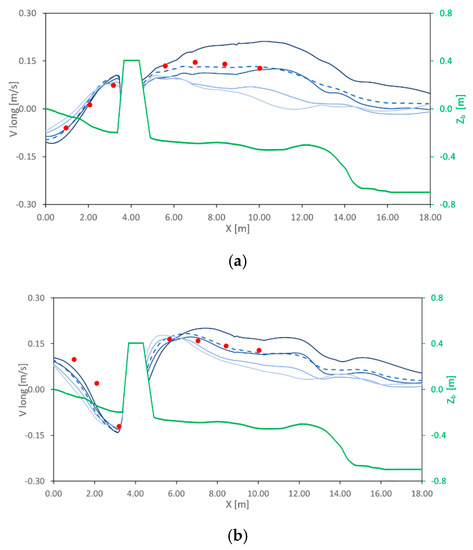
Figure 10.
Long-shore currents at (a) and (b). Dashed blue line: depth-averaged velocity field computed by the proposed model. Solid blue lines: velocity fields computed by the proposed model at a relative position from the free surface , , , , from lightest blue to darkest blue. Red circles: experimental results obtained by Gravens and Wang [33]. Green line: bottom elevation.
Figure 11 shows the comparison between the cross-shore currents computed by the proposed model and those experimentally measured by Gravens and Wang [33], at two different sections, (Figure 11a) and (Figure 11b). Similarly with Figure 10, the results are shown in terms of the depth-averaged velocity (dashed line) and in terms of velocities at different relative positions from the free surface , , , . The agreement between the simulated depth-averaged velocity and the one measured by [33] is shown to be quite good. From Figure 11b, it has to be noted that at , the simulated cross-shore current shows a different behavior from the measured one, in the zone between the shoreline and the structure, and overestimated in the offshore zone; furthermore, the numerical model overestimates the cross-shore current between and . As for the case of long-shore currents, even for the cross-shore currents, the deviation between the numerical and experimental results close to the structure (especially for section ) can be related to the difference between the structure and its numerical representation.
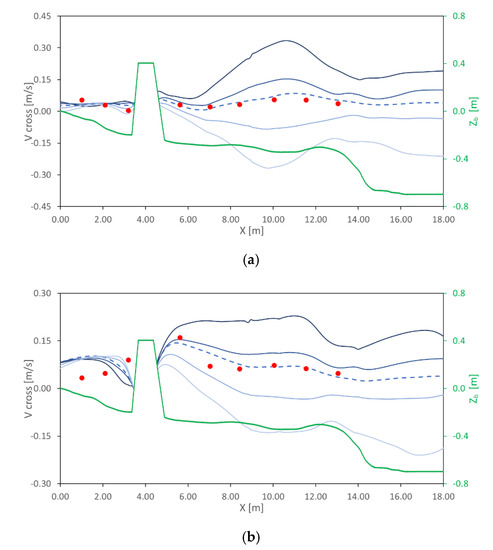
Figure 11.
Cross-shore currents at (a) and (b). Dashed blue line: depth-averaged velocity field computed by the proposed model. Solid blue lines: velocity fields computed by the proposed model at relative position from free-surface , , , , from lightest blue to darkest blue. Red circles: experimental results obtained by Gravens and Wang [33]. Green line: bottom elevation.
From Figure 10 and Figure 11, it can be deduced that the vertical distribution of the velocity can be of primary importance in the study of this test case. In fact, while for the long-shore currents, the changes at different depths are moderate, in the case of the cross-shore currents, the velocity fields change consistently with the variation of the depth. In particular, the presence of an offshore-oriented current near the bottom and an onshore-oriented current near the free surface is evident from Figure 11.
5. Conclusions
In this work, we proposed a novel numerical scheme that aims to simulate coastal flows in complex geometries in the presence of the structure. The numerical model presented is based on the model proposed by Cannata et al. [28] that solves the three-dimensional Navier–Stokes equations in an integral contravariant formulation on a time-dependent curvilinear grid. Differently from the numerical scheme proposed by [28], in the proposed numerical scheme an appropriate boundary conditions treatment allows the model to represent flows around sharp-cornered structures. Furthermore, the proposed scheme adopts an evaluation of the non-zero dynamic pressure at the free surface. The use of boundary-conforming grids combined with the adoption of the proposed numerical scheme makes it possible to represent complex natural morphologies and coastal structures. In order to test the model, a simulation consisting in a random wave train approaching a natural shore with a T-head groin structure was carried out and the numerical results were compared against the experimental measurements. From the comparison between the numerical and experimental results, we verified the ability of the model to reproduce three-dimensional hydrodynamic flows in complex domains with structures.
Author Contributions
Conceptualization and methodology, G.C. and F.G. Validation and investigation, G.C. and M.T. Writing and editing, M.T. Supervision, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moore, B.D.; Humiston, K.K. Composite T-Head Groins for Erosion Control. In Proceedings of the Coastal Structures 2003, Portland, OR, USA, 26–30 August 2003. [Google Scholar]
- Özölçer, İ.H.; Kömürcü, M.İ.; Birben, A.R.; Yüksek, Ö.; Karasu, S. Effects of T-Shape Groin Parameters on Beach Accretion. Ocean Eng. 2006, 33, 382–403. [Google Scholar] [CrossRef]
- Li, B.; Yu, X.; Yu, Y. Nonlinear dynamics of nearshore irregular waves: A threedimensional numerical model and its validation. Coast. Eng. J. 2007, 49, 103–126. [Google Scholar] [CrossRef]
- Gallerano, F.; Cannata, G.; De Gaudenzi, O.; Scarpone, S. Modeling Bed Evolution Using Weakly Coupled Phase-Resolving Wave Model and Wave-Averaged Sediment Transport Model. Coast. Eng. J. 2016, 58, 1650011. [Google Scholar] [CrossRef]
- Ma, G.; Chou, Y.J.; Shi, F. A wave-resolving model for nearshore suspended sediment transport. Ocean Model. 2014, 77, 33–49. [Google Scholar] [CrossRef]
- Nam, P.T.; Oumeraci, H.; Larson, M.; Hanson, H. Modeling undertow due to random waves. Ocean Dyn. 2014, 64, 1209–1219. [Google Scholar] [CrossRef]
- Hu, K.; Mingham, C.G.; Causon, D.M. Numerical simulation of wave overtopping of coastal structures using the non-linear shallow water equations. Coast. Eng. 2000, 41, 433–465. [Google Scholar] [CrossRef]
- Cannata, G.; Petrelli, C.; Barsi, L.; Fratello, F.; Gallerano, F. A dam-break flood simulation model in curvilinear coordinates. WSEAS Trans. Fluid Mech. 2018, 13, 60–70. [Google Scholar]
- Tonelli, M.; Petti, M. Shock-capturing Boussinesq model for irregular wave propagation. Coast. Eng. 2012, 61, 8–19. [Google Scholar] [CrossRef]
- Cannata, G.; Barsi, L.; Petrelli, C.; Gallerano, F. Numerical investigation of wave fields and currents in a coastal engineering case study. WSEAS Trans. Fluid Mech. 2018, 13, 87–94. [Google Scholar]
- Guerrini, M.; Bellotti, G.; Fan, Y.; Franco, L. Numerical modelling of long waves amplification at Marina di Carrara Harbour. Appl. Ocean Res. 2014, 48, 322–330. [Google Scholar] [CrossRef]
- Lynett, P.J. Nearshore wave modeling with high-order Boussinesq-type equations. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 348–357. [Google Scholar] [CrossRef]
- Chen, X. A fully hydrodynamic model for three-dimensional free-surface flows. Int. J. Numer. Meth. Fluids 2003, 42, 929–952. [Google Scholar] [CrossRef]
- Casulli, V.; Cheng, R.T. Semi-implicit finite-difference methods for three-dimensional shallow flow. Int. J. Numer. Meth. Fluids 1992, 15, 1045–1068. [Google Scholar] [CrossRef]
- De Marchis, M.; Napoli, E. Effects of irregular two-dimensional and three-dimensional surface roughness in turbulent channel flows. Int. J. Numer. Meth. Fluids 2012, 36, 7–17. [Google Scholar] [CrossRef]
- Bradford, S.F. Numerical Simulation of Surf Zone Dynamics. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 1–13. [Google Scholar] [CrossRef]
- Berberović, E.; van Hinsberg, N.P.; Jakirlić, S.; Roisman, I.V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. E 2009, 79, 036306. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Simulating coastal engineering processes with OpenFOAM®. Coast. Eng. 2013, 71, 119–134. [Google Scholar] [CrossRef]
- Montagna, F.; Bellotti, G.; Di Risio, M. 3D numerical modeling of landslide-generated tsunamis around a conical island. Nat. Hazards 2011, 58, 591–608. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Petit, H.A.H.; van den Bosch, P.; Klopman, G.; Broekens, R.D. Numerical Simulation of Wave Motion on and in Coastal Structures. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992. [Google Scholar]
- Romano, A.; Lara, J.L.; Barajas, G.; Di Paolo, B.; Bellotti, G.; Di Risio, M.; Losada, I.; De Girolamo, P. Numerical Modelling of Landslide-Generated Tsunamis with OpenFOAM®: A New Approach. In Proceedings of the Coastal Structures Conference 2019, Hannover, Germany, 30 September–2 October 2019. [Google Scholar]
- Lin, P.; Li, C.W. A σ-coordinate three-dimensional numerical model for surface wave propagation. Int. J. Numer. Meth. Fluids 2002, 38, 1045–1068. [Google Scholar] [CrossRef]
- Lin, P. A multiple-layer σ-coordinate model for simulation of wave–structure interaction. Comput. Fluids 2006, 35, 147–167. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43–44, 22–35. [Google Scholar] [CrossRef]
- Cannata, G.; Gallerano, F.; Palleschi, F.; Petrelli, C.; Barsi, L. Three-dimensional numerical simulation of the velocity fields induced by submerged breakwaters. Int. J. Mech. 2019, 13, 1–14. [Google Scholar]
- Napoli, E.; De Marchis, M.; Vitanza, E. PANORMUS-SPH. A new Smoothed Particle Hydrodynamics solver for incompressible flows. Comput. Fluids 2015, 106, 185–196. [Google Scholar] [CrossRef]
- Monaghan, J. Simulating free surface flows with SPH. J. Comput. Phys. V 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Cannata, G.; Petrelli, C.; Barsi, L.; Gallerano, F. Numerical integration of the contravariant integral form of the Navier–Stokes equations in time-dependent curvilinear coordinate systems for three-dimensional free surface flows. Continuum Mech. Therm. 2019, 31, 491–519. [Google Scholar] [CrossRef]
- Palleschi, F.; Iele, B.; Gallerano, F. Integral contravariant form of the Navier-Stokes equations. WSEAS Trans. Fluid Mech. 2019, 14, 101–113. [Google Scholar]
- Fadlun, E.A.; Verzicco, R.; Orlandi, P.; Mohd-Yusof, J. Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 2000, 161, 35–60. [Google Scholar] [CrossRef]
- Ma, G.; Farahani, A.A.; Kirby, J.T.; Shi, F. Modeling wave-structure interactions by an immersed boundary method in a σ-coordinate model. Ocean Eng. 2016, 125, 238–247. [Google Scholar] [CrossRef]
- Roman, F.; Napoli, E.; Milici, B.; Armenio, V. An improved immersed boundary method for curvilinear grids. Comput. Fluids 2009, 38, 1510–1527. [Google Scholar] [CrossRef]
- Gravens, M.B.; Wang, P. Data Report: LSTF Experiments—Transport by Waves and Currents & Tombolo Development Behind Headland Structures, Technical Report ERDC/CHL TR-04-9; Coastal and Hydraulics Laboratory, US Army Engineer Research and Development Center: Vicksburg, MS, USA, 2007. [Google Scholar]
- Spiteri, R.J.; Ruuth, S.J. A new class of optimal high-order strong-stability preserving time discretization methods. SIAM J. Numer. Anal. 2002, 40, 469–491. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Nam, P.T.; Larson, M. A model of wave and current fields around coastal structures. Proc. Coast. Dyn. 2009, 1–14. [Google Scholar] [CrossRef]
- Tamburrino, M.; Cannata, G. Simulation of wave run-up by means of the exact solution of the wet/dry Riemann problem. WSEAS Trans. Fluid Mech. 2019, 14, 114–123. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).