Calculation Methods of Icebreaking Capability for a Double-Acting Polar Ship
Abstract
1. Introduction
2. Mathematical Model
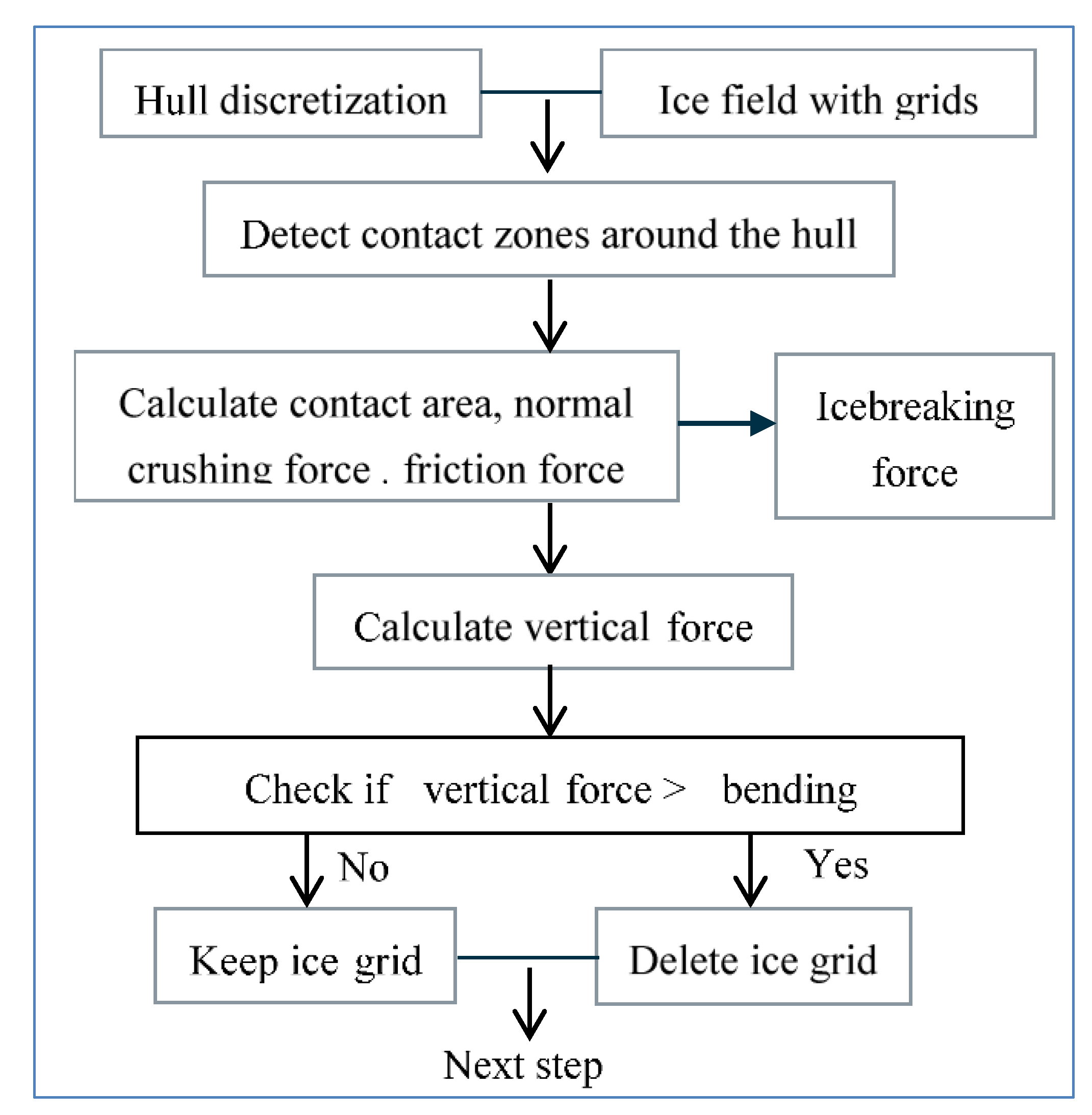
2.1. Static Method
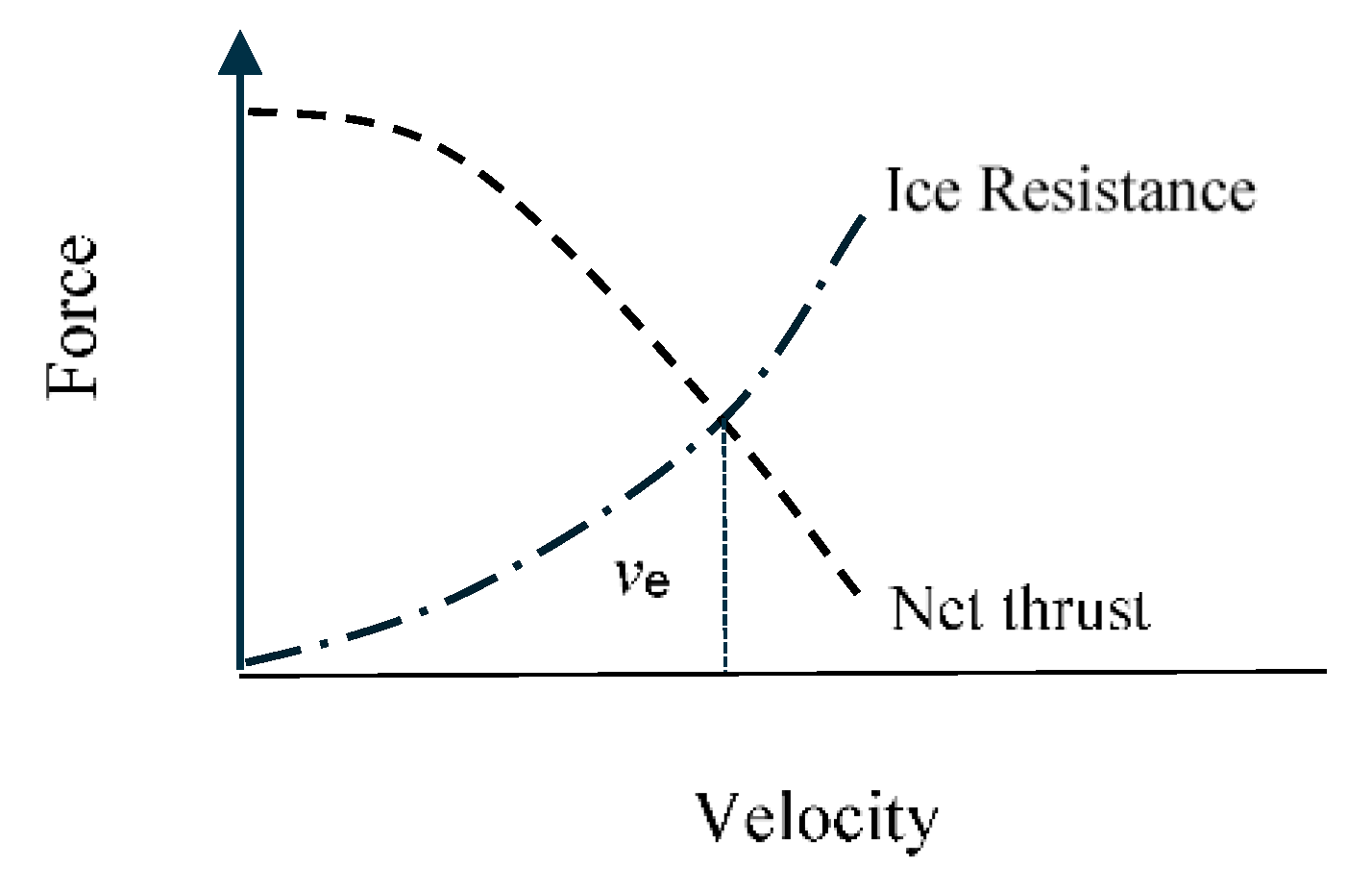
2.2. Dynamic Method
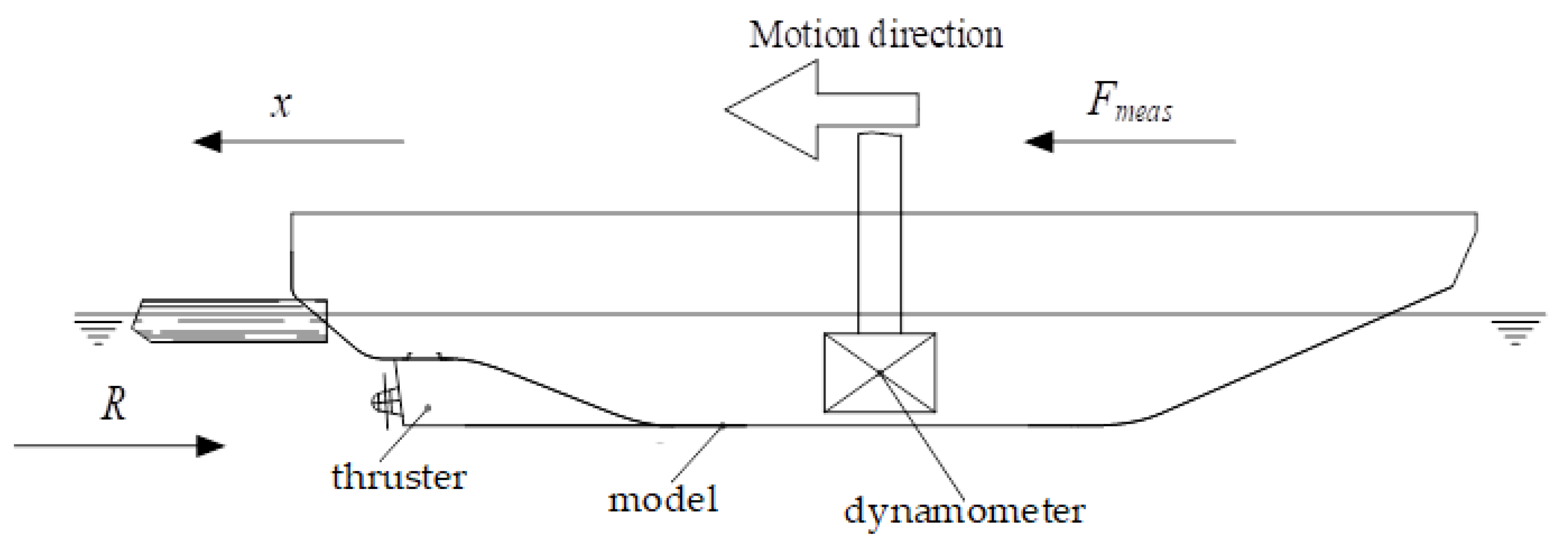
3. Model Tests in the Ice Basin
4. Numerical Simulation and Comparison
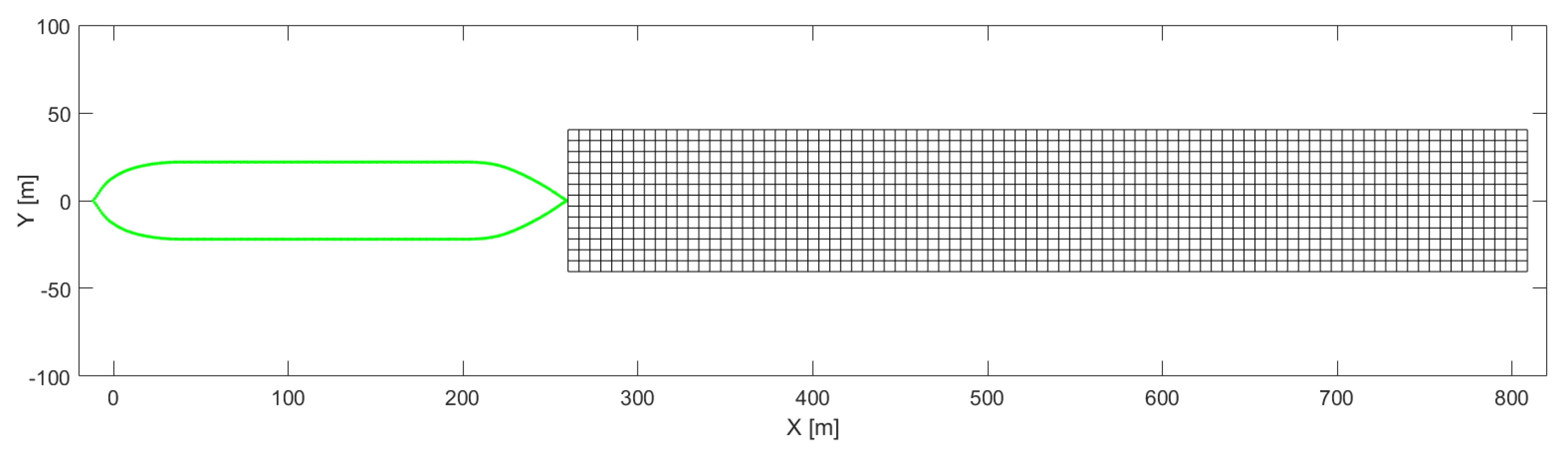
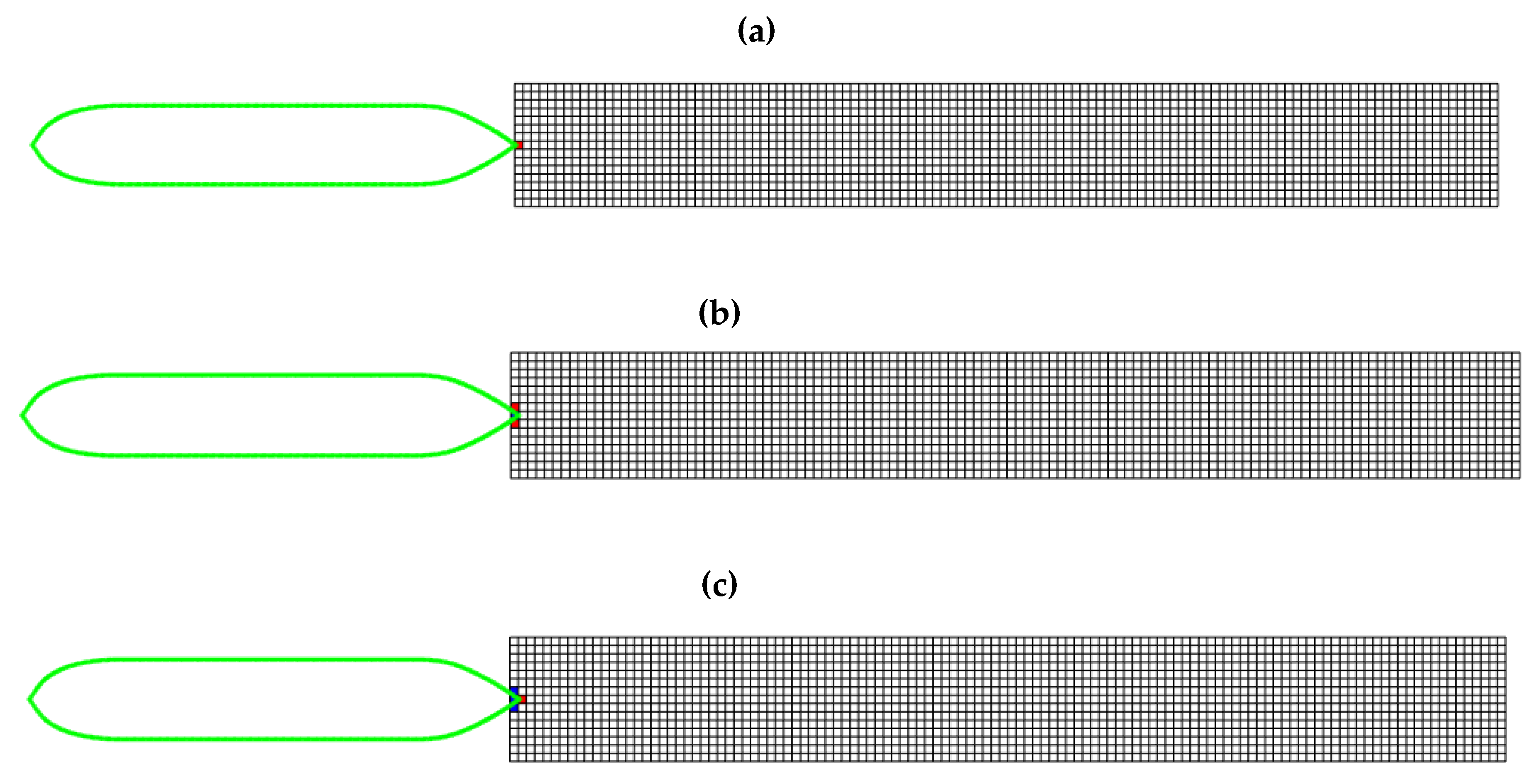
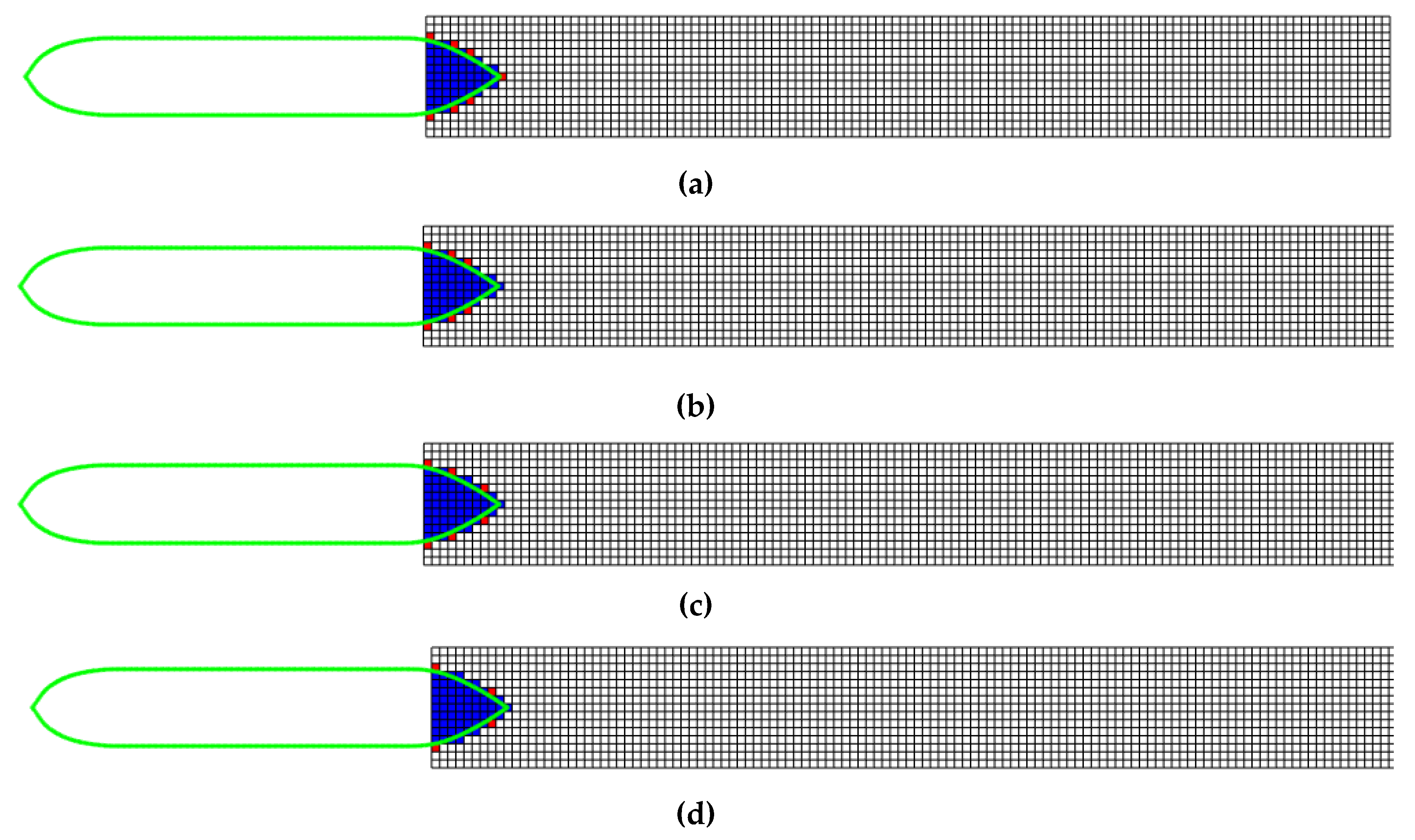
4.1. Simulation Setup
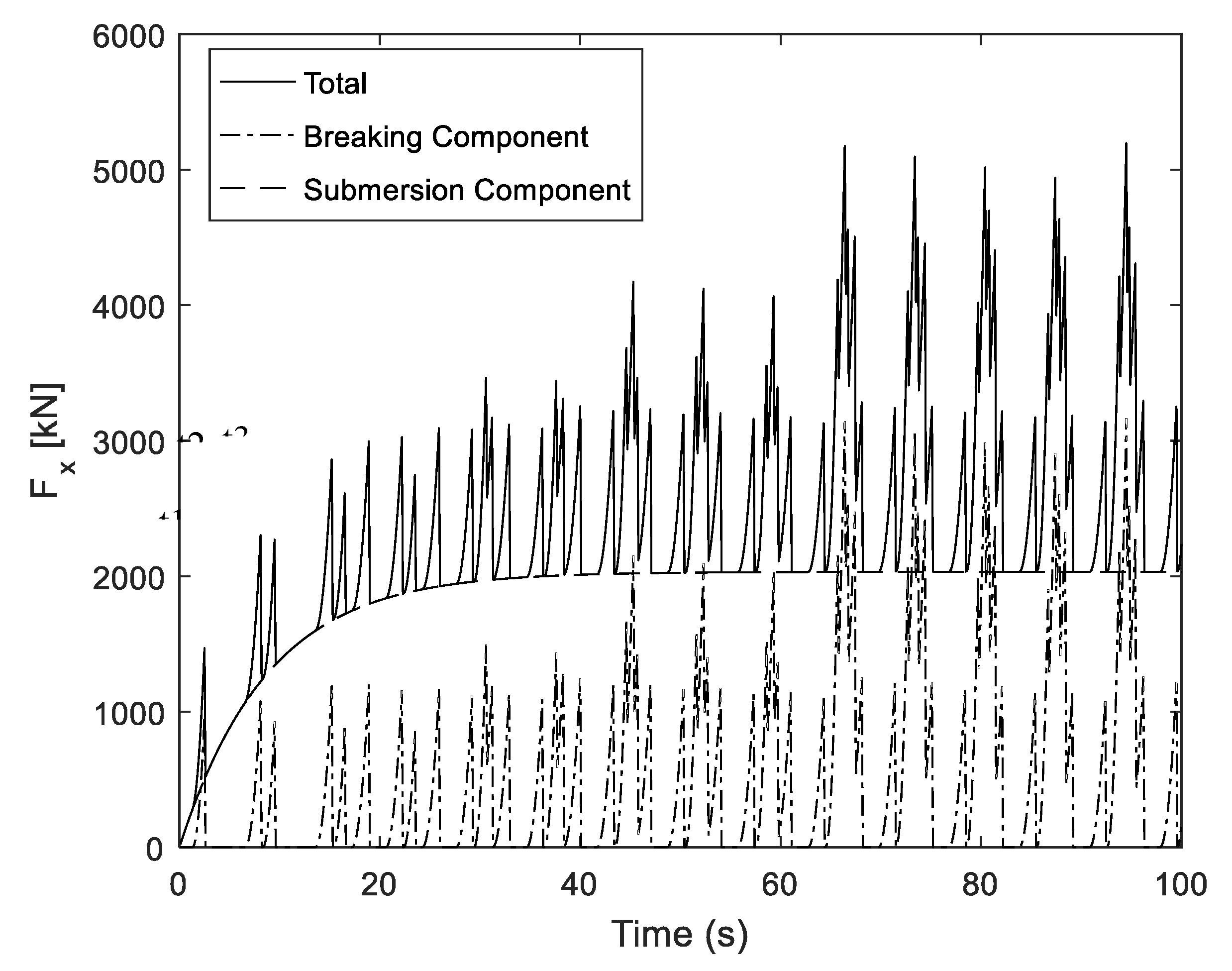
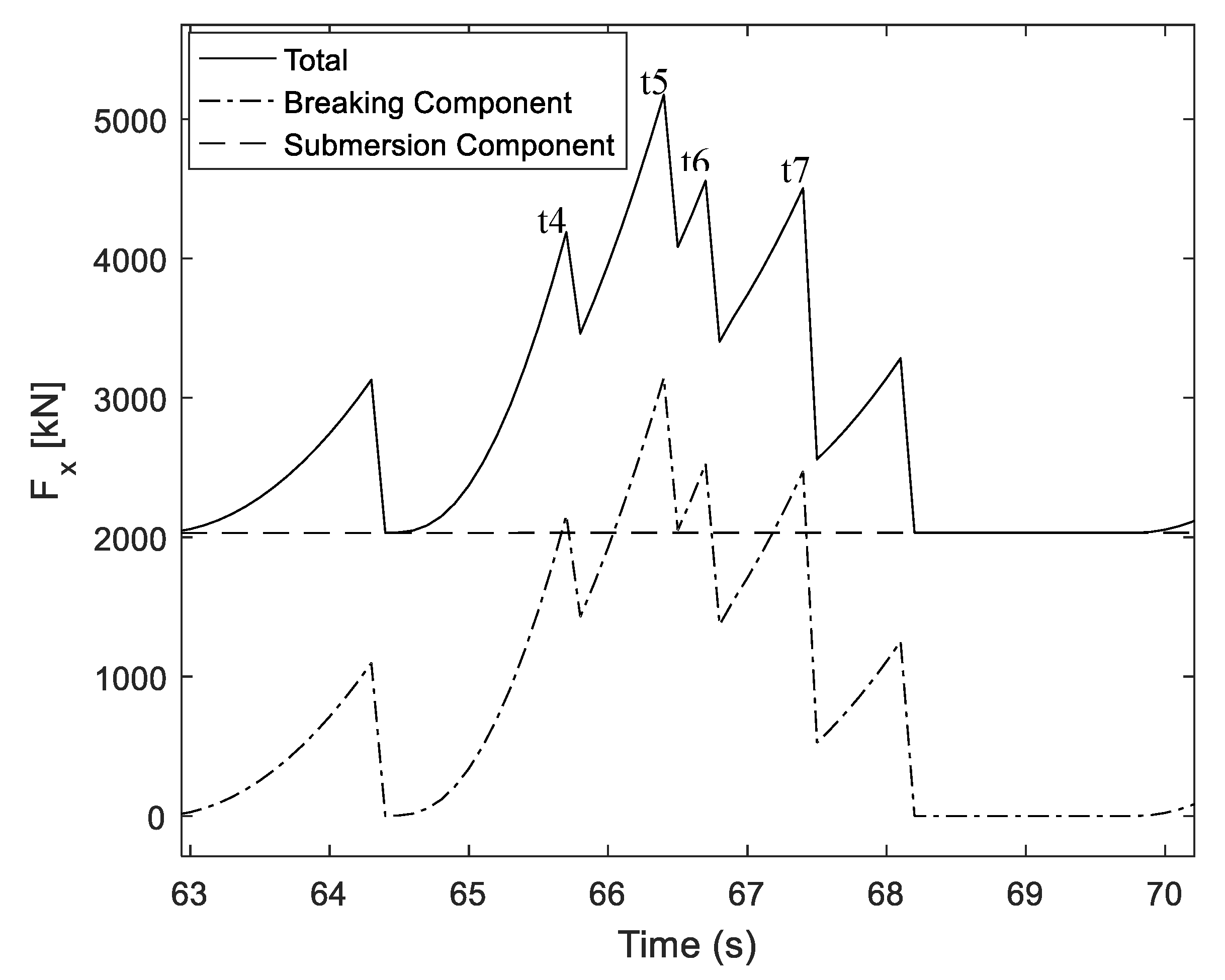
4.2. Simulation Examples
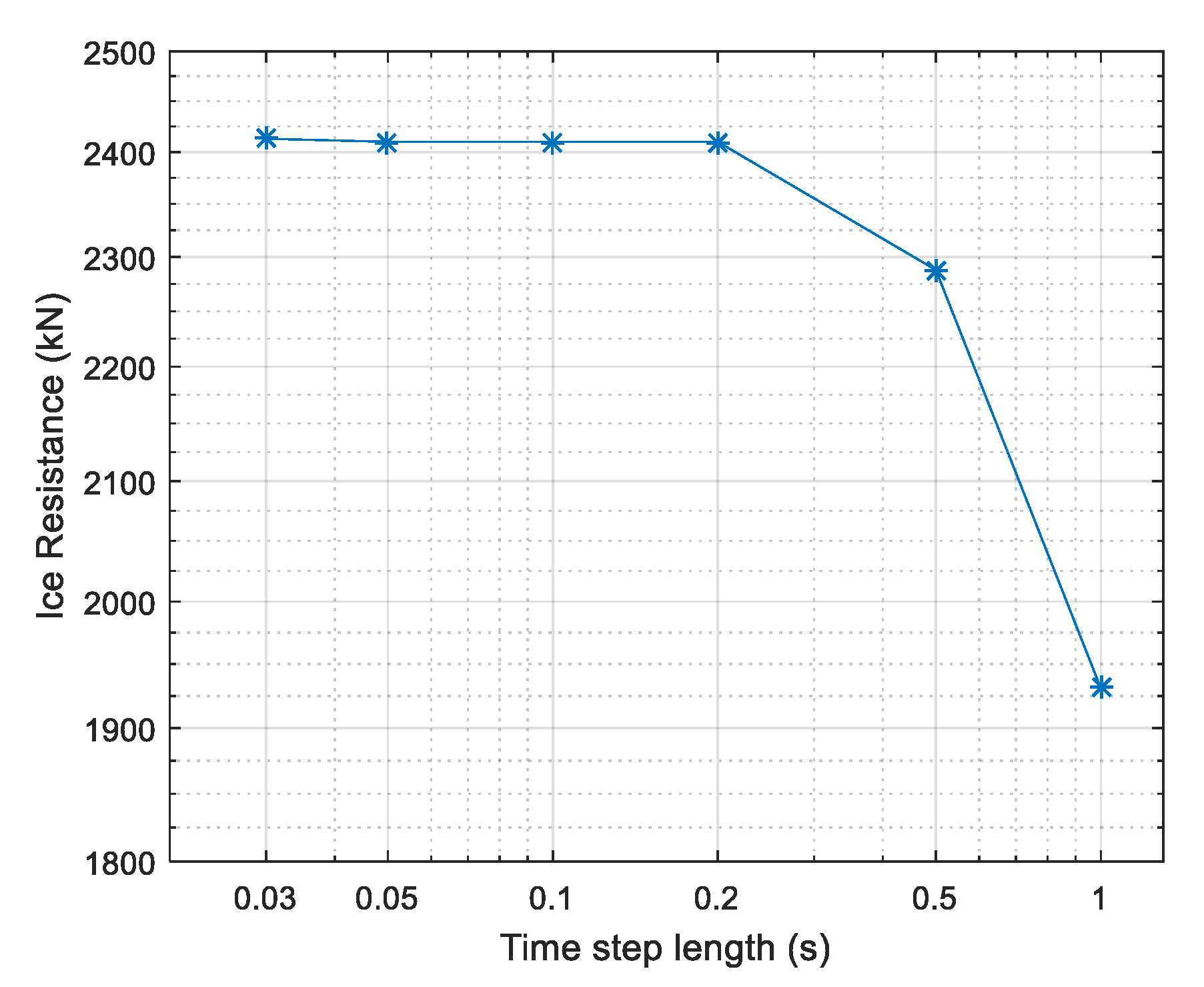
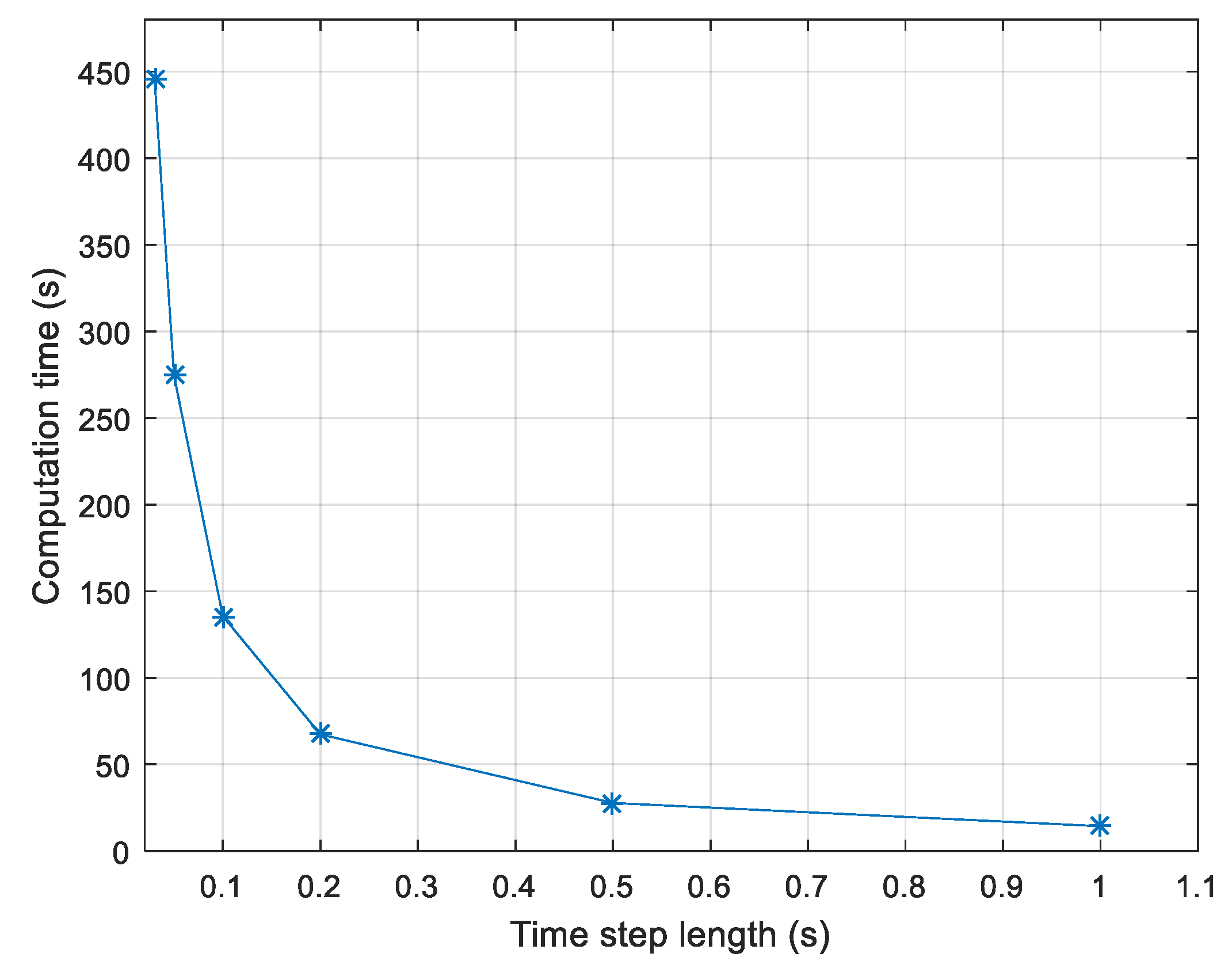
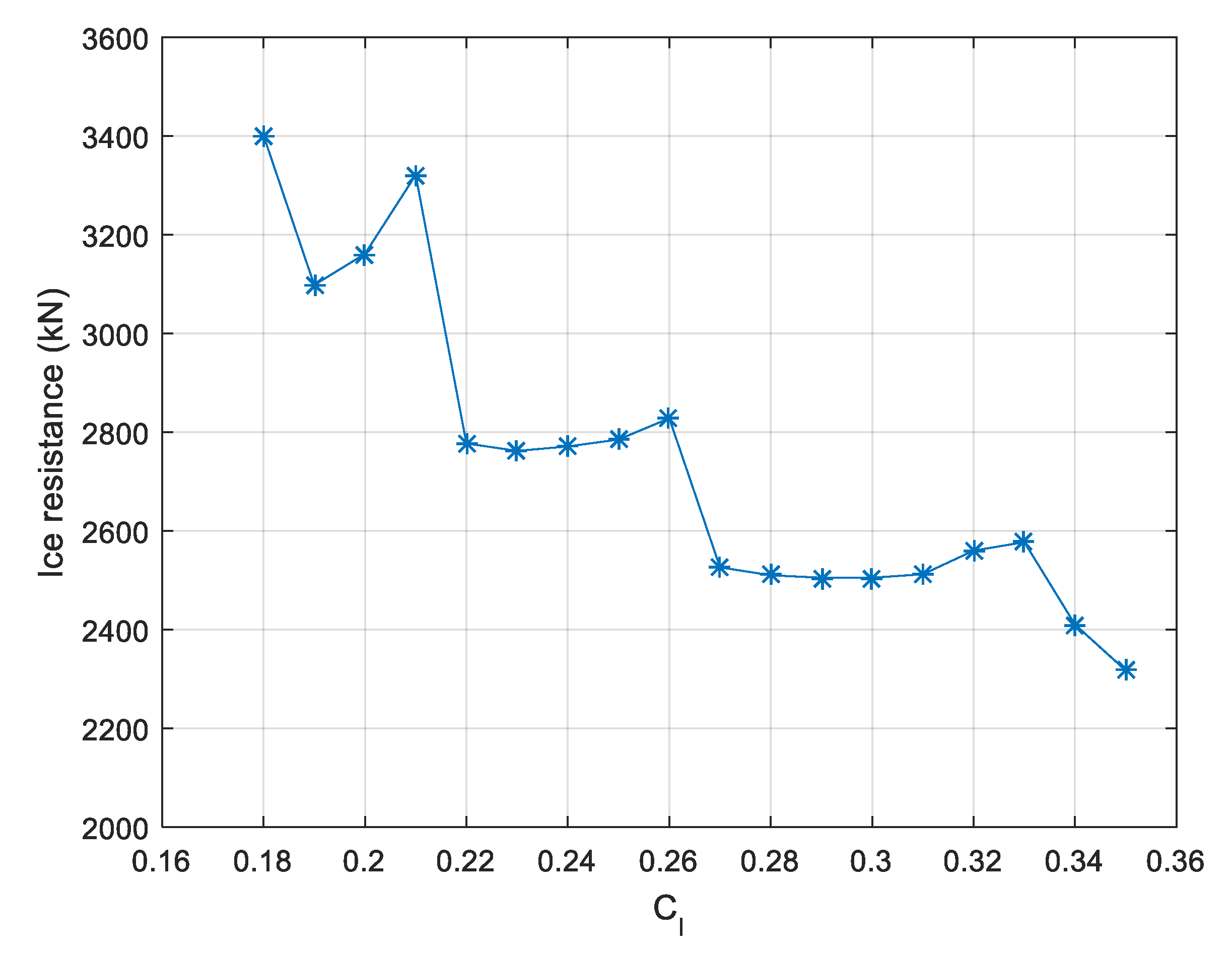
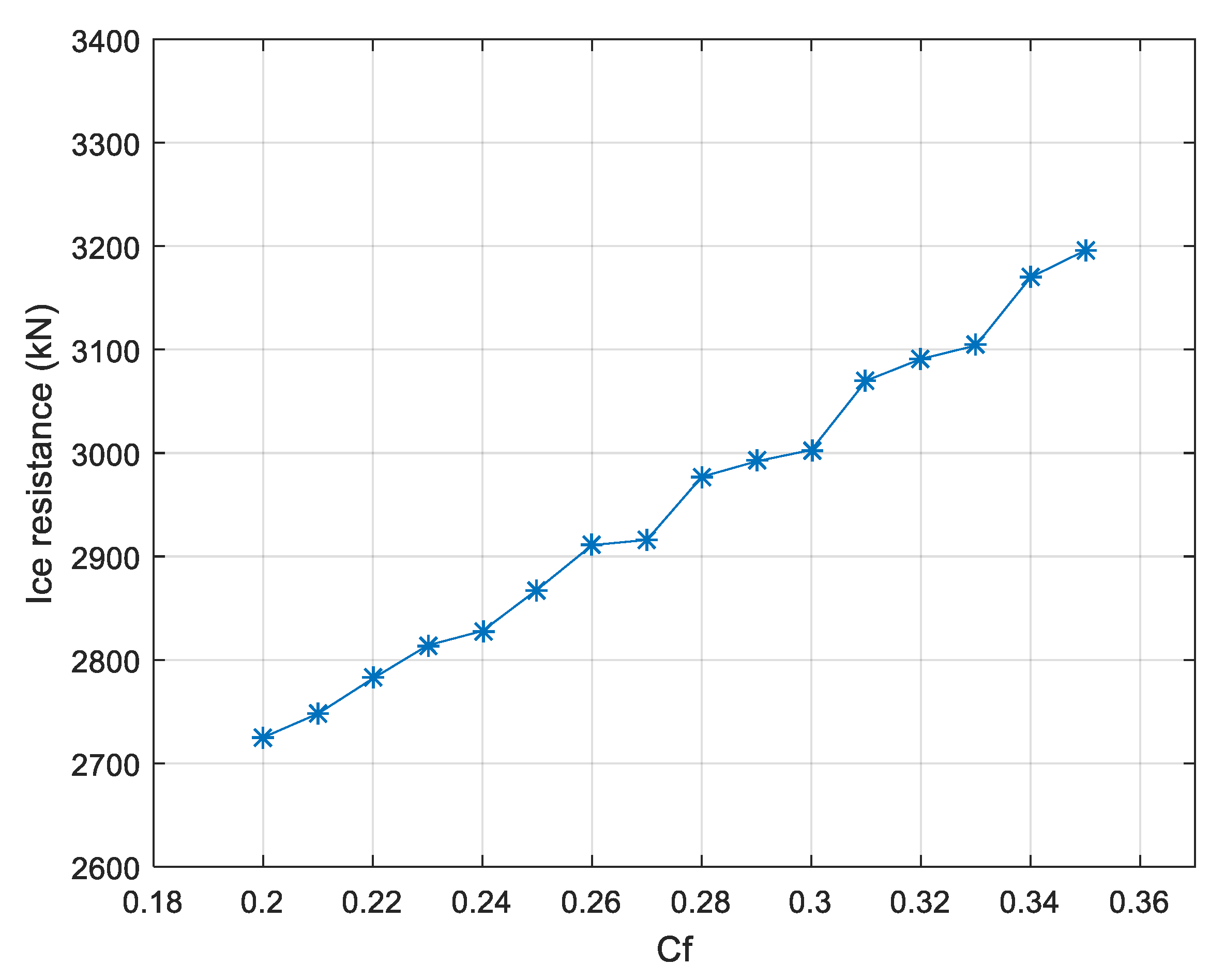
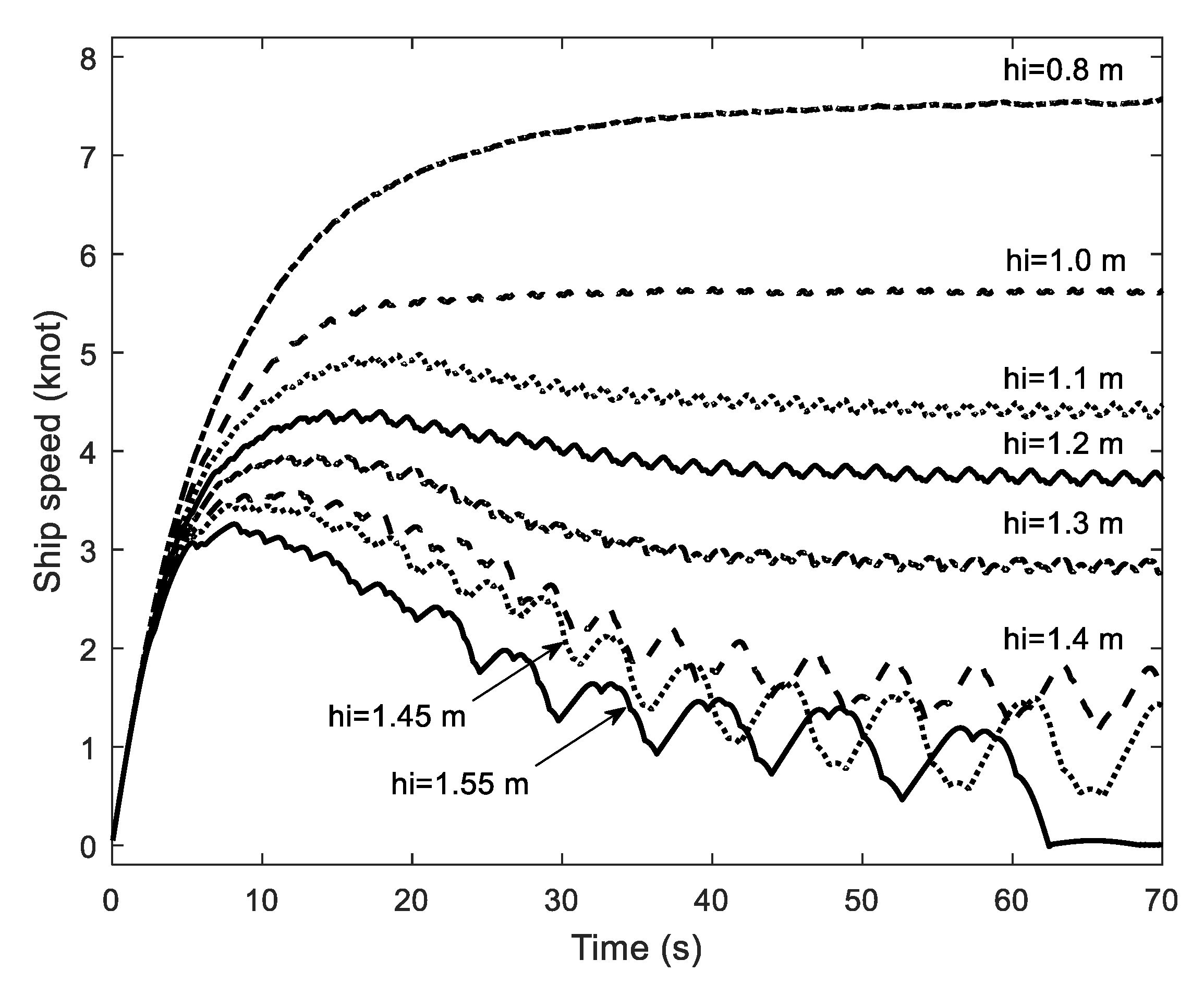
4.3. Sensitivity Study
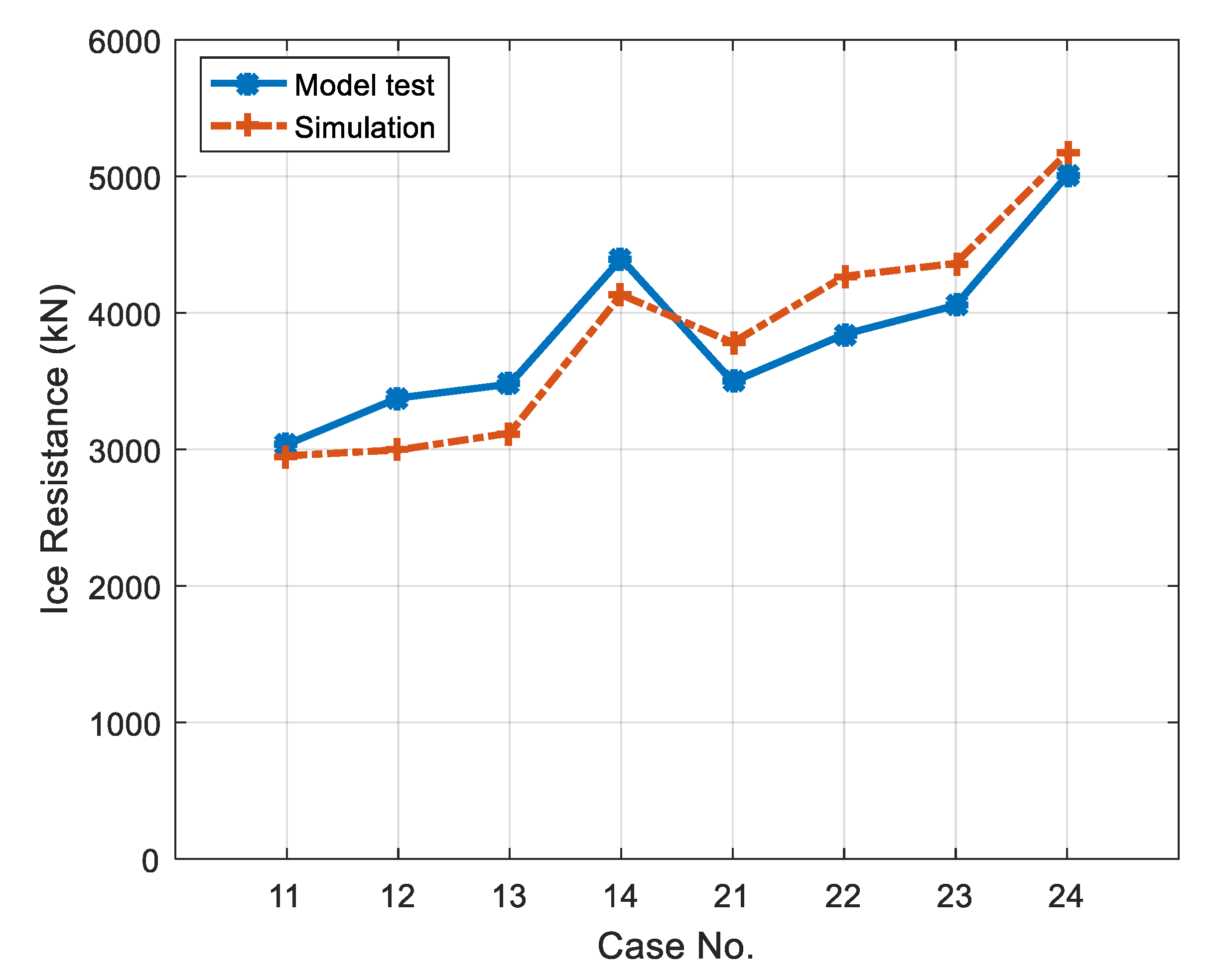
4.4. Ice Resistance Comparison
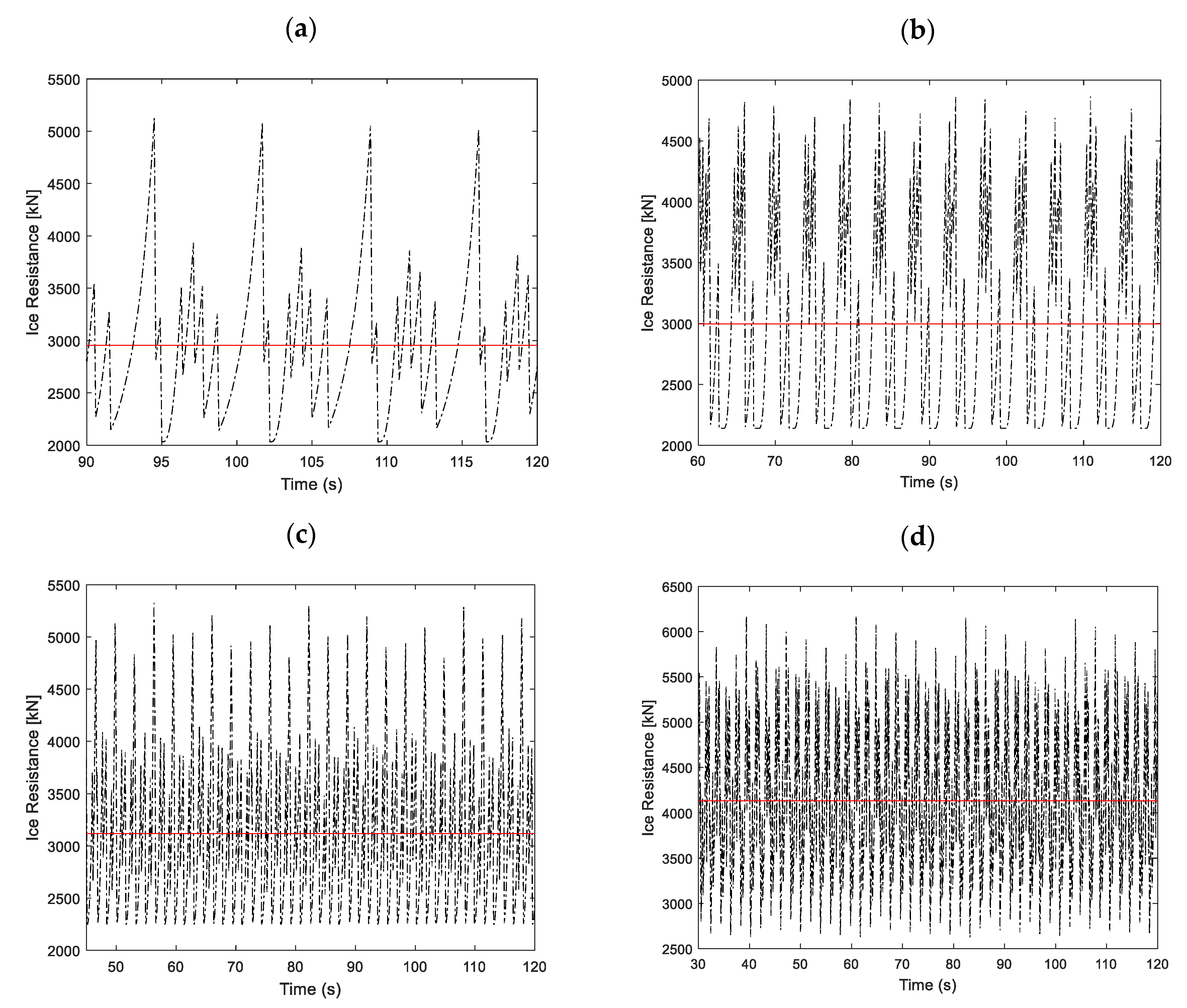
4.4.1. Icebreaking Ahead
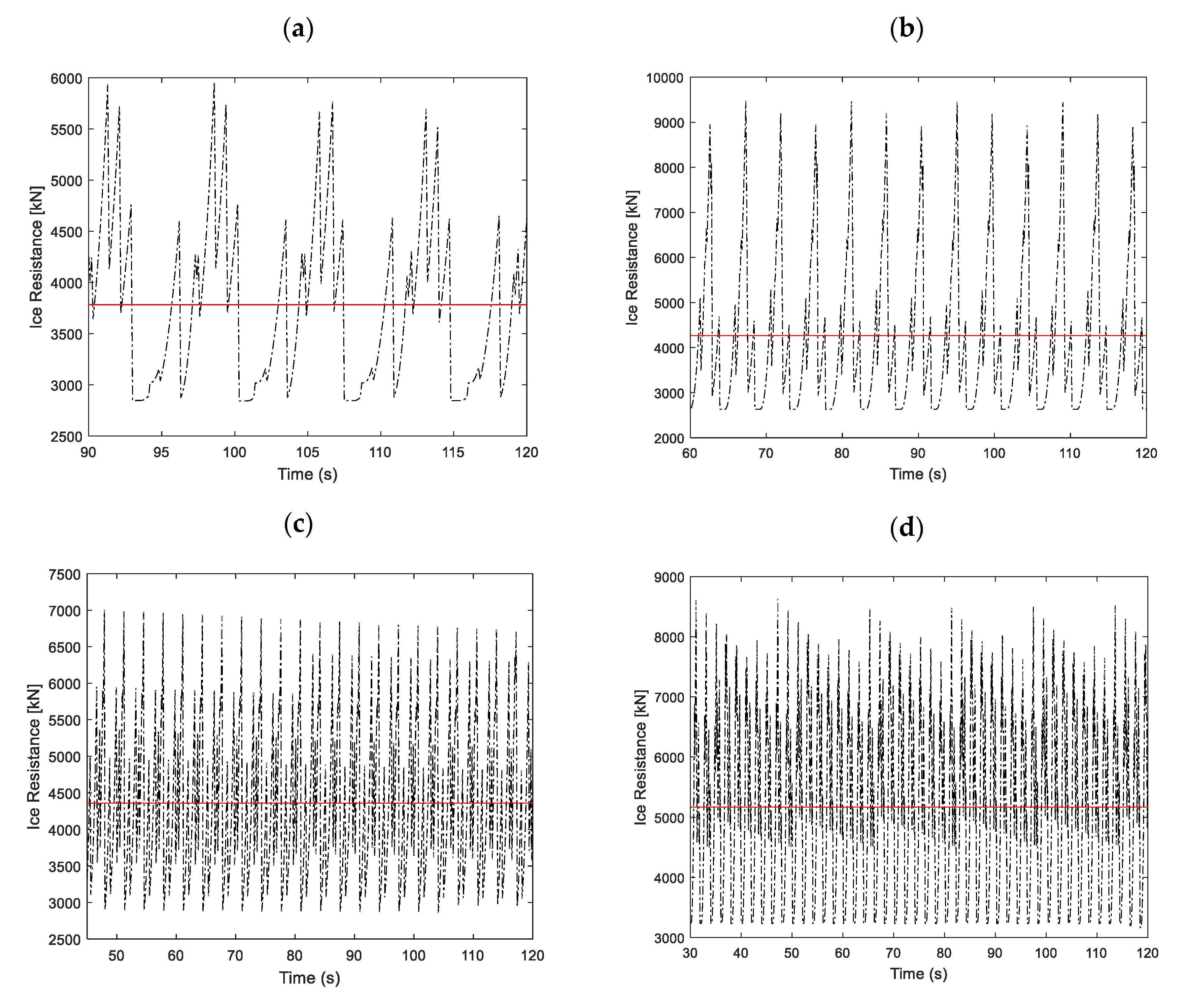
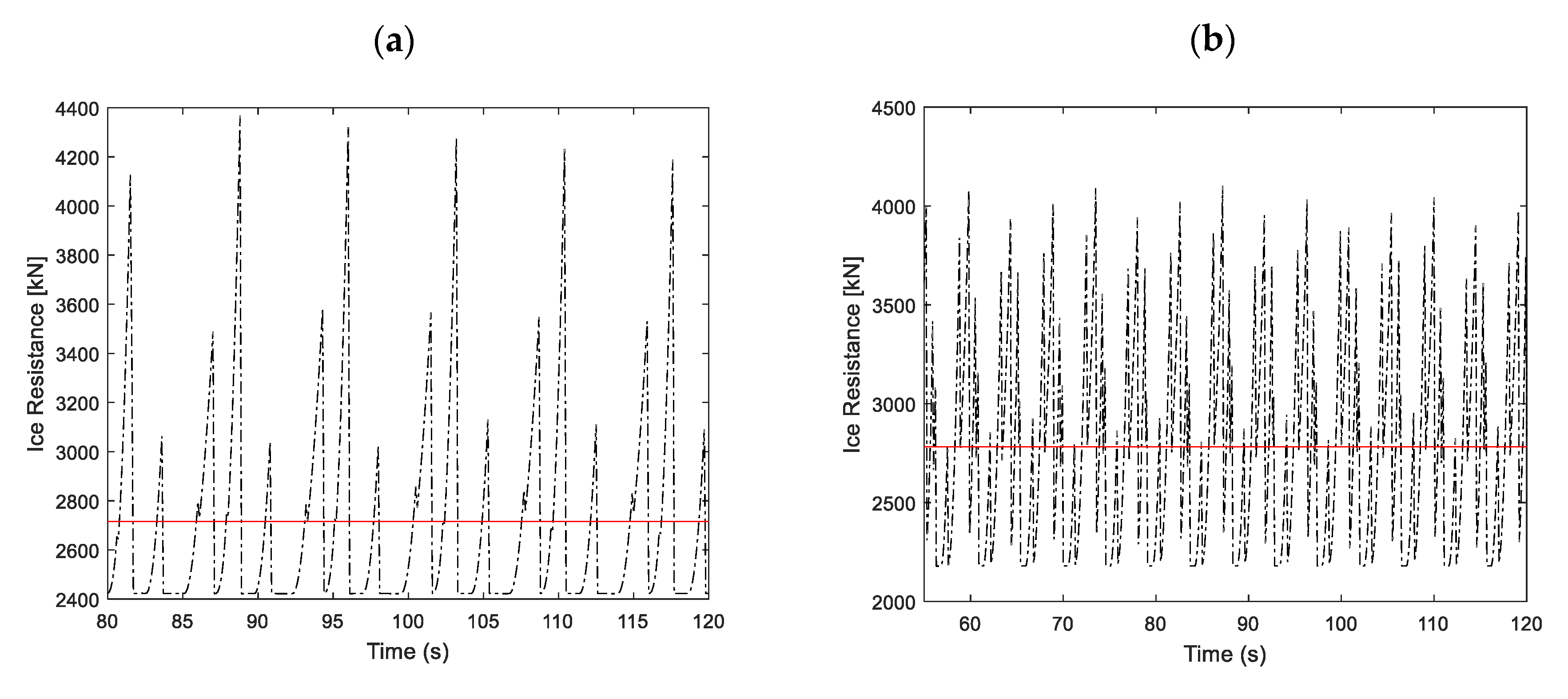
4.4.2. Icebreaking Astern
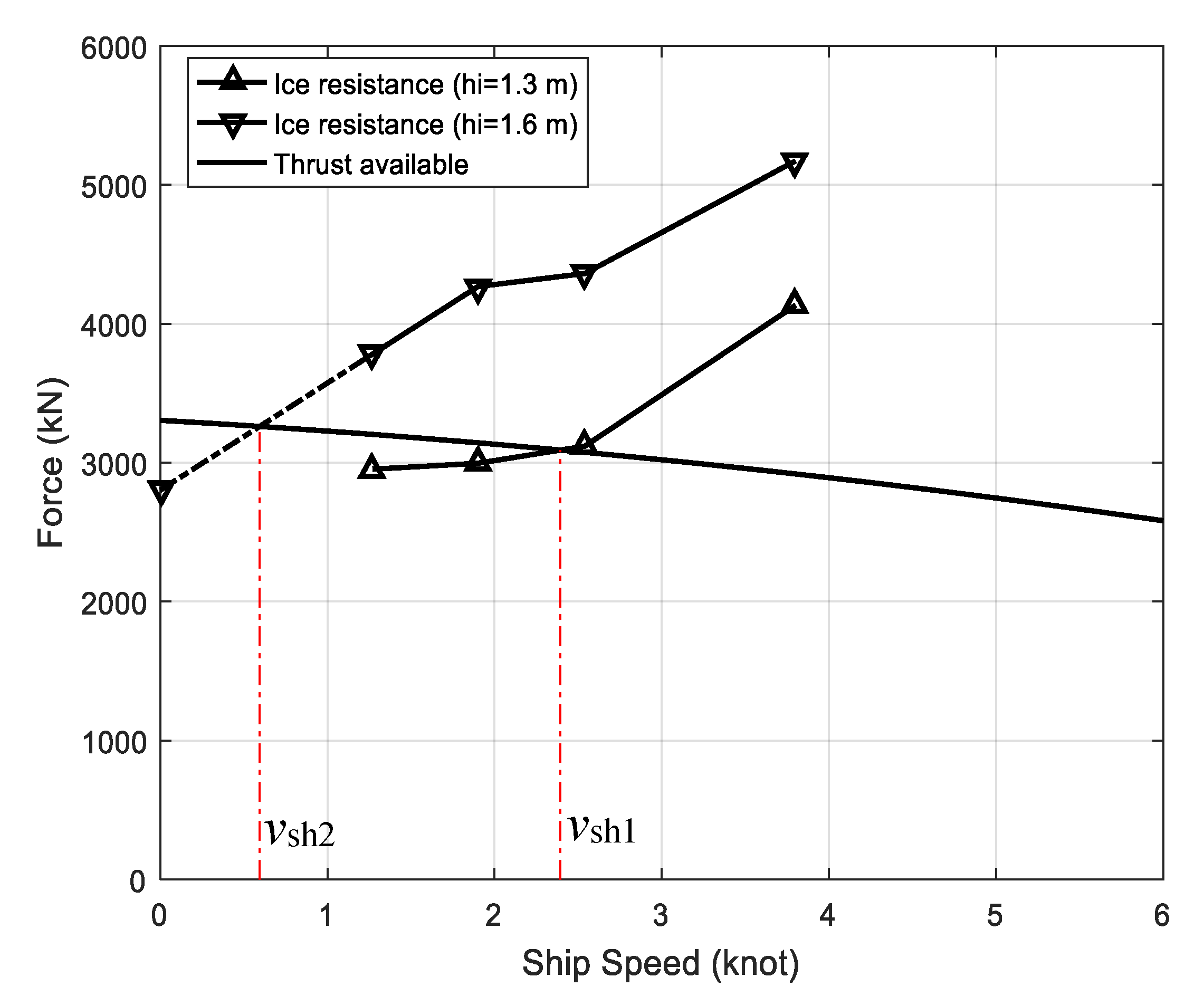
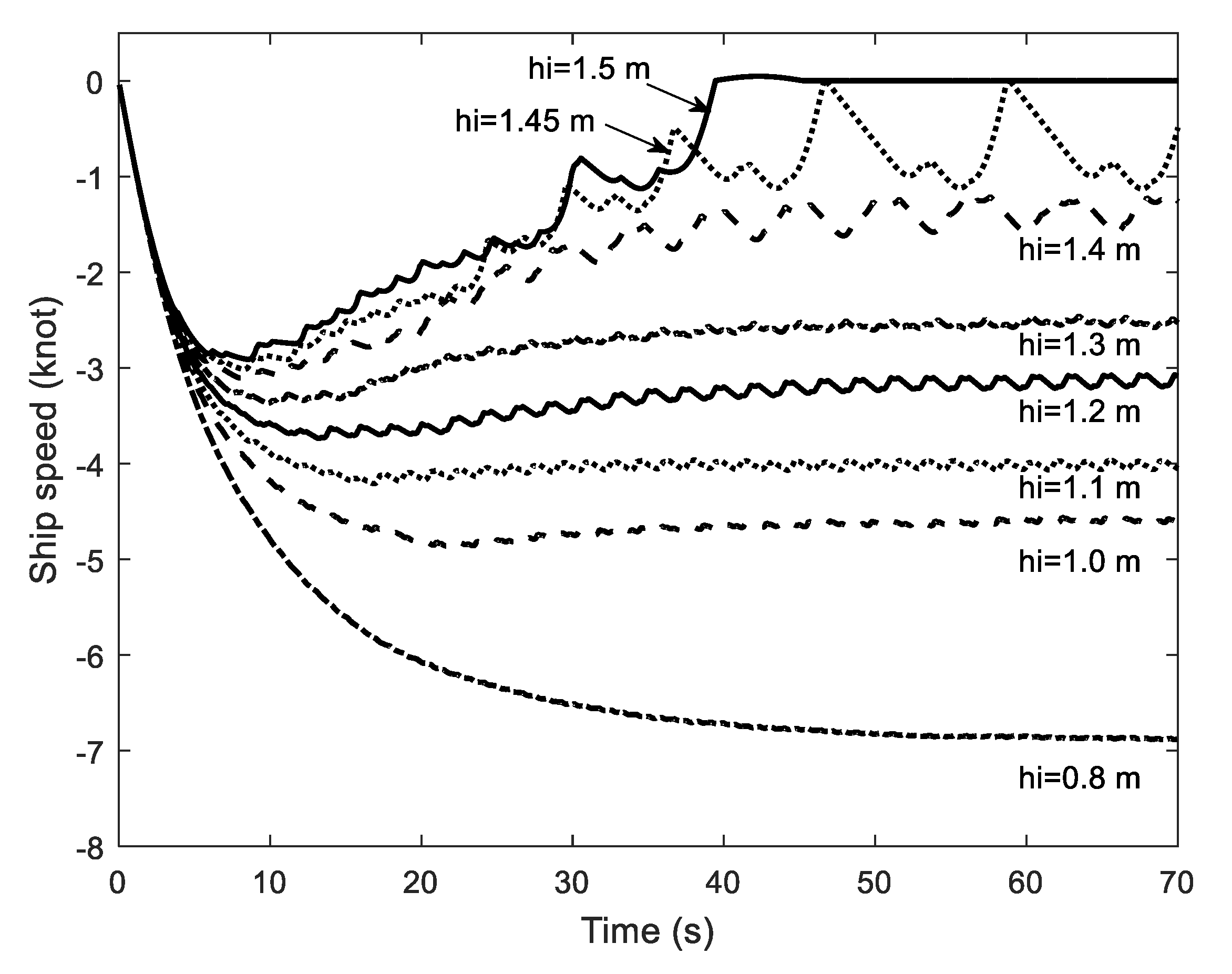
4.5. Comparison of Icebreaking Capability
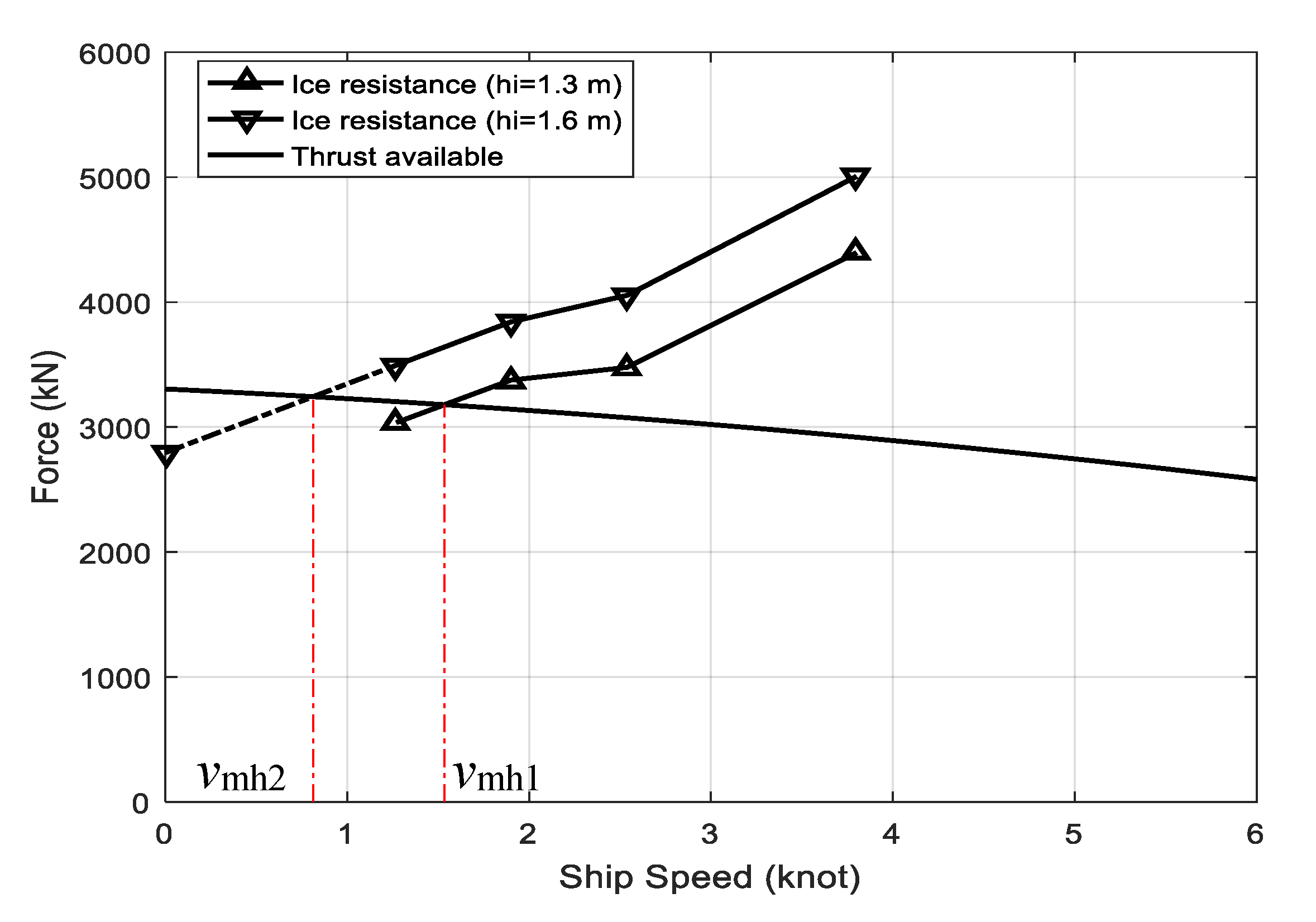
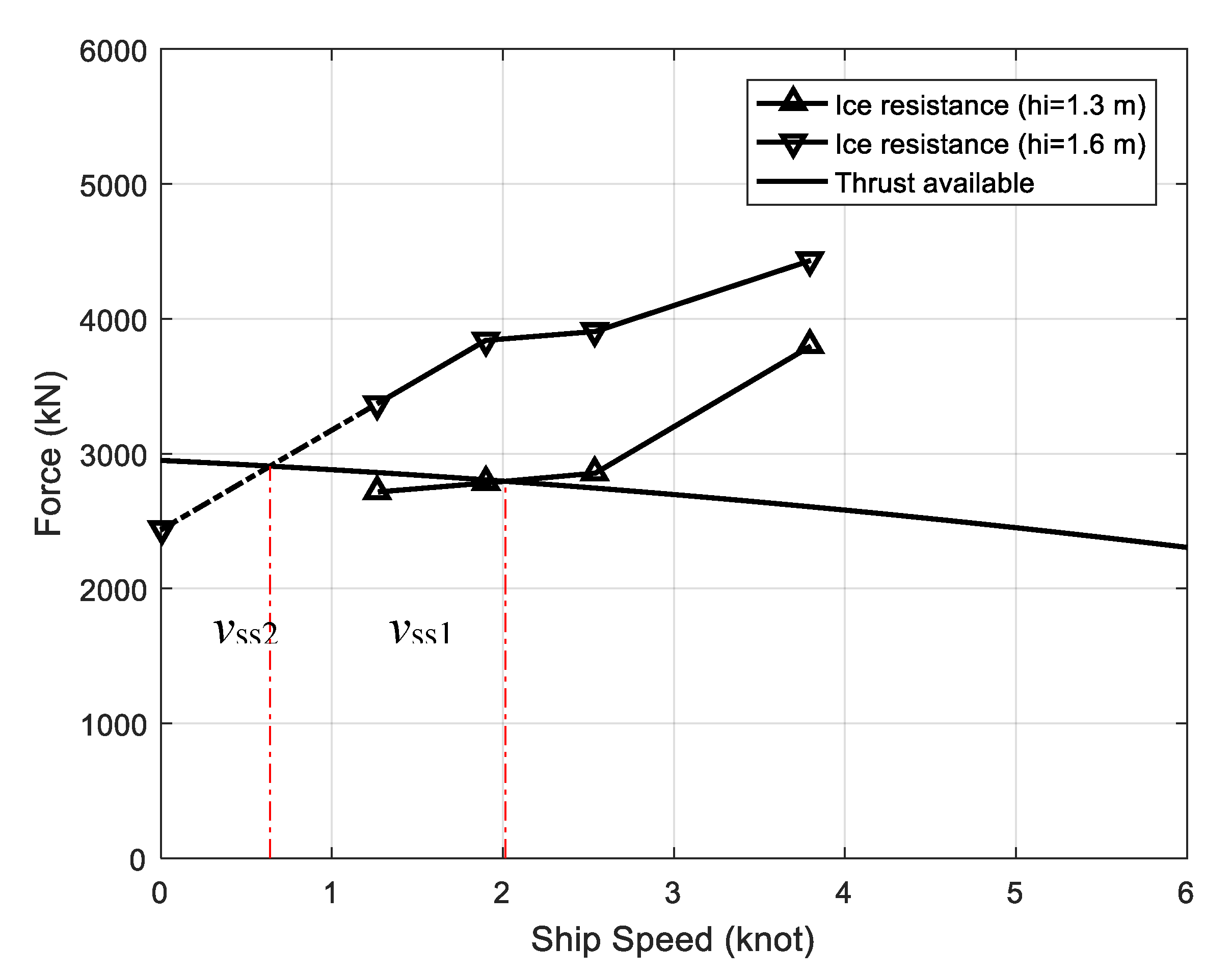
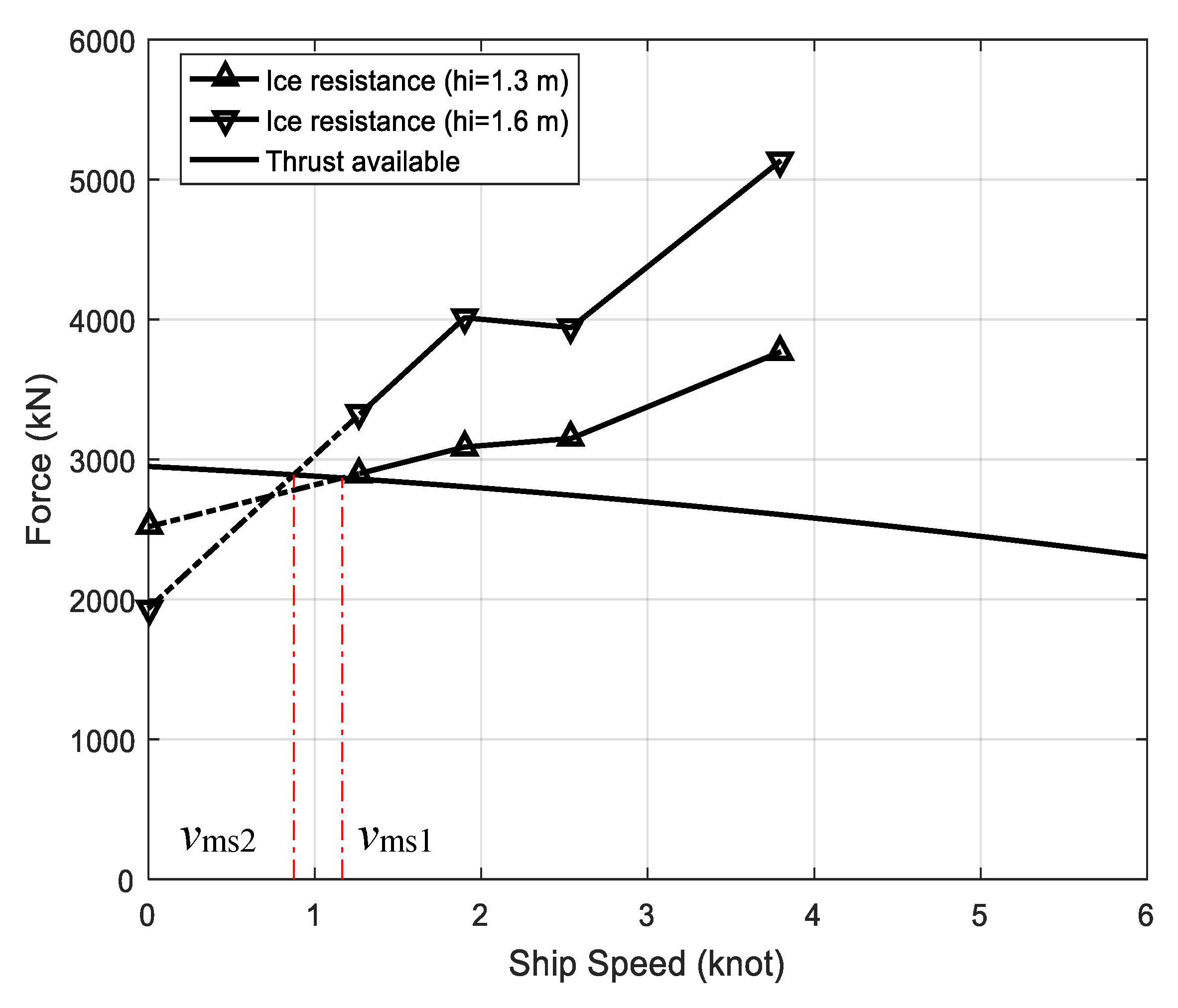
4.5.1. Static Method
4.5.2. Dynamic Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Fbi | Local forces |
| vrel | Relative velocity between the ship and the drifting level ice sheet |
| L | Length of the ship |
| ρi | Ice density |
| ρw | Water density |
| g | Acceleration of gravity |
| B | Width of the hull |
| T | Draught of the hull |
| μ | Friction coefficient between ice and hull |
| Af | Area of the bow |
| vow | Maximum open water speed |
| Tpull | Bollard pull of the ship |
| M | Inertial mass |
| A | Added mass matrix |
| B | Damping term |
| C | Hydrostatic restoring coefficient |
| Fb | Icebreaking force |
| Fs | Ice force due to ice submersion |
| Tnet | Thrust available from propellers |
| Cvs and Cls | Icebreaking radius |
| hi | Thickness of the ice |
| l | Characteristic length of the ice |
| Ei | Elastic modulus |
| γ | Poisson ratio |
| Cf | Ice bending capacity coefficient |
References
- Riska, K. Ship-ice interaction in ship design: Theory and practice. In Encyclopedia of Life Support Systems (EOLSS); Developed under the Auspices of the UNESCO; Eolss Publishers: Oxford, UK, 2010. [Google Scholar]
- Lindqvist, G. A Straightforward Method for Calculation of Ice Resistance of Ships. In Proceedings of the International Conference on Port and Ocean Engineering under Arctic Conditions (POAC), Lulea, Sweden, 12–16 June 1989; pp. 722–735. [Google Scholar]
- Keinonen, A.J.; Browne, R.; Revill, C.; Reynolds, A. Icebreaker Characteristics Synthesis. In Report for the Transportation Development Centre; Report TP 12812E; Transport Canada: Ottawa, ON, Canada, 1996. [Google Scholar]
- Riska, K.; Wilhelmson, M.; Englund, K.; Leiviskä, T. Performance of Merchant Vessels in the Baltic; Research Report No. 52; Winter Navigation Research Board; Helsinki University of Technology: Espoo, Finland, 1997. [Google Scholar]
- Valanto, P. The resistance of ships in level ice. Trans. Soc. Naval Archit. Mar. Eng. SNAME 2001, 109, 53–83. [Google Scholar]
- Liu, J.C.; Lau, M.; Williams, F.M. Mathematical modeling of ice–hull interaction for ship maneuvering in ice simulations. In Proceedings of the 7th International Conference and Exhibition on Performance of Ships and Structures in Ice (ICETECH), Banff, AB, Canada, 16–19 July 2006. [Google Scholar]
- Martio, J. Numerical Simulation of Vessel’s Maneuvering Performance in Uniform Ice; Report No. M-301; Ship Laboratory; Helsinki University of Technology: Espoo, Finland, 2007. [Google Scholar]
- Sawamura, J.; Tsuchiya, H.; Tachibana, T.; Osawa, N. Numerical modeling for ship maneuvering in level ice. In Proceedings of the 20th International Symposium on Ice (IAHR), Lahti, Finland, 14–17 June 2010. [Google Scholar]
- Su, B.; Riska, K.; Moan, T. A Numerical Method for the Prediction of Ship Performance in Level Ice. Cold Reg. Sci. Technol. 2010, 60, 177–188. [Google Scholar] [CrossRef]
- Lubbad, R.; Løset, S. A numerical model for real-time simulation of ship–ice interaction. Cold Reg. Sci. Technol. 2011, 65, 111–127. [Google Scholar] [CrossRef]
- Zhou, L.; Ding, S.F.; Song, M.; Han, Y. A Numerical Model for Towing Operations of Arctic Gravity based Structure in Managed Ice Fields. J. Mar. Sci. Eng. 2020. under review. [Google Scholar]
- Zhou, L.; Chuang, Z.; Ji, C. Ice forces acting on towed ship in level ice with straight drift. Part I: Analysis of model test data. Int. J. Naval Archit. Ocean Eng. 2018, 10, 60–68. [Google Scholar] [CrossRef]
- Su, B. Numerical Predictions of Global and Local Ice Loads on Ships. Ph.D. Thesis, Cesos, Norwegian University of Science and Technology, Trondheim, Norway, 2011. [Google Scholar]
- Zhou, L.; Chuang, Z.; Bai, X. Ice forces acting on towed ship in level ice with straight drift. Part II: Numerical simulation. Int. J. Naval Archit. Ocean Eng. 2018, 10, 119–128. [Google Scholar] [CrossRef]
- Zhou, L.; Riska, K.; Ji, C. Simulating transverse icebreaking process considering both crushing and bending failures. Mar. Struct. 2017, 54, 167–187. [Google Scholar] [CrossRef]
- Juva, M.; Riska, K. On the Power Requirement in the Finnish–Swedish Ice Class Rules; Research Report No. 47; Winter Navigation Research Board: Sweeden and Finland; Helsinki University of Technology Ship Laboratory: Espoo, Finland, 2002. [Google Scholar]
- Zhou, L.; Riska, K.; Moan, T.; Su, B. Numerical modelling of ice load on an icebreaking tanker: Comparing simulations with model tests. Cold Reg. Sci. Technol. 2013, 87, 33–46. [Google Scholar] [CrossRef]
- Zhou, L.; Gao, J.; Xu, S.; Bai, X. A numerical method to simulate ice drift reversal for moored ships in level ice. Cold Reg. Sci. Technol. 2018, 152, 35–47. [Google Scholar] [CrossRef]
- Timco, G.W.; Weeks, W.F. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]









| Parameter | Value | Unit |
|---|---|---|
| Beam o.a. | 44 | m |
| Length p.p. | 259.2 | m |
| Fore draught | 15.00 | m |
| Midship draught | 15.00 | m |
| Aft draught | 15.00 | m |
| Length by waterline | 270 | m |
| Wetted surface area | 16,604 | m2 |
| Displacement | 136,385 | m3 |
| block coefficient | 0.765 | - |
| Waterplane area coefficient | 0.892 | - |
| Midship section coefficient | 0.995 | - |
| Longitudinal center of buoyancy (from Lpp/2) | 7.593 | m |
| Test No. | Ice Thickness (m) | Tanker Speed (kn) | Operation Mode |
|---|---|---|---|
| 11 | 1.3 | 1.27 | Ahead running |
| 12 | 1.3 | 1.90 | |
| 13 | 1.3 | 2.54 | |
| 14 | 1.3 | 3.80 | |
| 21 | 1.6 | 1.27 | |
| 22 | 1.6 | 1.90 | |
| 23 | 1.6 | 2.54 | |
| 24 | 1.6 | 3.80 | |
| 15 | 1.3 | 1.27 | Astern running with operating propellers |
| 16 | 1.3 | 1.90 | |
| 17 | 1.3 | 2.54 | |
| 18 | 1.3 | 3.80 | |
| 25 | 1.6 | 1.27 | |
| 26 | 1.6 | 1.90 | |
| 27 | 1.6 | 2.54 | |
| 28 | 1.6 | 3.80 |
| Value | Unit | |
|---|---|---|
| Elastic modulus | 2000 | MPa |
| Bending strength | 500 | kPa |
| Crushing strength | 2300 | kPa |
| Poisson ratio | 0.3 | |
| Ice-hull friction coefficient | 0.1 | |
| Water density | 1025 | kg.m−3 |
| Ice density | 900 | kg.m−3 |
| Gravity acceleration | 9.81 | m.s−2 |
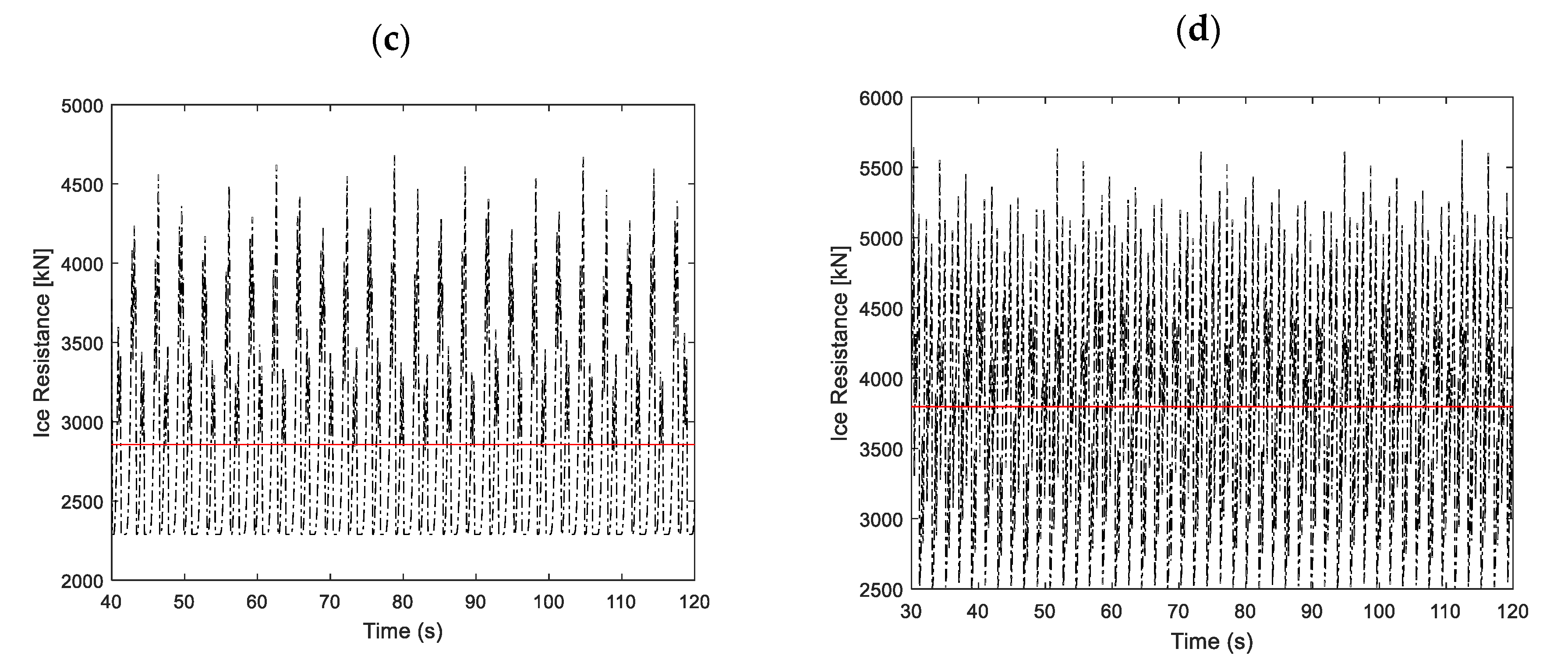
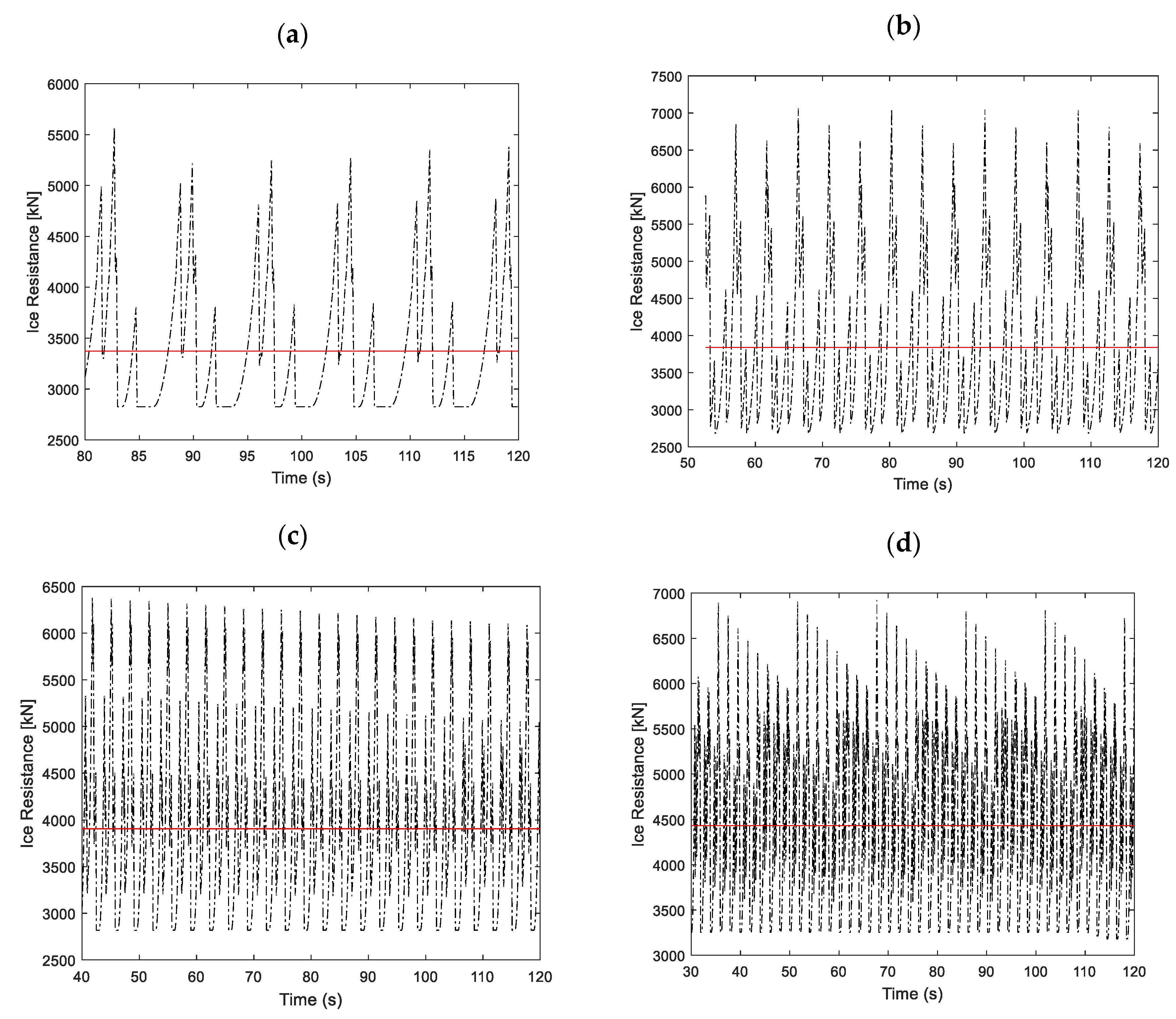
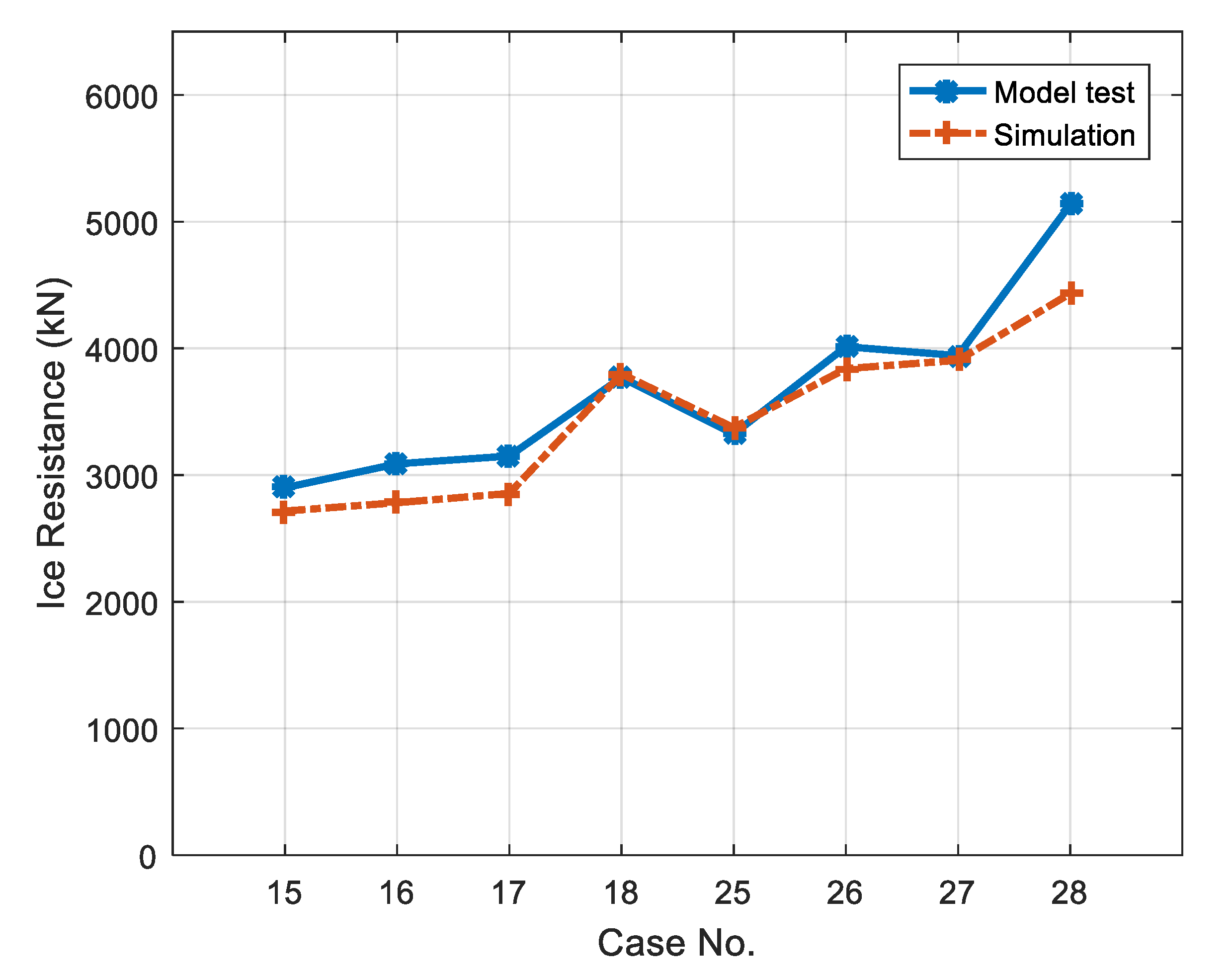
| Test No. | Model Test (kN) | Simulation (kN) | Absolute Error (%) | Operation Mode |
|---|---|---|---|---|
| 11 | 3036 | 2953 | 2.7 | Ahead running |
| 12 | 3376 | 2996 | 11.3 | |
| 13 | 3478 | 3119 | 10.3 | |
| 14 | 4396 | 4133 | 6.0 | |
| 21 | 3495 | 3782 | 8.2 | |
| 22 | 3842 | 4268 | 11.1 | |
| 23 | 4055 | 4362 | 7.6 | |
| 24 | 5007 | 5172 | 3.3 | |
| 15 | 2900 | 2716 | 6.3 | Astern running with operating propellers |
| 16 | 3089 | 2782 | 9.9 | |
| 17 | 3150 | 2855 | 9.4 | |
| 18 | 3770 | 3798 | 0.7 | |
| 25 | 3324 | 3374 | 1.5 | |
| 26 | 4013 | 3840 | 4.3 | |
| 27 | 3943 | 3906 | 0.9 | |
| 28 | 5136 | 4433 | 13.7 |
| Items | Ahead Running | Astern Running |
|---|---|---|
| Model test (m) | 1.52 | 1.47 |
| Simulation by static method (m) | 1.53 | 1.52 |
| Simulation by dynamic method (m) | 1.45 | 1.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Diao, F.; Song, M.; Han, Y.; Ding, S. Calculation Methods of Icebreaking Capability for a Double-Acting Polar Ship. J. Mar. Sci. Eng. 2020, 8, 179. https://doi.org/10.3390/jmse8030179
Zhou L, Diao F, Song M, Han Y, Ding S. Calculation Methods of Icebreaking Capability for a Double-Acting Polar Ship. Journal of Marine Science and Engineering. 2020; 8(3):179. https://doi.org/10.3390/jmse8030179
Chicago/Turabian StyleZhou, Li, Feng Diao, Ming Song, Yue Han, and Shifeng Ding. 2020. "Calculation Methods of Icebreaking Capability for a Double-Acting Polar Ship" Journal of Marine Science and Engineering 8, no. 3: 179. https://doi.org/10.3390/jmse8030179
APA StyleZhou, L., Diao, F., Song, M., Han, Y., & Ding, S. (2020). Calculation Methods of Icebreaking Capability for a Double-Acting Polar Ship. Journal of Marine Science and Engineering, 8(3), 179. https://doi.org/10.3390/jmse8030179





