Abstract
Mooring systems exhibit high failure rates. This is especially problematic for offshore renewable energy systems, like wave and floating wind, where the mooring system can be an active component and the redundancy in the design must be kept low. Here we investigate how uncertainty in input parameters propagates through the mooring system and affects the design and dynamic response of mooring and floaters. The method used is a nonintrusive surrogate based uncertainty quantification (UQ) approach based on generalized Polynomial Chaos (gPC). We investigate the importance of the added mass, tangential drag, and normal drag coefficient of a catenary mooring cable on the peak tension in the cable. It is found that the normal drag coefficient has the greatest influence. However, the uncertainty in the coefficients plays a minor role for snap loads. Using the same methodology we analyze how deviations in anchor placement impact the dynamics of a floating axi-symmetric point-absorber. It is shown that heave and pitch are largely unaffected but surge and cable tension can be significantly altered. Our results are important towards streamlining the analysis and design of floating structures. Improving the analysis to take into account uncertainties is especially relevant for offshore renewable energy systems where the mooring system is a considerable portion of the investment.
1. Introduction
Mooring systems play an important role in assuring the safe operation (to life and to the environment) of floating structures like oil and gas (O&G) platforms. The failure rates of mooring cables for O&G installations are surprisingly high. Brindley and Comley [1] analyzed the times to failure of mooring cables for semisubmersible mobile offshore drilling units (MODUs) operating in the North Sea during the years 1996–2005, concluding that there is an average time of 24 operational years per failure of single lines and 112 years for multiple lines. These numbers should be compared with the industry target times of 10,000 and 100,000 operational years [2]. The reasons for the failures are widespread. Kvitrud [3] reports on 16 line failures in the Norwegian Continental Shelf between 2010 and 2014. The failures were due to fatigue (four cases), overload (six cases), mechanical damage (four cases), and manufacturing errors (two cases). In other words, more than 60% of the failures were due to design errors. While a mooring failure of an O&G platform can cause severe consequences, often the catastrophic effects are prevented due to high redundancy in the mooring design.
In floating renewable energy technologies, due to their nature, mooring systems are not as critical to life and environment. They are, however, a significant part of the total budget (18%–30% [4,5], compared to 2% [4] for O&G). Due to the large portion of cost associated with the mooring system, the level of redundancy in the mooring design is kept low. Hence, failures of mooring systems have caused the loss of several offshore renewable energy prototypes [6].
To reduce the cost and optimize the performance of mooring systems, it is of interest to know which parameters have the greatest contribution to the final design and to the dynamics of the structure they keep on station. We also need to understand how uncertainty in input parameters propagates through the mooring system and affects the design and dynamic response. Two parameters that are subjected to uncertainty and can have a large influence on the dynamics of mooring systems are the hydrodynamic coefficients of mooring cables and the position of the anchors. It is hard, and most of the time impossible, to determine the actual values of hydrodynamic coefficients in full scale prototypes; as for the anchors, it is difficult to ensure that they are positioned exactly as specified during design, usually being allowed an installation tolerance around the expected position.
Hydrodynamic coefficients, being determined in small scale models, have the additional issues of their values suffering from scale effects and of depending on the experimental methods applied. For example, for the added mass coefficient of a cable used in Morison’s formulation for hydrodynamic forces, the software Orcaflex [7] uses the value 1.0 for chains, while in Marin’s aNySIM model [8] the default value is 0.6.
It is on the impact of hydrodynamic coefficients and anchor position on the dynamics of mooring cables and floating structures that we will focus our study. In Section 4.2 we will analyze the impact of uncertainty in the hydrodynamic coefficients in the peak tension of a catenary mooring system. Afterwards, in Section 4.3, we will analyze the impact that errors in anchor placement have on the dynamics of a floating buoy and respective mooring cable tension. To simulate the dynamics of cables and floating structures we will use numerical models, described in Section 2, while forward uncertainty propagation will be based on generalized Polynomial Chaos (gPC).
Generalized Polynomial Chaos, described in Section 3, provides a surrogate model, based on polynomial expansions, for stochastic processes. It was introduced by Norbert Wiener in 1938 as Homogeneous Chaos [9], using expansions based on the Normal Distribution and expanded by Xiu and Karniadakis in 2002 to generalized Polynomial Chaos [10] to include several other probability distribution laws. Its strength is the ability to, for the same inputs, provide almost the same results as the original model but at a fraction of the computational cost and time. Furthermore, for problems with low dimensionality (small number of uncertain inputs) gPC is much faster in converging to the solution than traditional methods, such as the Monte Carlo (MC) method. Generalized Polynomial Chaos is a well established procedure in uncertainty quantification and sensitivity analysis of computational fluid dynamics (CFD) simulations, see e.g., [11,12] and the references therein. It has been applied to study, for example, the dynamics of vehicles [13] and train wagons [14]. For renewable energy we note the study of wind turbines [15]. In coastal engineering gPC has been used to study the sensitivity of coastal inundation to parameters like Manning’s number [16,17], while in ocean engineering the method has been applied to phase-averaging spectral wave modeling [18], water wave propagation and transformation [19], wave scattering from an ice floe [20], and the motions of a heaving cylinder [21] in irregular waves. It is also seeing applications in the field of marine renewable energy and moored structures, in the prediction of extreme loads on wave energy converters [22], and long-term extreme responses of moored floating structures [23].
For completeness, we will first illustrate the use of gPC to the case of a simple taut linear string in Section 4.1. The most important results of our research will be summarized in Section 5.
2. Numerical Models
2.1. Mooring Equations
Let us consider the equation of perfectly flexible cables [24], applied to a cable of length , in a physical domain and a time domain , subject to initial and Dirichlet boundary conditions, Equation (1):
where ml is the mass per unit length of the cable, is the position of the cable point s, is the unstretched line coordinate, is the tension magnitude, ϵ is the extension, and are the external forces acting on the cable. is the initial deformation of the cable and and represent the boundary conditions at the ends of the cable. The external forces, , include the effects of buoyancy, weight, hydrodynamic forces (added mass and viscous drag), and ground forces (contact forces and Coulomb drag). The added mass and the drag forces are computed via Morison’s equations [25] based on the relative acceleration and velocity between the fluid and the cable, Equation (5):
and the effect of weight and buoyancy computed using Equation (6)
where fm is the added mass force, Ac is the cable cross section area, ρw is the fluid mass density, arf is the relative cable-fluid acceleration, Cm is the cable added mass coefficient, fd is the viscous drag force, D is the cable diameter, Cdt is the cable tangential drag coefficient, Cdn is the cable normal drag coefficient, vr,t is the relative fluid-cable tangential velocity, vr,n is the relative fluid-cable normal velocity, fb is the submerged weight of the cable, ρc is the mass density of the cable material, and g is the acceleration of gravity.
Interaction of the cable with the ground is modelled using a spring-damper system in the normal direction, Equation (7a), and a Coulomb friction model in the tangential direction, Equation (7c). The spring-damper system applies stiffness and damping forces when the cable is setting down, but when the cable is being lifted it applies only stiffness forces.
in which fc,z is vertical ground force, fc,xy is the horizontal ground force, K is the soil’s stiffness per unit area, rz is the height of the cable, zg is the height of the sea-bottom, ξ is the soil’s normal damping ratio, vz is the vertical component of the velocity of the cable, vx is the component of the velocity of the cable in the x direction, vy is the component of the velocity of the cable in the y direction, vc is the speed of fully developed friction force magnitude, and μ is the soil’s Coulomb friction coefficient.
2.2. Numerical Mooring Model
The dynamics of mooring cables are solved using the numerical code MooDy, introduced in Palm et al. [26]. MooDy solves Equation (1) using an hp-adaptive discontinuous Galerkin (DG) method. In doing so, the equation is first reformulated to be cast in conservative form. The DG method allows discontinuities across the element boundaries, using a numerical flux to couple elements together. This makes the DG method locally conservative and a good candidate for problems involving shocks, such as snap loads. A DG cable is illustrated in Figure 1, where the elements are approximated using a basis made up of Legendre polynomials (top right corner), and the numerical flux is made up of an approximate Riemann solver (bottom right corner), which in MooDy is the local Lax–Friedrich flux. For smooth solutions, MooDy exhibits convergence rates of () [26]. This allows high-resolution solutions using few degrees-of-freedom. The model advances in time using the explicit third-order strong-stability-preserving Runge–Kutta scheme.
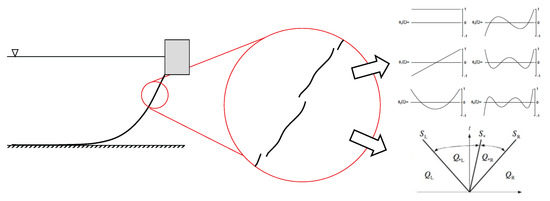
Figure 1.
Outline of the high-order DG modeling approach. The cable is discretised into finite elements of size h with approximation order p. The jumps are exaggerated for illustrative purposes.
When coupled to external codes, such as floating body solvers, at each rigid body time step, MooDy updates the position of the mooring fairlead and returns the corresponding mooring force. As the time step required for the cable dynamics is smaller than for the body motion, several substeps are performed in the mooring solver between each rigid body time step. Please note that in MooDy, the hydrodynamic forces of added mass and drag, Equation (5), are presently computed under the assumption of quiescent water. For details of MooDy please see [26,27].
2.3. Floating Body Model
In the cases presented here concerning moored floating structures, the dynamics of the floating structure are modeled using linear potential flow theory and Cummins’s Equation [28], Equation (8):
with being the generalized mass matrix of the the floating body, the added mass matrix at infinity frequency, the radiation impulse response function, the hydrostatic stiffness matrix, the vector of external forces, and , , and , respectively, the displacement, velocity, and acceleration vectors. The vector of external forces, , contains any wave excitation forces, and mooring forces, . The hydrodynamic coefficients are typically computed using a boundary element method (BEM) code for potential flow, such as WAMIT [29] or Nemoh [30].
The code used to solve Cummins’s Equation, or the dynamics of the floating structure, was WEC-Sim, a time-domain multibody dynamics model, developed by NREL and Sandia [31]. To simulate nonlinear mooring dynamics, WEC-Sim has to be coupled to external mooring simulation codes. The standard code coupled to WEC-Sim for mooring dynamics is the lumped-mass model MoorDyn [32]. However, the code we use for mooring dynamics is MooDy. The coupling of MooDy to WEC-Sim was introduced in [26] and further validated in [33].
3. Uncertainty Quantification
3.1. Generalized Polynomial Chaos
Consider a mathematical model f with uncertainty in one of its input variables. We can represent f by , where is the vector of deterministic input variables and Z is the input subjected to uncertainty. Z is a random variable that can take values in , from the sample space of possible outcomes Ω, in the form of events denoted by , with an associated probability P. This is denoted by . Using the property that continuous function in with bounded variation can be expressed as an infinite series, gPC provides a polynomial expansion surrogate model to :
in which are the polynomial coefficients and is the set of polynomial basis functions. For optimal convergence of to the results of the original model , the basis functions should be selected based on the probability distribution of Z according to the Wiener–Askey scheme [10]. Because Equation (9) is an infinite sum, in practical applications it must be truncated at specified polynomial degree p, being represented by a series approximation:
Usually, there is no prior knowledge about the minimum required degree of the polynomial approximation, which needs to be tuned by trial and error. For the particular case of smooth solutions, the coefficients decay rapidly with increasing order p, providing a means to determine the optimal value for p. An important feature of gPC is that the coefficients encode information about the moments of the probability distribution of the results. For example, is a scaled value of the mean, and the variance can be obtained by summing the squares of the set of coefficients in the expansion.
For problems with d independent input random variables, , in Equations (9) and (10) is replaced by a tensor product of polynomials corresponding to each random variable
where is the vector of input random variables, is a multi-index such that and , and is the polynomial basis function of the variable of degree .
3.2. Stochastic Collocation Method
The application of gPC to a mathematical model can take two different forms: the Stochastic Galerkin Method and the Stochastic Collocation Method [34]. We will be using the stochastic collocation method because it is a nonintrusive method, so it does not require any knowledge of the mathematical model under study. For the computation of the gPC model , we only need to postprocess the results of simulations using the mathematical model at preselected values of the uncertain input . The points where is to be evaluated depending on the method chosen to determine the coefficients . The two methods we will use are the projection method and the regression method.
In the projection method, the coefficients are determined by the inner product of and the polynomial basis, , with respect to the probability density function (PDF) of the random variable, , Equation (12):
Equation (12) is solved using quadrature rules, such as Gauss quadrature, which provide the points where the model is to be evaluated and the quadrature weights, . Because multivariable gPC is formulated as a tensor product, the number of points where the numerical model needs to be evaluated grows exponentially with the number d of random input variables: the dimension of the problem. This is known as the curse of dimensionality. For it is convenient to employ sparse quadratures, such as Smolyak’s quadrature [34]; however, for , even sparse quadratures can require hundreds or thousands of costly model evaluations. In this situation it is more efficient to apply a regression method or methods designed for high scalability with dimensions, e.g., [35].
In the regression method, the coefficients are determined by minimizing the error of fitting the values of the coefficients to the results of the numerical model, at randomly sampled values of . One of the procedures to fit the values of the coefficients is the Least Angle Regression (LAR) algorithm [36], which computes a set of candidate solutions and chooses the one with the smallest error. For the best results, the random should be sampled with a method which tries to cover the sample space evenly.
In multivariate models, we can limit the interaction between the different univariate polynomials in the tensor product by setting the value of the q-norm. A q-norm of 1 allows the tensor product of any set of univariate polynomials to reach the maximum selected polynomial order; decreasing the q-norm, until the minimum value of zero, decreases the maximum polynomial order allowed for products of univariate polynomials, reducing the total number of polynomial terms.
3.3. Model Equations with Random Input Variables
The stochastic equation of cable dynamics follows directly from Equation (1), by introducing a set of random variables , Equation (16):
We obtain the stochastic Cummins’s equation, Equation (17), from Equation (8) in a similar way as Equation (16):
3.4. Methodology
We applied the following methodology throughout all the cases presented in the article:
- select the process to be studied;
- select a physics-based mathematical model for the process;
- choose which parameters of the model are deterministic and which are random variables;
- define the values of the deterministic parameters;
- choose appropriate probability distributions for the random variables;
- choose the method to determine the gPC model coefficients (quadrature or LAR)
- compute (for the case of quadrature) or sample (for the case of LAR) the values of the input random variables where the physics-based model is to be evaluated;
- evaluate the physics-based model at the previously defined values of the random variables;
- apply the chosen method (quadrature or LAR) to the results of point 8 to obtain the coefficients of the gPC model;
- use the gPC model of the physics-based model to evaluate large samples of the random variables and build probability density functions.
For the computation of the gPC model we use UQLab’s version 1.3.0, Polynomial Chaos Expansions Module [36]. The probability density functions are estimated with the Kernel Density Estimation method with a Gaussian kernel, using MATLAB’s ksdensity function, with a logarithmic boundary correction. For solving the Cummin’s Equation (8) we employ WEC-Sim version 3.0.0, commit 27cfb3b [31].
4. Case Studies
4.1. Linear String
In this case we will study the effect of uncertainty in the tension and in the mass per unit length of a linear string in its geometry, at a certain time after being released from an unsteady position. The equation of motion of a taut linear string, Equation (18), is obtained from Equation (1) under the assumptions of constant extension, tension, mass per unit length, and small transverse displacements [37]:
with x the abscissa of the cable and y the ordinate. For a cable with length L, fixed at both ends, , and zero initial velocity, , the solution of Equation (18) is [37]:
where are the Fourier series coefficients of the function describing the initial displacement , and c is the transverse wave celerity, . For an initial displacement in the shape of a half sine, Figure 2a, we have , and Equation (19) becomes:
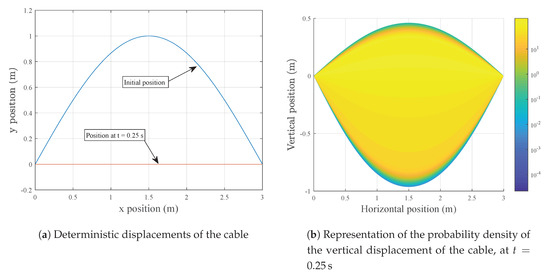
Figure 2.
Example of a taut linear cable.
There are six variables influencing the results of Equation (20)—A, L, x, T, m1, and t—of which only two are subjected to uncertainty: T and m1. For the reference deterministic case, against which we will compare the results of uncertainty quantification, we choose for the variables the values presented in Table 1. The reference values for L, T, and m1 were selected so that the cable would have an oscillation period of 1 s and that at odd multiples of 0.25 s it would be on a perfectly straight line, as illustrated in Figure 2a. For simplicity, we assign uniform distributions to T and ml: , .

Table 1.
Linear cable properties.
Because the two input distributions are uniform, following the Wiener–Askey scheme [10] for optimal convergence, we use Legendre polynomials for the basis functions. Since the uncertainty dimension is , we use the full quadrature to solve Equation (12). In addition, with , there is no need to limit the number of polynomial coefficients, so we choose a q-norm of 1. Thus, we use quadrature points to construct the gPC. All the results presented below are for a time instant t = 0.25 s.
Now we will use gPC to estimate the probability density function of the position of the cable. For that, we generated 500,000 random samples of T and ml and evaluated them in the gPC model. Even though we are not really concerned with the physics of the problem, let us analyze the results of the gPC computations. In Figure 2b, we illustrate the density function for the whole cable using p = 6. We can immediately notice two things: first, in spite of the simple distributions of T and ml, the distribution of the cable position is far from simple. Second, there is a wide range of cable positions significantly different from the deterministic one, which have a reasonable high probability of occurrence.
We use this simple case to illustrate the convergence of the gPC mooring cable surrogate model. Figure 3a illustrates how the PDF of position evolves as p is increased, for the midpoint of the cable (x = 1.5). For p = 1 we obtain a quite crude PDF, but for p = 2, the approximation is reasonable. A polynomial order p = 3 has practically converged to the final PDF. For polynomial p > 4 it is almost impossible to tell the plots apart, and so the PDF has converged. We find that the expected value of the position of the midpoint of the cable, computed using gPC, is 9.39 × 10−2 m, and the variance is 1.26 × 10−1 m2.
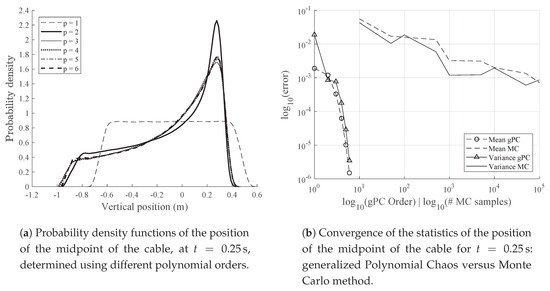
Figure 3.
Convergence of the gPC method for the taut linear cable case.
In Figure 3b we can see the evolution of the error in the mean and in the variance of the solution of Equation (20) at the midpoint, as a function of the polynomial order and number of Monte Carlo samples. The error is defined as the absolute value of the difference between the mean or variance at a certain order (or number of samples) and the value at a polynomial order , for gPC, or at 500,000 samples, for the MC method. Using gPC, the error decreases exponentially with increasing order p, whereas using the MC method the error decreases algebraically. Moreover, the error in the gPC method decreases monotonically, while in the MC method it does not. The large error in the first point of the variance plot in gPC occurs because the variance can only be computed for polynomial order p > 2.
4.2. Oscillating Mooring Cable
In this case we analyze the influence of uncertainty in the hydrodynamic coefficients of a mooring cable (added mass coefficient, Cm, normal drag coefficient, Cdn, and tangential drag coefficient, Cdt) on the tension at its upper end. The simulations reproduce experiments reported by Lindahl [38], whose data is available through ref. [39]. The experimental set-up is illustrated in Figure 4. It is composed of a submerged chain, with one end anchored to the bottom of a concrete tank and the other attached to a disk slightly above the water. The disk moves the top end of the chain in a circular motion, with a radius rm = 0.20 m, for two different periods: Tr = 1.25 s and Tr = 3.50 s. A summary of the relevant properties of the cable and of the numerical model is presented in Table 2. The cable was discretised using Nel = 10 elements of order p = 5, with a limitation on the time-stepping that the Courant–Friedrichs–Lewy value should not exceed 0.45.
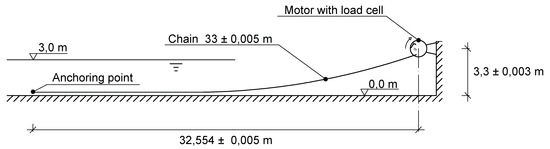
Figure 4.
Experimental set-up for the oscillating mooring cable case.

Table 2.
Deterministic or constant parameters of the cable and of the experimental set-up.
Figure 5 shows a comparison between numerical and experimental tension at the fairlead. There is a general good agreement. The oscillations in low tension regions are exaggerated in the numerical model. This is due to (i) the problem being ill-posed at slack conditions [40] and (ii) the ground interaction being modeled with the traditional elastic seabed approach (the so-called spring-mattress method), which is known to introduce spurious oscillations [41].
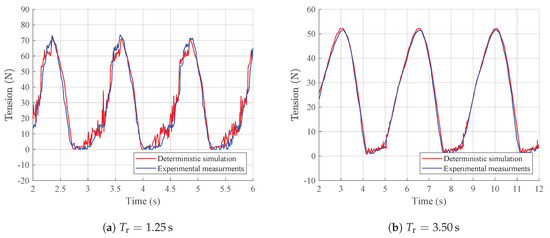
Figure 5.
Numerical simulation of the tension at the fairlead compared to experimental data from [39].
For each period, we analyze four different scenarios: one analyzing the effects of uncertainty on all the coefficients at the same time, and three which analyze the effects of uncertainty in each coefficient individually. The first scenario gives us insight about how general uncertainty in cable properties affects the cable dynamics, while the other scenarios give us information about the most relevant coefficients affecting the cable dynamics.
As there is very little data on the distribution of the hydrodynamic coefficients, we assume a uniform distribution centered around the deterministic values reported in [38], with a parameter range of half the mean value, Table 3. The values of Cm, Cdn and Cdt relate to the cable’s geometry and surface roughness and these coefficients are, therefore, dependent. However, because there is no data describing the correlation between the different coefficients to enable a multivariate probability modeling, and to simplify the analysis, we assumed that they are independent.

Table 3.
Parameters of the probability distributions of the hydrodynamic coefficients.
The polynomial coefficients for the gPC models of the cable dynamics were computed using a polynomial degree p of 5 and the full quadrature method (i.e., quadrature points are used to construct the gPC). Then, for each of the four scenarios, 3000 random samples of coefficient values were drawn from their distributions and evaluated in the gPC model, to build the probability density functions.
The results of the simulations are presented in Figure 6 for the case of Tr = 1.25 s and in Figure 7 for the case of Tr = 3.50 s. The most striking result is that, for both oscillating periods, despite the relatively large uncertainty in the coefficient values (50%), the range of variation in the tension cycles and maximum tensions is not very large. It is mostly the spread of tension values in the lower tension regions that is affected. This is more surprising in the case with an oscillating period Tr = 1.25 s, which shows snap loads. Snap loads, being generated by quick cable motions, are more dependent on the hydrodynamic coefficients, but, they nevertheless seem to be little influenced by the uncertainty.
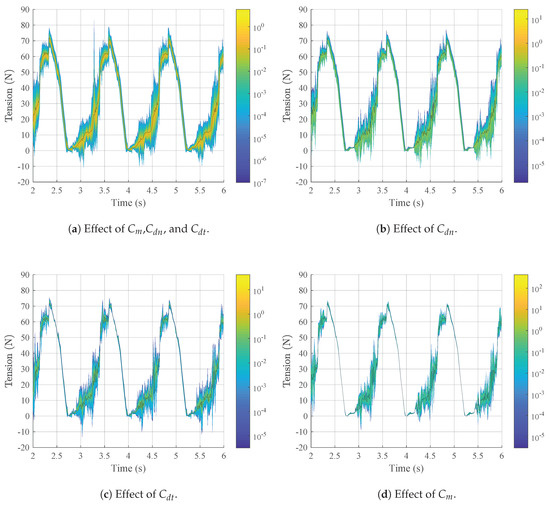
Figure 6.
Representation of the probability density of cable tension as a function of time, for Tr = 1.25 s, together with the mean tension (black line).
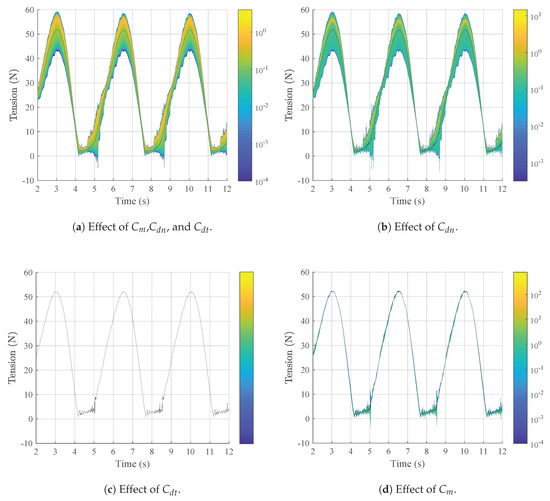
Figure 7.
Representation of the probability density of cable tension as a function of time, for Tr = 3.50 s, together with the mean tension (black line).
In all plots it is visible that when the tension is close to zero, the probability density and the confidence intervals extend slightly to negative values. This is not possible in a flexible cable, as it cannot sustain compression. However, it is well-known that in the absence of bending stiffness, Equation (1) is ill-posed in slack conditions [40]. This gives rise to numerical oscillations when the tension is close to zero, leading to a large variability of the results in this region. Because of this variability, it is difficult for any regression or surrogate model (like the gPC method) to accurately predict the trend of the original model.
For both oscillation periods—Tr = 1.25 s and Tr = 3.50 s—the maximum tensions happen when all the coefficients—Cm, Cdn and Cdt—are varied simultaneously: around 79 N for Tr = 1.25 s and around 69 N for Tr = 3.50 s. When the coefficients are varied individually, changes in Cdn lead to the highest peak tensions, which are equal to, or only slightly lower than, when the coefficients are varied simultaneously: around 75 N for Tm = 1.25 s and around 69 N for Tm= 3.50 s. Varying Cdt and Cm leads to the lowest peak tensions: 73 N to 74 N for Tm = 1.25 s and around 52 N for Tm = 3.50 s. Another result that is common to both oscillating periods is the spread of tension values, which is largest when all the coefficients are varied simultaneously, followed by when only Cdn is varied. Variations in Cdt and Cm cause significantly lower spread of the tension values. In fact, for Tm = 3.50 s, varying Cdt causes no noticeable changes in the tension values, so it is not possible to compute the PDF.
Focusing on the case with oscillating period Tm = 1.25 s, we can see that there is a higher dispersion of the tension when its value is close to 0 N and increasing, than when at its maximum and decreasing. This is probably caused by the instability of the equation of perfectly flexible cables, which becomes ill-posed when the tension is zero, leading to numerical oscillations. In spite of, as mentioned above, there being a larger dispersion of tension values when all the coefficients are varied simultaneously, looking at Figure 6, we see that, in the low tension region, the probability densities are generally higher when the coefficients are varied individually. This means that, although a wider range of tension values is possible when all the coefficients are varied simultaneously, extreme values are less likely to happen in this case than when the coefficients are varied individually. This points to a possible smoothing effect of the variation of the coefficients over one another, something that requires a deeper investigation.
For the oscillating period Tm = 3.50 s, the differences between the four scenarios are more marked than for Tm = 1.25 s. Variations in Cm have limited influence in the tension, and changes in Cdt have no effect at all; therefore, it was not possible to build a PDF for this case. It is variations in Cdn that cause most of the variations in the tension, as can be seen in Figure 7a,b. In contrast to the case with the oscillation period Tm = 1.25 s, for Tm = 3.50 s, the probability density and the mean have a smooth evolution in time.
Another way to study the impact of the hydrodynamic coefficients is through variance-based sensitivity analysis, which provides a global sensitivity analysis. A graphical representation of this is illustrated in Figure 8, for the scenario where all the coefficients are varied simultaneously. This figure shows the approximate contribution of each hydrodynamic coefficient to the variance of the tension as a function of time. It is based on the Total Sensitivity Indexes (TSI) suggested by Sobol, computed using the gPC coefficients, as described in [14,42]. In Figure 8, the TSIs are represented by their magnitude relative to each other like in [43], instead of their absolute value. For both rotation periods, Cm and Cdt have the greatest influence when the tension is close to 0 N. Cm has similar contributions in Tr = 1.25 s and in Tm = 3.50 s. For Tm = 1.25 s Cdt dominates in the low tension region, while Cdn dominates during the high tension part of the cycle. For Tm = 3.50 s Cdn dominates almost the entire time, with the exception of very short periods, right before the cable goes slack, when Cm dominates briefly.
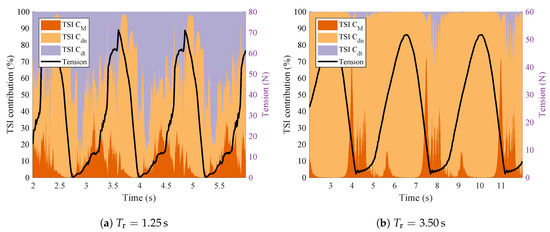
Figure 8.
Approximate relative contribution of each coefficient to the variance of the tension, together with the plot of the mean tension.
This analysis is in line with what was seen before. We have Cdn playing a major role when the tension is higher, because the cable is moving faster. When the tension is lower, Cm and Cdt have a greater, or even the greatest, contribution to the results. In both cases, Cdn seems to be the leading coefficient contributing to the value of the maximum tension. Since Cm and Cdt are of greatest importance when the tension is close to 0 N, it might be that their contribution is mostly to the stability of the numerical model, rather than to the tension, in a physical sense. Another hypothesis is the geometry of the catenary itself. In slack mooring cables, tangential motions happen mostly either in the very upper parts of the cable near the fairlead or on the portions of the cable that are lying on the sea-floor and dragging along it. So these results might also mean that when the tension is low, the dynamics of the cable might be dominated by the portions of the cable suspended immediately after the fairlead or those portions interacting with the sea-floor.
From what was presented above we can draw some important results, at least for the cases analyzed. First, in the simulation of cable dynamics, it seems to be more important to select an appropriate value of the normal drag coefficient, Cdn, than any other coefficient. Although it has been found in [44,45] that the hydrodynamic coefficients control the dynamics of submerged cables, the extent to which each of them does is not so well understood. This has now been made possible using gPC, which allowed thousands of values to be tested quickly. The relative importance of the tangential drag coefficient, Cdt, and of the added mass coefficient, Cm, depends on the period of the excitation: for shorter periods, Cdt has more influence than Cm, while for longer periods, the opposite happens. In other words, Cdt has more importance for fast motions, whereas Cm has more importance for slow motions. This happens because the drag forces depend on the square of the speed of the cable, so for slow motions the tangential drag force will be small and grow quickly as the speed increases.
4.3. Moored Cylinder
Here we analyze the influence that deviations in anchor placement have on the dynamics of a moored cylindrical buoy. The case study is based on physical model experiments of a vertical cylinder moored with spread mooring system composed of three catenaries, Figure 9 (see [46] for a close description of the physical experiments). This case has been investigated numerically by coupled mooring analysis using CFD [25] and using linear potential theory [33].

Figure 9.
Experimental set-up reproduced in the moored cylindrical buoy case.
The properties of the buoy used here follow [25], with a slightly modified mass and inertia to include styrofoam lid and metal support of the load cells. The properties of the model are presented in Table 4 for the buoy, Table 5 for the chain, and Table 6 for the soil and water. For the analysis, we selected three regular wave tests with a constant wave height H = 0.04 m and three different periods: T = 1.00 s, T = 1.20 s, and T = 1.40 s. The dynamics of the moored floating cylinder were modeled in a coupling of MooDy and WEC-Sim. The cables were modeled in MooDy, discretised elements of order p = 5, and a time-step such that the CFL condition was always smaller than 0.9. The buoy motion was modeled in WEC-Sim, using a time-step of 0.01 s.

Table 4.
Properties of the buoy. D—diameter; h—height; —inertia around the horizontal axis through the center of gravity; —center of gravity (distance from the top).

Table 5.
Chain properties.

Table 6.
Water and soil properties.
We modeled the uncertainty in the anchor position using the one-dimensional Gaussian distribution for each of the horizontal anchor coordinates: xAi and yAi, corresponding to cable i. The data relative to the probability distributions of the uncertainty is presented in Table 7. For the mean of the distribution of each coordinate we selected the deterministic value of the position of the anchor in the experimental set-up. For the standard deviation we chose the value of 0.025 m, based on reasonable estimates of the maximum error when installing the anchor in the physical model, given the dimensions of the set-up and the difficulty in handling the anchors. To obtain the gPC model of the moored buoy, we generated 150 samples of the positions of the anchors using the Latin Hyper Cube method and ran the numerical model for each of these sampled positions. Afterwards, we used the LAR algorithm to fit the coefficients to a gPC expansion of order p = 5, using Hermite polynomials and q-norm of 1. With the gPC model we evaluated 3000 random samples of anchor positions to build confidence intervals for the tension in the cables and for the surge, heave and pitch motions. These were then compared with the physical model measurements. The results are presented in Figure 10, Figure 11 and Figure 12.

Table 7.
Parameters of the probability distributions of the anchors’ positions.
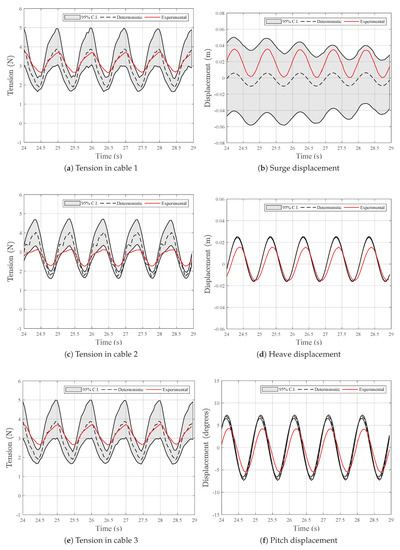
Figure 10.
95% confidence intervals together with deterministic simulation results using the mean value of the input random variables, for T = 1.00 s, H = 0.04 m.
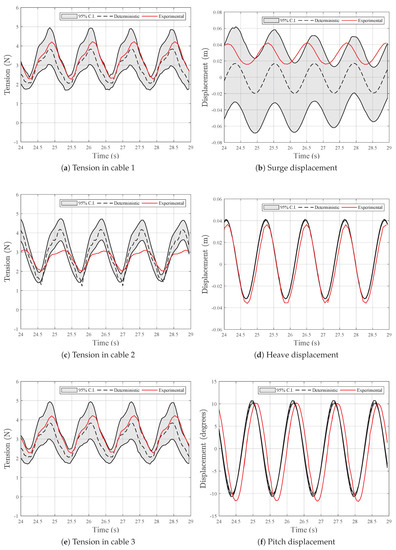
Figure 11.
95% confidence intervals together with deterministic simulation results using the mean value of the input random variables, for T = 1.20 s, H = 0.04 m.
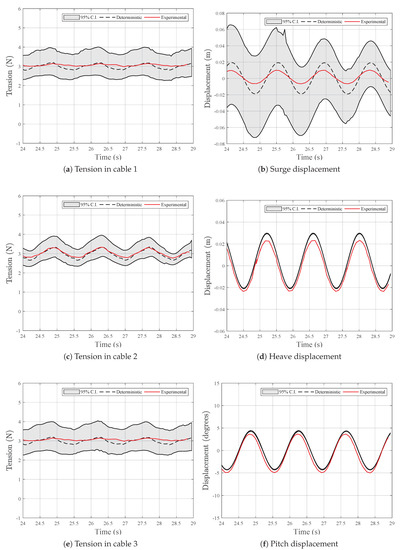
Figure 12.
95% confidence intervals together with deterministic simulation results using the mean value of the input random variables, for T = 1.40 s, H = 0.04 m.
Before analyzing the results of the gPC model we note that there are differences between the physical model results and the deterministic simulations, already analyzed in [25,33]. The main cause for the difference between the mean surge displacement in the simulations and the one measured in the experiments is the WEC-Sim simulations not accounting for second order drift forces. As the mean surge displacement and the tension in the cables are linked, more accurate results in the simulation of surge, such as for , lead to more accurate results in tension.
The results of the simulations are presented in Figure 10, Figure 11 and Figure 12. The confidence intervals represent fairly well the tension in the cables and the heave and pitch motions. In surge, there is a long period variation in the amplitude of the confidence intervals, as is clearly seen in Figure 12b. This is caused by transient motions of the buoy in the beginning of the simulations: although the anchors’ position change in each simulation, the buoy’s initial position is kept constant (in the one corresponding to the mean anchor position), causing it to start its motion slightly out of equilibrium.
Within the range applied in this work, the positions of the anchors have very little influence in the heave and pitch behavior. The surge motion and the tension, on the contrary, show a significant influence from the position of the anchors. With a large confidence interval, surge seems to be the most susceptible quantity to the effect anchor placement, which is partially due to having the mooring tension, which displays a notable uncertainty, as the only restoring force. These are important results for floating structures with working principles depending on heave and pitch dynamics, as neither the design nor the installation need to be too demanding when it comes to anchor placement accuracy. However, the influence played by the anchor position in surge and in the tension shows the need to account for installation errors during the design phase. This can be done using gPC, or another UQ method, to determine bounds of acceptable deviations in anchor positioning, which might relax design and deployment tolerances.
5. Conclusions
We applied generalized Polynomial Chaos (gPC) to build cost-effective surrogate models to perform uncertainty quantification of mooring cable dynamics. Two cases were considered: (i) the sensitivity of hydrodynamic coefficients on peak tension loads and (ii) the sensitivity of anchor position on tension loads and the resulting floater motion.
The study on hydrodynamic coefficients was based on numerical simulations of a single mooring cable subjected to forced oscillatory motion of its top end. The results showed that the normal drag coefficient has the greatest influence in the simulation results, while the tangential drag and the mass coefficients have almost negligible influence. As such, when simulating mooring cables, it is more important to get an accurate value of the normal drag coefficient than of the tangential drag or of the mass coefficients. However, a large uncertainty in the value of the coefficients (50%) causes only small changes in the value of the peak tension, even when snap loads are present. The results also show that when the tension is low, tangent motions along the ground might be relevant, but further investigation is required.
The test case for the impact of uncertainty in anchor position used numerical simulations to reproduce physical model experiments of a cylindrical buoy moored by three catenary chains. It was shown that deviations in the anchor position, relative to the expected one, have very little influence in heave or pitch dynamics. However, the surge motion and mooring cable tension can be significantly affected.
Through the use of cost-effective surrogate models (here based on gPC) it is possible to perform sensitivity analysis to better understand how some mooring system parameters are more relevant to the design than others. This will help designers and researchers choose where to focus their efforts when analyzing mooring systems, ultimately contributing to improved and more reliable mooring designs.
Author Contributions
Conceptualization, G.M.P., C.E. and A.P.E.-K; methodology, G.M.P., C.E. and A.P.E.-K.; simulation and analysis, G.M.P.; writing—original draft preparation, G.M.P.; writing—review and editing, C.E. and A.P.E.-K. All authors have read and agreed to the published version of the manuscript.
Funding
This project received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 752031.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BEM | Boundary Element Method |
| CFL | Courant–Friedrichs–Lewy |
| DG | Discontinuous Galerkin |
| gPC | generalized Polynomial Chaos |
| LARS | Least Angle Regression |
| MC | Monte Carlo |
| MODU | Mobile Offshore Drilling Unit |
| O&G | Oil and Gas |
| Probability Density Function | |
| TSI | Total Sensitivity Index |
| UQ | Uncertainty Quantification |
References
- Brindley, W.; Comley, A.P. North Sea mooring systems: How reliable are they? In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- DNV GL AS. Offshore Standards DNVGL-OS-E301 Position mooring. 2018. Available online: http://rules.dnvgl.com/docs/pdf/dnvgl/os/2018-07/dnvgl-os-e301.pdf (accessed on 28 February 2020).
- Kvitrud, A. Anchor Line Failures Norwegian Continental Shelf: 2010–2014; Technical Report; Petroleum Safety Authority Norway: Stavanger, Norway, 2014. [Google Scholar]
- Fitzgerald, J. Position Mooring of Wave Energy Converters. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2009. [Google Scholar]
- Martinelli, L.; Ruol, P.; Cortellazzo, G. On mooring design of wave energy convertes: The Seabreath application. In Proceedings of the 33rd Conference on Coastal Engineering; Coastal Engineering Research Council, Santander, Spain, 1–6 July 2012; Volume 33. [Google Scholar]
- Thomsen, J. Mooring Solutions for Large Wave Energy Converters. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2017. [Google Scholar] [CrossRef]
- Orcina Ltd. OrcaFlex Manual-Version 9.7a. 2015. Available online: https://www.orcina.com/releases/orcaflex-97/ (accessed on 28 February 2020).
- MARIN. aNySIM Documentation-Mooring. 2011. Available online: https://www.marin.nl/storage/uploads/3569/files/aNySIM_XMF.pdf (accessed on 28 February 2020).
- Wiener, N. The Homogeneous Chaos. Am. J. Math. 1938, 60, 897. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Le Maître, O.P.; Knio, O.M. Spectral Methods for Uncertainty Quantification; Scientific Computation; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Couaillier, V.; Savin, E. Generalized Polynomial Chaos for Nonintrusive Uncertainty Quantification in Computational Fluid Dynamics. In Uncertainty Management for Robust Industrial Design in Aeronautics; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 123–141. [Google Scholar] [CrossRef]
- Kim, K.K.K.; Shen, D.E.; Nagy, Z.K.; Braatz, R.D. Wiener’s Polynomial Chaos for the Analysis and Control of Nonlinear Dynamical Systems with Probabilistic Uncertainties [Historical Perspectives]. IEEE Control Syst. 2013, 33, 58–67. [Google Scholar] [CrossRef]
- Bigoni, D.; True, H.; Engsig-Karup, A.P. Sensitivity analysis of the critical speed in railway vehicle dynamics. Veh. Syst. Dyn. 2014, 52, 272–286. [Google Scholar] [CrossRef]
- Murcia, J.P.; Réthoré, P.E.; Dimitrov, N.; Natarajan, A.; Sørensen, J.D.; Graf, P.; Kim, T. Uncertainty propagation through an aeroelastic wind turbine model using polynomial surrogates. Renew. Energy 2018, 119, 910–922. [Google Scholar] [CrossRef]
- Ge, L.; Cheung, K.F. Spectral sampling method for uncertainty propagation in long-wave runup modeling. J. Hydraul. Eng. 2011, 137, 277–288. [Google Scholar] [CrossRef]
- Ricchiuto, M.; Congedo, P.; Delis, A. Runup and Uncertainty Quantification: Sensitivity Analysis via ANOVA Decomposition; Technical Report; INRIA: Bordeaux, France, 2014. [Google Scholar]
- Yildirim, B.; Karniadakis, G.E. Stochastic simulations of ocean waves: An uncertainty quantification study. Ocean Model. 2015, 86, 15–35. [Google Scholar] [CrossRef]
- Bigoni, D.; Engsig-Karup, A.P.; Eskilsson, C. Efficient uncertainty quantification of a fully nonlinear and dispersive water wave model with random inputs. J. Eng. Math. 2016, 101, 87–113. [Google Scholar] [CrossRef]
- Mosig, J.E.M.; Montiel, F.; Squire, V.A. Water wave scattering from a mass loading ice floe of random length using generalised polynomial chaos. Ocean Model. 2017, 70, 239. [Google Scholar] [CrossRef]
- Kreuzer, E.; Solowjow, E. Polynomial Chaos and the Heave Motion of a Cylinder in Random Seas. In Proceedings in Applied Mathematics and Mechanics; Springer: New York, NY, USA, 2015; Volume 15, pp. 559–560. [Google Scholar] [CrossRef]
- Nguyen, P.T.T.; Manuel, L.; Coe, R.G. On the development of an efficient surrogate model for predicting long-term extreme loads on a wave energy converter. J. Offshore Mech. Arct. Eng. 2019, 141, 061103. [Google Scholar] [CrossRef]
- Lim, H.; Manuel, L.; Low, Y.M. On efficient long-term extreme response estimation for a moored floating structure. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Montano, A.; Restelli, M.; Sacco, R. Numerical simulation of tethered buoy dynamics using mixed finite elements. Comput. Methods Appl. Mech. Eng. 2007, 196, 4117–4129. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Paredes, G.M.; Bergdahl, L. Coupled mooring analysis for floating wave energy converters using CFD: Formulation and validation. Int. J. Mar. Energy 2016, 16, 83–99. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Bergdahl, L. An hp-adaptive discontinuous Galerkin method for simulating snap loads in mooring cables. Ocean Eng. 2017, 144, 266–276. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C. MooDy User Manual—Version 1.0.0; Technical Report; Chalmers University of Technology: Gothernburg, Sweden, 2018. [Google Scholar]
- Cummins, W.E. The Impulse Response Function and Ship Motions; Technical Report; David Taylor Model Basin: Washington, DC, USA, 1962. [Google Scholar]
- WAMIT, Inc.WAMIT User Manual Version 7.0. 2013. Available online: https://www.wamit.com/manual.htm (accessed on 28 February 2020).
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015. [Google Scholar]
- National Renewable Energy Laboratory and Sandia Corporation. WEC-Sim (Wave Energy Converter SIMulator) — WEC-Sim Documentation. 2015. Available online: https://wec-sim.github.io/WEC-Sim/ (accessed on 28 February 2020).
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef]
- Paredes, G.M.; Eskilsson, C.; Palm, J.; Kofoed, J.P.; Bergdahl, L. Coupled BEM/hp-FEM Modelling of Moored Floaters. In Proceedings of the 1st Vietnam Symposium on Advances in Offshore Engineering; Springer: Hanoi, Vietnam, 2018; pp. 504–510. [Google Scholar]
- Xiu, D. Numerical Methods for Stochastic Computations—A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010; p. 144. [Google Scholar]
- Bigoni, D.; Engsig-Karup, A.P.; Marzouk, Y.M. Spectral tensor-train decomposition. SIAM J. Sci. Comput. 2016, 38, A2405–A2439. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab User Manual—Polynomial Chaos Expansions; Technical Report, Chair of Risk, Safety & Uncertainty Quantification; ETH Zurich: Zurich, Switzerland, 2018. [Google Scholar]
- Greiner, W. Classical Mechanics: Systems of Particles and Hamiltonian Dynamics; Springer: New York, NY, USA, 2003. [Google Scholar]
- Lindahl, J. Modellförsök med en Förankringskabel; Technical Report; Chalmers University of Technology: Gothernburg, Sweden, 1985. [Google Scholar]
- Bergdahl, L.; Palm, J.; Eskilsson, C.; Lindahl, J. Dynamically Scaled Model Experiment of a Mooring Cable. J. Mar. Sci. Eng. 2016, 4, 5. [Google Scholar] [CrossRef]
- Triantafyllou, M.; Howell, C. Dynamic response of cables under negative tension: An ill-posed problem. J. Sound Vib. 1994, 173, 433–447. [Google Scholar] [CrossRef]
- Low, C.; Nga, E.K.; Narasimalua, S.; Linc, F.; Kimb, Y. Numerical modelling of seabed impact effects on chain and small diameter mooring cables. Appl. Ocean. Res. 2018, 80, 248–277. [Google Scholar] [CrossRef]
- Marelli, S.; Lamas, C.; Sudret, B.; Konakli, K.; Mylonas, C. UQLab User Manual —Sensitivity Analysis; Technical Report, Chair of Risk, Safety and Uncertainty Quantification; ETH Zurich: Zürich, Switzerland, 2018. [Google Scholar]
- Bigoni, D. Uncertainty Quantification with Applications to Engineering Problems. Ph.D. Thesis, Technical University of Denmark, Kgs. Lyngby, Denmark, 2015. [Google Scholar]
- Triantafyllou, M.S.; Bliek, A.; Shin, H. Dynamic Analysis as a Tool for Open-Sea Mooring System Design. SNAME Trans. 1985, 93, 303–324. [Google Scholar]
- Papazoglou, V.J.; Mavrakos, S.A.; Triantafyllou, M.S. Non-linear cable response and model testing in water. J. Sound Vib. 1990, 140, 103–115. [Google Scholar] [CrossRef]
- Moura Paredes, G.; Palm, J.; Eskilsson, C.; Bergdahl, L.; Taveira-Pinto, F. Experimental investigation of mooring configurations for wave energy converters. Int. J. Mar. Energy 2016, 15, 56–67. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).