Extending Complex Conjugate Control to Nonlinear Wave Energy Converters
Abstract
1. Introduction
2. CCC and PDC3
3. Electrical Power Networks, Mechanical Oscillators, and Linear Limit Cycles
3.1. Electrical Power Networks
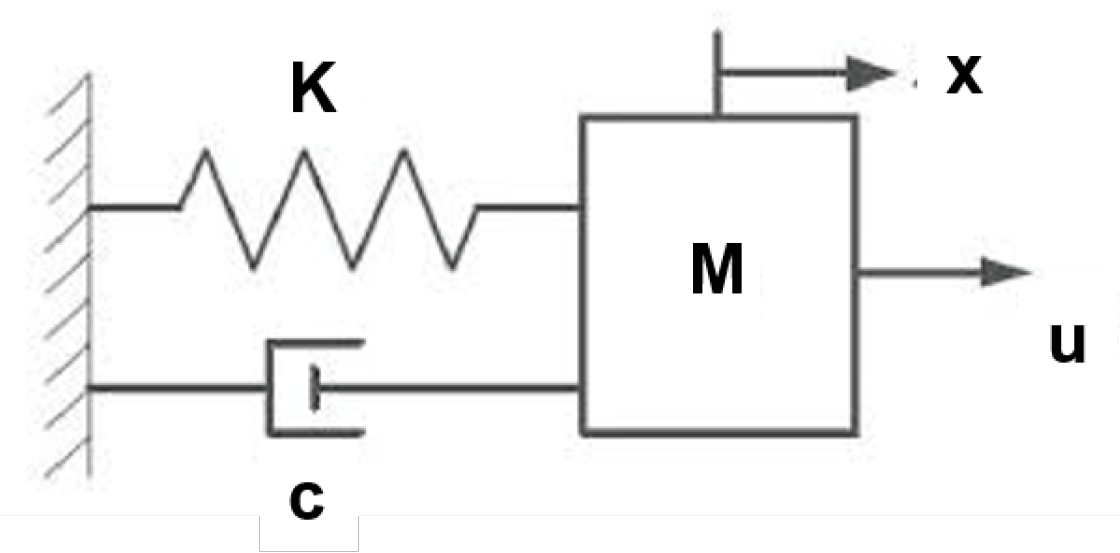
3.2. Mechanical Systems
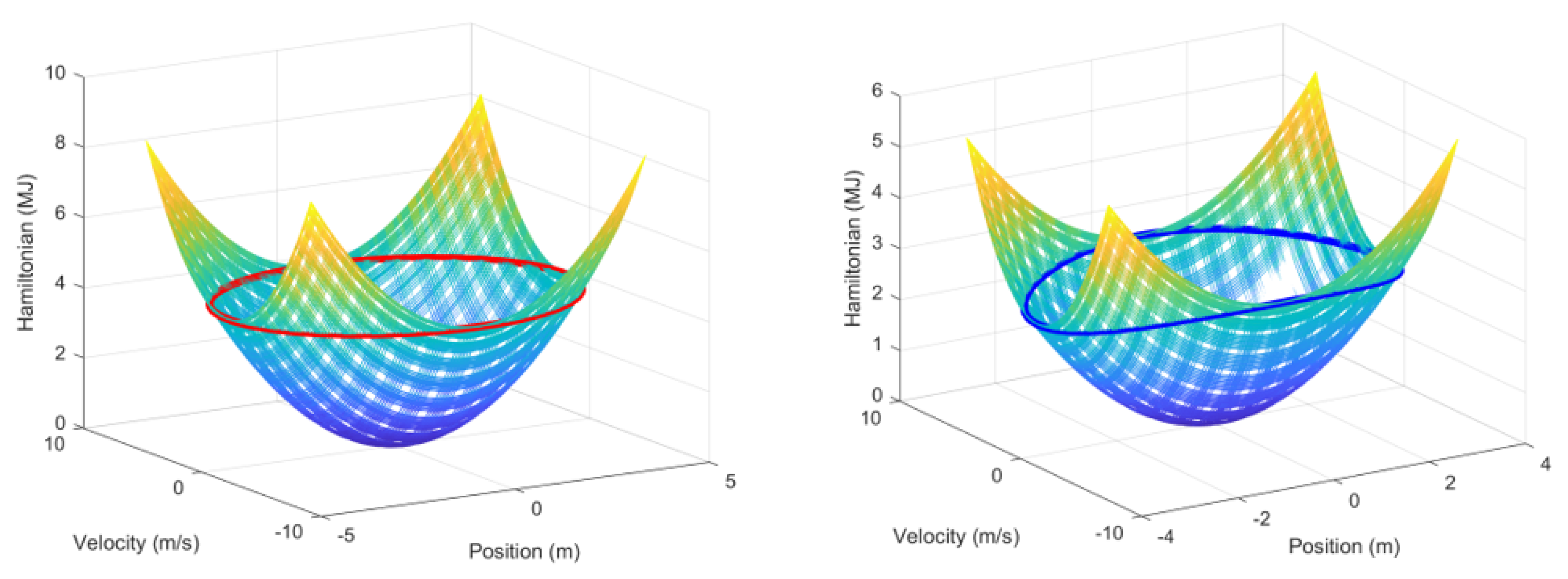
3.3. Linear Limit Cycles
4. Nonlinear Feedback Linearization and PDC3
5. HSSPFC and Nonlinear Limit Cycles
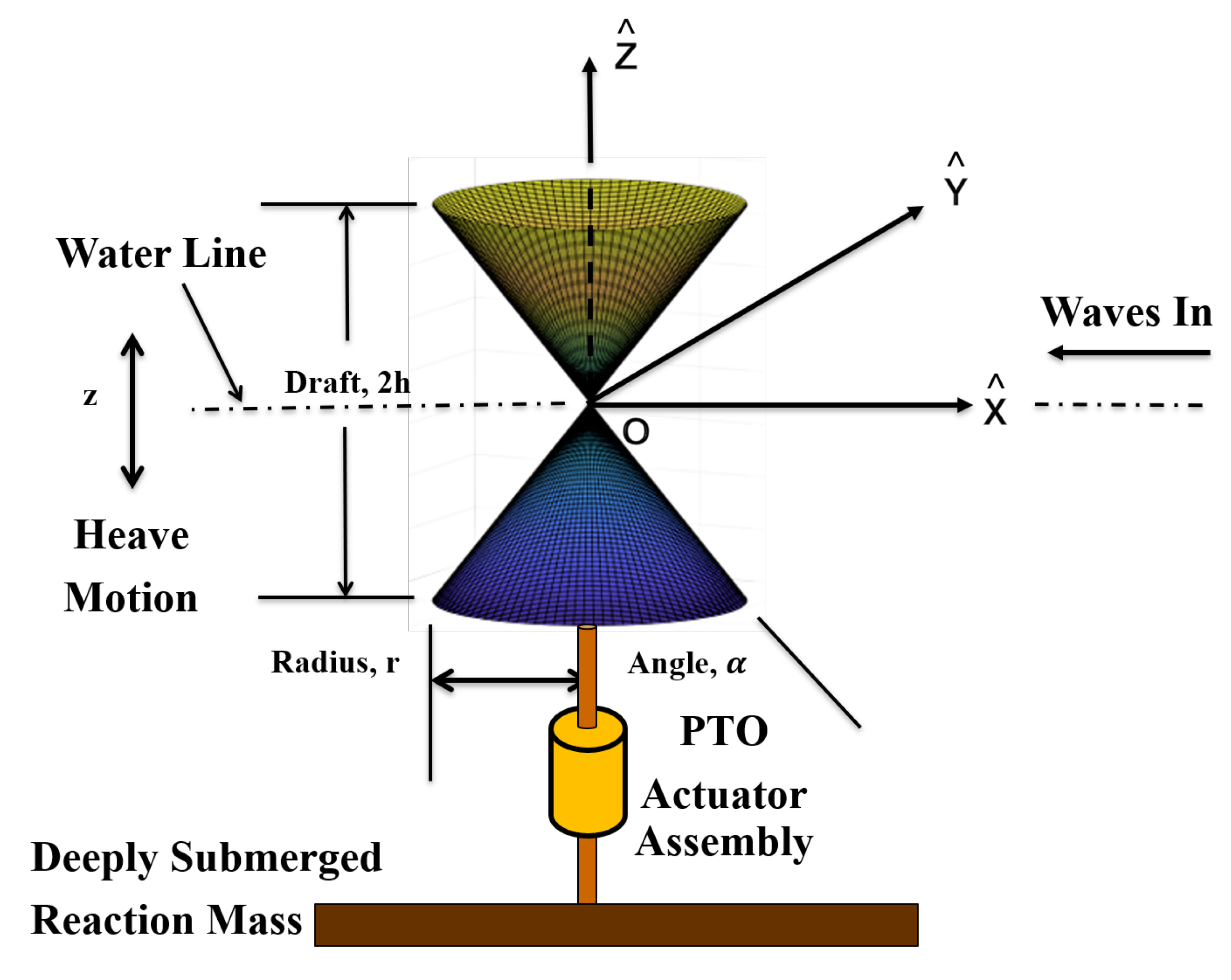
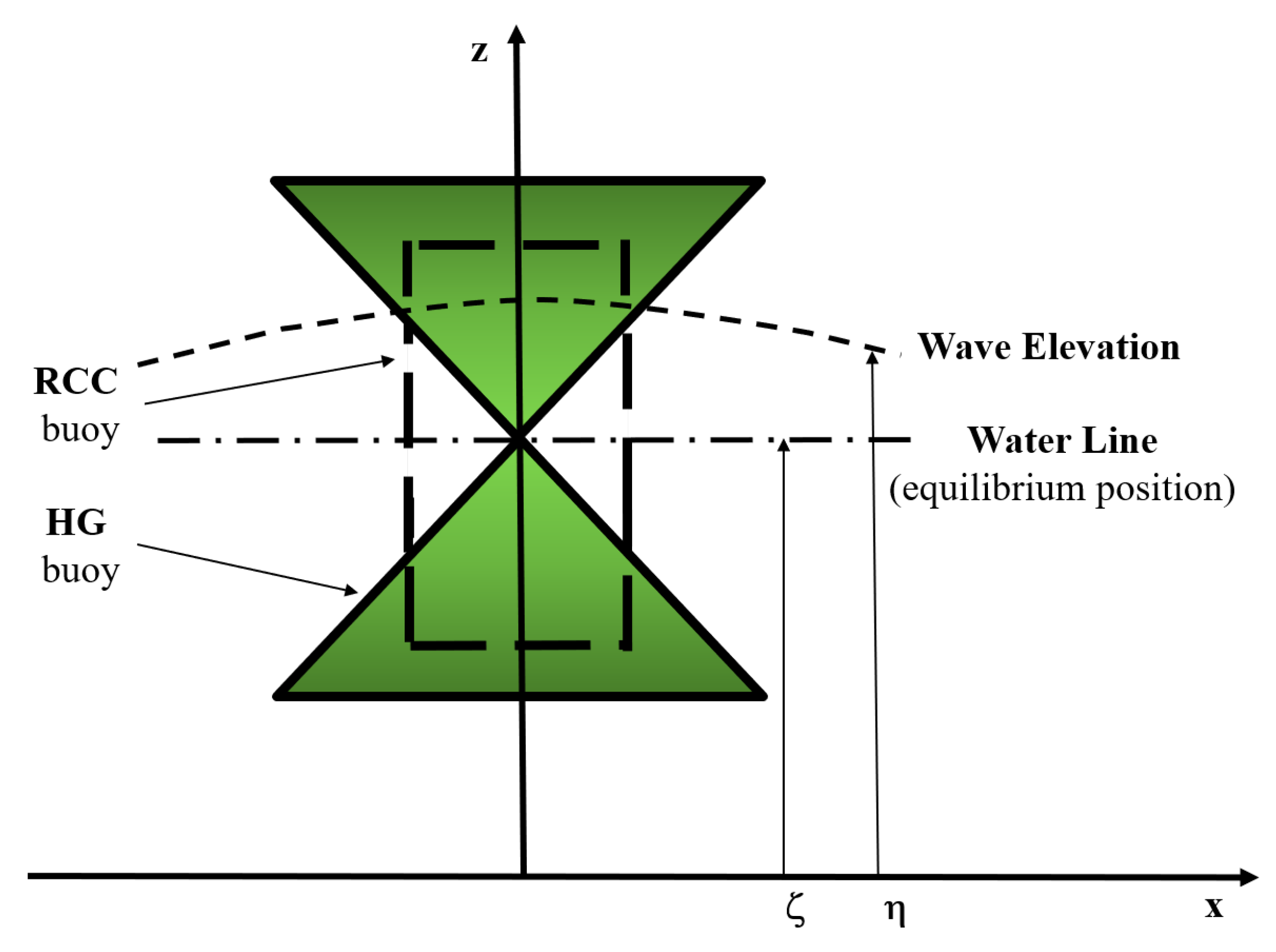
5.1. Hour-Glass (HG) WEC Design Model Development
5.2. RCC WEC Design Model Development
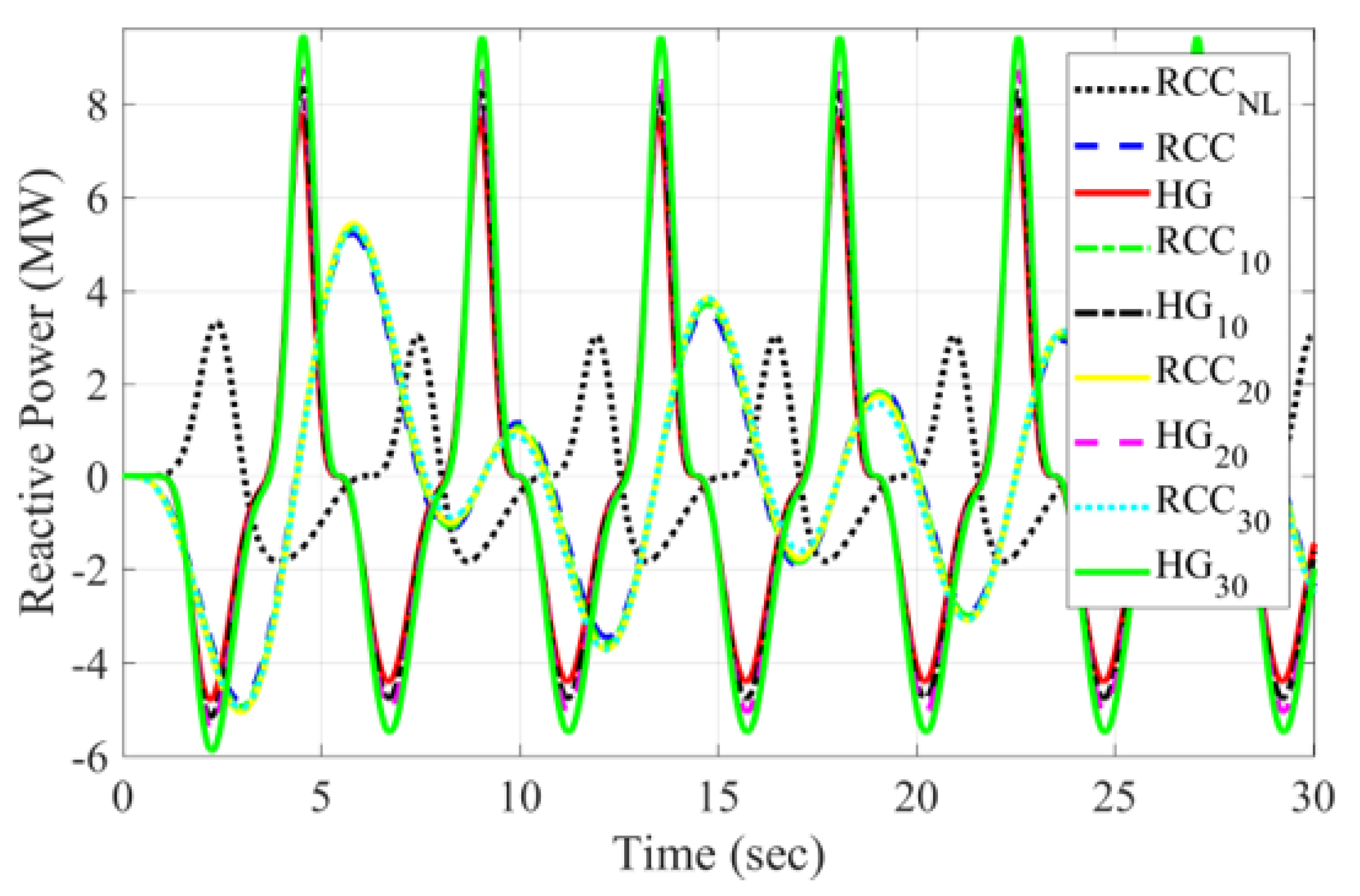
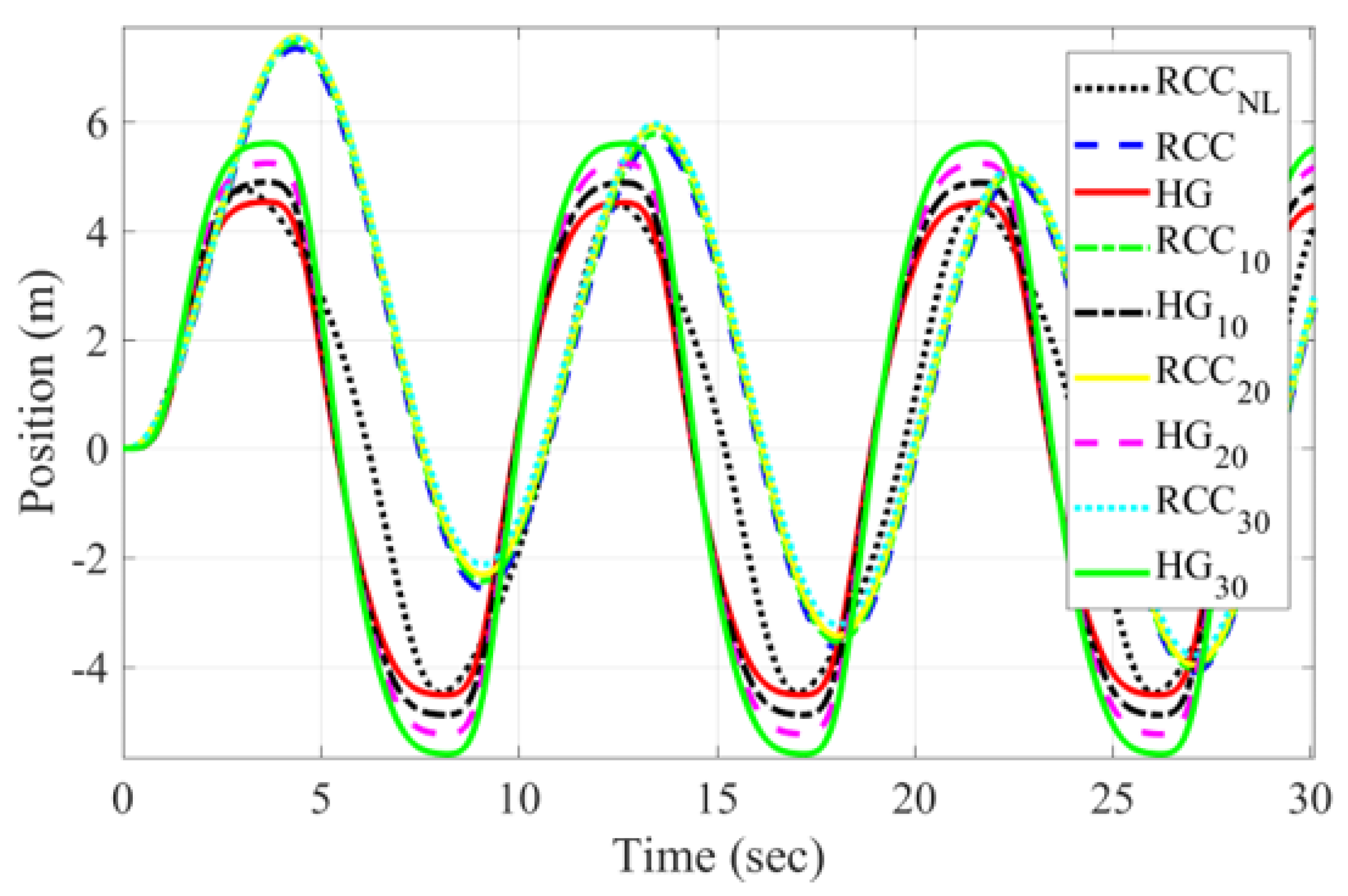
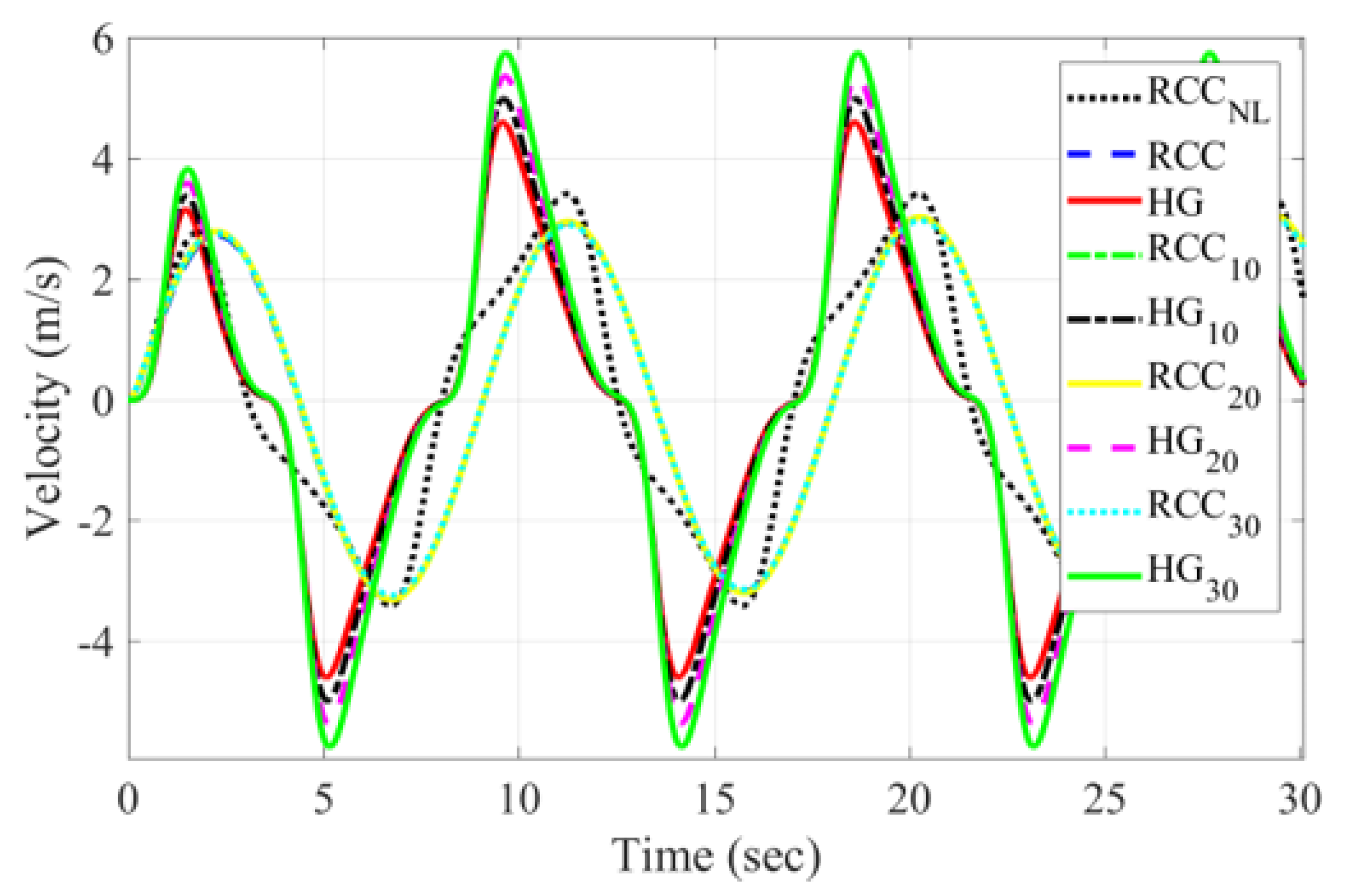
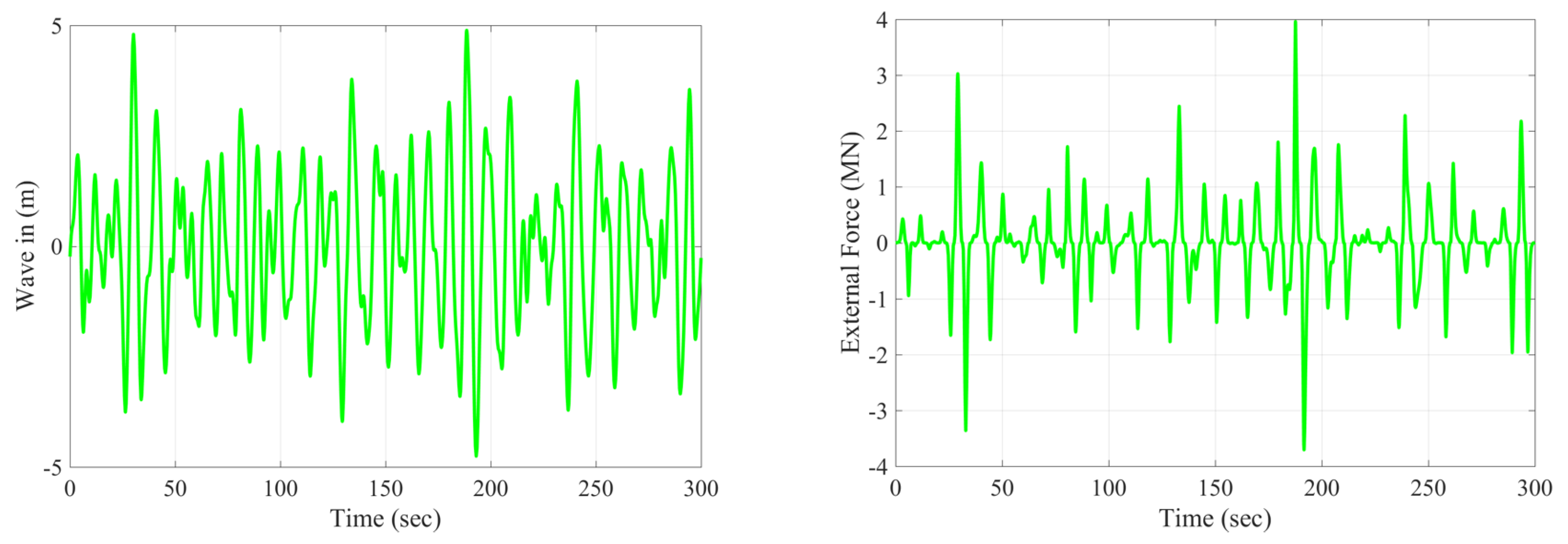
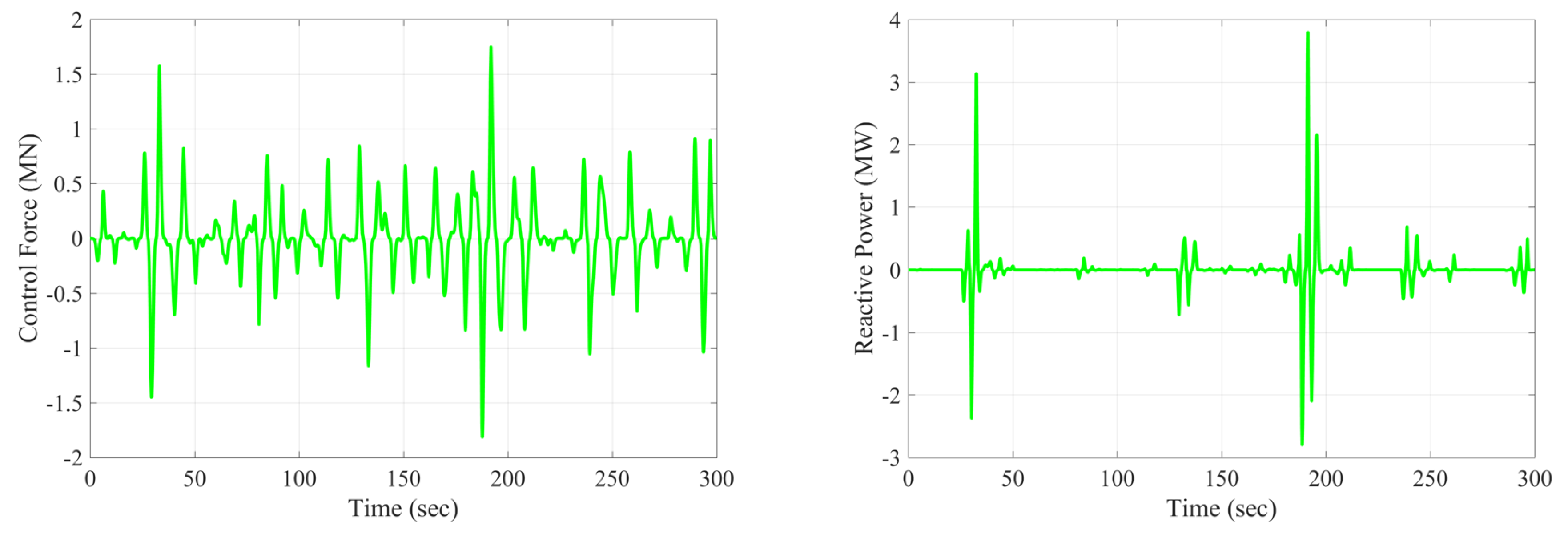
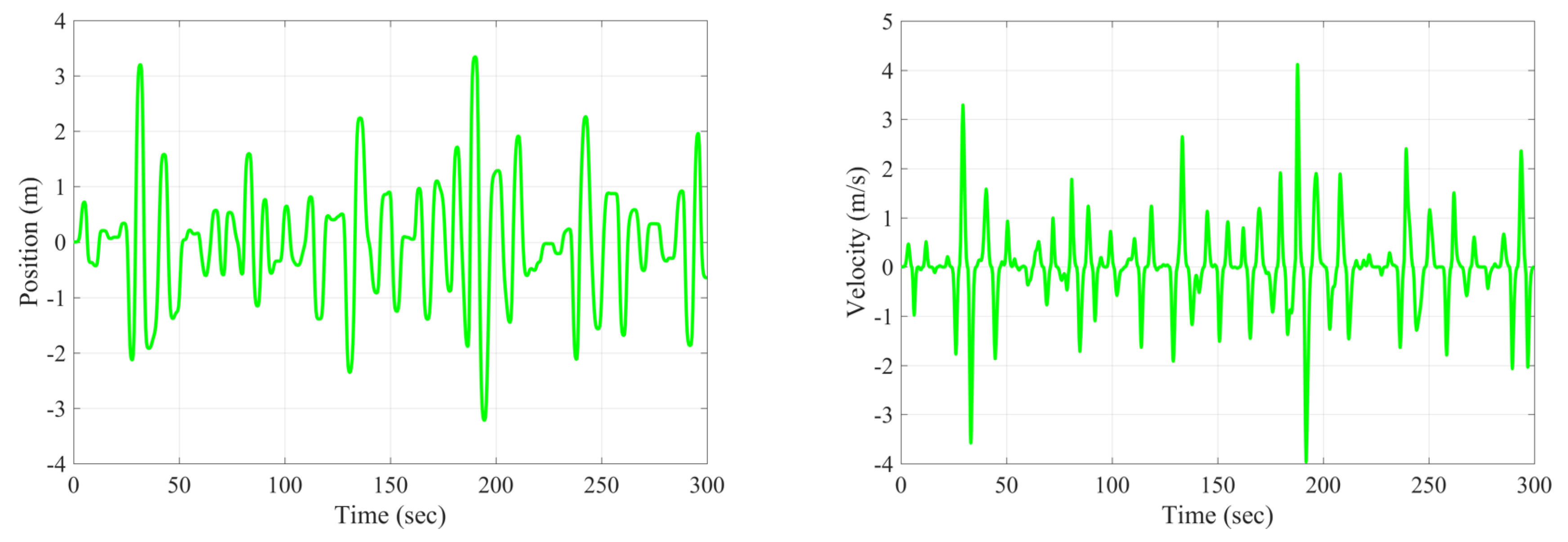
6. Case Study Simulation Results
6.1. Nonlinear Resonator Results
6.2. Single Frequency Results
6.3. Bretschneider Multi-Spectrum Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | SI Units |
| Estimate of parameter | - | |
| A | Cross-sectional area | m2 |
| HG buoy geometry cone steepness angle | deg | |
| b | Linear damping coefficient | N s/m |
| c | Linear damping coefficient | N s/m |
| Nonlinear damping coefficient | N | |
| Nonlinear damping coefficient | N/(m/s)2 | |
| C | Electrical capacitance | F |
| Maximum harvested energy | MJ | |
| Wave elevation | m | |
| External force | N | |
| Control force | N | |
| Nonlinear control force | N | |
| PDC3 control force | N | |
| Reactive force | N | |
| Real force | N | |
| Hydrostatic force | N | |
| Gravitation force | N | |
| Buoy force | N | |
| Bretschneider ith sea state spectral peak frequency | Hz | |
| External force magnitude | N | |
| g | Gravitational constant | m/s2 |
| Bretschneider significant wave height parameter | m | |
| h | Buoy height, HG, RCC | m |
| Height of buoy and one-half of total draft | m | |
| Hamiltonian over a cycle | J | |
| Hamiltonian, total energy with subscripts; electrical (e), mechanical (m) | J | |
| Hamiltonian rate, power flow with subscripts; electrical (e), mechanical (m) | W | |
| j | Sum index for number of force components | - |
| Stiffness coefficient | N/m | |
| Linear stiffness coefficient | N/m | |
| Nonlinear stiffness coefficient | N/m3 | |
| Nonlinear stiffness coefficient | N/m3 | |
| Proportional control gain | kg/s2 | |
| Derivative control gain | kg/s | |
| L | Electrical inductance | H |
| Mass of system | kg | |
| N | Maximum number of force components | - |
| Mechanical system natural frequency | rad/s | |
| Extern force excitation frequency | rad/s | |
| Electrical system natural frequency | rad/s | |
| Reactive power | MW | |
| Real power | MW | |
| q | Electrical charge | C |
| Electrical charge rate (equal to current) | C/s | |
| Electrical charge acceleration | C/s2 | |
| r | Buoy radius, HG, RCC | m |
| R | Electrical resistance | Ohms |
| Optimal damping coefficient | N s/m | |
| Effective optimal damping coefficient | N s/m | |
| Buoy material density | kg/m3 | |
| Non-uniform water plane area | m2 | |
| Bretschneider spectral density | m2s/rad | |
| Cycle time | sec | |
| t | time | sec |
| Kinetic energy with subscripts; electrical (e), mechanical (m) | J | |
| Bretschneider spectral peak period parameter | sec | |
| V | Volume with subscripts; cone, buoy, RCC, HG | m3 |
| Volume as a function of heave displacement | m3 | |
| External voltage magnitude | V | |
| Potential energy with subscripts; electrical (e), mechanical (m) | J | |
| x | Displacement | m |
| Velocity | m/s | |
| Acceleration | m/s2 | |
| x-coordinate | - | |
| y-coordinate | - | |
| z-coordinate | - | |
| z | Heave displacement | m |
| Heave velocity | m/s | |
| Heave acceleration | m/s2 | |
| Vertical position of the center of volume of buoy | m |
References
- Li, G.; Weiss, G.; Mueller, M.; Townley, S.; Belmont, M.R. Wave energy converter control by wave prediction and dynamic programming. Renew. Energy 2012, 48, 392–403. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Ringwood, J.; Bacelli, G.; Fusco, F. Energy-Maximizing Control of Wave-Energy Converters: The Development of Control System Technology to Optimize Their Operation. IEEE Control Syst. Mag. 2014, 34, 30–55. [Google Scholar] [CrossRef]
- Hals, J.; Falnes, J.; Moan, T. A Comparison of Selected Strategies for Adaptive Control of Wave Energy Converters. J. Offshore Mech. Arct. Eng. 2011, 133. [Google Scholar] [CrossRef]
- Cretel, J.; Lightbody, G.; Thomas, G.; Lewis, A. Maximisation of Energy Capture by a Wave-Energy Point Absorber Using Model Predictive Control. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; Volume 44, pp. 3714–3721. [Google Scholar]
- Bacelli, G.; Ringwood, J.V.; Gilloteaux, J.C. A control system for a self-reacting point absorber wave energy converter subject to constraints. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 11387–11392. [Google Scholar]
- Abdelkhalik, O.; Robinett, R.; Bacelli, G.; Coe, R.; Bull, D.; Wilson, D.; Korde, U. Control Optimization of Wave Energy Converters Using a Shape-Based Approach. In ASME Power & Energy 2015; ASME: San Diego, CA, USA, 2015. [Google Scholar]
- Abdelkhalik, O.; Robinett, R.; Zou, S.; Bacelli, G.; Coe, R.; Bull, D.; Wilson, D.; Korde, U. On the control design of wave energy converters with wave prediction. J. Ocean Eng. Mar. Energy 2016, 2, 473–483. [Google Scholar] [CrossRef]
- Faedo, N.; Olaya, S.; Ringwood, J.V. Optimal control, MPC and MPC-like algorithms for wave energy systems: An overview. IFAC J. Syst. Control 2017, 1, 37–56. [Google Scholar] [CrossRef]
- Abraham, E. Optimal Control and Robust Estimation for Ocean Wave Energy Converters. Ph.D. Thesis, Department of Aeronautics, Imperial College London, London, UK, 2013. [Google Scholar]
- Retes, M.; Giorgi, G.; Ringwood, J. A Review of Non-Linear Approaches for Wave Energy Converter Modelling. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Wolgamot, A.; Fitzgerald, C. Nonlinear Hydrodynamic and Real Fluid Effects on Wave Energy Converters. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 772–794. [Google Scholar] [CrossRef]
- Giorgi, G.; Retes, M.; Ringwood, J. Nonlinear Hydrodynamic Models for Heaving Buoy Wave Energy Converters. In Proceedings of the Asian Wave and Tidal Energy Conference (AWETEC 2016), Singapore, 24–28 October 2016. [Google Scholar]
- Abdelkhalik, O.; Darani, S. Optimization of nonlinear wave energy converters. Ocean Eng. 2018, 162, 187–195. [Google Scholar] [CrossRef]
- Darani, S.; Abdelkhalik, O.; Robinett, R.; Wilson, D. A hamiltonian surface-shaping approach for control system analysis and the design of nonlinear wave energy converters. J. Mar. Sci. Eng. 2019, 7, 48. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems, 1st ed.; Cambridge University Press: Cambridge, NY, USA, 2002. [Google Scholar]
- Song, J.; Abdelkhalik, O.; Robinett, R.; Bacelli, G.; Wilson, D.; Korde, U. Multi-Resonant Feedback Control of Heave Wave Energy Converters. Ocean Eng. 2016, 127, 269–278. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Zou, S.; Robinett, R.; Bacelli, G.; Wilson, D.; Coe, R.; Korde, U. Multi-Resonant Feedback Control of Three Degree-of-Freedom Wave Energy Converters. IEEE Trans. Sustain. Energy 2017, 8, 1518–1527. [Google Scholar] [CrossRef]
- Wilson, D.; Bacelli, G.; Coe, R.; Bull, D.; Abdelkhalik, O.; Korde, U.; Robinett, R. A Comparison of WEC Control Strategies; Sandia Report, URR, SAND2016-4293; Sandia National Laboratories: Albuquerque, NM, USA, 2016.
- Robinett, R.; Wilson, D. Nonlinear Power Flow Control Design: Utilizing Exergy, Entropy, Static and Dynamic Stability, and Lyapunov Analysis; Springer: London, UK, 2011. [Google Scholar]
- Wilson, D.; Bacelli, G.; Robinett, R.; Korde, U.; Abdelkhalik, O.; Glover, S. Order of Magnitude Power Increase from Multi-Resonance Wave Energy Converters. In Proceedings of the OCEANS 2017—Anchorage, Anchorage, AK, USA, 18–21 September 2017. [Google Scholar]
- Robinett, R.; Wilson, D. What is a Limit Cycle? Int. J. Control 2008, 81, 1886–1900. [Google Scholar] [CrossRef]
- Wikipedia. Limit Cycle. 2019. Available online: www.wikipedia.org (accessed on 27 January 2020).
- Ogata, K. Modern Control Engineering; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Smith, R. Circuits, Devices, and Systems: A First Course in Electrical Engineering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1976. [Google Scholar]
- Hartog, J.D. Mechanical Vibrations; McGraw-Hill: New York, NY, USA, 1934. [Google Scholar]
- Habiba, G.; Detroux, T.; Kerschen, G. Generalization of Den Hartog’s Equal-Peak Method for Nonlinear Primary Systems. In MATEC Web of Conferences, CSNDD 2014—International Conference on Structural Nonlinear Dynamics and Diagnosis; EDP Sciences: Les Ulis, France, 2014; Volume 16. [Google Scholar]
- Robinett, R.; Wilson, D. Nonlinear power flow control applied to power engineering. In Proceedings of the 2008 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM 2008), Ishchia, Italy, 11–13 June 2008. [Google Scholar]
- Slotine, J.J.; Li, W. Applied Nonlinear Control; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Wilson, D.; Robinett, R.; Abdelkhalik, O.; Bacelli, G. Nonlinear Control Design for Nonlinear Wave Energy Converters. In Proceedings of the John L. Junkins Dynamical Systems Symposium, College Station, TX, USA, 20–21 May 2018. [Google Scholar]
- Wilson, D.; Bacelli, G.; Weaver, W.; Robinett, R. 10x Power Capture Increased from Multi-Frequency Nonlinear Dynamics; Express LDRD Final Report, SAND2015-10446R; Sandia National Laboratories: Albuquerque, NW, USA, 2015.
- Perez, T.; Fossen, T. A Matlab Toolbox for Parametric Identification of Radiation-Force Models of Ships and Offshore Structures. Model. Identif. Control 2009, 30, 1–15. [Google Scholar] [CrossRef]




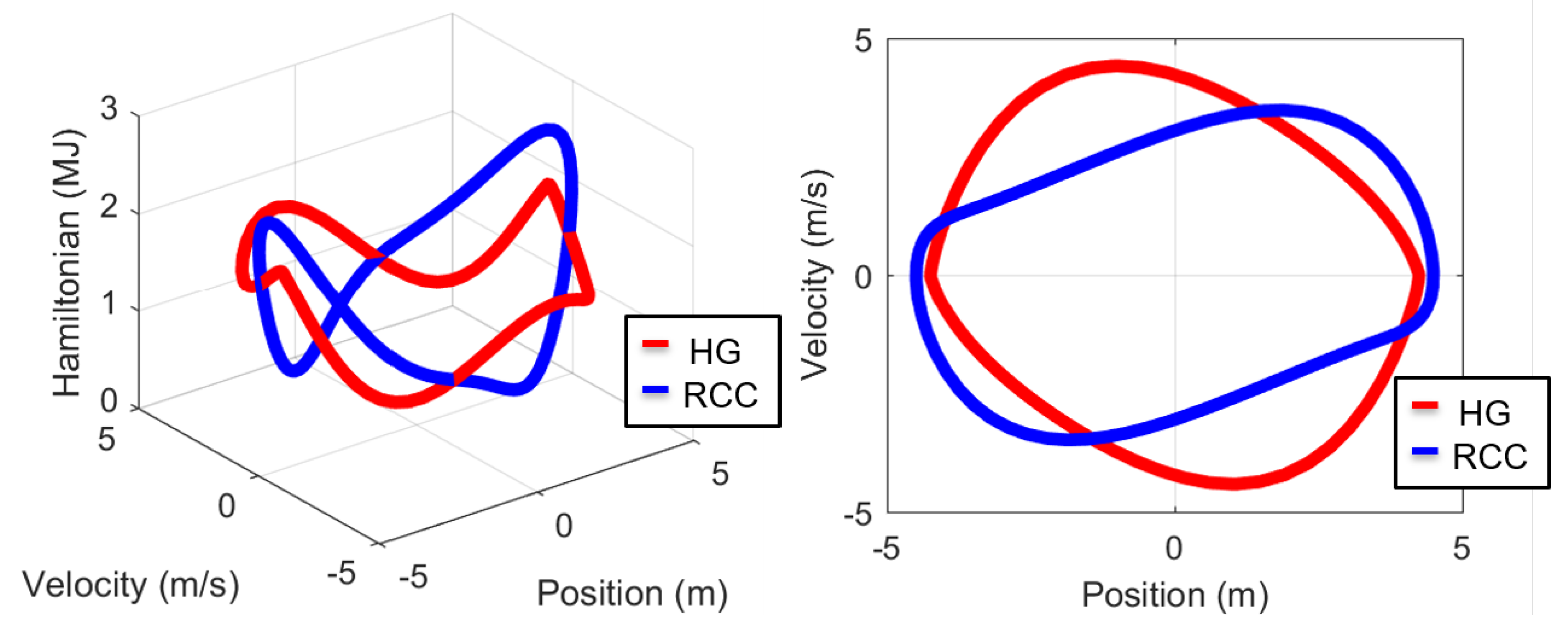

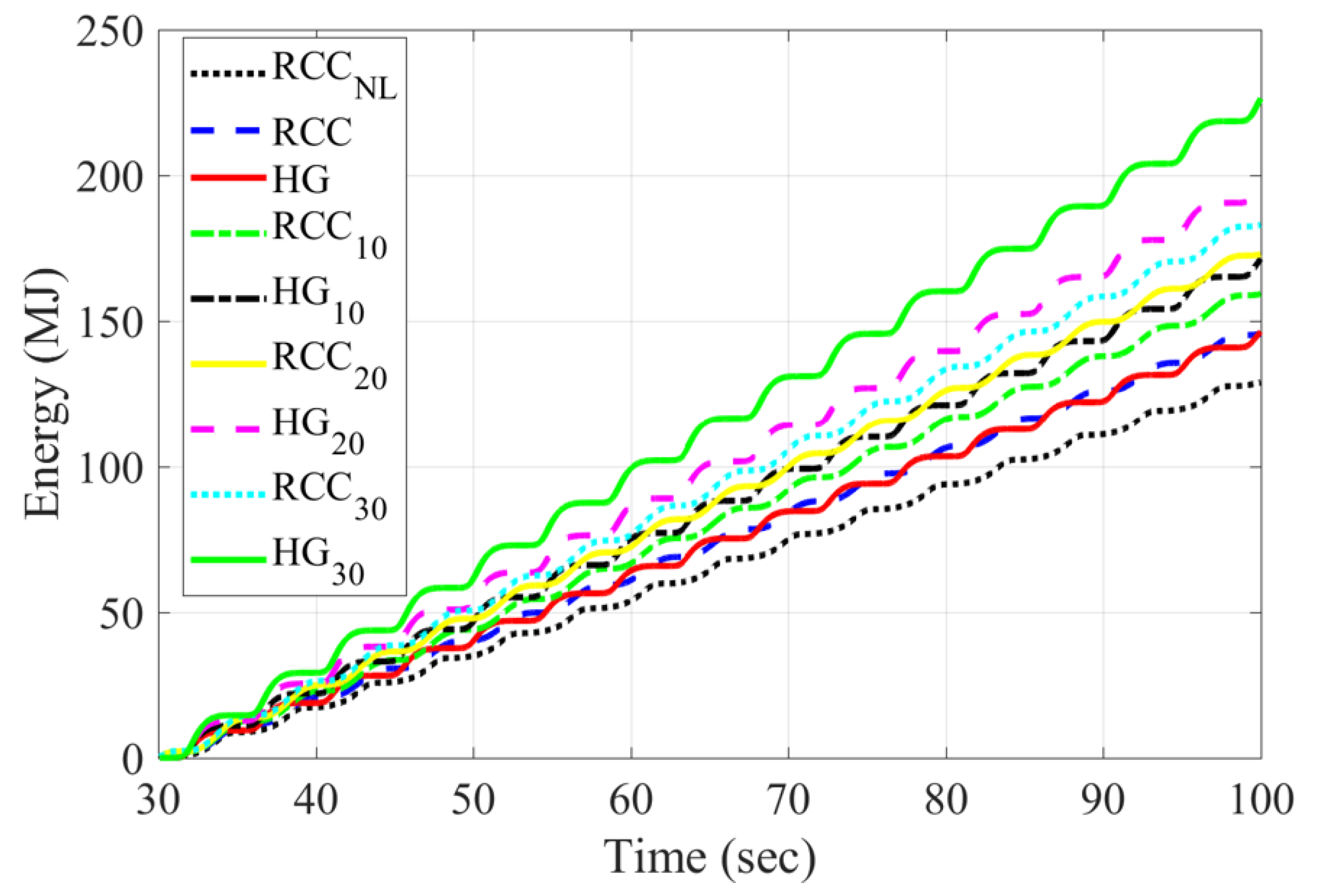
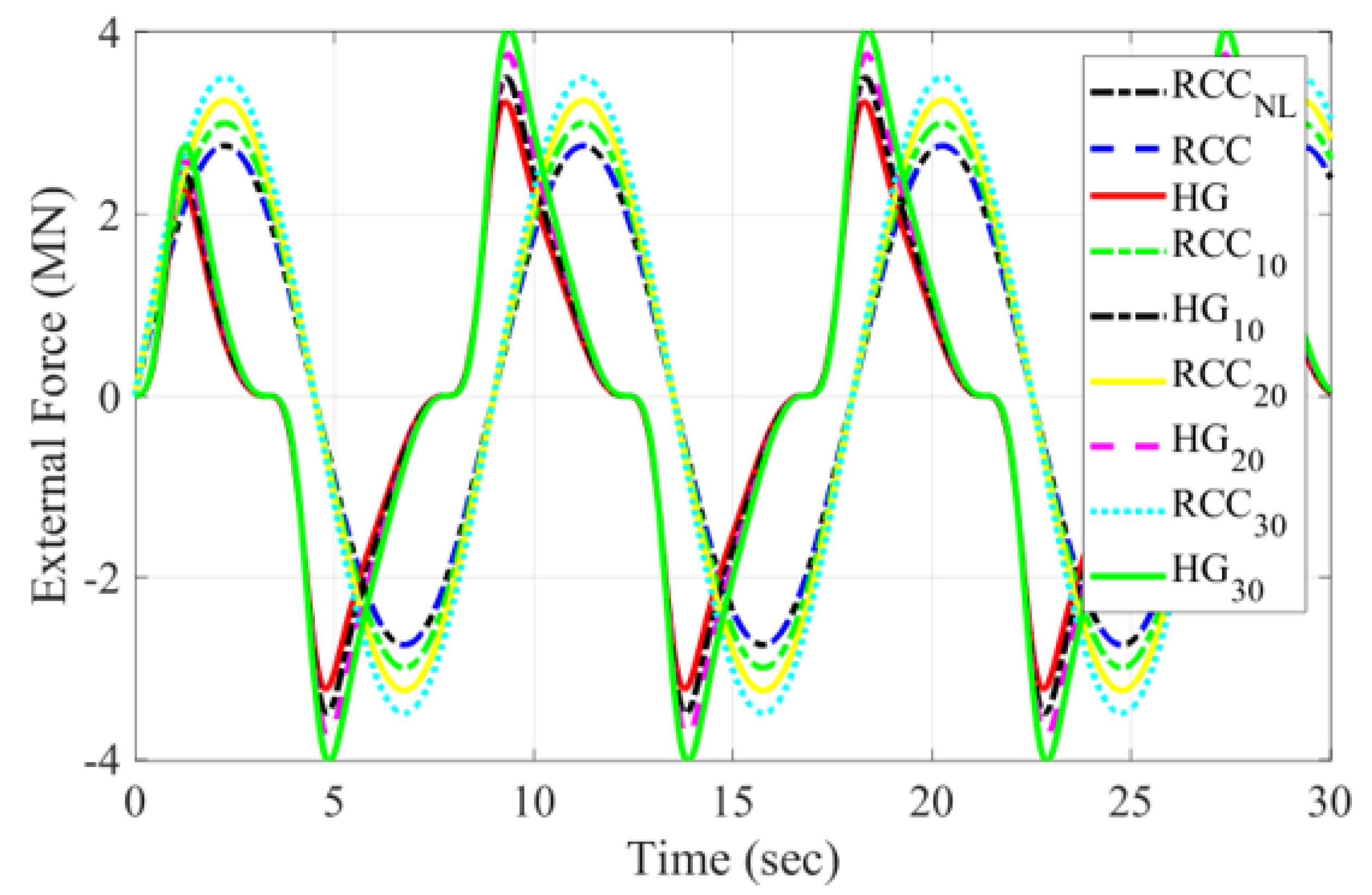
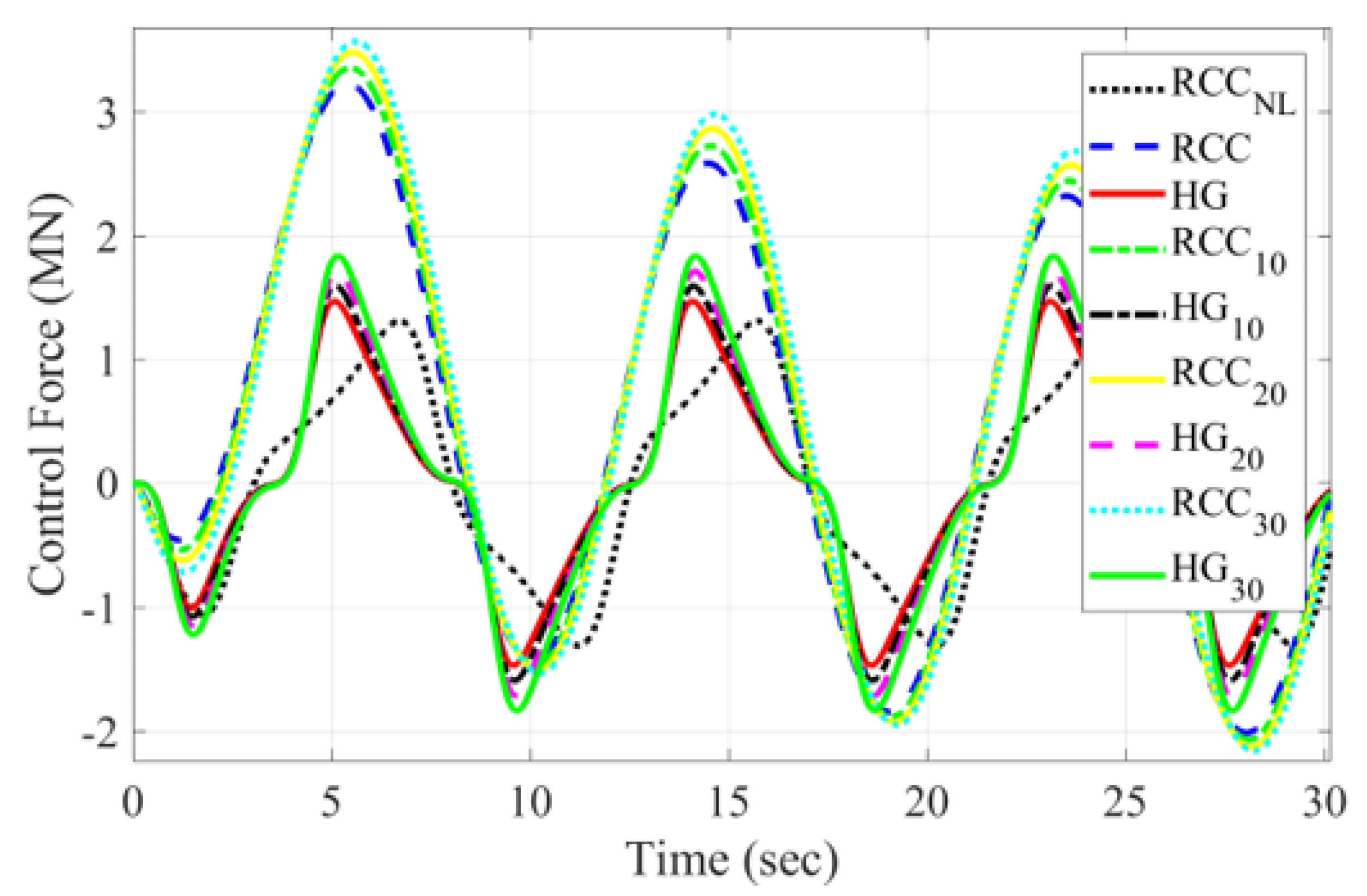




| Parameter | Symbol | HG Range | RCC Value | Unit |
|---|---|---|---|---|
| Radius | r | 5.72–10.0 | 4.47 | m |
| Height | h | 8.18–2.68 | 4.47 | m |
| Angle | 50–70 | 0.00 | deg |
| Parameter | Unit | RCCNL | RCC | HG | RCC10 | HG10 | RCC20 | HG20 | RCC30 | HG30 |
|---|---|---|---|---|---|---|---|---|---|---|
| deg | N/A | N/A | 59.5 | N/A | 56.5 | N/A | 53.5 | N/A | 50.9 | |
| 3.844 | 4.456 | N/A | 4.848 | N/A | 5.242 | N/A | 5.746 | N/A | ||
| m | 4.47 | 4.47 | 4.53 | 4.47 | 4.896 | 4.47 | 5.274 | 4.47 | 5.614 | |
| MJ | 129 | 146 | 146 | 160 | 171 | 173 | 197 | 183 | 226 |
| Sea State | (m) | (sec) | Duration (sec) |
|---|---|---|---|
| 1 | 5.7 | 8.0 | 300.0 |
| 2 | 6.6 | 6.6 | 300.0 |
| 3 | 7.8 | 7.8 | 300.0 |
| 4 | 6.9 | 11.0 | 300.0 |
| Angle | Draft | Sea State 1 | Sea State 2 | Sea State 3 | Sea State 4 |
|---|---|---|---|---|---|
| hhalf | Emax | Emax | Emax | Emax | |
| deg | m | MJ | MJ | MJ | MJ |
| 55 | 5.084 | 26.485 | 23.935 | 174.63 | 32.230 |
| 60 | 4.470 | 43.240 | 39.235 | SAT | 48.564 |
| 65 | 3.8767 | 67.170 | 61.550 | – | 69.790 |
| 70 | 3.2864 | SAT | 92.752 | – | SAT |
| 75 | 2.680 | – | SAT | – | – |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, D.G.; Robinett, R.D., III; Bacelli, G.; Abdelkhalik, O.; Coe, R.G. Extending Complex Conjugate Control to Nonlinear Wave Energy Converters. J. Mar. Sci. Eng. 2020, 8, 84. https://doi.org/10.3390/jmse8020084
Wilson DG, Robinett RD III, Bacelli G, Abdelkhalik O, Coe RG. Extending Complex Conjugate Control to Nonlinear Wave Energy Converters. Journal of Marine Science and Engineering. 2020; 8(2):84. https://doi.org/10.3390/jmse8020084
Chicago/Turabian StyleWilson, David G., Rush D. Robinett, III, Giorgio Bacelli, Ossama Abdelkhalik, and Ryan G. Coe. 2020. "Extending Complex Conjugate Control to Nonlinear Wave Energy Converters" Journal of Marine Science and Engineering 8, no. 2: 84. https://doi.org/10.3390/jmse8020084
APA StyleWilson, D. G., Robinett, R. D., III, Bacelli, G., Abdelkhalik, O., & Coe, R. G. (2020). Extending Complex Conjugate Control to Nonlinear Wave Energy Converters. Journal of Marine Science and Engineering, 8(2), 84. https://doi.org/10.3390/jmse8020084







