Simulation of Marine Towing Cable Dynamics Using a Finite Elements Method

Abstract

A numerical model to study the towing maneuver for floating and submerged bodies has been developed. The proposed model is based on the dynamic study of a catenary line moving between two bodies, one body with imposed motion, and the other free to move. The model improves previous models used to study the behavior of mooring systems based on a finite element method by reducing the noise of the numerical results considering the Rayleigh springs model for the tension of the line. The code was successfully validated using experimental results for experimental data from different authors and experiments found in the literature. Sensitivity analysis on the internal damping coefficient and the number of elements has been included in the present work, showing the importance of the internal damping coefficient. As an example of the application of the developed tool, simulations of towing systems on a real scale were analyzed for different setups. The variation of the loads at the towed body and the position of the body were analyzed for the studied configurations. The reasonable results allow us to say that the proposed model is a useful tool with several applications to towing system design, study or optimization.

1. Introduction

The rapid development of floating structures such as wave energy converters, floating wind turbines and aquaculture structures has increased the use of the marine space. The new uses involve more and complex marine operations, as part of industrialized operation and maintenance strategies, where apart from accessibility issues, device towing becomes a critical issue. Moreover, the installation of floating devices is usually done by a ship towing the device using a catenary line, as shown in Figure 1. However, submerged towing systems are also used in numerous ocean engineering applications such as sonars, seabed exploration, fishing or spotting sea mines.

All these activities require well planned actions to lower the risk and to raise the impact over the OPEX costs. Therefore, numerical models become a crucial tool for optimized marine operations. The purpose of this paper is to provide a numerical tool to analyze the towing maneuver of floating and submerged bodies, to be integrated into future operational systems.

Submerged and floated towing maneuvers involve a cable that connects a ship with the towed device. There are different alternatives in the literature to study the mooring systems of floating bodies. These methods are based in the study of the cable dynamics using a finite element method (FEM) [1,2] and lumped mass models (LM) [3,4]. All these authors use Morison equation for the fluid-cable interaction, neglecting viscous effects as the Vortex Induced Vibrations [5,6]. This simplification is also assumed for the present work. Zhu [7] proposed a new nodal position FEM (NP-FEM) to study the towing of submerged bodies. The possibility of improving the numerical results found in the literature for towing systems, and the model used for the tension term on the mooring or towing lines led to this paper, where an extension of these models is proposed, improving and adapting them for application in towing maneuvers.

The Environmental Hydraulics Institute already has an implementation of a numerical FEM model used to study mooring systems, based on References [1,8]. The scope of this work was to improve and adapt that implementation with the inclusion of the internal damping and the towing boundary conditions. In point of fact, this code has been modified to study the towing maneuvers, implying the modification of the boundary conditions used in the model. In the study of mooring lines, one boundary moves with the moored body, and the other boundary is fixed to the seabed. In this case, one boundary will move with enforced movements, simulating the motion of the towing ship, while the other boundary is free to move the body connected in it. The presented model is validated against experimental data published in the literature [7,9]. These experiments were chosen as good cases for checking correctness for computing snap tensions and cable positioning, respectively. Additionally, a sensitivity analysis for the number of elements used in the discretization of the line and the damping included in the model was performed.

The validated model has been used to study the towing of two bodies. The objective was to check that the code would yield reasonable results for real-scale problems. The first example studied was the simulation of the towing of a submerged body, such as a sonar, by a moving ship. Different line lengths and body weights were evaluated to study the final position at which the towed body navigated. In the second example, the towing body is floating, as shown in Figure 1. In this case, also, different line lengths were tested. The effect of including an intermediate body to add extra buoyancy, or weight, to the catenary, increasing or decreasing the vertical component of the force at the towed body was also tested. Finally, the influence of the vertical force was also evaluated, depending on the position of the intermediate body.

This paper continues with a brief description of the numerical model used to study mooring lines and the new boundary condition applied to the study of the towing maneuver in Section 2. Then, the validation of the proposed model using experimental works published in the literature is presented in Section 3. Finally, the proposed methodology is applied to the towing of two bodies, one submerged and one floating, in Section 4. The work ends up with a discussion of the work done, presented in Section 5.

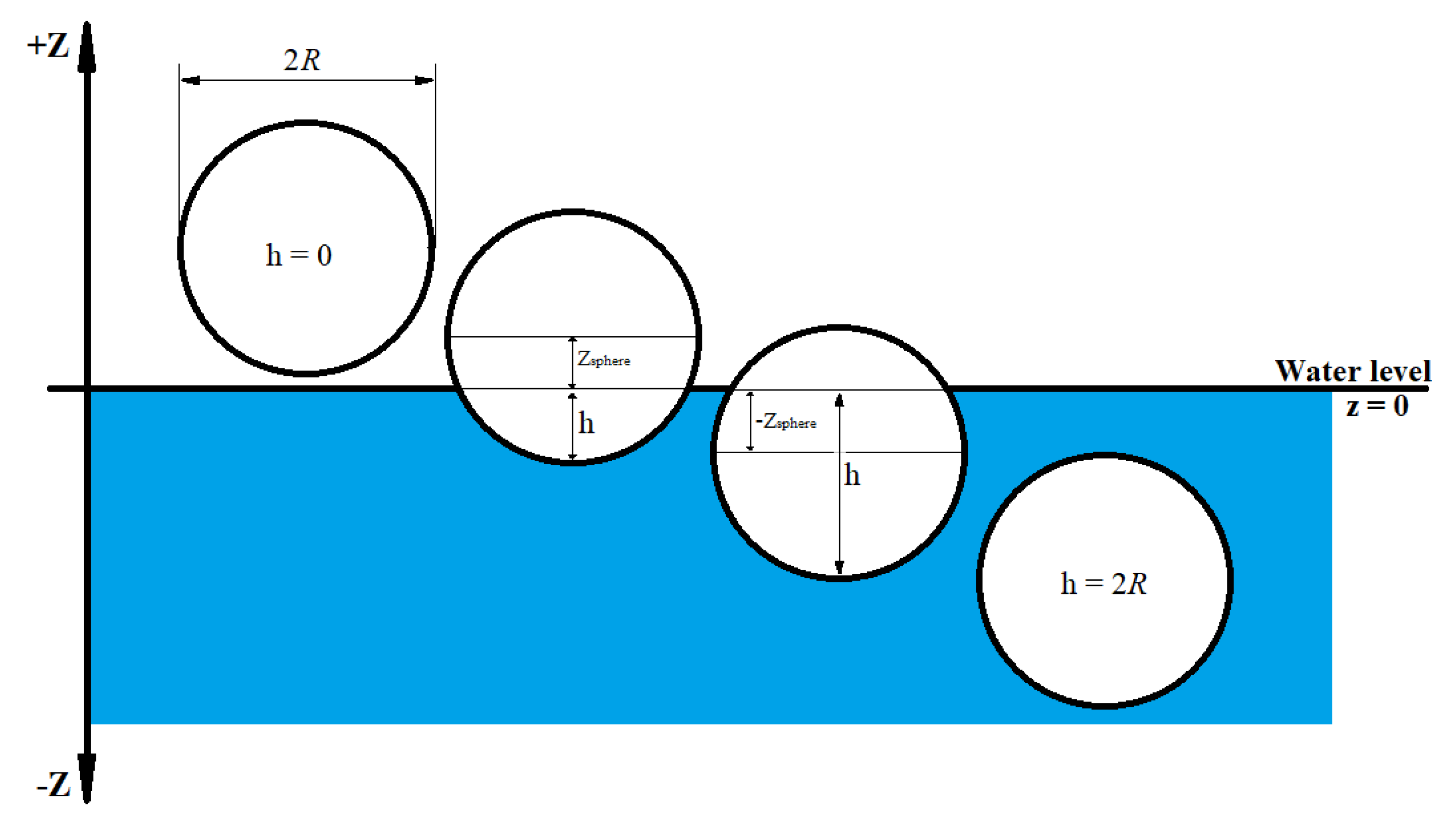
2. Numerical Model

In the current research on towing and mooring dynamics simulation, a finite element method (FEM) is used to solve the partial differential equation (PDE) ruling cable dynamics. The equation used in the literature generally ignores flexion and torsion effects and is based on the one-dimensional wave equation [1,2,3,4]:

$$\begin{array}{c}\hfill {\rho }_0\frac{{\partial }^2\mathbf{r}(t,s)}{\partial t^2}=\frac{\partial }{\partial s}\left(T(t,s)\mathit{t}(t,s)\right)+\mathbf{f}(t,s)(1+e(t,s)),\end{array}$$

(1)

where $\mathbf{r}(t,s)$ denotes the position of the cable parametrized by arc length, $s\in [0,L]$ represents the variable of the parametrization of the curve of the cable, t is the time variable, ${\rho }_0$ denotes the linear density of the cable, $T(s,t)$ is the tension of the cable, $\mathit{t}(t,s)$ is the unitary tangential vector to the cable, $\mathbf{f}(t,s)$ is the external force vector and $e(t,s)$ represents the strain of the cable.

The external forces $\mathbf{f}$, are composed of the buoyancy force ${\mathbf{f}}_{hg}$, normal ${\mathbf{f}}_{dn}$ and tangential ${\mathbf{f}}_{dt}$ hydrodynamic drag forces and the inertial forces ${\mathbf{f}}_{mn}$.

$$\begin{array}{c}\hfill \mathbf{f}={\mathbf{f}}_{hg}+{\mathbf{f}}_{dt}+{\mathbf{f}}_{dn}+{\mathbf{f}}_{mn}\end{array}.$$

(2)

These forces are defined as follows:

$$\begin{array}{ccc}\hfill {\mathbf{f}}_{hg}& =& {\rho }_0\frac{{\rho }_c-{\rho }_w}{(1+e){\rho }_c}\mathbf{g}\hfill \\ \hfill {\mathbf{f}}_{dn}& =& -\frac{1}{2}{C}_{dn}d{\rho }_w\left|{\mathbf{v}}_n\right|{\mathbf{v}}_n\hfill \\ \hfill {\mathbf{f}}_{dt}& =& -\frac{1}{2}{C}_{dt}d{\rho }_w\left|{\mathbf{v}}_t\right|{\mathbf{v}}_t\hfill \\ \hfill {\mathbf{f}}_{mn}& =& -C_{mn}\frac{\pi d^2}{4}{\rho }_w{\mathbf{a}}_n\hfill \end{array},$$

(3)

where ${\rho }_c$ is the density of the cable material, ${\rho }_w$ is the water density, $\mathbf{g}$ is the gravity acceleration, $C_{dn}$ and $C_{dt}$ are normal and tangential drag coefficients, respectively, $C_{mn}$ is hydrodynamic mass coefficient, d is the diameter of the cable, $\mathbf{v}$ and $\mathbf{a}$ denote velocity and acceleration, and subindices n and t denote normal or tangential components of the vector, respectively.

In Reference [1], first-order FEM is used to solve Equation (1) as follows—the PDE is transformed into the generalized problem, the Galerkin method is used, and the cable is discretized in $n+1$ points $\mathbf{r}(s,t)=({\mathbf{r}}_0,{\mathbf{r}}_1,\dots ,{\mathbf{r}}_n)$, where ${\mathbf{r}}_n$ is the position of the top support of the cable at the fairlead of the body, and ${\mathbf{r}}_0$ is the position of the opposite end of the cable, the position of a fixed anchor in Reference [1] and the position of the towed body in this research. In this way, a system of lineal ordinary differential equations (ODEs) is generated. The following approximation can be considered:

$$\begin{array}{c}\hfill {\dot{\mathbf{r}}}_{k-1}\approx {\dot{\mathbf{r}}}_k{\dot{\mathbf{r}}}_{k+1}\approx {\dot{\mathbf{r}}}_k{\ddot{\mathbf{r}}}_{k-1}\approx {\ddot{\mathbf{r}}}_k{\ddot{\mathbf{r}}}_{k+1}\approx {\ddot{\mathbf{r}}}_k,\end{array}$$

(4)

which allows for the matrices describing the system of ODE to become tridiagonal and gives simplified expressions for the elementary matrices and vectors—mass elementary matrix ${\mathbf{M}}_k$, drag elementary matrix ${\mathbf{D}}_k$, stiffness elementary vector ${\mathbf{k}}_k$ and external forces elementary vector ${\mathbf{g}}_k$ (only gravity considered here). The approximation supposes that each element separately cannot bend or rotate, and for the line, in general, that bending of the line does not result in any elastic forces being applied. The assembling of the elementary matrices results in the total system, where boundary conditions are applied by substituting identity matrices and expected acceleration vectors in the appropriate positions of the mass matrix and the total forces vector. In this work, this model is implemented, and the system is solved with LAPACK routines [10]. ODEPACK routines are used to obtain the time evolution of the problem—predictor-corrector Adams methods are chosen for nonstiff problems, and backwards differentiation formula-based methods are chosen for stiff problems [11]. To assure the correct solution of the system, the relative and absolute tolerances are chosen to be ${10}^{-7}$ and ${10}^{-9}$, respectively.

2.1. Damping Coefficient

In this work, as was done in References [8,12], the tension term in Equation (1) is computed by considering each element of a cable with section $A_0$ as a Rayleigh spring: a combination of a spring with the Young’s modulus E and a resistance with a damping coefficient $\beta$, as shown in Equation (5).

$$\begin{array}{c}\hfill T(t,s)=E{A}_0\left(e+\beta \frac{\partial e}{\partial t}\right).\end{array}$$

(5)

In other words, the term ${\displaystyle E{A}_0\beta \frac{\partial e}{\partial t}}$ is added to the Hook’s law equation $(T(t,s)=E{A}_{0}e)$. To use Equation (5) in the numerical model proposed in Reference [1], it is necessary to compute numerically ${\displaystyle \frac{\partial e}{\partial t}}$. The exact and the numerical expressions of $e(s,t)$ are given by Equation (6). For the numerical expression, the strain will be considered constant on each element.

$$\begin{array}{c}\hfill e(s,t)=\left|\frac{\partial \mathbf{r}(s,t)}{\partial s}\right|-1\approx \frac{1}{l}\left|{\mathbf{r}}_k-{\mathbf{r}}_{k-1}\right|-1=e_k\left(t\right),\end{array}$$

(6)

where l is the length of each element that is considered in the cable, $s\in \left(\right(k-1)·l,k·l)$ and $k\in \{1,\dots ,n\}$. Considering that ${\overrightarrow{r}}_k=\left(x_k\left(t\right),y_k\left(t\right),z_k\left(t\right)\right)$ Equation (6) can be rewritten as:

$$\begin{array}{c}\hfill e_k\left(t\right)=\frac{1}{l}·\sqrt{{\left(x_k\left(t\right)-x_{k-1}\left(t\right)\right)}^2+{\left(y_k\left(t\right)-y_{k-1}\left(t\right)\right)}^2+{\left(z_k\left(t\right)-z_{k-1}\left(t\right)\right)}^2}-1.\end{array}$$

(7)

Taking the derivative, consider that: ${\displaystyle \frac{\partial {\mathbf{r}}_k}{\partial t}={\dot{\mathbf{r}}}_k=\left({\dot{x}}_k,{\dot{y}}_k,{\dot{z}}_k\right)}$; a numerical expression for the time derivative of the cable strain is obtained in Equation (8).

$$\begin{array}{c}\hfill {\dot{e}}_k=\frac{1}{l}\frac{1}{\left|{\mathbf{r}}_k-{\mathbf{r}}_{k-1}\right|}\left[(x_k-x_{k-1})({\dot{x}}_k-{\dot{x}}_{k-1})+(y_k-y_{k-1})({\dot{y}}_k-{\dot{y}}_{k-1})+(z_k-z_{k-1})({\dot{z}}_k-{\dot{z}}_{k-1})\right].\end{array}$$

(8)

For the tension term, Hook’s law is used in Reference [1]. When the Voigt-Kelvin model is considered instead, the only expression that changes is the one for the elementary stiff matrix, as is shown in Equation (9).

$$\begin{array}{c}{\mathbf{k}}_k=\frac{EA}{l}\left[\left(\frac{|{\mathbf{r}}_k-{\mathbf{r}}_{k-1}|-l}{|{\mathbf{r}}_k-{\mathbf{r}}_{k-1}|}·({\mathbf{r}}_k-{\mathbf{r}}_{k-1})-\frac{|{\mathbf{r}}_{k+1}-{\mathbf{r}}_k|-l}{|{\mathbf{r}}_{k+1}-{\mathbf{r}}_k|}·({\mathbf{r}}_{k+1}-{\mathbf{r}}_k)\right)+\right.\hfill \\ \left.+\beta ·\left(\frac{{\dot{e}}_k}{|{\mathbf{r}}_k-{\mathbf{r}}_{k-1}|}·({\mathbf{r}}_k-{\mathbf{r}}_{k-1})-\frac{{\dot{e}}_{k+1}}{|{\mathbf{r}}_{k+1}-{\mathbf{r}}_k|}·({\mathbf{r}}_{k+1}-{\mathbf{r}}_k)\right)\right].\hfill \end{array}$$

(9)

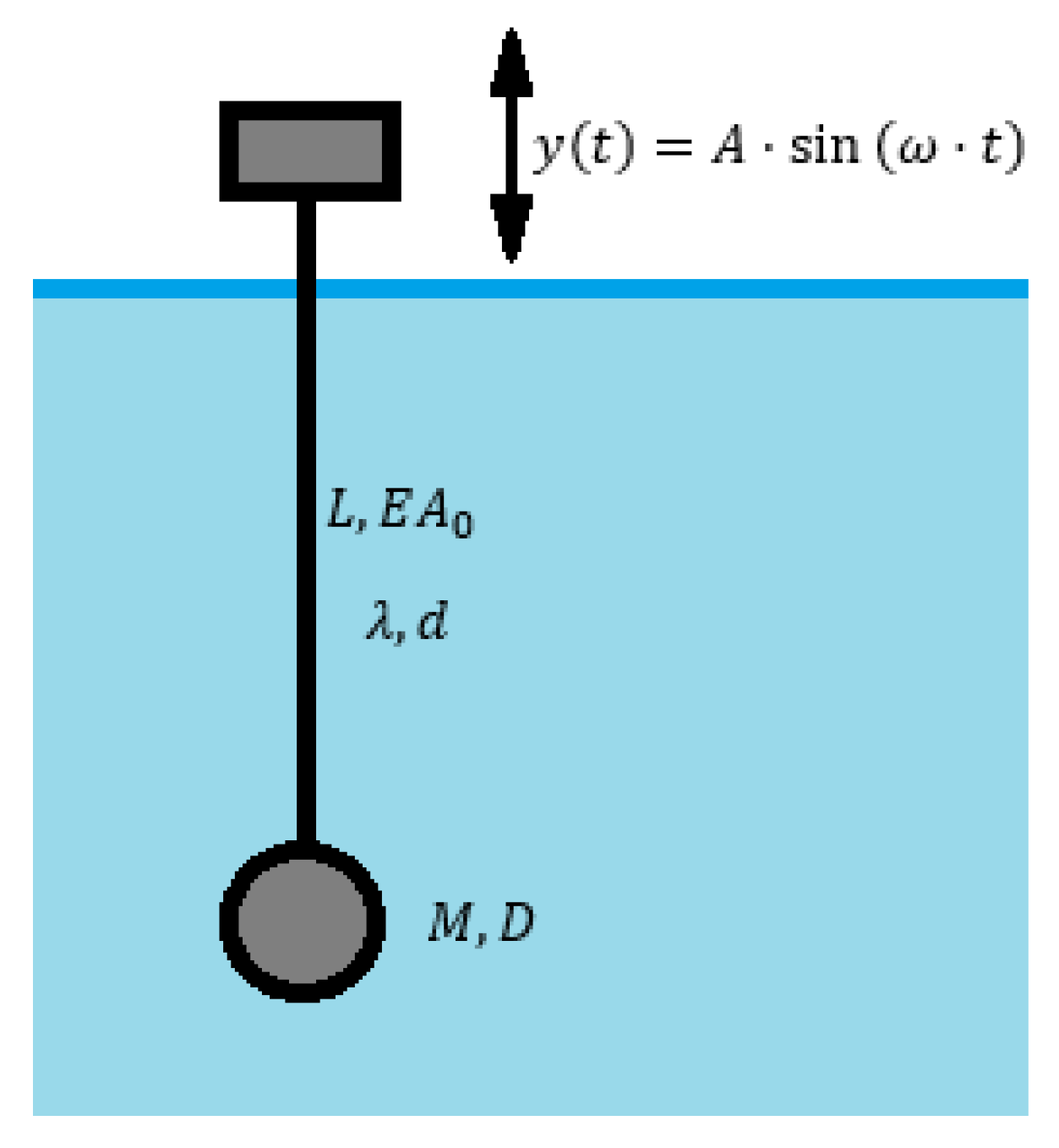
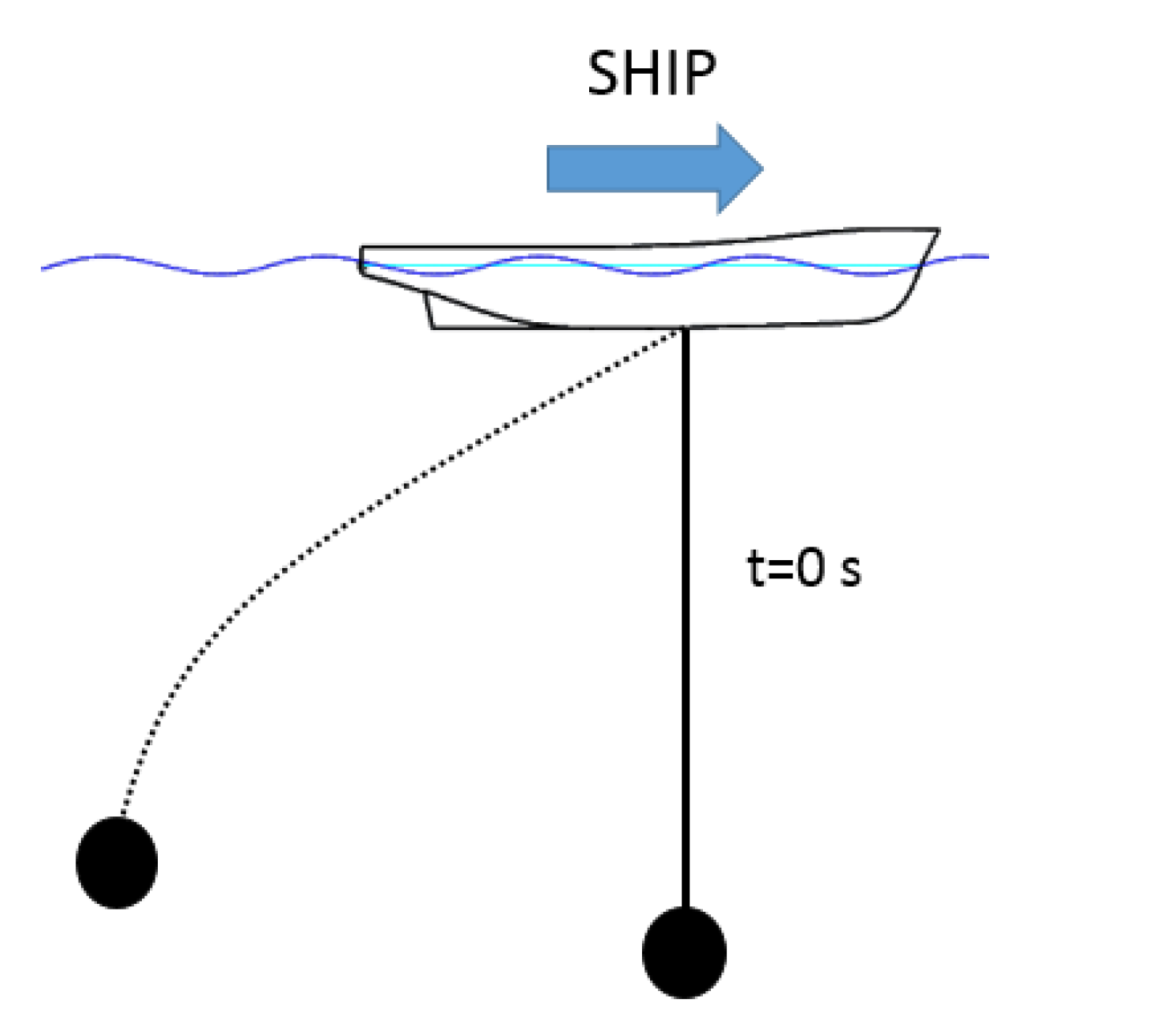
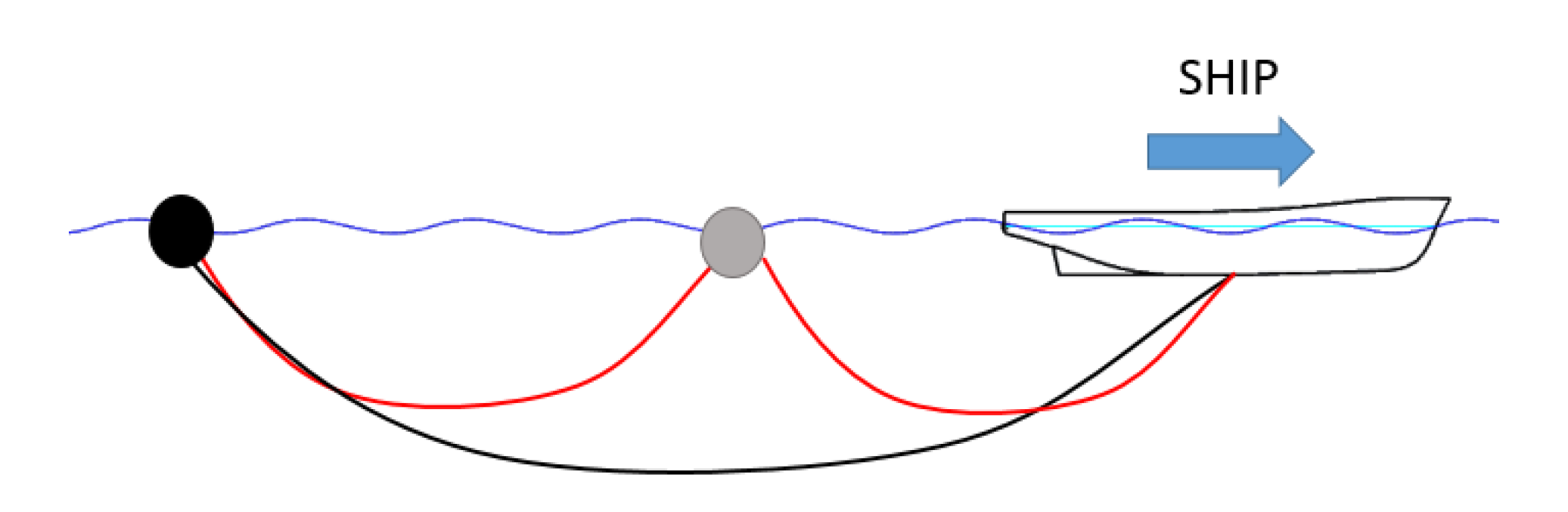
2.2. Towing Boundary Condition

To implement the boundary conditions of the towing problem, the expected acceleration at the fairlead of the towed body needs to be calculated. To perform this calculation, a potential flow theory or CFD may be used to compute the hydrodynamic forces and momenta over the towed body, using the position of the body, velocity and acceleration at the previous time-step. For the external forces and momenta, the known tension of the line at the towed body fairlead may be considered. With the sum of all these forces and momenta, the added mass matrix and the inertia matrix of the towed body, it is possible to find its acceleration for the six degrees of freedom. Using the solid body theory, the acceleration of the fairlead, for three degrees of freedom, can be computed. Finally, this acceleration is imposed on the node where the towed body is wanted.

Some approximations may be considered for towed bodies with certain symmetries, and it could be possible to ignore their rotations. For spherical body towing, the rotations can be ignored, the hydrodynamic forces are obtained using the Morison equation, and the hydrostatic forces can be computed theoretically. An example of approximately spherical body towing systems are the used in operations of installation of buoys or more sophisticated devices as wave energy converters [13]. For this reason, in this work, spherical body towing systems are studied as a particular example.

First, the hydrodynamic forces over the sphere were computed based on the Morison equation. In this case, it is assumed that the sphere is fully submerged for the computation of these forces. For an object submerged in a fluid with a certain flow, there will be a force parallel to the flow applied over the body. If the fluid density is $\rho$, the flow velocity is $\overrightarrow{u}$ and the body has volume V, cross-sectional area perpendicular to the flow A, drag coefficient $C_d$ and added mass coefficient $C_a$, the Morison Equation (10) is:

$$\begin{array}{c}\hfill {\overrightarrow{F}}_M=\rho C_{a}V·\dot{\overrightarrow{u}}+\frac{1}{2}\rho C_{d}A·\overrightarrow{u}|\overrightarrow{u}|.\end{array}$$

(10)

Additionally, other forces must be considered, such as gravity, buoyancy and tension of the line at the sphere. For gravity and buoyancy, if the body has a mass m and $\mathbf{g}$ is the gravity acceleration at sea level, the force can be written as:

$$\begin{array}{c}\hfill {\overrightarrow{F}}_{gb}=(V_u·\rho -m)·\mathbf{g},\end{array}$$

(11)

where $V_u$ is the volume under water, studied in detail later for the spherical case. For the tension force, since the body will be placed at the first node:

$$\begin{array}{c}\hfill {\overrightarrow{F}}_k=E{A}_0·(e_1+\beta ·{\dot{e}}_1)·\frac{{\mathbf{r}}_1-{\mathbf{r}}_0}{|{\mathbf{r}}_1-{\mathbf{r}}_0|}.\end{array}$$

(12)

Now, considering Equations (10)–(12), when the body is a sphere of radius R and mass m located at the first node, the acceleration of the body is:

$$\begin{array}{c}\hfill {\mathbf{a}}_{sphere}=\frac{{\overrightarrow{F}}_M+{\overrightarrow{F}}_{gb}+{\overrightarrow{F}}_k}{m+C_a\rho V},\end{array}$$

(13)

where the flow velocity or acceleration are taken to be the velocity or acceleration of the flow at the point where the first node is minus the velocity or acceleration of the first node, and:

• $A^{sphere}=\pi R^2$
• $V^{sphere}=\frac{4}{3}\pi R^3$
• $V_u^{sphere}=\frac{\pi h^2}{3}(3R-h)$
• $h=min\{2R,max\{0,R-z_{sphere}\}\}$
• $C_m^{sphere}=0.5$
• $C_d^{sphere}=0.47$

The volume and area of the sphere are well known, and the drag and mass coefficient expressions are given in the literature [14,15]. The expression for $V_u^{sphere}$ comes from the volume of a spherical cap where h is the height of the cap. The expression for h gives the height of the spherical cap that is under water, where $z_{sphere}$ is the z coordinate of the center of the sphere, as shown in Figure 2. The $min$ and $max$ of the h equation allow to consider the different possibilities for the relative position of the sphere with the water level: completely submerged, most of it submerged, most of it emerged and completely emerged.

For a sphere located in an inner node i of the cable, the acceleration at that node would be replaced by the acceleration in Equation (13), but using the inner or intermediate node position, velocity and acceleration. Then, ${\overrightarrow{F}}_k$ in Equation (12) is replaced by:

$$\begin{array}{c}\hfill {\overrightarrow{F}}_k=E{A}_0·\left[(e_i+\beta ·{\dot{e}}_i)·\frac{{\mathbf{r}}_{i-1}-{\mathbf{r}}_i}{|{\mathbf{r}}_{i-1}-{\mathbf{r}}_i|}+(e_{i+1}+\beta ·{\dot{e}}_{i+1})·\frac{{\mathbf{r}}_{i+1}-{\mathbf{r}}_i}{|{\mathbf{r}}_{i+1}-{\mathbf{r}}_i|}\right].\end{array}$$

(14)

For the case where nothing is hanging from the towing cable, the boundary condition was approached as the boundary condition for a sphere with the cable density and diameter.

3. Validation

To validate the numerical model proposed, two different benchmark cases were studied: a sphere hanging with a cable from a boat that oscillates vertically and a cable swinging after being released from one of the two supports that were holding both of its ends at the same height. The first case uses the experimental and numerical results shown in Reference [7] and the second case uses the results from Reference [9].

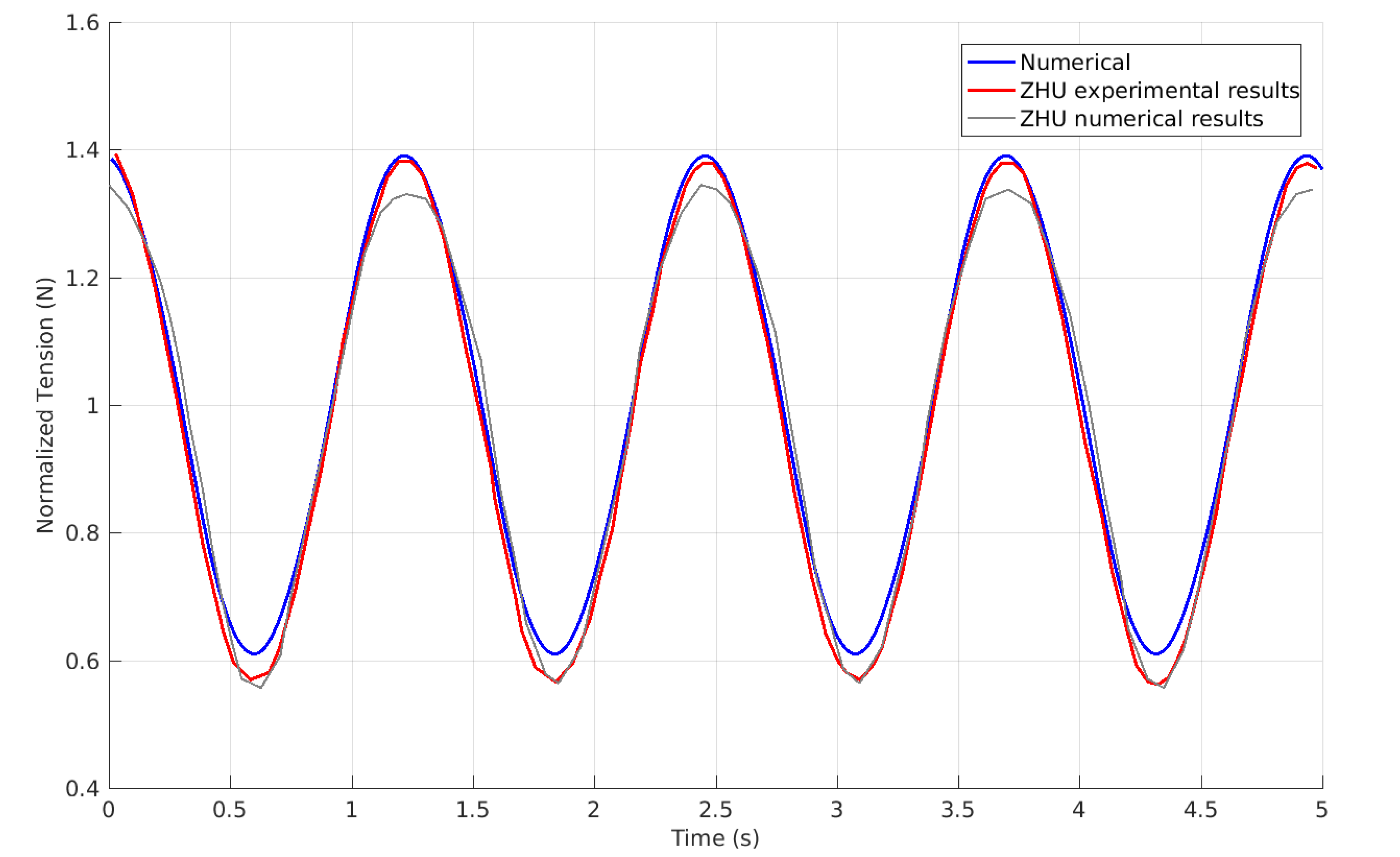
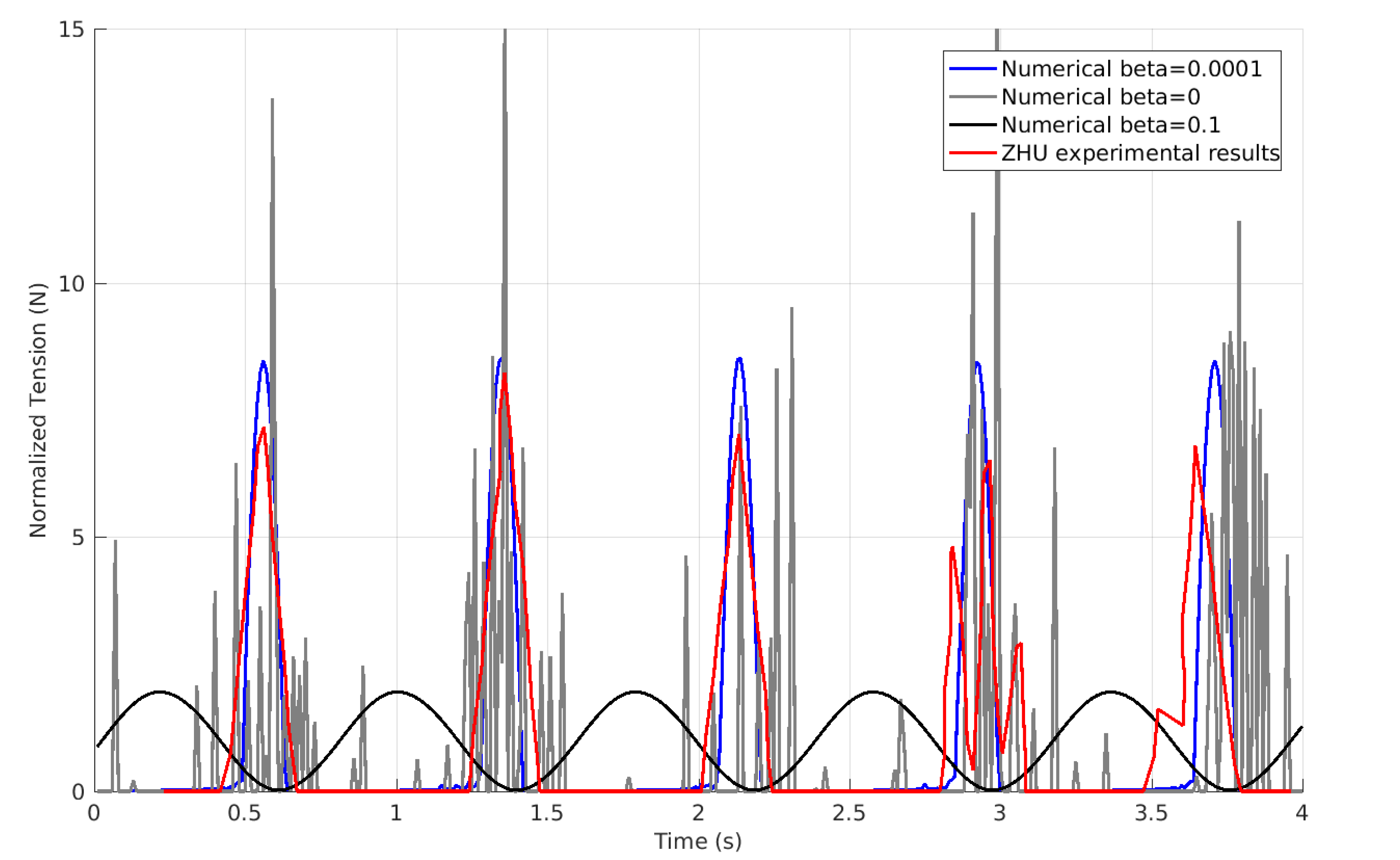
3.1. Zhu’s Experiment

This experiment considers a sphere hanging with a cable from a boat that oscillates vertically, as shown in Figure 3, and it studies the vertical tension at the top of the cable, done for two different frequencies (0.807 Hz and 1.27 Hz) and with a 78 mm amplitude of oscillation. In this paper, first, the numerical results of the optimal configuration of number of nodes and internal damping are shown and compared with the experimental results. Then, for the higher frequency, a sensitivity analysis of the numerical results for the number of nodes and for the internal damping coefficient is performed.

3.1.1. Optimal Simulation

The optimal simulation (see Section 3.1.2 and Section 3.1.3) uses 40 nodes, a 0.01 s time-step and an internal damping coefficient $\beta ={10}^{-4}$, and the numerical normalized tension results of the low frequency case are shown in Figure 4. In this case, the numerical results from the new method show great accuracy in predicting the peak tension, improving Zhu’s results as those predict a lower tension. This does not happen for the minimum tension, where Zhu’s results are better, and our results predict higher tension values. The overall performance of the numerical model is highly positive.

For the higher frequency results, displayed in Figure 5, the method presented shows lower noise than Zhu’s, a constant peak tension and an excellent agreement with the maximum peak tension registered in the experimental results, backing the method as a good predictor of the peak tension, as was seen for low frequency. The maximum tension registered in the experiment is accurately predicted numerically. However, some differences may be identified. The differences can be justified by horizontal dispersion of energy or effects of turbulence, which are not considered by the model. On the one hand, this approach shows the limitations of the model, but on the other hand, it is not needed to consider that many physical phenomena to predict maximum peak tensions in the cable, as it also shows that the most important physical processes are well captured.

3.1.2. Dependence on the Internal Damping Coefficient

The study of the dependence on the internal damping coefficient is presented in Figure 6 and shows that for zero internal damping, a great amount of noise is produced, similar to Zhu’s numerical results. This finding was expected, as introducing the internal damping coefficient is one of the main differences of the presented method with Zhu’s model. High internal damping coefficients cancel the snap tensions. Therefore, we can be assured that an appropriate election of the internal damping coefficient is essential to predict the maximum peak tensions accurately. The computational times for the 0, ${10}^{-4}$, and $0.1$ internal damping coefficients simulations were 30 s, 1.2 s and 1.9 s per second of simulation, respectively, which shows that introducing the $\beta$-coefficient implies lower computational time. Lower noise is closely related to lower computational cost: the lower the internal oscillations are, the faster the convergence of the ODE solvers is.

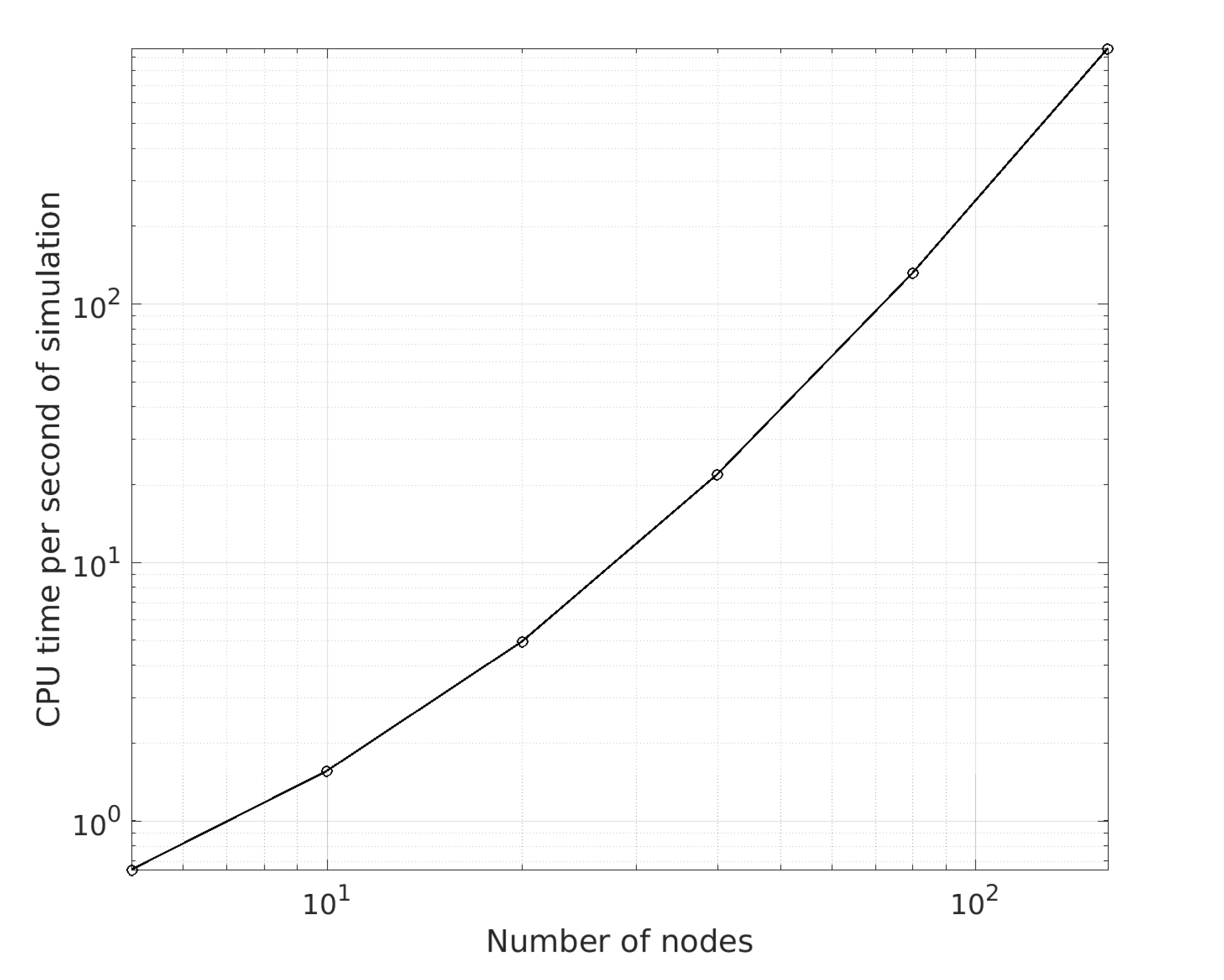
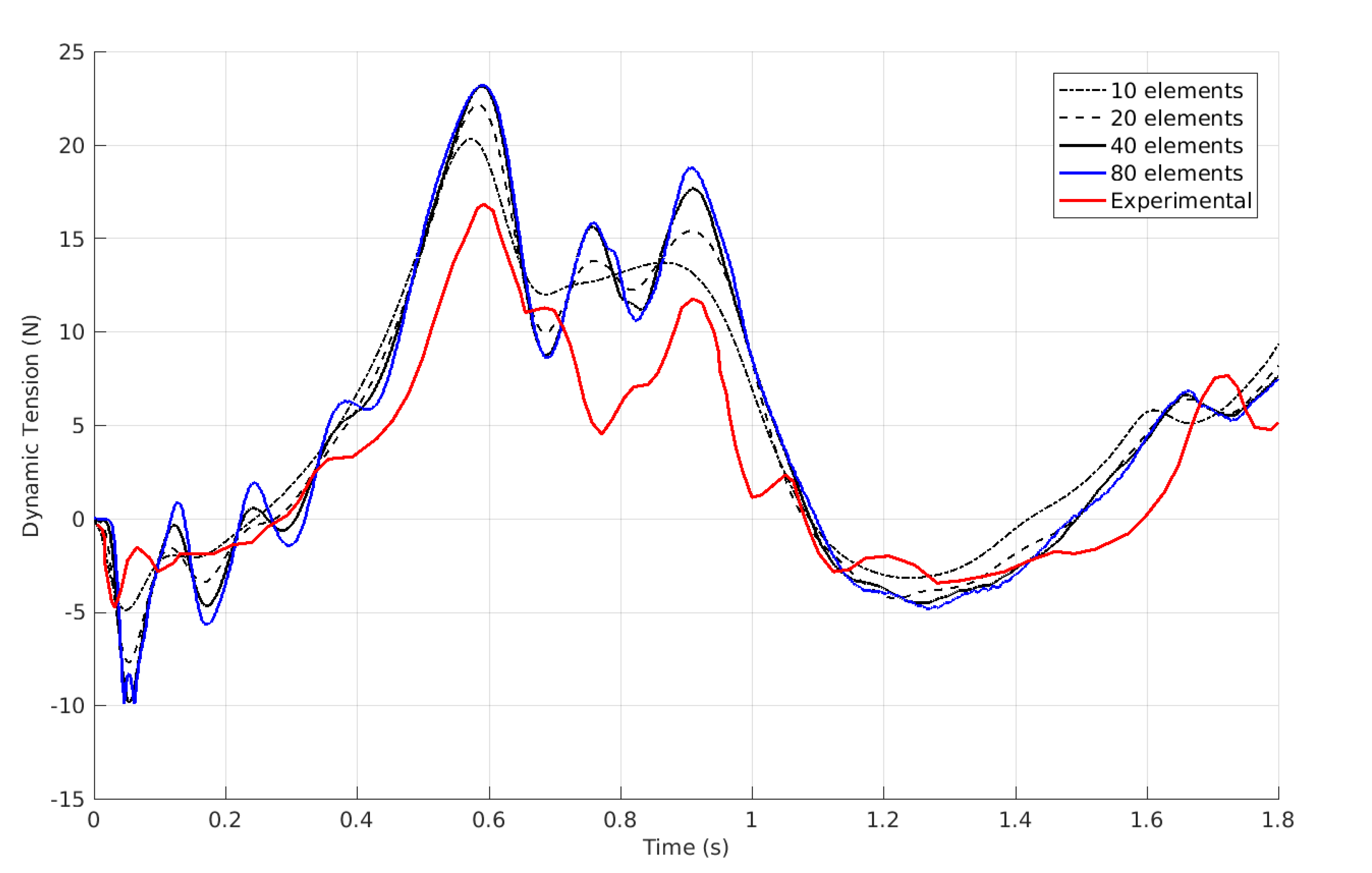
3.1.3. Dependence on the Number of Nodes

Furthermore, an analysis of the dependence on the number of nodes has been performed. Figure 7 and Figure 8 show low dependence on the number of nodes. The detailed figure shows better agreement with the maximum peak tension and a lower phase difference and noise for the higher number of nodes, as was expected. The computational times are shown in Figure 9. For this case, using a low number of elements, the results are slightly conservative (larger prediction for peaks), although this results may not be true in general. Additionally, the computational cost is smaller for the lower number of nodes, as was expected.

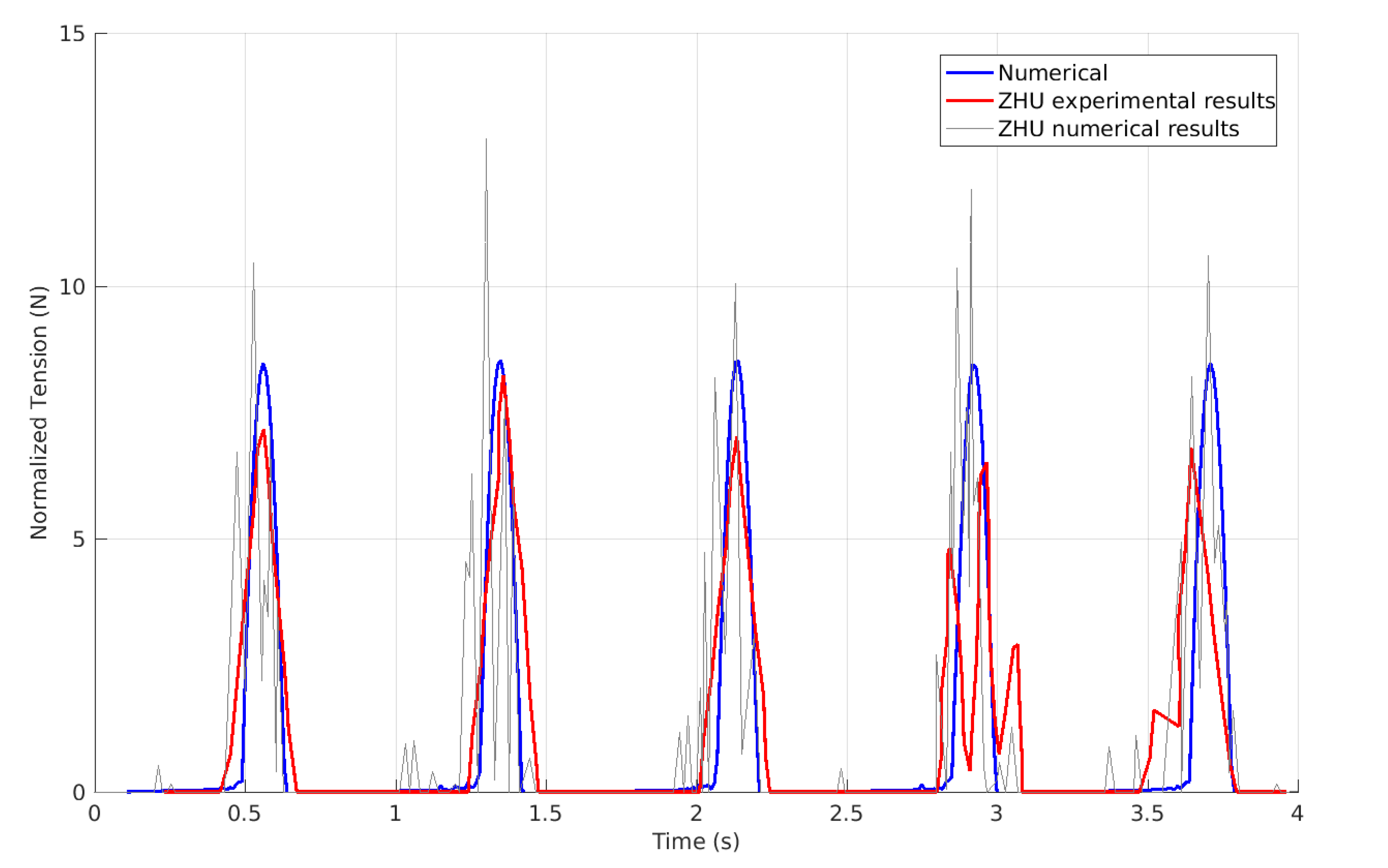
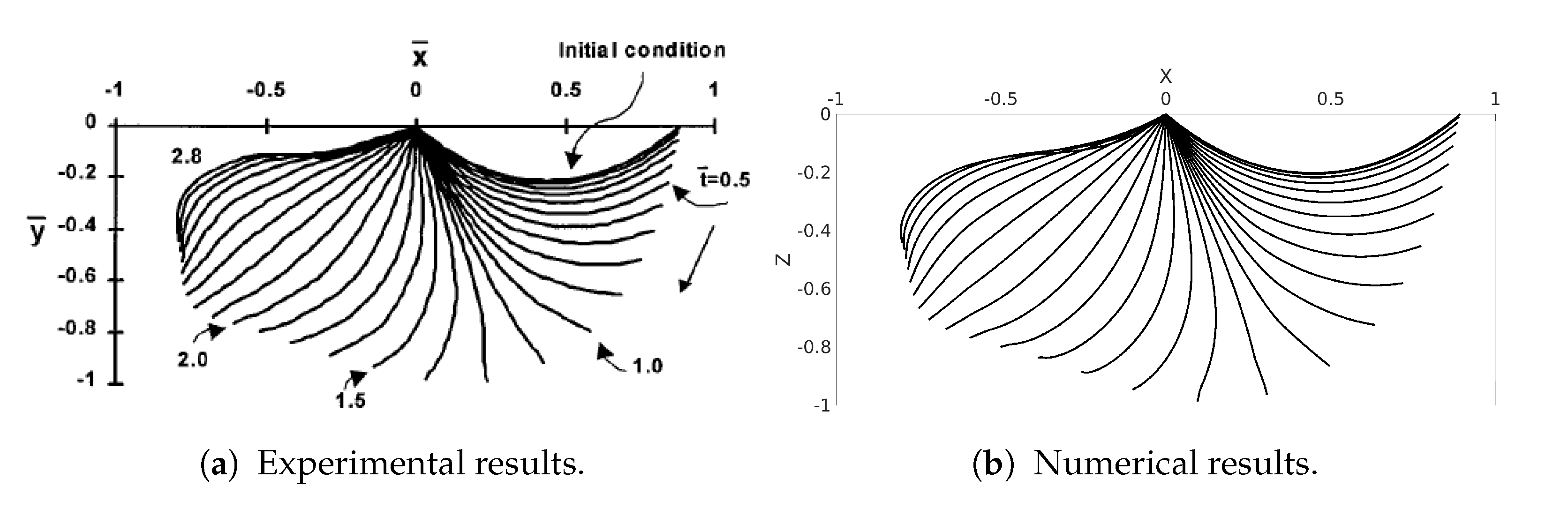
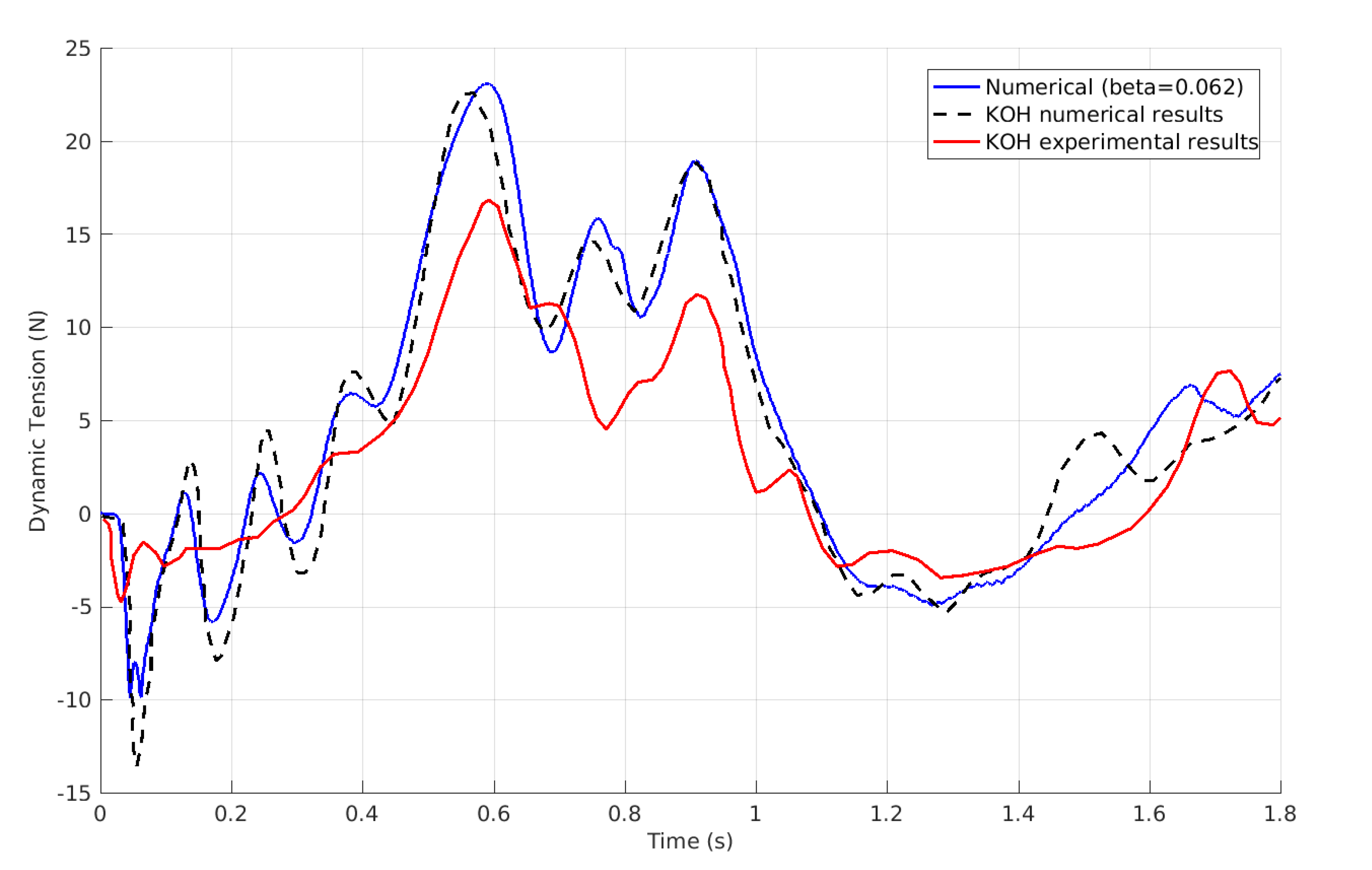
3.2. Koh’s Experiment

This experiment measures the shape of a cable and its tension at the top support when it swings. The cable is initially hanging as in the initial condition shown in Figure 10a. The swing is produced after the cable is released from one of the two ends. Further information of the experimental details can be found in Koh’s paper [9]. In this paper, the numerical results from the new method and Koh’s numerical and experimental results are compared for the shape of the cable and the tension. Additionally, the dependence of the tension results with the internal damping coefficient and the number of elements is studied.

3.2.1. Optimal Simulation

The optimal simulation uses 80 nodes, a ${10}^{-3}$ s time-step and an internal damping coefficient $\beta =6.2\times {10}^{-2}$, as Koh does in his paper. In Figure 11 the results of the new method for the tension are truly similar to Koh’s numerical results. The dynamic tension oscillation for the first 0.5 s is lower for the presented method, showing a slightly better agreement with the experimental results than Koh’s. For the peak tension at 0.6 s, Koh is slightly closer to the experimental results, but the presented method has better accuracy concerning when the snap tension shows. From 0.6 s to 1.4 s, both numerical results are almost the same but fail to accurately predict a minimum of the tension at 0.8 s. At 1.7 s, experimental results show one more snap tension peak, that the presented method predicts more accurately. Comparing Figure 10a,b shows that the shape of the cable swing is almost the same as the measured value in the experiment, and no remarkable differences can be observed. Overall the presented method is at least as reliable as Koh’s method.

3.2.2. Dependence on the Damping Coefficient

A similar behavior was observed in relation to the dependence of the results on the damping coefficient value, as before. Figure 12 shows that high internal damping smooths all the tension oscillations, zero internal damping results imply too much noise and the optimal internal damping, gives better results since it reduces abnormal peak tensions in the line. The computational times for the 0, 0.062, and 1 internal damping coefficients simulations are 59.0 s, 13.6 s and 15.7 s, respectively, reinforcing the conclusion observed before relating the computational cost and the oscillation of the results.

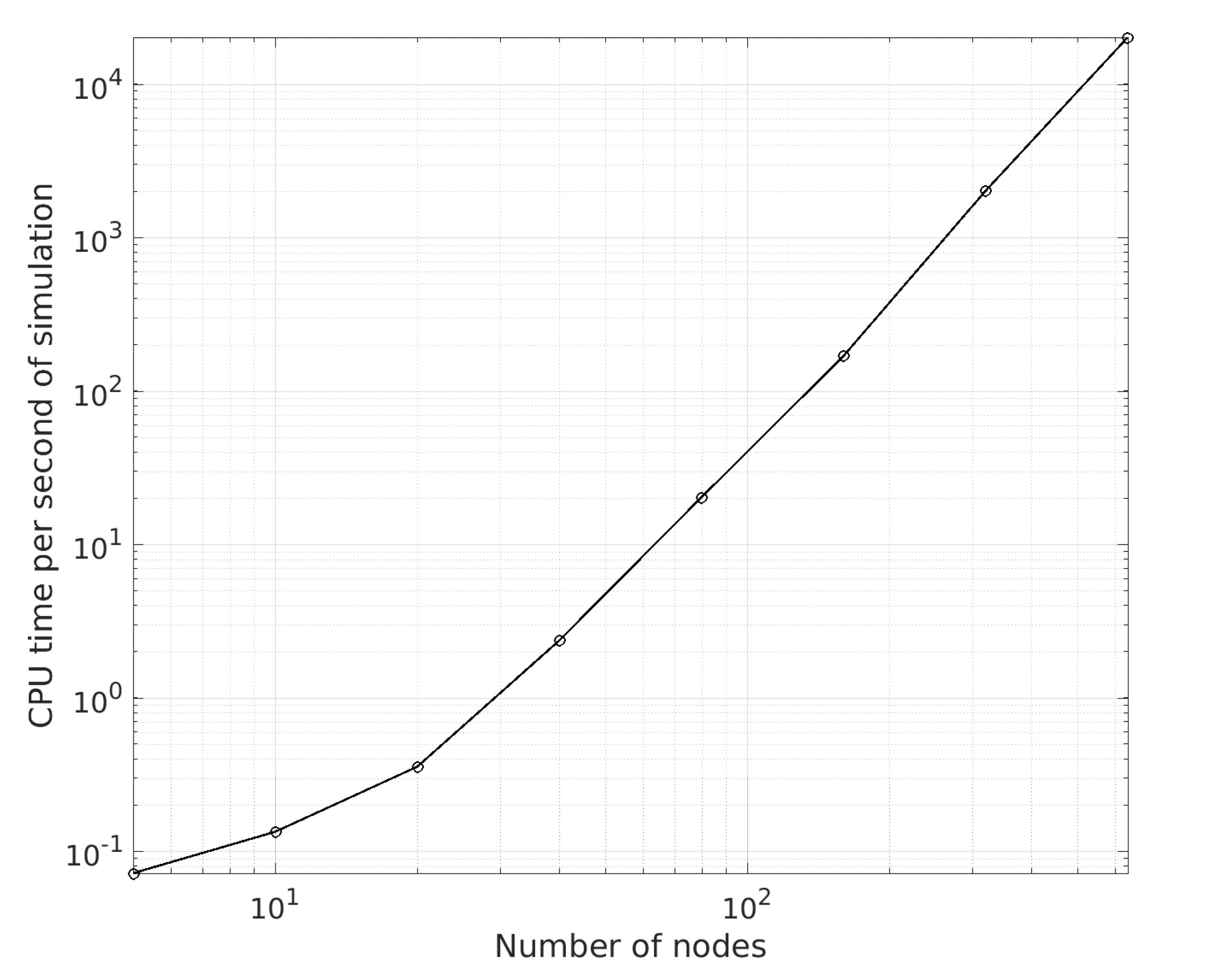
3.2.3. Dependence on the Number of Nodes

Again, a study of the dependence on the number of nodes was developed. Figure 13 shows that the lower the number of nodes is the smoother the oscillations are. It is also significant that the phase differences become larger. The computational times are shown in Figure 14. There is no significant difference in the results obtained with 40 and 80 elements, but the computational cost for 80 nodes is six times higher. Therefore, from the CPU cost point of view, it is important to find the balance between the number of elements and the physics represented. Moreover, the lack of agreement here evidenced is probably due to the physical phenomena that are not considered in the equation that is used: the forces caused by the flexion of the cable as it swings may be contributing to the movement of the cable and the tension at the top support.

Figure 14 shows the dependence of the computational time with the number of nodes. The higher number of nodes was considered to construct this figure (up to 120).

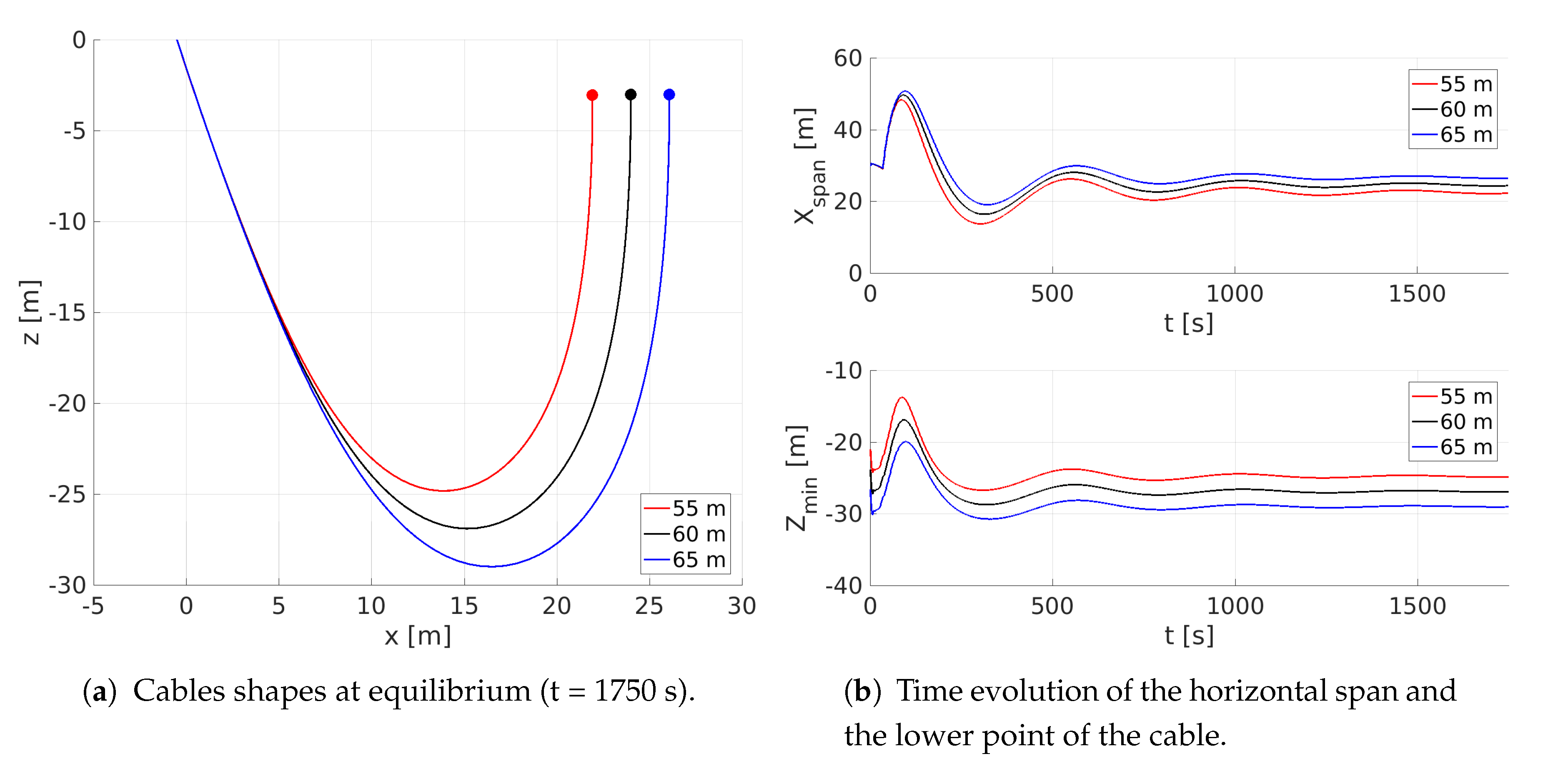
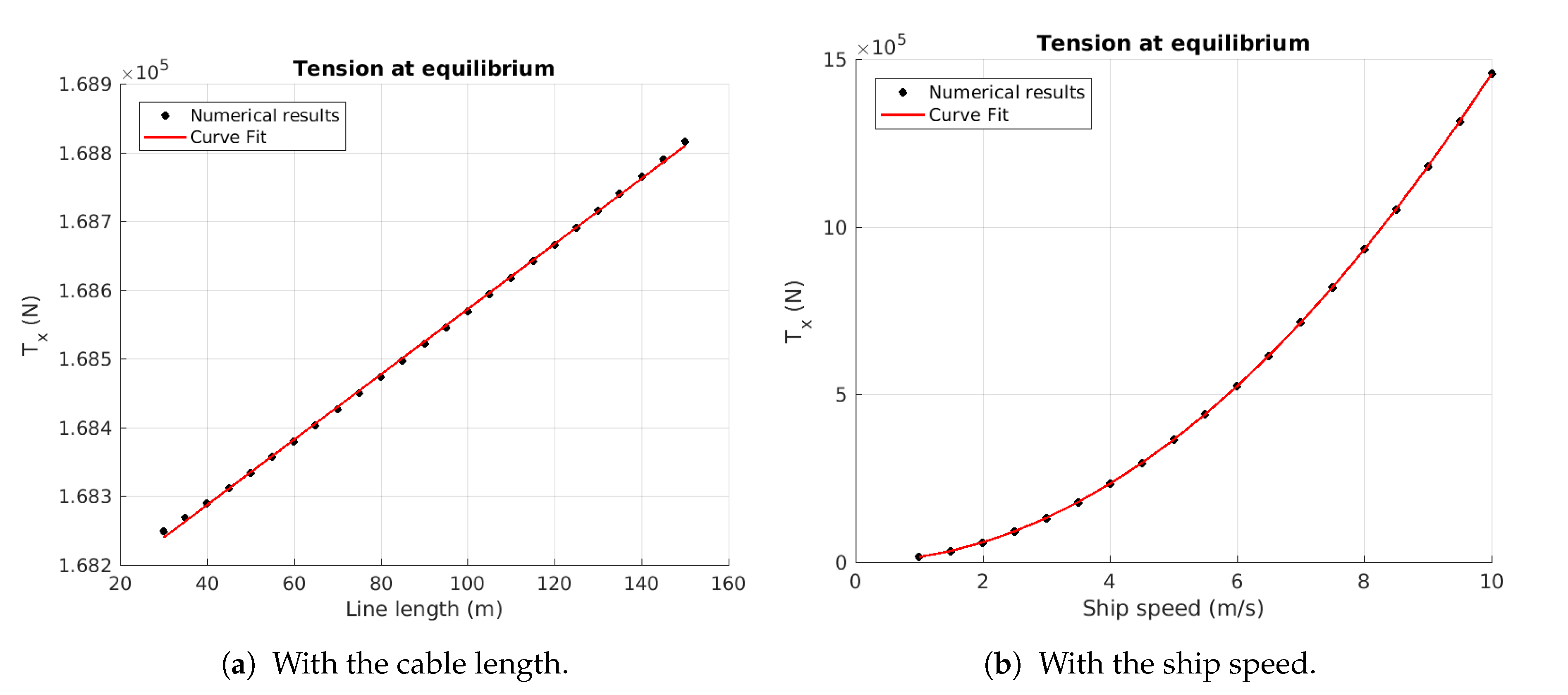
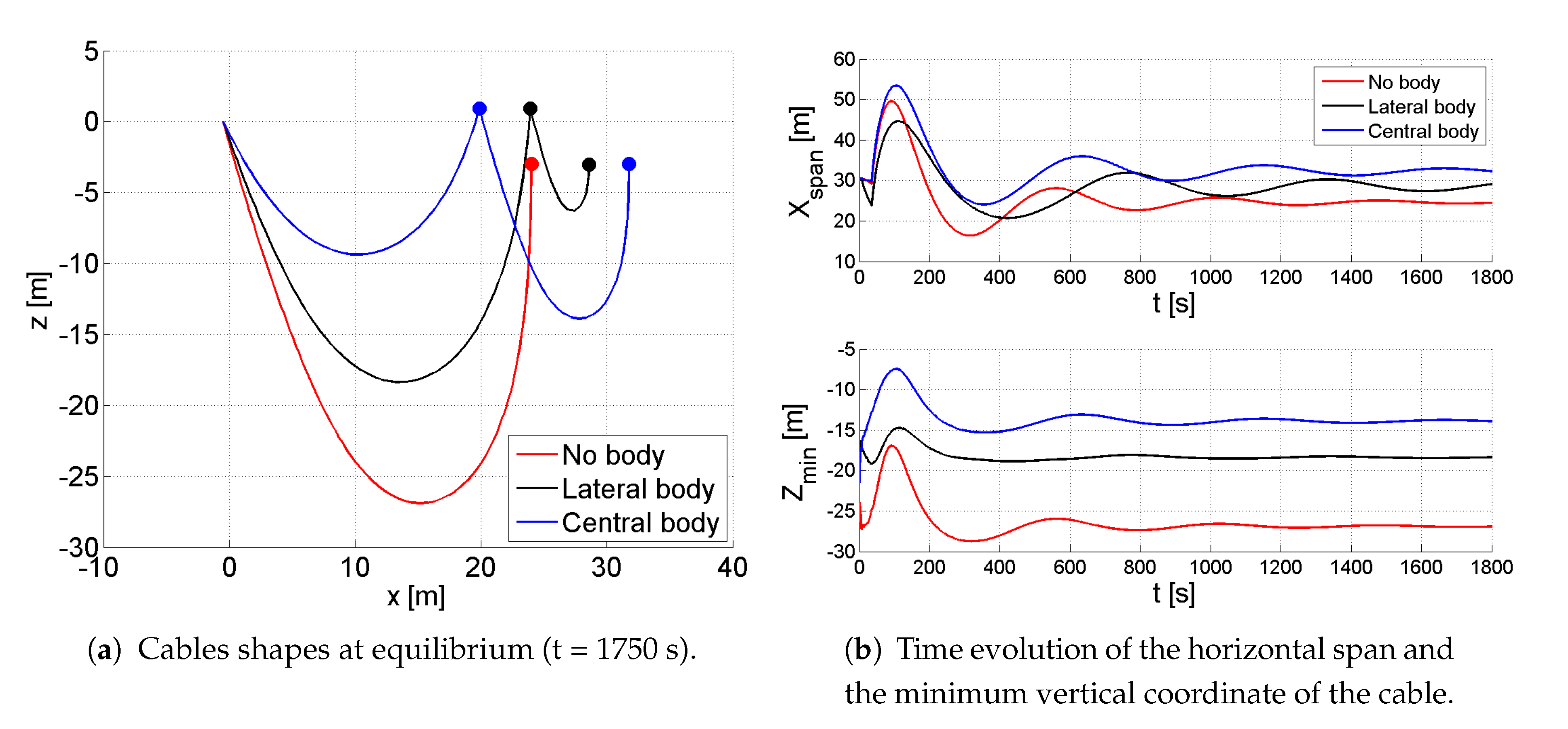
4. Analysis of Different Towing Systems

Once the model was validated, it was applied to the numerical analysis of towing procedures. In this section, different towing systems are studied: floating or submerged bodies. It is also interesting to study cases with intermediate bodies that may help to optimize the towing systems. To accomplish this goal, the cable is set on a certain boundary condition (vertical as in Zhu’s experiment or hanging horizontally as in Koh’s) and the boundary condition at the top support is imposed as horizontal displacement—it starts moving after 5 s of simulation (thus the system becomes stable before the top support starts moving) at a constant speed. In general, the final shape of the cable is studied, as well as the time dependence of some parameters, for example, the depth of the towed body. It is considered that the study of the final stationary condition is enough for a simple test with a real scale case of the proposed method. The study of the transitory behaviours and the dynamic effects of the waves was not included in the scope of this paper, and it could be included in future research, together with the coupling of the cable dynamics with the vessel and towed body dynamics.

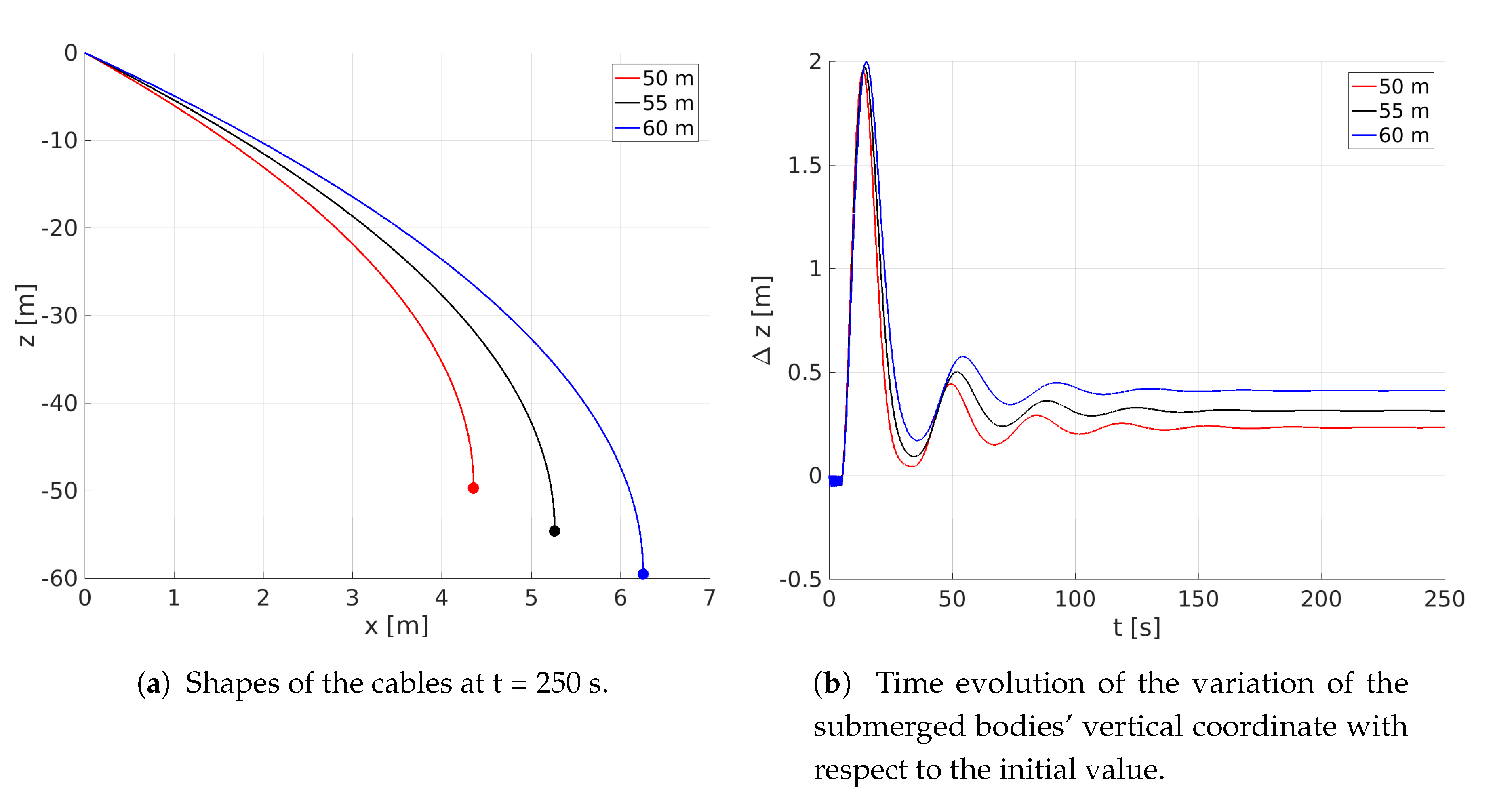
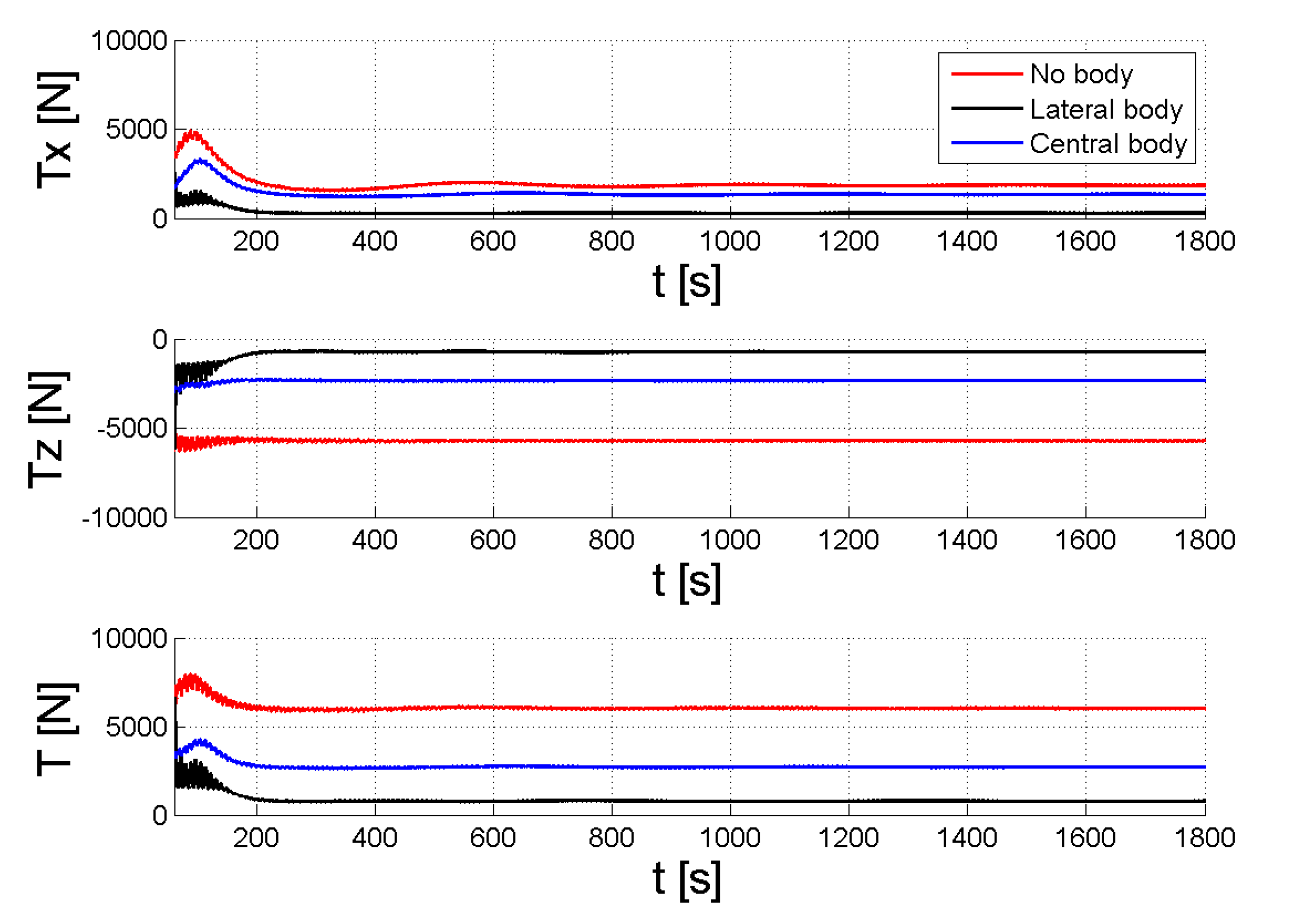
4.1. Towing of a Submerged Body

First, a towing system composed of a unique submerged body is analyzed. The shape of the body is a sphere with higher density than water (see

Table 1. Towing a submerged body data.

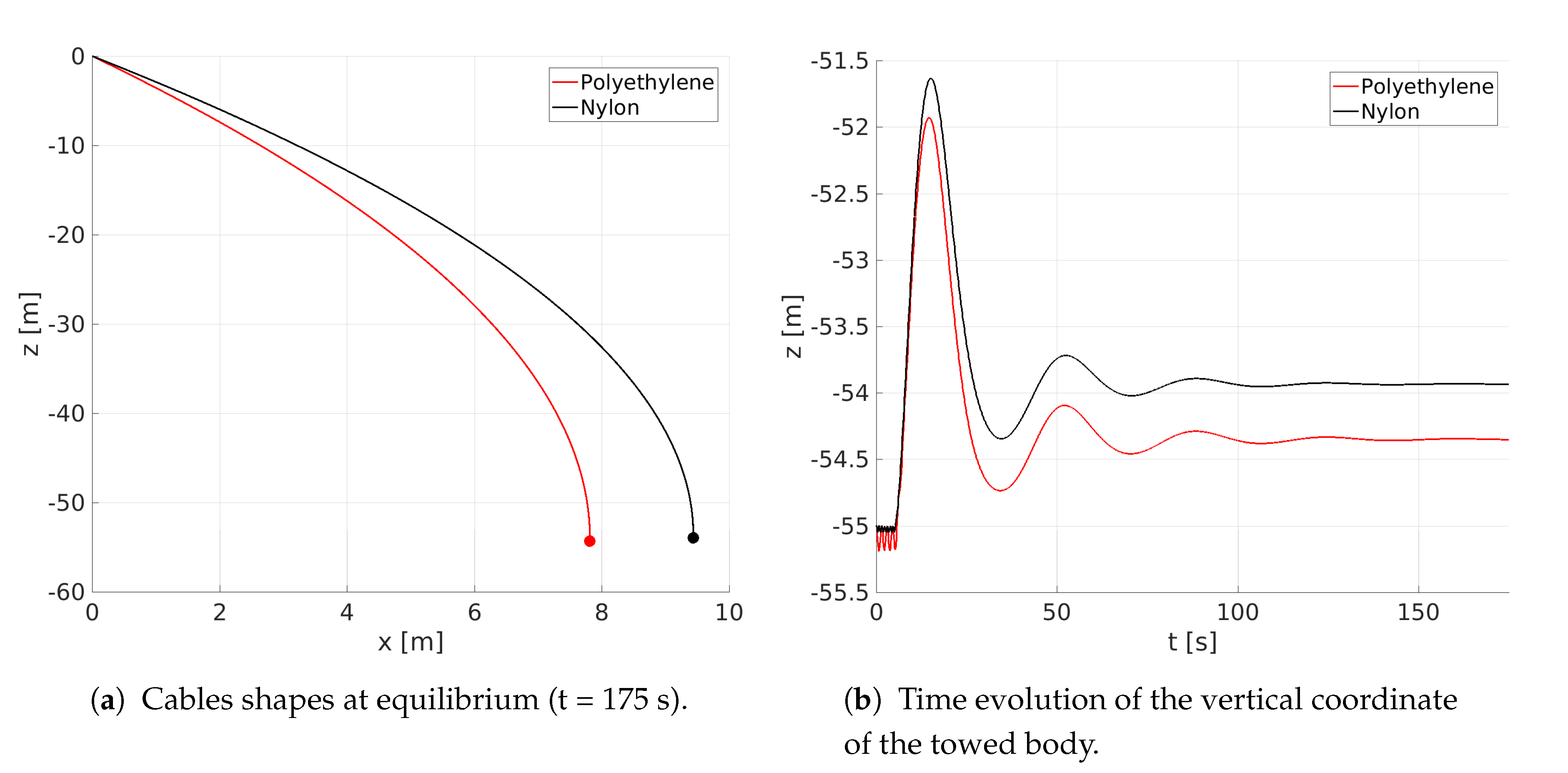
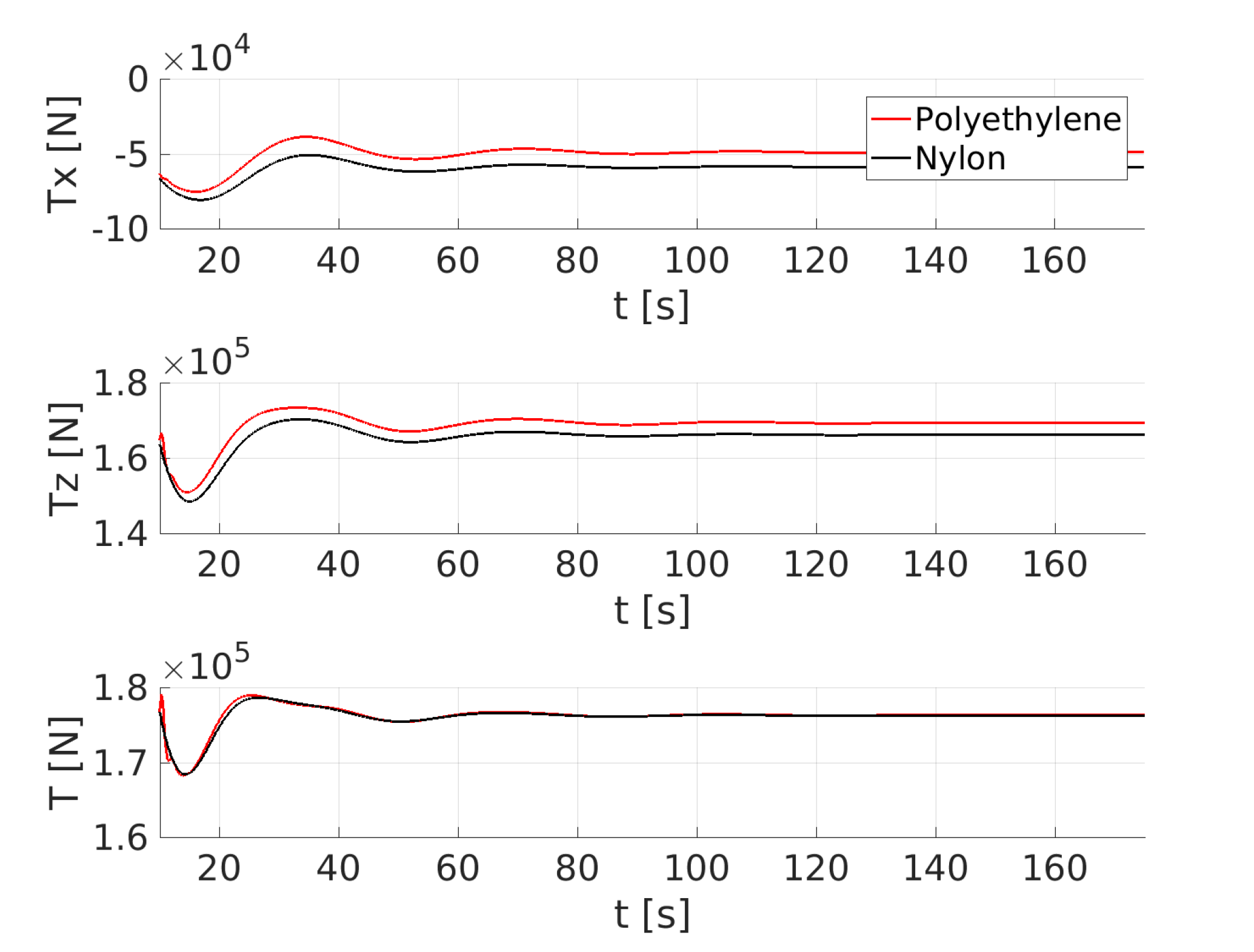
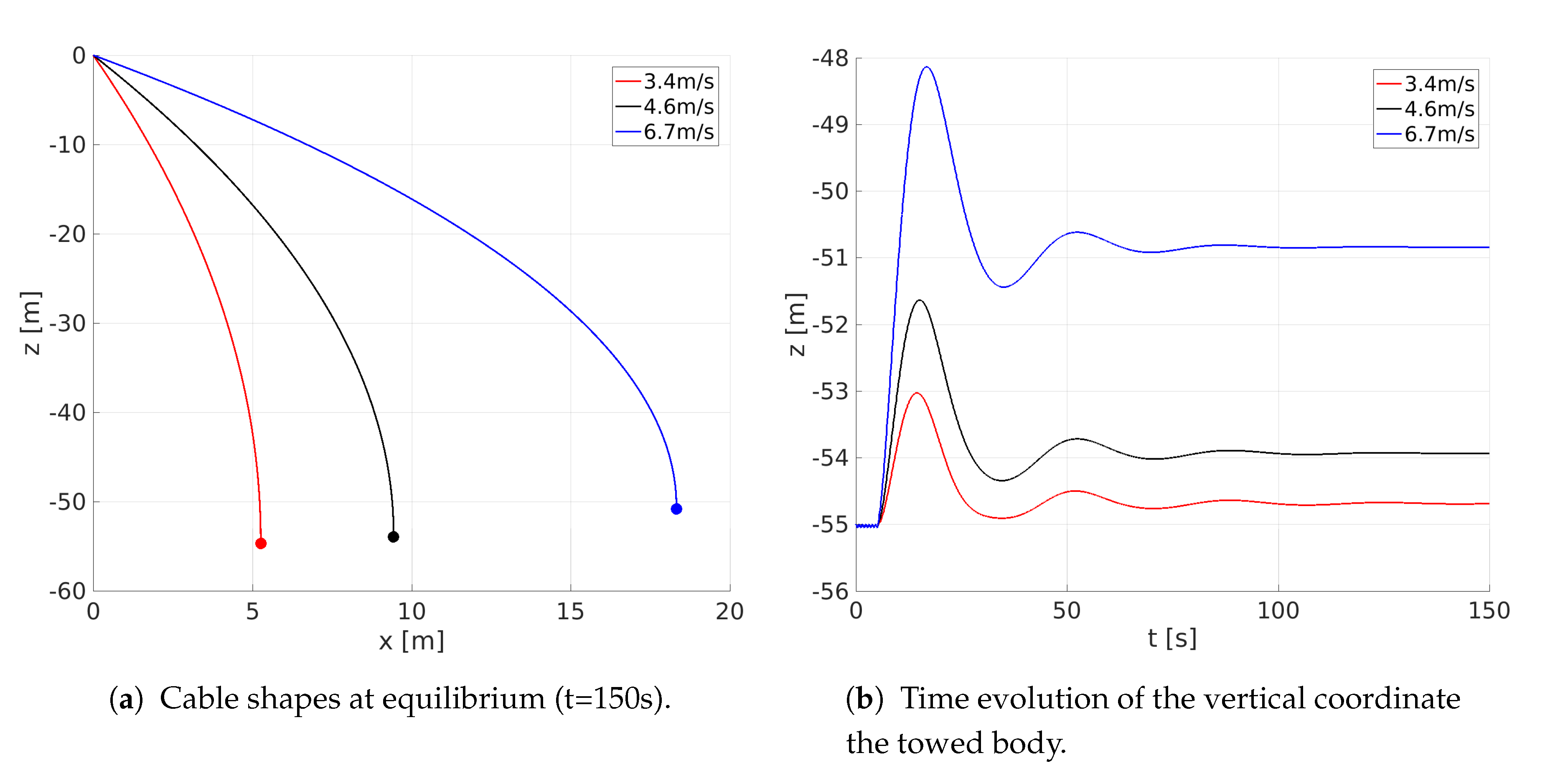
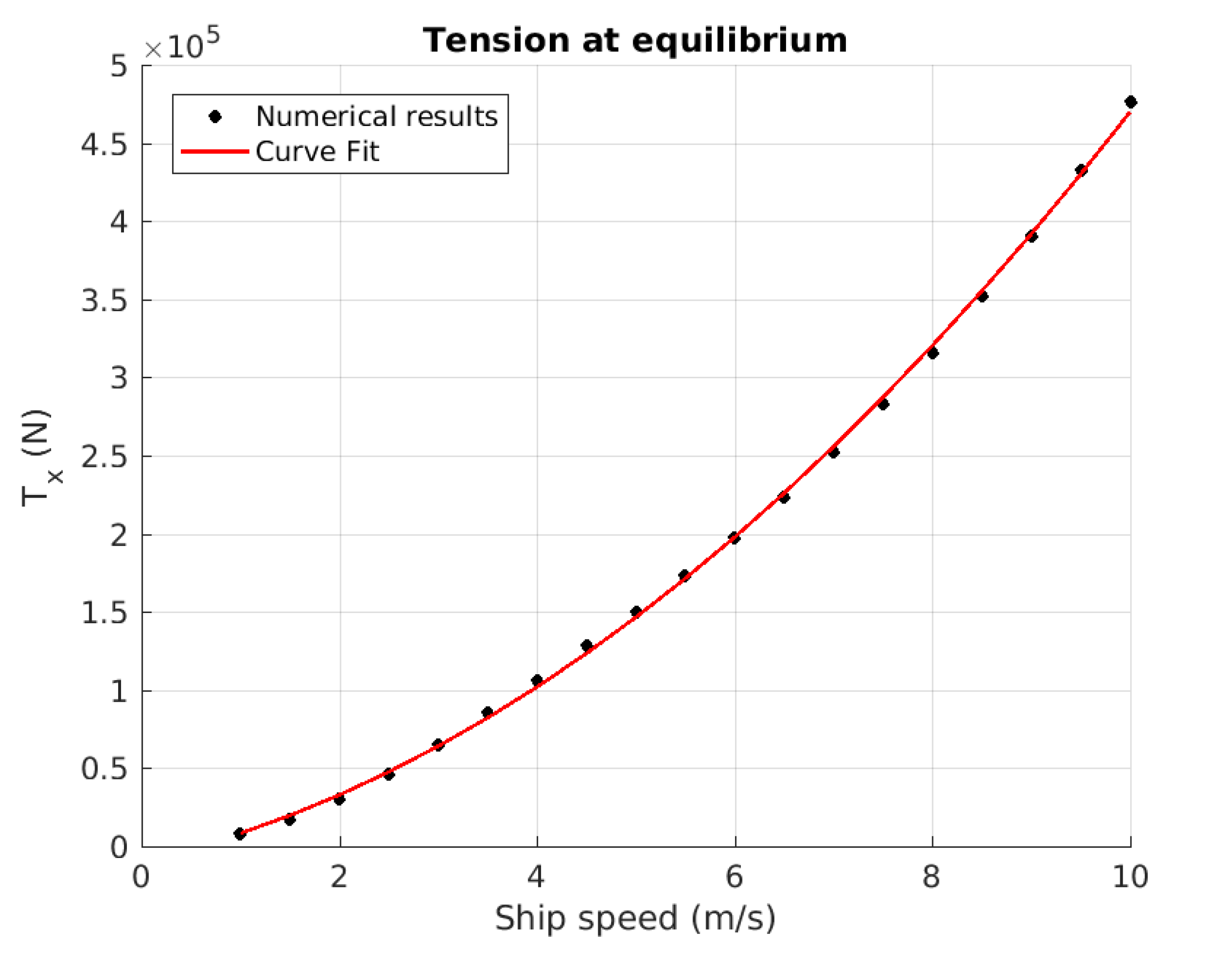
Cables			Towed Sphere
Material	Nylon	Polyethylene	D	4.8 m
$\rho$	1150 kg/m${}^3$	1175 kg/m${}^3$	m	$7.74\times {10}^4$ kg
E	$3.0\times {10}^9$ N/m${}^2$	$2.5\times {10}^9$ N/m${}^2$	$C_d$	$0.47$
L	55 m	55 m	$C_m$	$0.5$
d	88 mm	72 mm	-
$C_{dt}$	$0.01$	$0.01$	-
$C_{dn}$	$1.2$	$1.2$	-
$C_{mn}$	$1.0$	$1.0$	-

). The setup of the towing is shown in Figure 15. The initial condition is hanging vertically as in Zhu’s experiment. Two different cable configurations have been used. The characteristics of the system are shown in Table 1.

Figure 16a,b show the results for the shapes of the cables once they reach equilibrium and the time evolution of the depth of the sphere respectively for three different towing systems. These systems use the same spheres and the same cables, but three different lengths for the cables. The cable used was Nylon, and the speed of the boat was 3.4 m/s (6.6 knots). Figure 17a shows the dependence of the cable horizontal tension at the boat support with the length and Figure 17b shows the dependence of the cable spans on its length.

As expected, the longer the cable, the deeper and the farther away the towed body stays. Figure 16b also shows that the longer the cable is, the more the towed body rises due to the speed of the boat, and the time evolution of the depth of the body shows the same behavior disregarding the length of the cable. The line tension shows a larger horizontal component for longer cables, although the total tension remains almost the same. Figure 17a shows how fairlead’s horizontal tension increases with the cable length. The relationship could be expected to be linear, but tension increases more slowly for greater cable lengths. The horizontal span also becomes more significant for longer cable lengths. This finding explains why the tension line slope is lower for longer lengths—the cable stays more horizontal, tangential drag forces are lower than the normal drag forces, and then, the cable offers lower resistance to displacement.

These results may provide useful information on how to choose the length of a cable for this type of towing system within the length ranges that may be considered in a design, for example, in terms of efficiency, it could be more desirable that the cable tension pulls the boat vertically rather than horizontally, and longer cables would lead to lower consumption.

Figure 18a,b show the same results as the two previous figures, but here, the towing systems have two different cable materials instead of three different cable lengths. The cable length was kept constant at 55 m, and the speed of the boat was 4.6 m/s (8.9 knots). Figure 19 and

Table 2. Results at equilibrium of the tension on the boat’s end of the cable for submerged body towing systems with different cable materials.

Cable Material	$-{\mathit{T}}_{\mathit{x}}$ (N)	${\mathit{T}}_{\mathit{z}}$ (N)	$\left|\mathit{T}\right|$ (N)
Polyethylene	$4.909\times {10}^4$	$1.693\times {10}^5$	$1.763\times {10}^5$
Nylon	$5.882\times {10}^4$	$1.661\times {10}^5$	$1.762\times {10}^5$

show the cable tension at the boat support.

The nylon cable rises more than the polyethylene cable, although the density of nylon is higher. This rise is due to the higher normal drag forces on the cable due to its thicker diameter, which has a great effect on the tension at the boat support, as shown in Figure 19. It can be deduced that the thicker the cable, the more horizontal its shape is, and the larger the horizontal component of the tension becomes. This result should also be considered with the cable length, previously studied, when designing a towing system.

Figure 20a,b show the results for the shape of the cables once they reach equilibrium and the time evolution of the depth of the sphere, respectively, for three different cases. This system uses the same spheres and the same cable (the 55 m Nylon cable) for the three cases, but three different ship speeds. Figure 21 shows the dependence on the ship speed of the cable horizontal tension at the boat support.

These figures show that the higher the boat speed is, the lower the depth of the towed body is. As expected, Figure 21 shows that the horizontal tension of the cable at the fairlead is proportional to the second power of the ship speed.

4.2. Towing of a Floating Body

Finally, floating body towing systems are studied. To do so, a sphere with density lower than water is chosen, and the initial condition sets the cable hanging horizontally as in Koh’s experiment [9]. The setup of the towing is shown in Figure 22. Similar to the previous section, the dependence of the system on the length of the cable is studied. Figure 23a displays the shapes of the cables after they reach equilibrium, and Figure 23b displays the time evolution of the z-coordinate of the deepest point of the cable and the time evolution of the horizontal span between the top support and the towed body. The initial horizontal span is the same for the three systems. The boat speed is 3.4 m/s (6.6 knots), and the characteristics of the towing systems are shown in

Table 3. Data on towing a floating body.

Steel Cable		Towed Sphere		Intermediate Sphere
$\rho$	7870 kg/m${}^3$	D	$8.5$ m	D	$2.5$ m
$EA$	$2\times {10}^{11}$ N/m${}^2$	m	$3.11\times {10}^5$ kg	m	$3.11\times {10}^2$ kg
L	60 m	$C_d$	$0.5$	$C_d$	$0.47$
d	80 mm	$C_m$	$0.18$	$C_m$	$0.5$
$C_{dt}$	$0.01$	-		-
$C_{dn}$	$1.2$	-		-
$C_{mn}$	1	-		-

. Figure 24a shows the dependence of the cable horizontal tension at the boat support with the length, and Figure 24b shows the dependence of the cable horizontal tension at the boat support with the ship speed.

Figure 23a shows that when the system is stable, the depth of the cable and horizontal span increase with cable length. Figure 23b shows that both the horizontal span, $X_{span}$, and the cable depth, $Z_{min}$, are decreasing for the first 20 seconds because when the ship is not moving, the weight of the cable pulls the sphere towards the fairlead of the ship, and then the cable goes deeper. The same occurrence is observed in the next section. Once the ship starts moving, both $X_{span}$ and $Z_{min}$, increase rapidly. For minimum cable depth, in Figure 23b, a large difference can be observed among the three systems, as the initial horizontal span is set to be the same; thus, the longer cable hang deeper. There is a smaller difference among the three systems at final equilibrium, as the horizontal span is not the same anymore. For horizontal span, as expected, the initial span is the same, but as the system reaches equilibrium, the longer cables let the sphere hold more distance with the top support. The length difference leads to an almost constant horizontal tension, which is opposing the drag forces on the body, while the vertical tension increases as the longer cables are heavier. In this case, the relationship of the length of the cable and the horizontal fairlead tension is linear because in this case, the cable shape does not depend on the length. We can conclude that cable length does not have a significant impact on fuel consumption in floating body towing systems.

Figure 24b shows that the horizontal tension of the cable at the fairlead is proportional to the second power of the ship speed, which should be considered to compute the optimal speed for the ship in some cases, when the towing system size is large in comparison to the size of the ship.

Finally, the inclusion of an intermediate body in the towing systems is studied. To do so, the intermediate body boundary conditions described in Section 2.2 are imposed. This can be done for any internal node of the cable, and for different sizes and masses of the spheres chosen to be placed as an intermediate body. Figure 25a displays the final state of three towing systems of a floating body: again, one with no intermediate body, and two with a floating intermediate body, one on the center (central intermediate body) and the other one closer to the towed body (noncentral intermediate body), placed at nodes 50 and 80, respectively, where the total number of nodes was 100. Figure 25b shows the time evolution of the horizontal span, $X_{span}$, and the deepest point of the cable, $Z_{min}$, and Figure 26 shows the computed cable tension at the towed body. Apart from the intermediate body difference, all the remaining parameters are kept the same as in Table 3.

In Figure 25, the system with the intermediate body in the middle of the cable presents the largest horizontal span and the lowest depth of the cable. On the other hand, the system with no intermediate body shows the lowest span and the largest depth. The most important result here is that the tension of the wire at the fairlead of the ship is significantly lower for the systems with intermediate floating bodies, as shown in Figure 26 and

Table 4. Results at equilibrium of the tension at the towed body’s end of the cable for floating body towing systems with different intermediate body arrangements.

Int. Body	${\mathit{T}}_{\mathit{x}}$ (N)	$-{\mathit{T}}_{\mathit{z}}$ (N)	$\left|\mathit{T}\right|$ (N)
No int. body	$1.834\times {10}^3$	$5.711\times {10}^3$	$6.000\times {10}^3$
Central inter. body	$1.324\times {10}^3$	$2.349\times {10}^3$	$2.697\times {10}^3$
Lateral inter. body	$0.285\times {10}^3$	$0.725\times {10}^3$	$0.779\times {10}^3$

. For the noncentral intermediate body, the tension is the lowest among the three studied systems, valid both for vertical and horizontal tension. Therefore, attaching a floating body to the towing line at a point close to the towed body would result in a reduction of fuel consumption.

5. Conclusions

The numerical model introduced in Reference [1] has been extended with the implementation of different boundary conditions. This extension opened the door to the study of towing maneuvers. Additionally, the Rayleigh model for springs was used instead of the Hook’s law, as was done in Reference [8,12]. An internal damping coefficient was introduced in the equations. Moreover, the extension of the boundary conditions is not only valid for a specific case: a general methodology is considered, allowing for several setups, with several towing bodies and lines.

The results obtained with the model that was presented were validated using experimental results published in the literature. Specifically, Zhu’s [7] and Koh’s [9] experiments were considered for validation. The method that was presented showed good accuracy at predicting tension peaks for snapping cables when the bending effects were not important. However, the method failed at properly predicting the tension of a cable exposed to larger bending effects, as the model ignored such effects. Bending effects are negligible for most of the towing systems used in modern naval procedures, which is a reason to consider the proposed method a potential tool to design towing maneuvers.

The sensitivity analysis of the results for the internal damping coefficient and the number of nodes was studied. An appropriate election of the damping coefficient was necessary to predict the peak tension of the cable accurately. Introducing internal damping was found to lead to lower computational times due to its effect on reducing the vibrations in the cable, which helps the ODE solvers to achieve faster convergence. For the dependence on the number of nodes, the results showed that for simple problems it was enough with a low number of nodes, approximately 10. More complex problems, as the cable swung, required a higher number, at least 20. In both cases, increasing the number of nodes farther from the minimum requirements did not increase accuracy significantly, but it did increase computational time, and we can conclude that choosing an appropriate number of nodes, using calibration techniques, is essential to guarantee a correct result and a low computational time.

Finally, application cases of towing systems were studied to show how the method adapts to real-scale problems. Both for floating and submerged towed bodies, the results obtained were shown to be useful in towing system optimization—it is possible to compare different setups in terms of cable properties, speed of the ship and intermediate body disposition and properties. More specifically, for submerged towed bodies, cable length can play an important role in braking the ship. For floating towed bodies, attaching a floating body to the towing line at a point close to the towed body would result in a reduction of the horizontal tension at the fairlead of the ship, and for both types of towed bodies, the dependence of the drag forces on the towing system with the ship speed needs to be considered while computing optimal transport speed. Together with the precision obtained at computing snap tensions, these results are a step forward in the tools used in the design of towing maneuvers, allowing the user to minimize risks and fuel consumption.