Model of Bio-Colonisation on Mooring Lines: Updating Strategy Based on a Static Qualifying Sea State for Floating Wind Turbines
Abstract
1. Introduction
- a reduction of mooring line’s minimum tension, leading to an increased risk of “slack event” [7] (fast tensioning of the line).
- a reduction of line’s buoyancy, accelerating wearing by rubbing with the seabed.
- a shift of natural frequencies towards larger periods at which the floater has larger response amplitudes [8].
- an increase of effective tension’s variance [8].
2. Materials and Methods
2.1. An a Priori Spatial Distribution of Bio-Colonisation
2.1.1. Data
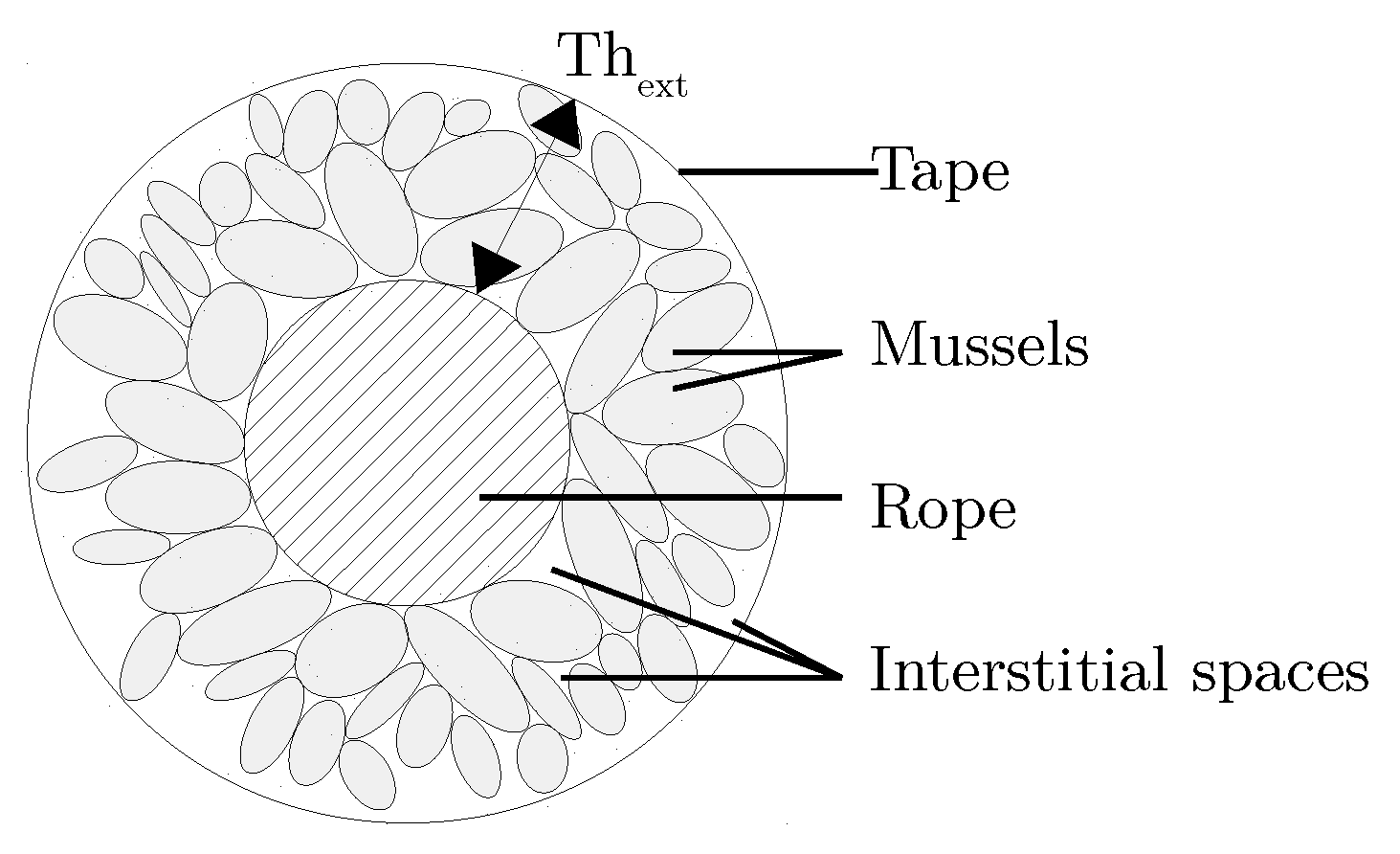
- Mussels colonisation is a so-called hard macro-colonisation. The fluid interaction with a solid body, instead of a soft body, can be modelled through the Morison equation.
- The settlement of mussels after the installation of the offshore structure is fast, usually in one year.
- Mussels are plentiful in the first 20 m under the Mean Water Level (MWL), but can also colonise deeper (cf. data from Spraul et al. [8]) because they sustain a wide range of temperature.
- In a certain extent, mussels can resist to mooring lines perturbations reinforcing their byssal threads, with which they attach themselves to the mooring line or others mussels. Mussels could then occupy the space during a long term [20].
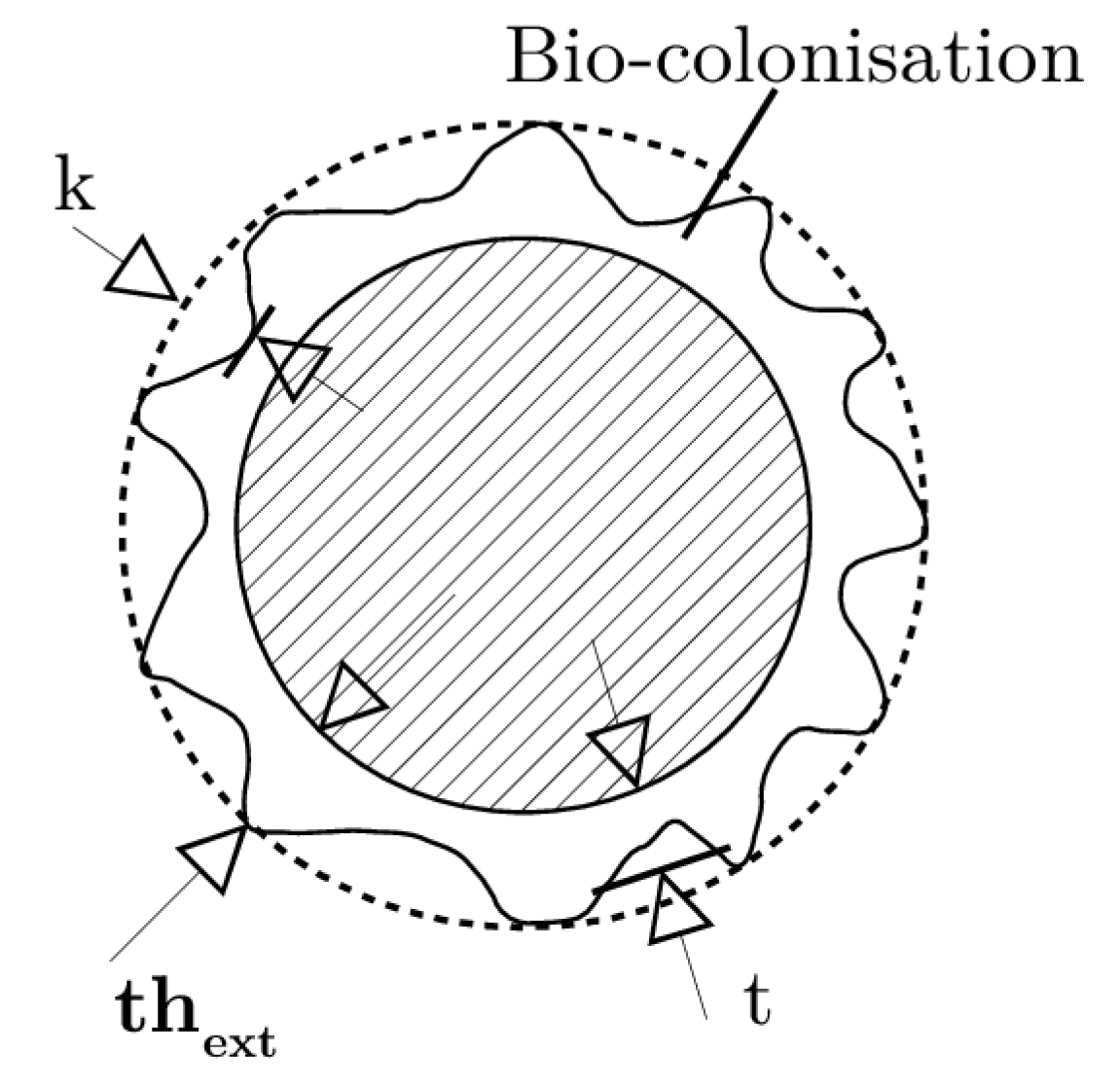
2.1.2. Modelling
- A decrease of thickness with depth.
- The emergence of bulbs or lumps identifiable by peaks and deeps of thickness along the line.
- A correlated geospatial process.
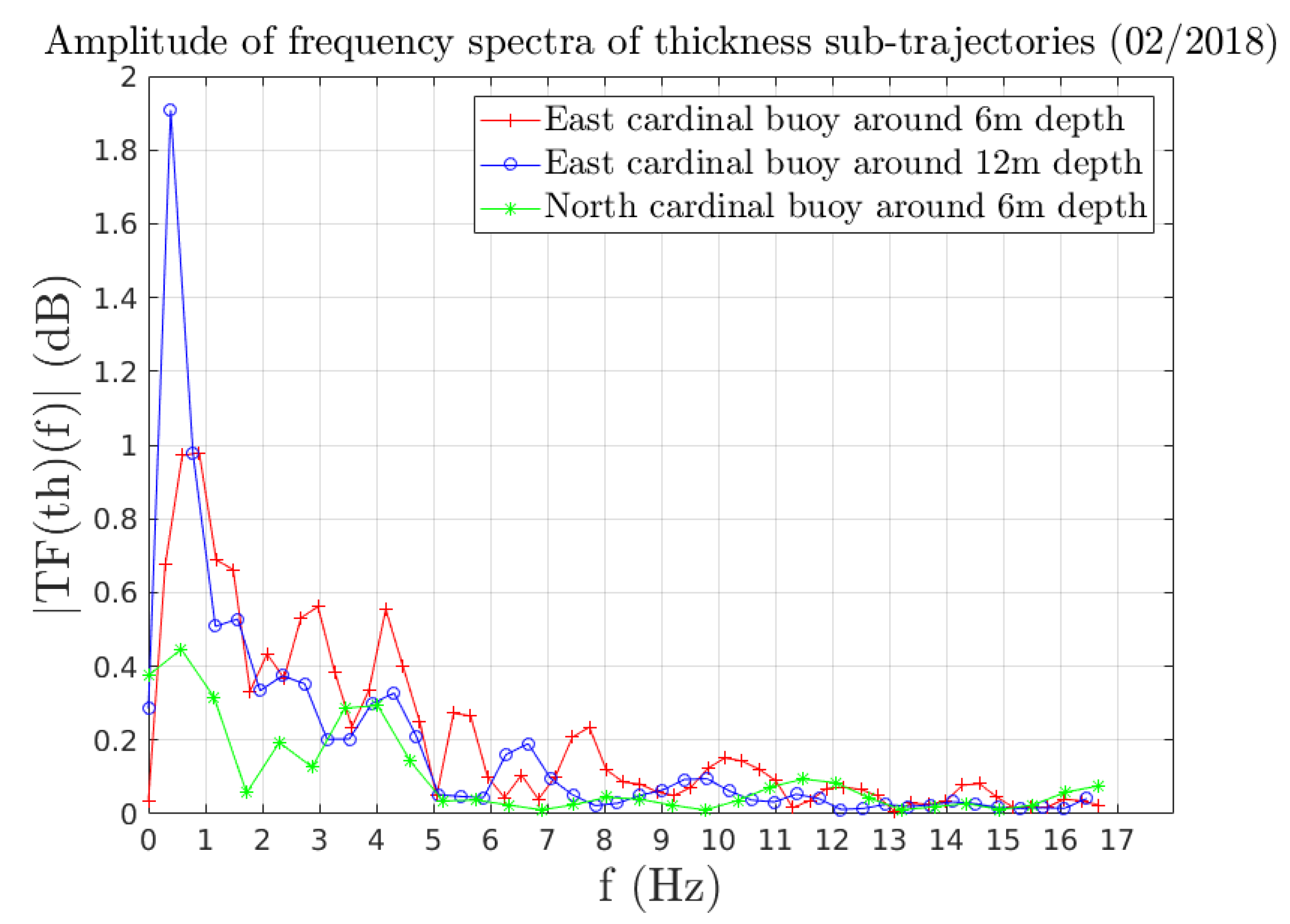
2.1.3. Parameters Identification & Model Uncertainty
2.1.4. Density of Bio-Colonisation
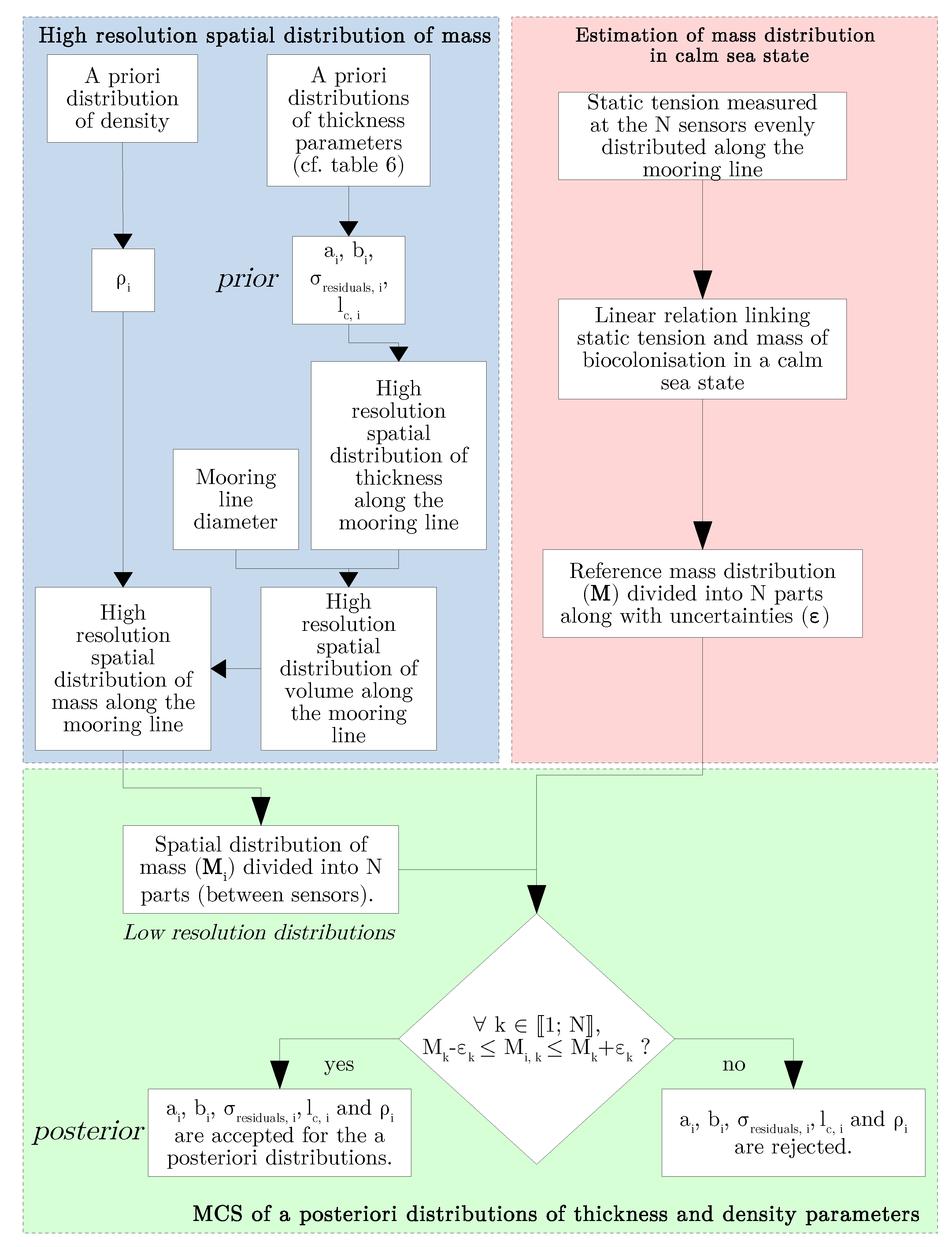
2.2. Reduction of the Uncertainty of our Prior Model
- the storms which can result in high accelerations and vibrations of the mooring lines and so lead to the unhooking of mussels clusters.
- the natural unhooking of multi-layered mussels clusters when they reach a critical size. The external layers can come down during a slack event of the line due to their fragile connection with below layers, which are directly hooked to the mooring line. This phenomenon is well-known by mussel farmers, who remove these external layers before they come down and let the underneath mussels grow.
- the mortality due to attacks of predators such as sea stars (Asterias rubens) or sparus fishes (Sparus aurata).
- the non-monotonous supply of phytoplankton which is depending on phytoplankton bloom and currents.
- The mortality or growth due to extreme variations of environmental parameters such as temperature.
- Pollution or diseases.
- define a realistic case study by presenting the chosen anchoring geometry, by configuring a tension sensing network on it and finally by proposing different realistic scenarii of bio-colonisation called reference mass distributions.
- present the methodology to build samples of posterior distributions of thickness and density parameters, which will depend on the number and the measurement error of tension sensors, and also on the reference mass distribution of bio-colonisation.
- introduce a robust estimator to quantify the reduction of uncertainty between prior and posterior distributions.
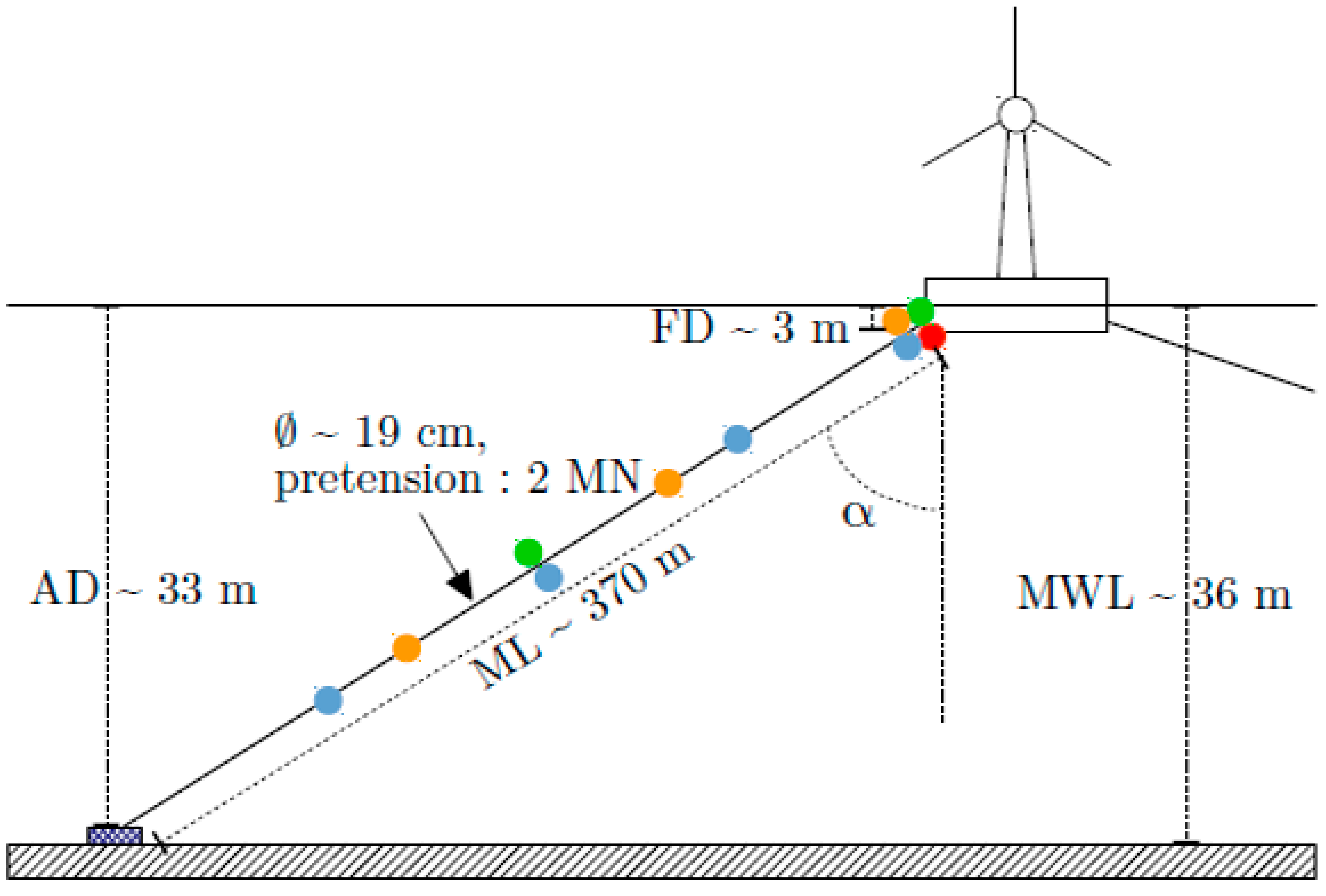
2.2.1. Realistic Mass Distributions of Bio-Colonisation and Parametrisation of Distributed Sensors on a Monitored Mooring Line of a FWT
- Only one tension sensor close to the fairlead (red in Figure 15).
- Two tension sensors (green). One close to the fairlead and a second in the middle of the line.
- Three tension sensors (orange). One close to the fairlead, a second at one-third of the line and a last at two-third of the line.
- Four tension sensors (blue). One close to the fairlead, a second at one-quarter of the line, a third in the middle of the line and a last at three-quarter of the line.
2.2.2. Updating a Priori Model from Measurements
- installation uncertainties:
- −
- the position of the anchor which influences and the pretension.
- −
- the position, orientations and draft of the floater which also influence and the pretension .
- manufacturing uncertainties:
- −
- the length and the diameter of the mooring line which influence the mass and volume of the mooring line.
2.2.3. Estimate for Uncertainty Reduction from SHM
3. Results and Discussion
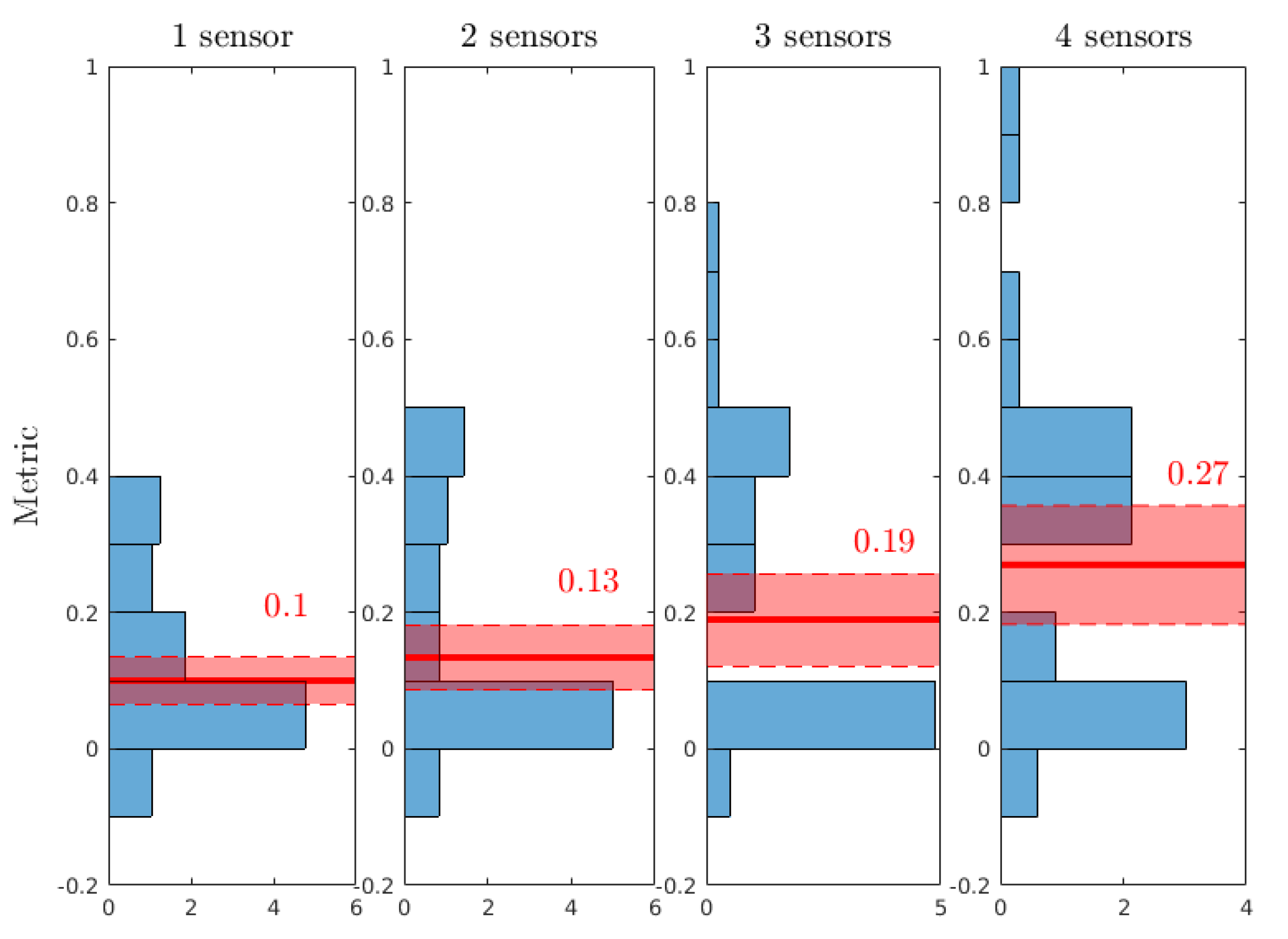
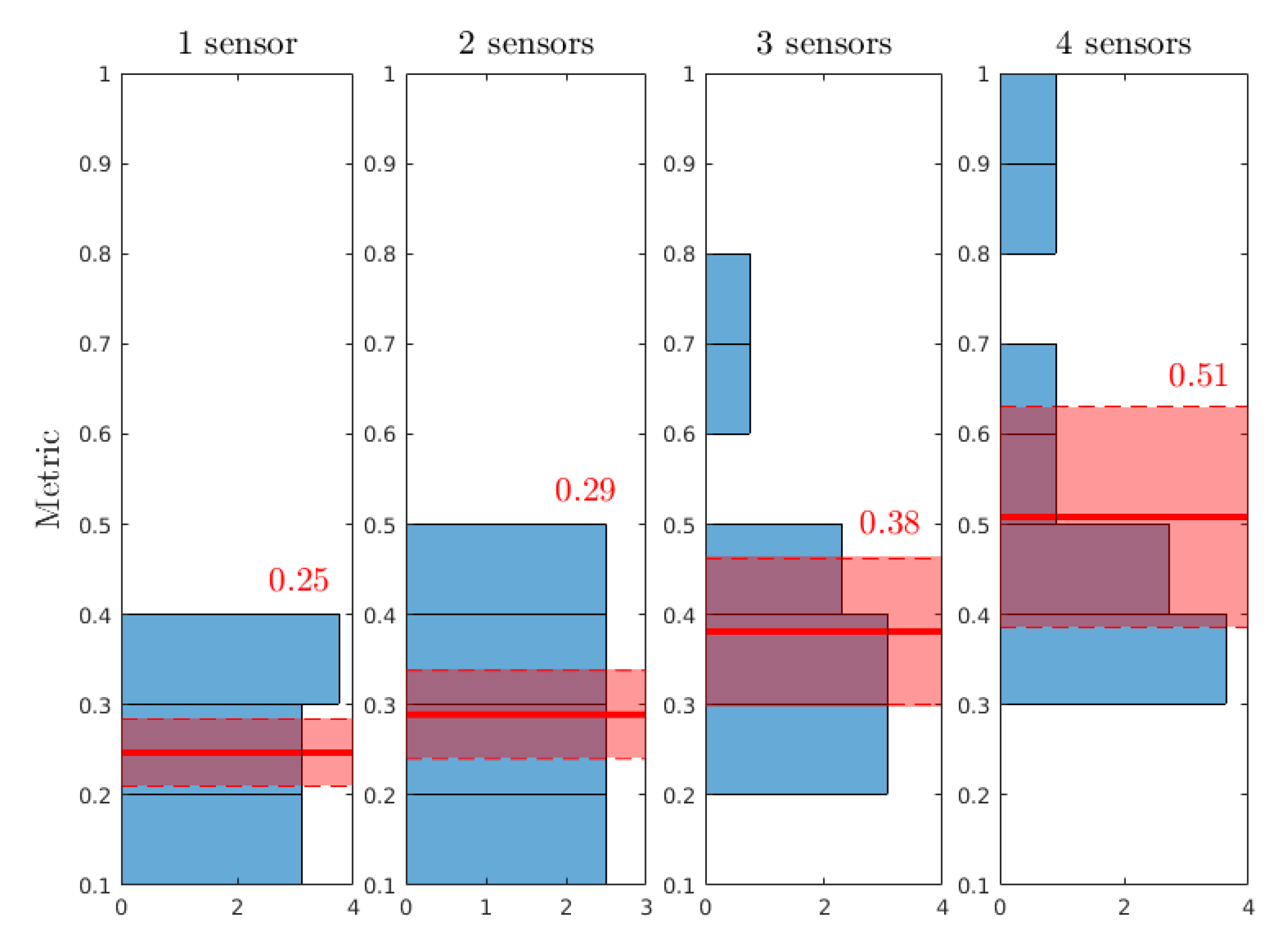
- Does the uncertainty narrow around the reference value (cf. Table 4)?
- For parameters whose uncertainty is reduced, is the metric linked with: the reference case? The error of measurement? The number of sensors?
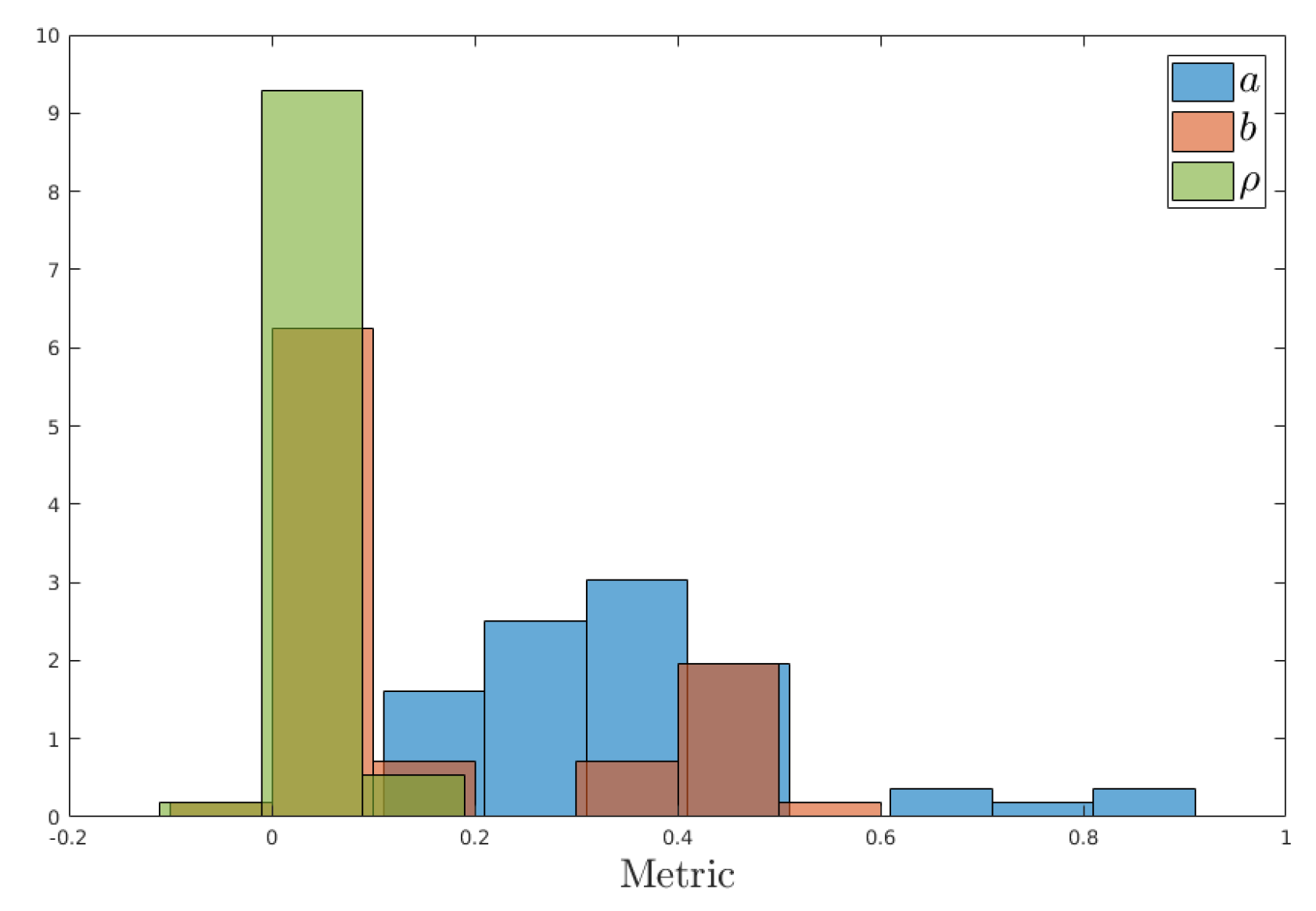
3.1. Efficiency of the Methodology
3.2. Sensitivity Analysis
- the reduction of uncertainty on a is strongly correlated with the number of sensors, strongly uncorrelated with the case of colonisation and uncorrelated with the error of measurement.
- the reduction of uncertainty on b is strongly correlated with the case of colonisation, correlated with the number of sensors and dimly correlated with the error of measurement.
- the reduction of uncertainty on is correlated with the number of sensors, dimly correlated with the error of measurement and strongly uncorrelated with the case of colonisation.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADF | Augmented Dickey-Fuller |
| AIC | Akaike Information Criterion |
| cdf | cumulative density function |
| CoV | Coefficient of Variation |
| DFT | Discrete Fourier Transform |
| FFT | Fast Fourier Transform |
| FPU | Floating Production Unit |
| FWT | Floating Wind Turbine |
| GEV | Generalised Extrem Value |
| KPSS | Kwiatkowski-Phillips-Schmidt-Shin |
| KS | Kolmogorov-Smirnov |
| LSE | Least-Squares Estimation |
| MCS | Monte-Carlo Sampling |
| MLE | Maximum Likelihood Estimation |
| MWL | Mean Water Level |
| probability density function | |
| QSS | Qualifying Sea State |
| RLHS | Random Latin Hypercube Sampling |
| SCAP | Spatial Correlation Assessment Procedure |
| SHM | Structural Health Monitoring |
| Std | Standard deviation |
| VIV | Vortex Induced Vibrations |
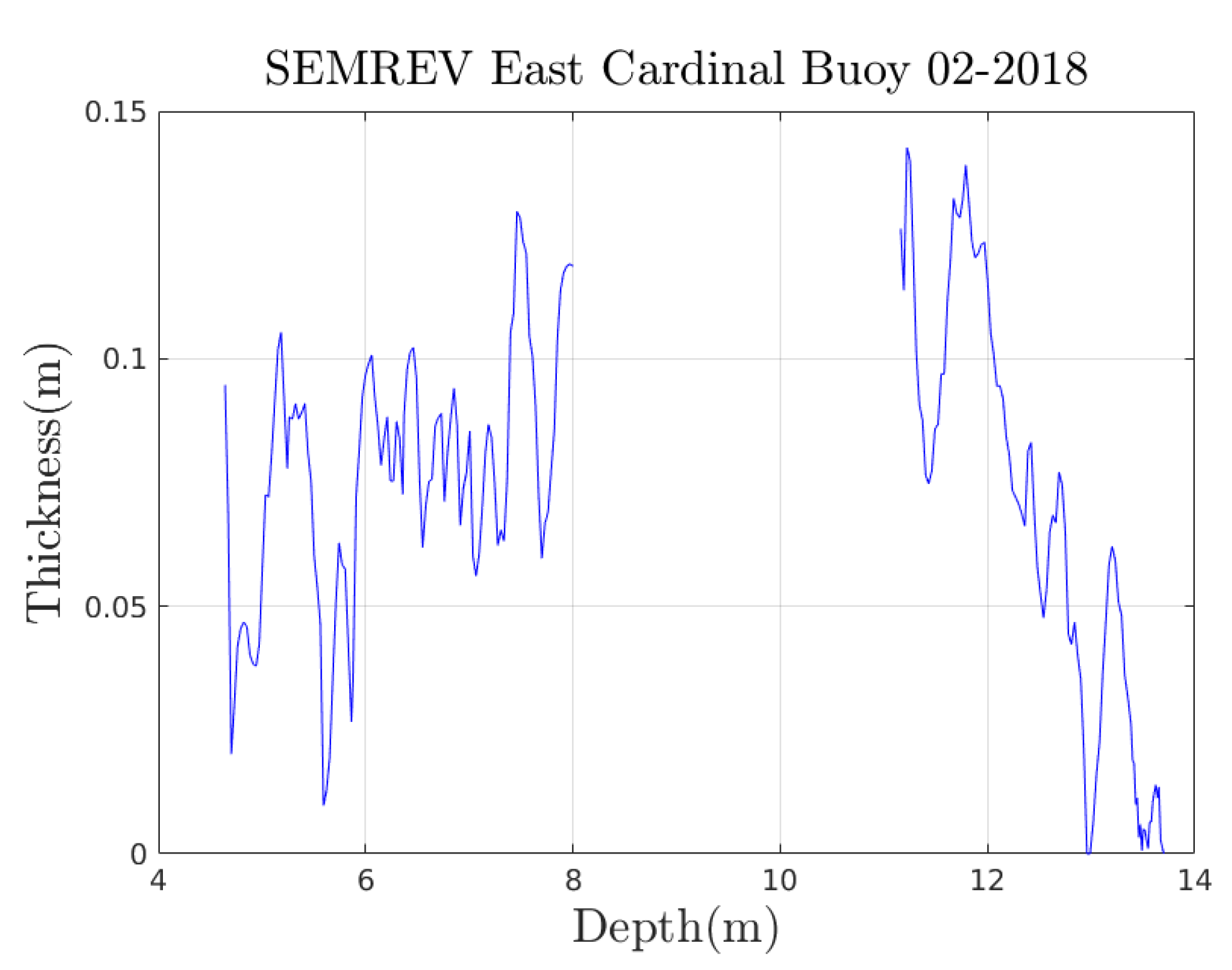
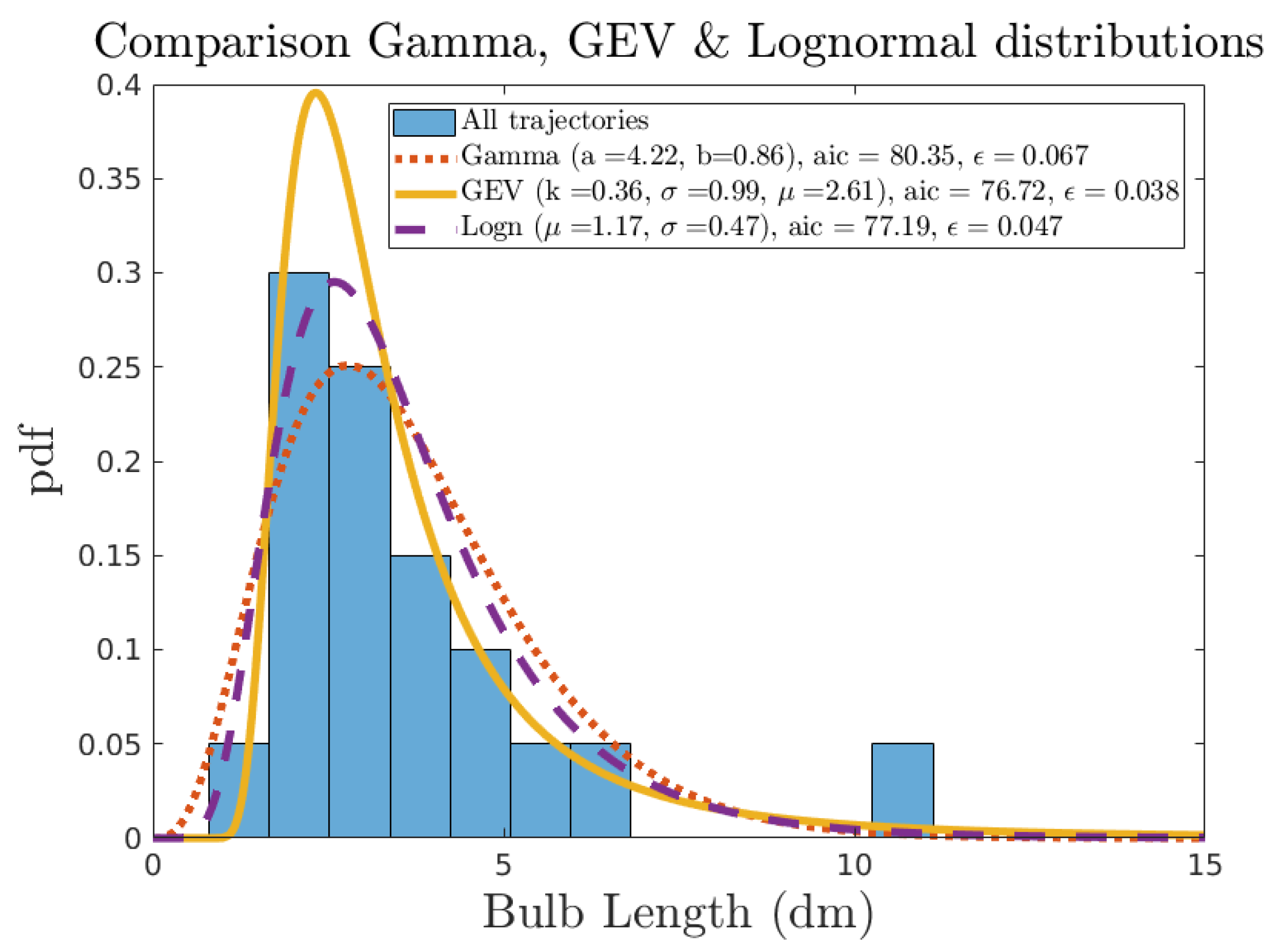
Appendix A. Experimental Trajectories
Appendix A.1. From a Previous Article on the SEMREV Test Site
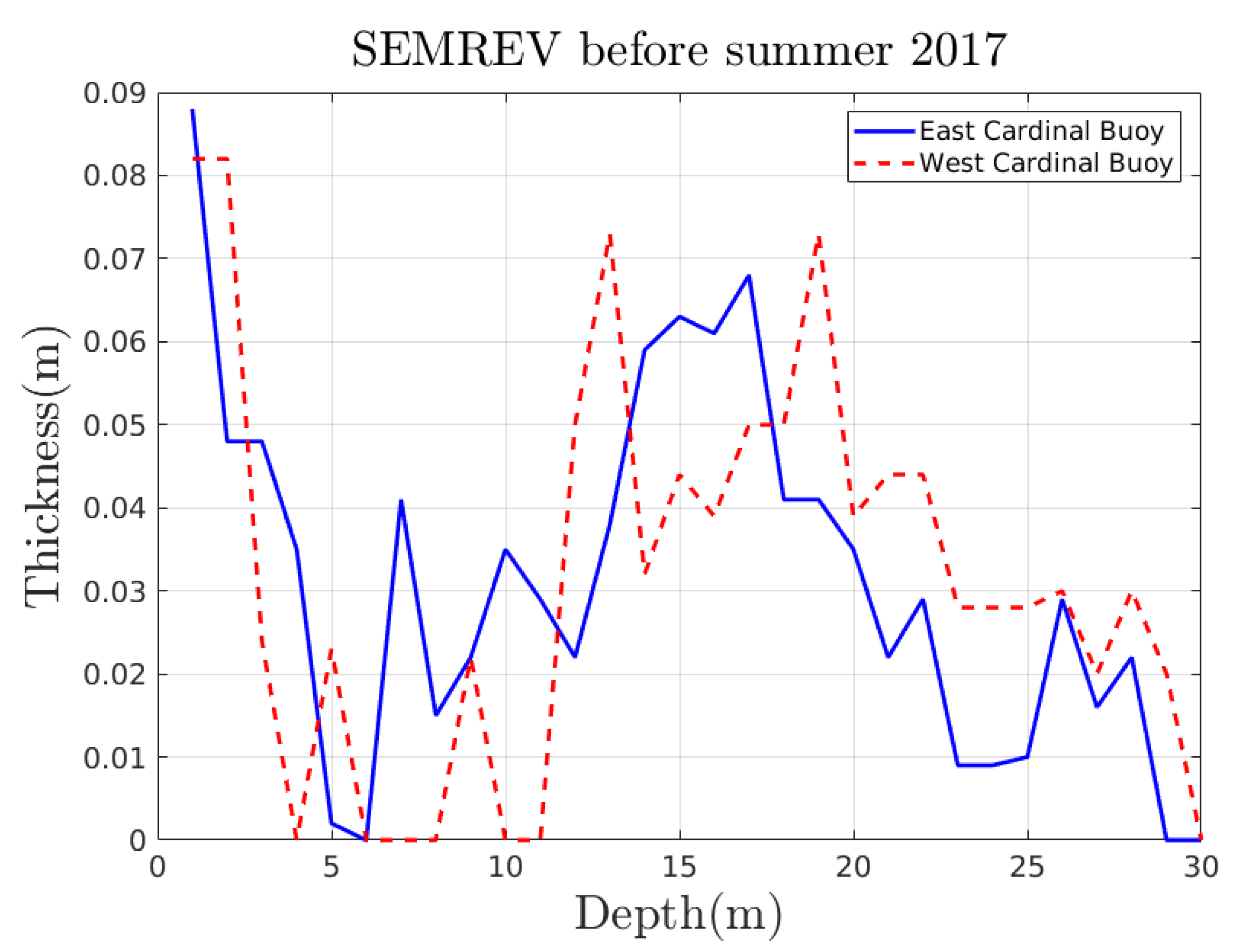
Appendix A.2. From Videotapes
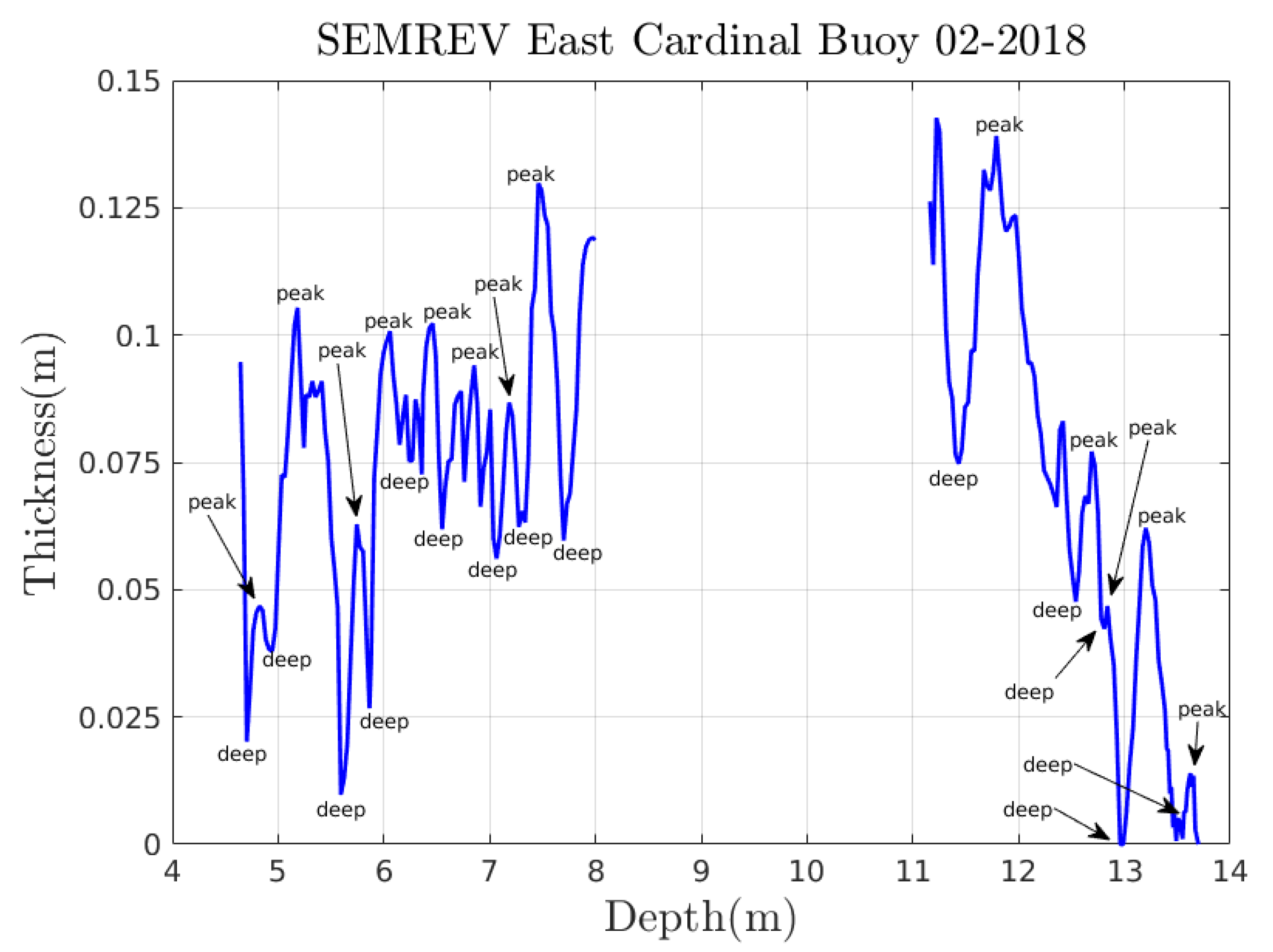
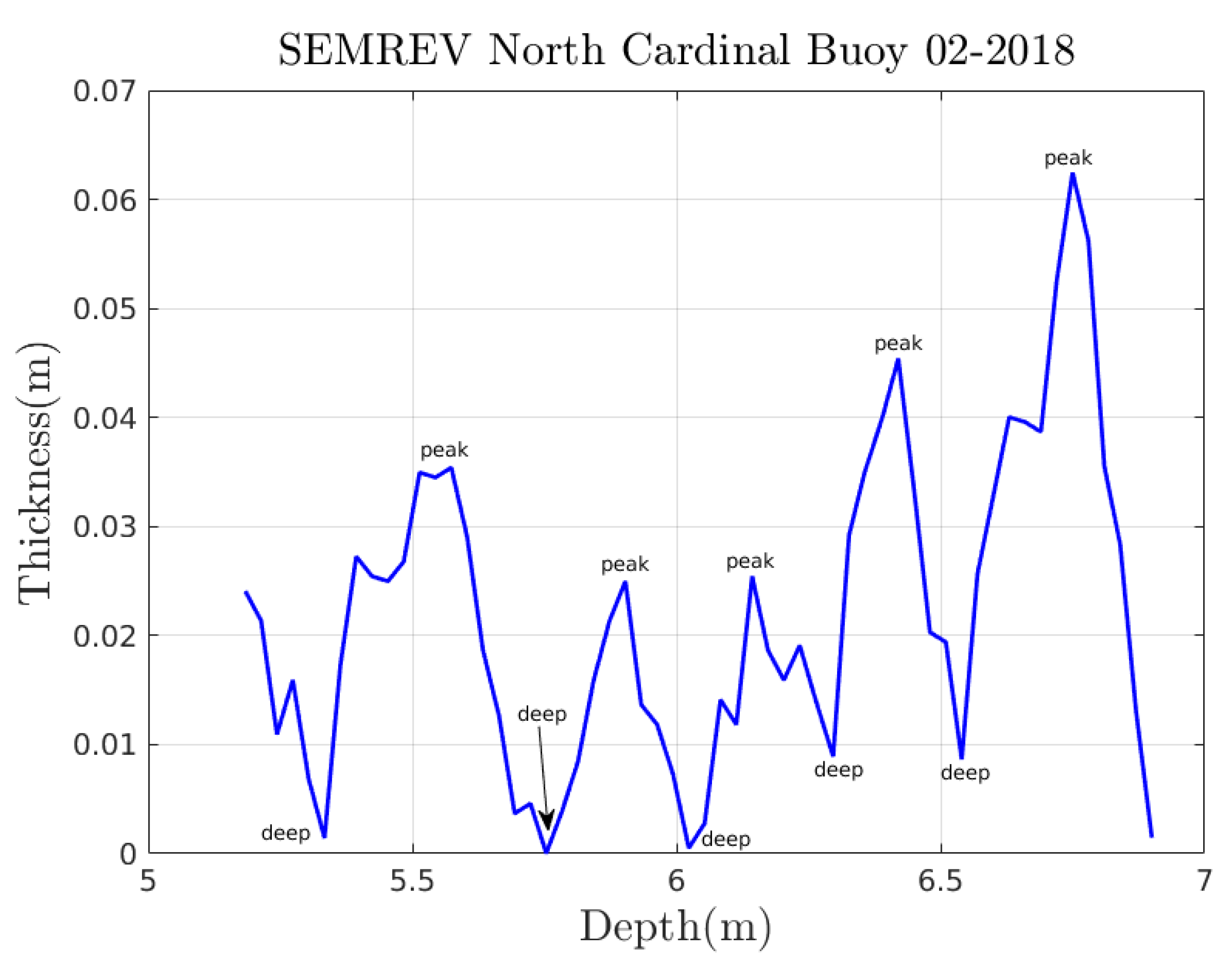

Appendix B. Generation of the Thicknesses for the Deeps
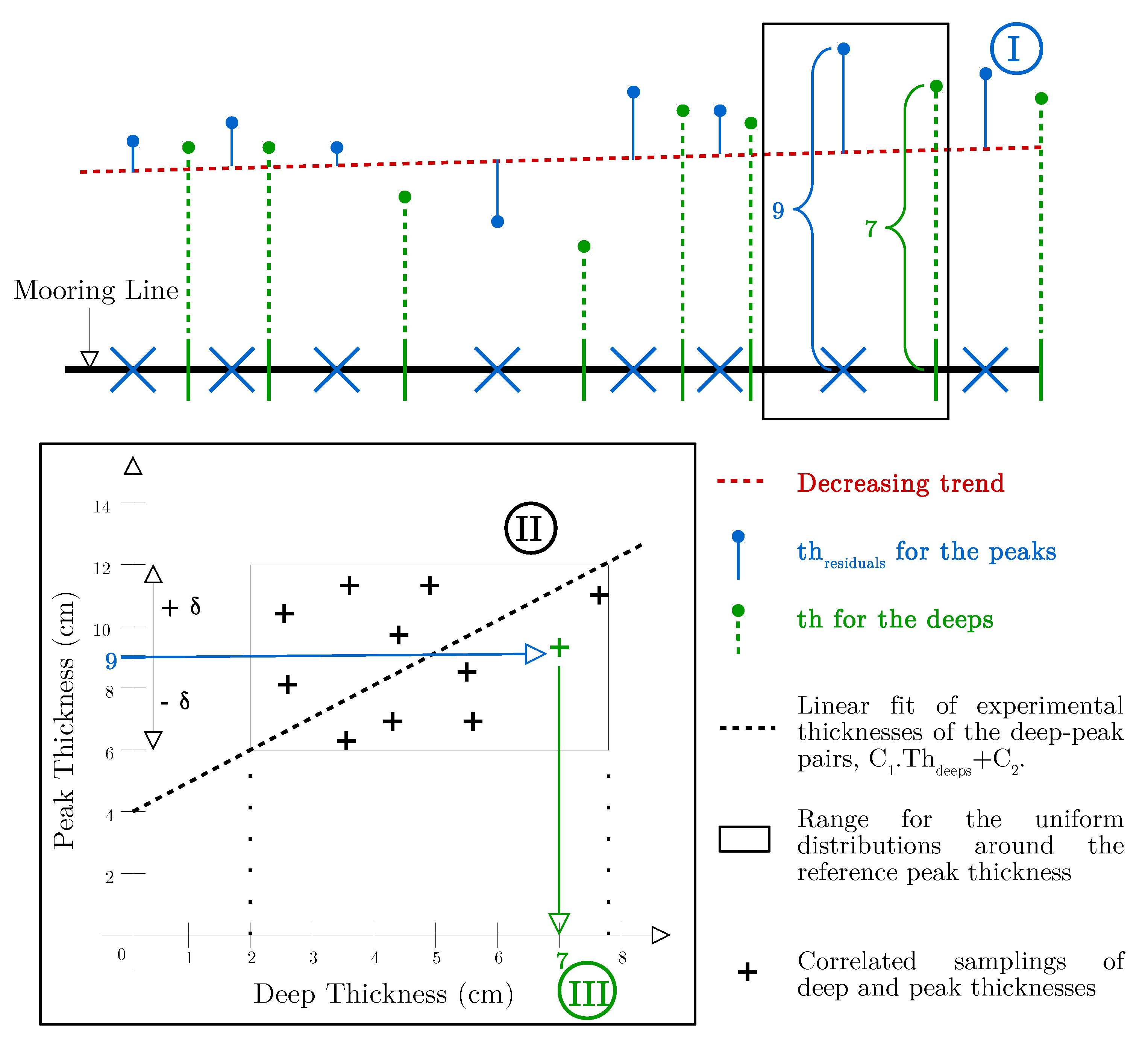
- First (I), we generate a Gaussian field for the residuals at peak positions (blue), following Equation (2) but with m .
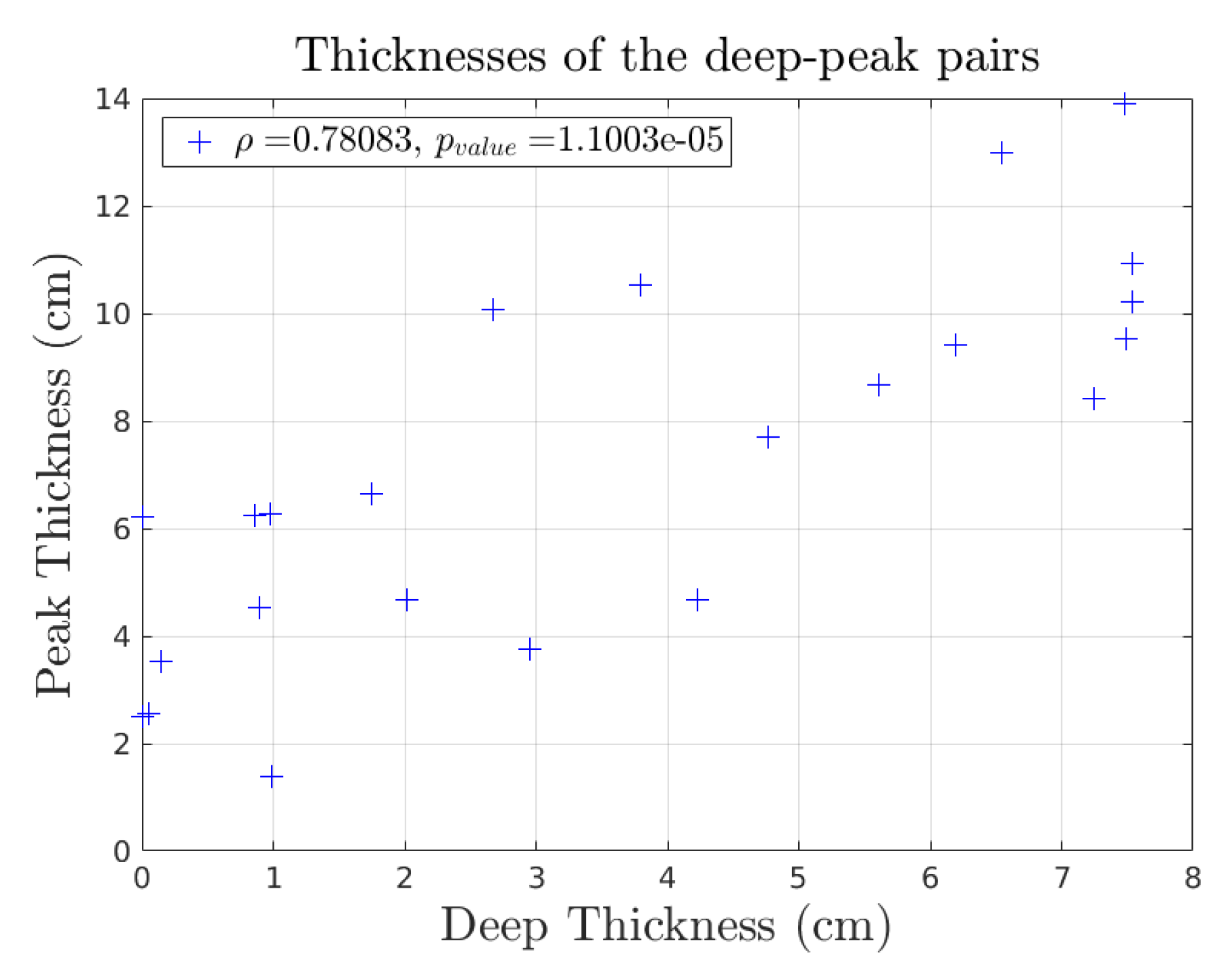
- Second (II), for each peak thickness, now considered to be the reference value ( in Figure A5), we generate correlated samplings of deep and peak thicknesses from uniform distributions around the reference value, using a Gaussian copula and a correlation coefficient . Peak thicknesses are uniformly sampled between and . The upper and lower bounds for the sampling of deep thicknesses (doted lines) are respectively the antecedents of and by the linear fit of experimental thicknesses of the deep-peak pairs (cf. Figure 9).
- Third (III), we stop the generation of samplings when we find a sampling whose peak thickness is close enough to the reference value ( m). The deep thickness of the selected sampling (7 in Figure A5) is then assigned to the deep position upstream the peak position of the reference peak thickness.
Appendix C. Differential Entropy of a Truncated Normal Distribution
References
- Fontaine, E.; Kilner, A.; Carra, C.; Washington, D.; Ma, K.; Phadke, A.; Laskowski, D.; Kusinski, G. Industry Survey of Past Failures, Pre-emptive Replacements and Reported Degradations for Mooring Systems of Floating Production Units. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar] [CrossRef]
- Pham, H.D.; Schoefs, F.; Cartraud, P.; Soulard, T.; Pham, H.H. Methodology for modeling and service life monitoring of mooring lines of floating wind turbines. Ocean Eng. 2019, 193. [Google Scholar] [CrossRef]
- Thies, P.R.; Johanning, L.; Harnois, V.; Smith, H.C.; Parish, D.N. Mooring line fatigue damage evaluation for floating marine energy converters: Field measurements and prediction. Renew. Energy 2014, 63, 133–144. [Google Scholar] [CrossRef]
- Ameryoun, H. Probabilistic Modeling of Wave Actions on Jacket Type Offshore Wind Turbines in Presence of Marine Growth. Ph.D. Thesis, Nantes University, Nantes, France, 2015. [Google Scholar]
- API. API RP 2A-WSD Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design. 2005. Available online: http://latorebondeng90245.tripod.com/api_rp2a.pdf (accessed on 3 February 2020).
- DNVGL. DNVGL-OS-E301 Position Mooring. 2018. Available online: http://rules.dnvgl.com/docs/pdf/dnvgl/os/2018-07/dnvgl-os-e301.pdf (accessed on 5 February 2020).
- Wright, C.; Pakrashi, V.; Murphy, J. The Dynamic Effects of Marine Growth on a Tension Moored Floating Wind Turbine; Progress in Renewable Energies Offshore: Lisbon, Portugal, 2016. [Google Scholar] [CrossRef]
- Spraul, C.; Pham, H.D. Effect of Marine Growth on Floating Wind Turbines Mooring Lines Responses; AFM, Association Française de Mécanique: Lille, France, 2017. [Google Scholar]
- Yang, S.H.; Ringsberg, J.; Johnson, E. The Influence of Biofouling on Power Capture and the Fatigue Life of Mooring Lines and Power Cables Used in Wave Energy Converters; Progress in Renewable Energies Offshore: Lisbon, Portugal, 2016; pp. 711–722. [Google Scholar] [CrossRef]
- Spraul, C. Suivi en Service de la DuréE de vie des Ombilicaux Dynamiques pour L’éolien Flottant. Ph.D. Thesis, Ecole Centrale Nantes, Nantes, France, 2018. [Google Scholar]
- Jusoh, I.; Wolfram, J. Effects of Marine Growth and Hydrodynamic Loading on Offshore Strucutres. J. Mek. 1996, 1, 77–98. [Google Scholar]
- Boukinda Mbadinga, M.L.; Quiniou Ramus, V.; Schoefs, F. Marine Growth Colonization Process in Guinea Gulf: Data Analysis. J. Offshore Mech. Artic Eng. 2007. [Google Scholar] [CrossRef]
- O’Byrne, M.; Pakrashi, V.; Schoefs, F.; Ghosh, B. A Stereo-Matching Technique for Recovering 3D Information from Underwater Inspection Imagery. Comput. Aided Civ. Infrastruct. Eng. 2018, 33, 193–208. [Google Scholar] [CrossRef]
- Ameryoun, H.; Schoefs, F.; Barillé, L.; Thomas, Y. Stochastic Modeling of Forces on Jacket-Type Offshore Structures Colonized by Marine Growth. J. Mar. Sci. Eng. 2019, 7, 158. [Google Scholar] [CrossRef]
- Berhault, C.; Le Crom, I.; Le Bihan, G. SEM-REV: un moyen d’essais en mer multi-fonctions pour les énergies marines renouvelables. La Houille Blanche 2015, 2. [Google Scholar] [CrossRef]
- Qvarfordt, S.; Kautsky, H.; Malm, T. Development of Fouling Communities on Vertical Structures in the Baltic Sea. Estuar. Coast. Shelf Sci. 2006, 67, 618–628. [Google Scholar] [CrossRef]
- Relini, G.; Tixi, F.; Torchia, G. The Macrofouling on Offshore Platforms at Ravenna. Int. Biodeterior. Biodegrad. 1997, 41, 41–55. [Google Scholar] [CrossRef]
- Wilhelmsson, D.; Malm, T. Fouling Assemblages on Offshore Wind Power Plants and Adjacent Substrata. Estuar. Coast. Shelf Sci. 2008, 79, 459–466. [Google Scholar] [CrossRef]
- Compère, C.; Segonzac, M. Marine Growths on Offshore Structures; Technical Report; IFREMER: Plouzané, France, 2000.
- Parks, T.; Sell, D.; Picken, G. Marine Growth Assessment of Alwyn North A in 1994; Technical Report; Auris Environmental LTD: Aberdeen, Scotland, 1995. [Google Scholar]
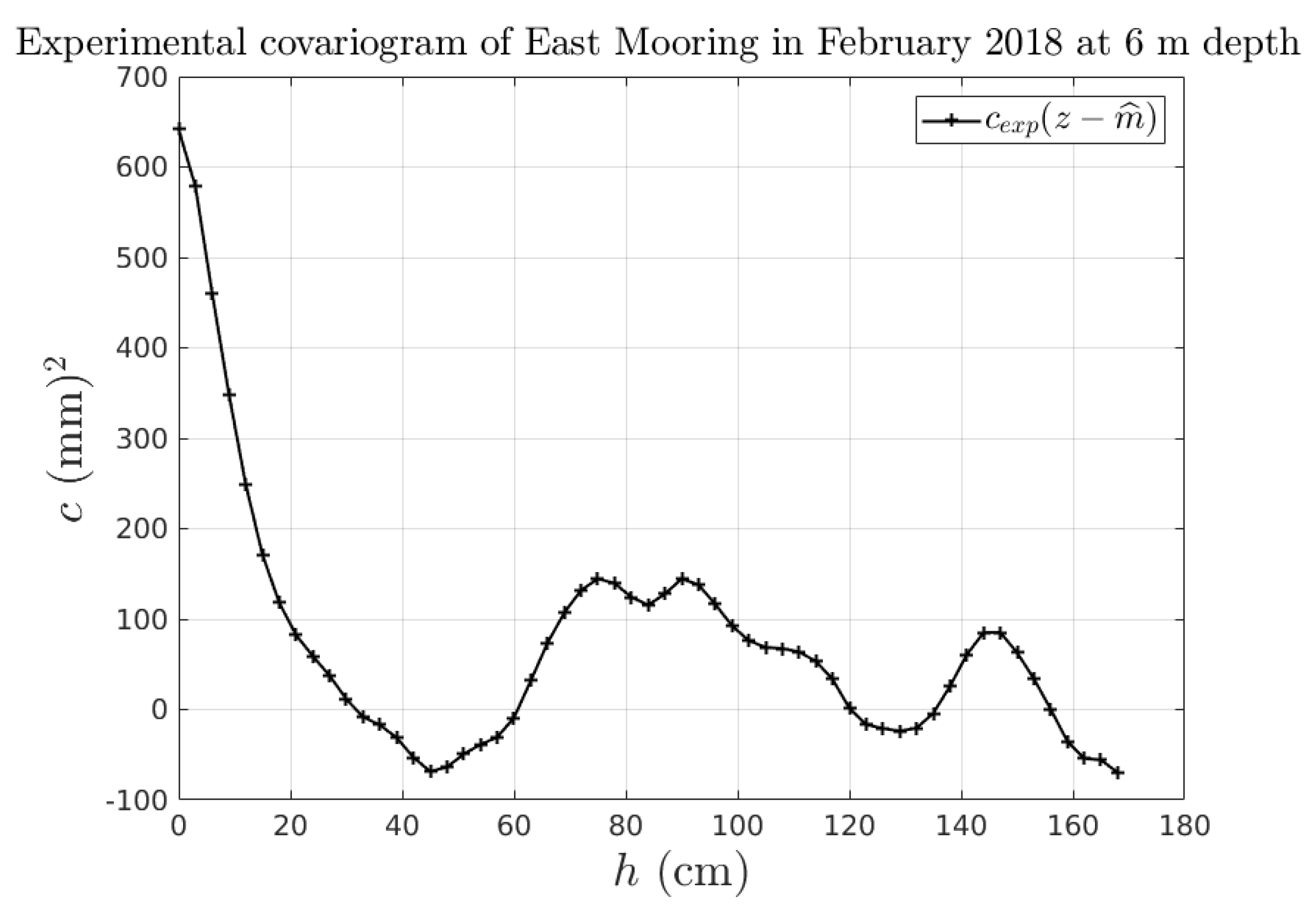
- Clerc, R.; Oumouni, M.; Schoefs, F. SCAP-1D: A Spatial Correlation Assessment Procedure from unidimensional discrete data. Reliab. Eng. Syst. Saf. 2019, 191. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference—A Practical Information—Theoretic Approach; Springer: Berlin, Germany, 2002. [Google Scholar]
- Dietrich, C.R.; Newsam, G.N. Fast and Exact Simulation of Stationary Gaussian Processes Through Circulant Embedding of the Covariance Matrix. SIAM J. Sci. Comput. 1997, 18, 1088–1107. [Google Scholar] [CrossRef]
- Parks, T.; Cunningham, A.; Sell, D. Marine Growth on Alwyn North B in 1991; Technical Report; Auris Environmental LTD: Aberdeen, Scotland, 1991. [Google Scholar]
- Molin, B. Hydrodynamique des Structures Offshore; Guides Pratiques Sur Les Ouvrages en Mer; Editions TECHNIP: Paris, France, 2002. [Google Scholar]
- Malings, C.; Pozzi, M. Conditional entropy and value of information metrics for optimal sensing in infrastructure systems. Struct. Saf. 2016, 60, 77–90. [Google Scholar] [CrossRef]
- Verdugo, L.; Pushpa, N.R. On the Entropy of Continuous Probability Distributions. IEEE Trans. Inf. Theory 1978, 24, 120–122. [Google Scholar] [CrossRef]
- Györfi, L.; Beirlant, J.; Dudewicz, E.J.; van der Meulen, E.C. Non-Parametric Entropy Estimation: An Overview. Int. J. Math. Stat. Sci. 2001, 6, 17–39. [Google Scholar]
- Hall, P.; Morton, S.C. On the Estimation of Entropy. Ann. Inst. Stat. Math. 1993, 45, 69–88. [Google Scholar] [CrossRef]








| a (m) | b | |
|---|---|---|
| East Mooring before summer 2017 | ||
| West Mooring before summer 2017 | ||
| East Mooring in February 2018 | ||
| East Mooring in May 2018 |
| (m) | (m) | ||
|---|---|---|---|
| East Mooring before summer 2017 | MLE | ||
| West Mooring before summer 2017 | MLE | ||
| East Mooring in February 2018 | LSE | ||
| East Mooring in May 2018 | MLE |
| Interstitial Water Volume | Intervalvular Water Mass | |
|---|---|---|
| The “open porosity” density () | ✓ | × |
| The “closed porosity” density () | × | ✓ |
| The “open and closed” porosity density () | ✓ | ✓ |
| Name of the Scenario | (m) | (m) | (m) | (kg·m) | |
|---|---|---|---|---|---|
| Unfavourable site (US) | 720 | ||||
| Favourable site after some months (FS) | 380 | ||||
| Full developed in favourable site (FD) | 550 | ||||
| After a storm (AS) | 2 | 550 |
| Name of the Scenario | 1 Sensor (kg) | 2 Sensors (kg) | 3 Sensors (kg) | 4 Sensors (kg) |
|---|---|---|---|---|
| Unfavourable site | 465 | |||
| Favourable site after some months | 848 | |||
| Full developed in favourable site | ||||
| After a storm | 2863 |
| Probabilistic Distribution | |
|---|---|
| a (m) | Uniform |
| b | Uniform |
| (m) | Truncated normal (Mean: m; Std: m; m; m) |
| (m) | Truncated normal (Mean: m; Std: m; m; m) |
| (kg·m) | Uniform |
| Differential Entropy in Nats | Source | |
|---|---|---|
| Uniform | [27] | |
Truncated normal | Appendix C |
| Reference Mass Distribution | Number of Sensors | Relative Error of Tension Measurement |
|---|---|---|
| Favourable site after some months | 4 | 5 |
| Full developed in favourable site | 3 4 | 5 5 |
| After a storm | 3 3 4 4 4 | 5 10 5 10 15 |
| a | b | ||||
|---|---|---|---|---|---|
| h | 1 | 1 | 0 | 0 | 1 |
| p-value |
| Nb Sensors | a | b | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| US | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | × | × | × | × | |
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | × | × | × | × | ||
| × | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | × | × | × | × | ||
| ✓ | × | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | × | × | × | × | ||
| FS | ✓ | ✓ | ✓ | □ | × | × | × | □ | ✓ | ✓ | ✓ | □ | |
| ✓ | ✓ | ✓ | ✓ | × | × | × | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| ✓ | ✓ | ✓ | ✓ | × | × | × | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| ✓ | ✓ | ✓ | ✓ | × | × | × | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| FD | ✓ | ✓ | □ | □ | ✓ | ✓ | □ | □ | Reference value | ||||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Prior mean = | |||||
| AS | × | × | □ | □ | × | × | □ | □ | Reference value | ||||
| × | × | □ | □ | × | × | □ | □ | ||||||
| × | × | ✓ | □ | × | × | ✓ | □ | ||||||
| × | × | ✓ | ✓ | × | × | ✓ | ✓ | Prior mean = | |||||
| Colonisation Case | Number of Sensors | Error of Measurement | |
|---|---|---|---|
| Pearson | Corr p-value | Corr p-value | Corr p-value |
| Spearman | Corr p-value | Corr p-value | Corr p-value |
| Colonisation Case | Number of Sensors | Error of Measurement | |
|---|---|---|---|
| Pearson | Corr p-value | Corr p-value | Corr p-value |
| Spearman | Corr p-value | Corr p-value | Corr p-value |
| Colonisation Case | Number of Sensors | Error of Measurement | |
|---|---|---|---|
| Pearson | Corr p-value | Corr p-value | Corr p-value |
| Spearman | Corr p-value | Corr p-value | Corr p-value |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Decurey, B.; Schoefs, F.; Barillé, A.-L.; Soulard, T. Model of Bio-Colonisation on Mooring Lines: Updating Strategy Based on a Static Qualifying Sea State for Floating Wind Turbines. J. Mar. Sci. Eng. 2020, 8, 108. https://doi.org/10.3390/jmse8020108
Decurey B, Schoefs F, Barillé A-L, Soulard T. Model of Bio-Colonisation on Mooring Lines: Updating Strategy Based on a Static Qualifying Sea State for Floating Wind Turbines. Journal of Marine Science and Engineering. 2020; 8(2):108. https://doi.org/10.3390/jmse8020108
Chicago/Turabian StyleDecurey, Benjamin, Franck Schoefs, Anne-Laure Barillé, and Thomas Soulard. 2020. "Model of Bio-Colonisation on Mooring Lines: Updating Strategy Based on a Static Qualifying Sea State for Floating Wind Turbines" Journal of Marine Science and Engineering 8, no. 2: 108. https://doi.org/10.3390/jmse8020108
APA StyleDecurey, B., Schoefs, F., Barillé, A.-L., & Soulard, T. (2020). Model of Bio-Colonisation on Mooring Lines: Updating Strategy Based on a Static Qualifying Sea State for Floating Wind Turbines. Journal of Marine Science and Engineering, 8(2), 108. https://doi.org/10.3390/jmse8020108






