Interaction of a Solitary Wave with Vertical Fully/Partially Submerged Circular Cylinders with/without a Hollow Zone
Abstract
1. Introduction
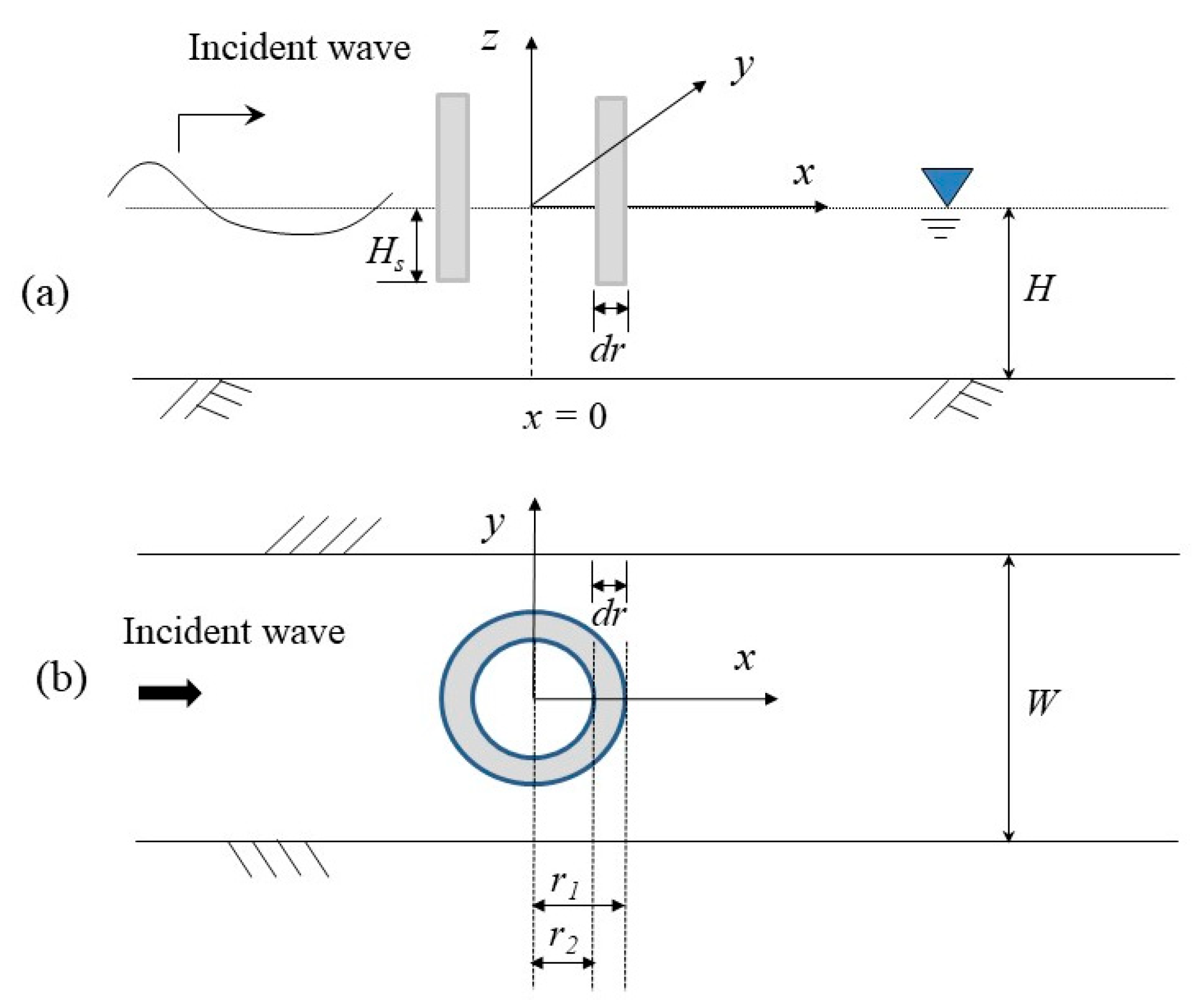
2. Flow-Field Equations
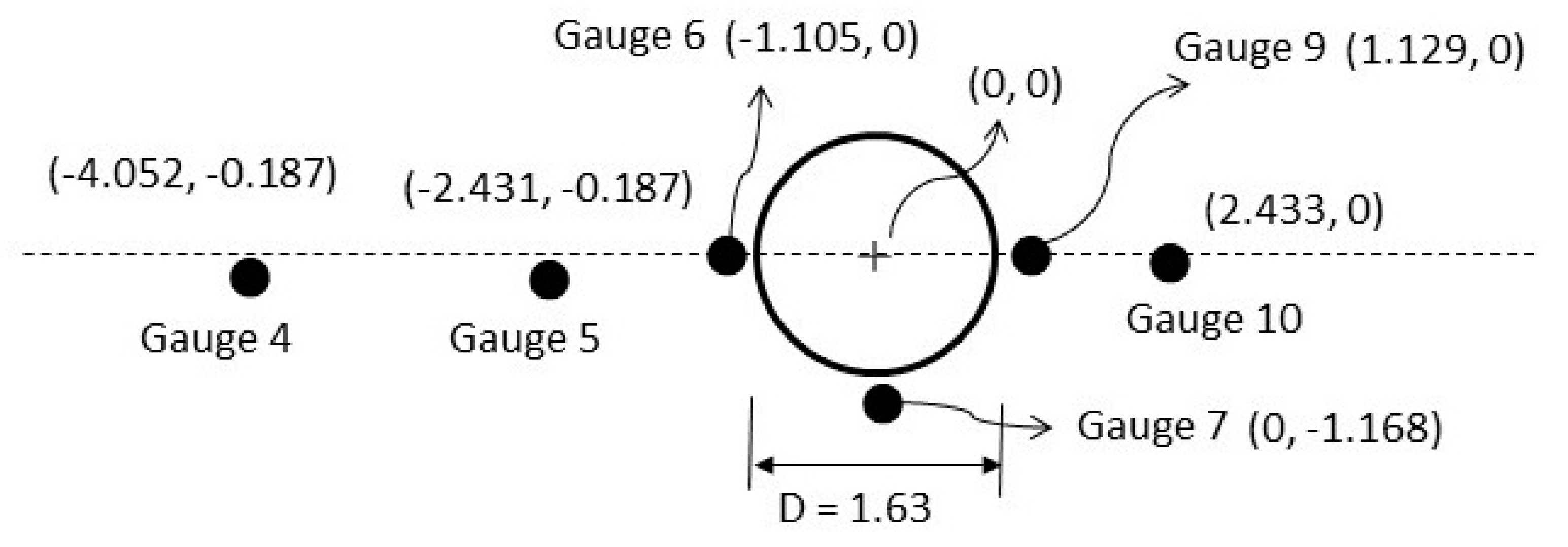
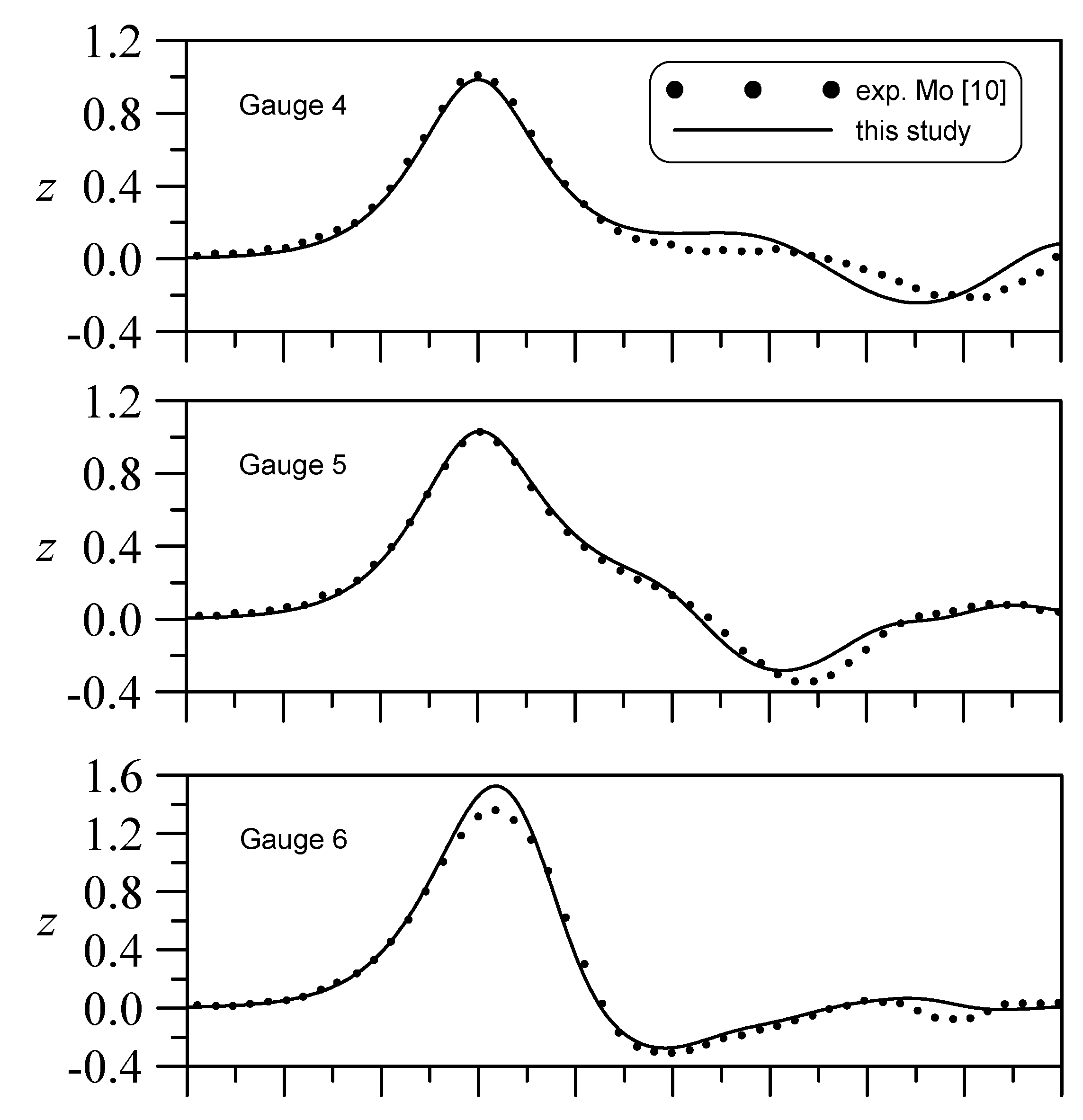
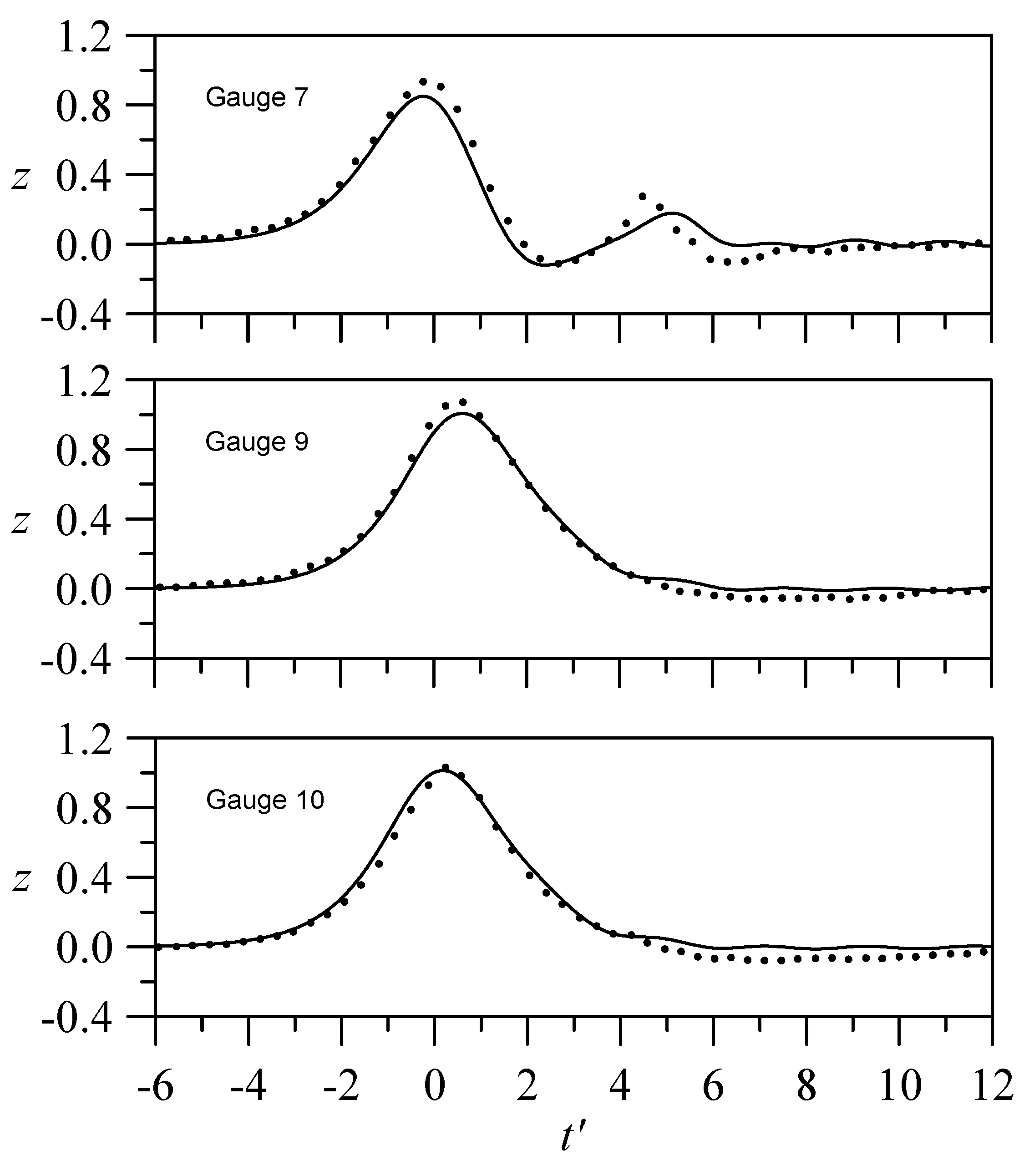
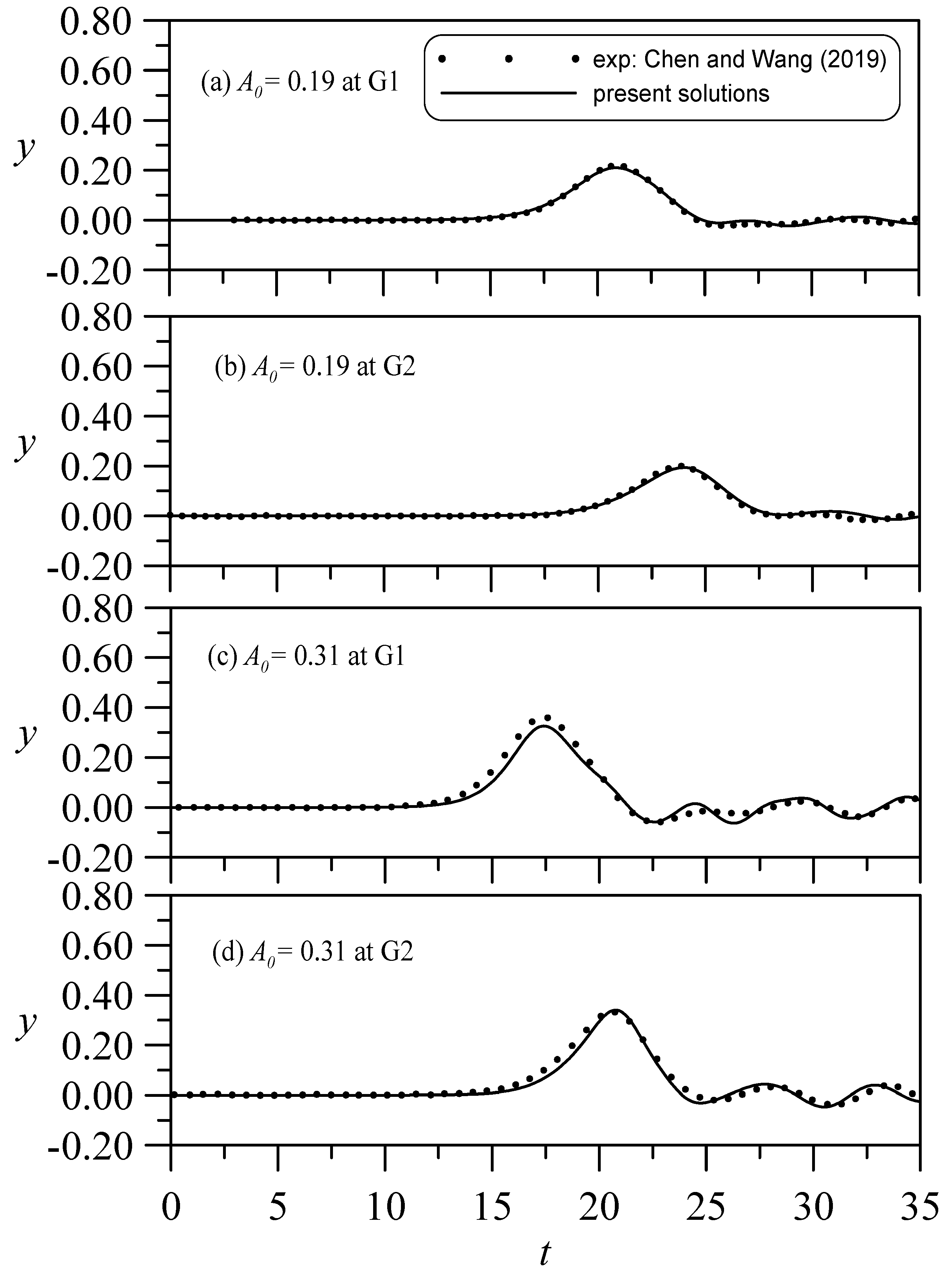
3. Validations
4. Results and Discussion
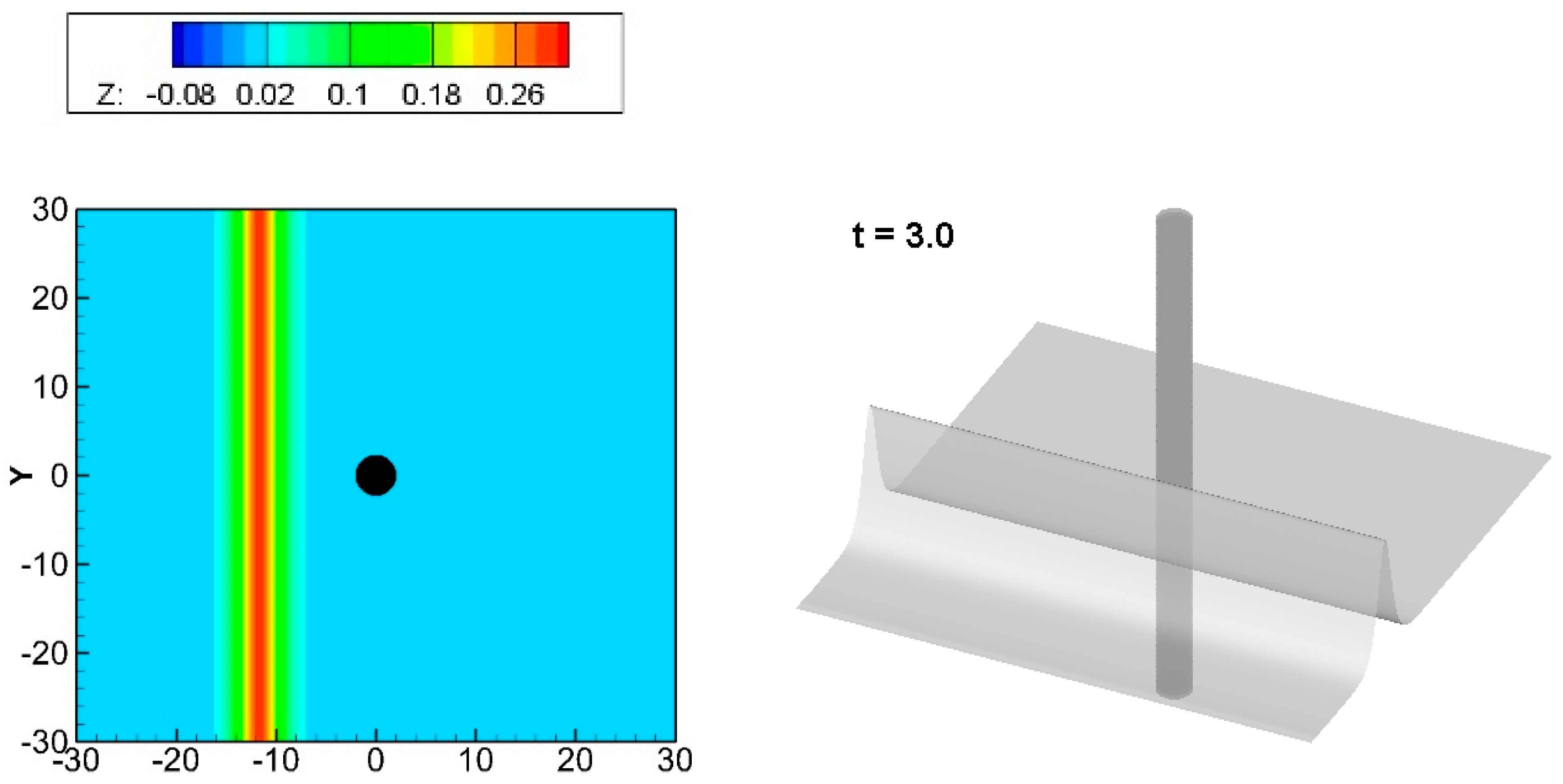
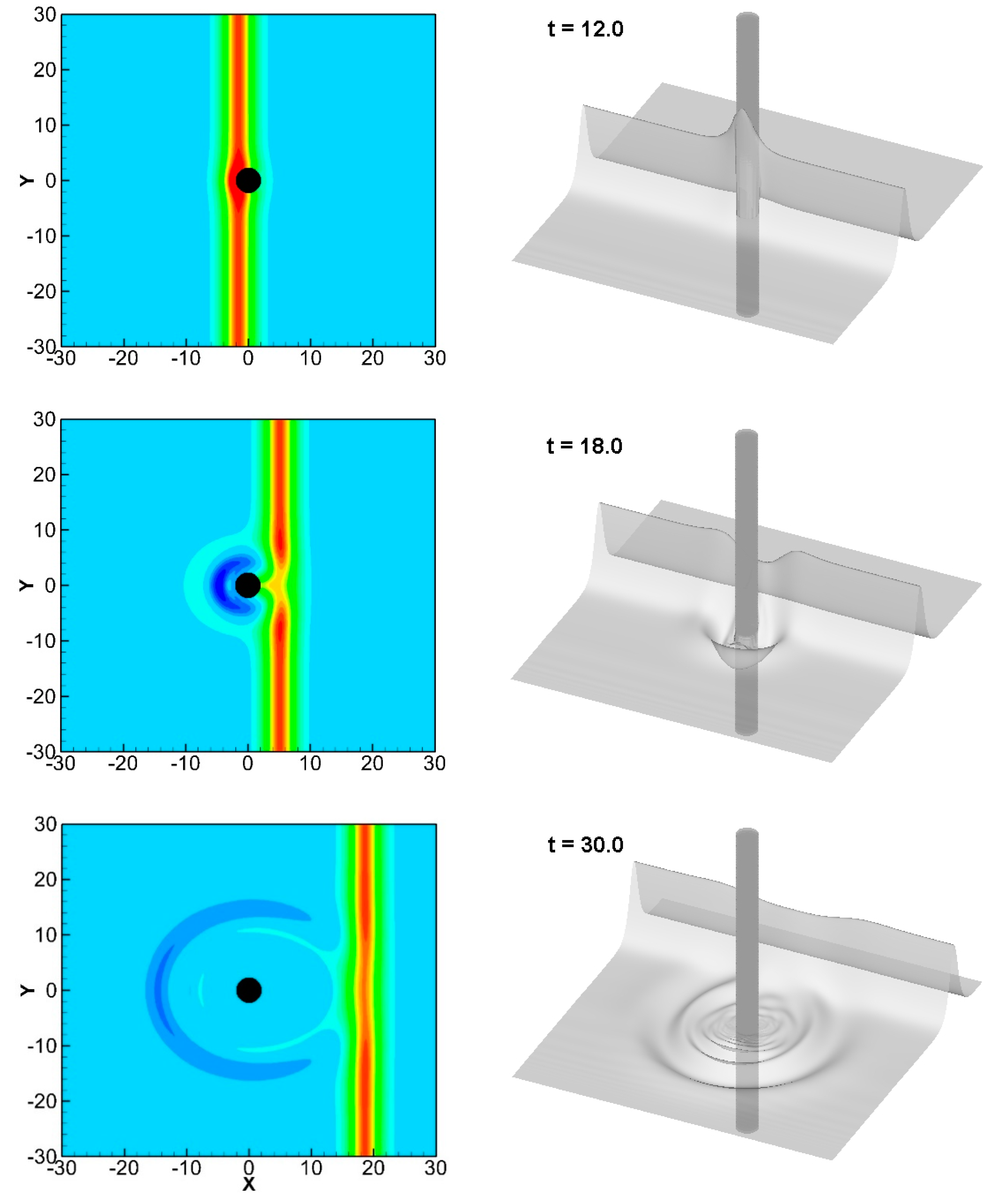
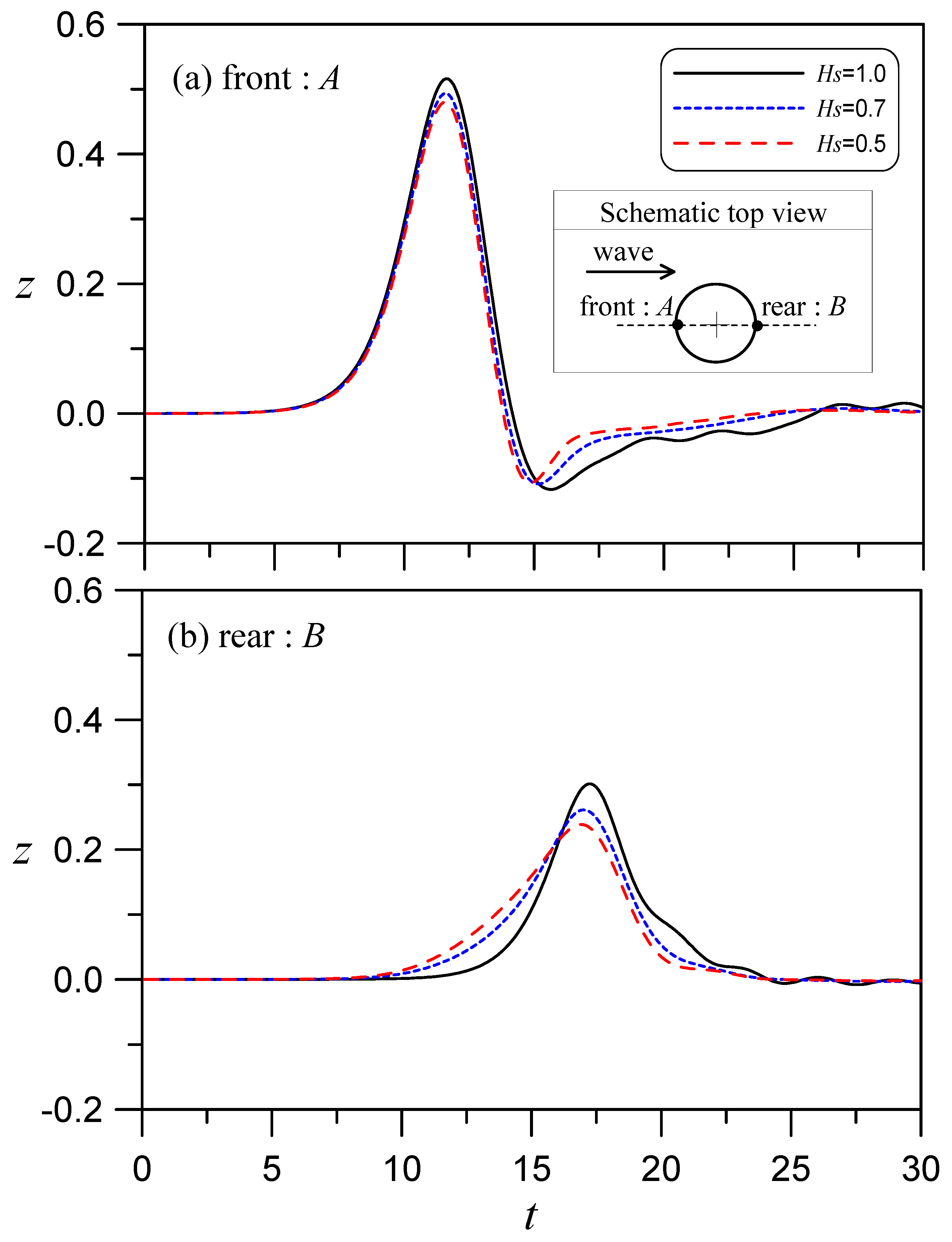
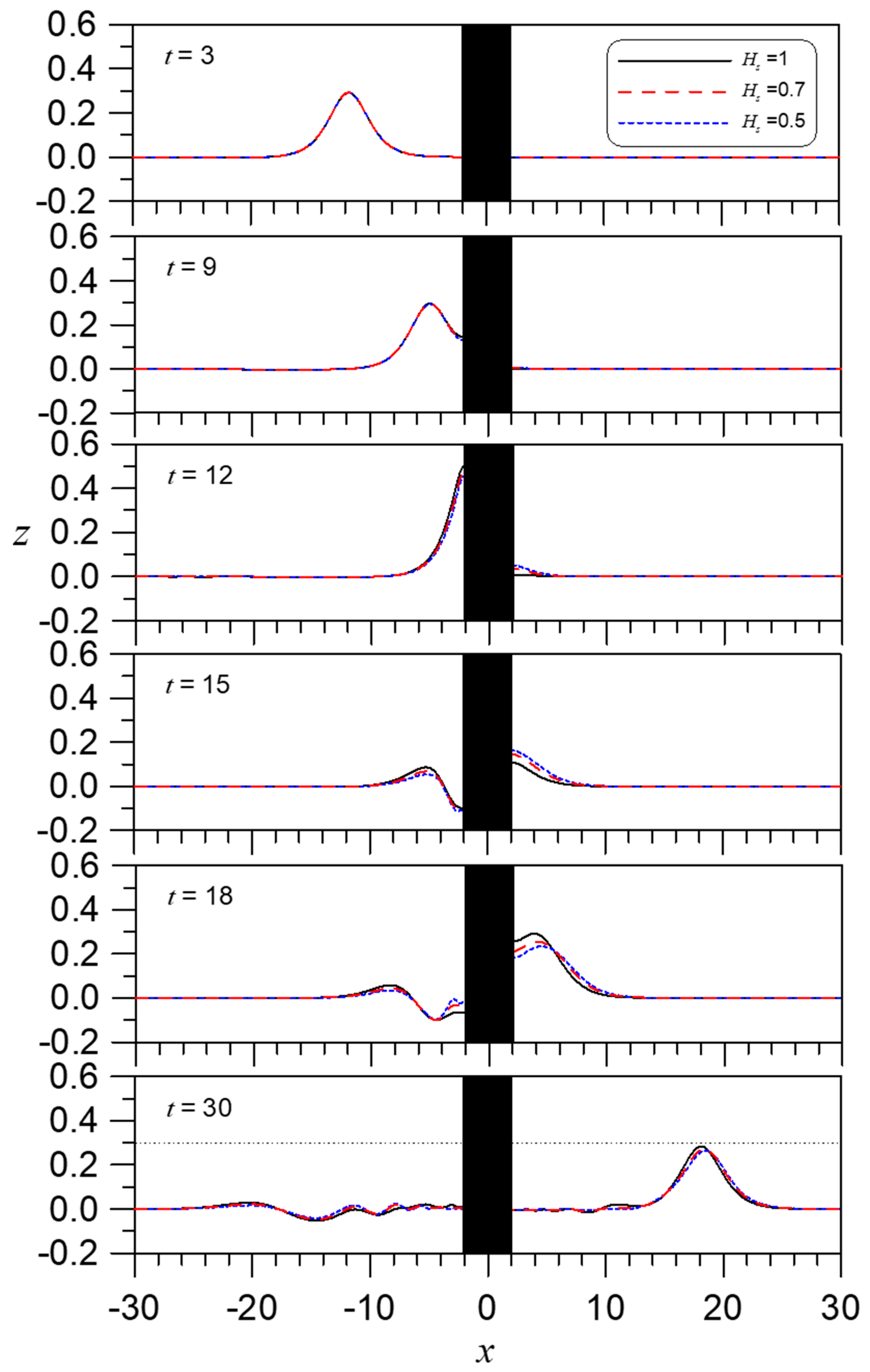
4.1. Solitary Wave Hitting a Circular Cylinder with Different Drafts and Sizes
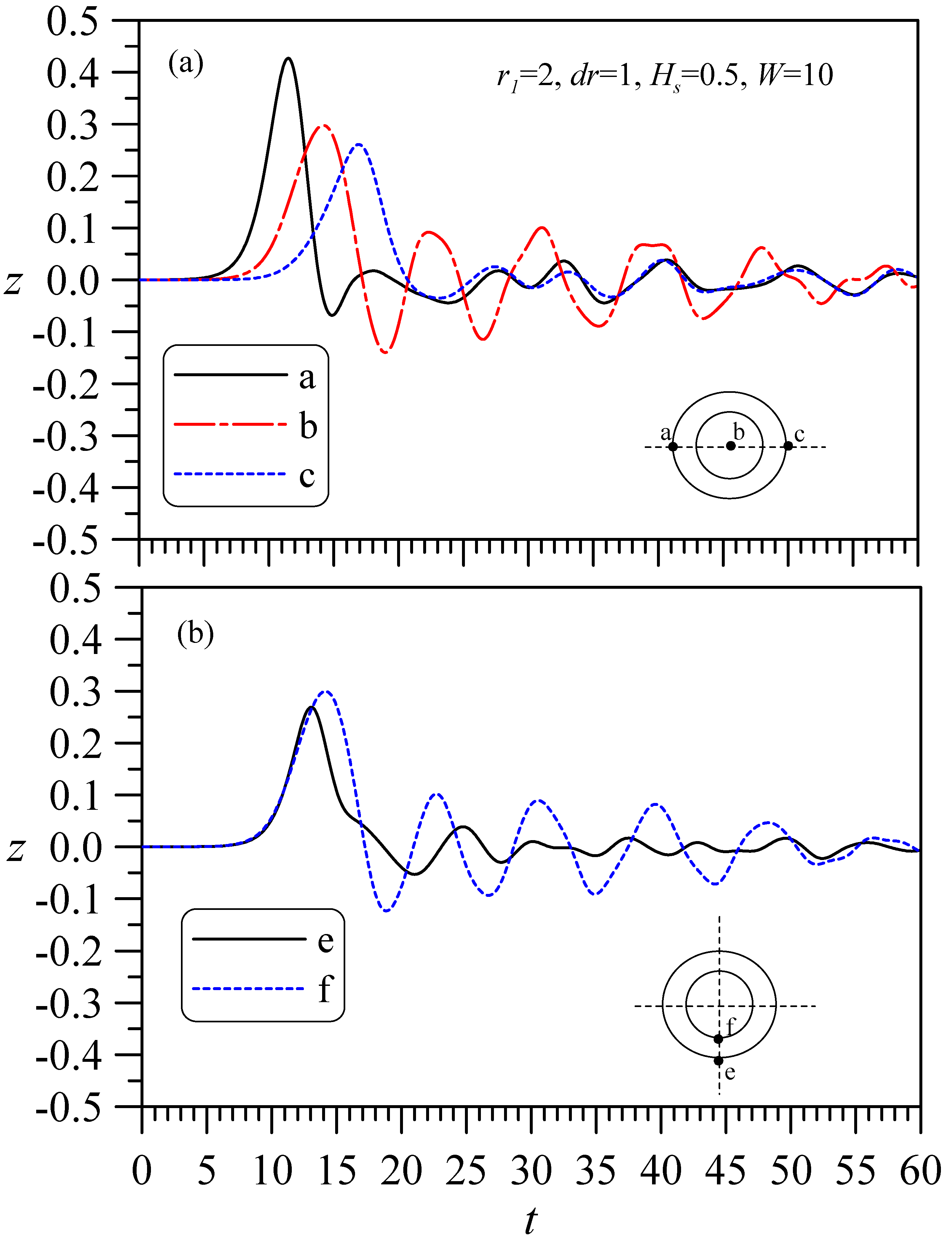
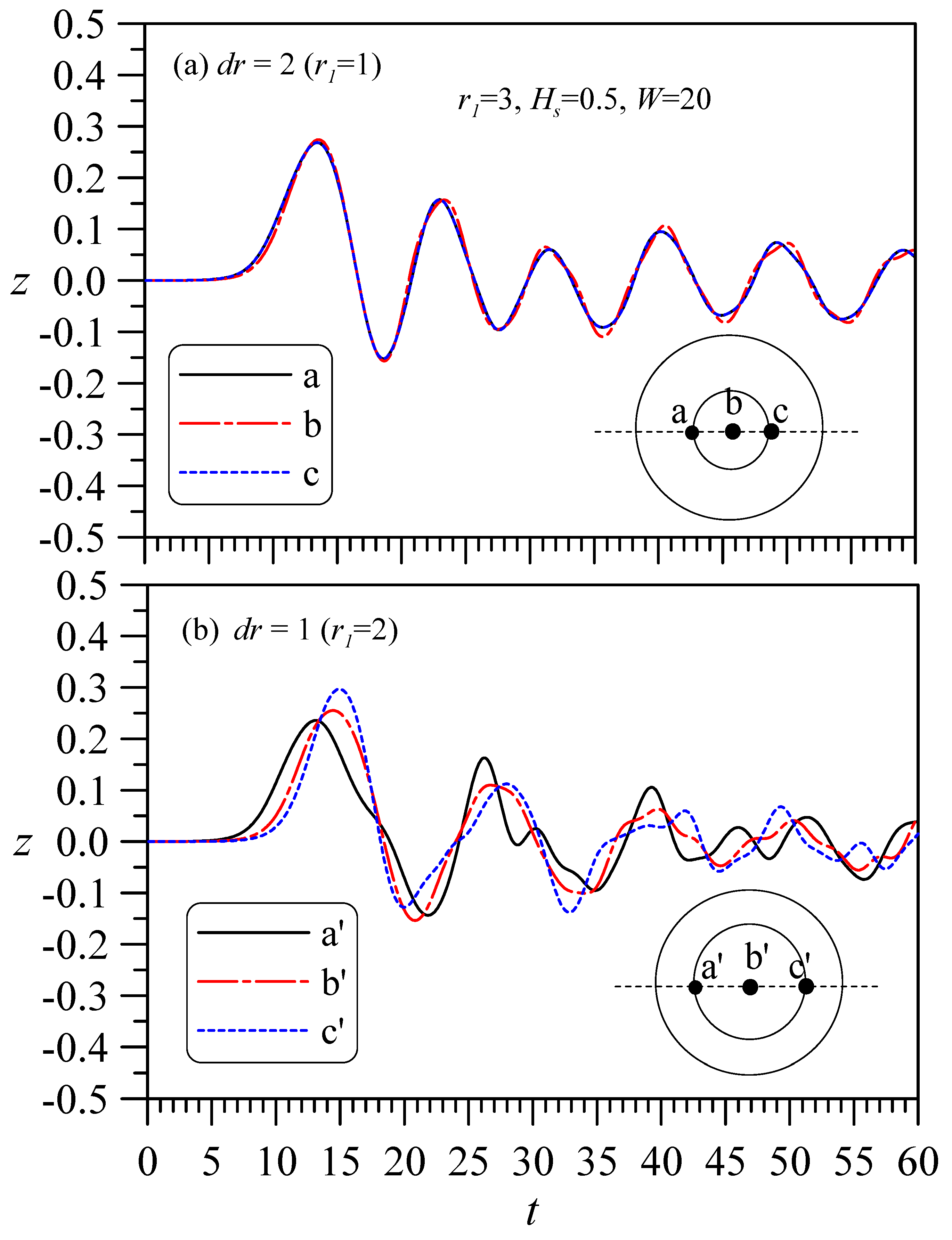
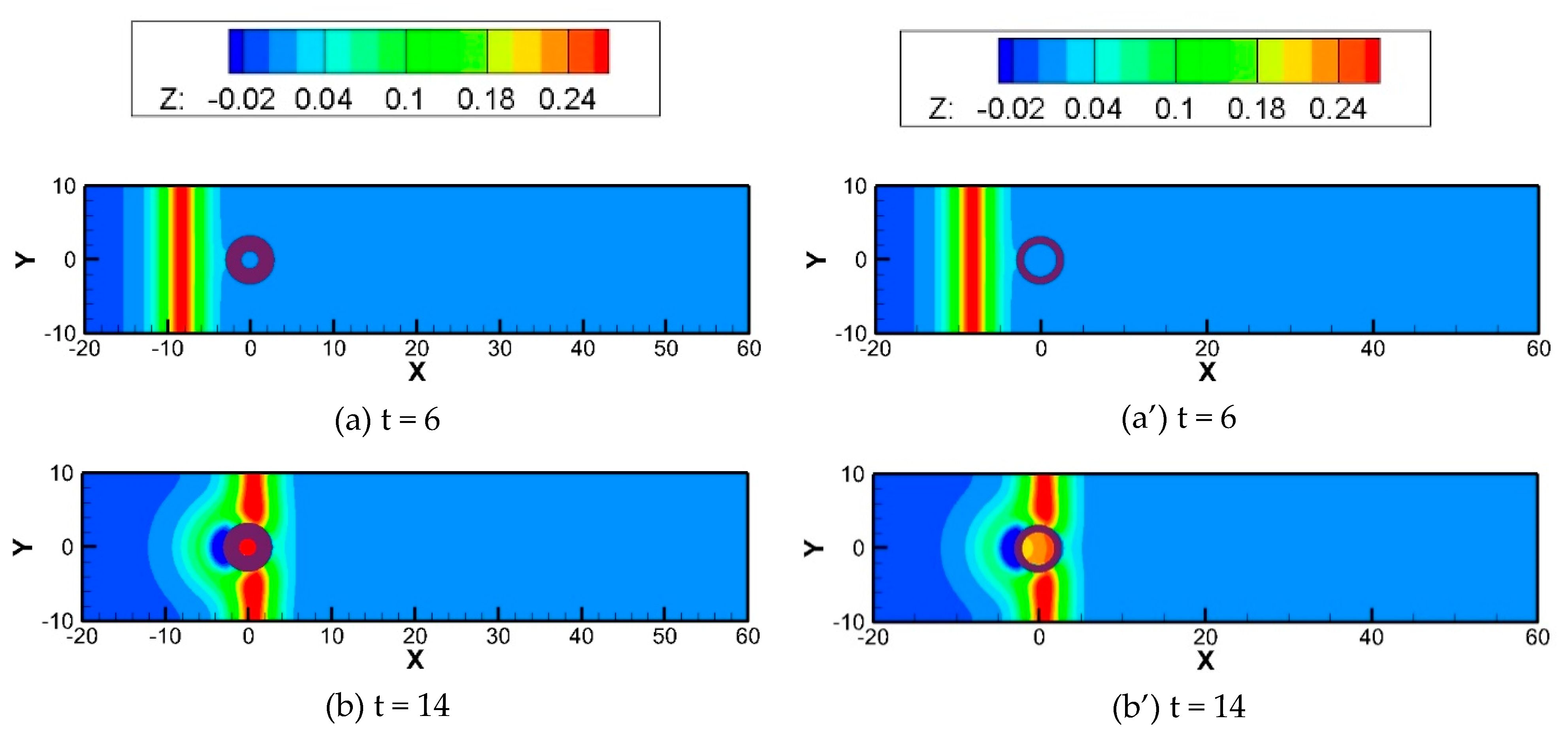
4.2. Solitary Wave Hits a Circular Cylinder with a Hollow Zone
4.2.1. Fixed Thickness, with Changes in the Outer and Inner Diameters
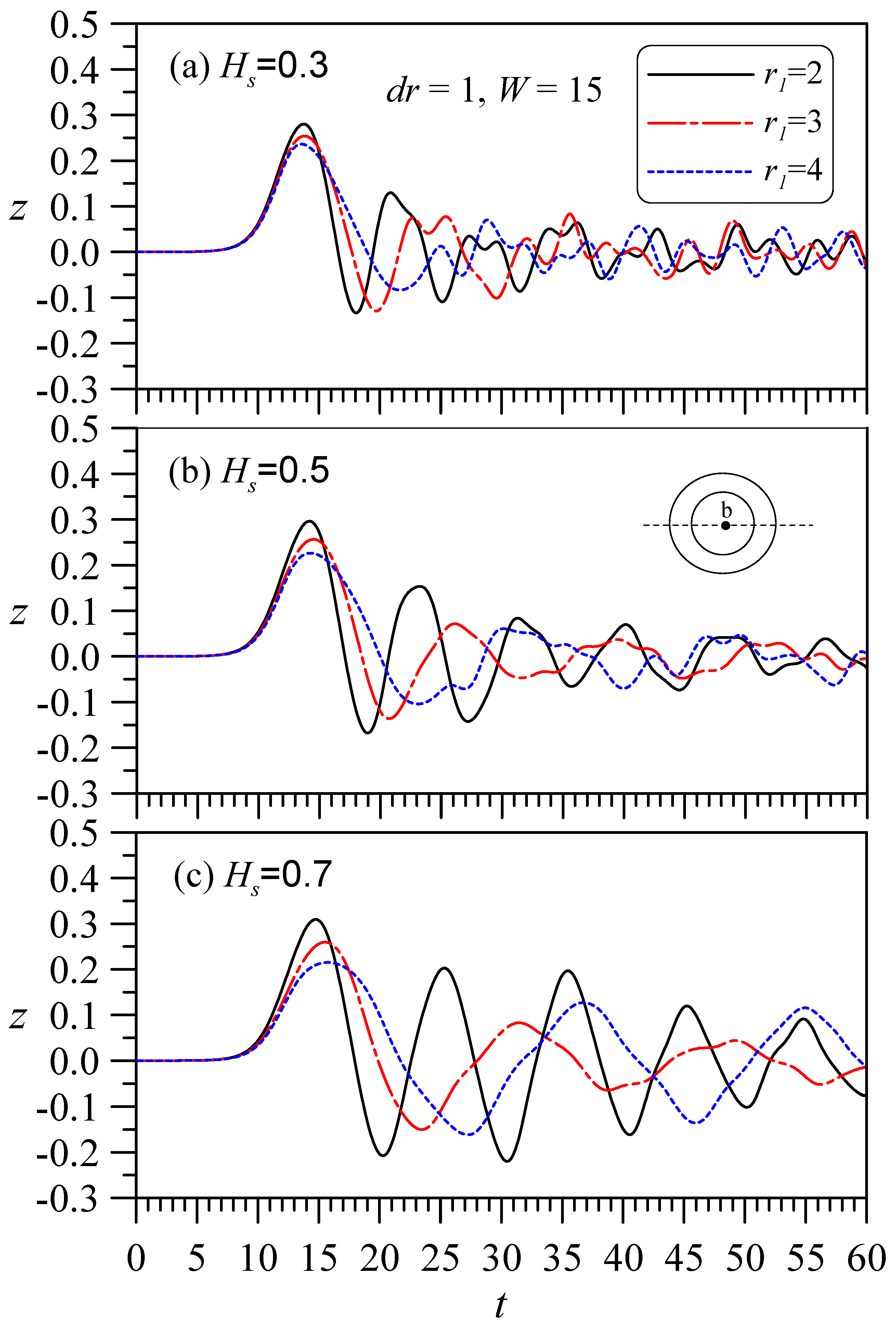
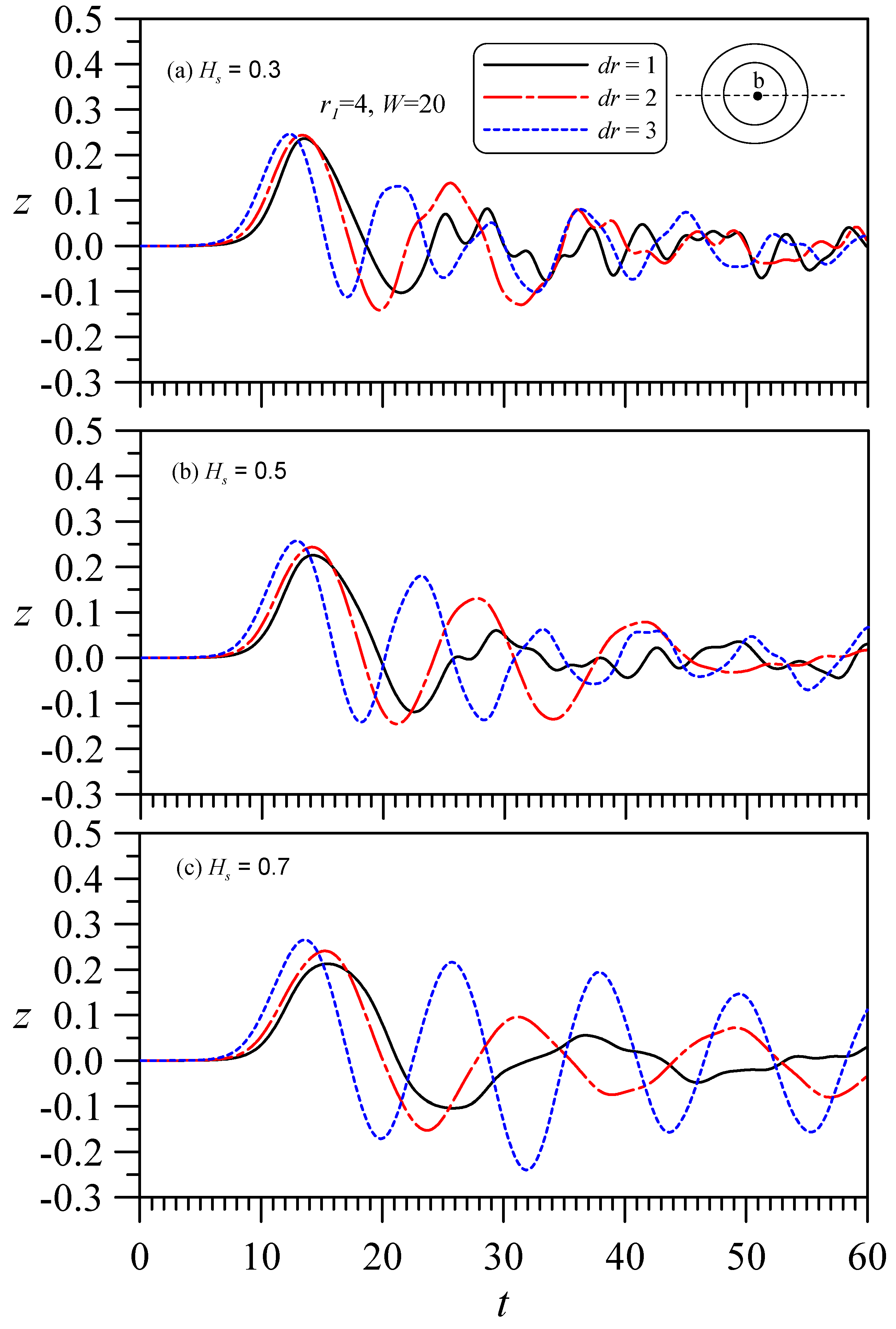
4.2.2. Fixed Inner Diameter, with Changes in the Outer Diameter and Thickness
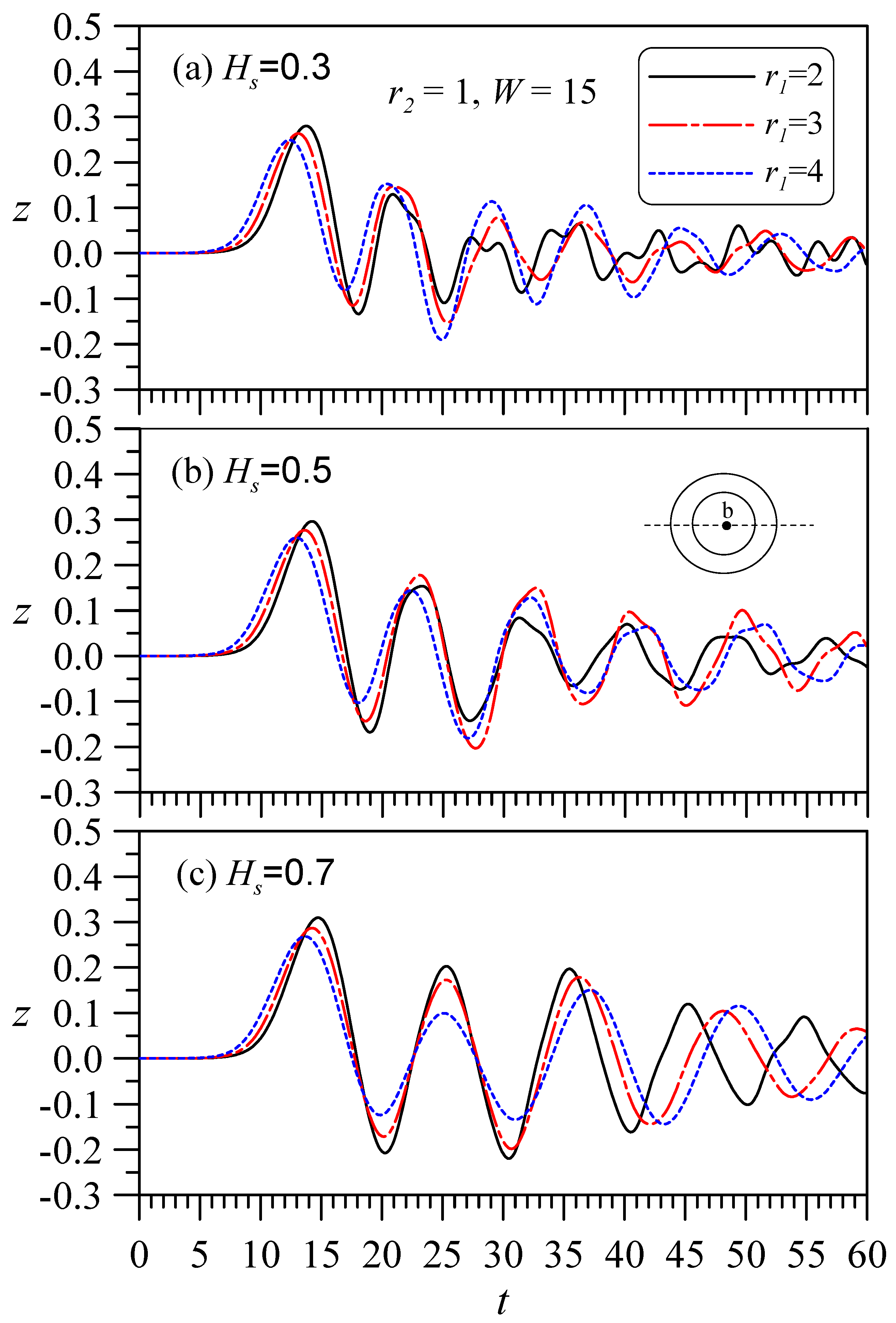
4.2.3. Fixed Outer Diameter, with Changes in the Inner Diameter and Thickness
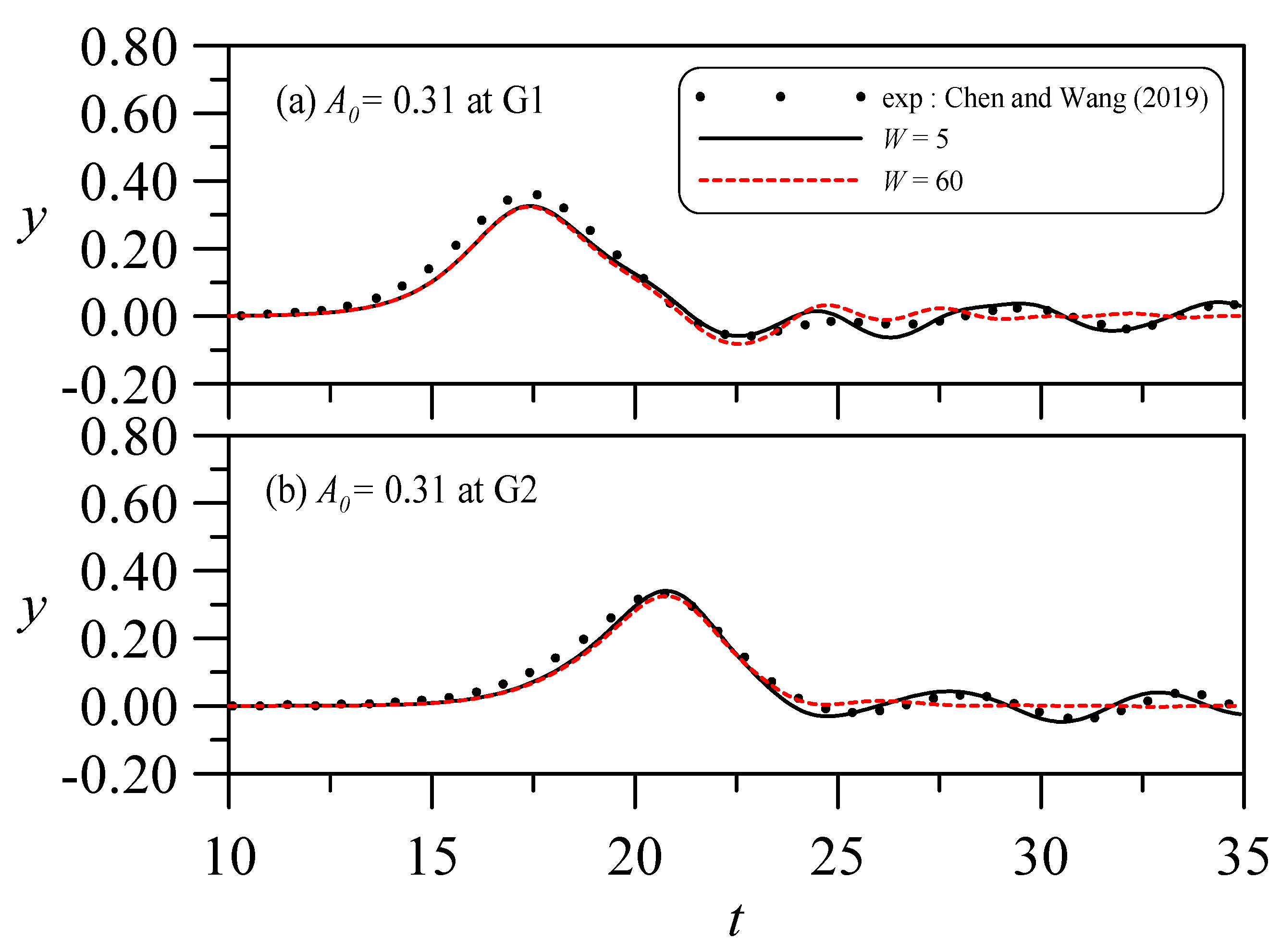
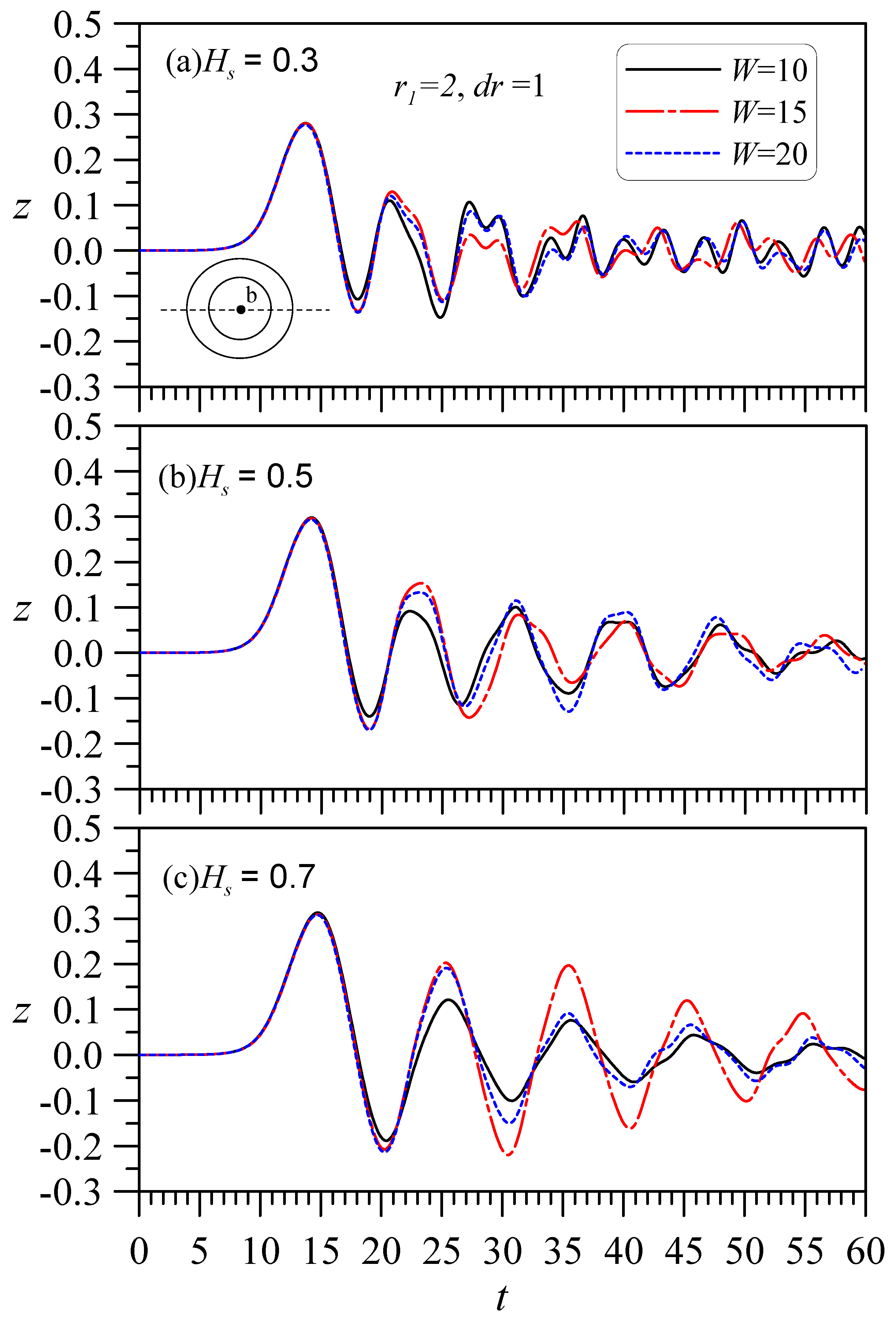
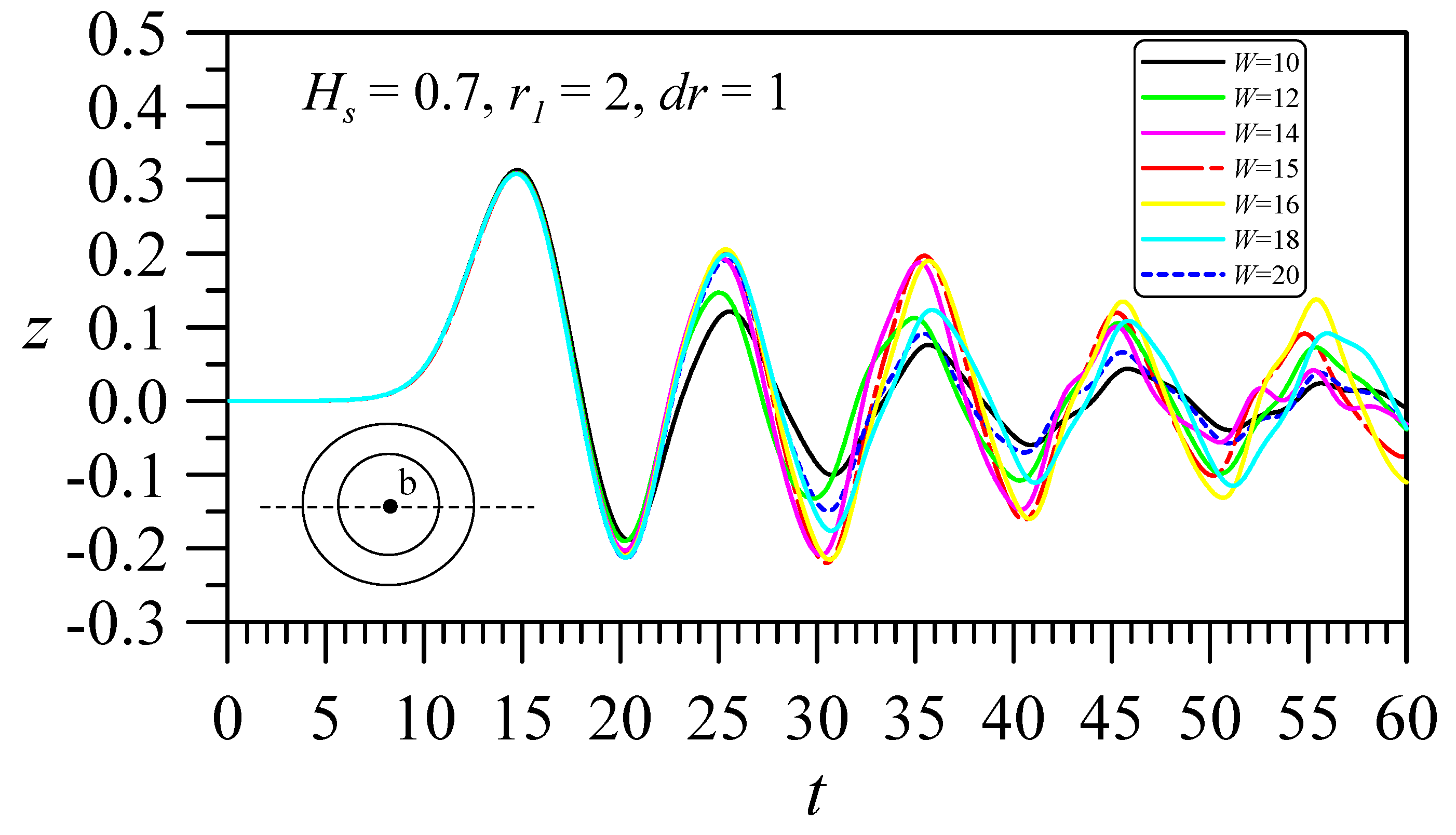
4.3. Influence of W on the Solitary Wave Hitting a Circular Cylinder with a Hollow Zone
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
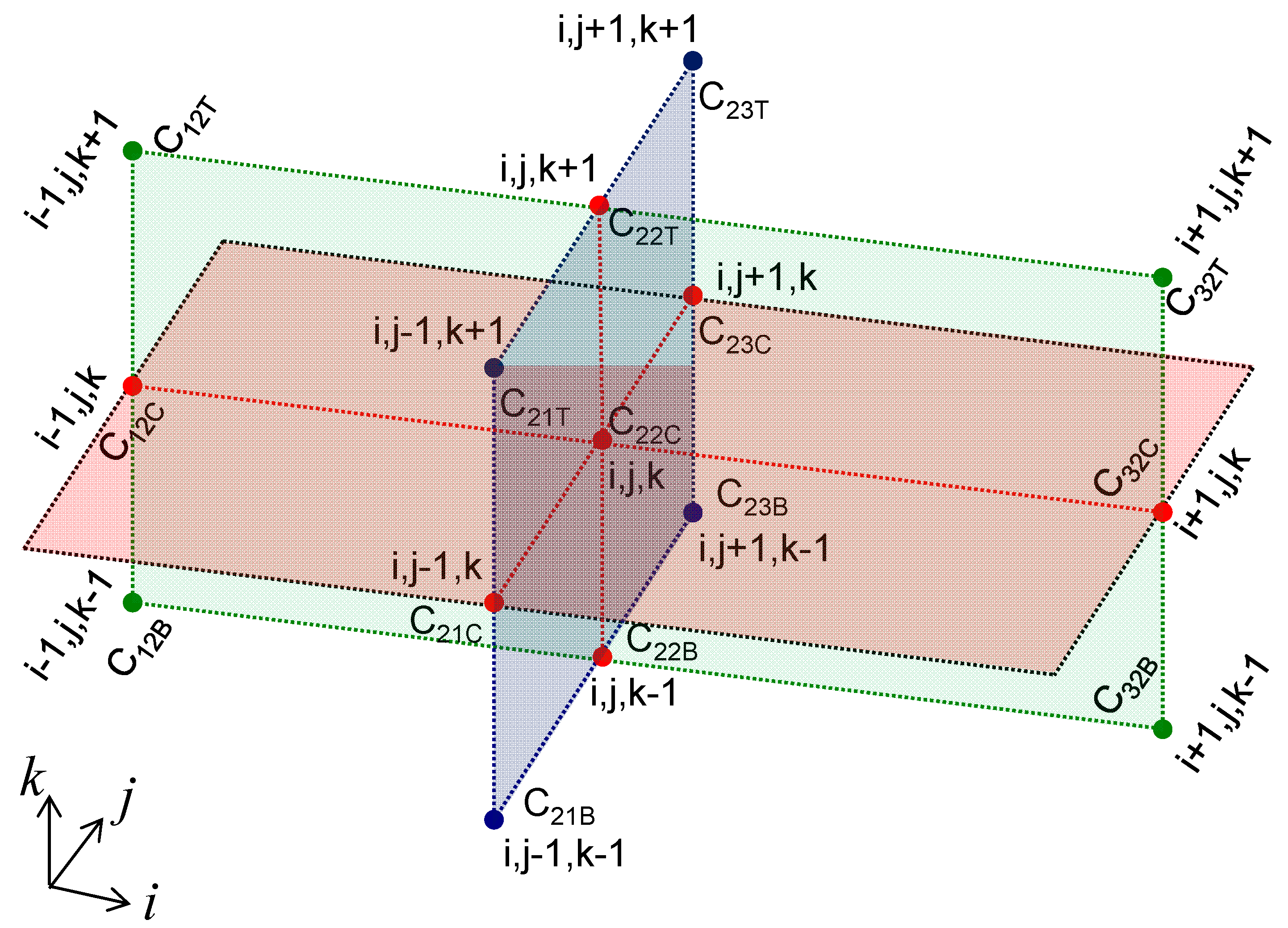
Appendix A.1. Grid Generations
Appendix A.2. Equation Transformation
Appendix A.3. Numerical Discretization
References
- Havelock, T.H. The pressure of water waves upon a fixed obstacle. Proc. R. Soc. Lond. 1940, 175, 409–421. [Google Scholar]
- Ursell, F. On the heaving motion of a circular cylinder on the surface of a fluid. Q. J. Mech. Appl. Math. 1949, 2, 218–231. [Google Scholar] [CrossRef]
- MacCamy, R.C.; Fuchs, R.A. Wave Forces on a Pile: A Diffraction Theory; Technical Memorandum 69; Beach Erosion Board Corps of Engineers: Washington, DC, USA, 1954. [Google Scholar]
- Finnegan, W.; Meere, M.; Goggins, J. The wave excitation forces on a truncated vertical cylinder in water of infinite depth. J. Fluids Struct. 2013, 40, 201–213. [Google Scholar] [CrossRef]
- Miles, J.W.; Gilbert, J.F. Scattering of gravity waves by a circular dock. J. Fluid Mech. 1968, 34, 783–793. [Google Scholar] [CrossRef]
- Garrett, C.J.R. Wave forces on a circular dock. J. Fluid Mech. 1971, 46, 129–139. [Google Scholar] [CrossRef]
- Black, J.L.; Mei, C.C.; Bray, C.G. Radiation and scattering of water waves by rigid bodies. J. Fluid Mech. 1971, 46, 151–164. [Google Scholar] [CrossRef]
- Molin, B. Second-order diffraction loads upon three-dimensional bodies. Appl. Ocean Res. 1979, 1, 197–202. [Google Scholar] [CrossRef]
- Yeung, R.W. Added mass and damping of a vertical cylinder in finite-depth waters. Appl. Ocean Res. 1981, 3, 119–133. [Google Scholar] [CrossRef]
- Sabuncu, T.; Calisal, S. Hydrodynamic coefficients for a vertical circular cylinders at finite depth. Ocean Eng. 1981, 8, 25–63. [Google Scholar] [CrossRef]
- Williams, A.N.; Demirbilek, Z. Hydrodynamic interactions in floating cylinder arrays–I. Wave scattering. Ocean Eng. 1988, 15, 549–583. [Google Scholar] [CrossRef]
- Bhatta, D.D.; Rahman, M. Wave loadings on a vertical cylinder due to heave motion. Int. J. Math. Math. Sci. 1995, 18, 151–170. [Google Scholar] [CrossRef]
- Bhatta, D.D.; Rahman, M. On scattering and radiation problem for a cylinder in water of finite depth. Int. J. Eng. Sci. 2003, 41, 931–967. [Google Scholar] [CrossRef]
- Bhatta, D.D. Computations of hydrodynamic coefficients, displacement-amplitude ratios and forces for a floating cylinder due to wave diffraction and radiation. Int. J. Non-Linear Mech. 2011, 46, 1027–1041. [Google Scholar] [CrossRef]
- Jiang, S.C.; Ning, D.Z. An analytical solution of wave diffraction problem on a submerged cylinder. J. Eng. Mech. 2014, 140, 225–232. [Google Scholar] [CrossRef]
- Li, A.J.; Liu, Y. New analytical solutions to water wave diffraction by vertical truncated cylinders. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 952–969. [Google Scholar] [CrossRef]
- Ghadimi, P.; Bandari, H.P.; Rostami, A.B. Determination of the heave and pitch motions of a floating cylinder by analytical solution of its diffraction problem and examination of the effects of geometric parameters on its dynamics in regular waves. Int. J. Appl. Math. Res. 2012, 1, 611–633. [Google Scholar] [CrossRef]
- Xu, D.; Stuhlmeier, R.; Stiassnie, M. Assessing the size of a twin-cylinder wave energy converter designed for real sea-states. Ocean Eng. 2018, 147, 243–255. [Google Scholar] [CrossRef]
- Taylor, R.E.; Hung, S.M. Second order diffraction forces on a vertical cylinder in regular waves. Appl. Ocean Res. 1987, 9, 19–30. [Google Scholar] [CrossRef]
- Taylor, R.E.; Hung, S.M. Semi-analytical formulation for second-order diffraction by a vertical cylinder in bichromatic waves. J. Fluids Struct. 1997, 11, 465–484. [Google Scholar] [CrossRef]
- Kriebel, D.L. Nonlinear wave interaction with a vertical circular cylinder. Part I: Diffraction theory. Ocean Eng. 1990, 17, 345–377. [Google Scholar] [CrossRef]
- Kim, J.W.; Kyoung, J.; Ertekin, R.C.; Bai, K.J. Wave diffraction of steep stokes waves by bottom-mounted vertical cylinders. In Proceedings of the ASME 22nd International Conference on Offshore Mechanics and Arctic Engineering, Cancun, Mexico, 8–13 June 2003. [Google Scholar]
- Yan, K.; Shen, L.D.; Shang, J.W.; Ma, L.; Zou, Z.L. Experimental study on crescent waves diffracted by a circular cylinder. China Ocean Eng. 2018, 32, 624–632. [Google Scholar] [CrossRef]
- Wang, K.H.; Wu, T.Y.; Yates, G.T. Three-dimensional scattering of solitary waves by vertical cylinder. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 551–566. [Google Scholar] [CrossRef]
- Yates, G.T.; Wang, K.H. Solitary wave scattering by a vertical cylinder: Experimental study. In Proceedings of the ISOPE-I-94-198, the Fourth International, Offshore and Polar Engineering Conference, Osaka, Japan, 10–15 April 1994. [Google Scholar]
- Wang, K.H.; Jiang, L. Solitary wave interaction with an array of two vertical cylinders. Appl. Ocean Res. 1994, 15, 337–350. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Teng, B. Numerical simulation of solitary wave scattering by a circular cylinder array. Ocean Eng. 2007, 34, 489–499. [Google Scholar] [CrossRef]
- Neill, D.R.; Hayatdavoodi, M.; Ertekin, R.C. On solitary wave diffraction by multiple, in-line vertical cylinders. Nonlinear Dyn. 2018, 91, 975–994. [Google Scholar] [CrossRef]
- Yuan, Z.; Huang, Z. Solitary wave forces on an array of closely-spaced circular cylinders. In Asian and Pacific Coasts, 2009; World Scientific: Singapore, 2009; pp. 136–142. [Google Scholar]
- Isaacson, M.D.S.Q. Solitary wave diffraction around large cylinders. Waterw. Port Coast. Ocean Eng. 1983, 109, 121–127. [Google Scholar] [CrossRef]
- Isaacson, M.D.S.Q. Nonlinear-wave effects on fixed and floating bodies. J. Fluid Mech. 1982, 20, 267–281. [Google Scholar] [CrossRef]
- Isaacson, M.Q.; Cheung, K.F. Time-domain second-order wave diffraction in three dimensions. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 496–517. [Google Scholar] [CrossRef]
- Ohyama, T. A numerical method of solitary wave forces acting on a large vertical cylinder. Coast. Eng. Proc. 1990, 1, 840–852. [Google Scholar]
- Yang, C.; Ertekin, R.C. Numerical simulation of nonlinear wave diffraction by a vertical cylinder. J. Offshore Mech. Arctic Eng. 1992, 114, 36–44. [Google Scholar] [CrossRef]
- Wang, H.W.; Huang, C.J. Wave and flow fields induced by a solitary wave propagating over a submerged 3D breakwater. J. Coast. Ocean Eng. 2006, 6, 1–22. (In Chinese) [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere: Washington, DC, USA, 1980. [Google Scholar]
- Mo, W.H. Numerical Investigation of Solitary Wave Interaction with Group of Cylinders. Ph.D. Thesis, Graduate School of Civil and Environmental Engineering of Cornell University, Ithaca, NY, USA, August 2010. [Google Scholar]
- Cao, H.J.; Wan, D.C. RANS-VOF solver for solitary wave run-up on a circular cylinder. China Ocean Eng. 2015, 29, 183–196. [Google Scholar] [CrossRef]
- Leschka, S.; Oumeraci, H. Solitary waves and bores passing three cylinders—Effect of distance and arrangement. Coast. Eng. Proc. 2014, 1. [Google Scholar] [CrossRef]
- Leschka, S.; Oumeraci, H.; Larsen, O. Hydrodynamic forces on a group of three emerged cylinders by solitary waves and bores: Effect of cylinder arrangements and distances. J. Earthq. Tsunami 2014, 8, 1440005. [Google Scholar] [CrossRef]
- Chen, Q.; Zang, J.; Kelly, D.M.; Dimakopoulos, A.S. A 3-D numerical study of solitary wave interaction with vertical cylinders using a parallelized particle-in-cell solver. J. Hydrodyn. 2017, 29, 790–799. [Google Scholar] [CrossRef]
- Kang, A.; Lin, P.; Lee, Y.J.; Zhu, B. Numerical simulation of wave interaction with vertical circular cylinders of different submergences using immersed boundary method. Comput. Fluids 2015, 106, 41–53. [Google Scholar] [CrossRef]
- Lin, P. A multiple-layer σ-coordinate model for simulation of wave–structure interaction. Comput. Fluids 2006, 35, 147–167. [Google Scholar] [CrossRef]
- Zhou, B.Z.; Wu, G.X.; Meng, Q.C. Interactions of fully nonlinear solitary wave with a freely floating vertical cylinder. Eng. Anal. Bound. Elem. 2016, 69, 119–131. [Google Scholar] [CrossRef]
- Chen, Y.H.; Wang, K.H. Experiments and computations of solitary wave interaction with fixed, partially submerged, vertical cylinders. J. Ocean Eng. Mar. Energy 2019, 5, 189–204. [Google Scholar] [CrossRef]
- Garrett, C.J.R. Bottomless harbours. J. Fluid Mech. 1970, 43, 433–449. [Google Scholar] [CrossRef]
- Zhu, S.; Mitchell, L. Diffraction of ocean waves around a hollow cylindrical shell structure. Wave Motion 2009, 46, 78–88. [Google Scholar] [CrossRef]
- Simon, M.J. Wave-energy extraction by a submerged cylindrical duct. J. Fluid Mech. 1981, 104, 159–187. [Google Scholar] [CrossRef]
- Miles, J.W. On surface-wave radiation from a submerged cylindrical duct. J. Fluid Mech. 1982, 122, 339–346. [Google Scholar] [CrossRef]
- Harun, F.N. Analytical solution for wave diffraction around cylinder. Res. J. Recent Sci. 2013, 2, 5–10. [Google Scholar]
- Mavrakos, S.A. Wave loads on a stationary floating bottomless cylindrical body with finite wall thickness. Appl. Ocean Res. 1985, 7, 213–224. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Hydrodynamic coefficients for a thick walled bottomless cylindrical body floating in water of finite depth. Ocean Eng. 1988, 15, 213–229. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Hydrodynamic coefficients in heave of two concentric surface-piercing truncated circular cylinders. Appl. Ocean Res. 2004, 26, 84–97. [Google Scholar] [CrossRef]
- Shipway, B.J.; Evans, D.V. Wave trapping by axisymmetric concentric cylinders. In Proceedings of the 21st International Conference on Offshore Mechanics and Artic Engineering (OMAE’2002), Oslo, Norway, 23–28 June 2002. [Google Scholar]
- McIver, P.; Newman, J.N. Trapping structures in the three-dimensional water-wave problem. J. Fluid Mech. 2003, 484, 283–301. [Google Scholar] [CrossRef]
- Hassan, M.; Bora, S.N. Exciting forces for a pair of coaxial hollow cylinder and bottom-mounted cylinder in water of finite depth. Ocean Eng. 2012, 50, 38–43. [Google Scholar] [CrossRef]
- Hassan, M.; Bora, S.N. Hydrodynamic coefficients in surge for a radiating hollow cylinder placed above a coaxial cylinder at finite ocean depth. J. Mar. Sci. Technol. 2014, 19, 450–461. [Google Scholar] [CrossRef]
- Simonetti, I.; Cappietti, I.; El Safti, H.; Oumeraci, H. 3D numerical modelling of oscillating water column wave energy conversion devices: Current knowledge and OpenFoam implementation. In Proceedings of the 1st International Conference on Renewable Energies Offshore—RENEW2014, Lisbon, Portugal, 24–26 November 2014. [Google Scholar]
- Kamath, A.; Bihs, H.; Arntsen, Ø.A. Comparison of 2D and 3D simulations of an OWC device in different configurations. Coast. Eng. Proc. 2014, 1, 66. [Google Scholar] [CrossRef]
- Lee, K.H.; Kim, T.G. Three-dimensional numerical simulation of airflow in oscillating water column device. J. Coast. Res. 2018, 85, 1346–1350. [Google Scholar] [CrossRef]
- Kim, J.R.; Koh, H.J.; Ruy, W.S.; Cho, I.H. Experimental study on the hydrodynamic behaviors of two concentric cylinders. In Proceedings of the 2013 World Congress on Advances in Structural Engineering and Mechanics (ASEM13), Jeju, Korea, 8–12 September 2013. [Google Scholar]
- Stokers, J.J. Water Waves: The Mathematical Theory with Application; John Wiley & Sons: New York, NY, USA, 1957; pp. 9–12. ISBN 978-0-471-57034-9. [Google Scholar]
- Schember, H.R. A New Model for Three-Dimensional Nonlinear Dispersive Long Waves. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1982; p. 24. [Google Scholar]
- Wang, K.H. Diffraction of solitary waves by breakwaters. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 49–69. [Google Scholar] [CrossRef]
- Wu, T.Y. Long waves in ocean and coastal waters. J. Eng. Mech. Div. ASCE 1981, 107, 501–522. [Google Scholar]
- Dommermuth, D.G.; Yue, D.K.P. A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 1987, 184, 267–288. [Google Scholar] [CrossRef]
- Zhuang, Y.; Wan, D. Review: Recent development of high-order-spectral method combined with computational fluid dynamics method for wave-structure interactions. J. Harbin Inst. Technol. 2020, 27, 170–188. [Google Scholar]
- Chang, C.H.; Wang, K.H. Fully nonlinear water waves generated by a submerged object moving in an unbounded fluid domain. ASCE J. Eng. Mech. 2011, 137, 101–112. [Google Scholar] [CrossRef]
- Thompson, J.F.; Thames, F.C.; Mastin, C.W. TOMCAT—A code for numerical generation of boundary-fitted curvilinear coordinate systems on fields containing any number of arbitrary two-dimensional bodies. J. Comput. Phys. 1977, 24, 274–302. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-H. Interaction of a Solitary Wave with Vertical Fully/Partially Submerged Circular Cylinders with/without a Hollow Zone. J. Mar. Sci. Eng. 2020, 8, 1022. https://doi.org/10.3390/jmse8121022
Chang C-H. Interaction of a Solitary Wave with Vertical Fully/Partially Submerged Circular Cylinders with/without a Hollow Zone. Journal of Marine Science and Engineering. 2020; 8(12):1022. https://doi.org/10.3390/jmse8121022
Chicago/Turabian StyleChang, Chih-Hua. 2020. "Interaction of a Solitary Wave with Vertical Fully/Partially Submerged Circular Cylinders with/without a Hollow Zone" Journal of Marine Science and Engineering 8, no. 12: 1022. https://doi.org/10.3390/jmse8121022
APA StyleChang, C.-H. (2020). Interaction of a Solitary Wave with Vertical Fully/Partially Submerged Circular Cylinders with/without a Hollow Zone. Journal of Marine Science and Engineering, 8(12), 1022. https://doi.org/10.3390/jmse8121022



