An Explicit Algebraic Closure for Passive Scalar-Flux: Applications in Channel Flows at a Wide Range of Reynolds Numbers
Abstract
1. Introduction
2. Younis’ Formulation
3. Quadratic Dependence on Reynolds Stress
4. Proposed Formulation
4.1. Redistributive Term
4.2. Model Calibration
5. Model Assessment
5.1. Poiseuille Flows
5.1.1. Low Reynolds Number Cases
5.1.2. High Reynolds Number Cases
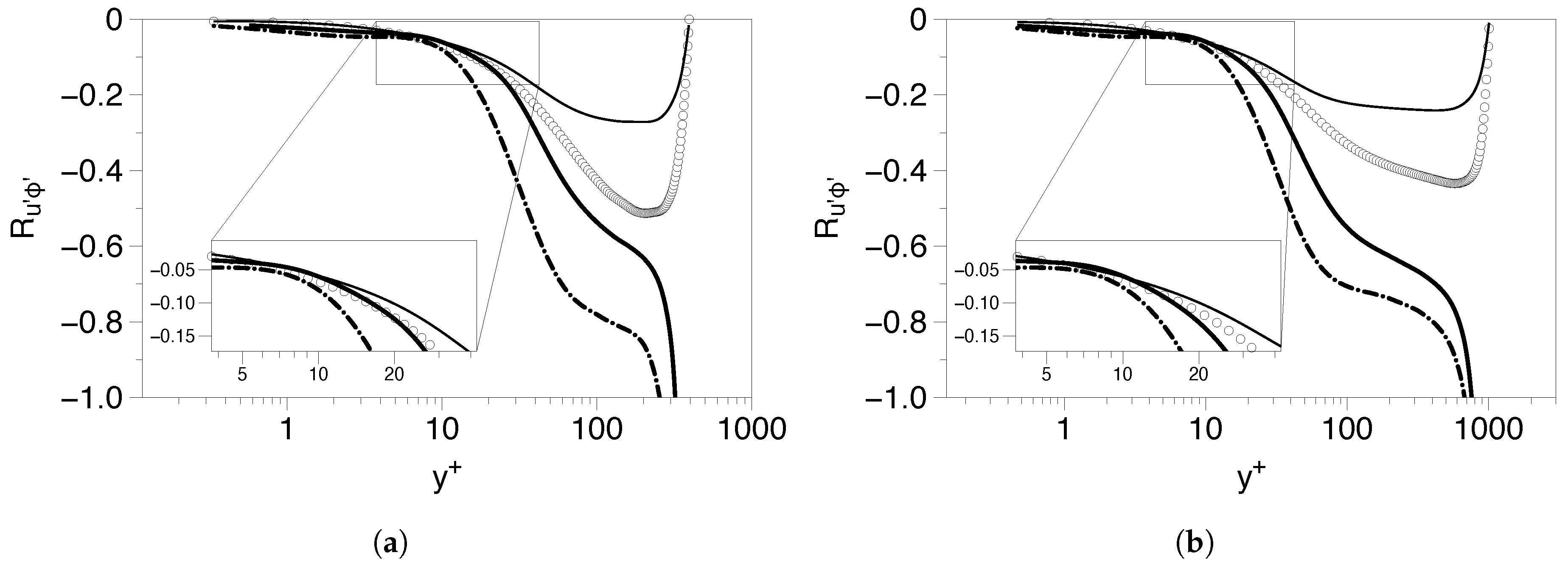
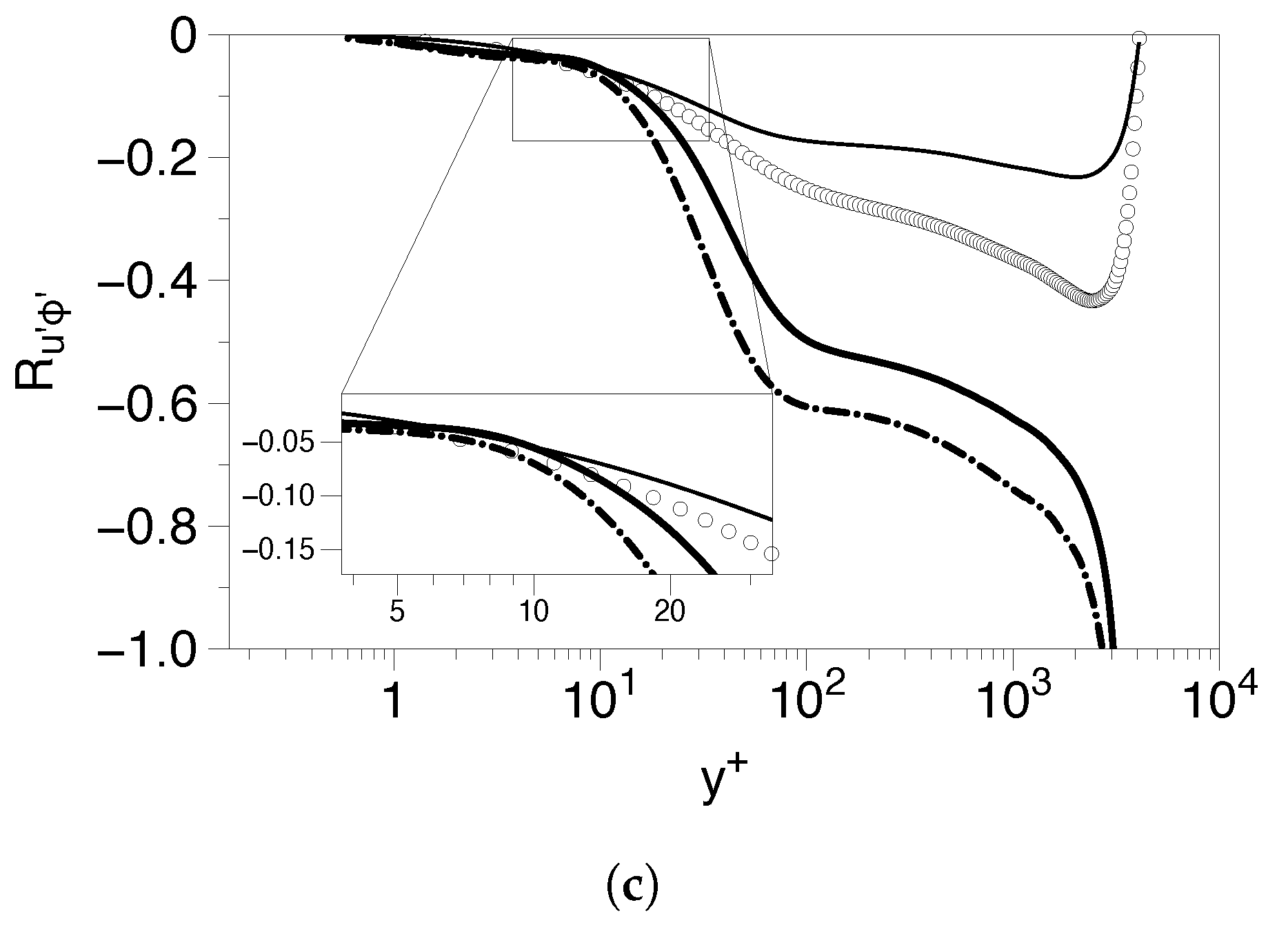
5.1.3. Inclination Angle of the Scalar-Flux Vector Near the Wall Boundary
5.2. Couette Flows
5.3. Higher Pr Case
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| , | model constants of function |
| channel’s half height | |
| dissipation rate of kinetic energy | |
| molecular diffusivity | |
| turbulent kinetic energy | |
| mean scalar gradient vector, | |
| kinematic viscosity | |
| mean vorticity tensor, | |
| , , | instantaneous, mean and fluctuating scalar field |
| fluid density | |
| time scale, | |
| turbulent scalar-flux | |
| A | Lumley’s stress flatness parameter, |
| second invariant of , | |
| third invariant of , | |
| anisotropic stress tensor, | |
| optimized constants of function | |
| components of function | |
| correction function for | |
| effective gradient, | |
| mean velocity gradient tensor, | |
| p, | instantaneous and fluctuating pressure |
| Peclet number, |
| Prandtl number, | |
| Reynolds stress tensor, | |
| normalized Reynolds stress tensor, | |
| scalar-flux ratio, | |
| friction Reynolds number, | |
| turbulence Reynolds number, | |
| “slip” Reynolds number, | |
| mean strain rate tensor, | |
| friction velocity | |
| , | instantaneous, mean, and fluctuating velocity components |
| wall velocity |
Appendix A. Determination of Correction Function
Appendix A.1. Boundary Limiting Behavior
Appendix A.2. Details Regarding the Functional form of
References
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Verstappen, R. When does eddy viscosity damp subfilter scales sufficiently? J. Sci. Comput. 2011, 49, 94–110. [Google Scholar] [CrossRef]
- Rozema, W.; Bae, H.J.; Moin, P.; Verstappen, R. Minimum-dissipation models for large-eddy simulation. Phys. Fluids 2015, 27, 085107. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Verstappen, R. How much eddy dissipation is needed to counterbalance the nonlinear production of small, unresolved scales in a large-eddy simulation of turbulence? Comput. Fluids 2016, 176, 276–284. [Google Scholar] [CrossRef]
- Trias, F.; Folch, D.; Gorobets, A.; Oliva, A. Building proper invariants for eddy-viscosity subgrid-scale models. Phys. Fluids 2015, 27, 065103. [Google Scholar] [CrossRef]
- Rozema, W.; Verstappen, R.W.C.P.; Veldman, A.E.P.; Kok, J.C. Low-Dissipation Simulation Methods and Models for Turbulent Subsonic Flow. Arch. Comput. Methods Eng. 2018, 27, 299–330. [Google Scholar] [CrossRef]
- Batchelor, G. Diffusion in a field of homogeneous turbulence. Aust. J. Sci. Res. Ser. A 1949, 2, 437–450. [Google Scholar] [CrossRef]
- Daly, B.; Harlow, F. Transport equations of turbulence. Phys. Fluids 1970, 13, 2634–2649. [Google Scholar] [CrossRef]
- Suga, K.; Abe, K. Nonlinear eddy viscosity modelling for turbulence and heat transfer near wall and shear-free boundaries. Int. J. Heat Fluid Flow 2000, 21, 37–48. [Google Scholar] [CrossRef]
- Rodi, W. The Prediction of Free Turbulent Boundary Layers by Use of a Two-Equation Model of Turbulence. Ph.D. Thesis, Department of Heat Transfer, Imperial College, London, UK, 1972. [Google Scholar]
- Girimaji, S.; Balachandar, S. Analysis and modeling of buoyancy-generated turbulence using numerical data. Int. J. Heat Mass Trans. 1998, 41, 915–929. [Google Scholar] [CrossRef]
- Wikstrom, P.; Wallin, S.; Johansson, A. Derivation and investigation of a new explicit algebraic model for the passive scalar flux. Phys. Fluids 2000, 12, 688–702. [Google Scholar] [CrossRef]
- Lazeroms, W.; Brethouwer, G.; Wallin, S.; Johansson, A. An explicit algebraic Reynolds-stress and scalar-flux model for stably stratified flows. J. Fluid Mech. 2013, 723, 91–125. [Google Scholar] [CrossRef]
- Younis, B.; Speziale, C.; Clark, T. A rational model for the turbulent scalar fluxes. Proc. R. Soc. A 2005, 461, 575–594. [Google Scholar] [CrossRef]
- Younis, B.; Weigand, B.; Spring, S. An Explicit Algebraic Model for Turbulent Heat Transfer in Wall-Bounded Flow With Streamline Curvature. J. Heat Transf. 2007, 129, 425–433. [Google Scholar] [CrossRef]
- Dakos, T.; Gibson, M. On modelling the pressure terms of the scalar flux equations. In Turbulent Shear Flows 5; Springer: Berlin/Heidelberg, Germany, 1987; pp. 7–18. [Google Scholar]
- Yoshizawa, A. Statistical analysis of the anisotropy of scalar diffusion in turbulent shear flows. Phys. Fluids 1985, 28, 3226–3231. [Google Scholar] [CrossRef]
- Kaltenbach, H.; Gerz, T.; Schumann, U. Large-eddy simulation of homogeneous turbulence and diffusion in stably stratified shear flow. J. Fluid Mech. 1994, 280, 1–40. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence Statistics in Fully Developed Channel Flow at Low Reynolds Number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef]
- Younis, B.; Weigand, B.; Mohr, F.; Schmidt, M. Modeling the Effects of System Rotation on the Turbulent Scalar Fluxes. J. Heat Transf. 2010, 132, 051703. [Google Scholar] [CrossRef]
- Launder, B. On the computation of convective heat transfer in complex turbulent flows. J. Heat Transf. 1988, 110, 1112–1128. [Google Scholar] [CrossRef]
- Abe, K.; Suga, K. Towards the development of a Reynolds-averaged algebraic turbulent scalar-flux model. Int. J. Heat Fluid Flow 2001, 22, 19–29. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P. Transport of Passive Scalars in a Turbulent Channel Flow. In Turbulent Shear Flows; Andre, J.C., Cousteix, J., Durst, F., Launder, B., Schmidt, F., Whitelaw, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; Volume 6. [Google Scholar]
- Jones, W.; Musonge, P. Closure of the Reynolds stress and scalar flux equations. Phys. Fluids 1987, 31, 3589–3604. [Google Scholar] [CrossRef]
- Monin, A. On the symmetry of turbulence in the surface layer of air. Izv. Atmos. Ocean. Phys. 1965, 1, 45–54. [Google Scholar]
- Launder, B.E. On the effects of a gravitational field on the turbulent transport of heat and momentum. J. Fluid Mech. 1975, 67, 569–581. [Google Scholar] [CrossRef]
- Kawamura, H.; Abe, H.; Shingai, K. DNS of turbulence and heat transport in a channel flow with different Reynolds and Prandtl numbers and boundary conditions. In Proceedings of the 3rd International Symposium on Turbulence, Heat and Mass Transfer, Nagoya, Japan, 3–6 April 2000; Nagano, Y., Hanjalic, K., Tsuji, T., Eds.; Aichi Shuppan: Tokyo, Japan, 2000; Volume 6. [Google Scholar]
- Kozuka, M.; Seki, Y.; Kawamura, H. Direct Numerical Simulation Data Base for Turbulent Channel Flow with Heat Transfer. Available online: https://www.rs.tus.ac.jp/t2lab/db/ (accessed on 5 October 2020).
- Kassinos, S.; Reynolds, W. A Structure-Based Model with Stropholysis Effects; Annual Research Briefs; Center for Turbulence Research, NASA Ames/Stanford University: Santa Clara County, CA, USA, 1998; pp. 197–209. [Google Scholar]
- Panagiotou, C.; Kassinos, S. A structure-based model for the transport of passive scalars in homogeneous turbulent flows. Int. J. Heat Fluid Flow 2016, 57, 109–129. [Google Scholar] [CrossRef]
- Panagiotou, C.; Kassinos, S. A structure-based model for transport in stably stratified homogeneous turbulent flows. Int. J. Heat Fluid Flow 2017, 65, 309–322. [Google Scholar] [CrossRef]
- Panagiotou, C.; Stylianou, F.; Kassinos, S. Structure-based transient models for scalar dissipation rate in homogeneous turbulence. Int. J. Heat Fluid Flow 2020, 82, 108557. [Google Scholar] [CrossRef]
- Tomita, Y.; Kasagi, N.; Kuroda, A. Establishment of the Direct Numerical Simulation Databases of Turbulent Transport Phenomena. Available online: https://thtlab.jp/ (accessed on 5 November 2020).
- Abe, H.; Kawamura, H.; Matsuo, Y. Surface heat-flux fluctuations in a turbulent channel flow up to Reτ=1020 with Pr=0.025 and 0.71. Int. J. Heat Fluid Flow 2004, 25, 404–419. [Google Scholar] [CrossRef]
- Pirozzoli, S.; Bernardini, M.; Orlandi, P. Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 2016, 788, 614–639. [Google Scholar] [CrossRef]
- Pirozzoli, S.; Bernardini, M.; Orlandi, P. Turbulent Channel Flow With Passive Scalars—DNS Database Up to Reτ = 4000. Available online: http://newton.dma.uniroma1.it/scalars/stat/ (accessed on 5 November 2020).

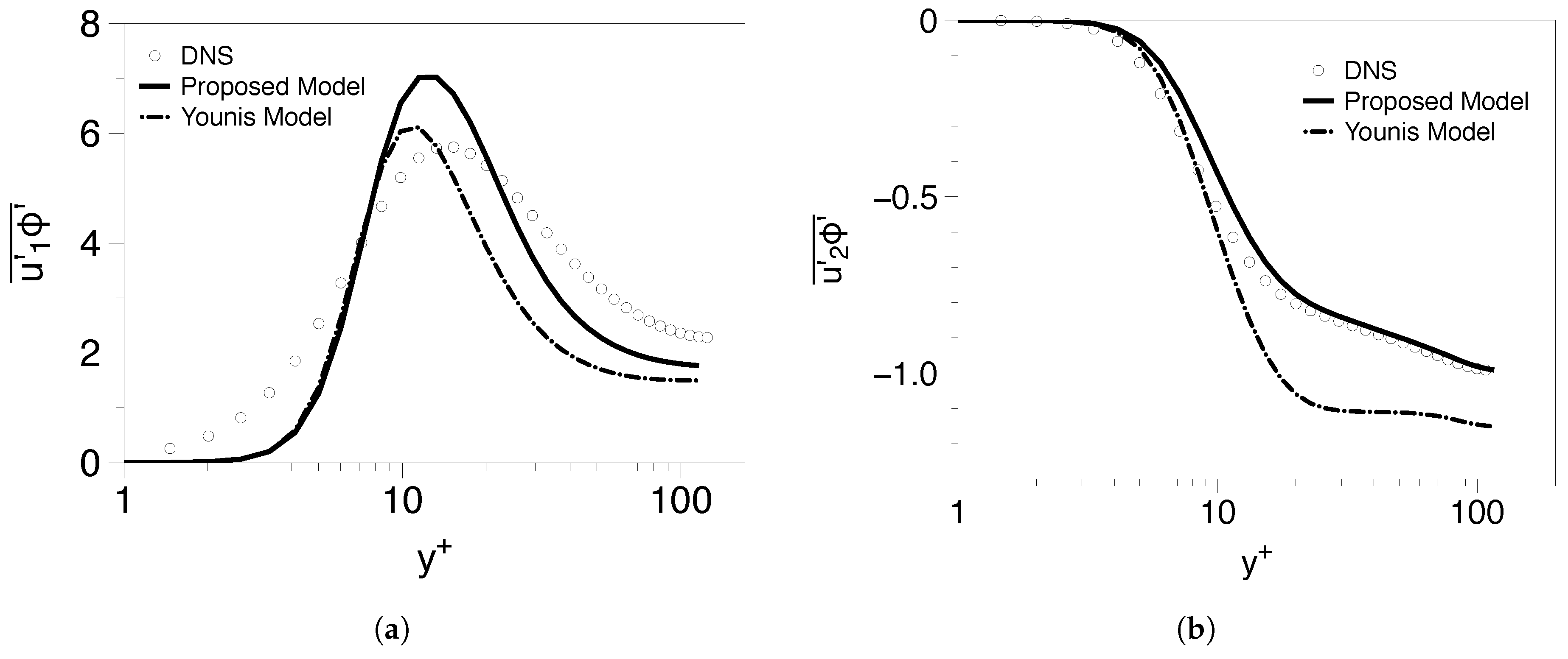
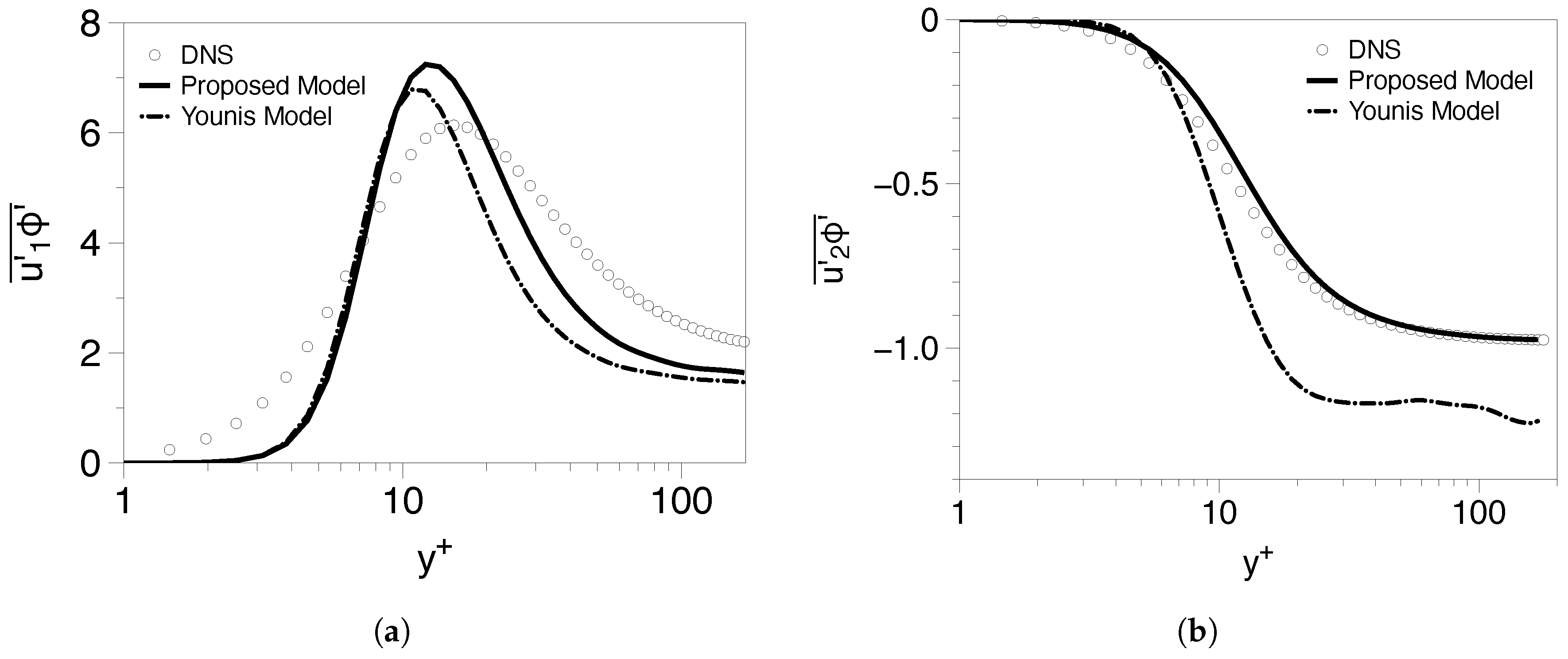
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagiotou, C.F.; Stylianou, F.S.; Gravanis, E.; Akylas, E.; Michailides, C. An Explicit Algebraic Closure for Passive Scalar-Flux: Applications in Channel Flows at a Wide Range of Reynolds Numbers. J. Mar. Sci. Eng. 2020, 8, 916. https://doi.org/10.3390/jmse8110916
Panagiotou CF, Stylianou FS, Gravanis E, Akylas E, Michailides C. An Explicit Algebraic Closure for Passive Scalar-Flux: Applications in Channel Flows at a Wide Range of Reynolds Numbers. Journal of Marine Science and Engineering. 2020; 8(11):916. https://doi.org/10.3390/jmse8110916
Chicago/Turabian StylePanagiotou, Constantinos F., Fotos S. Stylianou, Elias Gravanis, Evangelos Akylas, and Constantine Michailides. 2020. "An Explicit Algebraic Closure for Passive Scalar-Flux: Applications in Channel Flows at a Wide Range of Reynolds Numbers" Journal of Marine Science and Engineering 8, no. 11: 916. https://doi.org/10.3390/jmse8110916
APA StylePanagiotou, C. F., Stylianou, F. S., Gravanis, E., Akylas, E., & Michailides, C. (2020). An Explicit Algebraic Closure for Passive Scalar-Flux: Applications in Channel Flows at a Wide Range of Reynolds Numbers. Journal of Marine Science and Engineering, 8(11), 916. https://doi.org/10.3390/jmse8110916





