Simplified Numerical Models to Simulate Hollow Monopile Wind Turbine Foundations
Abstract
1. Introduction
2. State of the Art: Numerical Simulations of Wind Turbine Foundations
3. Methodology
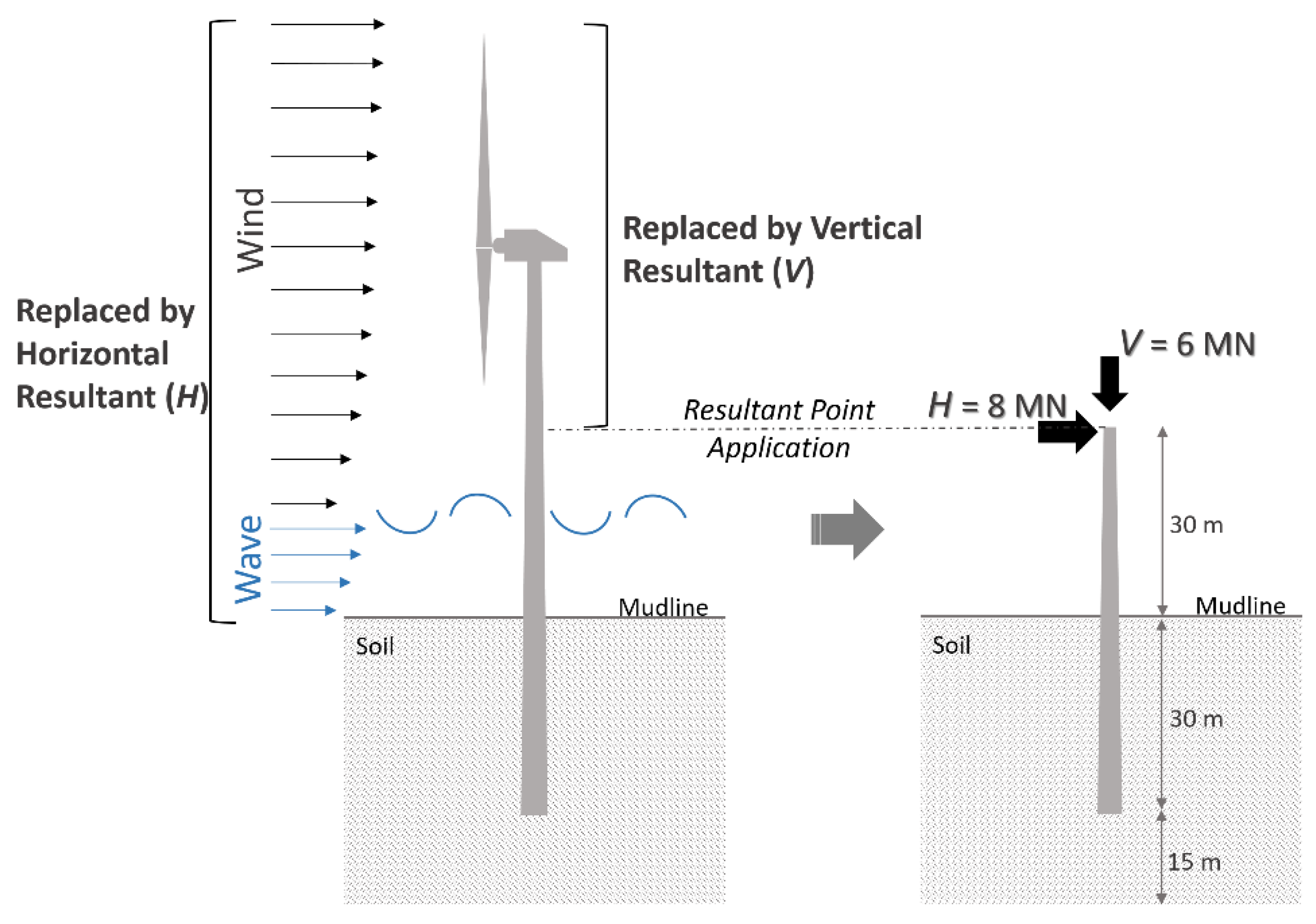
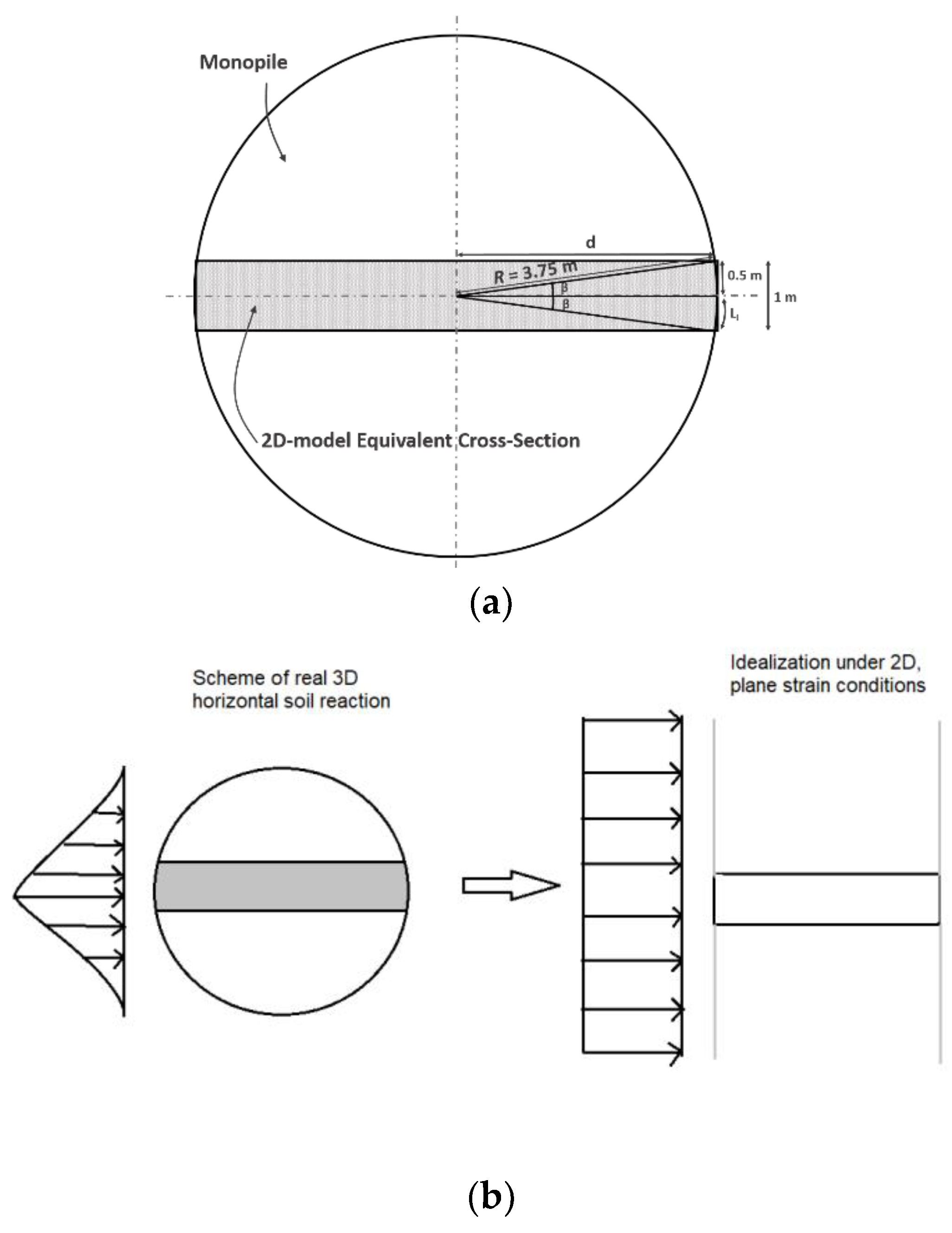
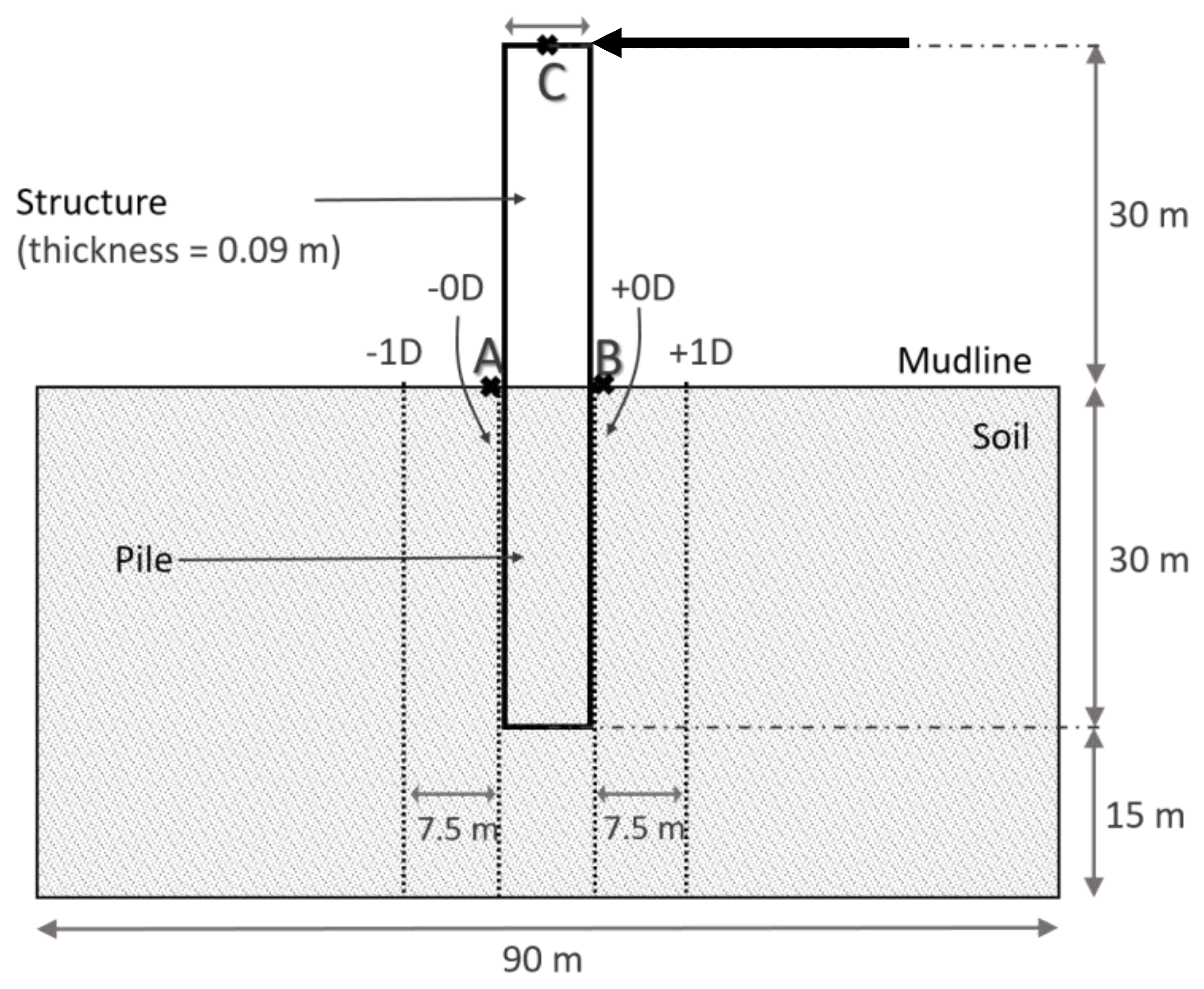
3.1. Geometry of the Models
3.2. Material Properties
3.3. Input Loads
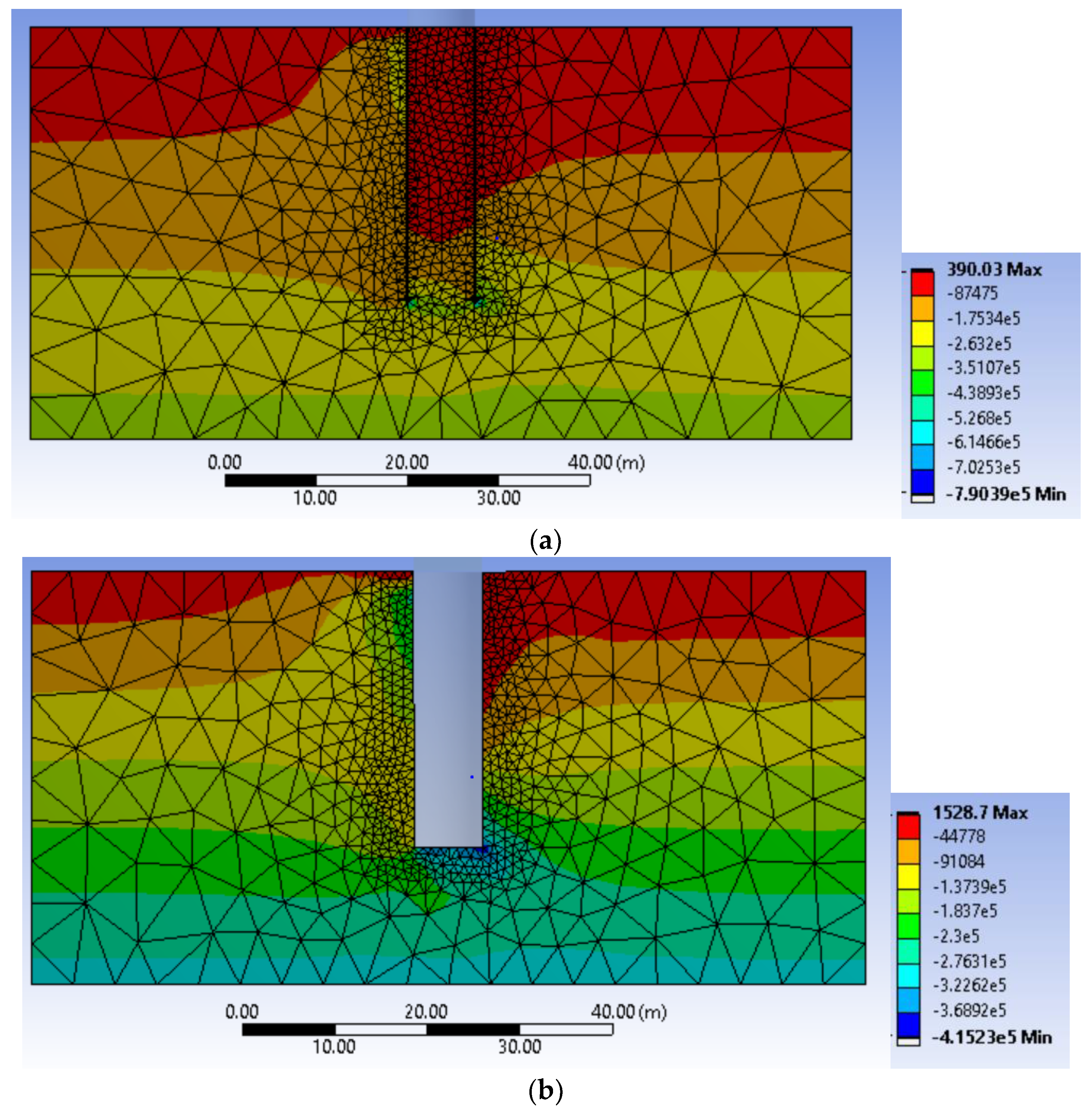
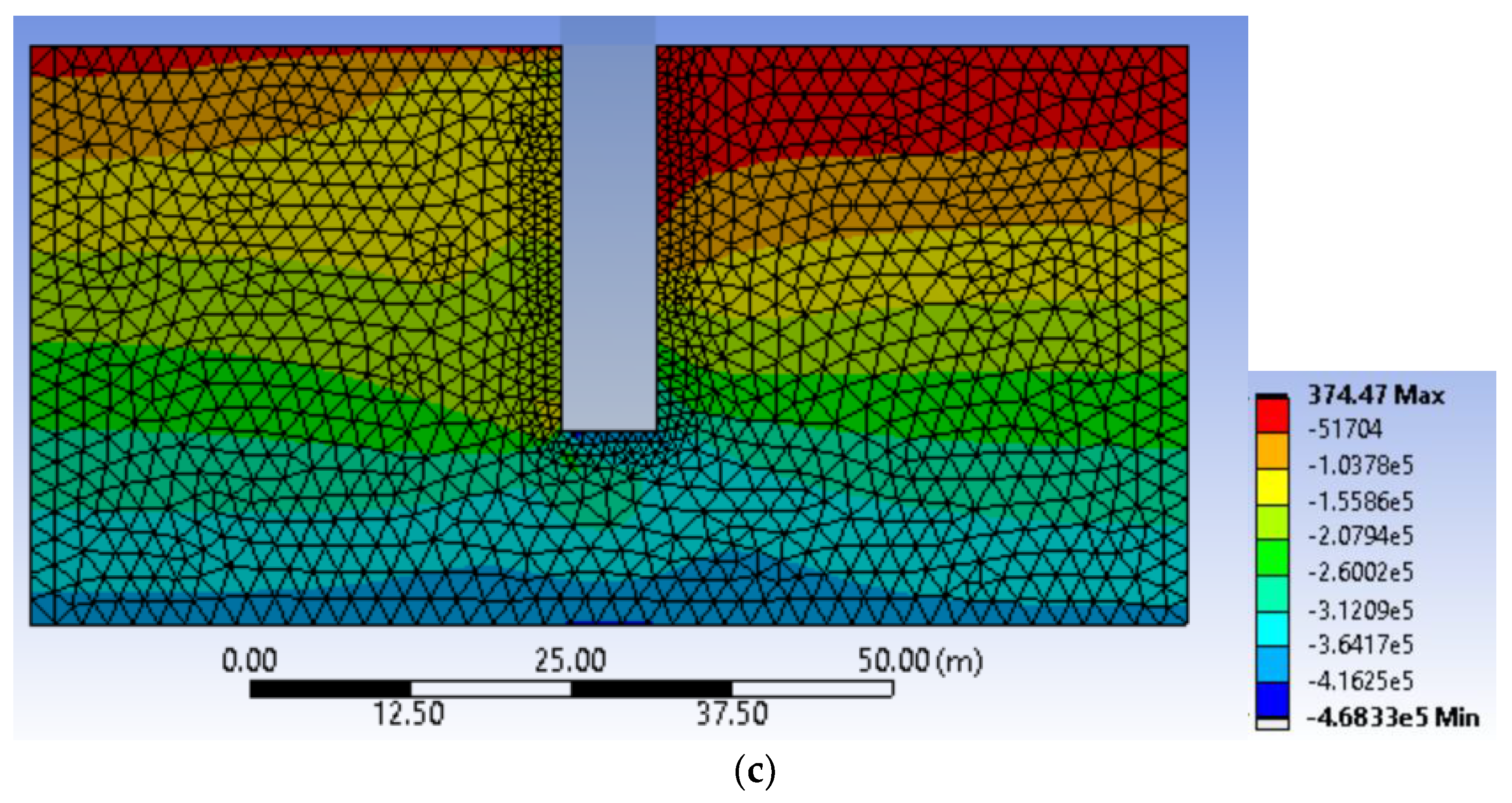
3.4. Details of the Finite Element Model
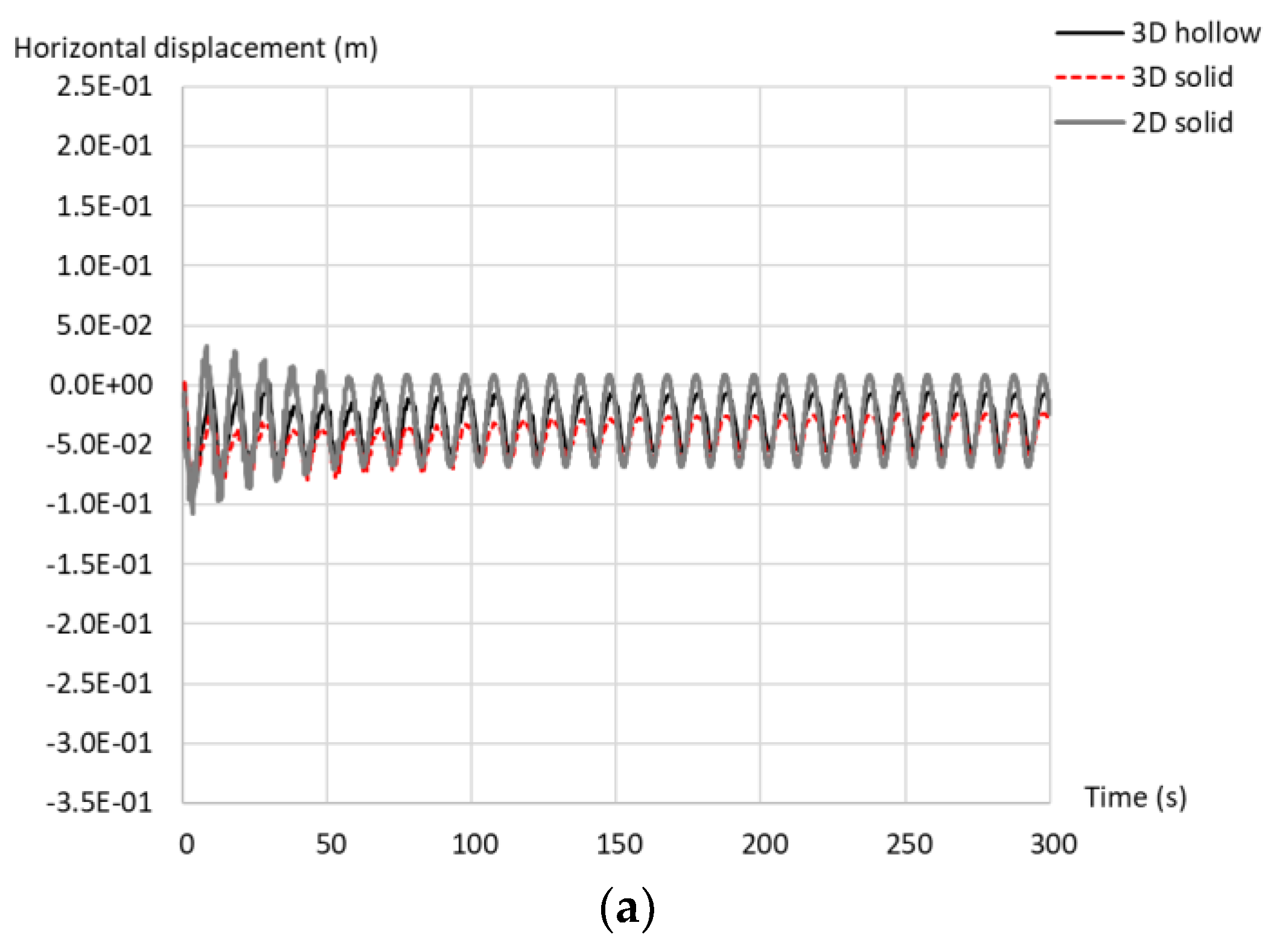
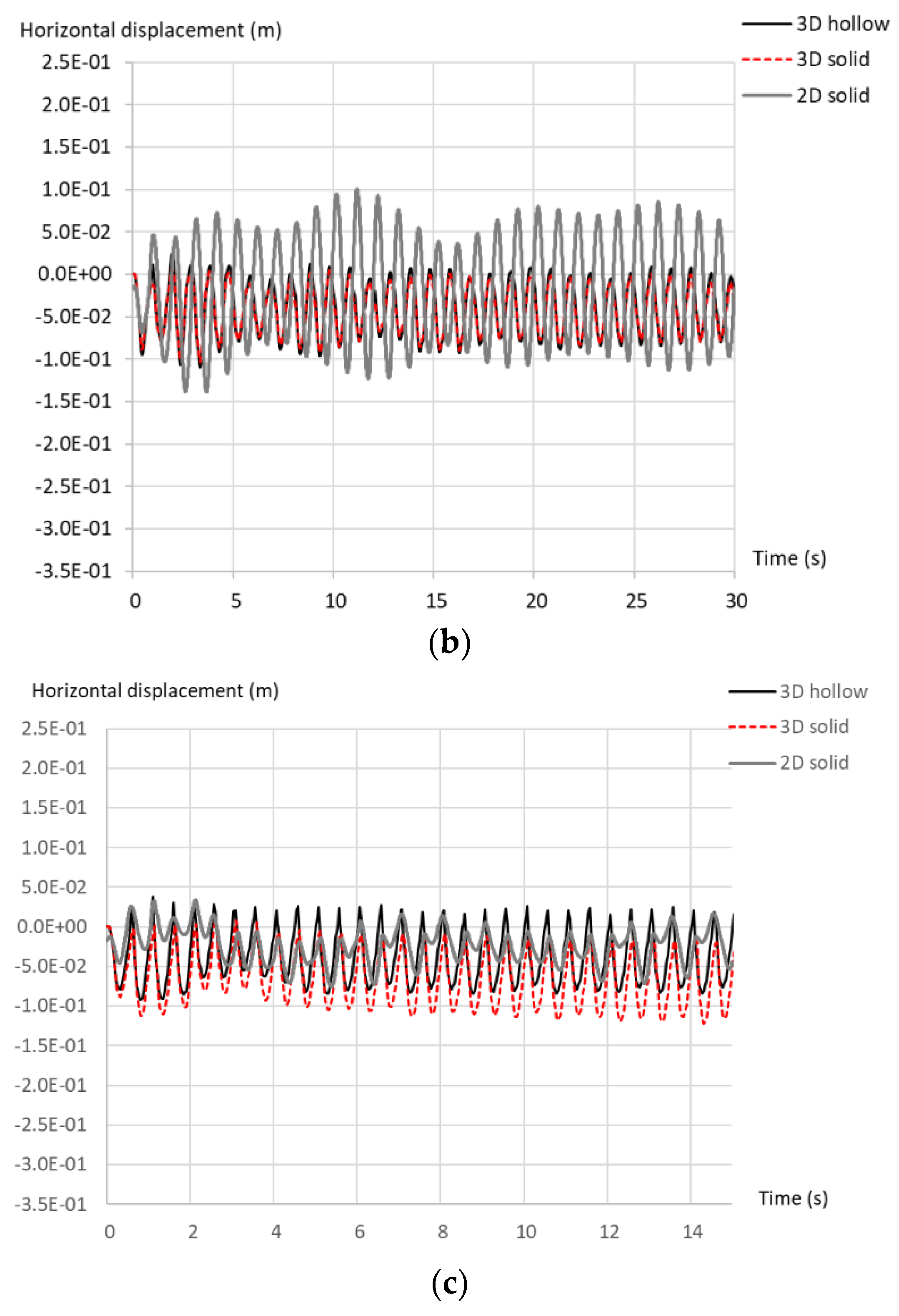
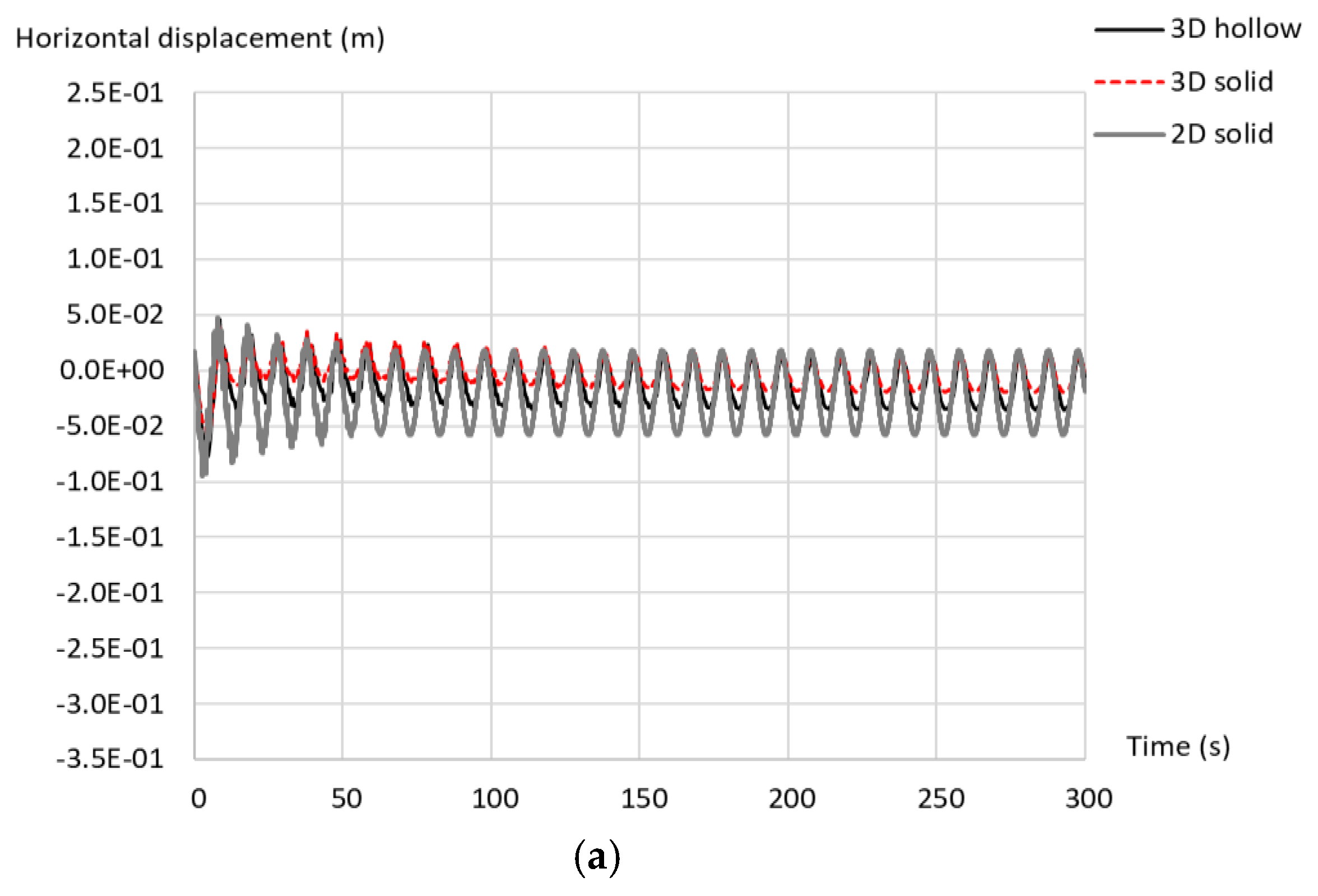
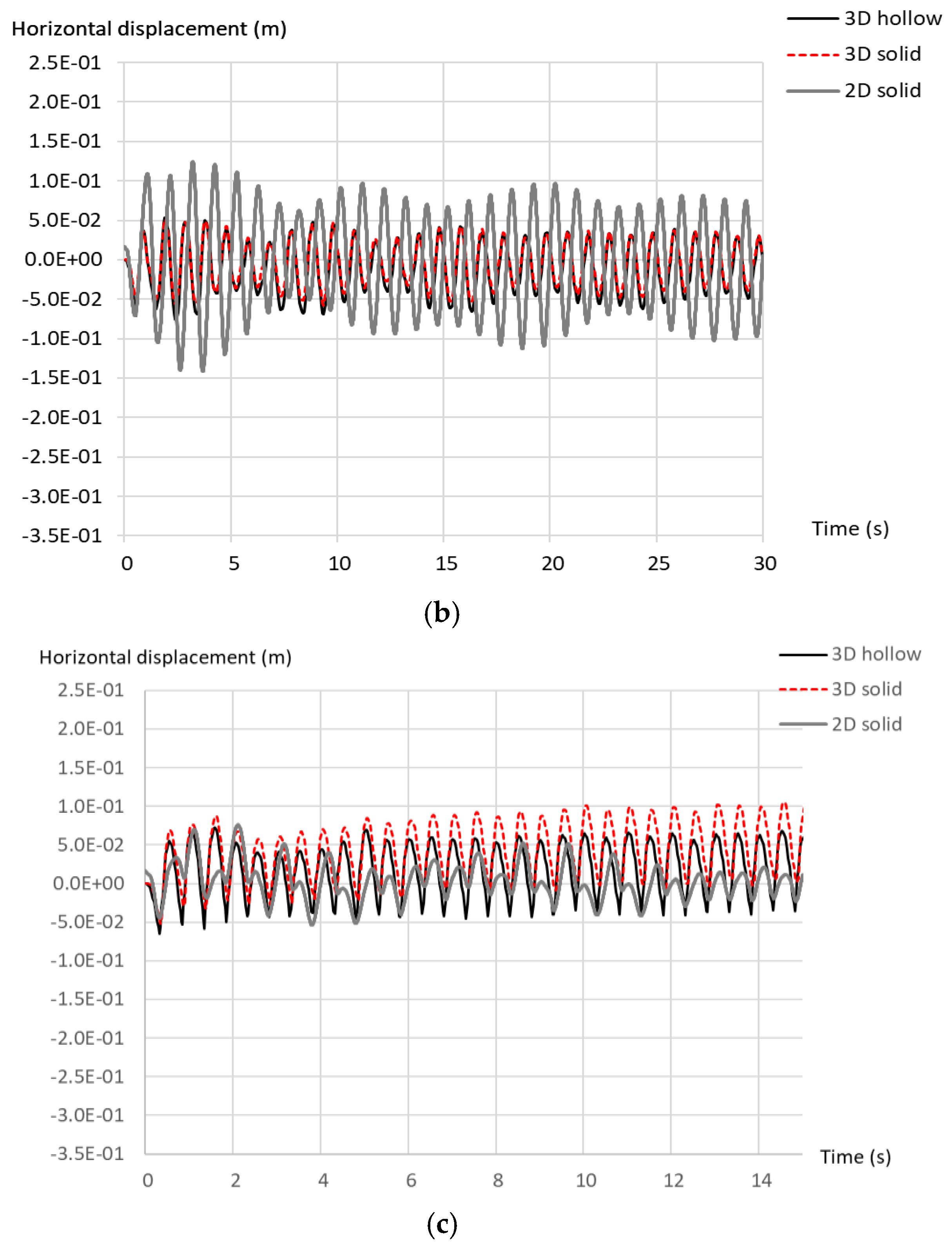
4. Results and Discussion
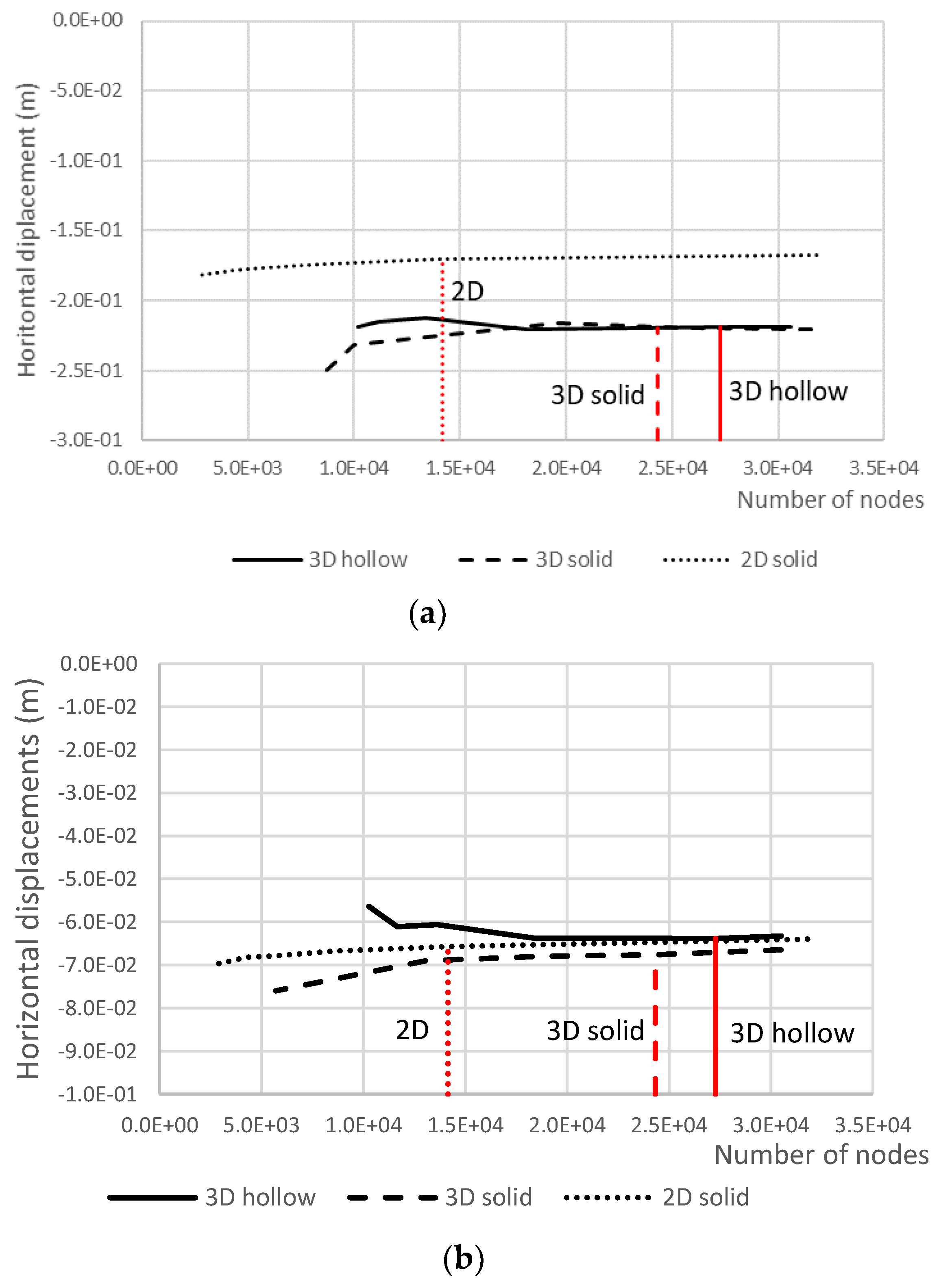
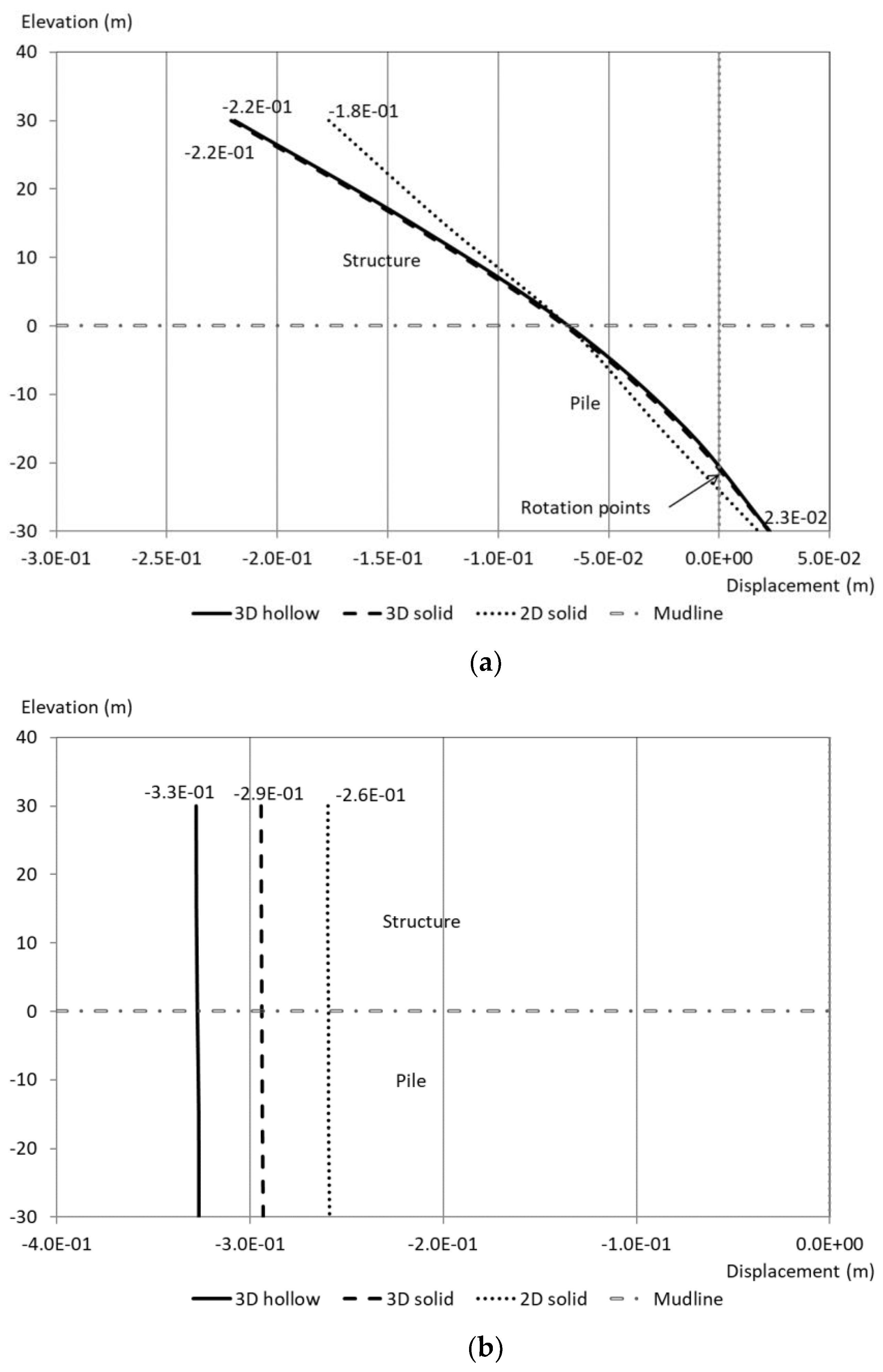
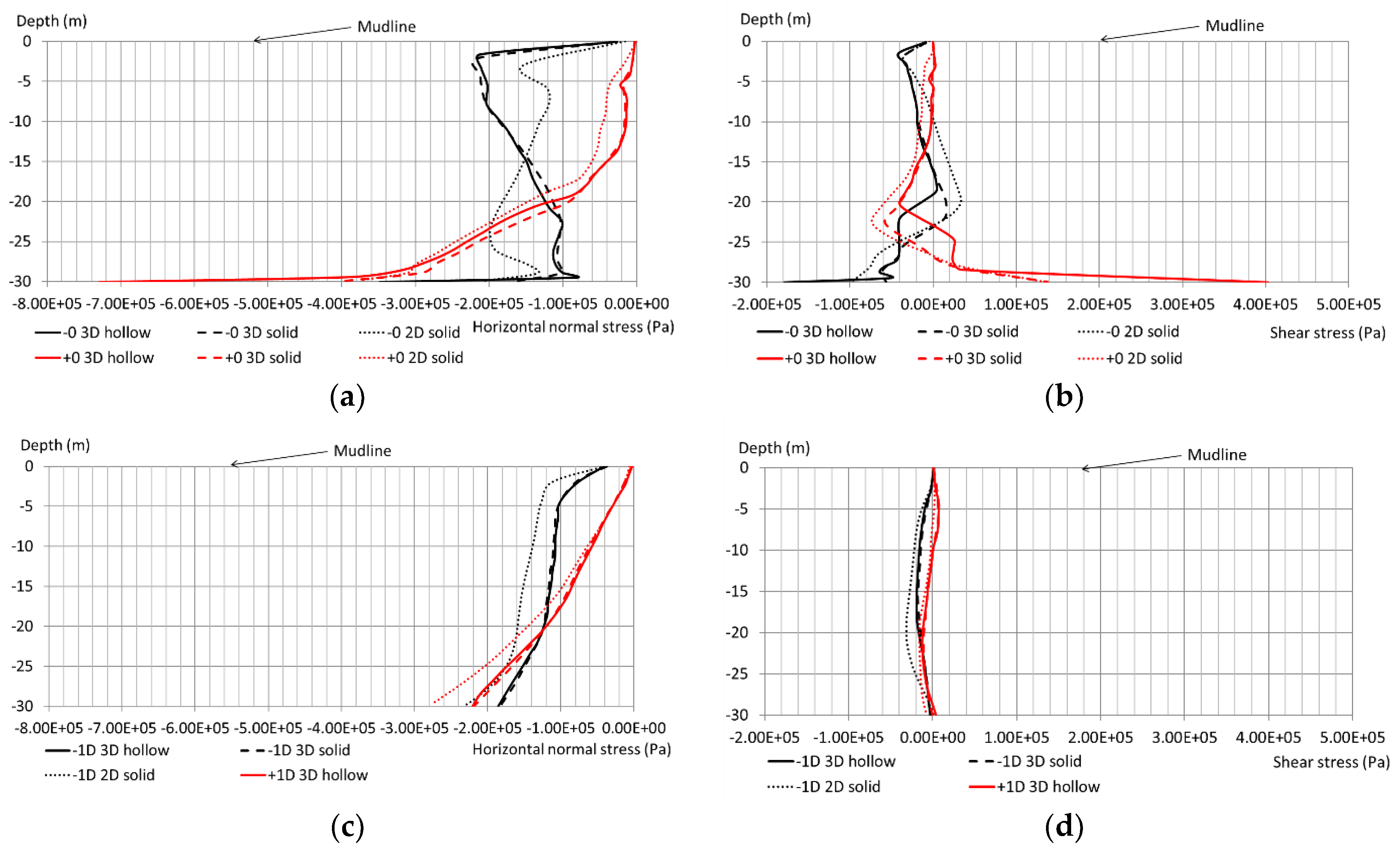
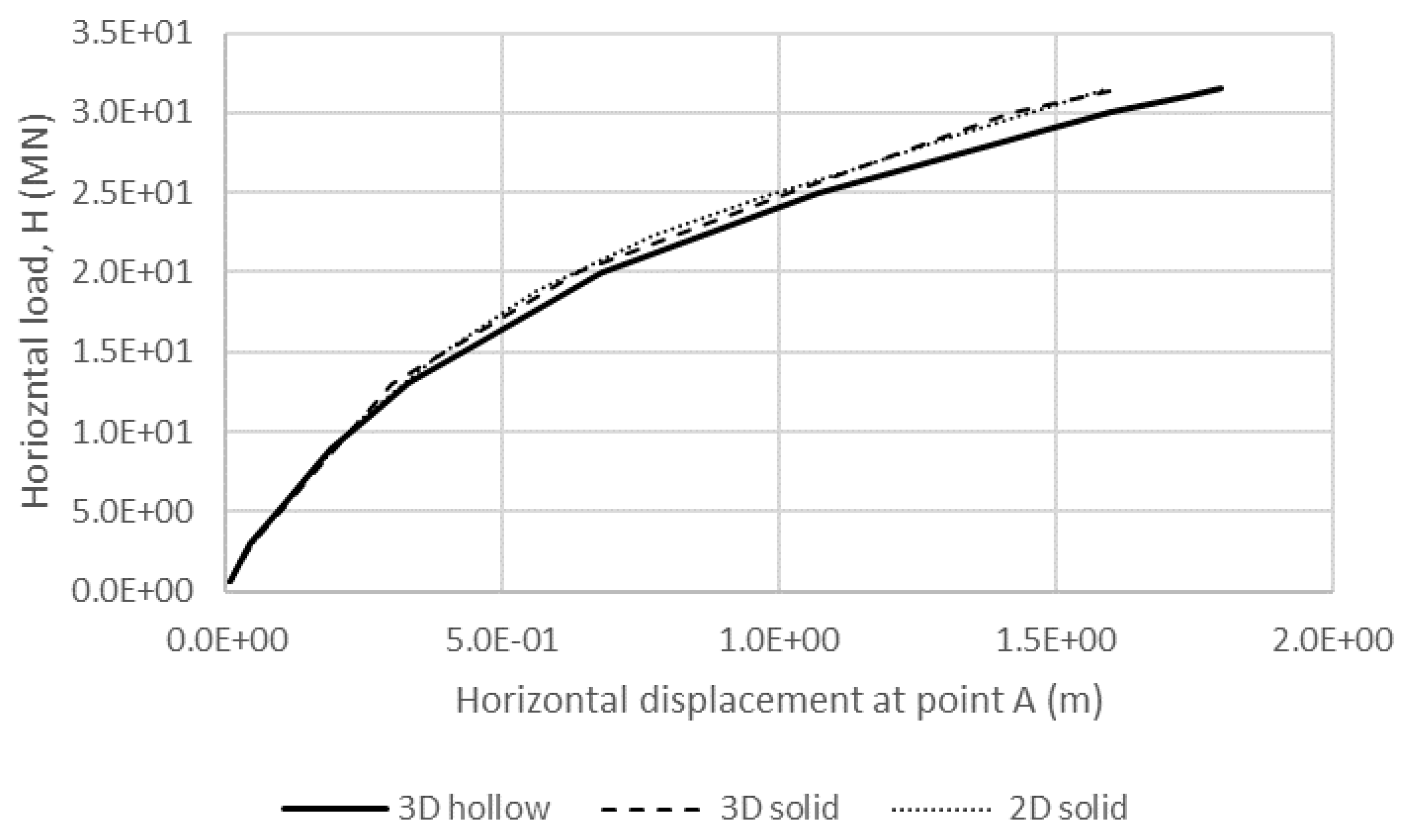
4.1. Static Analysis
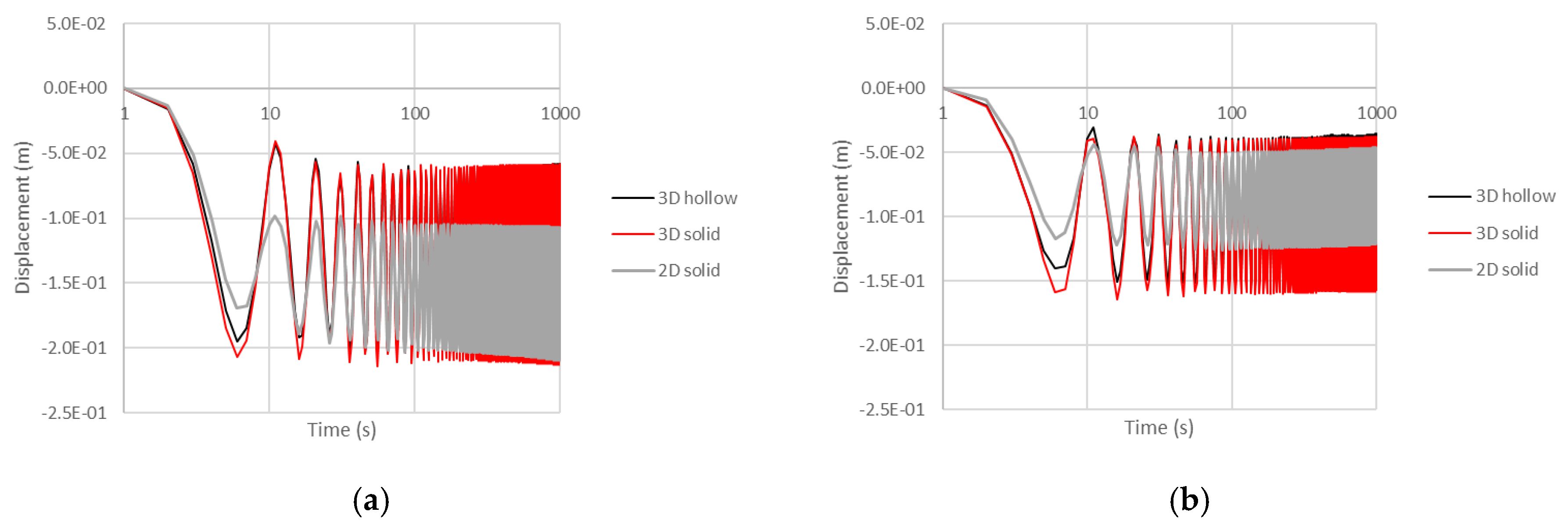
4.2. Dynamic Analyses
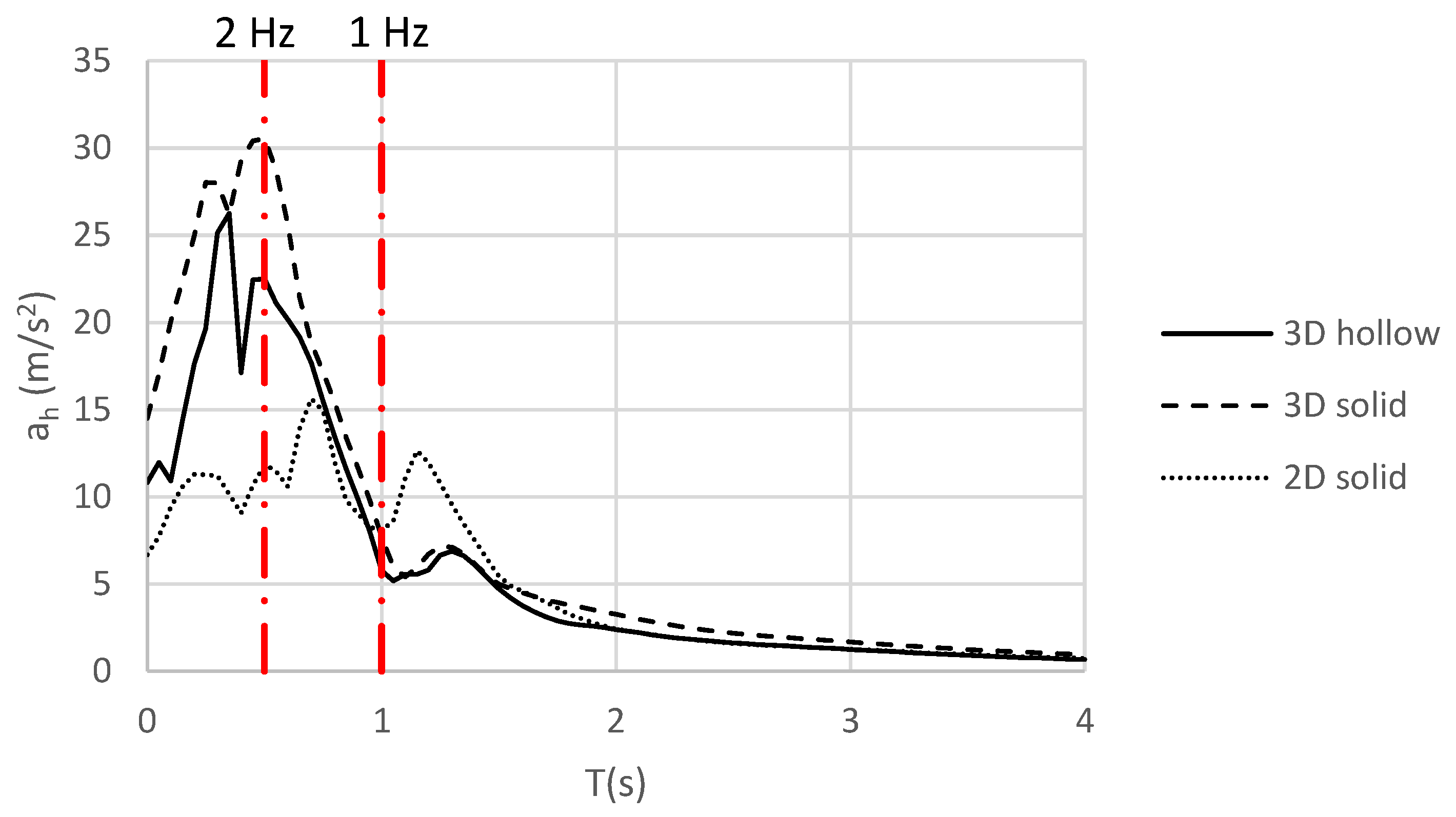
4.2.1. Free Vibration
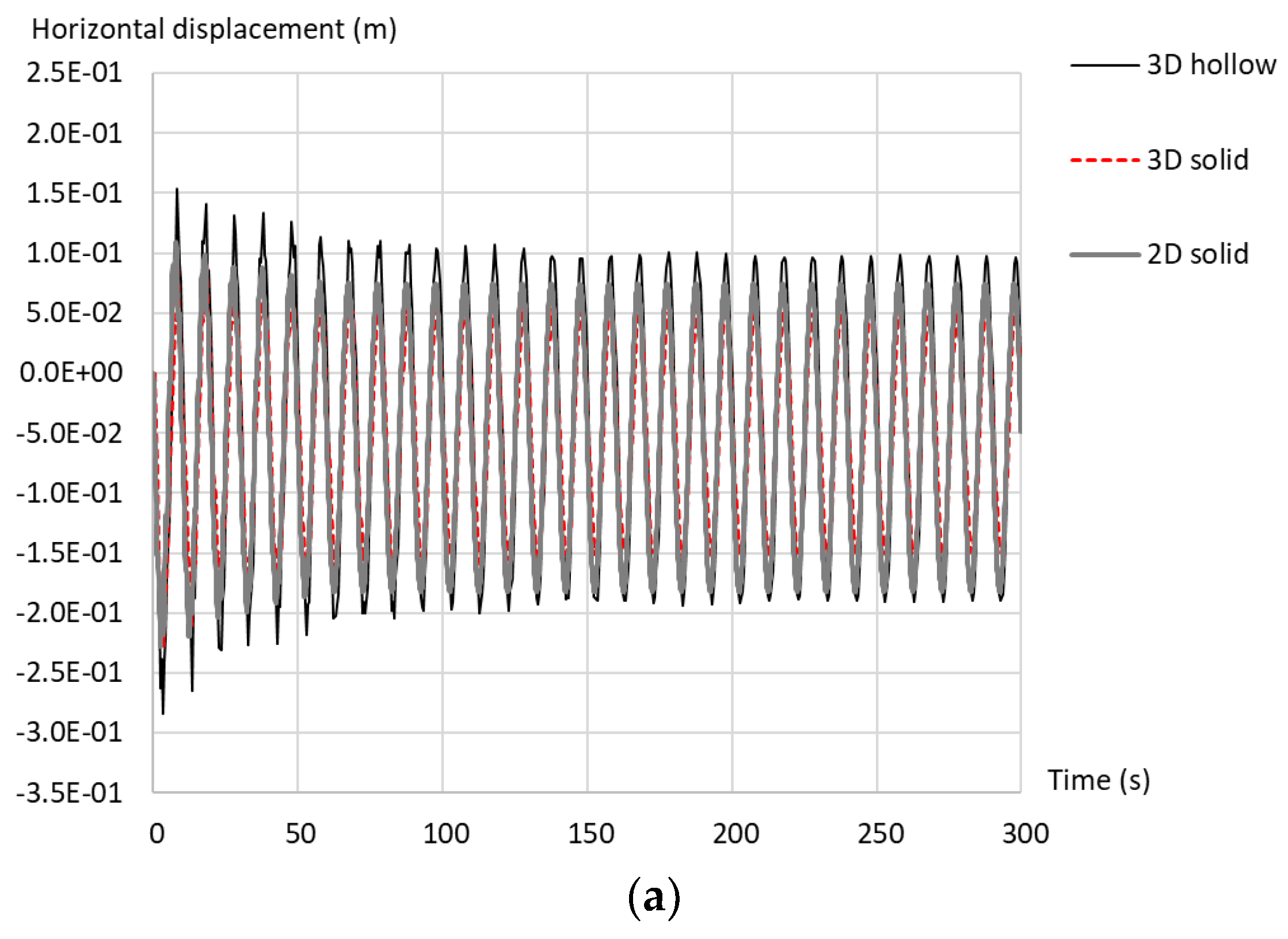
4.2.2. Forced Vibration in Homogeneous Soil
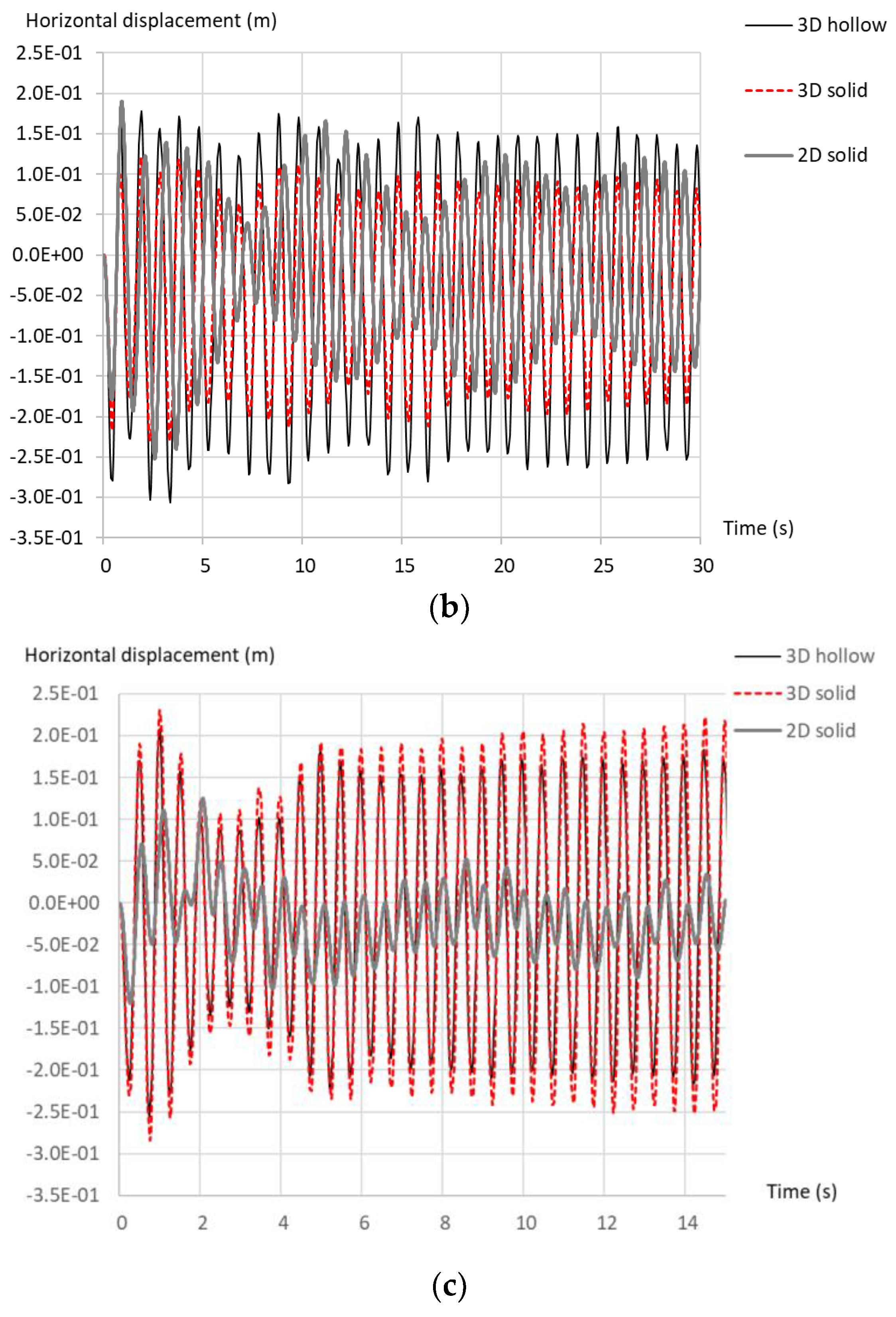
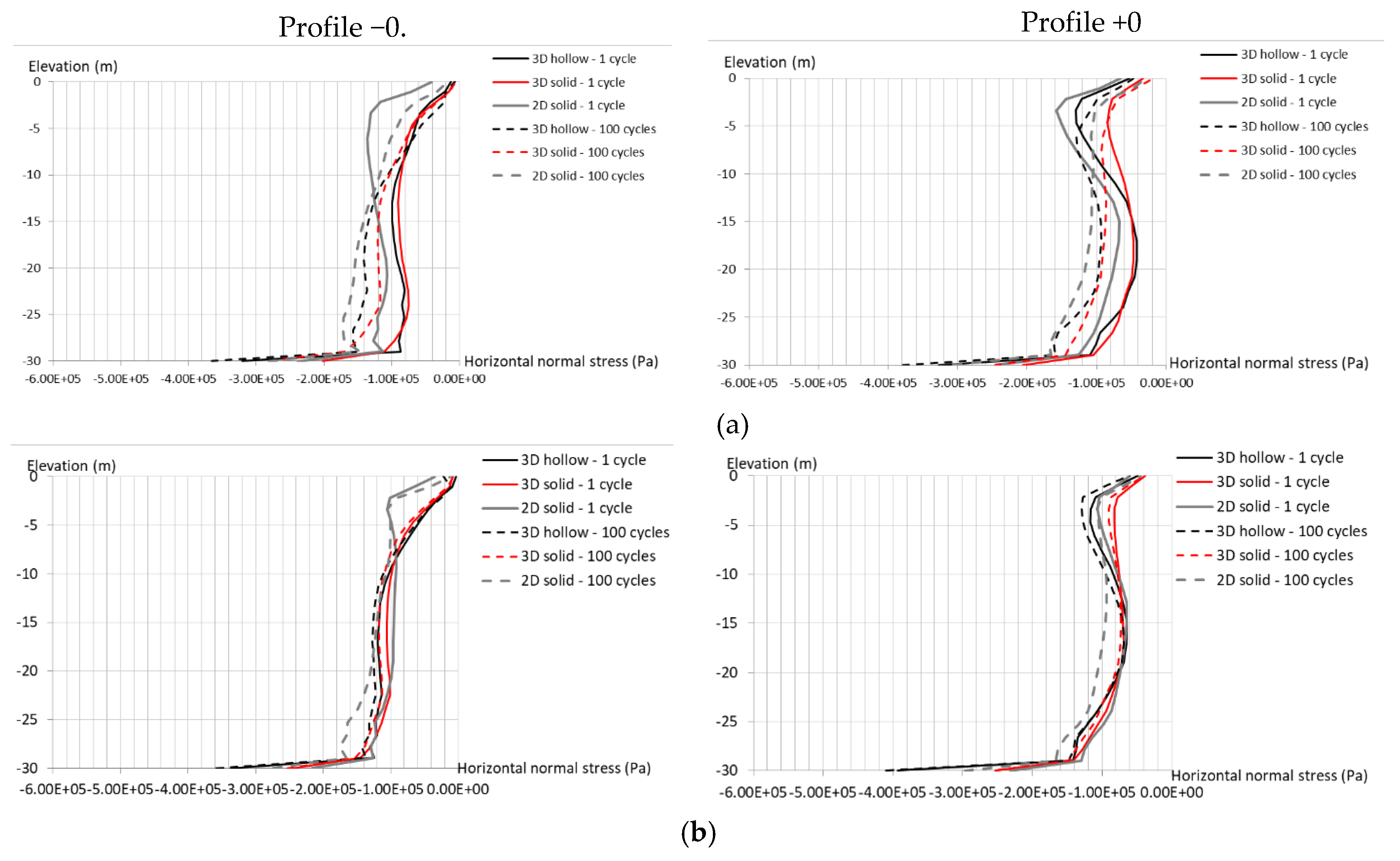
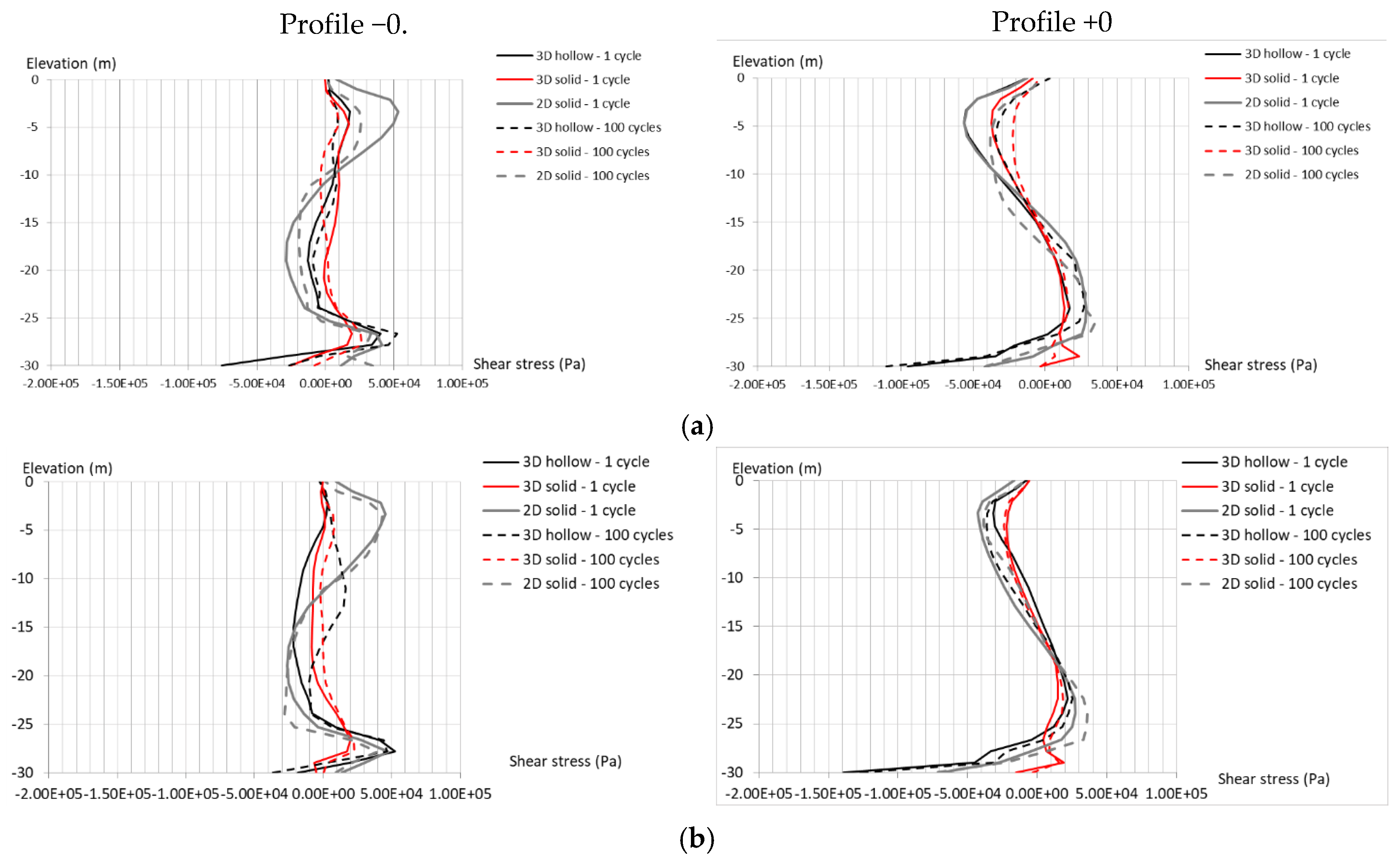
4.2.3. Forced Vibration in Depth-Dependent Stiffness Soil with Degradation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Esteban, M.; Leary, D. Current developments and future prospects of offshore wind and ocean energy. Appl. Energy 2012, 90, 128–136. [Google Scholar] [CrossRef]
- Cuéllar, P. Pile Foundations for Offshore Wind Turbines: Numerical and Experimental Investigations on the Behaviour under Short-Term and Long-Term Cyclic Loading. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2011. [Google Scholar]
- Bhattacharya, S.; Nikitas, N.; Garnsey, J.; Alexander, N.; Cox, J.; Lombardi, D.; Wood, D.M.; Nash, D. Observed dynamic soil–structure interaction in scale testing of offshore wind turbine foundations. Soil Dyn. Earthq. Eng. 2013, 54, 47–60. [Google Scholar] [CrossRef]
- ISO. Petroleum and Natural Gas. Industries—Fixed Steel Offshore Structures; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- DNV. Offshore Standard-Design of Offshore Wind Turbine Structures, DNV-OS-J101; Det Norske Veritas AS.: Oslo, Norway, 2014. [Google Scholar]
- Cuéllar, P.; Mira, P.; Pastor, M.; Fernández-Merodo, J.; Baeßler, M.; Rücker, W. A numerical model for the transient analysis of offshore foundations under cyclic loading. Comput. Geotech. 2014, 59, 75–86. [Google Scholar] [CrossRef]
- Achmus, M.; Kuo, Y.-S.; Abdel-Rahman, K. Behavior of monopile foundations under cyclic lateral load. Comput. Geotech. 2009, 36, 725–735. [Google Scholar] [CrossRef]
- Poulos, H.G.; Hull, T.S. The Role of Analytical Geomechanics. In Foundation Engineering: Current Principles and Practices; American Society of Civil Engineers: New York, NY, USA, 1989; Volume 2, pp. 1578–1606. Available online: https://cedb.asce.org/CEDBsearch/record.jsp?dockey=0063226 (accessed on 24 October 2020).
- Randolph, M.F. The response of flexible piles to lateral loading. Géotechnique 1981, 31, 247–259. [Google Scholar] [CrossRef]
- Niemunis, A.; Wichtmann, T.; Triantafyllidis, T. A high-cycle accumulation model for sand. Comput. Geotech. 2005, 32, 245–263. [Google Scholar] [CrossRef]
- Bransby, F. Difference between Load-Transfer Relationships for Laterally Loaded Pile Groups: Active p-y or Passive p -? J. Geotech. Eng. 1996, 122, 1015–1018. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Martin, G. Soil–structure interaction for landslide stabilizing piles. Comput. Geotech. 2002, 29, 363–386. [Google Scholar] [CrossRef]
- Hazzar, L.; Karray, M.; Bouassida, M.; Hussien, M.N. Ultimate Lateral Resistance of Piles in Cohesive Soil. DFI J. J. Deep. Found. Inst. 2013, 7, 59–68. [Google Scholar] [CrossRef]
- Hazzar, L.; Hussien, M.N.; Karray, M. Two-dimensional modelling evaluation of laterally loaded piles based on three-dimensional analyses. Géoméch. Geoengin. 2019, 1–18. [Google Scholar] [CrossRef]
- Bourgeois, E.; Rakotonindriana, M.; Le Kouby, A.; Mestat, P.; Serratrice, J. Three-dimensional numerical modelling of the behaviour of a pile subjected to cyclic lateral loading. Comput. Geotech. 2010, 37, 999–1007. [Google Scholar] [CrossRef]
- López-Querol, S.; Cui, L.; Bhattacharya, S. Numerical Methods for SSI Analysis of Offshore Wind Turbine Foundations. In Wind Energy Engineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 275–297. [Google Scholar]
- Zdravkovic, L.; Taborda, D.M.G.; Potts, D.; Jardine, R.; Sideri, M.; Schroeder, F.; Byrne, B.; McAdam, R.; Burd, H.; Houlsby, G.; et al. Numerical modelling of large diameter piles under lateral loading for offshore wind applications. In Frontiers in Offshore Geotechnics III; Informa UK Limited: London, UK, 2015; pp. 759–764. [Google Scholar]
- McClelland, B.; Focht, J. Soil modulus for laterally loaded piles. J. Soil Mech. Found. Div. 1956, 82, 1–22. [Google Scholar]
- Reese, L.C.; Matlock, H. Non-dimensional Solutions for Laterally Loaded Piles with Soil Modulus Assumed Proportional to Depth. In Proceedings of the 8th Texas Conference on Soil Mechanics and Foundation Engineering, Austin, TX, USA, 14–15 September 1956. [Google Scholar]
- Reese, L.C.; Cox, W.R.; Koop, F.D. Analysis of Laterally Loaded Piles in Sand. In Proceedings of the Offshore Technology Conference, Society of Petroleum Engineers (SPE), Houston, TX, USA, 6–8 May 1974; Volume 2. [Google Scholar]
- Winkler, E. Die Lehre Von Elasticzitat Und Festigkeit; Scientific Research Publishing Inc.: Prague, Czech Republic, 1867; Available online: https://www.scirp.org/(S(vtj3fa45qm1ean45vvffcz55))/reference/ReferencesPapers.aspx?ReferenceID=2521358 (accessed on 24 October 2020).
- API. Planning, Designing, and Constructing Fixed Offshore Platforms, 22nd ed.; RP 2A-WSD.; American Petroleum Institute: Washington, DC, USA, 2014; Available online: https://infostore.saiglobal.com/en-us/Standards/API-2A-WSD-2014-98372_SAIG_API_API_206553/ (accessed on 24 October 2020).
- Achmus, M.; Albiker, J.; Peralta, P.; tom Wörden, F. Scale Effects in the Design of Large Diameter Monopoles; EWEA: Brussels, Belgium, 2011; pp. 326–328. [Google Scholar]
- Jardine, R.J. Geotechnics, energy and climate change: The 56th Rankine Lecture. Géotechnique 2020, 70, 3–59. [Google Scholar] [CrossRef]
- Randolph, M.F.; Dolwin, J.; Beck, R. Design of driven piles in sand. Géotechnique 1994, 44, 427–448. [Google Scholar] [CrossRef]
- Trochanis, A.; Bielak, J.; Christiano, P. Three-dimensional nonlinear study of piles. J. Geotech. Eng. ASCE. 1991, 117, 429–447. [Google Scholar] [CrossRef]
- Damgaard, M.; Bayat, M.; Andersen, L.V.; Ibsen, L.B. Assessment of the dynamic behaviour of saturated soil subjected to cyclic loading from offshore monopile wind turbine foundations. Comput. Geotech. 2014, 61, 116–126. [Google Scholar] [CrossRef]
- Ong, D. Benchmarking of FEM technique involving deep excavation, pile-soil interaction and embankment construction. In Proceedings of the 12th International Conference of International Association for Computer Methods and Advanced in Geomechanics (IACMAG), Goa, India, 1–6 October 2008. [Google Scholar]
- Sidali, R. Comparison between 2D and 3D analysis of mono-pile under lateral cyclic load. In Proceedings of the 5th Maghreb Conference in Geotechnical Engineering, Marrakech, Morocco, 26–27 October 2016. [Google Scholar]
- ANSYS. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Construction_production_(volume)_index_overview (accessed on 15 July 2020).
- Page, A.M.; Grimstad, G.; Eiksund, G.R.; Jostad, H.P. A macro-element model for multidirectional cyclic lateral loading of monopiles in clay. Comput. Geotech. 2019, 106, 314–326. [Google Scholar] [CrossRef]
- Page, A.M.; Skau, K.S.; Jostad, H.P.; Eiksund, G.R. A new foundations model for integrated analyses of monopile-based offshore wind turbines. In Proceedings of the 14th Deep Sea Offshore R&D Conference (EERA DeepWind’2017), Thondheim, Norway, 18–20 January 2017. [Google Scholar]
- Gelagoti, F.M.; Kourkoulis, R.S.; Georgiou, I.A.; Karamanos, S.A. Soil–Structure Interaction Effects in Offshore Wind Support Structures under Seismic Loading. J. Offshore Mech. Arct. Eng. 2019, 141, 061903-39. [Google Scholar] [CrossRef]
- Murphy, G.; Igoe, D.; Doherty, P.; Gavin, K. 3D FEM approach for laterally loaded monopile design. Comput. Geotech. 2018, 100, 76–83. [Google Scholar] [CrossRef]
- Shao, W.; Yang, N.; Shi, D.; Liu, Y. Degradation of lateral bearing capacity of piles in soft clay subjected to cyclic lateral loading. Mar. Georesources Geotechnol. 2019, 37, 999–1006. [Google Scholar] [CrossRef]
- Taborda, D.M.G.; Zdravković, L.; Potts, D.M.; Burd, H.J.; Byrne, B.; Gavin, K.G.; Houlsby, G.T.; Jardine, R.J.; Liu, T.; Martin, C.M.; et al. Finite-element modelling of laterally loaded piles in a dense marine sand at Dunkirk. Géotechnique 2020, 70, 1024–1029. [Google Scholar] [CrossRef]



| Material | Young Modulus, E (MPa) | Poisson’s Ratio, ν | Density, ρ (Kg/m3) | Friction Angle, φ (o) | Dilatancy, δ (o) | Cohesion, c (kPa) |
|---|---|---|---|---|---|---|
| Soil (Mohr–Coulomb) | 40.0 | 0.25 | 2000.0 | 35 | 5 | 1 |
| Steel (elastic) | 2.1 × 105 | 0.30 | 7850.0 | - | - | - |
| Structure (elastic—simplified models) | 1.94 × 104 | 0.30 | 372.2 | - | - | - |
| Pile (elastic—simplified models) | 1.95 × 104 | 0.30 | 2277.43 | - | - | - |
| Type of Sand | Oedometric Stiffness Parameter, κ | Oedometer Stiffness Parameter, λ | Degradation Parameter, b1 | Degradation Parameter, b2 |
|---|---|---|---|---|
| Medium dense | 400 | 0.60 | 0.16 | 0.38 |
| Dense | 600 | 0.55 | 0.2 | 5.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez-Querol, S.; Spyridis, M.; Moreta, P.J.M.; Arias-Trujillo, J. Simplified Numerical Models to Simulate Hollow Monopile Wind Turbine Foundations. J. Mar. Sci. Eng. 2020, 8, 837. https://doi.org/10.3390/jmse8110837
Lopez-Querol S, Spyridis M, Moreta PJM, Arias-Trujillo J. Simplified Numerical Models to Simulate Hollow Monopile Wind Turbine Foundations. Journal of Marine Science and Engineering. 2020; 8(11):837. https://doi.org/10.3390/jmse8110837
Chicago/Turabian StyleLopez-Querol, Susana, Michail Spyridis, Pedro J. M. Moreta, and Juana Arias-Trujillo. 2020. "Simplified Numerical Models to Simulate Hollow Monopile Wind Turbine Foundations" Journal of Marine Science and Engineering 8, no. 11: 837. https://doi.org/10.3390/jmse8110837
APA StyleLopez-Querol, S., Spyridis, M., Moreta, P. J. M., & Arias-Trujillo, J. (2020). Simplified Numerical Models to Simulate Hollow Monopile Wind Turbine Foundations. Journal of Marine Science and Engineering, 8(11), 837. https://doi.org/10.3390/jmse8110837






