A Low-Cost Stereo Video System for Measuring Directional Wind Waves
Abstract
1. Introduction
2. Materials and Methods
2.1. Camera Calibration
2.2. Acquisition System and Frame Synchronization
2.3. Mean Sea-Level
2.4. Experimental Setup and Conditions
3. Results
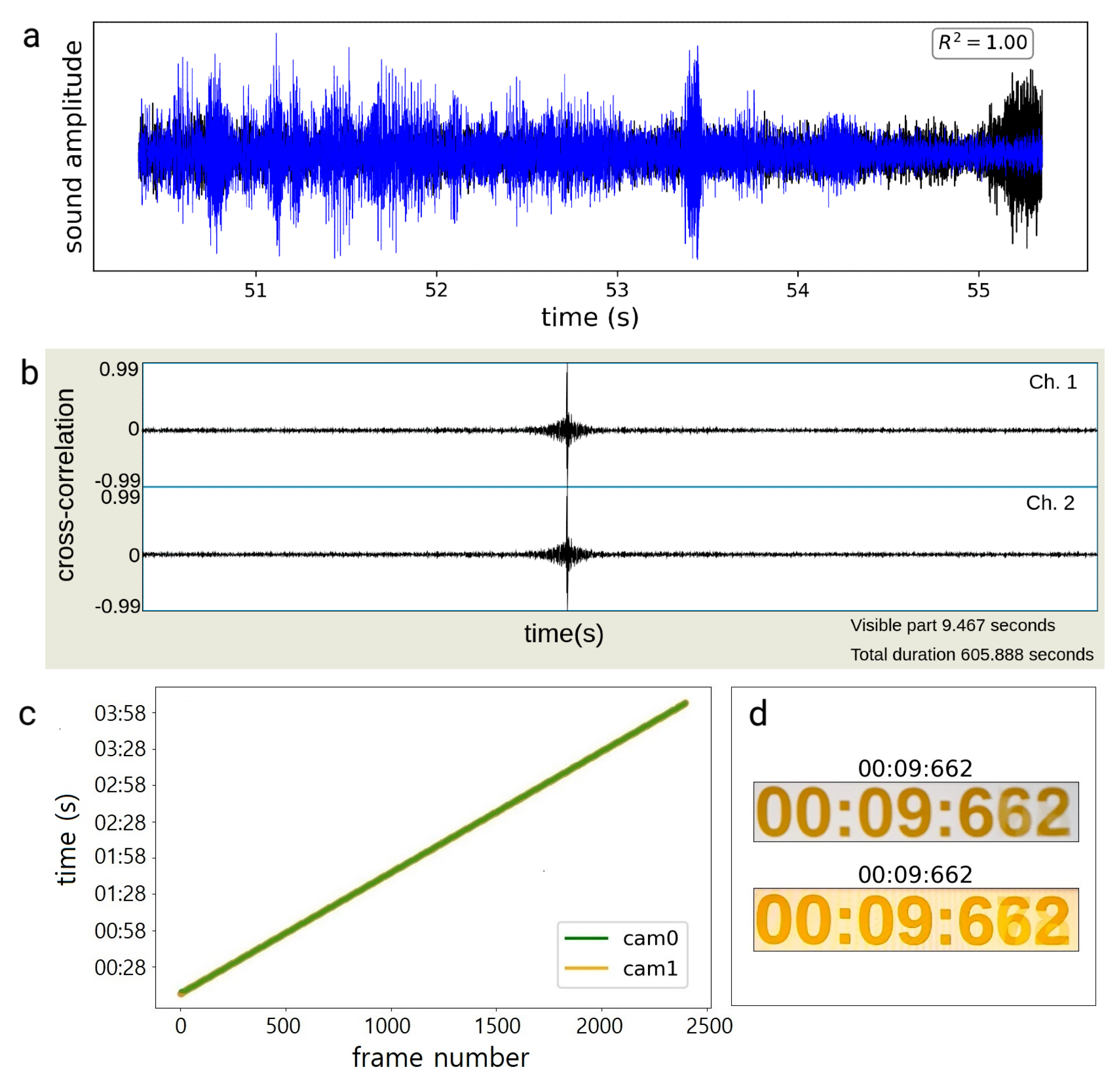
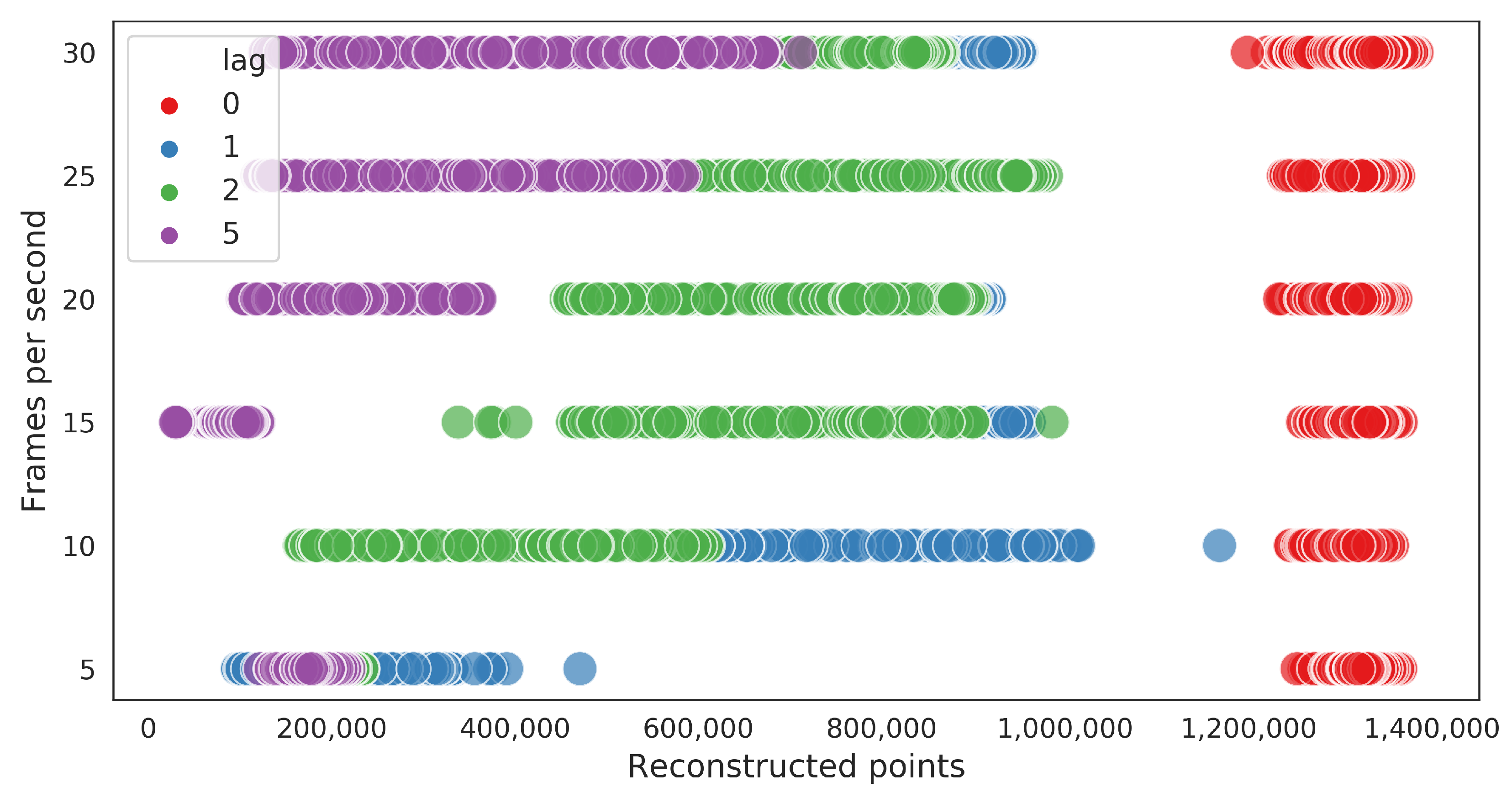
3.1. Frame Synchronization
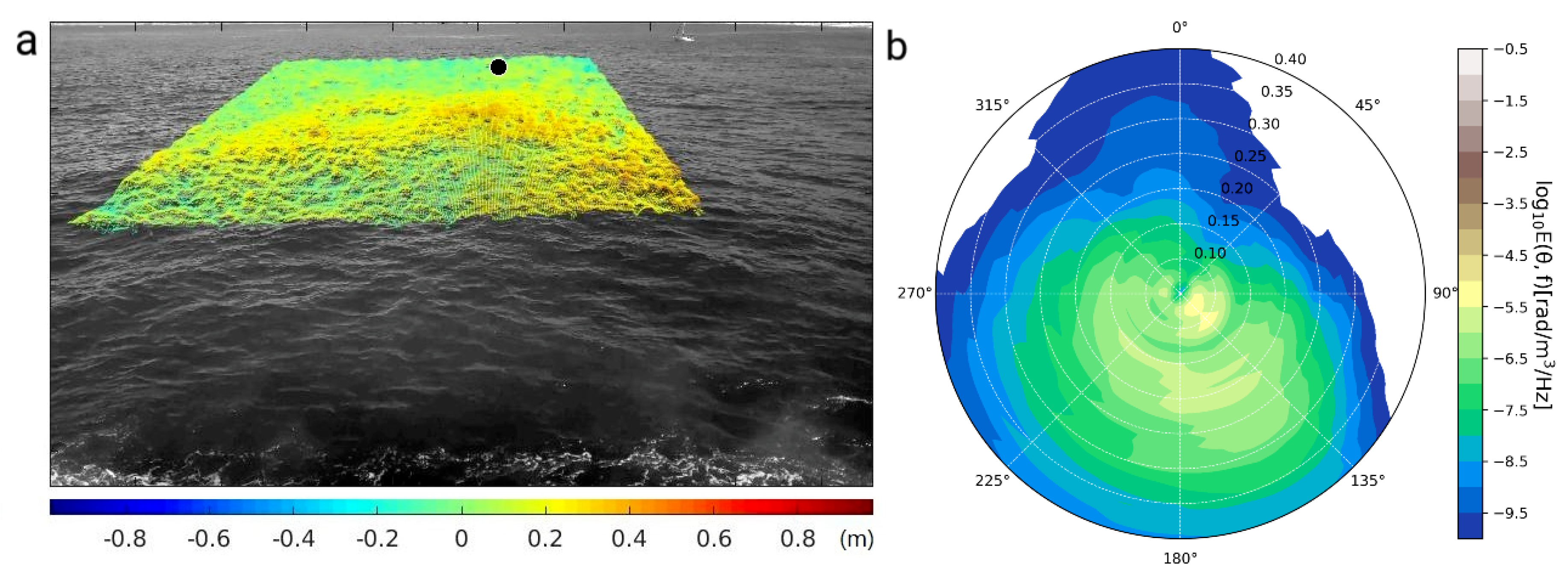
3.2. Stereo Video
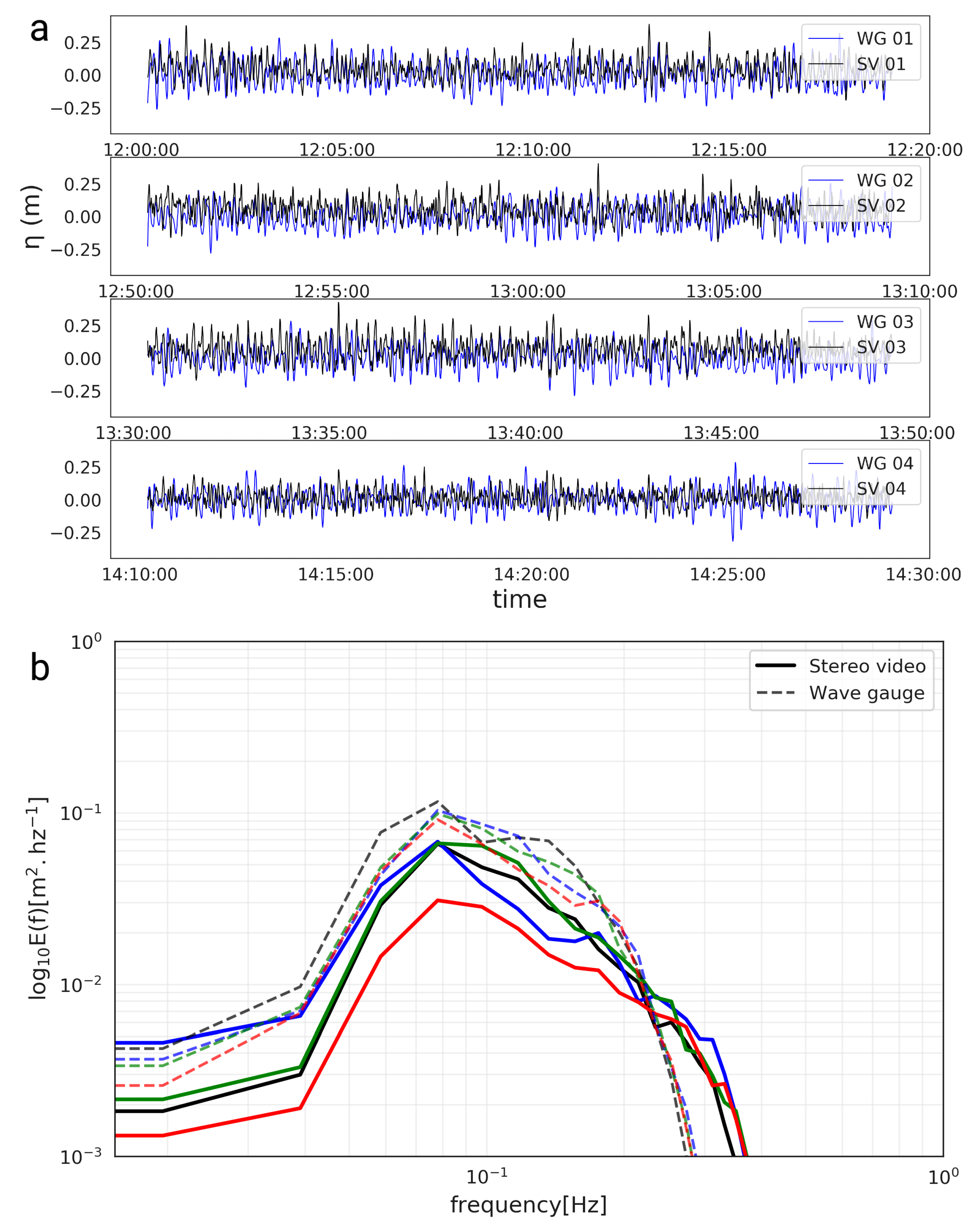
3.3. Validation against In Situ Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Statistics Of The Sea Surface Derived From Sun Glitter. J. Mar. Res. 1954, 13, 198–227. [Google Scholar]
- Monaldo, F.M.; Kasevich, R.S. Daylight Imagery of Ocean Surface Waves for Wave Spectra. J. Phys. Oceanogr. 1981, 11, 272–283. [Google Scholar] [CrossRef][Green Version]
- Stilwell, D., Jr. Directional energy spectra of the sea from photographs. J. Geophys. Res. (1896–1977) 1969, 74, 1974–1986. [Google Scholar] [CrossRef]
- Stilwell, D., Jr.; Pilon, R.O. Directional spectra of surface waves from photographs. J. Geophys. Res. (1896–1977) 1974, 79, 1277–1284. [Google Scholar] [CrossRef]
- Jähne, B.; Riemer, K.S. Two-dimensional wave number spectra of small-scale water surface waves. J. Geophys. Res. 1990, 95, 11531–11546. [Google Scholar] [CrossRef]
- Rapizo, H.; d’Avila, V.; Violante-Carvalho, N.; Pinho, U.; Parente, C.E.; Nascimento, F. Simple Techniques for Retrieval of Wind Wave Periods and Directions from Optical Images Sequences in Wave Tanks. J. Coast. Res. 2016, 32, 1227–1234. [Google Scholar] [CrossRef]
- Banner, M.L.; Jones, I.S.F.; Trinder, J.C. Wavenumber spectra of short gravity waves. J. Fluid Mech. 1989, 198, 321–344. [Google Scholar] [CrossRef]
- Benetazzo, A. Measurements of short water waves using stereo matched image sequences. Coast. Eng. 2006, 53, 1013–1032. [Google Scholar] [CrossRef]
- Mironov, A.S.; Yurovskaya, M.V.; Dulov, V.A.; Hauser, D.; Guérin, C.A. Statistical characterization of short wind waves from stereo images of the sea surface. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Shemdin, O.H.; Tran, H.M.; Wu, S.C. Directional measurement of short ocean waves with stereophotography. J. Geophys. Res. Oceans 1988, 93, 13891–13901. [Google Scholar] [CrossRef]
- Wanek, J.; Wu, C. Automated Trinocular stereo imaging system for three-dimensional surface wave measurements. Ocean Eng. 2006, 33, 723–747. [Google Scholar] [CrossRef]
- Banner, M.L.; Barthelemy, X.; Fedele, F.; Allis, M.; Benetazzo, A.; Dias, F.; Peirson, W.L. Linking reduced breaking crest speeds to unsteady nonlinear water wave group behavior. Phys. Rev. Lett. 2014, 112, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Leckler, F.; Ardhuin, F.; Peureux, C.; Benetazzo, A.; Bergamasco, F.; Dulov, V. Analysis and interpretation of frequency-wavenumber spectra of young wind waves. J. Phys. Oceanogr. 2015, 45, 2484–2496. [Google Scholar] [CrossRef]
- Benetazzo, A.; Barbariol, F.; Bergamasco, F.; Torsello, A.; Carniel, S.; Sclavo, M. Stereo wave imaging from moving vessels: Practical use and applications. Coast. Eng. 2016, 109, 114–127. [Google Scholar] [CrossRef]
- Alvise, B.; Francesco, B.; Filippo, B.; Sandro, C.; Mauro, S. Space-time extreme wind waves: Analysis and prediction of shape and height. Ocean Model. 2017, 113, 201–216. [Google Scholar] [CrossRef]
- Laxague, N.; Haus, B.; Bogucki, D.; Özgökmen, T. Spectral characterization of fine-scale wind waves using shipboard optical polarimetry. J. Geophys. Res. Oceans 2015, 120, 3140–3156. [Google Scholar] [CrossRef]
- Guimarães, P.V. Sea Surface and Energy Dissipation. Ph.D. Thesis, École centrale de Nantes, Nantes, France, 2018. [Google Scholar]
- Schwendeman, M.S.; Thomson, J. Sharp-Crested Breaking Surface Waves Observed from a Ship-Based Stereo Video System. J. Phys. Oceanogr. 2017, 47, 775–792. [Google Scholar] [CrossRef]
- Guimarães, P.V.; Ardhuin, F.; Sutherland, P.; Accensi, M.; Hamon, M.; Pérignon, Y.; Thomson, J.; Benetazzo, A.; Ferrant, P. A surface kinematics buoy (SKIB) for wave–current interaction studies. Ocean Sci. 2018, 14, 1449–1460. [Google Scholar] [CrossRef]
- Schumacher, A. Stereophotogrammetrische Wellenaufnahmen. In Wissenschaftliche Ergebnisse Der Deutschen Atlantischen Expedition Auf Dem Forschungs- Und Vermessungss. "Meteor”. 1925–1927; Walter de Gruyter: Berlin, Germany, 1939. [Google Scholar]
- Chase, J.L. The Directional Spectrum of a Wind Generated Sea as Determined from Data Obtained by the Stereo Wave Observation Project; New York University, College of Engineering, Research Division, Department of Meteorology and Oceanography and Engineering Statistics Group: New York, NY, USA, 1957. [Google Scholar]
- Sugimori, Y. A study of the application of the holographic method to the determination of the directional spectrum of ocean waves. Deep Sea Res. Oceanogr. Abstr. 1975, 22, 339–350. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Observations of the Directional Distribution of Ocean-Wave Energy in Fetch-Limited Conditions. J. Phys. Oceanogr. 1983, 13, 191–207. [Google Scholar] [CrossRef]
- Gallego, G.; Benetazzo, A.; Yezzi, A.; Fedele, F. Wave Statistics and Spectra via a Variational Wave Acquisition Stereo System. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- Fedele, F.; Benetazzo, A.; Gallego, G.; Shih, P.C.; Yezzi, A.; Barbariol, F.; Ardhuin, F. Space-time measurements of oceanic sea states. Ocean Model. 2013, 70, 103–115. [Google Scholar] [CrossRef]
- Leckler, F. Observation et Modélisation du Déferlement des Vagues. Ph.D. Thesis, Université de Bretagne Occidentale, Bretagne, France, 2013. [Google Scholar]
- Peureux, C.; Benetazzo, A.; Ardhuin, F. Note on the directional properties of meter-scale gravity waves. Ocean Sci. 2018, 14, 41–52. [Google Scholar] [CrossRef]
- Bergamasco, F.; Torsello, A.; Sclavo, M.; Barbariol, F.; Benetazzo, A. WASS: An open-source pipeline for 3D stereo reconstruction of ocean waves. Comput. Geosci. 2017, 107, 28–36. [Google Scholar] [CrossRef]
- Vieira, M.; Guimarães, P.V. Measuring Sea Surface Gravity Waves Using Smartphones. In Ports 2019: Port Planning and Development; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 184–192. [Google Scholar]
- Benetazzo, A.; Bergamasco, F.; Yoo, J.; Cavaleri, L.; Kim, S.S.; Bertotti, L.; Barbariol, F.; Shim, J.S. Characterizing the signature of a spatio-temporal wind wave field. Ocean Model. 2018, 129, 104–123. [Google Scholar] [CrossRef]
- Benetazzo, A.; Ardhuin, F.; Bergamasco, F.; Cavaleri, L.; Guimarães, P.V.; Schwendeman, M.; Sclavo, M.; Thomson, J.; Torsello, A. On the shape and likelihood of oceanic rogue waves. Sci. Rep. 2017, 7, 8276. [Google Scholar] [CrossRef]
- Filipot, J.F.; Guimaraes, P.; Leckler, F.; Hortsmann, J.; Carrasco, R.; Leroy, E.; Fady, N.; Accensi, M.; Prevosto, M.; Duarte, R.; et al. La Jument lighthouse: A real-scale laboratory for the study of giant waves and their loading on marine structures. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20190008. [Google Scholar] [CrossRef]
- Guimarães, P.V.; Ardhuin, F.; Bergamasco, F.; Leckler, F.; Filipot, J.F.; Shim, J.S.; Dulov, V.; Benetazzo, A. A data set of sea surface stereo images to resolve space-time wave fields. Sci. Data 2020, 7, 145. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Soatto, S.; Kosecká, J.; Sastry, S. An Invitation to 3-D Vision; Springer: New York, NY, USA, 2004. [Google Scholar]
- Benetazzo, A.; Fedele, F.; Gallego, G.; Shih, P.C.; Yezzi, A. Offshore stereo measurements of gravity waves. Coast. Eng. 2012, 64, 127–138. [Google Scholar] [CrossRef]
- Bouguet, J.Y. Camera Calibration Toolbox for Matlab; Technical Report; California Institute of Technology: Pasadena, CA, USA, 2004. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Boersma, P.; Weenink, D. Praat: Doing Phonetics by Computer [Computer Program] Version 6.1.09. 2020. Available online: http://www.praat.org/ (accessed on 20 August 2018).
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Jähne, B. Spatio-Temporal Image Processing: Theory and Scientific Applications; Springer: Berlin/Heidelberg, Germany, 1993; Volume 751. [Google Scholar]
- Rodriguez, J.J.; Aggarwal, J.K. Stochastic analysis of stereo quantization error. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 467–470. [Google Scholar] [CrossRef]
- Benetazzo, A.; Barbariol, F.; Bergamasco, F.; Torsello, A.; Carniel, S.; Sclavo, M. Observation of Extreme Sea Waves in a Space–Time Ensemble. J. Phys. Oceanogr. 2015, 45, 2261–2275. [Google Scholar] [CrossRef]

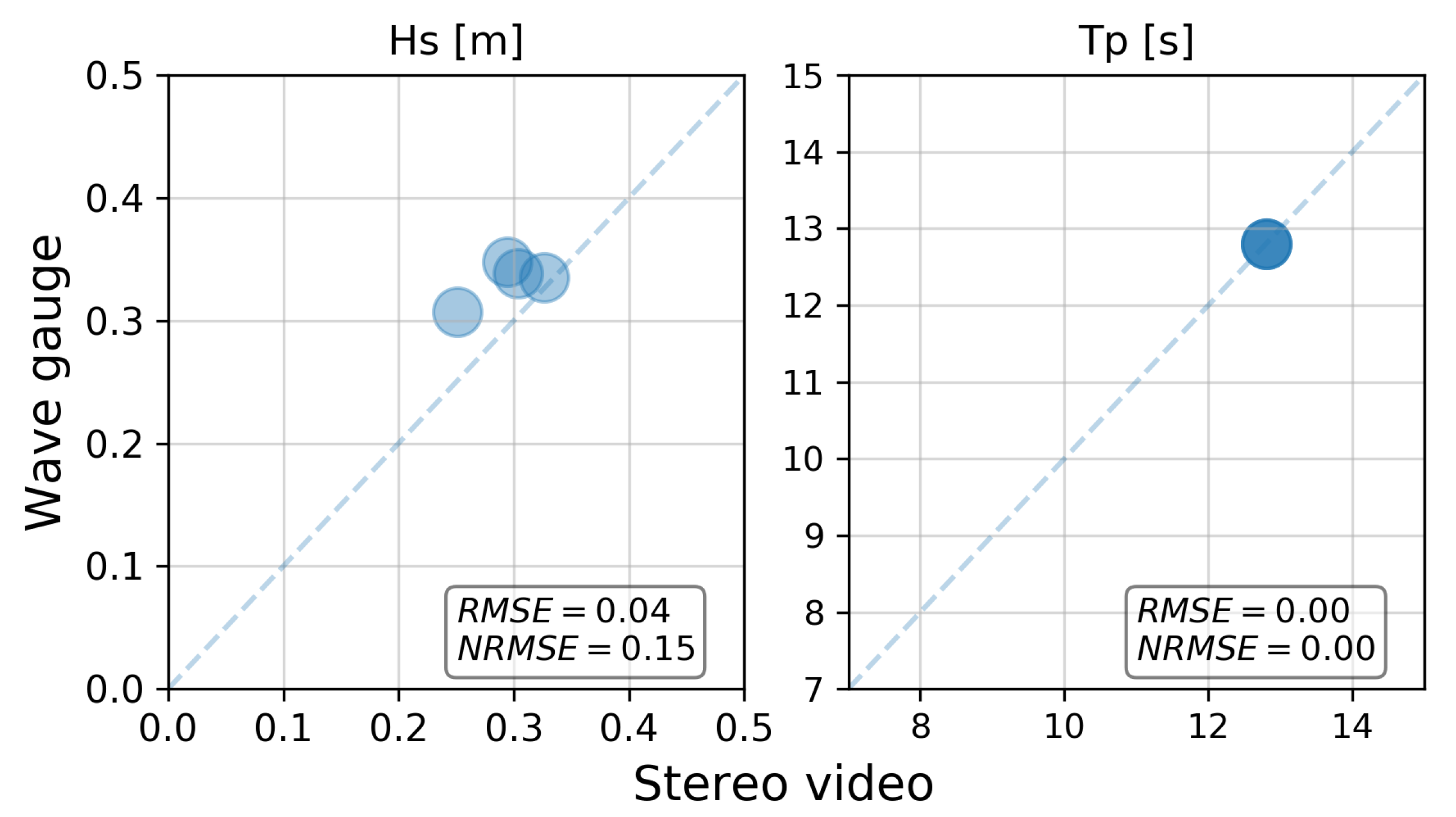
| Sensor | Hs (m) | Tp (s) | RMSE (m) | Bias (m) |
|---|---|---|---|---|
| SV 01 | 0.29 | 12.8 | 0.10 | −0.04 |
| WG | 0.35 | 12.8 | ||
| SV 02 | 0.30 | 12.8 | 0.12 | −0.05 |
| WG | 0.34 | 12.8 | ||
| SV 03 | 0.33 | 12.8 | 0.12 | −0.06 |
| WG | 0.33 | 12.8 | ||
| SV 04 | 0.35 | 12.8 | 0.10 | −0.01 |
| WG | 0.30 | 12.8 |
| Traditional Stereo Video | Low-Cost Stereo Video | |
|---|---|---|
| Video cameras | 2 Wired connected dedicated cameras and 2 lens | 2 Smartphones or video cameras with audio built-in |
| Power supply | External power supply + cables | Optional |
| Synchronization | Proprietary trigger box or trigger controller | Offline TLCC method |
| Acquisition system | Fast computer and dedicated software | Smartphones App |
| Cameras mounting system | Dedicated camera cases | Tripod and Smartphone support |
| Images quality | Higher | Lower |
| Storage space required | Higher | Lower (due to video compression) |
| Calibration procedure | Same for booth system | |
| Fixed platform | Same for booth system | |
| Lighting and environmental conditions | Same for both system | |
| Postprocessing time | Near the same * | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, M.; Guimarães, P.V.; Violante-Carvalho, N.; Benetazzo, A.; Bergamasco, F.; Pereira, H. A Low-Cost Stereo Video System for Measuring Directional Wind Waves. J. Mar. Sci. Eng. 2020, 8, 831. https://doi.org/10.3390/jmse8110831
Vieira M, Guimarães PV, Violante-Carvalho N, Benetazzo A, Bergamasco F, Pereira H. A Low-Cost Stereo Video System for Measuring Directional Wind Waves. Journal of Marine Science and Engineering. 2020; 8(11):831. https://doi.org/10.3390/jmse8110831
Chicago/Turabian StyleVieira, Matheus, Pedro Veras Guimarães, Nelson Violante-Carvalho, Alvise Benetazzo, Filippo Bergamasco, and Henrique Pereira. 2020. "A Low-Cost Stereo Video System for Measuring Directional Wind Waves" Journal of Marine Science and Engineering 8, no. 11: 831. https://doi.org/10.3390/jmse8110831
APA StyleVieira, M., Guimarães, P. V., Violante-Carvalho, N., Benetazzo, A., Bergamasco, F., & Pereira, H. (2020). A Low-Cost Stereo Video System for Measuring Directional Wind Waves. Journal of Marine Science and Engineering, 8(11), 831. https://doi.org/10.3390/jmse8110831









