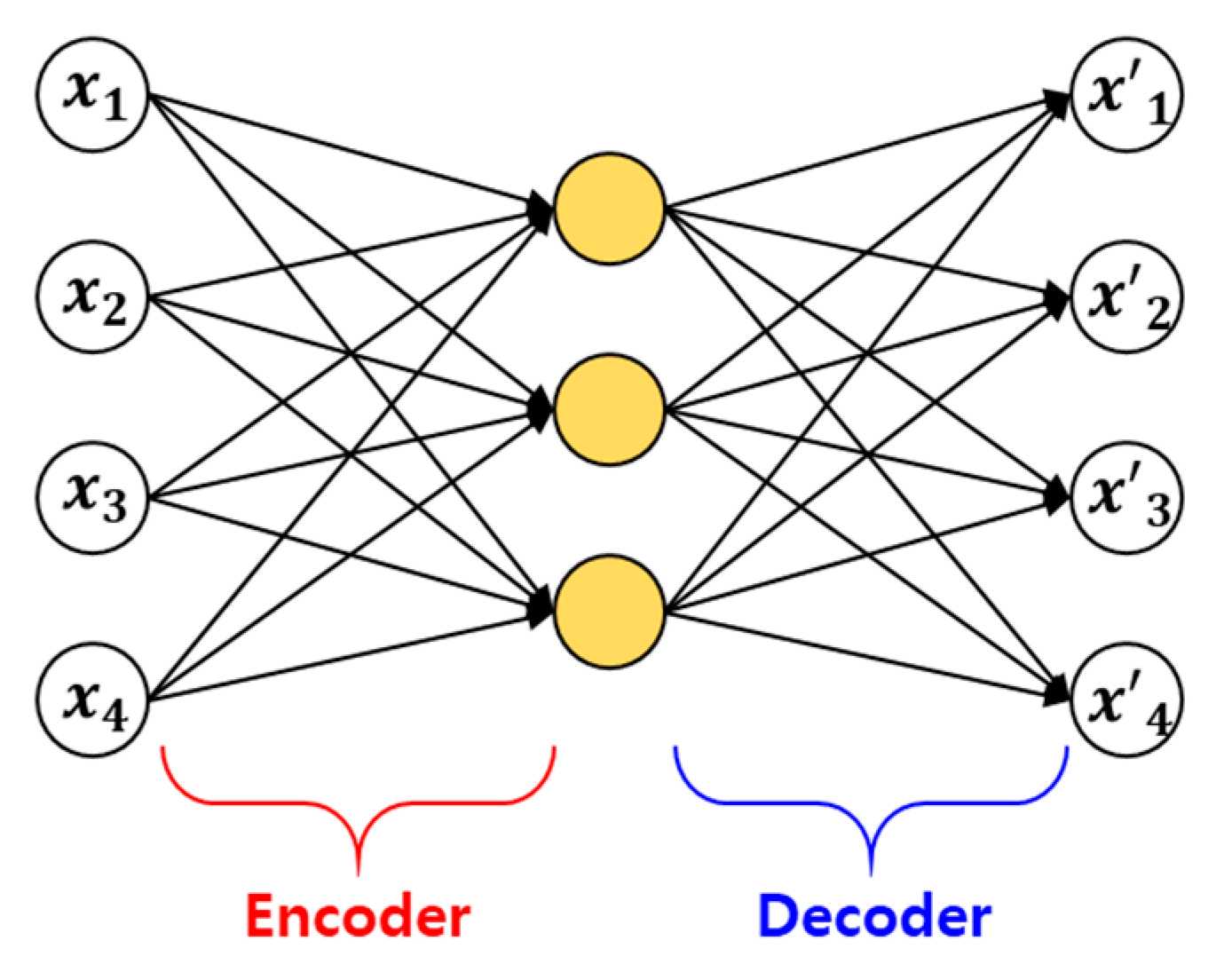
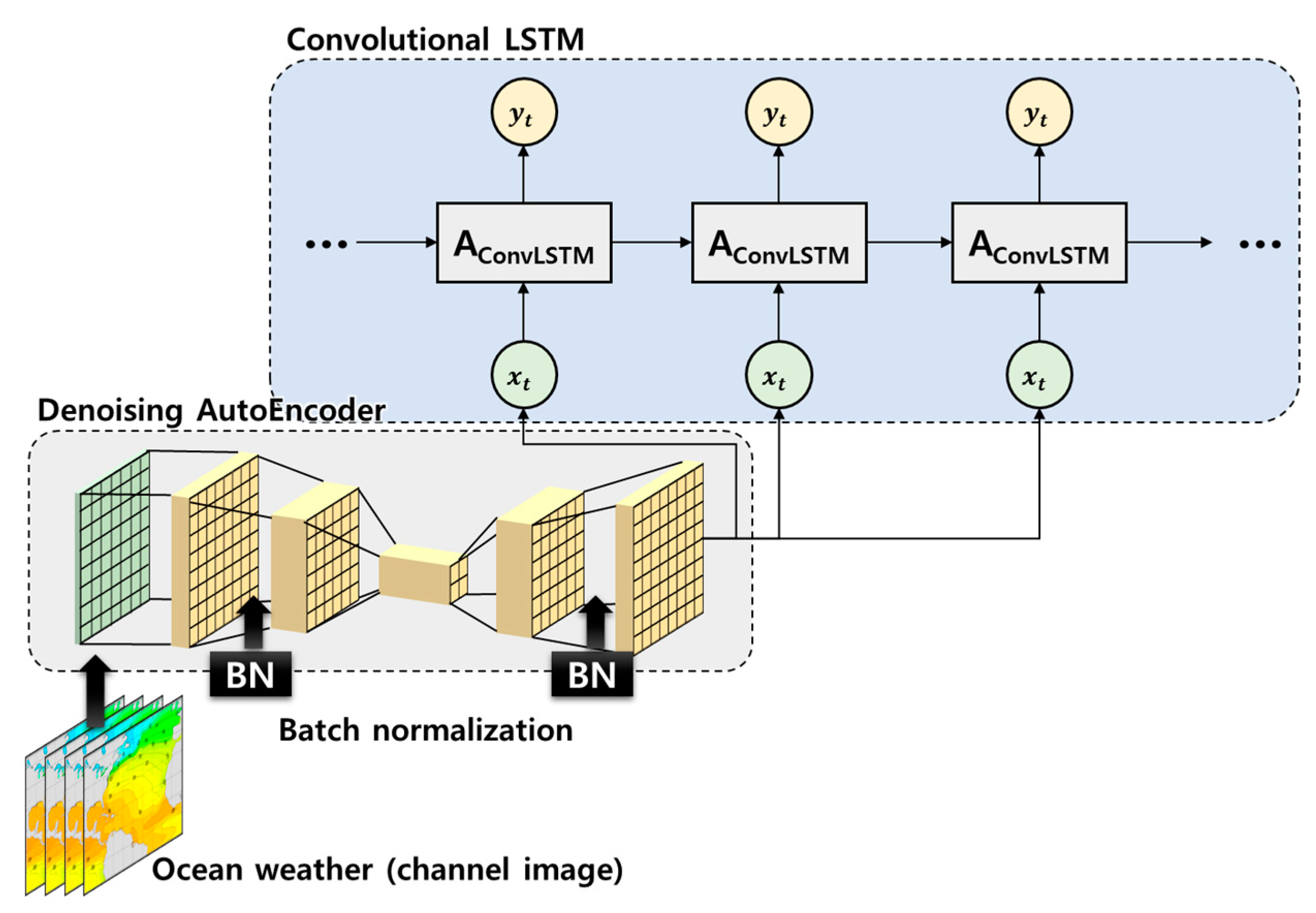
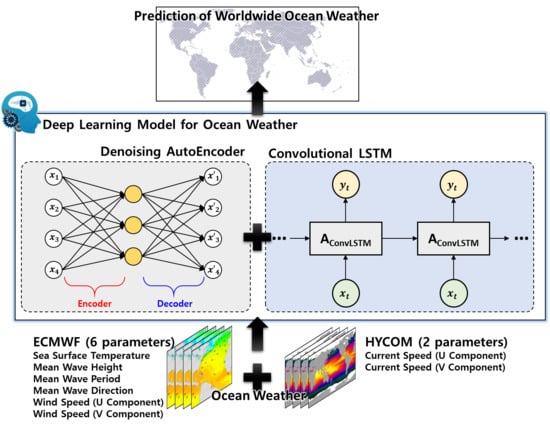
4.1. Hyperparameters of the Learning Model
Hyperparameters for the ConvLSTM include the epoch number, batch size, and loss function type. Eight parameters of ocean weather were trained through a model combining the denoising AutoEncoder and the ConvLSTM. In the case of six parameters of ocean weather obtained from ECMWF, since it is a total of 20 years of data, the initial 16 years of data were used as a training set, and the remaining 4 years of data were used as a validation set (2 years) and a test set (2 years). In addition, in the case of two parameters of ocean weather obtained from HYCOM, since it is a total of 4 years and 4 months of data, the initial 4 years of data were used as a training set and the remaining 4 months of data were used as a validation set (2 months) and a test set (2 months). The batch size and number of epochs were tracked for the training set, validation set, and test set. The epoch number was determined using the convergence step from the line where no overfitting occurred. As a result of training progress, most models typically converge between 40 and 50 epochs. In this study, MAE was used in all cases for accuracy comparison. Since RMSE tends to overestimate outliers in the overall data, MAE is more appropriate for this study using time-series data for the long term. In the case of average error, the whole data are firstly calculated as MAE by comparing them with the original data and averaged. In addition, the land included in each area was also excluded from the error calculation. Due to the nature of the ConvLSTM, an image was used as an input, and the value of the land was calculated as 0. If the error of the land is included in the error, the total error will be smaller. In this study, we grasped this, calculated MAE for all areas and time series, and averaged it.
4.2. Effect of the Denoising AutoEncoder
The model described in
Table 4 of
Section 4.3 was trained using a model combining a denoising AutoEncoder and the ConvLSTM, as mentioned in
Section 3.1. However, before that, we attempted to confirm the effect of the denoising AutoEncoder. For this, SST, which has a strong periodicity, was used. The results obtained using only the ConvLSTM model and those obtained using the denoising AutoEncoder and ConvLSTM models proposed in this study were compared.
Prior to comparing the two models, to determine whether the delay prediction result occurs even when training SST, the look forward value was changed under the same conditions by using a single channel of SST as input data, and the accuracy was compared.
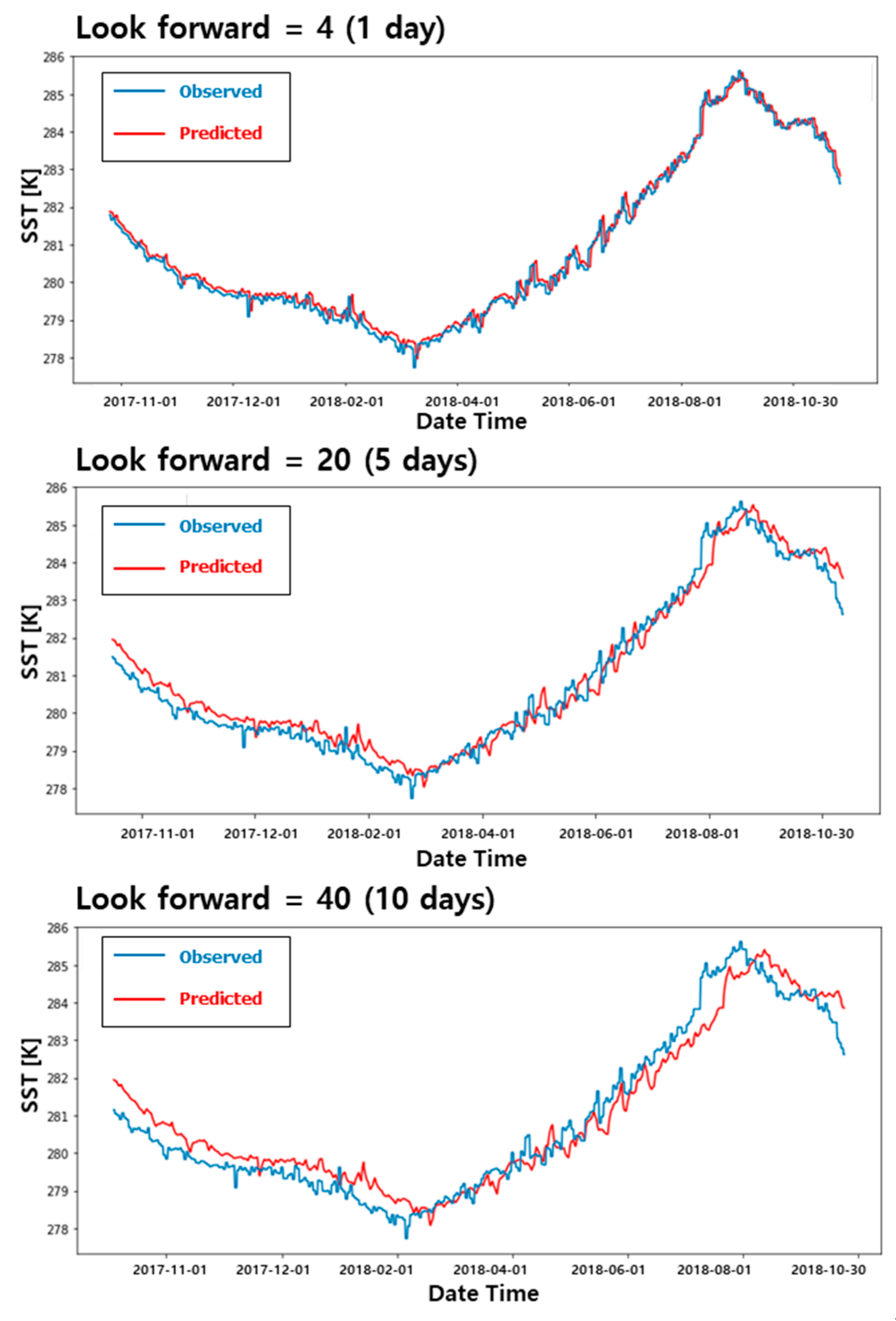
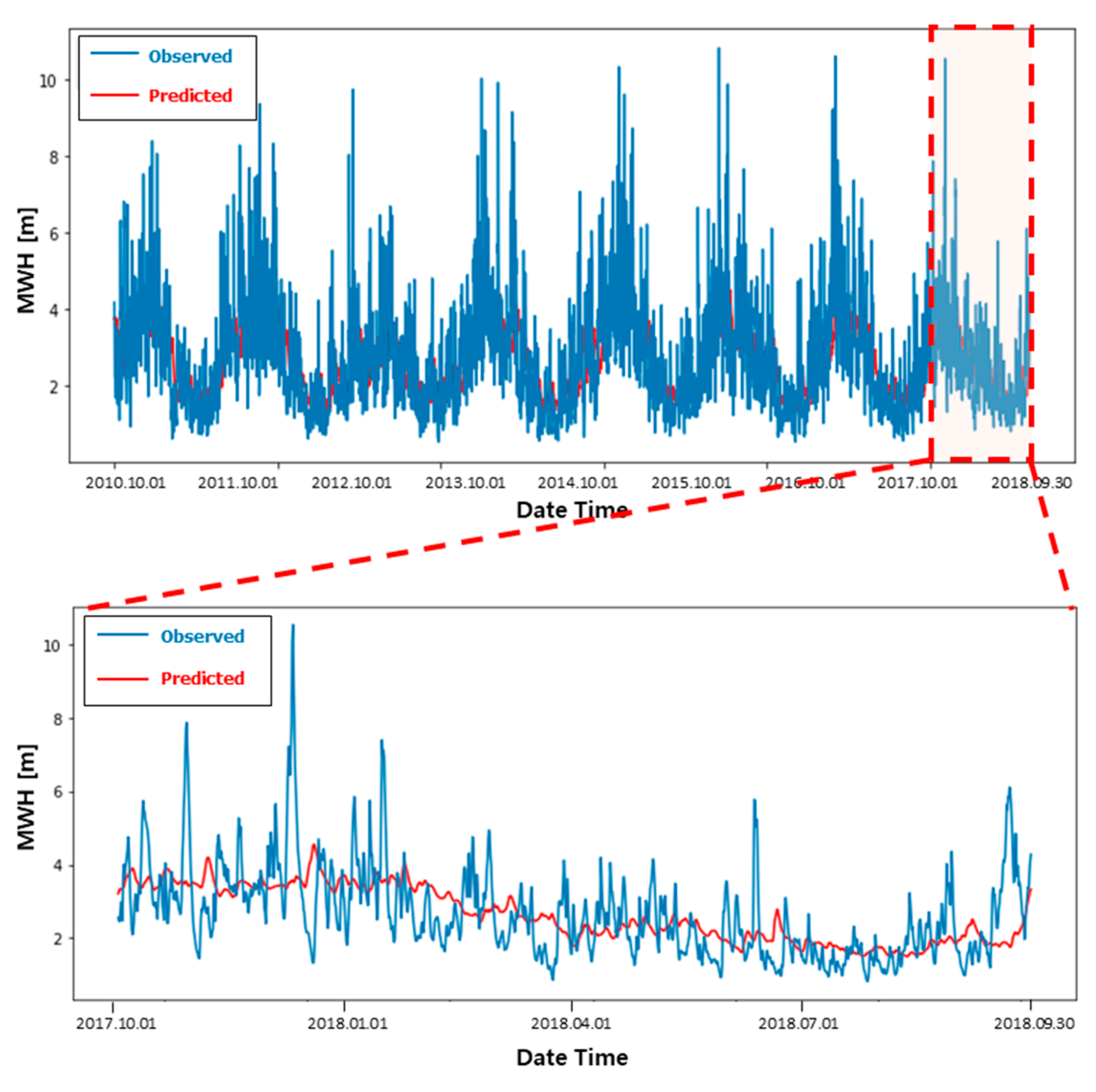
Figure 8 shows the results of SST predictions for the Yellow Sea in South Korea for approximately a year in 2018. It shows the difference in prediction results according to the look forward value. When the look forward value was set to 4, 1 day later, a little difference was found between the observed value and the predicted value. However, evidently, the predicted value is similar to the shape when the observed value graph is slightly shifted to the right. When the look forward value is increased to 20 (5 days) and 40 (10 days), the delay prediction result can be clearly confirmed. Notably, the look forward value increases, and the delay prediction problem of the prediction result becomes more pronounced. This occurs because, as explained in
Section 2.3, the learning model does not accurately grasp the data pattern because of the noise. As the look forward value increases, the farther the value to be predicted is from the current time when the prediction is made so that the current value can be scaled as it is and inferred as a prediction result. To address this problem, the noise should be removed by adding a denoising AutoEncoder to the ConvLSTM model.
To analyze the effect of using the denoising AutoEncoder, SST of South Korea’s Yellow Sea was selected as a prediction target, as in the previous example. A total of 8 years of data were used, and a training set of 6 years and a test set of 2 years were used. The data were only used for this section and are different from the data mentioned in
Section 4.1.
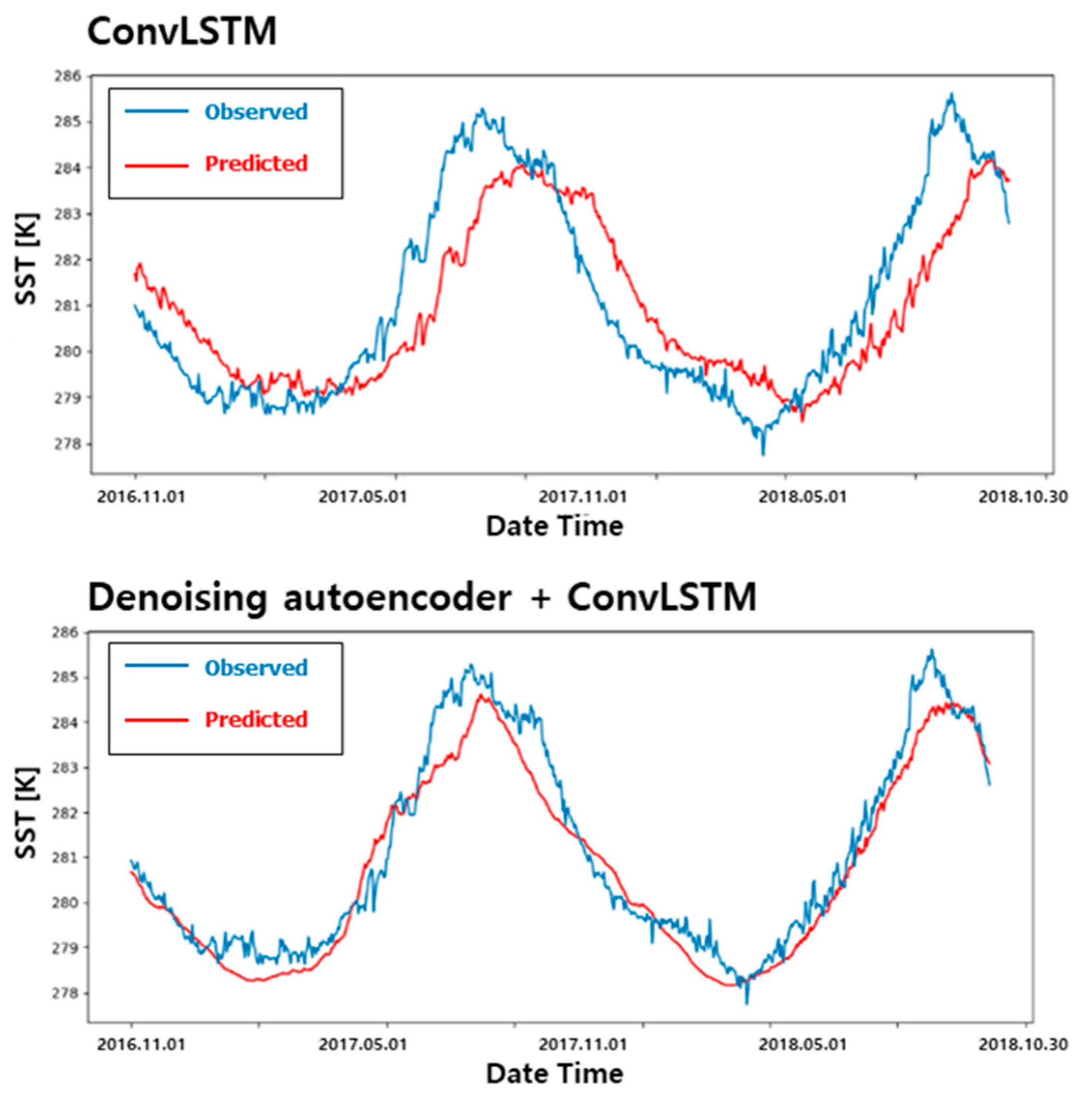
Figure 9 shows the result of SST prediction. The upper graph is the prediction result using only the ConvLSTM, and the lower graph is the prediction result using the denoising AutoEncoder as the input of the ConvLSTM model. In the test case, models predicting a month (30 days) from the present were trained and compared whether the delayed problem is clearly visible or not. The result shows the last 2 years (from November 2016 to October 2018) of the predicted range, which was not used for training. The two data used in
Figure 8 and
Figure 9 are the same. However, in
Figure 9, the graph was drawn using 2 years of data to show the effect of the denoising AutoEncoder clearly.
In
Figure 9, the result using only the ConvLSTM shows a significantly delayed predicted result, as in
Figure 8. The average error of the test set is 0.998 K, and when converted at a ratio according to the maximum and minimum value, it has an error of 10.97%. For the model using an additional denoising AutoEncoder, the delay prediction is clearly resolved. The average error of the test set is 0.474 K, showing an error of 5.26%. This is a 53% reduction in error compared with learning using the ConvLSTM alone, and as mentioned, the delay prediction problem has been solved. Therefore, in this study, a model combining a denoising AutoEncoder and the ConvLSTM was used to predict ocean weather.
4.3. Description of the Learning Models for Worldwide Data
The disadvantage of not using the ConvLSTM described in
Section 2.2 is that the characteristics of space and correlation between each parameter of ocean weather cannot be considered for learning. In addition, when using a conventional LSTM, an LSTM learning model must be created for each point where the prediction of ocean weather is desired.
Figure 10 predicts MWH using the ConvLSTM. A total of 8 years of data were used for learning, 6 years were used as a training set, 1 year was used as a validation set, and the last 1 year was used as a test set. A model for predicting MWH after 7 days was trained using a total of 30 days of data. The batch size was 128, the number of hidden layers was 1, and the total number of nodes in the hidden layer was 32. The study was performed for 40 epochs until the model converged sufficiently. The lower graph in
Figure 10 is an enlarged prediction result of the test set. The MAE of the test set was predicted relatively accurately at 0.78 m (4.8% error).
The conventional models of deep learning, such as DFN and LSTM, use data for specific locations to learn. Therefore, it is challenging to compare the ConvLSTM to DFN or LSTM directly. A large number of learning models are required to target worldwide data. Although the total number of models differs depending on how the resolution of the training model is set, 64,800 (= 180 × 360) models are needed worldwide to build a learning model for the ocean weather with resolutions of 1 degree in longitude and latitude. The recent increase in computing power has accelerated learning speed, but it takes considerable time to train 64,800 models. Therefore, in this study, the world was divided into 12 areas, and the proposed learning model was applied.
Figure 11 shows the 12 areas used in this study. Dividing the latitude from −67.5° to 67.5° into three equal parts and the longitude from −180° to 180° into four equal parts divided the world into 12 equal pieces.
The structure of the learning model is important. However, setting the input, output, and hyperparameters of the learning model has a significant influence also in the learning efficiency. Therefore, this study attempted to analyze its effects through case studies of various input and output changes. A total of 240, 90, and 84 input data (look back) were used. Since the time interval of the ocean weather is 6 h, if there are 240 input data, this indicates that 60 days of data are used as input. In the case of ocean weather, trends over time should be considered. Therefore, if possible, it is good to have a long look back period. However, lengthening the look back period infinitely is impossible because there are limitations on the computation power of memory. In this manner, we used six hours of data. Therefore, assuming 90 steps as a look back, and it means using 22.5 days of data as input. However, when the interval of data is set to 1 day, a total of 90 days of data can be used as a look back. The accuracy, according to the interval of the ocean weather, was also analyzed.
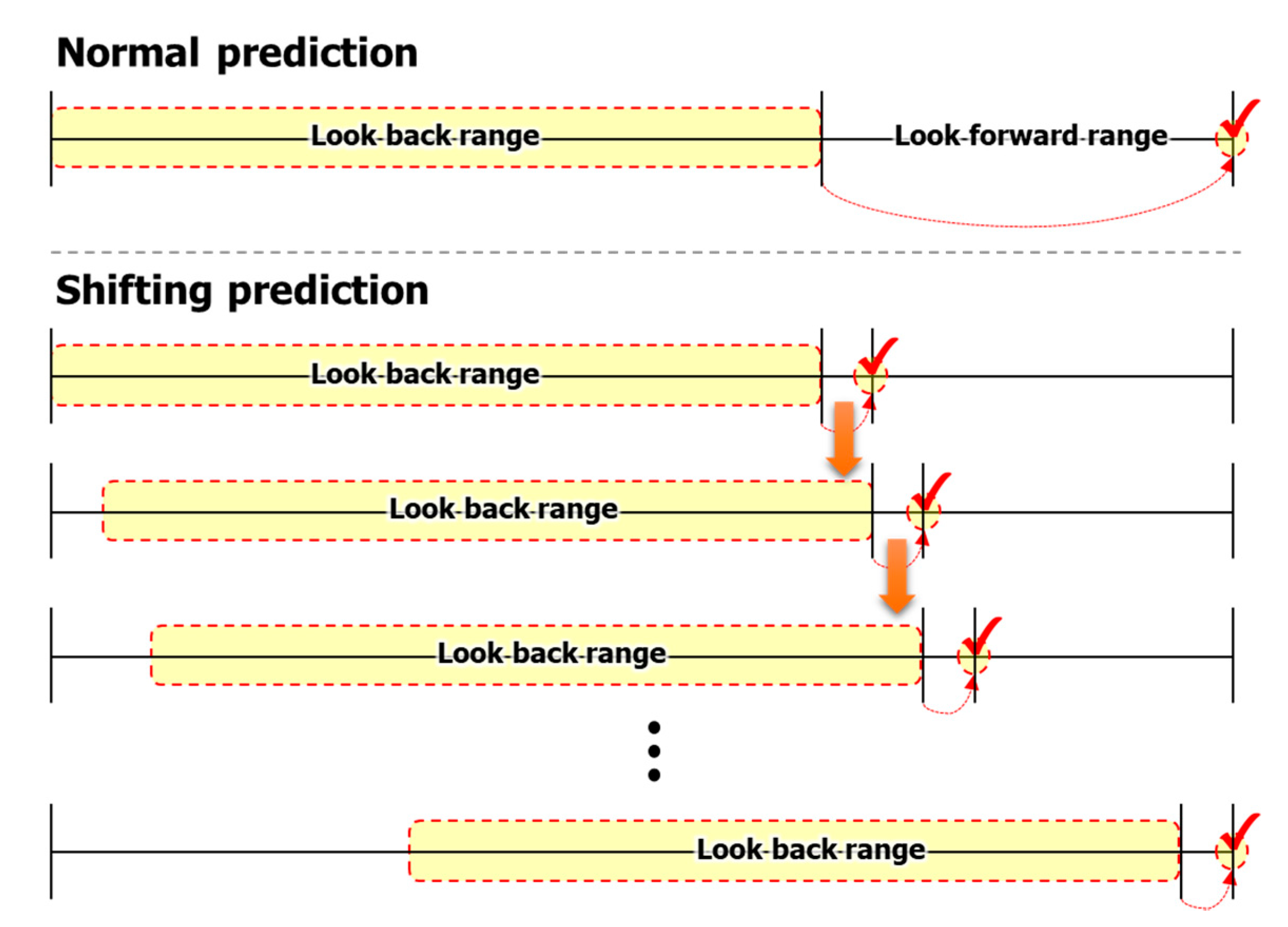
In the case of output data (look forward), it denotes at which point the ocean weather is predicted through the look back data. In general, as the prediction time interval from the input data decreases, the accuracy increases. For example, predicting 1 day after the present is more accurate than predicting 1 week later. In this study, the accuracy was analyzed by changing the look forward to 4, 8, 12, and 28 steps. The look forward is similar to the look back. If the data interval is 6 h, 4 steps means a day later. Similarly, if the weather data are on a daily basis, 4 steps means 4 days later. In addition, in the case of look forward, shifting prediction is possible.
The shifting prediction is a method of predicting a specific point and using the predicted data as an input to predict the following continuously. For example, if the learning model is trained as a model that predicts one step forward, it cannot predict after four steps. In this case, the result of predicting the first step forward can be used as input again to predict the second step forward. By repeating this process, we can predict 4 steps forward and even can predict 100 steps forward.
Figure 12 shows a comparison between normal prediction and shifting prediction. In the process of using deep learning models, we confirmed various studies on shifting prediction. Rasp et al. [
21] performed a similar approach and named it “iterative prediction”. If the satellite communication is lost, we cannot get nowcasting information. However, we can predict any days in the future from past data by generating our own prediction model. In addition, using shifting forecasting allows for predicting the far future as well; thus, we can make a long-term plan. In this study, the difference in accuracy between the two methods was analyzed.
As explained earlier, it takes a lot of time and effort to train models by dividing the world into 12 areas. Therefore, it is necessary to find the appropriate number of input data to shorten the training time and to achieve affordable prediction accuracy. The original data are in intervals of 6 h. However, by adjusting it to an interval of one day, we compared the accuracy of making predictions using data from a longer period as a look back. Finally, as explained in
Section 3.3, we compared and analyzed whether it is accurate to predict eight parameters of data with a single model and to divide the model through correlation analysis.
Table 4 shows the types of models trained in this study for comparison. Case 1 shows how much look back range could be accepted for the performance of the computer used in this study. Cases 3, 4, 5, 6, and 7 were compared to analyze the accuracy of the prediction model as the look forward increased. When predicting the same time, Cases 6 and 8 were used to determine whether it is correct to predict the time right or to make a shifting prediction. By comparing Cases 7 and 9, when predicting the same time, it was confirmed whether the prediction accuracy is maintained even if the number of data points for prediction is reduced. In Case 8, six channels (SST, MWH, MWP, MWD, WU, and WV) constituted a single learning model. In Case 9, a total of two models was trained. One is a prediction model that includes only one channel (SST), and the other is a prediction model that includes five channels (MWH, MWP, MWD, WU, and WV) to consider the correlation of each channel. The last two cases were selected to see which one was more accurate.
For accurate verification, K fold cross-validation is generally used, and training is performed commonly through a total of 10 fold cross-validation [
22]. However, since the model of this study takes about one week for training each model, it is difficult to perform all cross-validation at the laboratory level. Due to this limitation, the cross-validation was not implemented here.
4.4. Case Studies and Discussion
All accuracy for case studies was measured using “Area 4” out of the 12 areas shown in
Figure 11. The training time for computing varies depending on the look back range and the channel, but on average, it took approximately a week to train one model.
Table 5 shows the accuracy of 11 cases. Accuracy was covered for all areas, including land. Since the training was performed with the image data, some data that are not on the land, such as SST or MWH, are assumed to be 0, and an image is generated and used as input.
In general, as the look back range increases, so does the prediction accuracy. However, the longer the look back range, the more memory allocation is required exponentially to train the models. If it is assumed to train the model for one area, the input data becomes an image of ocean weather during the look back range. Following the look back range, the number of images required for training increased significantly. In addition, if we use images of multiple channels, the number of images required for training is multiplied by the number of channels. If a multi-channel image is used as the input for the model using the lock back range of Case 1, training is impossible due to a memory problem. That is, if training is performed with the computing specifications in
Table 3, training will not progress because of insufficient memory. Due to the limitation of computing power, it was determined that one channel was the maximum look back range for 240 steps in this study. In the case of Case 1, because training was performed with one channel of SST, there was not an insufficient memory issue. However, when training is conducted through one channel, the causality between each type of data cannot be considered. Therefore, to proceed with training in multiple channels, the look back range was reduced from the maximum allowed by the memory.
Cases 3–7 set the look back range to 22.5 days (90 steps) and performed training using six channels (SST, MWH, MWP, MWD, WU, and WV) of data. In Case 2, look forward was set to 6 h (1 step), and in Cases 4, 5, 6, and 7, training was performed after 1 day (4 steps), 2 days (8 steps), 3 days (12 steps), and 7 days (28 steps). When comparing the four cases, as the look forward increases, the prediction error also increases. The average errors of Cases 3–7 are 3.1%, 4.6%, 4.6%, 5.6%, and 5.1%, respectively. For accurate prediction, look forward should be small. However, the accuracy relatively remained over a range of look forward. In a typical prediction model for the ocean weather, the longer the forecast period, the higher the error, as shown in
Figure 13. However, as the results presented in this study, it can be seen that the error does not increase after a certain period. Unlike the general prediction model based on physical phenomena, the deep learning-based prediction model presented in this study is a data-driven prediction model. Therefore, even if the prediction period is lengthened, the error does not increase indefinitely by considering the periodic and seasonal characteristics of the data at the same time.
When the same time was predicted in Cases 6 and 8, we determined whether the normal prediction or the shifting prediction was more accurate. As shown in
Figure 12, shifting prediction is a method of predicting the next time point using the predicted data as input again and can easily predict the far future, regardless of the size of the look forward. Therefore, in this study, the accuracy of the two methods was compared through Cases 6 and 8. In Case 5, the look forward was set to 3 days (12 steps), and in Case 7, the result was predicted after 3 days by shifting; the model trained to predict after 6 h (1 step) was used. Cases 3 and 8 are the same learning model, but the error is much more significant when shifting prediction is performed. Case 5 showed an average error of 5.6%, but Case 7 showed a relatively high error of 10.0% because of the accumulation of errors during shifting. In Case 2, the SST and MWD errors were relatively high compared with the other data types. Since the errors accumulate and become more significant during shifting, in Case 7, SST and MWD are 23.1% and 18.3%, respectively, and the error was significantly increased compared with the other data types. By comparing the results of Cases 6 and 8, it can be observed that when predicting a relatively far future, it is more accurate to train the model as a normal prediction model than as a learning model for shifting prediction.
When the data at the same time were predicted in Cases 8 and 9, the data intervals used in the two models were different. Cases 8 and 9 used an interval of 1 day (originally, 4 steps). In this way, even if the same look forward was used, there was an advantage that prediction could be performed considering a longer period (longer look back range). Case 6 was a model that predicted 7 days later (look forward was 28 steps) using 22.5 days of data (look back range was 90). In Case 8, the look back range was also 90. However, because the interval of the data used for training was one, it was a model that predicts 7 days later using data from 90 days. Case 6 had an average error of 5.1%. In Case 8, the average error was 5.6%. When using the same look back range, it is more accurate to have a dense data interval. However, the difference in the error was not as large as it was in other comparisons.
In Cases 8 and 9, two models were compared in terms of accuracy. One was a learning model that consists of six channels of data in ECMWF, and the other one was a learning model where SST and five other parameters of data were divided into two models, as described in
Section 3.3. The error of Case 8 was 5.6%, and the error of Case 9 was similar to that of Case 6, with an error of 5.1%. By comparing Cases 8 and 9, it was confirmed that it is more accurate to separate the model considering the causality. Therefore, this study consists of three models for predicting ocean weather. One was a single model of SST, and one was for the five remaining ECMWF data (MWH, MWP, MWD, WU, and WV). The last one was a model for HYCOM data (CU and CV).
Actually, it is hard to directly compare the accuracy of the model in this study with that of the general prediction model provided by weather centers. To compare the accuracy between them, the ocean weather data up to now should be obtained, and the proposed model should be generated using those data. However, ECMWF and HYCOM provide only data from several months ago; hence, it is difficult to obtain the data for generating the model at a specific point in time. In addition, even for predictions at a specific point in the past, they only provide actual data from the past, not data of how they predicted the weather at that time (i.e., past forecast data).
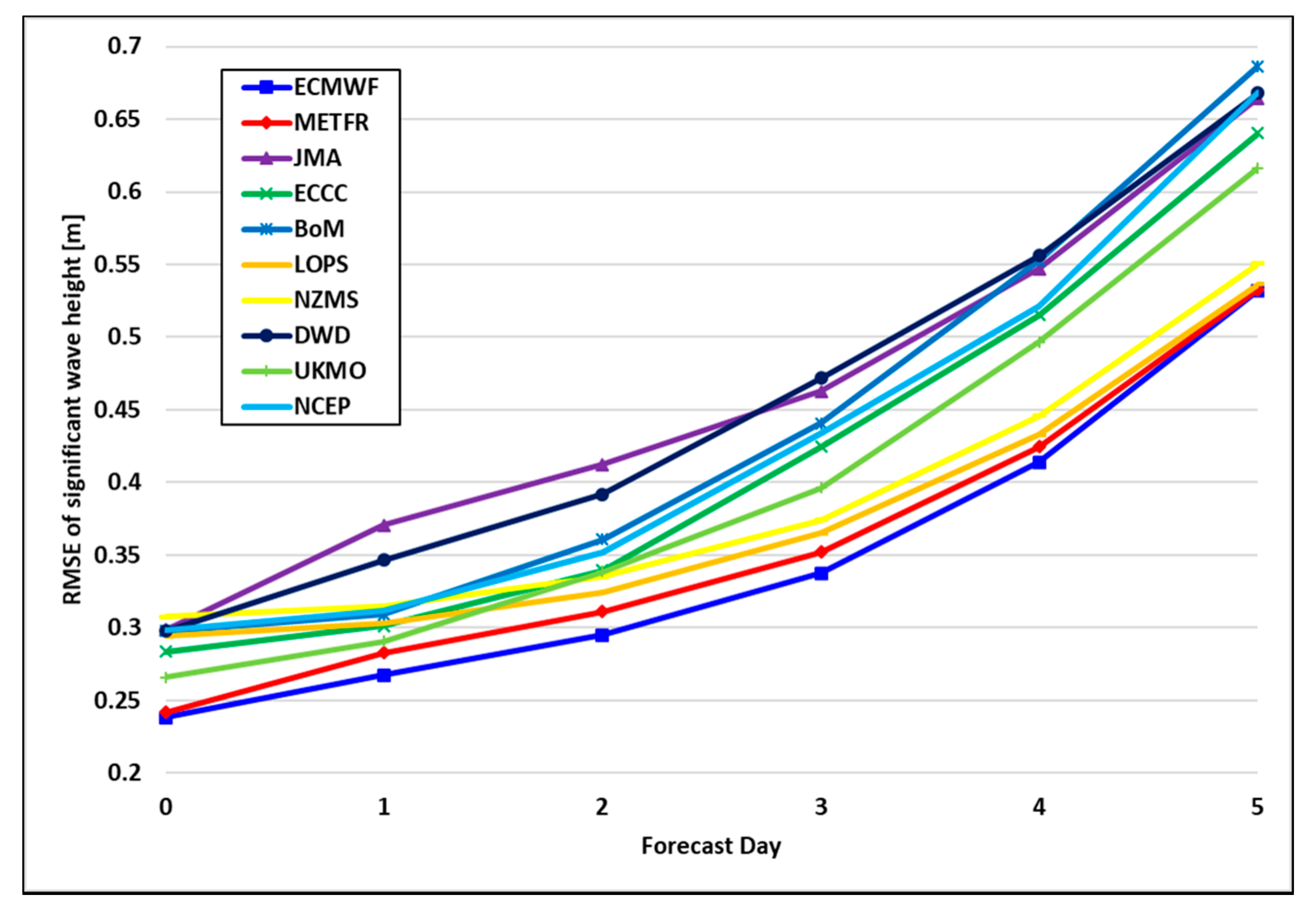
However, for indirect comparison, three parameters of verification data for the ocean weather (significant wave height (SWH), peak wave period (PWP), and wind speed (WS)) provided by the Weather Meteorological Organization (WMO) and ECMWF (2020) were additionally investigated. According to the verification data, it can be seen that the error rate accumulates and increases as the forecast period increases in the prediction models of weather centers. A total of ten organizations surveyed by the WMO compared the result of error between predicted ocean weather after three days and the actual value. The error of SWH is about 0.3–0.5 m, PWP is about 2.0–2.6 s, and WS is about 2.7–3.4 m/s, respectively.
Figure 13 shows the RMSE of SWH presented in WMO and ECMWF [
23]. In this study, the results of predicting the ocean weather after three days using the proposed model were presented in
Section 4.4 (Case 5). As a result of predicting the ocean weather after three days using the proposed method in Case 5, the error was 0.22 m for MWH, 0.48 s for MWP, 2.46 m/s for WU, and 2.24 m/s for WV, respectively. It can be seen that it shows a similar error rate presented by WMO and ECMWF (2020). Therefore, if there is no experience to make a numerical prediction model for the ocean weather, the proposed method is expected to be helpful.
4.5. Prediction Results of Worldwide Ocean Weather
We proposed a learning model for predicting ocean weather using the ConvLSTM model and denoising AutoEncoder. In addition, through the case studies in
Section 4.4, the accuracy of the learning models according to various look back and look forward ranges was compared and analyzed. Based on the comparison, the model used in Case 9 was applied to training the models worldwide. As described in
Section 3.2, the eight parameters of data used in this study consist of data that have 6-h intervals and spatial intervals of 0.75° in longitude and latitude. If the 0.75° interval data are used for one region shown in
Figure 11, an image size of 120 × 30 pixels should be applied. This induced practical difficulty in training because of the specifications of
Table 3 in terms of memory. Therefore, data were organized at intervals of 1.5° in longitude and latitude. Finally, training was performed using an image of 60 × 30 pixels per area.
In addition, as described in
Section 4.4, three models per area in the 12 areas were used for prediction, and 36 prediction models were used to predict the ocean weather worldwide. In the case of look back, 84 days of data (12 weeks) was used, and a model for predicting after 7 days was constructed.
Table 6 shows the prediction accuracy for the eight parameters of ocean weather in the 12 areas.
In
Table 6, the area with the lowest error is shown in blue, and the area with the highest error is shown in red, for each parameter of ocean weather. In addition, the area with the lowest average error was marked with blue shade, and the area with the highest error was marked with a red shade. The average error for the eight parameters of data worldwide was 6.7%, and the results were quite different in each area, ranging from 4.1% to 9.7%. When comparing the error rates for each area, it can be seen that Areas 1, 3, 4, and 6 have higher average errors than the other areas. This is because it is challenging to consider spatial influences in learning because the land is included in these areas. However, in Areas 10 and 11, the error rate is significantly higher than in other areas, even though these areas contain little land. This is because, despite the fact that the area includes a large ocean area, the ocean weather varied so much that the learning model could not grasp the pattern correctly.
By analyzing the error rate for each type of data, the error rate of the current is significantly lower than that of the other types. In this study, the HYCOM data were used for training the CU and CV, and the data range was relatively short (4.4 years data) compared with the ECMWF data. However, the error rate was low compared with the other types of data. It was expected to be easy for the learning model to grasp the pattern because the current is relatively small, and there is little change compared with the other data. Conversely, in the case of MWD, the error rate was significantly higher than that of other data, which may have occurred because the fluctuation range is very severe and there is no periodicity relative to the other types of data.