Abstract
Scour induced by currents is one of the main causes of the bridge failure in rivers. Fundamental knowledge and mechanisms on scour processes due to currents are often taken as a basis for scour studies, which are the focus of this review. Scour development induced by waves and in combined wave–current conditions are also briefly discussed. For the design of structure foundations, the maximum scour depths need to be estimated. The mechanisms of local scour and predictions of maximum local scour depths have been studied extensively for many years. Despite the complexity of the scour process, a lot of satisfying results and progresses have been achieved by many investigators. In order to get a comprehensive review of local scour for vertical piles, major progresses made by researchers are summarized in this review. In particular, maximum scour depth influencing factors including flow intensity, sediments, pile parameters and time are analyzed with experimental data. A few empirical equations referring to temporary scour depth and maximum scour depth were classified with their expressing forms. Finally, conclusions and future research directions are addressed.
1. Introduction
In river hydraulics, bridge failures due to local scour occurred frequently. In the U.S., a large amount of bridges are vulnerable to scour, and many of them are being scoured critically. More than 1000 bridges in the United States have failed, with 60% of those failures being due to local scour [1]. 40% of failed bridges in China are due to local scour between 2007 and 2015 [2]. Ettema [3] stated that scour damage to pile foundations, especially for bridges over small rivers, is still an important issue in bridge safety. Meanwhile, in the new field areas of offshore oil and gas engineering, submerged structures such as caissons, platform foundations, local scour cannot be neglected either [4].
Local scour around vertical piles in steady currents have been studied for a long time. It was divided into clear-water scour and live-bed scour by Chabert and Engeldinger [5]. When the critical velocity associated to the sediments is smaller than the approach velocity, the whole bed scours. Local scour is in live-bed scour condition. On the contrary, clear-water scouring refers to the absence of sediment in the incoming stream. The advances in hydrodynamic theory, sediment transport theory, experimental measurement techniques and the numerical simulations have promoted deeper understandings of the mechanisms of local scour. The process of flow passed a pile is a complex three dimensional phenomenon [6,7], as is shown in Figure 1. When the flow passes a vertical pile, it is blocked and the flow velocity will decrease to zero on the upstream face of the pile. This causes an increased pressure on the pile face and a pressure gradient that opposes flow direction. In the far field, the flow is assumed to have a logarithmic vertical profile [4], velocity together with pressure on the pile face decreases from flow surface to bed. The pressure gradient along the stagnation line (x/D = –0.5, y/D = –0.5 in Figure 1) will cause a downward flow, and create a scour hole immediately. As a result, the bed boundary layers of the flow surface separate along the bed in three dimensions, leading to forming horseshoe vortexes (Figure 1). The separated boundary layer then forms spiral vortices near the pile, which will be carried downstream by the current. The overall effect of these changes is generally to increase the local sediment transport in the case of an erodible bed, resulting in a local scour around the pile [6].
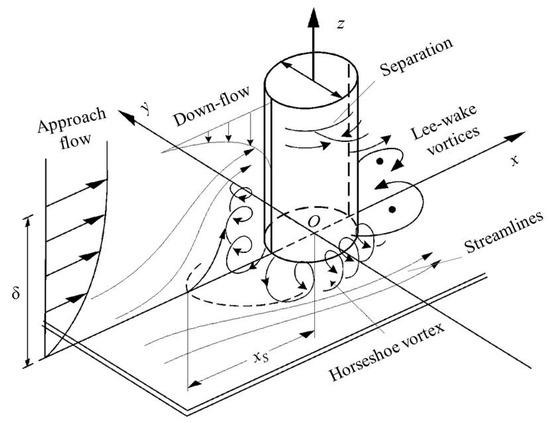
Figure 1.
Brief sketch of the local scour mechanisms (adapted from Roulund et al. [6], with permission from Journal of Fluid Mechanics, 2005). δ is boundary layer thickness, is the size of horseshoe vortex.
Large amounts of studies have been conducted to study the local scour regime [3,4,5,6,7,8,9]. By using an acoustic Doppler velocity meter (Micro-ADV) in three-dimensional analysis of bursting process, for instance, Keshavarzi et al. [7] predicted the transition probabilities, occurrence probabilities and directions of sediment particles movements. Moreover, [6,10,11] studied the shear stress under a horseshoe vortex in rigid beds, finding that the bed shear stress changed to more than 1.5 times larger than the undisturbed bed shear stress. Again, with a high-resolution two-dimensional particle image velocimetry (2D PIV) system, Guan et al. [12] found that the horseshoe vortex, which was along the upstream scour slope of the developing scour hole, evolved from one initial small vortex to a main large vortex, a small vortex upstream of the main vortex and a small junction vortex. Relationships between the scour hole and the horseshoe vortex have been observed, which indicated that both the strength and the size of the main vortex increased with the increasing scour hole. Mattioli et al. [13] used particle tracking velocimetry tracked the sediments particles and concluded that the downstream clockwise vortices and the upstream anticlockwise vortices influence sediments particles significantly on stirring them up. These findings have complemented the mechanisms of local scour from [14,15], who ignored the importance of vortex structure in local scour. Manes and Brocchini [16] examined the experimental and numerical results from [17,18] and found that the scour hole bottom around the point of the maximum scour depth is consistently flat. With the Kolmogorov’s theory of turbulence [19,20], Manes and Brocchini [16] derived the interactions between large-scale and small-scale eddies impinging the scour hole surface. More recently, Li et al. [21] used a 2D PIV system to study the relationships between turbulence horseshoe vortex and shear stress around the piles. The instantaneous bed shear stress was found to be directly associated with the dynamics of the turbulence horseshoe vortex. Sediments transport rate based on the mean shear stress could be underestimated as much as 70% compared to the instantaneous shear stress in clear-water scour conditions. The contracted streamlines around the pile were also thought to play an important role in local scour [6]. Zhao et al. [15] observed that local scour always began at the side edges of the pile in clear-water scour conditions. This phenomenon was attributed to the concentrated streamlines [6,22]. Baker [10] found that the contracted streamlines at the side edges of the pile amplified the shear stress five to 11 times larger than that of upstream approach flow. When sediments were transported from upstream of the pile, vortices shedding were believed to transport them downstream [14]. Dargahi [23] found the wake scouring was caused by the primary wake vortices and concentrated streamlines. The upstream and wake scouring interactions are accomplished by the action of the three dimensional horseshoe vortexes, according to [23].
While the scouring process in currents is mainly induced
by the horseshoe vortex, scour processes in waves have been observed to be more affected by vortex shedding at the lee side of the pile [14,24,25,26], particularly for small Keulegan–Carpenter (KC) numbers. Sumer and Fredsøe [14] summarized the results from former studies and found that apart from the influencing factors in currents, the KC number (, is the maximum value of the undisturbed orbital velocity at the bed, D is the cylinder diameter and is the wave period) affects the local scour most in waves. If KC is less than 6, no horseshoe vortex would be formed in front of the cylindrical pile (For square piles the value is 4). Sumer and Fredsøe [14] has also derived an empirically driven prediction approach for combined wave-current conditions. Rudolph and Bos [27] have performed laboratory tests on the scour development at monopiles under combined wave-current conditions in low KC numbers. In addition, Qi and Gao [28] carried out physical model tests on the scour development in combined wave-current conditions with small KC numbers and included the assessment of the influence of pore pressure on the scour process. Zanke et al. [29] have developed an empirically based prediction approach by introducing a new function between the wave and current generated scour at a singular pile.
Based on these laws, Miozzi et al. [30] conducted an experimental test with KC = 10. By using the defocusing digital PIV technique, the dynamic equilibrium scouring state was described by a Eulerian in-phase analysis of the sand particle motion, which was inferred from Lagrangian data collected over a large number of wave passages. The five main mobilization or transport mechanisms identified by [30] are the (i) generation of a coherent structure reminiscent of a horseshoe vortex at the toe, (ii) intense scouring at the top of the flatbed region, (iii) vortex shedding in the wake during onshore flow, (iv) shear crossflow on the lee-side of the cylinder and (v) large vertical shearing in the flatbed region during the offshore flow. Within the phases of wt = 0–48°, sediments particles were lift up by the horseshoe vortex in front of the pile. An intense acceleration of the flow that interacted strongly with the bed at the rear side pile was observed. Within the phases of wt = 96–136°, the reverse flow that started from downstream of the pile interacted with the onshore flow, resulting in shear crossflow on the lee-side of the cylinder, would lead to the backfilling of the sediments around the rear side of the pile. Sediments would be mobilized towards upstream once the velocity of whole water space was offshore direction. The general backfilling mechanism and timescale in case of combined waves and current conditions was investigated by Sumer et al. [31].
In the backfilling studies, Sumer et al. [25] conducted experimental tests upon equilibrium scour holes. When KC was smaller than 10, the time for backfilling was far more than scouring time. When KC was larger than 10, the backfilling time was less than scouring time. Apparently, when waves are imposed in local scour, the phases governing velocity periodic oscillation at bed bottom makes it different from the currents cases only.
Laws for flow field around the pile, including velocity and pressure distributions in three dimensions, characteristics of horseshoe vortex and vortices shedding, boundary layer and shear stress near the bed were successfully obtained by scholars [6,10,17,21,23]. The transportation of a single sediment particle was traced in detail [30,32,33], which contributed to the calculation of the sediment transport rate. In a project design for scouring protection, the most concerned is the maximum scour depth, so numerous researchers have studied the factors that influence scour depths. As a result, many semi-empirical and empirical formulas for sediment transportation of local scour have been established [16,34,35,36,37,38,39,40].
The paper does not study the new findings of recent work from the authors, but mainly reviews the mechanisms, influencing factors and empirical equations in literature. Investigations and laws of local scour were adopted and analyzed, especially in flow intensity, sediments particles diameters and sediments uniformity, pile widths and heights, depth of water and scouring time that affect the maximum local scour depths. Temporary and equilibrium scour depth equations proposed in literature are also reviewed. A best method of scouring time for scouring equilibrium is obtained by comparing these definitions in equilibrium scour time. The empirical equations are summarized and classified into four expressing forms.
2. Influencing Factors
Reference [14] summarized that the local scour was mainly influenced by the Shields number, sediment gradation, ratio of boundary layer thickness to pile diameter, ratio of sediment diameter to pile diameter, geometric parameters of pile, approach flow velocity and its attacking angle and scour time. That means the flow intensity, water depth, sediment size and its gradation, geometric parameters of pile and time control the scour process and the scour depth. Due to these influencing factors, local scour is a complexed process and is very difficult to study. However, laws could still be obtained when some conditions are restrained. This paper reviewed and studied conditions of steady currents, circular and square cross vertical piles, non-cohesive sediments and perpendicular flow angle attacks.
2.1. Intensity of Flow
Flow intensity is a parameter affecting scour depth, which is widely used in most published papers [15,41,42]. It is defined as the ratio of the average approach flow velocity U to critical average velocity for the onset of a sediment particle motion . The critical average velocity is calculated by Equation (1)
where the critical shear velocity is determined using the Shields diagram; h is the water depth and is the medium sediments diameter.
The flow intensity is also a criterion for determining whether a sediment particle is activated. When is smaller than 1 in uniform sediments bed conditions, no sediment particles are activated, and the local scour hole does not have sediment supplement from upstream. For uniform sediment materials, live-bed scour occurs when is larger than 1. However, for non-uniform sediment, scour conditions are controlled by the limiting armoring velocity . In this sense, clear-water scour and live-bed scour exist for and separately [41].
The authors collected a number of experimental data from literature as is seen in Table 1. As is seen in Figure 2a, the maximum local scour depth occurs at in uniform sediments conditions, and decreases within a period of increasing . This phenomenon is easy to understand. When is smaller than 1, the bed is under clear-water scour condition. Sediments at upstream cannot be mobilized by the currents. No sediment will be transported into the scour hole around the pile. Scour depth will be deeper when the flow intensity is higher, leading to an almost linearly relationship between and relative scour depth before the first threshold peak. When surpasses 1 in uniform sediments, the bed is under live-bed scour condition. With flow intensity increasing, the relative scour depth decreases to a minimum value. After that, it increases to the second peak, which is called live-bed peak (Figure 2a). Aksoy et al. [43] obtained this threshold of flow intensity , and thought this peak occurred at about the transition flat bed stage of sediments transport on the bed. The authors collected a number of experimental data from literature and drew envelope curves, as is presented in Figure 2b. When the flow intensity is less than 1, scour depth increased rapidly with flow intensity. In relatively weak live-bed scour conditions (), the quantity of sediment particles that transported into the scour hole is larger than that moved out of the scour hole. When the flow intensity surpasses 2.1, the envelope curve is found to be horizontal. What is more, the former increases faster than the latter. As a result, the maximum scour depth decreases. However, when the flow intensity gets strong enough, the quantity of sediment particles in the scour hole will be moved out more than that of supplements from upstream, leading to scour depth to the live-bed peak.

Table 1.
Range of experimental data.
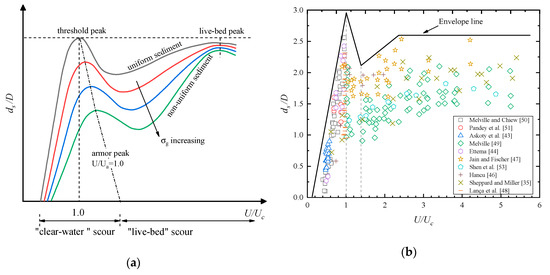
Figure 2.
Relative local scour depth variations with flow intensity. (a) Reproduced from Melville [44], with permission from Fourth International Conference on Scour and Erosion, 2008. (b) Experimental data from literature.
When it comes to non-uniform sediment, the armor layer will take part in. Baker [56] observed that the maximum local scour depths occurred at . Raudkivi and Ettema [57] found the armoring effects affected local scour in two different types. One was bed armoring, which was responsible for bed forms. The other was scour hole armoring, which would reduce the local scour depth. For the difference between the armor layers in the scour hole and on a streambed, Raudkivi and Ettema [57] pointed that the former did not have significant fines. The maximum scour depths would not be affected when the gradation coefficient of the sediments was less than 2.0. However, different conclusions were obtained from Melville [44]. Figure 2a presents the experimental conclusions made by Melville [44]. The for green line is about 5. It could be seen that increased with the increasing for a given . Apparently, Melville [44] has a higher credibility. The increasing leaded to a decreasing of threshold peak. Figure 2a is also significant for the influences of sediments. It will be mentioned later in this paper.
2.2. Flow Depth
As velocity distributions along flow depth are not a constant value, flow depth will have an influence on the onset of the sediment particles. However, for a given value of the ratio of approach flow friction velocity to critical shear velocity for sediment particles , it is identical that the scour depth will not increase with flow depth when it gets to a threshold value. To explain this phenomenon, early researchers have done a series of experiments to study it. Among them, the analysis from Ettema et al. [46] is most popular. The influence of flow depth h on scour depth ds depended on the relative size of the pile h/D and the relative medium sediments diameter . When is less than 2, the volume of down-flow diverted into the scour hole diminished. When is larger than 3, the interactions between anti-clockwise damming near the water surface and the horseshoe vortex in clockwise will fade to zero. As a result, the horseshoe vortex can act on sediment scour completely. When is below 1, a nearly to the water surface height bar will be formed behind the pile, which will weaken the strength of wake vortex. For the influence of , Raudkivi and Ettema [57] came to the conclusion that the scour depth was independent with when was in high values. However, the scour depth did not seem to stop increasing with for a given value of .
Researches on the relationships between flow depth and scour depth have shown the complexity in their interactions. However, based on experimental or field data, some laws were obtained by researchers. Hjorth [11] found that when the flow depth was shallower than some undetermined multiple of the boundary roughness, the strength of the horseshoe vortex increased with flow depth. Baker [56] found this increase stopped when the relative flow depth was 4. Similarly, Baykal [42] obtained by analyzing experimental data from former researchers. Later, [45] divided h/D into regions of narrow pile (), wide pile () and intermediate wide pile (). Melville and Chiew [51] stated that the scour depth was independent with flow depth in narrow pile cases, but increased with flow depth in wide conditions. For intermediate wide piles, scour depths were between them. When the flow surface was blocked by a pile, an anti-clockwise damming would interact with the clockwise horseshoe vortex. However, the interaction will fade to zero when the water depth is deep enough ().
A large number of experimental data have been given by researchers (Table 1). Among the conclusions obtained by these researchers, Melville [50] obtained for independence of through their own experimental data as well as data from Sheppard et al. [53]. To investigate the relationships between and , data was used from Table 1 and presented in Figure 3a,b. For a safe design, the envelope line presented in Figure 3a was recommended. Although more data for deeper flow experiments needs to be studied, the envelope line tends to be a constant value when is larger than 4. When the experimental data was kept for the same conditions except the water depths, a trend was clearly seen in Figure 3b. The test numbers in Figure 3b were numbers where [46,47,50] numbered in their own tests. By collecting these experimental data, the authors found that the relative scour depths increased with the increasing relative water depth until to their own thresholds. Apparently, due to their differential experimental parameters, the threshold values of vary with the researchers. The results of Ettema et al. [46], who obtained the critical value , are consistent with the envelope line in Figure 3a. The others were a little larger or smaller than [39], but were nearby . By analyzing a large number of field data and laboratory data, Park et al. [58] stated that the laboratory data were more dependent on the flow depth than the field data. With flow depth increased, scour depths in laboratory tended to overestimate more than that of the field data.
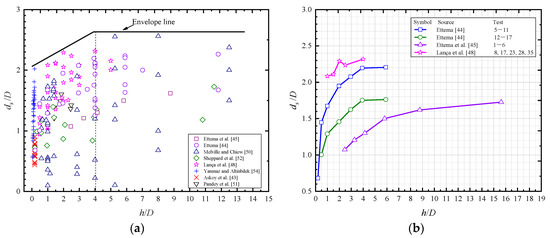
Figure 3.
Relationships of water depth with maximum scour depth. (a) Envelope line of maximum scour depth. (b) Trends of the water depth with maximum scour depth.
2.3. Sediments
Effect of bed materials on local scour depths has been a subject of research for many years. It is logical that the equilibrium scour depth depends on the size of bed materials. As sediments are mostly non-uniform in the field, studies of influences on local scour depths about the sediments gradation are necessary. The sediment gradation is characterized by geometric standard deviation of sediment grain size , and could be calculated in ways of . Some researchers have distinguished the uniform sediment with σg. Dey [59] classified the sediment material into uniform sediment () and non-uniform sediment (). Hoffmans [60] defined as uniform sediment, and stated that sediments non-uniformity was about 1.8 in natural rivers. Researchers found that the scouring rate and scour depth decreased significantly with increased [61,62,63]. Chiew and Melville [62], for an example, observed that the finer particles would be armored by coarse particles both on the upstream bed and at the scour hole. The scour depth decreased with when was less than 5. In accord with Figure 2a,b, Zanke et al. [29] obtained that the scour depth rarely depended on the sediments non-uniformity in high flow intensity cases. As is shown in Figure 2a, relative scour depths were almost the same when flow intensity surpassed 4, though the sediment non-uniformity σg were different. In non-uniform sediments, flow intensity was determined as the ratio of approach flow velocity U to the armoring velocity . The armoring effects were found to increase with by Melville [64]. For this reason, the first threshold peaks (Figure 2a) tended to decrease with the increasing .
As many physical variables such as flow velocity, shear stress and sediments transport rate are depicted in average, the sediment medium size is widely used as a character in scour and deposition. Melville and Chiew [51] stated that when was finer than about 0.6–0.7, ripples would be formed when the sediments bed was scoured. Then the movement of sediments particles would be affected significantly by the ripples. Later, the relationships between ripples and relative scour depths were obtained by Melville [64]. As is shown in Figure 4, thresholds values of local scour depths occurred in the two curves when flow intensity increased to 1. However, the maximum scour depth for non-ripple forming bed is larger than that of ripple forming. However, when flow intensity surpasses 1, a drop of the maximum scour depth happens in live-bed scour conditions. This is due to the fact that sediments were transported to the scour hole from upstream of the pile just as described in the analysis of flow intensity above. The similar trend was found in Ettema et al. [46], who concluded the maximum scour depth was 0.3–2.3D, depending on the distributions of the sediment sizes. Chiew and Melville [62] argued that the formed ripples on bed were responsible for these variations. Ripples made bed more roughness and increased quantity of sediments particles transported from upstream, resulting that more sediments particles were transported into scour hole around the pile.
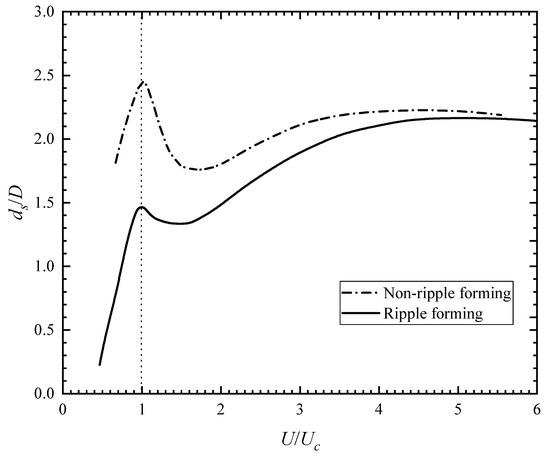
Figure 4.
Influence of ripples on maximum scour depth (Adapted from Melville [64], with permission from Journal of Hydraulic Engineering, 1997).
The influences of sediment medium size d50 on scour depths have been developed to a deeper understanding. In early years, many researchers believed that the relative scour depth increased with the increase of relative medium sediments diameter when was smaller than 25–50. When it surpassed 50, would be independent with . Nevertheless, with relatively larger flume experiments and long-time scouring, Sheppard et al. [53] put forward a different view for cases. As is shown in Figure 5, ds/D decreased with D/d50 increased. Later, a similar trend was found by Lee and Sturm [65]. However, what differs from Sheppard et al. [53] is that when , is independent on it.
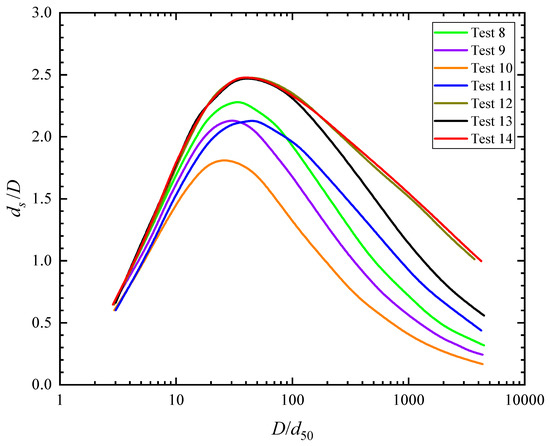
Figure 5.
Dependence of ds/D on D/d50 (Adapted from Sheppard et al. [53], with permission from Journal of Hydraulic Engineering, 2004).
2.4. Pile
There are many shapes of piles used in engineering, and their effects on the scour are significant. In this paper, only the most popular piles of vertical circular piles and rectangular piles are presented. For unsubmerged piles, their widths have been reviewed and discussed in terms of relative flow depth and sediment size. As is depicted in Figure 6a, scour depth increases with pile diameter. The wider the pile is, the more significantly it blocks the approach flow, and thus forming a deeper scour hole in vicinity of the pile Sarkar et al. [66]. However, when the scour depth is normalized with pile width, it decreases. This trend can also be viewed as the rate of scour depth with pile width. Sooner or later, the rate will tend to be zero, and thus a threshold of scour depth for independence on pile width will be obtained. For the influence of pile height (Figure 6b), it is similar with flow depth effect when the pile is unsubmerged. In the submerged conditions, scour depth increases with pile height when the other factors are kept the same.
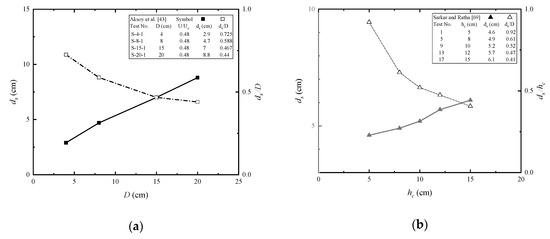
Figure 6.
Influence of pile width and height on scour depth. (a) Influence of pile width on scour depth. (b) Influence of pile height on scour depth (submerged).
A few researchers such as Roulund et al. [6] and Sumer and Fredsøe [14] stated that the height to diameter ratio and submergence ratio h/hc affected the relative scour depth significantly. This section focused on the submerged pile characterized in height to diameter ratio and submergence ratio . Although, these were not studied as early as those reviewed above, some progressive results were obtained by a few scholars. Table 2 is submerged experimental data collected from the literature. Except for data from Zhao et al. [15], they are all in clear-water scour conditions. To depict the experimental data concisely, tests numbers in Table 2 were numbered with their own tests numbers.

Table 2.
Submerged experimental data.
Figure 7 was drawn with data chosen from Table 2, each of which was controlled with its same sediment characters , , flow intensity , water depth h and scour time t. It can be seen that the dimensionless scour depth increases with the relative pile height hc/D when is smaller than 3–4. Except the diamond data from Zhao et al. [15], which was in live-bed scour condition and fitted with a blue line, there is not a curve reflecting the independence of for . Zhao et al. [15] found the maximum scour depth was independent with when was larger than about 2. The vortices shedding behind the pile was weakened when the height of the pile was small. No scour was seen behind the edge of the pile when was smaller than 0.25. With numerical simulations methods, Zhao et al. [15] obtained shear stress around the pile, and found a significant decrease in smaller value of .
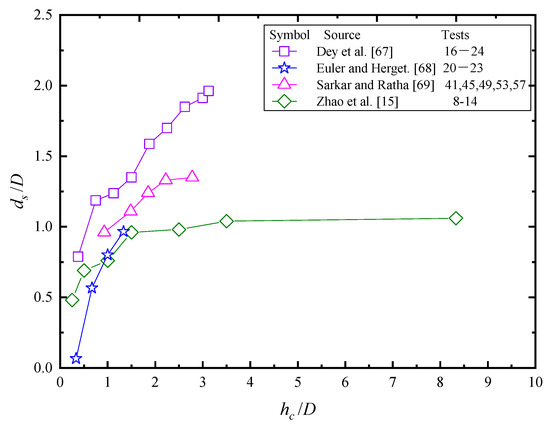
Figure 7.
Influence of pile width on scour depth.
The relationships between h/hc and ds/D for submerged cases are also investigated by a few researchers. According to Hunt et al. [1] and Tsutsui [70], there was a reverse flow and a separation bubble on the top of the pile instead of the anti-clockwise damming in front of the pile when the pile was submerged. The additional water down wash flowed on the side and behind the pile. Consequently, local scour for submerged piles or structures needs to be studied too. However, as far as the authors are aware, local scour researches in submerged vertical piles were only seen in [4,15,67,68,69,71]. Among them, influences of flow depth studies were even fewer. Dey et al. [67] observed that an increase in h/hc would reduce the block of flow, and thus the horseshoe vortex was weakened in strength and dimension. They also pointed out that the downward pressure gradient for the submerged pile was less than that of the unsubmerged pile. In addition, the interaction between the free surface and the wake region behind the pile was analyzed by Sarkar and Ratha [69]. They found that free surface was not seen to interact with the wake region when 2.3 < h/hc < 3. However, for h/hc < 2.3, upper layer mixes with wake and intensity increases with Froude number, resulting in a weakened vortices shedding behind the pile. For experimental data in Figure 8, the relative scour depth ds/D decreased rapidly with the increasing submergence of the pile h/hc, especially for clear-water conditions [67,68,69]. It does not seem to stop at some value of h/hc as data of [15].
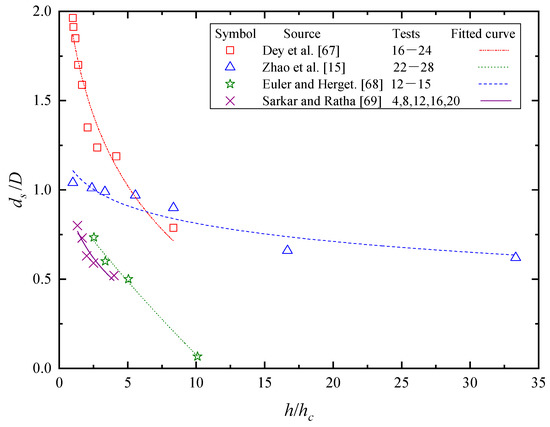
Figure 8.
Influence of pile height on scour depth.
It is no doubt that local scour is a complicated process depended on a series of factors including intensity of water, water depth, sediments and pile parameters. To value the influences of each parameter, researchers analyzed them in different ways. Muller [72] used partial residuals and multiple linear regressions to identify the key variables influencing scour depth. With a large number of experimental data and field data, Muller [72] found that pile width was the most important variable for estimating the equilibrium of scour depth. The same finding was given by Bateni [73], in which they applied artificial neural networks and adaptive neuro-fuzzy inference system to estimate equilibrium of scour depth and obtained that the pile width affected more than that of other parameters such as water depth, flow intensity and sediment size. However, Yao et al. [71] thought flow intensity was the most important factor that controls the equilibrium of scour depth.
2.5. Time
The time for an equilibrium scour varies with flow fields and piles [74]. In live-bed scour conditions, the time needed for the scouring balance is little and accompanied with upper and lower shocks near the equilibrium position [14,71,75]. In clear-water scour conditions, equilibrium needs a much longer period of time. An example for this was presented in Figure 9 in which clear-water scour and live-bed scour tests were taken from Melville and Chiew [51] and Chang et al. [76]. The maximum scour depth increased asymptotically with time and tended to be a threshold value when it was given enough scouring time in clear-water water scour conditions. On the contrary, live-bed scour reached a large scour depth value in very short time and oscillated nearby the equilibrium line, though the maximum scour depth was as much as 15 cm larger than the minimum scour depth when the scour depth was oscillating.
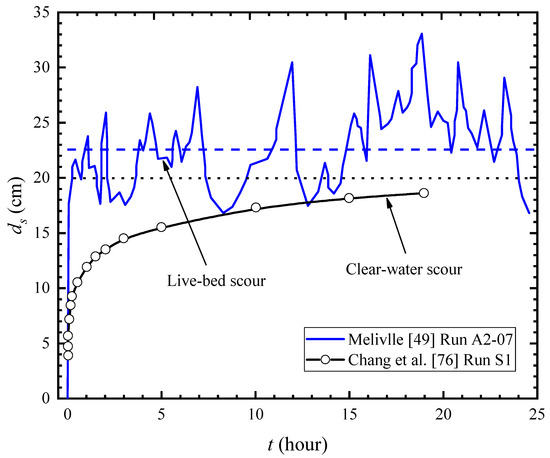
Figure 9.
Clear-water and live-bed scour evolution.
Due to the fact that most equilibrium scour depth equations were derived from experimental data, it is critically important to determine the time for an equilibrium scour depth in an experimental test. Summarizing from the literature, the authors obtained three concepts of the scour equilibrium. Most of them are empirical formulas derived from experimental data or field data rather than theoretical analysis. In fact, it has not been unified yet.
2.5.1. Finite Time
In local scour studies, many researchers have done their experiments in a finite time due to the fact that the equilibrium of scour is time consuming. Mia and Nago [34] defined that equilibrium of scour was achieved when scour depth increased by no more than 5%D in 24 hours. Kumar et al. [77] stopped the experiment when the depth of scouring was less than 1 mm for 3 hours. By assuming that, they considered the scouring equilibrium was reached. Bozkus and Yildiz [78] and Karimi et al. [79] found it was appropriate to reach the equilibrium state after 2 hours of scouring. However, Aksoy et al. [43] concluded that data obtained for less time, such as 10 hours, could underestimate scour depth as much as 50% of the equilibrium scour depth.
2.5.2. According to Asymptotically Functions
However, some researchers [35,46,80,81,82,83] believe that the equilibrium should be obtained according to fitted curves just as Figure 10 showed. The curves are unusually fitted by asymptotic functions such as exponential laws [14,34], logarithmic laws [64] and hyperbolic laws [53,84]. These functions will be discussed in more detail in Section 3. To fit a curve for experimental data, they proposed some formulas depending on the currents or pile parameters according to their experiments. Summarizing from experimental data, Ettema et al. [46] classified the curves into three paragraphs. In the initial phase, a rapid scour rate is caused by the down-flow in front of the pile. As the horseshoe vortex grows, the scour hole develops slower, but lasts for a longer time. The equilibrium phase is determined by factors of pile size, sediment and flow field.
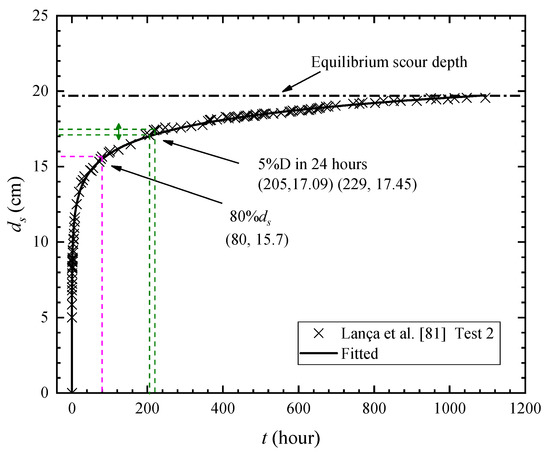
Figure 10.
Evolution of maximum scour depth (Reproduced from Lança et al. [81], with permission from River flow, 2010).
2.5.3. According to Critical Shear Stress
Another idea of the equilibrium is about the critical shear stress of sediment particles. References [16,52] thought that when shear stress reduced to critical shear stress of a sediment particle in a scour hole, no sediment would be stirred up by the horseshoe vortex. Kumar et al. [77] used a critical sediment size of dc, above which the sediment could not be mobilized. Scouring would be in an equilibrium state when the sediment in scour hole was larger than the calculated dc. For non-uniform sediment, the equivalent sediment size of mixing layer dm was chosen to represent dc. Nevertheless, the critical shear stress of sediment particles in scour hole is usually measured indirectly in laboratory. An example of bed shear stress associated with turbulence horseshoe vortex was given by Li et al. [21]. With a 2D PIV system, Li et al. [21] measured the time-averaged flow field in approach flow and the instantaneous velocity in front of the pile. Instantaneous bed shear stress was obtained by , with is water dynamic viscosity, is the eddy viscosity in the approach flow and and are the streamwise velocity and vertical position of the first measurement point above the bed. The direct methods need to be helped with numerical simulations. Manes and Brocchini [16] assumed the length scale of large eddies approximates the maximum scour hole depth. Through dimensional analyses and drag force acting on the cylinder, Manes and Brocchini [16] proposed an approach that combined theoretical analyses with empirical considerations in equilibrium scour depth estimation. In clear-water scour condition, the equilibrium scour depth was expressed as (where is assumed a constant drag coefficient), which contained all the non-dimensional groups identified by [41,71,85]. The dimensionless equation obtained from Figure 4 in [16] can be written as .
In order to compare these definitions above, a long-time scour experiment numbered test 2 in [81] is selected. The test parameters are shown in Table 3. Comparisons of equilibrium scour depths are calculated with criteria of [16,34,46,77,79,81]. The scour evolutions are presented in Figure 10 and the calculated results are shown in Table 4. The minimum value is from Karimi et al. [79], who stated scouring for 2 hours was enough for equilibrium in clear-water scour conditions. However, Figure 10 shows that scouring for 80% of equilibrium scour depth just needs 80 hours, which accounts for only 7.3% of 1094.5 hours. In fact, it can be seen from Figure 9 and Figure 10 that scour depth reached a relatively large proportion for a very short time in initial stage. In accord with Ettema et al. [46], Melville and Chiew [51] found the scour rate decreased gradually during a scouring process. The scouring rate reached 31%, 38% and 49% respectively within 0.3%, 0.6% and 1.7% of the equilibrium time, while the scouring rate reached 87% and 95% respectively at 33% and 67% of the equilibrium scouring time. Recently, Yao et al. [71] found that flow intensity had a much greater impact in time-scale than changes in aspect ratio.

Table 3.
Parameters of Test 2 in Lança et al. [81].

Table 4.
Comparisons of equilibrium scour depths.
For non-uniform scour, Chang et al. [76] conducted a series of tests, finding that the equilibrium time and the maximum scour depth decreased with σg. This conclusion is in good agreement with [43,86].
3. Empirical Equations
To predict the maximum scour depth related to time, investigating the temporary scour depth is necessary. As is defined by Pandey et al. [87], it was the variation of maximum scour depth near the pile or other hydraulic structure that developed with different time intervals. Based on laboratory experiments, prototype data or numerical simulations, several formulas have been proposed in the literature.
By solving the sediments continuity equations, Chiew and Melville [36] proposed a semi-empirical formula to predict temporary scour depths in uniform bed and steady currents conditions. Guo [37] developed a semi-analytical model for temporal clear-water scour at prototype piles. Kothyari et al. [86] attributed the scour to the horseshoe vortex, and computed the temporary scour depth with critical shear stress. Later, based on the similitude of Froude, [38] and [61] developed new relationships by relating the scour depth to the difference between the actual and entrainment densimetric particle Froude numbers. Mia and Nago [34] proposed a method for calculating the scour depth at any time by studying the effect of flow history on the local scour depth, and obtained the dimensionless formula of temporary scour depth. Lança et al. [81] conducted five long time scouring experimental tests, and developed the polynomial functions proposed by Bertoldi and Jones [88]. Analyzing some available formulas, Choi and Choi [89] obtained a new dimensionless formula. Pandey et al. [87] compared the formulas of [34,38,41,61,89,90] and obtained that the most accurate in predicting the maximum scour depth was the formula proposed by [61]. They stated that [87] showed more agreement in the equilibrium of scour time.
Since experiments were carried out in different sizes, piles materials, flow fields, sediments, measuring methods and equilibrium criteria, formulas of temporary scour depth were proposed with different types. According to their expression forms, the formulas can be classified with exponential, logarithmic, hyperbolic and numerical functions.
3.1. Exponential Formulas
It was first proposed by Breusers [91], and was developed by [14,34,39,92]. The model is in a form of equation (2). To determine coefficient C, exponent n and time scale T, they studied factors that affected the equilibrium scour depth and fitted them with curves. This equation is meaningful for evaluating the maximum scour depth with various times. Nevertheless, as the coefficient C, exponent n, and time scale T are variables that change with scour conditions, equilibrium scour depth could not be calculated without equation (2). Moreover, this equation is strictly limited with conditions of narrow pile width, uniform sediments and unsubmerged vertical circular piles.
A widely used formula in the literature was proposed by Sumer and Fredsøe [14], who attributed the local scour to Shields parameter θ, and involved other factors such as pile width, medium sediment diameter and boundary layer thickness. The semi-empirical formula Equation (3) obtained by them adopted the sediments particles inception theory and the fitted curves with experimental data gave a relatively satisfactory solution in recent years.
where is the time scale of scour, is non-dimensional time scale of scour, is the Shields parameter due to skin friction, is friction velocity associated with skin friction, is shear stress due to skin friction, , ρ is the flow density, g is the acceleration due to gravity, s is the specific gravity of sand, δ is the boundary layer thickness and κ is the Kármán constant.
3.2. Logarithmic Formulas
With Equation (4) proposed by Melville [41], Melville [64] used Equation (5) for predicting the time variation with maximum scour depth. The equation they proposed is easy to use, but is not accurate for different sizes of pile width. Limitations of flow intensity U/Uc are restricted for the range of 0.4–1.0. In addition, the pile shape should be vertical circular piles. Nevertheless, as was stated by Melville [64], D and U must be expressed in a consistent system of units, e.g., meters and meters per second, respectively. The formula for calculating the equilibrium time of scour depth te is dimensional inconsistency.
where , , , , and are empirical expressions of the flow depth, flow intensity, sediment size, pile shape, pile alignment and channel geometry separately.
where , when h > 6D and when h ≤ 6D.
Another equation in the logarithmic form was proposed by Oliveto and Hager [61,82]. It was developed by Kothyari [38] with Equation (6). They believed that the dominant parameter controlling the scour process was a densimetric particle Froude number Fd. Equation (6) is very meaningful, for it could be used for circular and rectangular piles in clear-water scour. Moreover, the sediments non-uniformity was included. As scour depth is an incremental function of time T in Equation (6), scour depth will be infinite when the time is infinite. Fortunately, they obtained Equation (9) for the equilibrium time of scour depth Te. However, some limitations were given by them too. Firstly, the dimensionless sediments gain sizes D* should be less than 15. Where , ν is kinematic fluid viscosity. Secondly, approach flow depth h cannot be smaller than 5 cm in a rectangular channel. Thirdly, the ratio of pile width to channel width should be less than 0.05. What is more, the densimetric particle Froude number is required to be far more larger than the densimetric particle Froude number of scour entrainment . Lastly, Equation (6) could only be used in clear-water scour conditions with a threshold Froude number Ft < 1.2.
where z is the maximum scour depth, is the reference length for the circular or rectangular pile, is the densimetric particle Froude number, , U is the approach flow velocity, is the relative gravitational acceleration, is the sediments density, ρ is the flow density, d50 is the sediments median grain size, t is the scour time, is the dimensionless time and is the relative time.
The densimetric particle Froude number of scour entrainment was calculated by Equation (7).
where is the densimetric particle Froude number for incipient sediment entrainment in the approach flow channel and is calculated by Equation (8), shape parameter for circular and rectangular piles, is submergence parameter, is cascade parameter, for circular and rectangular piles, is ratio of pile width to channel width and is the hydraulic radius.
where is the dimensionless grain size, ν kinematic fluid viscosity.
where is the threshold approach flow velocity.
3.3. Hyperbolic Functions
A few studies found that the hyperbolic functions predicted the scour depth versus scouring time better [4,35,88]. With more than 15 days scouring data for cylindrical piles, Bertoldi and Jones [88] proposed Equation (11) to fit evolutions of scour depths in clay bed. Zhao et al. [4] conducted a series of live-bed scour experiments with square piles in sandy bed and concluded that Equation (11) fitted better than Equation (3).
where is the equilibrium scouring time.
Sheppard and Miller [35] and Lança et al. [81] fitted their local clear-water scour experimental data with a hyperbolic function as is seen in Equation (12) and Equation (13). The hyperbolic function gives a more fitted curve for the development of the scour with time. However, it is purely mathematical rather than physical when compared to the other types of empirical formulas.
where a, b, c, d are coefficients fitted with experimental data.
where , , , and are coefficients fitted with experimental data.
3.4. Numerical Functions
Based on sediment continuity equations and sediment pickup function proposed by Dey and Debnath [93], Yanmaz [40] developed a semi-empirical equation for estimating the temporal variation of clear water scour at circular cylinders. It considered flow, pile, sediment properties and time. Though Equation (13) could predict time-dependent scour depths well in some cases, the calculation is a complex solving process with differentiation and derivation. It has a validation scope for its own flow intensity, relative pile width, and parameter α.
where , and is dimensionless sediment size, is the transport-stage parameter due to scour, , ϕ is the sediment angle of repose, is the bed shear stress on flat bed and τbc is the critical bed shear stress on flat bed.
The equilibrium scour depth under wave-only conditions is found to be mainly dependent on the KC number. Sumer et al. [90] proposed an empirical formula as follows:
where is equilibrium scour depth under wave-only conditions.
The equilibrium scour depth under combined wave-current conditions is dependent on both (the relative velocity ) and KC number, and may be calculated by the equation from Sumer and Fredsøe [14]:
where is equilibrium scour depth under combined wave-current conditions, is equilibrium scour depth under steady current conditions and A and B are fitted factors, and .
Since the above equation is only validated in the range KC > 4 and the predicted results showed obvious deviation for lower KC numbers, the Raaijmakers and Rudolph [94] formula (16) can be adopted. It was extended from the current-only scour formula of Breusers et al. [91] to combined wave-current conditions by introducing a parameter Kw to account for the wave effects.
where is the correction factor of the pile height to account for piles that are partly submerged in water and is the correction factor accounting for the wave action, .
For current-only conditions, the shedding frequency and vorticity of wake vortices can account for the discrepancy between the large and small piles [46,95]. For wave-only conditions, the main mechanisms for local scour around pile with relatively large pile, i.e., the case of smaller KC numbers, are due to the wave-induced steady streaming flow [96], which is different from the vortices system (e.g., horseshoe vortex and vortex shedding) around the slender pile [90].
4. Conclusions
Local scour at pile foundations is an important issue due to its complexity and practical application. Recent works on the local scour of the vertical piles due to current were systematically reviewed.
In this work, a literature review was also presented with a brief description of local scour induced by wave and current. This review highlighted the main progresses of local scour in currents. Mechanisms of local scour including the factors affecting the maximum scour depth were summarized. A number of experimental data were adopted for illustrating the relationships between them. Existing equations developed for predicting or estimating the maximum scour depths were analyzed. The main conclusions could be drawn as follows.
- (1)
- A local scour around a vertical pile involves interactions between sediments and flow fields, which is a process with complicated three-dimensional turbulence. Down-flow in front of a pile and the existed incoming boundary layer are essential in forming the horseshoe vortex. Shear stress at the pile edges, which are produced by the concentrated streamlines, will be amplified to a range of 5–10 times compared to that of the approach flow. Due to this amplification, scour was found to start at the pile upstream corners. Interactions between the three-dimensional horseshoe vortex and vortices shedding are responsible for scour behind the pile.
- (2)
- The flow intensity in uniform sediments or non-uniform sediments connects the approach flow velocity and sediment particles. In clear-water scour conditions, flow intensity is smaller than 1. Maximum scour depths were found at the transition from clear-water scour to live-bed scour conditions. The existing equilibriums of local scour in clear-water scour conditions indicated that shear stress in scour hole was smaller than the critical shear stress of sediment particle. In live-bed scour conditions, due to the supplements of sediments particles from upstream, equilibrium scour depth oscillates near the mean value. Both uniform and non-uniform sediments attained to their second scour depth peaks when the flow intensity was about 4.0.
- (3)
- Flow depth is an important factor in local scour. The unsubmerged vertical piles have been studied far more than that of submerged cases. In unsubmerged conditions, the maximum scour depth increased with the increasing flow depth until to a critical value. A curve (Figure 3a), which enveloped large amounts of experimental data, could give a reference in scour depth design when considering the flow depth effects. Due to the different flow fields, more studies are needed in submerged cases such as caissons, manifolds in offshore engineering.
- (4)
- Sediments parameters of medium size and non-uniformity in local scour were connected with flow intensity. Armoring effects, which decreased scour depth in non-uniform sediments, were found to increase with the increasing sediments gradation. However, reviews and conclusions in this paper were only for non-cohesive sediments.
- (5)
- Scour depth increases with pile width and pile height. In submerged cases, relative scour depth decreases with the increasing submergence ratio . For live-bed scour conditions, the relative scour depth tends to be a constant value when the submergence ratio surpasses 2.
- (6)
- Certifications for equilibrium of scour depth used by researchers vary broadly. Categories of finite time, according to asymptotically functions and according to the shear stress in scour hole were classified. Different equations based on these certifications with experimental data have been adopted in literature. Empirical equations were categorized into four types: exponential formula, logarithmic formula, hyperbolic functions and numerical functions.
However, due to the complexity of the scouring process, there is not an equation in estimating the maximum local scour depth based on the theoretical analysis completely. The turbulent boundary layer, variations of fluid with time and the mechanisms of sediments transport in scour pit also limit the development of scour equations. In addition, there are many other factors affecting scour depth such as pile shapes, cohesive sediments, flow attack angle, pile groups, measurement methodologies, etc.
As steady currents are ideal flow that could be only seen in laboratory or numerical model other than the fields, empirical equations were mostly fitted with experimental data. These models have limited accuracy when applied to estimating scour depth in engineering. In future works, larger scales and more advanced experiments need to be conducted so that to minimize the scale effects and to approach the prototype conditions in fields.
As theoretical solutions of mathematics and physics in solving the maximum scour depths may take a long time for researchers to attain to, alternative ways for modeling the maximum scour depth may needed. Numerical software, such as Fluent [97], Flow3D [98], SSSIIM2 [99] and open source software EllipSys3D [6], OpenFOAM [100], REEF 3D [101], etc. have been found functional in modeling the local scour process and may be able to resolve these issues.
Author Contributions
Data curation, formal analysis, funding acquisition, investigation, methodology, supervision and writing—review and editing were contributed by B.L. Data curation, formal analysis, investigation, methodology, resources, software, validation and writing—original draft were contributed by S.D. Formal analysis, methodology, supervision and writing—review and editing were contributed by X.P. Resources, supervision and writing—reviewing part of wave & current conditions and editing were contributed by L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Fund grant number [51739010, 51679223], 111 Project grant number [B14028], and a grant from the 7th Generation Ultra-Deep-water Drilling Rig Innovation Project.
Acknowledgments
The authors acknowledge the reviews’ constructive suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hunt, J.C.R.; Abell, C.J.; Peterka, J.A.; Woo, H. Kinematical studies of the flows around free or surface-mounted obstacles: Applying topology to flow visualization. J. Fluid Mech. 1978, 86, 179–200. [Google Scholar] [CrossRef]
- Liu, K.; Liu, J.L.; Yu, W.C. Statistical Analysis of Bridges Caused by Floods from 2007 to 2015. Urban Roads Bridges Flood Control 2017, 1, 90–92. [Google Scholar]
- Ettema, R. Scour at Bridge Piers; Report No. 216; University of Auckland: Auckland, New Zealand, 2016. [Google Scholar]
- Zhao, M.; Zhu, X.; Cheng, L.; Teng, B. Experimental study of local scour around subsea caissons in steady currents. Coast. Eng. 2012, 60, 30–40. [Google Scholar] [CrossRef]
- Chabert, J.; Engeldinger, P. Etude des Affouillements Autour des Piles des Ponts; Laboratoire National d’Hydraulique: Chatou, France, 1956. [Google Scholar]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Melville, B.; Ball, J. Three-dimensional analysis of coherent turbulent flow structure around a single circular bridge pier. Environ. Fluid Mech. 2004, 14, 821–847. [Google Scholar] [CrossRef]
- Okamoto, S.; Sunabashiri, Y. Vortex shedding from a circular cylinder of finite length placed on a ground plane. J. Fluids Eng. 1992, 114, 512–521. [Google Scholar] [CrossRef]
- Pattenden, R.J.; Turnock, S.R.; Zhang, X. Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Exp. Fluids 2005, 39, 10–21. [Google Scholar] [CrossRef]
- Baker, C.J. The laminar horseshoe vortex. J. Fluid Mech. 1979, 95, 344–367. [Google Scholar] [CrossRef]
- Hjorth, P. Studies on the Nature of Local Scour. Ph.D. Thesis, Department of Water Resources Engineering, Lund Institute of Technology, University of Lund, Scania, Sweden, 1975. [Google Scholar]
- Guan, D.W.; Chiew, Y.M.; Wei, M.X.; Hsieh, S.C. Characterization of horseshoe vortex in a developing scour hole at a cylindrical bridge pier. Int. J. Sediment Res. 2019, 34, 118–124. [Google Scholar] [CrossRef]
- Mattioli, M.; Alsina, J.M.; Mancinelli, A.; Miozzi, M.; Brocchini, M. Experimental investigation of the nearbed dynamics around a submarine pipeline laying on different types of seabed: The interaction between turbulent structures and particles. Adv. Water Resour. 2012, 48, 31–46. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. The Mechanics of Scour in the Marine Environment, 4th ed.; World Scientific: Singapore, 2002; pp. 149–228. [Google Scholar]
- Zhao, M.; Cheng, L.; Zang, Z. Experimental and numerical investigation of local scour around a submerged vertical circular cylinder in steady currents. Coast. Eng. 2010, 57, 709–721. [Google Scholar] [CrossRef]
- Manes, C.; Brocchini, M. Local scour around structures and the phenomenology of turbulence. J. Fluid Mech. 2015, 779, 309–324. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G.; Ettema, R. Coherent structures in the flow field around a circular cylinder with scour hole. J. Hydraul. Eng. 2008, 134, 572–587. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: New York, NY, USA, 1995; 296p. [Google Scholar]
- Li, J.; Qi, M.; Fuhrman, D.R.; Chen, Q. Influence of turbulent horseshoe vortex and associated bed shear stress on sediment transport in front of a cylinder. Exp. Therm. Fluid Sci. 2018, 97, 444–457. [Google Scholar] [CrossRef]
- Tseng, M.H.; Yen, C.L.; Song, C.C.S. Computation of three-dimensional flow around square and circular piers. Int. J. Numer. Methods Fluids. 2000, 34, 207–227. [Google Scholar] [CrossRef]
- Dargahi, B. The turbulent flow field around a circular cylinder. Exp. Fluids 1989, 8, 1–12. [Google Scholar] [CrossRef]
- Kobayashi, T.; Oda, K. Experimental study on developing process of local scour around a vertical cylinder. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; Volume 93, pp. 1284–1297. [Google Scholar]
- Sumer, B.M.; Fredsøe, J.; Christiansen, N. Scour around vertical pile in waves. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 15–31. [Google Scholar] [CrossRef]
- Sumer, B.M.; Christiansen, N.; Fredsøe, J. The horseshoe vortex and vortex shedding around a vertical wall-mounted cylinder exposed to waves. J. Fluid Mech. 1997, 332, 41–70. [Google Scholar] [CrossRef]
- Rudolph, D.; Bos, K.J. Scour around a monopile under combined wave current conditions and low KC-numbers. In Proceedings of the Third International Conference on Scour and Erosion, Amsterdam, The Netherlands, 1–3 November 2006; pp. 582–588. [Google Scholar]
- Qi, W.G.; Gao, F.P. Physical modeling of local scour development around a large diameter monopile in combined waves and current. Coast. Eng. 2014, 83, 72–81. [Google Scholar] [CrossRef]
- Zanke, U.C.E.; Hsu, T.W.; Roland, A.; Link, O.; Diab, R. Equilibrium scour depths around piles in noncohesive sediments under currents and waves. Coast. Eng. 2011, 58, 986–991. [Google Scholar] [CrossRef]
- Miozzi, M.; Corvaro, S.; Pereira, F.A.; Brocchini, M. Wave-induced morphodynamics and sediment transport around a slender vertical cylinder. Adv. Water Resour. 2019, 129, 263–280. [Google Scholar] [CrossRef]
- Sumer, B.M.; Petersen, T.U.; Locatelli, L.; Fredsøe, J.; Musumeci, R.E.; Foti, E. Backfilling of a scour hole around a pile in waves and current. J. Waterw. Port Coast. Ocean Eng. 2013, 139, 9–23. [Google Scholar] [CrossRef]
- Agudo, J.R.; Luzi, G.; Han, J.; Hwang, M.; Lee, J.; Wierschem, A. Detection of particle motion using image processing with particular emphasis on rolling motion. Rev. Sci. Instrum. 2017, 88, 051805. [Google Scholar] [CrossRef] [PubMed]
- Dey, S.; Ali, S.Z. Stochastic mechanics of loose boundary particle transport in turbulent flow. Phys. Fluids 2017, 29, 055103. [Google Scholar] [CrossRef]
- Mia, F.; Nago, H. Design method of time-dependent local scour at circular bridge pier. J. Hydraul. Eng. 2003, 129, 420–427. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Miller, W. Live-bed local pier scour experiments. J. Hydraul. Eng. 2006, 132, 635–642. [Google Scholar] [CrossRef]
- Chiew, Y.M.; Melville, B.W. Local scour around bridge piers. J. Hydraul. Res. 1987, 25, 15–26. [Google Scholar] [CrossRef]
- Guo, J.K. Semi-analytical model for temporal clear-water scour at prototype piers. J. Hydraul. Res. 2014, 52, 366–374. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hager, W.H.; Oliveto, G. Generalized approach for clear-water scour at bridge foundation elements. J. Hydraul. Eng. 2007, 133, 1229–1240. [Google Scholar] [CrossRef]
- Cheng, N.S.; Chiew, Y.M.; Chen, X.W. Scaling Analysis of Pier-Scouring Processes. J. Eng. Mech. 2016, 142, 06016005. [Google Scholar] [CrossRef]
- Yanmaz, A.M. Temporal variation of clear-water scour at cylindrical bridge piers. Can. J. Civ. Eng. 2006, 33, 1098–1102. [Google Scholar] [CrossRef]
- Melville, B.M.; Sutherland, A.J. Design method for local scour at bridge piers. J. Hydraul. Eng. 1988, 114, 1210–1226. [Google Scholar] [CrossRef]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R.; Jacobsen, N.G.; Fredsøe, J. Numerical investigation of flow and scour around a vertical circular cylinder. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140104. [Google Scholar] [CrossRef] [PubMed]
- Aksoy, A.O.; Bombar, G.; Arkis, T.; Guney, M.S. Study of the time-dependent clear water scour around circular bridge piers. J. Hydrol. Hydromech. 2017, 65, 26–34. [Google Scholar] [CrossRef]
- Melville, B. The physics of local scour at bridge piers. In Proceedings of the Fourth International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008; pp. 228–238. [Google Scholar]
- Ettema, R. Scour at Bridge Piers. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 1980. [Google Scholar]
- Ettema, R.; Kirkil, G.; Muste, M. Similitude of large-scale turbulence in experiments on local scour at cylinders. J. Hydraul. Eng. 2006, 132, 33–40. [Google Scholar] [CrossRef]
- Hancu, S. Sur le calcul des affouillements locaux dans la zone des piles des ponts. In Proceedings of the 14th AHR Congress International Association for Hydro Research (IAHR), Paris, France, 29 August–3 September 1971; Volume 3, pp. 299–313. [Google Scholar]
- Jain, S.C.; Fischer, E.E. Scour around Bridge Piers at High Froude Numbers; Report No. FH-WA-RD-79-104; Federal Highway Administration: Washington, DC, USA, 1979. [Google Scholar]
- Lança, R.M.; Fael, C.S.; Maia, R.J.; Pêgo, J.P.; Cardoso, A.H. Clear-water scour at comparatively large cylindrical piers. J. Hydraul. Eng. 2013, 139, 1117–1125. [Google Scholar] [CrossRef]
- Melville, B.W. Live-bed scour at bridge sites. J. Hydraul. Eng. 1984, 110, 1234–1247. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.M. Time scale for local scour at bridge piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Karna, N. Maximum scour depth around bridge pier in gravel bed streams. Nat. Hazards 2018, 91, 819–836. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Odeh MGlasser, T. Large scale clear-water local pier scour experiments. J. Hydraul. Eng. 2004, 130, 957–963. [Google Scholar] [CrossRef]
- Shen, H.W.; Schneider, V.R.; Karaki, S.S. Mechanics of Local Scour. National Bureau of Standards; Institute of Applied Technology, U.S. Department of Commerce: Washington, DC, USA, 1966. [Google Scholar]
- Yanmaz, M.; Altinbilek, H.D. Study of time-dependent local scour around bridge piers. J. Hydraul. Eng. 1991, 117, 1247–1268. [Google Scholar] [CrossRef]
- Baker, C.J. The position of points of maximum and minimum shear stress upstream of cylinders mounted normal to flat plates. J. Wind Eng. Ind. Aerodyn. 1985, 18, 263–274. [Google Scholar] [CrossRef]
- Raudkivi, A.J.; Ettema, R. Clear-water scour at cylindrical piers. J. Hydraul. Eng. 1983, 131, 338–350. [Google Scholar] [CrossRef]
- Park, C.W.; Park, H.I.; Cho, Y.K. Evaluation of the applicability of pier local scour formulae using laboratory and field data. Mar. Georesour. Geotechnol. 2017, 35, 1–7. [Google Scholar] [CrossRef]
- Dey, S. Three-dimensional vortex flow field around a circular cylinder in a quasi-equilibrium scour hole. Sādhanā 1995, 12, 771–785. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M.; Verheij, H.J. Scour Manual, A.A, 2nd ed.; Balkema: Rotterdam, The Netherlands, 1997; 205p. [Google Scholar]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Chiew, Y.M.; Melville, B.W. Local scour at bridge piers with non-uniform sediments. Proceedings of the institution of civil engineers. Publ. Telford Ltd. 1989, 87, 215–224. [Google Scholar]
- Mir, B.H.; Lone, M.A.; Bhat, J.A.; Rather, N.A. Effect of Gradation of Bed Material on Local Scour Depth. Geotech. Geol. Eng. 2018, 36, 2505–2516. [Google Scholar] [CrossRef]
- Melville, B.W. Pier and abutment scour: Integrated approach. J. Hydraul. Eng. 1997, 123, 125–136. [Google Scholar] [CrossRef]
- Lee, S.O.; Sturm, T.W. Effect of sediment size scaling on physical modeling of bridge pier scour. J. Hydraul. Eng. 2009, 135, 793–802. [Google Scholar] [CrossRef]
- Sarkar, K.; Chakraborty, C.; Mazumder, B.S. Variations of bed elevations due to turbulence around submerged cylinder in sand beds. Environ. Fluid Mech. 2016, 16, 659–693. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.; Roy, A. Scour at Submerged Cylindrical Obstacles under Steady Flow. J. Hydraul. Eng. 2008, 134, 105–109. [Google Scholar] [CrossRef]
- Euler, T.; Herget, J. Obstacle-Reynolds-number based analysis of local scour at submerged cylinders. J. Hydraul. Res. 2011, 49, 267–271. [Google Scholar] [CrossRef]
- Sarkar, A.; Ratha, D. Flow around submerged structures subjected to shallow submergence over plane bed. J. Fluids Struct. 2014, 44, 166–181. [Google Scholar] [CrossRef]
- Tsutsui, T. Flow around a cylindrical structure mounted in a plane turbulent boundary layer. J. Wind Eng. Ind. Aerodyn. 2012, 104, 239–247. [Google Scholar] [CrossRef]
- Yao, W.D.; An, H.W.; Draper, S.; Cheng, L.; Harris, J.M. Experimental investigation of local scour around submerged piles in steady current. Coast. Eng. 2018, 142, 27–41. [Google Scholar] [CrossRef]
- Muller, D.S. Local Scour at Bridge Piers in Non-uniform Sediment under Dynamic Conditions. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2011. [Google Scholar]
- Bateni, S.M.; Borghei, S.M.; Jeng, D.S. Neural network and neuro-fuzzy assessments for scour depth around bridge piers. Eng. Appl. Artif. Intell. 2007, 20, 401–414. [Google Scholar] [CrossRef]
- Guo, J.K. Time-dependent clear-water scour for submerged bridge flows. J. Hydraul. Res. 2011, 49, 744–749. [Google Scholar] [CrossRef]
- Ettema, R.; Constantinescu, G.; Melville, B.W. Flow-Field Complexity and Design Estimation of Pier-Scour Depth: Sixty Years since Laursen and Toch. J. Hydraul. Eng. 2017, 143, 03117006. [Google Scholar] [CrossRef]
- Chang, W.Y.; Lai, J.S.; Yen, C.L. Evolution of scour depth at circular bridge piers. J. Hydraul. Eng. 2004, 130, 905–913. [Google Scholar] [CrossRef]
- Kumar, V.; Rangaraju, K.G.; Vittal, N. Reduction of local scour around bridge piers using slot and collar. J. Hydraul. Eng. 1999, 125, 1302–1305. [Google Scholar] [CrossRef]
- Bozkus, Z.; Yildiz, O. Effects of inclination of bridge piers on scouring depth. J. Hydraul. Eng. 2004, 130, 827–832. [Google Scholar] [CrossRef]
- Karimi, N.; Heidarnejad, M.; Masjedi, A. Scour depth at inclined bridge piers along a straight path: A laboratory study. Eng. Sci. Technol. Int. J. 2017, 20, 1302–1307. [Google Scholar] [CrossRef]
- Cardoso, A.H.; Bettess, R. Effects of time and channel geometry on scour at bridge abutments. J. Hydraul. Eng. 1999, 125, 388–399. [Google Scholar] [CrossRef]
- Lança, R.; Fael, C.; Cardoso, A. Assessing equilibrium clear-water scour around single cylindrical piers. River Flow 2010, 1207–1213. [Google Scholar]
- Oliveto, G.; Hager, W.H. Further results to time-dependent local scour at bridge elements. J. Hydraul. Eng. 2005, 131, 97–105. [Google Scholar] [CrossRef]
- Simarro, G.; Fael, C.; Cardoso, A. Estimating equilibrium scour depth at cylindrical piers in experimental studies. J. Hydraul. Eng. 2011, 137, 1089–1093. [Google Scholar] [CrossRef]
- Briaud, J.L.; Ting, F.C.K.; Cheng, H.C.; Gudavalli, R.; Perugu, S.; Wei, G.S. SRICOS: Prediction of scour rate in cohesive soils at bridge piers. J. Geotech. Environ. Eng. 1999, 125, 237–246. [Google Scholar] [CrossRef]
- Ettema, R.; Constantnescu, G.; Melville, B. Evaluation of Bridge Scour Research: Pier Scour Processes and Predictions; University of Auckland: Auckland, New Zealand, 2011; NCHRP, Rep. 175. [Google Scholar]
- Kothyari, U.C.; Garde, R.J.; Ranga, K.G. Temporal variation of scour around circular bridge piers. J. Hydraul. Eng. 1992, 118, 1091–1106. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K. Evaluation of existing equations for temporal scour depth around circular bridge piers. Environ. Fluid Mech. 2017, 17, 981–995. [Google Scholar] [CrossRef]
- Bertoldi, D.A.; Jones, J.S. Time to scour experiments as an indirect measure of stream power around bridge piers. In Proceedings of the International Water Resource Engineering Conference, Memphis, Tennessee, 3–7 August 1998; pp. 264–269. [Google Scholar]
- Choi, S.U.; Choi, B. Prediction of time-dependent local scour around bridge piers. Water Environ. J. 2016, 30, 14–21. [Google Scholar] [CrossRef]
- Sumer, B.M.; Christiansen, N.; Fredsoe, J. Time scale of scour around a vertical pile. In Proceedings of the Second International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers, San Francisco, CA, USA, 14–19 June 1992. [Google Scholar]
- Breusers, H.N.C.; Nicollet, G.; Shen, H.W. Local scour around cylindrical piers. J. Hydraul. Resour. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Franzetti, S.; Larcan, E.; Mignosa, P. Influence of tests duration on the evaluation of ultimate scour around circular piers. In Proceedings of the International Conference on the Hydraulic Modeling of Civil Engineering Structures, Coventry, England, 22–24 September 1982; British Hydromechanics Research Association: Harrogate, UK, 1982; pp. 381–396. [Google Scholar]
- Dey, S.; Debnath, K. Sediment pickup on streamwise sloping beds. J. Irrig. Drain. Eng. 2011, 127, 39–43. [Google Scholar] [CrossRef]
- Raaijmakers, T.; Rudolph, D. Time-dependent scour development under combined current and wave conditions—Laboratory experiments with online monitoring technique. In Proceedings of the 4th International Conference of Scour Erosion, Tokyo, Japan, 5–7 November 2008; pp. 152–161. [Google Scholar]
- Ettema, R.; Melville, B.W.; Barkdoll, B. Scale effect in pier scour experiments. J. Hydraul. Eng. 1998, 124, 639–642. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour around pile in combined waves and current. J. Hydraul. Eng. 2001, 127, 403–411. [Google Scholar] [CrossRef]
- Zhao, Z.; Fernando, H.J.S. Numerical simulation of scour around pipelines using an Euler–Euler coupled two-phase model. Environ. Fluid Mech. 2007, 7, 121–142. [Google Scholar] [CrossRef]
- Nielsen, A.W.; Liu, X.F.; Sumer, B.M.; Fredsøe, J. Flow and bed shear stresses in scour protections around a pile in a current. Coast. Eng. 2013, 72, 20–38. [Google Scholar] [CrossRef]
- Baranya, S.; Olsen, B.; Stoesser, T.; Sturm, T.W. A nested grid based computational fluid dynamics model to predict bridge pier scour. Water Manag. 2014, 167, 259–268. [Google Scholar] [CrossRef]
- Liu, X.F.; García, M.H. Three-Dimensional Numerical Model with Free Water Surface and Mesh Deformation for Local Sediment Scour. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 203–217. [Google Scholar] [CrossRef]
- Ahmad, N.; Myrhaug, D.; Kamath, A.; Arntsen, Ø.A. Numerical modelling of pipeline scour under the combined action of waves and current with free-surface capturing. Coast. Eng. 2019, 148, 19–35. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).