Video Sensing of Nearshore Bathymetry Evolution with Error Estimate
Abstract
:Highlights
- New method of depth-inversion error estimate using tides
- Guidelines on the limits of video-based depth inversion
- Three-year analysis of low tide terrace evolution from video cameras
1. Introduction
2. Methods
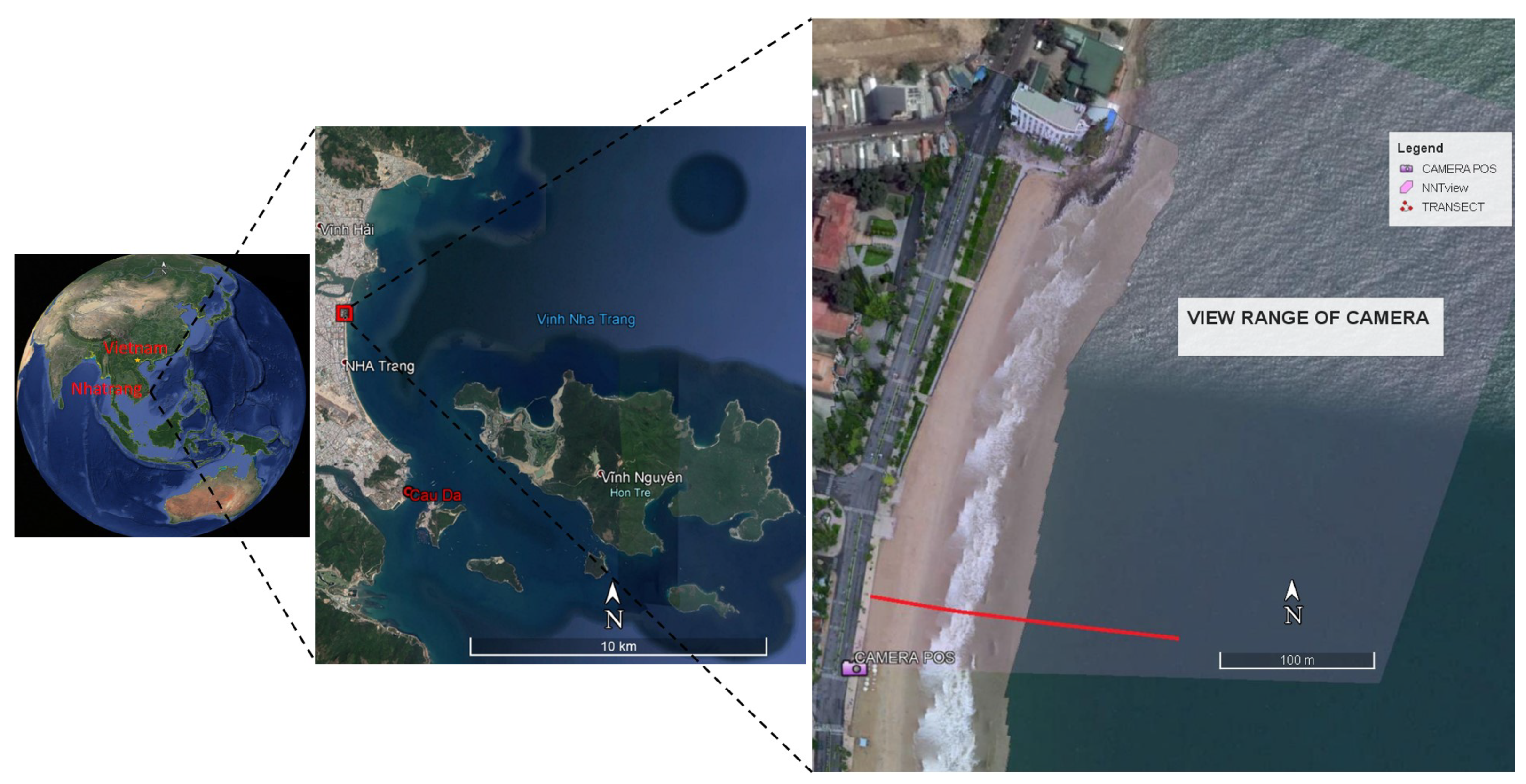
2.1. Study Area
2.2. Video Data
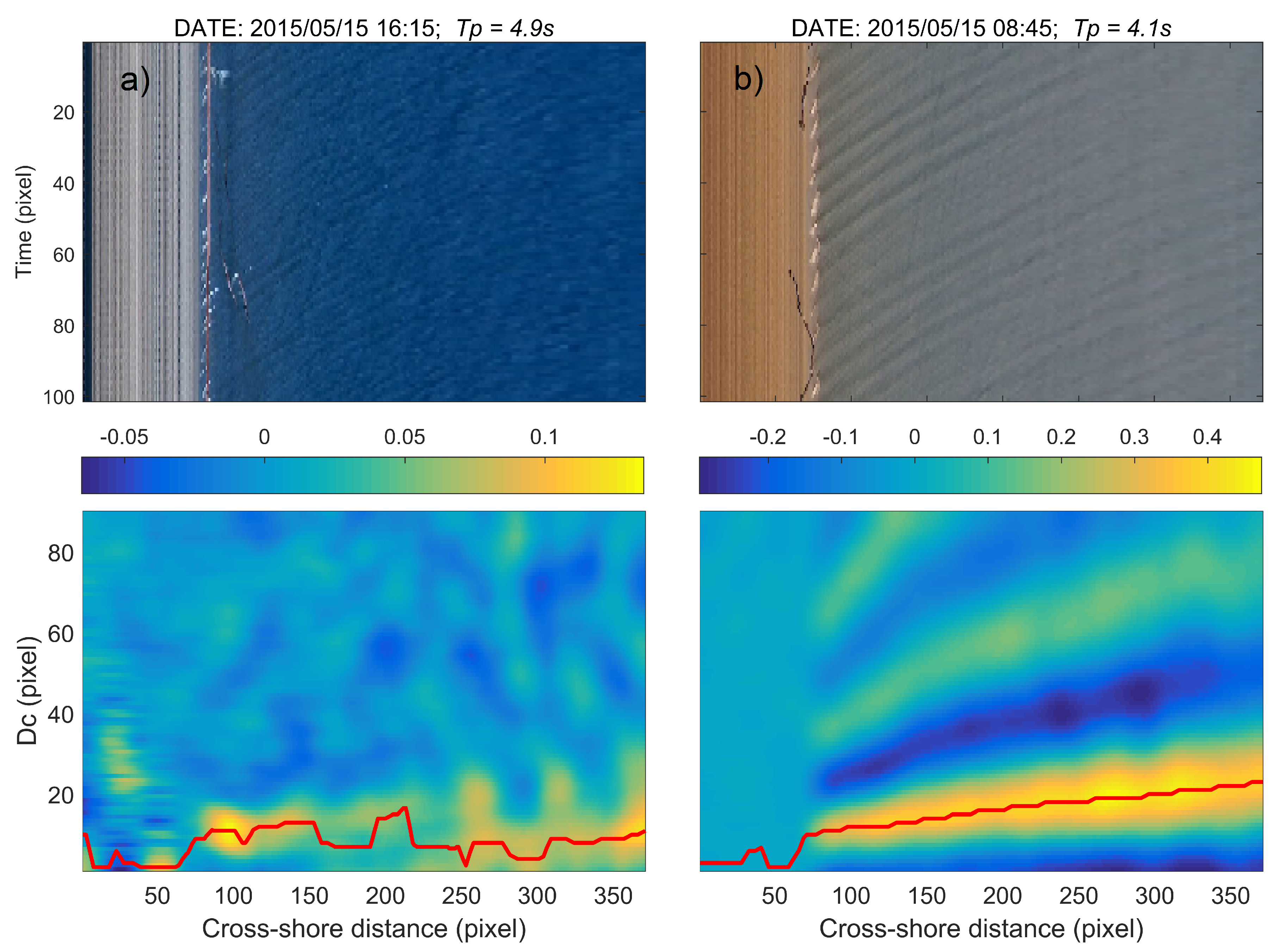
2.3. Depth Inversion along a Cross-Shore Transect
2.4. Using Tide as a Quality Proxy
3. Analysis of Beach Profile Evolution
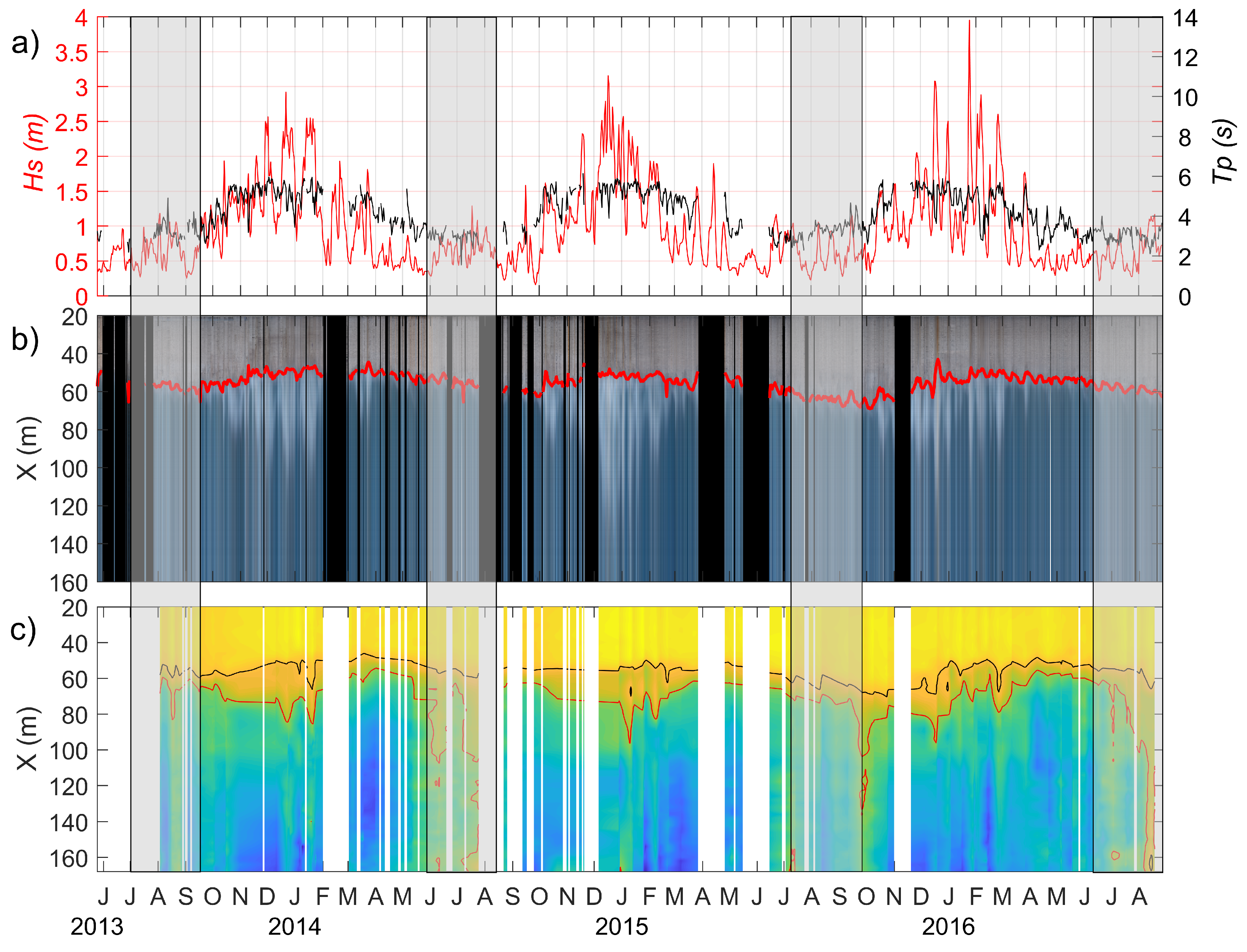
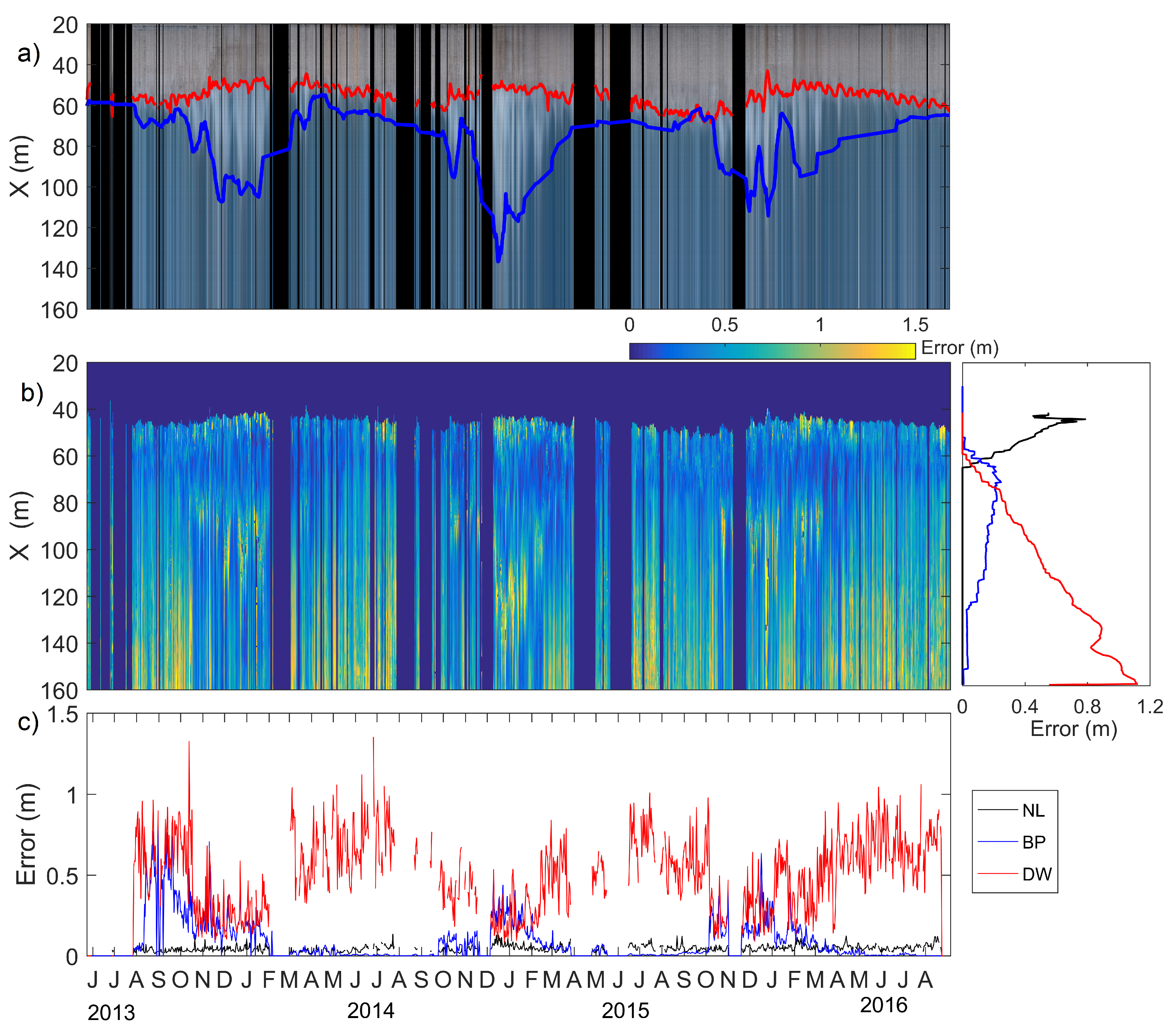
3.1. Bathymetry Evolution
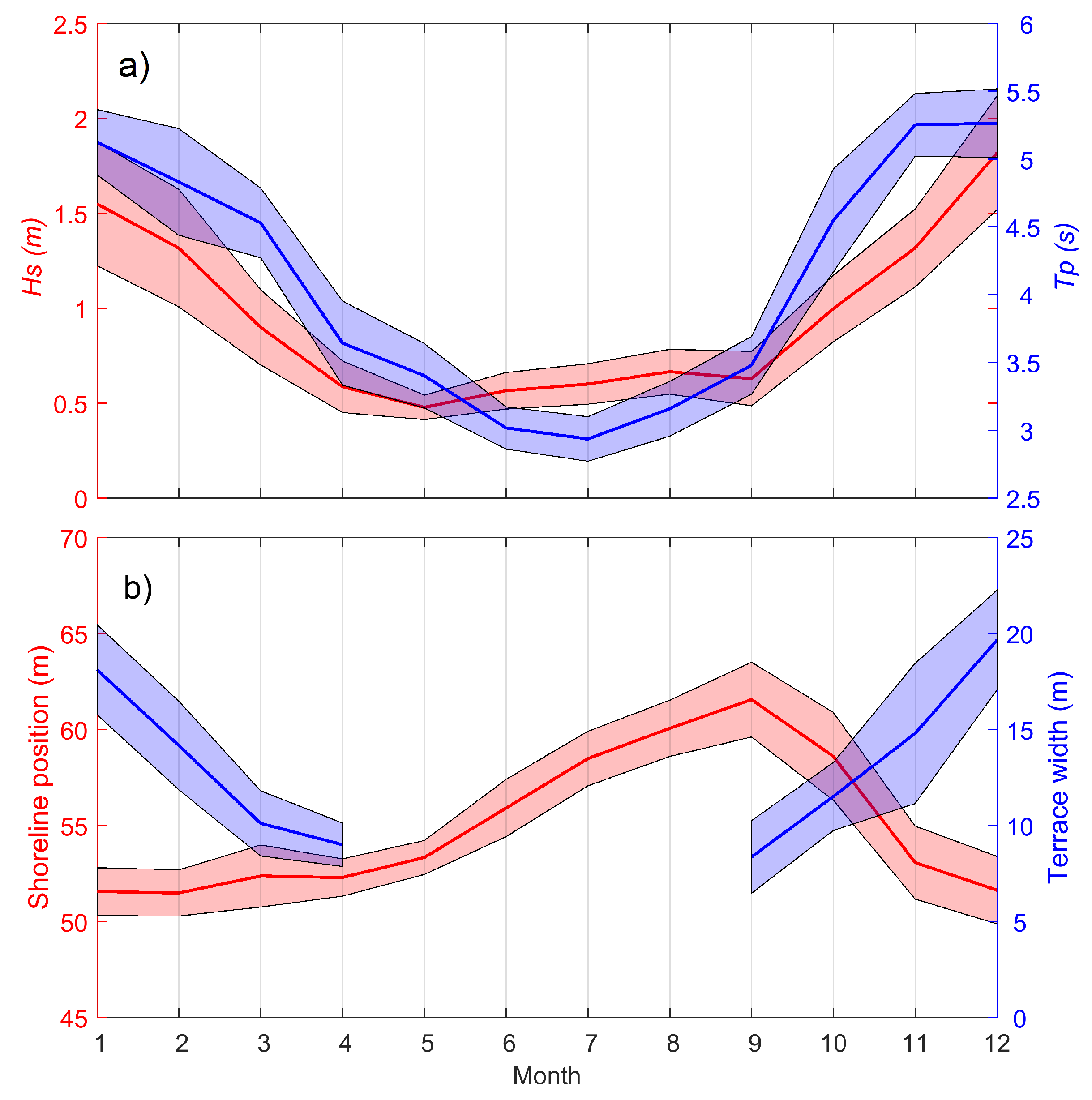
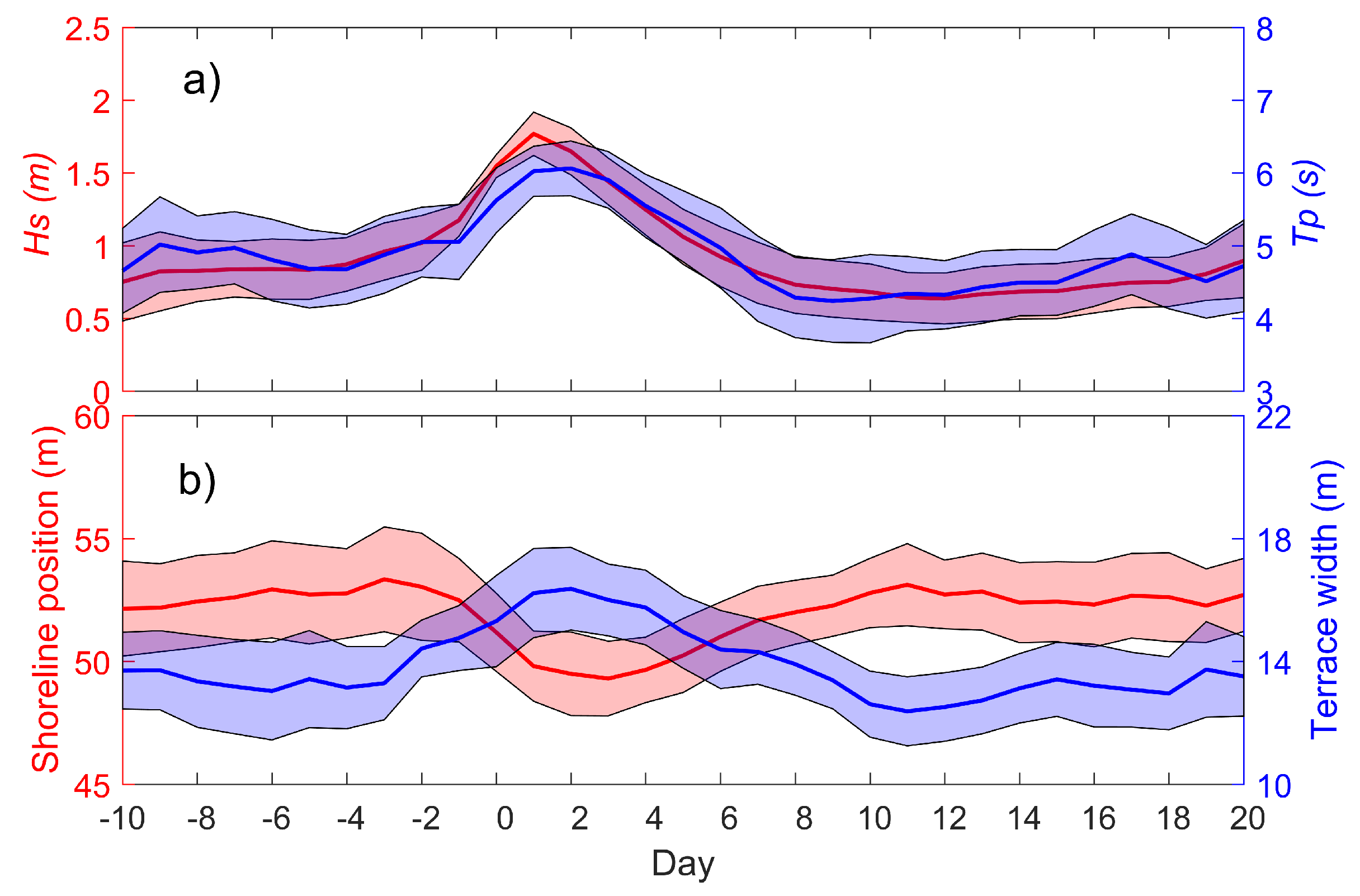
3.2. Seasonal Pattern
3.3. Impact of Winter Monsoon Events
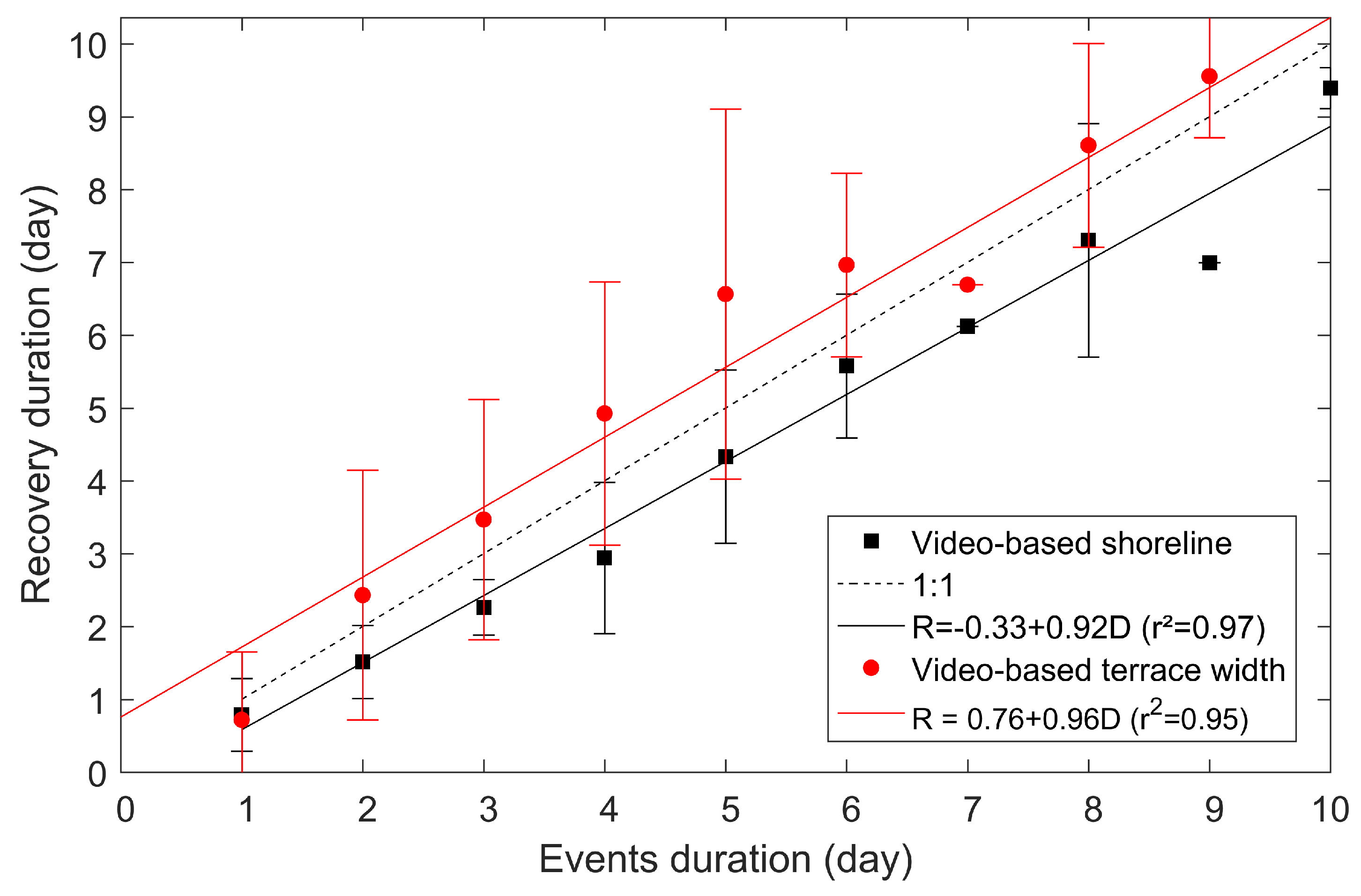
3.4. LTT Beach State Dynamics and Recovery
4. Discussion on Error Estimate
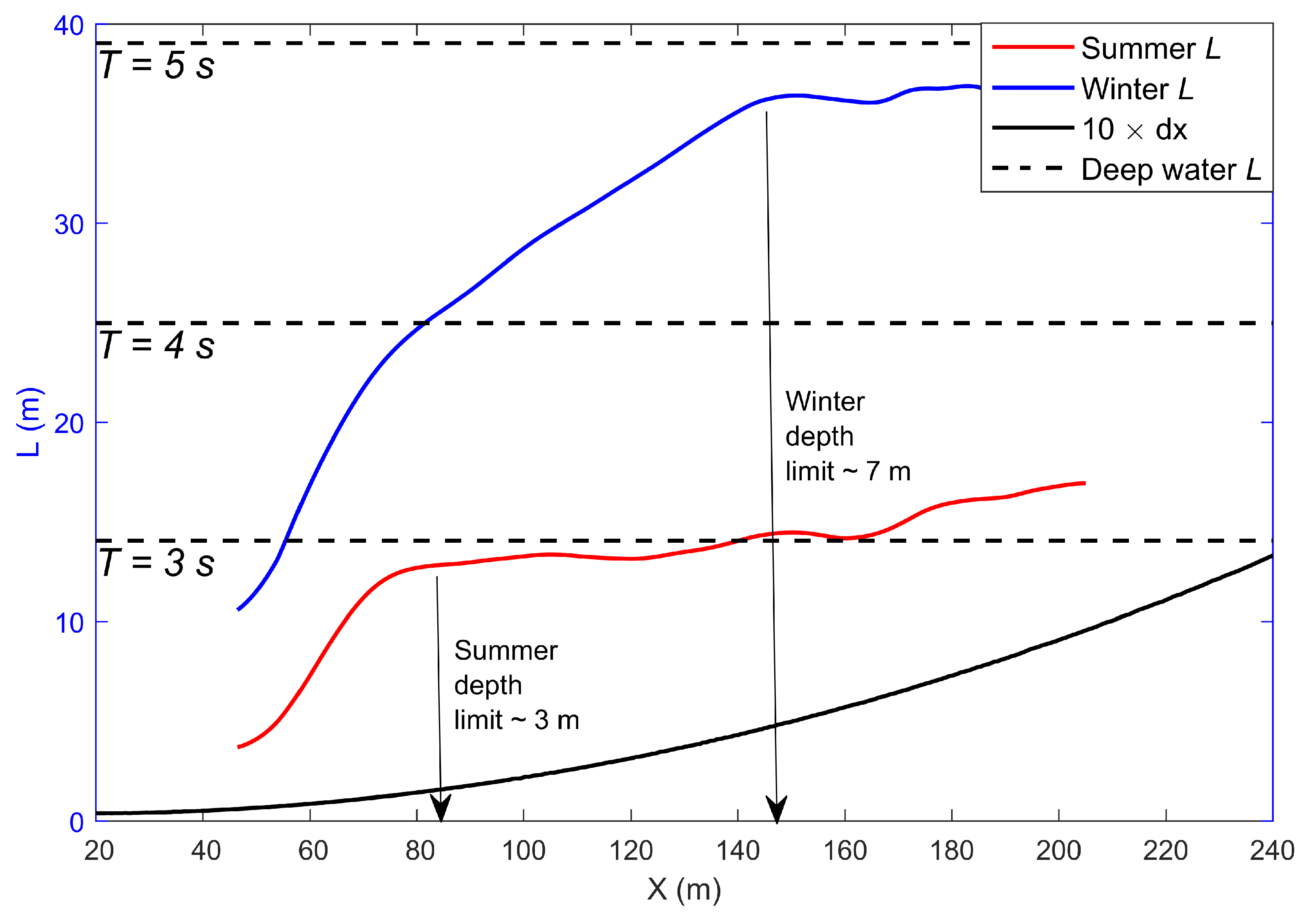
4.1. Nonlinear Effects during Shoaling and in Shallow Water
4.2. Breakpoint Optical Effect
4.3. Deep Water Asymptote
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abessolo Ondoa, G.; Bonou, F.; Tomety, F.S.; du Penhoat, Y.; Perret, C.; Degbe, C.G.E.; Almar, R. Beach Response to Wave Forcing from Event to Inter-Annual Time Scales at Grand Popo, Benin (Gulf of Guinea). Water 2017, 9, 447. [Google Scholar] [CrossRef]
- Wright, L.; Short, A.D. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Short, A.D. The role of wave height, period, slope, tide range and embaymentisation in beach classifications: A review. Rev. Chil. Hist. Nat. 1996, 69, 589–604. [Google Scholar]
- Short, A.; Jackson, D. Beach morphodynamics. Treatise Geomorphol. 2013, 10, 106–129. [Google Scholar]
- Karunarathna, H.; Horrillo-Caraballo, J.M.; Ranasinghe, R.; Short, A.D.; Reeve, D.E. An analysis of the cross-shore beach morphodynamics of a sandy and a composite gravel beach. Mar. Geol. 2012, 299, 33–42. [Google Scholar] [CrossRef]
- Troels, A.; Rolf Deigaard, D.F. (Eds.) Transient Surf Zone Circulation Induced by Rhythmic Swash Zone at a Reflective Beach; Number 131; Kulturværftet: Helsingør, Denmark, 2017. [Google Scholar]
- Miles, J.; Russell, P. Dynamics of a reflective beach with a low tide terrace. Cont. Shelf Res. 2004, 24, 1219–1247. [Google Scholar] [CrossRef]
- Masselink, G.; Short, A.D. The effect of tide range on beach morphodynamics and morphology: A conceptual beach model. J. Coast. Res. 1993, 9, 785–800. [Google Scholar]
- Almar, R.; Almeida, P.; Blenkinsopp, C.; Catalan, P. Surf-swash interactions on a low-tide terraced beach. J. Coast. Res. 2016, 75, 348–352. [Google Scholar] [CrossRef]
- Short, A.D. Australian beach systems—Nature and distribution. J. Coast. Res. 2006, 22, 11–27. [Google Scholar] [CrossRef]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Holman, R.; Haller, M.C. Remote sensing of the nearshore. Annu. Rev. Mar. Sci. 2013, 5, 95–113. [Google Scholar] [CrossRef] [PubMed]
- Holman, R.A.; Brodie, K.L.; Spore, N.J. Surf zone characterization using a small quadcopter: Technical issues and procedures. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 2017–2027. [Google Scholar] [CrossRef]
- Brodie, K.L.; Palmsten, M.L.; Hesser, T.J.; Dickhudt, P.J.; Raubenheimer, B.; Ladner, H.; Elgar, S. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Coast. Eng. 2018, 136, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Bergsma, E.; Conley, D.; Davidson, M.; O’Hare, T. Video-based nearshore bathymetry estimation in macro-tidal environments. Mar. Geol. 2016, 374, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Bergsma, E.W.; Almar, R. Video-based depth inversion techniques, a method comparison with synthetic cases. Coast. Eng. 2018, 138, 199–209. [Google Scholar] [CrossRef]
- Holman, R.A.; Holland, K.T.; Lalejini, D.M.; Spansel, S.D. Surf zone characterization from Unmanned Aerial Vehicle imagery. Ocean. Dyn. 2011, 61, 1927–1935. [Google Scholar] [CrossRef]
- Aarnink, J. Bathymetry Mapping Using Drone Imagery. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Bergsma, E.W.; Conley, D.C.; Davidson, M.A.; O’Hare, T.J.; Almar, R. Multi-scale coastal monitoring through video-based bathymetry estimation. Sub Mar. Geol. 2018. [Google Scholar]
- Bruno, M.F.; Molfetta, M.G.; Pratola, L.; Mossa, M.; Nutricato, R.; Morea, A.; Nitti, D.O.; Chiaradia, M.T. A combined approach of field data and earth observation for coastal risk assessment. Sensors 2019, 19, 1399. [Google Scholar] [CrossRef]
- Benveniste, J.; Cazenave, A.; Vignudelli, S.; Fenoglio-Marc, L.; Shah, R.; Almar, R.; Andersen, O.; Birol, F.; Bonnefond, P.; Bouffard, J.; et al. Requirements for a Coastal Hazards Observing System. Front. Mar. Sci. J. 2019. [Google Scholar] [CrossRef]
- Pianca, C.; Holman, R.; Siegle, E. Shoreline variability from days to decades: Results of long-term video imaging. J. Geophys. Res. Ocean. 2015, 120, 2159–2178. [Google Scholar] [CrossRef]
- Angnuureng, D.B.; Almar, R.; Senechal, N.; Castelle, B.; Addo, K.A.; Marieu, V.; Ranasinghe, R. Shoreline resilience to individual storms and storm clusters on a meso-macrotidal barred beach. Geomorphology 2017, 290, 265–276. [Google Scholar] [CrossRef]
- Thuan, D.H.; Binh, L.T.; Viet, N.T.; Hanh, D.K.; Almar, R.; Marchesiello, P. Typhoon impact and recovery from continuous video monitoring: A case study from Nha Trang Beach, Vietnam. J. Coast. Res. 2016, 75, 263–267. [Google Scholar] [CrossRef]
- Almar, R.; Marchesiello, P.; Almeida, L.P.; Thuan, D.H.; Tanaka, H.; Viet, N.T. Shoreline Response to a Sequence of Typhoon and Monsoon Events. Water 2017, 9, 364. [Google Scholar] [CrossRef]
- Liu, H.; Arii, M.; Sato, S.; Tajima, Y. Long-term nearshore bathymetry evolution from video imagery: A case study in the Miyazaki coast. Coast. Eng. Proc. 2012, 1, 60. [Google Scholar] [CrossRef]
- Almeida, L.P.; Almar, R.; Blenkinsopp, C.; Martins, K.; Sénéchal, N.; Floc’H, F.; Bergsma, E.; Marchesiello, P.; Benshila, R.; Caulet, C.; et al. Tide control on the swash dynamics of a steep beach with low-tide terrace. Sub to Mar. Geol. 2018. [Google Scholar]
- Lefebvre, J.P.; Almar, R.; Viet, N.T.; Thuan, D.H.; Binh, L.T.; Ibaceta, R.; Duc, N.V. Contribution of swash processes generated by low energy wind waves in the recovery of a beach impacted by extreme events: Nha Trang, Vietnam. J. Coast. Res. 2014, 70, 663–668. [Google Scholar] [CrossRef]
- Morio, O.; Garlan, T.; Guyomard, P. Etude dánalyse Granulométrique de Prélévements Sédimentaires Effectués lors de la Campagne COASTVAR Vietnam 2015. In Report; SHOM: Toulouse, France, 06 February 2017. [Google Scholar]
- Lippmann, T.C.; Holman, R.A. Quantification of sand bar morphology: A video technique based on wave dissipation. J. Geophys. Res. Ocean. 1989, 94, 995–1011. [Google Scholar] [CrossRef]
- Holman, R.A.; Sallenger, A.H., Jr.; Lippmann, T.C.; Haines, J.W. The Application of Video Image Processing to the Study of Nearshore Processes. Oceanography 1993, 6, 78–85. [Google Scholar] [CrossRef] [Green Version]
- Plant, N.G.; Holman, R.A. Intertidal beach profile estimation using video images. Mar. Geol. 1997, 140, 1–24. [Google Scholar] [CrossRef]
- Viet, N.T.; Duc, N.V.; Binh, L.T.; Thuan, D.H.; Tung, T.T.; Thin, N.V.; Uu, D.V.; Lefebvre, J.P.; Almar, R.; Tanaka, H. Seasonal evolution of shoreline changes in Nha Trang bay, Vietnam. In Proceedings of the 19th Congress of the Aisa and Pacific Division of the International Association of Hydraulic Engineering and Research (IAHR-APD), Hanoi, Vietnam, 21–24 September 2014. [Google Scholar]
- Duc, N.V.; Viet, N.T.; Thuan, D.H.; Binh, L.T.; Hung, D.V.; Binh, N.T.; Lefebvre, J.P.; Almar, R. Evaluation of long term variation of intertidal topography of Nha Trang beach based on high frequency video processing. In Proceedings of the 19th Congress of the Aisa and Pacific Division of the International Association of Hydraulic Engineering and Research (IAHR-APD), Hanoi, Vietnam, 21–24 September 2014. [Google Scholar]
- Holland, K.T.; Holman, R.A.; Lippmann, T.C.; Stanley, J.; Plant, N. Practical use of video imagery in nearshore oceanographic field studies. IEEE J. Ocean. Eng. 1997, 22, 81–92. [Google Scholar] [CrossRef]
- Heikkila, J.; Silven, O. A four-step camera calibration procedure with implicit image correction. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 1106–1112. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Almar, R.; Bonneton, P.; Senechal, N.; Roelvink, D. Wave celerity from video imaging: A new method. Coast. Eng. Proc. 2008, 661–673. [Google Scholar] [CrossRef]
- Abessolo Ondoa, G.; Almar, R.; Castelle, B.; Testut, L.; Leger, F.; Bonou, F.; Bergsma, E.; Meyssignac, B.; Larson, M. On The Use Of Shore-Based Video Camera To Monitor Sea Level At The Coast: A case study in Grand Popo, Benin (Gulf of Guinea, West Africa). Sub to J. Atmos. Ocean. Technol. 2018. [Google Scholar]
- Tissier, M.; Bonneton, P.; Almar, R.; Castelle, B.; Bonneton, N.; Nahon, A. Field measurements and non-linear prediction of wave celerity in the surf zone. Eur. J. -Mech.-B/Fluids 2011, 30, 635–641. [Google Scholar] [CrossRef]
- Dorsch, W.; Newland, T.; Tassone, D.; Tymons, S.; Walker, D. A Statistical Approach to Modelling the Temporal Patterns of Ocean Storms. J. Coast. Res. 2008, 24, 1430–1438. [Google Scholar] [CrossRef]
- Castelle, B.; Marieu, V.; Bujan, S.; Splinter, K.D.; Robinet, A.; Sénéchal, N.; Ferreira, S. Impact of the winter 2013–2014 series of severe Western Europe storms on a double-barred sandy coast: Beach and dune erosion and megacusp embayments. Geomorphology 2015, 238, 135–148. [Google Scholar] [CrossRef]
- Masselink, G.; Scott, T.; Poate, T.; Russell, P.; Davidson, M.; Conley, D. The extreme 2013/2014 winter storms: Hydrodynamic forcing and coastal response along the southwest coast of England. Earth Surf. Process. Landf. 2016, 41, 378–391. [Google Scholar] [CrossRef]
- Davidson, M.; Splinter, K.; Turner, I. A simple equilibrium model for predicting shoreline change. Coast. Eng. 2013, 73, 191–202. [Google Scholar] [CrossRef]
- Splinter, K.D.; Turner, I.L.; Davidson, M.A.; Barnard, P.; Castelle, B.; Oltman-Shay, J. A generalized equilibrium model for predicting daily to interannual shoreline response. J. Geophys. Res. Earth Surf. 2014, 119, 1936–1958. [Google Scholar] [CrossRef] [Green Version]
- Bell, P.S. Shallow water bathymetry derived from an analysis of X-band marine radar images of waves. Coast. Eng. 1999, 37, 513–527. [Google Scholar] [CrossRef]
- Holman, R.; Stanley, J. cBathy Bathymetry Estimation in the Mixed Wave-Current Domain of a Tidal Estuary. J. Coast. Res. 2013, 1391–1396. [Google Scholar] [CrossRef]
- Holman, R.; Plant, N.; Holland, T. cBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. Ocean. 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A. Estimation of wave phase speed and nearshore bathymetry from video imagery. J. Geophys. Res. Ocean. 2000, 105, 22015–22033. [Google Scholar] [CrossRef]
- Wilson, G.; Özkan-Haller, T.; Holman, R.; Kurapov, A. Remote sensing and data assimilation for surf zone bathymetric inversion. Coast. Eng. Proc. 2012, 1, 44. [Google Scholar] [CrossRef]
- Birrien, F.; Castelle, B.; Marieu, V.; Dubarbier, B. On a data-model assimilation method to inverse wave-dominated beach bathymetry using heterogeneous video-derived observations. Ocean. Eng. 2013, 73, 126–138. [Google Scholar] [CrossRef]
| 1 | The Exner equation states that the time change of bed elevation h varies with the divergence of sediment flux : , where is the grain packing density. |



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thuan, D.H.; Almar, R.; Marchesiello, P.; Viet, N.T. Video Sensing of Nearshore Bathymetry Evolution with Error Estimate. J. Mar. Sci. Eng. 2019, 7, 233. https://doi.org/10.3390/jmse7070233
Thuan DH, Almar R, Marchesiello P, Viet NT. Video Sensing of Nearshore Bathymetry Evolution with Error Estimate. Journal of Marine Science and Engineering. 2019; 7(7):233. https://doi.org/10.3390/jmse7070233
Chicago/Turabian StyleThuan, Duong Hai, Rafael Almar, Patrick Marchesiello, and Nguyen Trung Viet. 2019. "Video Sensing of Nearshore Bathymetry Evolution with Error Estimate" Journal of Marine Science and Engineering 7, no. 7: 233. https://doi.org/10.3390/jmse7070233
APA StyleThuan, D. H., Almar, R., Marchesiello, P., & Viet, N. T. (2019). Video Sensing of Nearshore Bathymetry Evolution with Error Estimate. Journal of Marine Science and Engineering, 7(7), 233. https://doi.org/10.3390/jmse7070233




